id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
27,087 | On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow Metro from "Taganskaya" station to "Kievskaya" station, and in the evening - back (see diagram).
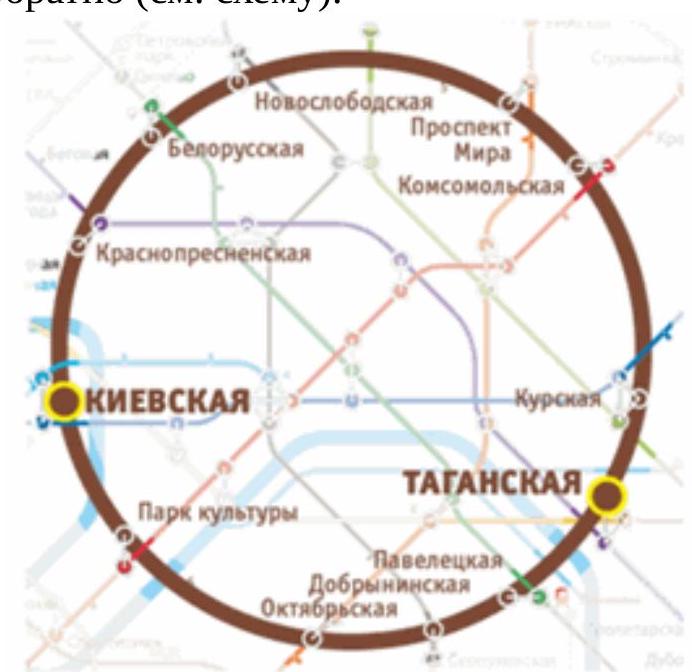
Upon entering the station, the Scientist boards the first arriving train. It is known that trains run in both directions with approximately equal intervals, and that the train traveling on the northern route (via "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while on the southern route (via "Paveletskaya") it takes 11 minutes. Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives. The same is true for "Taganskaya".
- the trip from home to work takes the Scientist on average 1 minute less than the trip from work to home. Find the expected interval between trains traveling in the same direction. | 3 |
27,101 | Problem 4. Point $O$ is the center of the circumcircle of triangle $ABC$ with sides $BC=8$ and $AC=4$. Find the length of side $AB$ if the length of the vector $4 \overrightarrow{OA} - \overrightarrow{OB} - 3 \overrightarrow{OC}$ is 10. | 5 |
27,103 | 11. (1973 USA Mathematical Olympiad) In a given regular $(2n+1)$-sided polygon, three different vertices are chosen at random. If all such choices are equally likely, find the probability that the center of the polygon lies in the interior of the triangle formed by the randomly chosen points. | \frac{n+1}{2(2n-1)} |
27,106 | 12. (15th All-Russian Mathematical Olympiad, 1989) Insert “+” or “-” signs between the numbers $1, 2, 3, \cdots, 1989$. What is the smallest non-negative number that can be obtained from the resulting sum? | 1 |
27,111 | Example 13 For all $a, b, c \in \mathbf{R}^{+}$, find the minimum value of $\frac{a}{\sqrt{a^{2}+8 b c}}$ $+\frac{b}{\sqrt{b^{2}+8 a c}}+\frac{c}{\sqrt{c^{2}+8 a b}}$. | 1 |
27,147 | 5. The bisectors $\mathrm{AD}$ and $\mathrm{BE}$ of triangle $\mathrm{ABC}$ intersect at point I. It turns out that the area of triangle ABI is equal to the area of quadrilateral CDIE. Find the greatest possible value of angle ACB. | 60 |
27,152 | 4. Let $A B C$ be a triangle with $A B=3, A C=8, B C=7$ and let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively. Point $T$ is selected on side $B C$ so that $A T=T C$. The circumcircles of triangles $B A T, M A N$ intersect at $D$. Compute $D C$. | \frac{7\sqrt{3}}{3} |
27,162 | 11.4. On the coordinate plane, the parabola $y=x^{2}$ is drawn. On the positive $O y$-axis, a point $A$ is taken, and through it, two lines with positive slopes are drawn. Let $M_{1}, N_{1}$ and $M_{2}, N_{2}$ be the points of intersection with the parabola of the first and second line, respectively. Find the ordinate of point $A$, given that $\angle M_{1} O N_{1}=\angle M_{2} O N_{2}$, where $O$ is the origin. | 1 |
27,169 | 11.174. A regular truncated hexagonal pyramid is inscribed in a sphere of radius $R$, with the plane of the lower base passing through the center of the sphere, and the lateral edge forming an angle of $60^{\circ}$ with the base plane. Determine the volume of the pyramid. | \frac{21R^{3}}{16} |
27,213 | # Task No. 8.1
## Condition:
Given triangle $\mathrm{ABC}$, where $2 \mathrm{BC}=\mathrm{AC}$ and angle $\mathrm{C}=74^{\circ}$. On ray $\mathrm{BC}$, segment $\mathrm{CD}=\mathrm{CB}$ is laid out. Then, from point $\mathrm{D}$, a perpendicular is drawn to the line containing the median of triangle $\mathrm{ABC}$, drawn from vertex $\mathrm{B}$, and the intersection point is $\mathrm{F}$. What is the measure of angle CDF? Express your answer in degrees. | 37 |
27,214 | 8.4. It is known that $a^{2}+2=b^{4}, b^{2}+2=c^{4}, c^{2}+2=a^{4}$. What is the value of the product $\left(a^{2}-1\right)\left(b^{2}-1\right)\left(c^{2}-1\right)$? Find all possible values and prove that there are no others. | 1 |
27,217 | 42. As shown in the figure, in isosceles trapezoid $A B C D$, $A D / / B C, \angle B=45^{\circ}, P$ is a point on side $B C$, the area of $\triangle P A D$ is $\frac{1}{2}, \angle A P D=90^{\circ}$, then the minimum value of $A D$ is $\qquad$ | \sqrt{2} |
27,226 | 32nd BMO 1996 Problem 4 Find all positive real solutions to w + x + y + z = 12, wxyz = wx + wy + wz + xy + xz + yz + 27. | w=x=y=z=3 |
27,232 | Determine the number of ten-thousands in $A=5^{5^{5^{5^{5}}}}$.
Determine the number of ten-thousands in $A=5^{5^{5^{5^{5}}}}$. | 0 |
27,234 | 1. Find all values of $x$, for each of which one of the three given numbers $\log _{x^{2}}\left(x^{2}-7 x+12\right)$, $\log _{x^{2}} \frac{x^{2}}{x-3}$, and $\log _{x^{2}} \frac{x^{2}}{x-4}$ is equal to the sum of the other two. | 5 |
27,235 | 4.5 Try to find the number of positive integer solutions to the indeterminate equation $\frac{1}{x+1}+\frac{1}{y}+\frac{1}{(x+1) y}=\frac{1}{1991}$.
(Japan Mathematical Olympiad, 1991) | 64 |
27,244 | Find the smallest number $a$ such that a square of side $a$ can contain five disks of radius 1 so that no two of the disks have a common interior point. | 2+2\sqrt{2} |
27,250 | 10.55 Find the digital sum of the product (as a function of $n$)
$$
9 \cdot 99 \cdot 9999 \cdot \cdots \cdot\left(10^{2^{n}}-1\right) \text {. }
$$
where the number of digits of each factor is twice the number of digits of the preceding factor.
(21st United States of America Mathematical Olympiad, 1992) | 9\cdot2^{n} |
27,270 | White and Black play the following game. In the corners of the chessboard stand two kings: White on a1, Black on h8. The players take turns making moves. White starts. A player can place their king on any adjacent square (provided it is free), adhering to the following rules: the distance between the kings cannot be increased (the distance between two squares is the minimum number of steps the king can take to move from one square to another: thus, at the beginning of the game, the distance between the kings is 7 moves). The player who places their king on the opposite edge of the board wins (the White king on the h-file or the 8th rank, the Black king on the a-file or the 1st rank). Who will win with correct play? | White |
27,282 | [Example 1.3.8] Let $l, m$ be two skew lines, and on $l$ there are three points $A, B, C$ such that $AB = BC$. Through $A, B, C$ respectively, draw perpendiculars to $m$ at points $D, E, F$. It is known that $AD = \sqrt{15}, BE = \frac{7}{2}, CF = \sqrt{10}$. Find the distance between $l$ and $m$. | \sqrt{6} |
27,285 | # Problem 5. (3 points)
In the cells of a $7 \times 7$ table, pairwise distinct non-negative integers are written. It turns out that for any two numbers in the same row or column, the integer parts of their quotients when divided by 8 are different. What is the smallest value that the largest number in the table can take? | 54 |
27,289 | 10 Let $A, B$ be the two foci of a hyperbola, and $C$ a point on the hyperbola. It is known that the three sides of $\triangle A B C$ form an arithmetic sequence, and $\angle A C B=120^{\circ}$. Then the eccentricity of the hyperbola is $\qquad$ | \frac{7}{2} |
27,294 | ## Subject III (7 p)
Let the set $A=\{\overline{a b c d}, \overline{a b}=\overline{c d}+4\}$
a) Determine whether 2016 and 2024 belong to the set A.
b) Find the remainder of the division of any number from A by 101.
c) If $\mathrm{S}$ is the sum of all numbers in $\mathrm{A}$, show that $\mathrm{S}$ is not a perfect square. | 97 |
27,296 | The Law of Sines
In triangle $ABC$, it is known that $AB = BC, \angle BAC = 45^{\circ}$. Line $MN$ intersects side $AC$ at point $M$ and side $BC$ at point $N$, with $AM = 2 \cdot MC, \angle NMC = 60^{\circ}$. Find the ratio of the area of triangle $MNC$ to the area of quadrilateral $ABNM$. | \frac{7-3\sqrt{3}}{11} |
27,302 | 64th Putnam 2003 Problem A3 Find the minimum of |sin x + cos x + tan x + cot x + sec x + cosec x| for real x. | 2\sqrt{2}-1 |
27,307 | 4. 2. 25 ** Let $n$ be a given positive integer, $n \geqslant 2, a_{1}, a_{2}, \cdots, a_{n} \in(0,1)$. Find the maximum value of $\sum_{i=1}^{n} \sqrt[6]{a_{i}\left(1-a_{i+1}\right)}$, where $a_{n+1}=a_{1}$. | \frac{n}{\sqrt[3]{2}} |
27,313 | Problem 1. Consider the parallelogram $A B C D$, whose diagonals intersect at $O$. The angle bisectors of $\angle D A C$ and $\angle D B C$ intersect at $T$. It is known that $\overrightarrow{T D}+\overrightarrow{T C}=\overrightarrow{T O}$. Determine the measures of the angles of triangle $A B T$. | 60 |
27,354 | Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that for all natural numbers $a$ and $b$:
$$
f(f(a)+f(b))=a+b
$$ | f(n)=n |
27,361 | 4. If a natural number can be divided by both 20 and 22, and it has exactly 2022 factors, it is called a “2022 Lucky Number”. There are $\qquad$ “2022 Lucky Numbers”. | 4 |
27,374 | 20. (2002 National High School Competition) Real numbers $a$, $b$, $c$ and a positive number $\lambda$ make $f(x)=x^{3}+a x^{2}+b \dot{x}+c$ have three real roots $x_{1}$, $x_{2}$, $x_{3}$, and satisfy
(1) $x_{2}-x_{1}=\lambda$;
(2) $x_{3}>\frac{1}{2}\left(x_{1}+x_{2}\right)$.
Find the maximum value of $\frac{2 a^{3}+27 c-9 a b}{\lambda^{3}}$. | \frac{3\sqrt{3}}{2} |
27,403 | 7th Balkan 1990 Problem 4 The function f is defined on the positive integers and f(m) ≠ f(n) if m - n is prime. What is the smallest possible size of the image of f. Solution | 4 |
27,431 | 8. Let the set $A=\{1,2, \cdots, n\}$. If there exist non-empty sets $B$ and $C$ such that $B \cap C=\varnothing, B \cup C=A$, and the sum of the squares of the elements in $B$ is $M$, the sum of the squares of the elements in $C$ is $N$, satisfying $M-N=2016$, find the minimum value of $n$. | 19 |
27,434 | 10. (40 points) On the board, there are 2015 pairwise distinct positive real numbers. It turns out that for any number $a>0$, the number of numbers on the board that are less than 2014/a, and the number of numbers that are greater than a, have the same parity. What can the product of all the numbers be? | 2014^{1007}\sqrt{2014} |
27,484 | 30th IMO 1989 shortlist Problem 15 Given a convex n-gon A 1 A 2 ... A n with area A and a point P, we rotate P through an angle x about A i to get the point P i . Find the area of the polygon P 1 P 2 ... P n . | 4\sin^2(\frac{x}{2})A |
27,489 | 2. Given positive numbers $a, b, c, d$. Find the minimum value of the expression
$$
A=\left(a^{2}+\frac{1}{b c}\right)^{3}+\left(b^{2}+\frac{1}{c d}\right)^{3}+\left(c^{2}+\frac{1}{d a}\right)^{3}+\left(d^{2}+\frac{1}{a b}\right)^{3}
$$ | 32 |
27,496 | 5. Circles $K_{1}$ and $K_{2}$ with centers at points $O_{1}$ and $O_{2}$ have the same radius $r$ and touch the circle $K$ of radius $R$ with center at point $O$ internally. The angle $O_{1} O O_{2}$ is $120^{\circ}$. Find the radius $q$ of the circle that touches $K_{1}$ and $K_{2}$ externally and the circle $K$ internally. | \frac{R(R-r)}{R+3r} |
27,500 | Example 1 (1993 National High School League Question) The last two digits of $\left[\frac{10^{93}}{10^{31}+3}\right]$ are $\qquad$ (where [x] denotes the greatest integer not greater than $x$.) | 8 |
27,548 | # 8. Variant 1
In trapezoid $A B C D(A D \| B C)$, the bisectors of angles $D A B$ and $A B C$ intersect on side $C D$. Find $A B$, if $A D=5, B C=2$. | 7 |
27,555 | 8. Find the least value of the expression $(x+y)(y+z)$, under the condition that $x, y, z$ are positive numbers satisfying the equation
$$
x y z(x+y+z)=1 \text {. }
$$ | 2 |
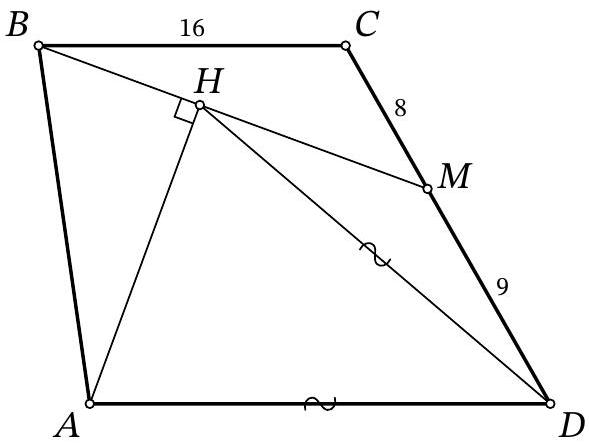
27,563 | Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
 | 18 |
27,573 | Shnol D....
Given a triangle $ABC$ and an excircle with center $O$, touching side $BC$ and the extensions of sides $AB$ and $AC$. Point $O_{1}$ is symmetric to point $O$ with respect to line $BC$. Find the measure of angle $A$, if it is known that point $O_{1}$ lies on the circumcircle of triangle $ABC$. | 60 |
27,588 | 13. In the triangle $A B C, \angle A=20^{\circ}, \angle C=90^{\circ}, O$ is a point on $A B$ and $D$ is the midpoint of $O B$. Suppose the circle centered at $O$ with radius $O D$ touches the side $A C$ at $T$. Determine the size of $\angle B C D$ in degrees. | 35 |
27,592 | 19. If a positive integer $N$ can be expressed as $\lfloor x\rfloor+\lfloor 2 x\rfloor+\lfloor 3 x\rfloor$ for some real numbers $x$, then we say that $N$ is "visible"; otherwise, we say that $N$ is "invisible". For example, 8 is visible since $8=\lfloor 1.5\rfloor+\lfloor 2(1.5)\rfloor+\lfloor 3(1.5)\rfloor$, whereas 10 is invisible. If we arrange all the "invisible" positive integers in increasing order, find the $2011^{\text {th }}$ "invisible" integer. | 6034 |
27,595 | 29th Putnam 1968 Problem A5 Find the smallest possible α such that if p(x) ≡ ax 2 + bx + c satisfies |p(x)| ≤ 1 on [0, 1], then |p'(0)| ≤ α. Solution | 8 |
27,630 | Example 3.1.3 Given nine points in space, where no four points are coplanar, connect several line segments among these nine points so that there is no tetrahedron in the graph. How many triangles can there be at most in the graph? | 27 |
27,653 | 13. Does there exist a natural number that decreases by 1981 times when the first digit of its decimal representation is erased? | No |
27,654 | Question 99, In $\triangle ABC$, the perimeter is 20, the area is $10 \sqrt{3}$, and $2 \angle A = \angle B + \angle C$.
(1) Find the length of $BC$;
(2) If point $P$ is a point on the incircle $\odot I$ of $\triangle ABC$, and $\overrightarrow{A I} = x \overrightarrow{A B} + y \overrightarrow{A C}$,
(1) Find the value of $x + y$;
(2) Find the range of $|\overrightarrow{A P} + \overrightarrow{B P} + \overrightarrow{C P}|$. | [2\sqrt{3},4\sqrt{3}] |
27,667 | Example 6 Function $f$ is defined on the set of real numbers, and for all real numbers $x$ it satisfies the equations
$f(2-x)=f(2+x)$ and $f(7-x)=f(7+x)$. Suppose $x=0$ is a root of $f(x)=0$, and let $N$ be the number of roots of $f(x)=0$ in the interval $[-1000,1000]$. Find the minimum value of $N$. | 401 |
27,672 | Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
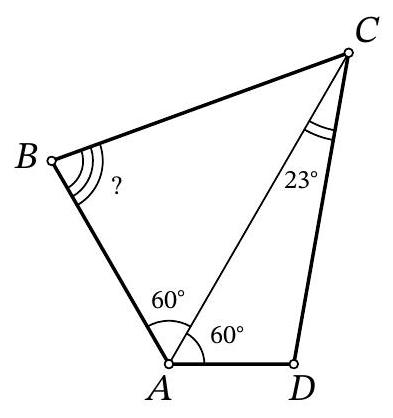 | 83 |
27,694 | [Area of a triangle (using two sides and the angle between them).]
A circle is circumscribed around triangle $ABC$. The median $AD$ is extended to intersect this circle at point $E$. It is known that $AB + AD = DE, \angle BAD = 60^{\circ}, AE = 6$. Find the area of triangle $ABC$. | \frac{9\sqrt{3}}{4} |
27,697 | There are 13 cities in a certain kingdom. Between some pairs of cities two-way direct bus, train or plane connections are established. What is the least possible number of connections to be established in order that choosing any two means of transportation one can go from any city to any other without using the third kind of vehicle? | 18 |
27,726 | 10. As shown in the figure, $\triangle A B C$ is an isosceles right triangle, $E$ is a point on side $B C$ such that $B E=3 C E$, and points $D, A, F$ are collinear. Let the height from $D$ to $B E$ in $\triangle D B E$ be $h_{1}$, and the height from $F$ to $E C$ in $\triangle F E C$ be $h_{2}$. We have $3 h_{1}+h_{2}=3$ cm. The sum of the areas of $\triangle D B E$ and $\triangle F E C$ is 6 square cm, then the area of $\triangle A B C$ is $\qquad$ square cm. | 64 |
27,730 | 2. Determine $x, y \in \mathbb{Q}$ that satisfy $\frac{x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}=-11 x+2 y$ and $\frac{2 x y}{\left(x^{2}+y^{2}\right)^{2}}=2 x+11 y$. | \frac{1}{5},-\frac{2}{5} |
27,739 | 9.5. On the side $AC$ of triangle $ABC$, a point $M$ is taken. It turns out that $AM = BM + MC$ and $\angle BMA = \angle MBC + \angle BAC$. Find $\angle BMA$. | 60 |
27,757 | 5. Seven fishermen stand in a circle. The fishermen have a professional habit of exaggerating numbers. Each fisherman has a measure of lying (each has their own, an integer) - how many times the number mentioned by the fisherman is greater than the true value. For example, if a fisherman with a lying measure of 3 catches two fish, he will say he caught six fish. In response to the question: "How many fish did your left neighbor catch?", the answers (not necessarily in the order in which the fishermen stand) were $12,12,20,24,32,42$ and 56. In response to the question: "How many fish did your right neighbor catch?", six fishermen answered $12,14,18,32$, 48,70. What did the seventh fisherman answer? | 16 |
27,781 | Example 5 Let $x, y, z, w$ be four real numbers, not all zero. Find:
$S=\frac{x y+2 y z+z w}{x^{2}+y^{2}+z^{2}+w^{2}}$ the maximum value.
(1985 Austrian-Polish League) | \frac{1}{2}(1+\sqrt{2}) |
27,789 | (21) The center of the ellipse $C$ is the origin $O$, with foci on the $y$-axis, the distance from the foci to the corresponding directrix, and the eccentricity are both $\frac{\sqrt{2}}{2}$. The line $l$ intersects the $y$-axis at point $P(0, m)$, and intersects the ellipse $C$ at two distinct points $A$ and $B$, and $\overrightarrow{A P}=\lambda \overrightarrow{P B}$.
(1) Find the equation of the ellipse;
(2) If $\overrightarrow{O A}+\lambda \overrightarrow{O B}=4 \overrightarrow{O P}$, find the range of $m$. | (-1,-\frac{1}{2})\cup(\frac{1}{2},1) |
27,808 | At what angle does the hypotenuse of a right-angled triangle with a perimeter of 2 units appear when viewed from a point on the internal angle bisector of the right angle, $\sqrt{2}$ units away from the vertex? | 45 |
27,818 | 5. Let $x, y, z \in \mathbf{R}^{+}$, satisfying $x+y+z=x y z$, then the minimum value of the function $f(x, y, z)=x^{2}(y z-1)+y^{2}(z x-1)+z^{2}(x y-1)$ is $\qquad$ . | 18 |
27,839 | 29.3.14 Xuan Yuan seeks the smallest natural number $n$ with the property that any $n$-element subset of $\{1,2, \cdots, 60\}$ must contain three numbers that are pairwise coprime. | 41 |
27,843 | The elements of the sequence $\mathrm{Az}\left(x_{n}\right)$ are positive real numbers, and for every positive integer $n$,
$$
2\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{4}=\left(x_{1}^{5}+x_{2}^{5}+\ldots+x_{n}^{5}\right)+\left(x_{1}^{7}+x_{2}^{7}+\ldots+x_{n}^{7}\right)
$$
Determine the elements of the sequence. | x_{n}=n |
27,877 | Four. (This question is worth 35 points) Given a set of points on a plane $P=\left\{P_{1}, P_{2}, \cdots, P_{1994}\right\}$, where no three points in $P$ are collinear. Divide all the points in $P$ into 83 groups arbitrarily, such that each group has at least 3 points, and each point belongs to exactly one group. Then connect any two points in the same group with a line segment, and do not connect points in different groups. This results in a pattern $G$. Different grouping methods result in different patterns. Let the number of triangles in pattern $G$ with vertices from points in $P$ be denoted as $m(G)$.
(1) Find the minimum value $m_{0}$ of $m(G)$.
(2) Let $G^{*}$ be a pattern such that $m\left(G^{*}\right)=m_{0}$. If the line segments in $G^{*}$ (referring to line segments with endpoints from points in $P$) are colored with 4 different colors, and each line segment is colored with exactly one color, prove that there exists a coloring scheme such that $G^{*}$, after coloring, does not contain a triangle with all three sides of the same color. | 168544 |
27,897 | 4. (13 points) The lateral edges of a triangular pyramid are pairwise perpendicular, and the sides of the base are equal to $\sqrt{85}$, $\sqrt{58}$, and $\sqrt{45}$. The center of the sphere that touches all the lateral faces lies on the base of the pyramid. Find the radius of this sphere. | \frac{14}{9} |
27,899 | 1. Let $\triangle A B C$ be a right triangle with right angle at $B$. Let the points $D, E$, and $F$ be on $A B, B C$, and $C A$, respectively, such that $\triangle D E F$ is an equilateral triangle and $E C=F C$. If $D B=5 \sqrt{3}, B E=3$, and $\sin \angle A C B=4 \sqrt{3} / 7$, find the perimeter of $\triangle A D F$. | 35\sqrt{3}+63+2\sqrt{21} |
27,917 | B5. Three wheels are pressed against each other so that they do not slip when rotating. The circumferences of the wheels are 14, 10, and \(6 \, \text{cm}\) respectively. Each wheel has an arrow pointing straight down. The largest wheel is set in motion, and the other wheels rotate along with it. They stop at the first moment when all three arrows point down again. A whistle sounds whenever one of the arrows points straight up.
If two or three arrows point up at the same time, only one whistle sounds. How many whistles sound in total?
## C-Problems
For the C-Problems, the answer is not the only thing that matters; a reasoning must also be provided that shows your answer is correct. Each correctly worked-out C-Problem is worth 10 points. Partial solutions can also earn points. Therefore, write everything clearly and submit your scratch paper as well.
NOTE: Solve each C-Problem on a separate sheet of paper and submit the corresponding scratch paper per problem. | 57 |
27,929 | 10.25 Find the smallest natural number, such that when its last digit is moved to the first position, its value increases by 5 times.
(13th All-Russian Mathematical Olympiad, 1987) | 142857 |
27,932 | 17 (12 points) In the Cartesian coordinate system, it is known that circle $C_{1}$ intersects with circle $C_{2}$ at points $P, Q$, and the coordinates of point $P$ are $(3, 2)$. The product of the radii of the two circles is $\frac{13}{2}$. If circles $C_{1}$ and $C_{2}$ are both tangent to the line $l: y=k x$ and the $x$-axis, find the equation of the line $l$. | 2\sqrt{2}x |
27,941 | Calculate the Minkowski dimensions of the following objects: a point, the interval $[0,1]$, the rationals in $[0,1]$, the triadic Cantor set $C(3)$. | \frac{\log(2)}{\log(3)} |
27,951 | 11. $[7]$ FInd the value of
$$
\sum_{k=1}^{60} \sum_{n=1}^{k} \frac{n^{2}}{61-2 n}
$$ | -18910 |
27,953 | 1. Given complex numbers $z$ and $\omega$ satisfy the following two conditions:
$$
\text { (1) } z+\omega+3=0 \text {; }
$$
(2) $|z|, 2, |\omega|$ form an arithmetic sequence.
Is there a maximum value for $\cos (\arg z-\arg \omega)$? If so, find it. | \frac{1}{8} |
27,986 | Problem 11.5. In a chess tournament, a team of schoolchildren and a team of students, each consisting of 15 people, are competing against each other. During the tournament, each schoolchild must play against each student exactly once, and each person must play no more than one game per day. The number of games played on different days may vary.
At some point in the tournament, the organizer noticed that the schedule for the next day can be arranged in exactly 1 way with 15 games, and in $N$ ways with 1 game (the order of the games in the schedule does not matter, only who plays against whom). Find the maximum possible value of $N$. | 120 |
28,001 | In triangle $A B C$, the altitudes $A A_{1}$ and $C C_{1}$ intersect at point $H$, which lies inside the triangle. It is known that $H$ is the midpoint of $A A_{1}$, and $C H: H C_{1}=2: 1$. Find the measure of angle $B$. | 45 |
28,004 | 5. Given points $A(0,3), B(0,6), C(0,-2), D(0,2)$, point $P$ is a moving point, and satisfies $\frac{|P A|}{|P B|}=\frac{1}{2}$. Let line $l$ be the perpendicular bisector of $P C$, and it intersects line $P D$ at point $Q$. Then, as point $P$ moves, the equation of the trajectory of point $Q$ is $\qquad$ | y^{2}-\frac{x^{2}}{3}=1 |
28,010 | Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
 | 83 |
28,012 | Problem 1
Determine all finite nonempty sets $S$ of positive integers satisfying $\frac{i+j}{(i, j)} \quad$ is an element of $S$ for all $i, j$ in $S$, where $(i, j)$ is the greatest common divisor of $i$ and $j$. | {2} |
28,023 | 28th Putnam 1967 Problem A3 Find the smallest positive integer n such that we can find a polynomial nx 2 + ax + b with integer coefficients and two distinct roots in the interval (0, 1). Solution | 5 |
28,029 | A tetrahedron is cut by planes parallel to its faces and tangent to the inscribed sphere, resulting in four smaller tetrahedra. What is the radius of the sphere inscribed in the original tetrahedron if the radii of the spheres inscribed in the smaller tetrahedra are 9, 12, 36, and 39 units long? | 48 |
28,043 | 3. Given $0 \leq a_{k} \leq 1(k=1,2, \ldots, 2020)$, let $a_{2021}=a_{1}, a_{2022}=a_{2}$, then the maximum value of $\sum_{k=1}^{2020}\left(a_{k}-\right.$ $\left.a_{k+1} a_{k+2}\right)$ is $\qquad$ | 1010 |
28,048 | If there are $2 k(k \geqslant 3)$ points on a plane, where no three points are collinear. Draw a line segment between any two points, and color each line segment red or blue. A triangle with three sides of the same color is called a monochromatic triangle, and the number of monochromatic triangles is denoted as $S$. For all possible coloring methods, find the minimum value of $S$. | \frac{k(k-1)(k-2)}{3} |
28,052 | Question 17: Let the function $f(x)$ be defined on $[0,1]$, satisfying: $f(0)=f(1)$, and for any $x, y \in[0,1]$ there is $|f(x)-f(y)|<|x-y|$. Try to find the smallest real number $m$, such that for any $f(x)$ satisfying the above conditions and any $x, y \in[0,1]$, we have $|f(x)-f(y)|<m$. | \frac{1}{2} |
28,055 | For an arbitrary point $P$ on an ellipse, the projection of $P$ onto the major axis is $Q$, and the midpoint of the segment $O Q$ is $R$, where $O$ is the center of the ellipse. What can we say about the ellipse if the line perpendicular to $P R$ at $P$ is exactly the tangent at $P$? | ^2=2b^2 |
28,061 | 6. The parabola $C_{1}: x^{2}=2 p y$ has a focus at $F$, and the hyperbola $C_{2}: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ has foci at $F_{1}$ and $F_{2}$. Point $P$ is a common point of the two curves in the first quadrant. If $P F F_{1}$ are collinear, and $C_{1}$ and $C_{2}$ have a common tangent line at $P$, then the eccentricity of $C_{2}$ is | \sqrt{2} |
28,072 | 10. (15 points) If $a, b, c \in \mathbf{R}^{+}$, and $a+b+c=1$, find the maximum value of the real number $\lambda$ such that the inequality $a^{2}+b^{2}+c^{2}+\lambda \sqrt{a b c} \leqslant 1$ always holds. | 2\sqrt{3} |
28,075 | Three, (25 points) For a positive integer $k$, find the greatest common divisor $d$ of all positive even integers $x$ that satisfy the following conditions:
(1) $\frac{x+2}{k}$ and $\frac{x}{k}$ are both integers, and the difference in the number of digits of these two numbers equals the difference between these two numbers;
(2) The product of the digits of $\frac{x}{k}$ is a perfect cube. | 1998 |
28,097 | 11.5 The tangents to the circumscribed circle of the right triangle $A B C$ ( $\angle C=$ $90^{\circ}$ ) at points $A$ and $C$ intersect at point $T$. The rays $A B$ and $T C$ intersect at point $S$. It is known that the areas of triangles $\triangle A C T$ and $\triangle B C S$ are equal. Find the ratio of the areas of triangles $\triangle A B C$ and $\triangle A T S$. | \frac{1}{3} |
28,116 | 3. Given arithmetic sequences $\left(x_{i}\right)_{i=1}^{\infty}$ and $\left(y_{i}\right)_{i=1}^{\infty}$ have the same first term and the following property: there exists an index $k(k>1)$, for which the equalities
$$
x_{k}^{2}-y_{k}^{2}=53, \quad x_{k-1}^{2}-y_{k-1}^{2}=78, \quad x_{k+1}^{2}-y_{k+1}^{2}=27 .
$$
hold. Find all such indices $k$. | 54 |
28,128 | 5. Given that $f(x)$ is a linear function, $f[f(1)]=-1$, the image of $f(x)$ symmetric to the line $x-y=0$ is $C$, if the point $\left(n, \frac{a_{n+1}}{a_{n}}\right)\left(n \in \mathbf{N}^{\cdot}\right)$ lies on the curve $C$, and $a_{1}=1, \frac{a_{n+1}}{a_{n}}-\frac{a_{n}}{a_{n-1}}=1(n \geqslant 2)$.
(1) Find the analytical expression of $f(x)$ and the equation of the curve $C$;
(2) Let $S_{n}=\frac{a_{1}}{3!}+\frac{a_{2}}{4!}+\frac{a_{3}}{5!}+\cdots+\frac{a_{n}}{(n+2)!}$, for all $n \in \mathbf{N}^{\cdot}$, if $S_{n}>m$ always holds, find the maximum value of the natural number $m$. | 0 |
28,135 | Three rays originating from a single point form pairwise angles of $60^{\circ}$. A unit radius sphere is tangent to all three rays. Calculate the distance from the center of the sphere to the starting point of the rays. | \sqrt{3} |
28,141 | 4. Determine the largest integer $k$ with the following property: no matter how the numbers $1,2, \ldots, 64$ are written in the cells of an $8 \times 8$ board, there exist two adjacent cells such that the difference between the numbers written in these cells is not less than $k$. (Two cells are adjacent if they share at least one common vertex.) | 9 |
28,160 | Let's write down the equation of the line that is tangent to the curve given by the equation $y=3 x^{4}-4 x^{3}$ at two different points.
---
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
---
Write down the equation of the line that is tangent to the curve given by the equation $y=3 x^{4}-4 x^{3}$ at two different points. | -\frac{8}{9}x-\frac{4}{27} |
28,163 | Example 12. Calculate the circulation of the vector field given in cylindrical coordinates: $2=\rho \sin \varphi \mathrm{e}_{\rho}+\rho z \mathrm{e}_{\varphi}+\rho^{3} \mathrm{e}_{z}$, along the curve L: $\{\rho=\sin \varphi, z=0,0 \leqslant \varphi \leqslant \pi\}$ directly and using Stokes' theorem. | 0 |
28,170 | Example 6. Solve the differential equation
$$
\left(1+x^{2} y^{2}\right) y+(x y-1)^{2} \cdot x \cdot y^{\prime}=0
$$ | xy-\frac{1}{xy}-2\ln|y|=C |
28,187 | 17. In $\triangle A B C, A C>A B$, the internal angle bisector of $\angle A$ meets $B C$ at $D$, and $E$ is the foot of the perpendicular from $B$ onto $A D$. Suppose $A B=5, B E=4$ and $A E=3$. Find the value of the expression $\left(\frac{A C+A B}{A C-A B}\right) E D$. | 3 |
28,190 | # Problem 7.
B-1 The height $B D$ of an acute-angled triangle $A B C$ intersects with its other heights at point $H$. Point $K$ lies on segment $A C$ such that the measure of angle $B K H$ is maximized. Find $D K$, if $A D=2, D C=3$. | \sqrt{6} |
28,204 | Let $n$ be a positive integer. Consider the set of $(n+1)^{3}-1$ points in three-dimensional space:
$$
S=\{(x, y, z): x, y, z \in\{0,1, \ldots, n\}, x+y+z>0\}
$$
Determine the minimum number of planes such that their union contains all points of the set $S$, but does not contain the point $(0,0,0)$. | 3n |
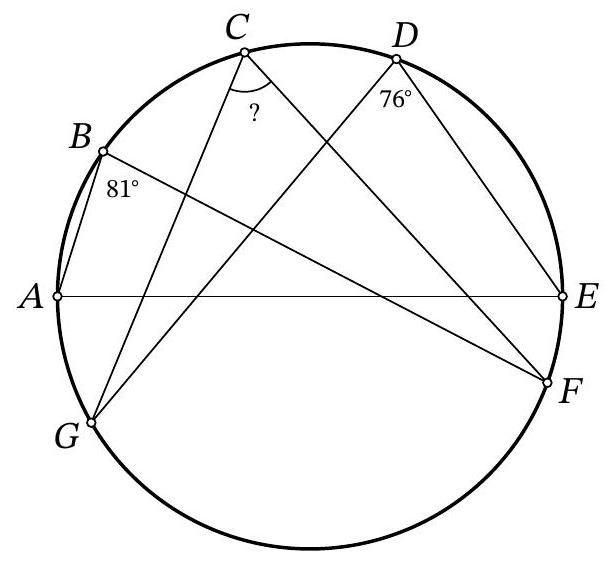
28,216 | Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
 | 67 |
28,240 | 4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-7.5,7.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$. | 240 |
28,244 | $6 \cdot 103$ Find the smallest positive integer $n$ (where $n>1$) such that the quadratic mean of the first $n$ natural numbers is an integer. Here, the quadratic mean of $n$ numbers $a_{1}, a_{2}, \cdots, a_{n}$ is defined as
$$
\left(\frac{a_{1}^{2}+a_{2}^{2}+\cdots+a_{n}^{2}}{n}\right)^{\frac{1}{2}} .
$$ | 337 |
28,257 | 26th Putnam 1965 Problem A5 How many possible bijections f on {1, 2, ... , n} are there such that for each i = 2, 3, ... , n we can find j < n with f(i) - f(j) = ± 1? Solution | 2^{n-1} |
28,259 | # 5. CONDITION
A right triangle $ABC$ with hypotenuse $AB$ is inscribed in a circle. A point $D$ is taken on the larger leg $BC$ such that $AC = BD$, and point $E$ is the midpoint of the arc $AB$ containing point $C$. Find the angle $DEC$. | 90 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.