id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
25,000 | A function \( f(x) \) defined on the interval \([1,2017]\) satisfies \( f(1)=f(2017) \), and for any \( x, y \in [1,2017] \), \( |f(x) - f(y)| \leqslant 2|x - y| \). If the real number \( m \) satisfies \( |f(x) - f(y)| \leqslant m \) for any \( x, y \in [1,2017] \), find the minimum value of \( m \). | 2016 |
25,002 | Two motorcyclists departed simultaneously from points \( A \) and \( B \) towards each other and met 50 km from point \( B \). After arriving at points \( A \) and \( B \), the motorcyclists immediately turned back and met for the second time 25 km from point \( A \). How many kilometers are there from \( A \) to \( B \)? | 125 |
25,024 | In trapezoid \(ABCD\), \(AD\) is parallel to \(BC\). \(\angle A = \angle D = 45^\circ\), while \(\angle B = \angle C = 135^\circ\). If \(AB = 6\) and the area of \(ABCD\) is 30, find \(BC\). | 2\sqrt{2} |
25,026 | Determine the radius of the sphere that touches the faces of the unit cube passing through vertex $A$ and the edges passing through vertex $B$. | 2 - \sqrt{2} |
25,037 | A right truncated pyramid is inscribed around a sphere of radius $r$, with its base being a square. What is the volume of this truncated pyramid, if the diagonal of its base is $4 r$? | \frac{28r^{3}}{3} |
25,044 | Problem 6. (Option 1).
In the right triangle $ABC: \angle ACB=90^{\circ}, AC=6, BC=4$. On the line $BC$, a point $D (CD>BD)$ is marked such that $\angle ADC=45^{\circ}$. On the line $AD$, a point $E$ is marked such that the perimeter of triangle $CBE$ is the smallest possible. Then, on the line $DC$, a point $F$ is marked such that the perimeter of triangle $AFE$ is the smallest possible. Find $CF$.
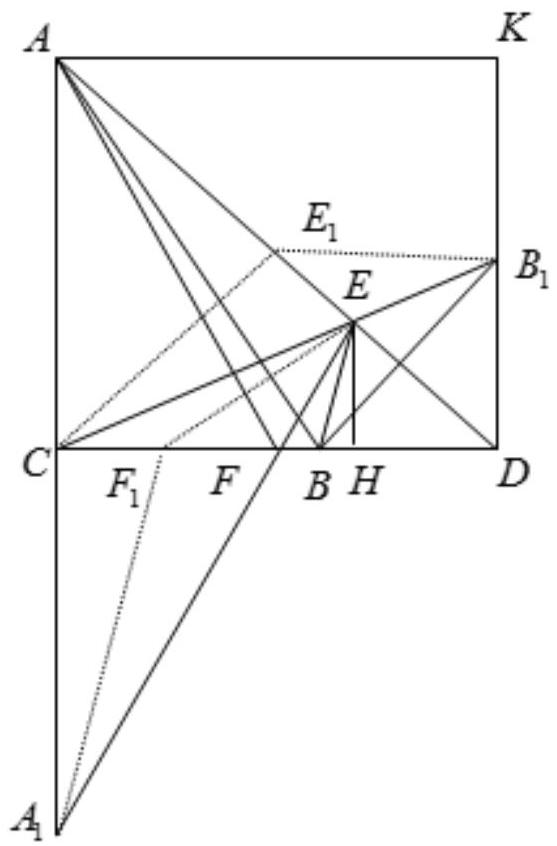
## Construction and Proof:
For convenience, construct a square ACDK (AD is its diagonal, since $\angle ADC=45^{\circ}$. Mark point $B_1$ on side $DK (B_1D=BD \Rightarrow B_1B \perp AD)$.
Draw line $B_1C$, which intersects $AD$ at point $E$.
The perimeter of triangle $CBE$ is the smallest because among all possible points $E_1$ on line $AD$, the sum of the lengths of segments $B_1E + EC$ is the smallest ($B_1E + EC < B_1E_1 + E_1C$ - triangle inequality) and $B_1E = EB$. Similarly, mark point $A_1$ on side $AC$ ($A_1C = AC$). Draw line $A_1E$, which intersects $CD$ at point $F$.
The perimeter of triangle $AFE$ is the smallest because among all possible points $F_1$ on line $AD$, the sum of the lengths of segments $A_1F + EF$ is the smallest ($A_1F + EF < A_1F_1 + F_1E$ - triangle inequality) and $A_1F = FA$. | 3.6 |
25,061 | Francisco has 3 daughters: Alina, Valentina, and Civela. An interesting fact is that all three daughters were born on March 18. Today, March 18, 2014, is their birthday. Noting another curious fact, Francisco says:
- Alina, your age is now double the age of Valentina.
a) Show that this could never have happened before and that, after the next birthday of Valentina, it will never happen again.
Then, Alina, who was very clever, exclaimed:
- Dad, exactly 10 years ago, the age of one of us three was double the age of another, and in 10 years, the same fact will happen again!
b) It is known that the oldest of the daughters is over 30 years old. How old is Civela? | 15 |
25,071 | 15. Given the ellipse $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ with left and right foci $F_{1}, F_{2}$, and the right vertex $A$, and $P$ is any point on the ellipse $C$. It is known that the maximum value of $\overrightarrow{P F_{1}} \cdot \overrightarrow{P F_{2}}$ is 3, and the minimum value is 2.
(1) Find the equation of the ellipse $C$;
(2) If the line $l: y=k x+m$ intersects the ellipse $C$ at points $M, N$ (where $M, N$ are not the left or right vertices), and the circle with diameter $M N$ passes through point $A$. Prove that the line $l$ passes through a fixed point, and find the coordinates of this fixed point. | (\frac{2}{7},0) |
25,072 | Third question Given ten points in space, where no four points lie on the same plane. Connect some of the points with line segments. If the resulting figure contains no triangles and no spatial quadrilaterals, determine the maximum number of line segments that can be drawn. | 15 |
25,080 | 4.9 On a $10 \times 10$ grid paper, there are 11 horizontal grid lines and 11 vertical grid lines. A line segment connecting two adjacent nodes on the same straight line is called a "link segment". How many link segments need to be erased at least, so that at most 3 link segments remain at each node? | 41 |
25,084 | Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
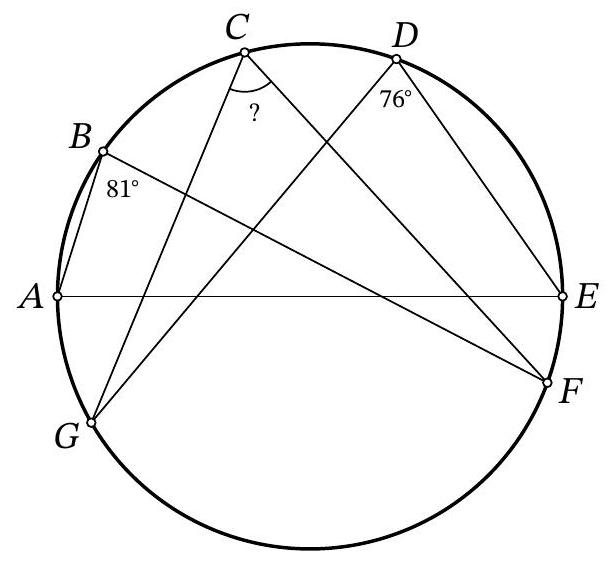 | 67 |
25,089 | Zaslavsky A.A.
Let $O, I$ be the centers of the circumcircle and incircle of a right triangle; $R, r$ be the radii of these circles; $J$ be the point symmetric to the right-angle vertex with respect to $I$. Find $O J$. | R-2r |
25,098 | [ Inscribed and Circumscribed Circles ] [ Inscribed Angle Subtended by a Diameter ]
A circle with radius 1 is circumscribed around triangle $A P K$. The extension of side $A P$ beyond vertex $P$ intercepts a segment $B K$ from the tangent to the circle at vertex $K$, and $B K$ is equal to 7. Find the area of triangle $A P K$, given that the angle $A B K$ is $\operatorname{arctg} \frac{2}{7}$. | \frac{28}{53} |
25,118 | 9. Given is a regular tetrahedron of volume 1 . We obtain a second regular tetrahedron by reflecting the given one through its center. What is the volume of their intersection? | \frac{1}{2} |
25,133 | 42nd Putnam 1981 Problem B2 What is the minimum value of (a - 1) 2 + (b/a - 1) 2 + (c/b - 1) 2 + (4/c - 1) 2 , over all real numbers a, b, c satisfying 1 ≤ a ≤ b ≤ c ≤ 4. Solution | 12-8\sqrt{2} |
25,136 | 14th ASU 1980 Problem 12 Some unit squares in an infinite sheet of squared paper are colored red so that every 2 x 3 and 3 x 2 rectangle contains exactly two red squares. How many red squares are there in a 9 x 11 rectangle? | 33 |
25,141 | 30th IMO 1989 shortlist Problem 23 155 birds sit on a circle center O. Birds at A and B are mutually visible iff ∠AOB ≤ 10 o . More than one bird may sit at the same point. What is the smallest possible number of mutually visible pairs? Solution | 270 |
25,143 | 22. (12 points) Given the function
$$
f(x)=\frac{m x-n}{x}-\ln x \quad (m, n \in \mathbf{R}) \text{.}
$$
(1) If the tangent line to the function $f(x)$ at the point $(2, f(2))$ is parallel to the line $x-y=0$, find the value of the real number $n$;
(2) Discuss the maximum value of the function $f(x)$ on the interval $[1,+\infty)$;
(3) If $n=1$, the function $f(x)$ has exactly two zeros $x_{1}, x_{2} \left(0 < x_{1} < x_{2}\right)$. Prove that $x_{1} + x_{2} > 2$. | 6 |
25,171 | 5. [5] The function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfies $f\left(x^{2}\right) f^{\prime \prime}(x)=f^{\prime}(x) f^{\prime}\left(x^{2}\right)$ for all real $x$. Given that $f(1)=1$ and $f^{\prime \prime \prime}(1)=8$, determine $f^{\prime}(1)+f^{\prime \prime}(1)$. | 6 |
25,176 | One, (40 points) Find the smallest positive integer $m$ such that the equation
$$
2^{x}+3^{y}-5^{z}=2 m
$$
has no positive integer solutions for $x, y, z$. | 11 |
25,183 | 10. $n>10$ teams take part in a soccer tournament. Each team plays every other team exactly once. A win gives two points, a draw one point and a defeat no points. After the tournament, it turns out that each team has won exactly half of its points in the games against the 10 worst teams (in particular, each of these 10 teams has scored half of its points against the 9 remaining teams). Determine all possible values of $n$, and give an example of such a tournament for these values.
## 1st solution
We call the 10 worst teams the losers, the $n-10$ best teams the winners. We repeatedly use the following fact: If $k$ teams play against each other, then the total number of points won is exactly $k(k-1)$. We count the total number of points won in two ways. On the one hand, this is exactly $n(n-1)$. On the other hand, the 10 losers in the games among themselves receive exactly $10 \cdot 9=90$ points. By assumption, this is exactly half of the total number of points that these 10 teams have achieved. Consequently, the total number of points scored by the losers is 180. The $n-10$ winners scored a total of $(n-10)(n-11)$ points in the games among themselves. Again, this is half of the total number of points, the latter is therefore equal to $2(n-10)(n-11)$. A comparison yields the equation
$$
n(n-1)=180+2(n-10)(n-11)
$$
This is equivalent to $n^{2}-41 n+400=0$ and has the solutions $n=16$ and $n=25$.
According to the above calculations, it also follows that the average score of the $n-10$ winners is equal to 2( $n-11)$, the average score of the 10 losers is equal to 18.
Of course, $2(n-10) \geq 18$ must now apply, i.e. $n \geq 20$. Consequently, $n=16$ is not possible.
Finally, we show that such a tournament exists for $n=25$. The 10 losers always play to a draw among themselves, as do the $n-10$ winners among themselves. The following diagram shows the games of the 15 winners $G_{i}$ against the 10 losers $V_{j}$. Where 2 means a win for $G_{i}$, 0$ a win for $V_{j}$ and 1 a draw.
| | $G_{1}$ | $G_{2}$ | $G_{3}$ | $G_{4}$ | $G_{5}$ | $G_{6}$ | $G_{7}$ | $G_{8}$ | $G_{9}$ | $G_{10}$ | $G_{11}$ | $G_{12}$ | $G_{13}$ | $G_{14}$ | $G_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $V_{1}$ | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 0 |
| $V_{2}$ | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 1 | 2 | 2 | 2 | 0 |
| $V_{3}$ | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 1 | 2 | 2 | 2 |
| $V_{4}$ | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 1 | 2 | 2 | 2 |
| $V_{5}$ | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 1 | 2 | 2 |
| $V_{6}$ | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 0 | 1 | 2 | 2 |
| $V_{7}$ | 2 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 0 | 1 | 2 |
| $V_{8}$ | 2 | 2 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 0 | 1 | 2 |
| $V_{9}$ | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 0 | 1 |
| $V_{10}$ | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 0 | 1 |
In total, the final score of each winner is 28, of which exactly 14 points come from games against the losers. Each loser has a final score of 18, half of which again comes from games against the other losers. This shows everything.
## 2nd solution
Here is another example of such a tournament. Again, the losers and the winners play each other to a draw. Now assume that a winner never loses to a loser. A winner scores a total of 14 points against the other winners, so he must also score 14 points against the losers. To do this, he must win four times and draw six times. Similarly, each loser draws nine times. We can now divide the $10 \times 15$ table from above into $2 \times 3$ boxes and obtain the following table with the same notations:
| | $G_{1}, G_{2}, G_{3}$ | $G_{4}, G_{5}, G_{6}$ | $G_{7}, G_{8}, G_{9}$ | $G_{10}, G_{11}, G_{12}$ | $G_{13}, G_{14}, G_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $V_{1}, V_{2}$ | 1 | 1 | 1 | 2 | 2 |
| $V_{3}, V_{4}$ | 2 | 1 | 1 | 1 | 2 |
| $V_{5}, V_{6}$ | 2 | 2 | 1 | 1 | 1 | 1 |
| $V_{7}, V_{8}$ | 1 | 2 | 2 | 1 | 1 |
| $V_{9}, V_{10}$ | 1 | 1 | 2 | 2 | 1 | | 25 |
25,186 | 3.48. The height of the cone is $H$, the angle between the slant height and the height is $\alpha$. A smaller cone is inscribed in this cone such that the vertex of the smaller cone coincides with the center of the base of the larger cone, and the corresponding slant heights of both cones are perpendicular to each other. Find the volume of the inscribed cone. | \frac{1}{3}\piH^{3}\sin^{4}\alpha\cos^{2}\alpha |
25,254 | Given a positive integer $n$ greater than 2004, fill the numbers $1, 2, \cdots, n^2$ into an $n \times n$ chessboard (consisting of $n$ rows and $n$ columns of squares) such that each square contains exactly one number. If a number in a square is greater than the numbers in at least 2004 other squares in its row and at least 2004 other squares in its column, then this square is called a "super square." Determine the maximum number of "super squares" on the chessboard.
(Feng Yuefeng, problem contributor) | n(n-2004) |
25,257 | 5. Given the hyperbola $C_{1}: 2 x^{2}-y^{2}=1$, and the ellipse $C_{2}$ : $4 x^{2}+y^{2}=1$. If $M$ and $N$ are moving points on the hyperbola $C_{1}$ and the ellipse $C_{2}$ respectively, $O$ is the origin, and $O M \perp O N$, then the distance from point $O$ to the line $M N$ is $\qquad$ | \frac{\sqrt{3}}{3} |
25,265 | Some unit-radius circles are drawn on the plane, and we color the center of each circle blue. We mark some points on the circumference of the circles in red such that exactly 2 red points lie on each circumference. What is the maximum number of blue points if there are a total of 25 colored points? | 20 |
25,268 | The first question: Let real numbers $a_{1}, a_{2}, \cdots, a_{2016}$ satisfy
$$
\begin{array}{l}
9 a_{i}>11 a_{i+1}^{2}(i=1,2, \cdots, 2015) \text {. Find } \\
\quad\left(a_{1}-a_{2}^{2}\right)\left(a_{2}-a_{3}^{2}\right) \cdots\left(a_{2015}-a_{2016}^{2}\right)\left(a_{2016}-a_{1}^{2}\right)
\end{array}
$$
the maximum value. | \frac{1}{4^{2016}} |
25,272 | [Theorem on the lengths of a tangent and a secant; the product of the entire secant and its external part [Pythagorean Theorem (direct and inverse).
A circle is tangent to side $B C$ of triangle $A B C$ at its midpoint $M$, passes through point $A$, and intersects segments $A B$ and $A C$ at points $D$ and $E$ respectively. Find the angle $A$, if it is known that $B C=12, A D=3.5$ and $E C=\frac{9}{\sqrt{5}}$.
# | 90 |
25,280 | 10. (20 points) Let positive numbers $x, y$ satisfy $x^{3}+y^{3}=$ $x-y$. Find the maximum value of the real number $\lambda$ such that $x^{2}+\lambda y^{2} \leqslant 1$ always holds. | 2+2\sqrt{2} |
25,286 | Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
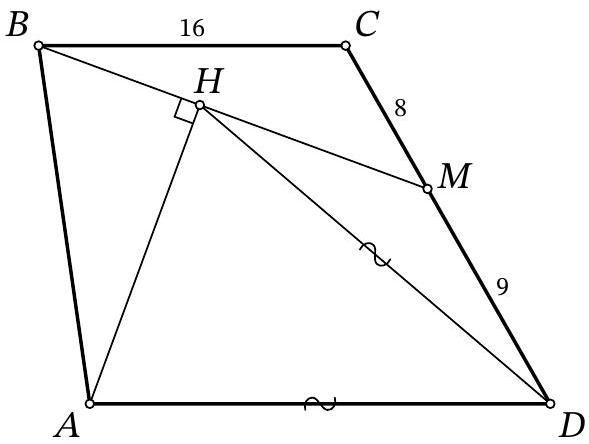 | 18 |
25,288 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{\sqrt{2}} \frac{x^{4} \cdot d x}{\left(4-x^{2}\right)^{3 / 2}}
$$ | 5-\frac{3\pi}{2} |
25,291 | 4. Find all triples of real numbers $x, y, z$ for which
$$
\lfloor x\rfloor-y=2 \cdot\lfloor y\rfloor-z=3 \cdot\lfloor z\rfloor-x=\frac{2004}{2005}
$$
where $\lfloor a\rfloor$ denotes the greatest integer not exceeding the number $a$.
The second round of category B takes place
on Tuesday, March 22, 2005
so that it starts in the morning and the contestants have 4 hours of pure time to solve the problems. For each problem, a contestant can earn 6 points, and a successful solver is a student who scores 10 points or more. Allowed aids are writing and drawing supplies, school MF tables, and calculators without a graphic display. This information will be communicated to the students before the start of the competition. | 2+\frac{1}{2005},1+\frac{1}{2005},1+\frac{1}{2005} |
25,293 | Krekov D:
In an acute scalene triangle $ABC$, the altitudes $AA'$ and $BB'$ intersect at point $H$, and the medians of triangle $AHB$ intersect at point $M$. The line $CM$ bisects the segment $A'B'$. Find the angle $C$. | 45 |
25,306 | $4 \cdot 20$ Given 9 points in space, where no 4 points are coplanar. Connect several line segments between the 9 points so that there is no tetrahedron in the graph. How many triangles can there be at most in the graph? | 27 |
25,319 | 31. Let $Z=\{1,2, \cdots, n\}, k$ be a positive integer, $\frac{n}{2} \leqslant k \leqslant n$, find the number of mappings $f: Z \rightarrow Z$ that satisfy the following conditions:
(i) $f^{2}=f$;
(ii) The image of $f(x)$, $f(Z)$, contains exactly $k$ distinct elements;
(iii) For each $y \in f(Z)$, there are at most two $x \in Z$ such that $f(x)=y$. | \frac{n!}{(n-k)!(2k-n)!} |
25,336 | 11. (20 points) Let point $Z$ move on the circle $|z|=3$ in the complex plane, and let $w=\frac{1}{2}\left(z+\frac{1}{z}\right)$. The trajectory of $w$ is the curve $\Gamma$. A line $l$ passes through the point $P(1,0)$ and intersects the curve $\Gamma$ at points $A$ and $B$, and intersects the imaginary axis at point $M$. If $\overrightarrow{M A}=t \overrightarrow{A P}$ and $\overrightarrow{M B}=s \overrightarrow{B P}$, find the value of $t+s$. | -\frac{25}{8} |
25,357 | 3.95. The base of the pyramid is an isosceles triangle with an angle $\alpha$ between the lateral sides. The pyramid is placed in a certain cylinder such that its base is inscribed in the base of this cylinder, and the vertex coincides with the midpoint of one of the cylinder's generators. The volume of the cylinder is $V$. Find the volume of the pyramid. | \frac{V}{3\pi}\sin\alpha\cos^{2}\frac{\alpha}{2} |
25,367 | $4 \cdot 20$ There is a $\triangle A B C, a 、 b 、 c$ are the sides opposite to $\angle A 、 \angle B 、 \angle C$ respectively. If $b$ is the arithmetic mean of $a 、 c$, and $\operatorname{tg} \frac{B}{2}$ is the geometric mean of $\operatorname{tg} \frac{A}{2} 、 \operatorname{tg} \frac{C}{2}$, try to form a quadratic equation with $\operatorname{tg} \frac{A}{2}, \operatorname{tg} \frac{C}{2}$ as its roots. | 3x^{2}-2\sqrt{3}x+1=0 |
25,368 | 4. In a given circular cone, with height $H$ and base radius $R$, a cylinder with maximum volume is inscribed. In this cylinder, a cone is inscribed, and in that cone, another cylinder with maximum volume is inscribed, etc. (the bases of the cylinders and cones are in the same plane). Find the sum of the volumes of the inscribed cylinders. | \frac{4}{23}\piR^{2}H |
25,375 | 6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=147 \\
y^{2}+y z+z^{2}=9 \\
z^{2}+x z+x^{2}=156
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 42 |
25,376 | Question 144, As shown in the figure, plane \(ABDE \perp\) plane \(\mathrm{ABC}\), \(\triangle \mathrm{ABC}\) is an isosceles right triangle, \(A C = B C = 4\), quadrilateral \(\mathrm{ABDE}\) is a right trapezoid, \(\mathrm{BD} / / \mathrm{AE}, \mathrm{BD} \perp \mathrm{AB}, \mathrm{BD} = 2, \mathrm{AE} = 4\), points \(O\) and \(\mathrm{M}\) are the midpoints of \(\mathrm{CE}\) and \(\mathrm{AB}\) respectively. Find the sine value of the angle formed by line \(\mathrm{CD}\) and plane \(\mathrm{ODM}\). | \frac{\sqrt{30}}{10} |
25,380 | 5th USAMO 1976 Problem 3 Find all integral solutions to a 2 + b 2 + c 2 = a 2 b 2 . Solution | 0,0,0 |
25,405 | Four, (50 points) Let $T$ be the set of all positive divisors of $2020^{100}$, and set $S$ satisfies:
(1) $S$ is a subset of $T$;
(2) No element in $S$ is a multiple of another element in $S$.
Find the maximum number of elements in $S$. | 10201 |
25,413 | 9.2. The bisectors of the external angles $B$ and $C$ of triangle $ABC$ intersect at point $M$. a) Can angle $BMC$ be obtuse? b) Find angle $BAC$ if it is known that $\angle BMC = \frac{\angle BAM}{2}$. | 120 |
25,419 | [ Diameter, main properties ] [ Signs and properties of the tangent ]
A circle passes through the midpoints of the hypotenuse $A B$ and the leg $B C$ of a right triangle $A B C$ and is tangent to the leg $A C$. In what ratio does the point of tangency divide the leg $A C$. | 1:3 |
25,442 | 6. Given the line $6 x-5 y-28=0$ and
the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\left(a>b>0\right.$, and $\left.a^{2} 、 b \in \mathbf{Z}\right)$
intersect at points $A$ and $C$. Let $B(0, b)$ be the upper vertex of the ellipse, and the centroid of $\triangle A B C$ is the right focus $F_{2}$ of the ellipse. Then the equation of the ellipse is $\qquad$. | \frac{x^{2}}{20}+\frac{y^{2}}{16}=1 |
25,453 | Example 5 Let $x, y, z, w$ be four real numbers, not all zero. Find:
$S=\frac{x y+2 y z+z w}{x^{2}+y^{2}+z^{2}+w^{2}}$'s maximum value. | \frac{1}{2}(1+\sqrt{2}) |
25,466 | 8. (10 points) In $\triangle A B C$, $B D=D E=E C$, $C F: A C=1: 3$. If the area of $\triangle A D H$ is 24 square centimeters more than the area of $\triangle H E F$, find the area of triangle $A B C$ in square centimeters? | 108 |
25,470 | 3. In a convex quadrilateral $A B C D$, the lengths of sides $A B$ and $B C$ are equal, $D B$ is the bisector of angle $A D C$, and $A D: D C=4: 3$. Find the cosine of angle $A K B$, where $K$ is the intersection point of diagonals $A C$ and $B D$, and $B K: K D=1: 3$. (16 points) | \frac{1}{4} |
25,484 | Example 3 Let $a \leqslant b<c$ be the side lengths of a right-angled triangle. Find the maximum constant $M$ such that $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geqslant \frac{M}{a+b+c}$.
(1991 China National Training Team Test) | 5+3\sqrt{2} |
25,485 | (JBMO 2002 - Shorlist, Problem G3), treated in class
Let $A B C$ be an isosceles triangle at $A$, with $\widehat{C A B}=20^{\circ}$. Let $D$ be a point on the segment $[A C]$, such that $A D=B C$. Calculate the angle $\widehat{B D C}$. | 30 |
25,487 | 6. For the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$, the left and right foci are $F_{1}, F_{2}$, and $P$ is any point on the ellipse that does not coincide with the left or right vertices. Points $I, G$ are the incenter and centroid of $\triangle P F_{1} F_{2}$, respectively. Given that for any point $\boldsymbol{P}, \boldsymbol{I} \boldsymbol{G}$ is always perpendicular to the $\boldsymbol{x}$-axis, the eccentricity of the ellipse is $\qquad$ | \frac{1}{3} |
25,503 | Blinkov A.D:
On the side $AB$ of rectangle $ABCD$, a point $M$ is chosen. Through this point, a perpendicular to the line $CM$ is drawn, which intersects the side $AD$ at point $E$. Point $P$ is the foot of the perpendicular dropped from point $M$ to the line $CE$. Find the angle $APB$. | 90 |
25,504 | A convex body is bounded by 4 regular hexagonal and 4 regular triangular faces. At each vertex of the body, 2 hexagons and 1 triangle meet. What is the volume of the body if the length of its edges is unit length? | \frac{23\sqrt{2}}{12} |
25,515 | 1. Let real numbers $a_{1}, a_{2}, \cdots, a_{2016}$ satisfy $9 a_{i}>11 a_{i+1}^{2}(i=1,2, \cdots, 2015)$. Find the maximum value of $\left(a_{1}-a_{2}^{2}\right)\left(a_{2}-a_{3}^{2}\right) \cdots\left(a_{2015}-a_{2016}^{2}\right)\left(a_{2016}-a_{1}^{2}\right)$. | \frac{1}{4^{2016}} |
25,521 | Example 3 Find the largest positive integer $n$, such that in three-dimensional space there exist $n$ points $P_{1}, P_{2}, \cdots, P_{n}$, where no three points are collinear, and for any $1 \leqslant i<j<k \leqslant n, \triangle P_{i} P_{j} P_{k}$ is not an obtuse triangle. | 8 |
25,523 | 5th Chinese 1990 Problem B1 Given a positive integer n, for what real u, v do the simultaneous equations a 2 + b 2 + c 2 = 169n 2 , a 2 (ua 2 + vb 2 ) + b 2 (ub 2 + vc 2 ) + c 2 (uc 2 + va 2 ) = (2u + v)(13n) 4 /4 have a solution in positive integers a, b, c? Solution | 2u |
25,527 | 19. In $\triangle A B C$, $A B=A C, \angle A=100^{\circ}, I$ is the incenter, $D$ is a point on $A B$ such that $B D=B I$. Find the measure of $\angle B C D$.
(Problem 1073 from Mathematical Bulletin) | 30 |
25,532 | Fibonacci numbers Euclidean algorithm
For each natural $n$, provide an example of a rectangle that would be cut into exactly $n$ squares, among which there should be no more than two identical ones. | F_{n}\timesF_{n+1} |
25,534 | 3. Let $l$ and $m$ be two skew lines, and on $L$ there are three points $A$, $B$, and $C$, with $A B = B C$. Through $A$, $B$, and $C$, perpendiculars $A D$, $B E$, and $C F$ are drawn to $m$, with the feet of the perpendiculars being $D$, $E$, and $F$ respectively. Given that $A D = \sqrt{15}$, $B E = \frac{7}{2}$, and $C F = \sqrt{10}$, find the distance between $l$ and $m$. | \sqrt{6} |
25,553 | 9. Given the parabola $C: x^{2}=2 p y(p>0)$, draw two tangent lines $R A$ and $R B$ from the point $R(1,-1)$ to the parabola $C$, with the points of tangency being $A$ and $B$. Find the minimum value of the area of $\triangle R A B$ as $p$ varies. | 3\sqrt{3} |
25,556 | 20. Let $n(n \geqslant 3)$ be a positive integer, and let positive numbers $\alpha$ and $\beta$ satisfy $\frac{\alpha}{\beta}=\frac{n-1}{n-2}$. Also, $x_{i} \in \mathbf{R}_{+}(i=1,2, \cdots, n)$, and $\sum_{i=1}^{n} x_{i}^{\alpha}=1$, find the minimum value of $\sum_{i=1}^{n} \frac{x_{i}^{\beta}}{1-x_{i}^{\alpha}}$. | \frac{n}{n-1}\cdot\sqrt[n-1]{n} |
25,576 | 12. Given the ellipse $\frac{x^{2}}{6}+\frac{y^{2}}{2}=1$ with its right focus at $F$, the line $y=k(x-2)$ through $F$ intersects the ellipse at points $P$ and $Q$ $(k \neq 0)$. If the midpoint of $P Q$ is $N$, and $O$ is the origin, the line $O N$ intersects the line $x=3$ at $M$.
(1) Find the size of $\angle M F Q$;
(2) Find the maximum value of $\frac{|P Q|}{|M F|}$. | \sqrt{3} |
25,591 | 8.32 Find all natural numbers $n$ such that $2^{8}+2^{11}+2^{n}$ is a perfect square of a natural number.
(6th All-Russian Mathematical Olympiad, 1980) | 12 |
25,605 | 11. Given positive real numbers $a, b, c$ satisfying $a b+b c+c a=1$, find the minimum value of $\sqrt{a^{2}+a b+b^{2}}+\sqrt{b^{2}+b c+c^{2}}+\sqrt{c^{2}+c a+a^{2}}$. | 3 |
25,611 | 4. Find all natural numbers $n$ such that $n-4$, $2n+2$, and $4n+1$ are perfect cubes. | 31 |
25,616 | 6. (7 points) Petya showed Vasya 37 identical-looking cards laid out in a row. He said that on the hidden sides of the cards, all numbers from 1 to 37 are written (each exactly once) such that the number on any card starting from the second is a divisor of the sum of the numbers written on all preceding cards. Then Petya showed Vasya that the number on the first card is 37, and on the second card is 1. Vasya said that he then knows what number is written on the third card. What is it? | 2 |
25,626 | 12. For a regular tetrahedron $P Q R S$, there are four vertices and six edges, each labeled with a number, making a total of 10 numbers. These 10 numbers are $1, 2, 3, 4, 5, 6, 7, 8, 9, 11$. Each number is used exactly once, and each number on an edge represents the sum of the numbers at the two vertices it connects. The number on edge $P Q$ is 9, then the number on edge $R S$ is $\qquad$ . | 5 |
25,636 | 12. (20 points) Given the ellipse $\frac{x^{2}}{6}+\frac{y^{2}}{2}=1$ with its right focus at $F$, the line $y=k(x-2)(k \neq 0)$ passing through $F$ intersects the ellipse at points $P$ and $Q$. If the midpoint of $PQ$ is $N$, and $O$ is the origin, the line $ON$ intersects the line $x=3$ at point $M$, find
(1) the size of $\angle M F Q$;
(2) the maximum value of $\frac{P Q}{M F}$. | \sqrt{3} |
25,642 | Example 3 Let $A A_{1} B_{1} B$ be the axial section of a cylinder, $C$ be a point on the circumference of the base circle, $A A_{1}=1, A B=4, \angle B A C=$ $60^{\circ}$. Find the dihedral angle formed by the plane $A_{1} C B_{1}$ and the base $A B$ of the cylinder. | 30 |
25,661 | 5. [5 points] A magician has a set of $16^{2}$ different cards. Each card has one side red and the other side blue; on each card, there is a natural number from 1 to 16 written on both sides. We will call a card a duplicate if the numbers on both sides of the card are the same. The magician wants to draw two cards such that at least one of them is a duplicate, and no number appears on both drawn cards simultaneously. In how many ways can he do this? | 3480 |
25,669 | 15. Given the sequence $\left\{a_{n}\right\}, a_{n}+a_{n+1}=n \cdot(-1)^{\frac{n(n+1)}{2}}$, the sum of the first $n$ terms is $S_{n}$, and $m+S_{2015}=-1007, a_{1} m>0$. Then the minimum value of $\frac{1}{a_{1}}+\frac{4}{m}$ is . $\qquad$ | 9 |
25,670 | 5. In each cell of a $15 \times 15$ table, a number $-1, 0$, or $+1$ is written such that the sum of the numbers in any row is non-positive, and the sum of the numbers in any column is non-negative. What is the smallest number of zeros that can be written in the cells of the table? | 15 |
25,672 | 5. The sequence $\left\{a_{n}\right\}$ satisfies: $a_{1}=1$, and for each $n \in \mathbf{N}^{*}, a_{n}, a_{n+1}$ are the roots of the equation $x^{2}+3 n x+b_{n}=0$, then $\sum_{k=1}^{20} b_{k}=$ $\qquad$ . | 6385 |
25,701 | 18. C6 (FRA 2) Let $O$ be a point of three-dimensional space and let $l_{1}, l_{2}, l_{3}$ be mutually perpendicular straight lines passing through $O$. Let $S$ denote the sphere with center $O$ and radius $R$, and for every point $M$ of $S$, let $S_{M}$ denote the sphere with center $M$ and radius $R$. We denote by $P_{1}, P_{2}, P_{3}$ the intersection of $S_{M}$ with the straight lines $l_{1}, l_{2}, l_{3}$, respectively, where we put $P_{1} \neq O$ if $l_{1}$ meets $S_{M}$ at two distinct points and $P_{1}=O$ otherwise ( $i=$ $1,2,3)$. What is the set of centers of gravity of the (possibly degenerate) triangles $P_{1} P_{2} P_{3}$ as $M$ runs through the points of $S$ ? | \frac{2R}{3} |
25,720 | Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
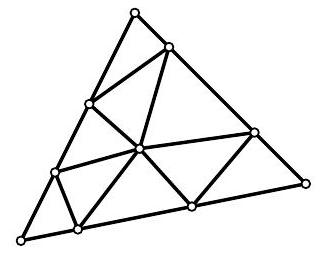 | 40 |
25,725 | 8. Let $a_{1}, a_{2}, \cdots, a_{105}$ be a permutation of $1,2, \cdots, 105$, satisfying: for any $m \in\{3,5,7\}$, for all $n$ such that $1 \leqslant n<n+m \leqslant 105$, we have $m \mid\left(a_{n+m}-a_{n}\right)$. Then the number of different permutations that meet the requirement is $\qquad$ (answer with a specific number). | 3628800 |
25,732 | A natural number $N$ greater than 20 can be represented as a palindrome in both base 14 and base 20 (a palindrome is a number that reads the same forward and backward, for example, $12321$ and $3443$ are palindromes, while 12331 is not a palindrome). The minimum value of $N$ is $\qquad$ (answer in decimal). | 105 |
25,743 | 14. Given a sequence $\left\{a_{n}\right\}$ with all terms being positive, the sum of the first $n$ terms is $S_{n}$, and $a_{n}+1=2 \sqrt{S_{n}}\left(n \in \mathbf{Z}_{+}\right)$.
(1) Find the general term formula for the sequence $\left\{a_{n}\right\}$;
(2) Let $b_{n}=\frac{a_{n+2}}{a_{n} a_{n+1} 2^{n}}$, the sum of the first $n$ terms of the sequence $b_{n}$ is $T_{n}$, prove: $\frac{5}{6} \leqslant T_{n}<1$. | \frac{5}{6}\leqslantT_{n}<1 |
25,763 | $14 \cdot 25$ Find the smallest natural number $n$ such that the equation $\left[\frac{10^{n}}{x}\right]=1989$ has an integer solution $x$.
(23rd All-Soviet Union Mathematical Olympiad, 1989) | 7 |
25,769 | 8.3. Given a triangle $A B C$, a point $D$ is chosen on side $B C$ and a point $H$ on side $A C$. Additionally, $D K$ is the angle bisector of triangle $B D A$. It turns out that angles $C H D$ and $H D K$ are right angles. Find $H C$, if $A C=2$. | HC=1 |
25,797 | A full score of 20 points) Let $x, y$ be non-zero real numbers, and satisfy $\frac{x \sin \frac{\pi}{5}+y \cos \frac{\pi}{5}}{x \cos \frac{\pi}{5}-y \sin \frac{\pi}{5}}=\tan \frac{9 \pi}{20}$.
(1) Find the value of $\frac{y}{x}$; (2) In $\triangle A B C$, if $\tan C=\frac{y}{x}$, find the maximum value of $\sin 2 A+2 \cos B$. | \frac{3}{2} |
25,813 | In an equilateral triangle $A B C$, an equilateral triangle $D E F$ is inscribed, see the figure. The vertices $D, E$, and $F$ lie on the sides $A B, B C$, and $A C$ such that the sides of triangle $D E F$ are perpendicular to the sides of triangle $A B C$. Furthermore, the segment $D G$ is a median in triangle $D E F$, and point $H$ is the intersection of the lines $D G$ and $B C$.
Determine the ratio of the areas of triangles $H G C$ and $B E D$.
(E. Patáková)
 | \frac{1}{4} |
25,826 | 23.7. Using the result of problem 23.6, calculate the following sums and products:
a) $\operatorname{ctg}^{2} \frac{\pi}{2 n+1}+\operatorname{ctg}^{2} \frac{2 \pi}{2 n+1}+\ldots+\operatorname{ctg}^{2} \frac{n \pi}{2 n+1}$;
b) $\frac{1}{\sin ^{2} \frac{\pi}{2 n+1}}+\frac{1}{\sin ^{2} \frac{2 \pi}{2 n+1}}+\ldots+\frac{1}{\sin ^{2} \frac{n \pi}{2 n+1}}$;
c) $\sin \frac{\pi}{2 n+1} \sin \frac{2 \pi}{2 n+1} \ldots \sin \frac{n \pi}{2 n+1}$.
## 23.3. Roots of Unity
A root of the $n$-th degree from unity is a complex number $\varepsilon$ for which $\varepsilon^{n}=1$. A primitive root of the $n$-th degree from unity is a complex number $\varepsilon$ for which $\varepsilon^{n}=1$ and $\varepsilon^{k} \neq 1$ for $k=1,2, \ldots, n-1$. | \frac{\sqrt{2n+1}}{2^{n}} |
25,830 | 11.58 (1) In a square consisting of $7 \times 7$ cells, mark the centers of $k$ cells such that no four of the marked points form the vertices of a rectangle with sides parallel to the grid lines. Find the maximum value of $k$.
(2) Solve the same problem for a square consisting of $13 \times 13$ cells. | 52 |
25,831 | [Theorem of Three Perpendiculars]
The base of the pyramid is a rectangle with an area of S. Two lateral faces are perpendicular to the base plane, while the other two are inclined to it at angles of $30^{\circ}$ and $60^{\circ}$. Find the volume of the pyramid. | \frac{1}{3}S\sqrt{S} |
25,846 | $p$ is a prime number such that the period of its decimal reciprocal is 200 . That is,
$$
\frac{1}{p}=0 . X X X X \ldots
$$
for some block of 200 digits $X$, but
$$
\frac{1}{p} \neq 0 . Y Y Y Y \ldots
$$
for all blocks $Y$ with less than 200 digits. Find the 101st digit, counting from the left, of $X$. | 9 |
25,848 | 10. (43rd Greek IMO Selection Test) Let $x, y, a$ be real numbers, and satisfy $x+y=x^{3}+y^{3}=x^{5}+y^{5}=a$. Find all possible values of $a$.
untranslated text remains unchanged. | -2,-1,0,1,2 |
25,850 | 9. As shown in the figure, the four vertices of square $A B C D$ are on the graphs of the inverse proportion functions $y=\frac{12}{x}$ and $y=\frac{20}{x}$ in the first quadrant, with the diagonals of the square parallel to the $x$-axis and $y$-axis, respectively. Then the x-coordinate of point $B$ is | 4 |
25,854 | 7. Suppose $A B C D$ is an isosceles trapezoid in which $\overline{A B} \| \overline{C D}$. Two mutually externally tangent circles $\omega_{1}$ and $\omega_{2}$ are inscribed in $A B C D$ such that $\omega_{1}$ is tangent to $\overline{A B}, \overline{B C}$, and $\overline{C D}$ while $\omega_{2}$ is tangent to $\overline{A B}, \overline{D A}$, and $\overline{C D}$. Given that $A B=1, C D=6$, compute the radius of either circle. | \frac{3}{7} |
25,855 | $[$ Properties and characteristics of the tangent $]$
In a circle with radius $R=4$, a chord $A B$ and a diameter $A K$ are drawn, forming an angle of $\frac{\pi}{8}$ with the chord. A tangent is drawn at point $B$, intersecting the extension of the diameter $A K$ at point $C$. Find the median $A M$ of triangle $A B C$. | 2\sqrt{9+6\sqrt{2}} |
25,857 | 7.3. Find the number of all integer solutions of the inequality $\sqrt{1+\sin \frac{\pi x}{4}-3 \cos \frac{\pi x}{2}}+\sqrt{6} \cdot \sin \frac{\pi x}{4} \geq 0$, belonging to the interval [1991; 2013]. | 9 |
25,897 | [Similar auxiliary triangles $]$ [ Right triangle with an angle at ]
On the cathetus $A C$ of the right triangle $A B C$, a circle is constructed with $A C$ as its diameter. It intersects side $A B$ at point $E$. A point $G$ is taken on side $B C$ such that segment $A G$ intersects the circle at point $F$, and segments $E F$ and $A C$ are parallel, $B G=2 C G$ and $A C=2 \sqrt{3}$. Find $G F$. | 1 |
25,902 | 6th Putnam 1946 Problem A5 Let T be a tangent plane to the ellipsoid x 2 /a 2 + y 2 /b 2 + z 2 /c 2 = 1. What is the smallest possible volume for the tetrahedral volume bounded by T and the planes x = 0, y = 0, z = 0? Solution | \frac{\sqrt{3}abc}{2} |
25,905 | Example 8 Let $f(a, b, c)=\frac{1}{\sqrt{1+2 a}}+\frac{1}{\sqrt{1+2 b}}+\frac{1}{\sqrt{1+2 c}}$, where $a, b, c>0$ and $abc=1$, find the minimum value of the constant $\lambda$ such that $f(a, b, c)<\lambda$ always holds. | 2 |
25,906 | 4. Let $H$ be the orthocenter of $\triangle A B C$ and let $A_{1}, B_{1}, C_{1}$ be the feet of the altitudes dropped from $A, B, C$ respectively. Let $\frac{\overline{A H}}{\overline{H A_{1}}}+\frac{\overline{B H}}{\overline{H B_{1}}}+\frac{\overline{C H}}{\overline{H C_{1}}}=2008$. Calculate the product $\frac{\overline{A H}}{\overline{H A_{1}}} \cdot \frac{\overline{B H}}{\overline{H B_{1}}} \cdot \frac{\overline{C H}}{\overline{H C_{1}}}$. | 2010 |
25,908 | $12 \cdot 60$ In a right-angled triangle with side lengths all being positive integers, one of the legs is 1575 less than the hypotenuse, and the other leg is less than 1991. Find the length of the hypotenuse of this right-angled triangle.
(China Beijing High School Grade 1 Mathematics Competition, 1991) | 1799 |
25,909 | Maria ordered a certain number of televisions for the stock of a large store, paying $\mathrm{R} \$ 1994.00$ per television. She noticed that, in the total amount to pay, the digits 0, 7, 8, and 9 do not appear. What is the smallest number of televisions she could have ordered? | 56 |
25,912 | Problem 5. (5 points) In a tournament, 55 boxers participated, and after each match, the winner left the tournament. The matches were held consecutively. It is known that in each match, boxers whose difference in the number of victories (at that moment) was no more than 1, met. How many matches could the winner of the tournament have played at most? | 8 |
25,952 | 15. $[\mathbf{9}]$ Compute $\tan \left(\frac{\pi}{7}\right) \tan \left(\frac{2 \pi}{7}\right) \tan \left(\frac{3 \pi}{7}\right)$. | \sqrt{7} |
25,957 | 9. Two circles are said to be orthogonal if they intersect in two points, and their tangents at either point of intersection are perpendicular. Two circles $\omega_{1}$ and $\omega_{2}$ with radii 10 and 13 , respectively, are externally tangent at point $P$. Another circle $\omega_{3}$ with radius $2 \sqrt{2}$ passes through $P$ and is orthogonal to both $\omega_{1}$ and $\omega_{2}$. A fourth circle $\omega_{4}$, orthogonal to $\omega_{3}$, is externally tangent to $\omega_{1}$ and $\omega_{2}$. Compute the radius of $\omega_{4}$. | \frac{92}{61} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.