id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
25,998 | 8,9
[ Ratio in which the bisector divides the side ]
In an isosceles triangle $A B C$, a rhombus $D E C F$ is inscribed such that vertex $E$ lies on side $B C$, vertex $F$ on side $A C$, and vertex $D$ on side $A B$. Find the length of the side of the rhombus if $A B=B C=12, A C=6$. | 4 |
26,005 | 3. In quadrilateral $A B C D$, side $A B$ is equal to diagonal $A C$ and is perpendicular to side $A D$, and diagonal $A C$ is perpendicular to side $C D$. A point $K$ is taken on side $A D$ such that $A C=A K$. The bisector of angle $A D C$ intersects $B K$ at point $M$. Find the angle $A C M$. (R. Zhenodarov) | 45 |
26,007 | 9.5. On a circle, $n>1$ points, called positions, are marked, dividing it into equal arcs. The positions are numbered clockwise from 0 to $n-1$. Vasya places a chip in one of them. Then the following actions, called moves, are repeated an unlimited number of times: Petya names some natural number, and Vasya moves the chip clockwise or counterclockwise by the number of positions specified by Petya. If at some point after Vasya's move, the chip lands in position number 0, Vasya loses, and Petya wins. For which $n$ can Petya always win, regardless of Vasya's moves? | 2^{k} |
26,029 | 2. The octahedron $A B C D E F$ has a square $A B C D$ as its base, while the line $E F$ is normal to the plane determined by the square $A B C D$ and passes through its center. It is known that the sphere that touches all faces of the octahedron and the sphere that touches all lateral edges (i.e., $E A, E B, E C, E D, F A, F B, F C$ and $F D$) have the same center, and that the sphere that touches the lateral edges has a surface area that is $50\%$ larger. Find the ratio $\frac{E F}{A B}$. | \sqrt{2} |
26,036 | 8.6. The altitudes of an acute-angled scalene triangle $ABC$ intersect at point $H$. $I$ is the incenter of triangle $ABC$, $O$ is the circumcenter of triangle $BHC$. It is known that point $I$ lies on the segment $OA$. Find the angle $BAC$. | 60 |
26,037 | Task 3. (15 points) Solve the system of equations
$$
\left\{\begin{array}{l}
x^{2}-23 y+66 z+612=0 \\
y^{2}+62 x-20 z+296=0 \\
z^{2}-22 x+67 y+505=0
\end{array}\right.
$$ | (-20,-22,-23) |
26,040 | 31. A circle inscribed in an angle with vertex $O$ touches its sides at points $A$ and $B$. Ray $O X$ intersects this circle at two points $C$ and $D$ such that $O C=C D=1$. If $M$ is the point of intersection of ray $O X$ and segment $A B$, then what is the length of segment $O M$? | \frac{4}{3} |
26,057 | [ The product of the lengths of the chord segments $\underline{\text { and }}$ the lengths of the secant segments ] Complex [The ratio of the areas of triangles with a common base or common height]
Diagonal $A C$ of the convex quadrilateral $A B C D$ is the diameter of the circumscribed circle around it. Find the ratio of the areas of triangles $A B C$ and $A C D$, given that diagonal $B D$ divides $A C$ in the ratio 2:5 (measured from point $A$), and $\angle B A C=45^{\circ}$. | \frac{29}{20} |
26,072 | 47th Putnam 1986 Problem A2 What is the remainder when the integral part of 10 20000 /(10 100 + 3) is divided by 10? Solution | 3 |
26,080 | 5.22 Let \( r \) and \( s \) be positive integers. Derive a formula for the number of ordered quadruples of positive integers \((a, b, c, d)\) that satisfy the following condition:
\[
3^{r} \cdot 7^{s} = [a, b, c] = [a, b, d] = [a, c, d] = [b, c, d] \text{.}
\]
The notation \([x, y, z]\) denotes the least common multiple of \(x, y, z\).
(41st Putnam Mathematical Competition, 1980) | (1+4r+6r^2)(1+4s+6s^2) |
26,083 | 2. Given that the circumcenter of $\triangle A B C$ is $O$, the orthocenter is $H, O \neq H$, and the midpoints of sides $B C, C A$ are $D, E$ respectively. Let $D^{\prime}, E^{\prime}$ be the points symmetric to $D, E$ with respect to $H$. If the line $A D^{\prime}$ intersects the line $B E^{\prime}$ at point $K$, find the value of $\frac{|K O|}{|K H|}$. | \frac{3}{2} |
26,102 | What is the largest possible number of subsets of the set $\{1,2, \ldots, 2 n+1\}$ such that the intersection of any two subsets consists of one or several consecutive integers? | (n+1)^2 |
26,119 | Given a cube $A B C D A 1 B 1 C 1 D 1$. A sphere touches the edges $A D, D D 1, C D$ and the line $B C 1$. Find the radius of the sphere, if the edge of the cube is 1. | 2\sqrt{2}-\sqrt{5} |
26,120 | 10. (20 points) Given a moving point $P$ on the parabola $y^{2}=4 x$, the focus $F(1,0)$, and $O$ as the origin. Find the maximum value of the inradius $r$ of $\triangle O P F$.
untranslated text remains unchanged. | \frac{2\sqrt{3}}{9} |
26,125 | Bakayev E.v.
Petya places 500 kings on the cells of a $100 \times 50$ board so that they do not attack each other. And Vasya places 500 kings on the white cells (in a chessboard coloring) of a $100 \times 100$ board so that they do not attack each other. Who has more ways to do this? | Vasya |
26,159 | Try to use a function of $n$ to represent the product
$$
9 \times 99 \times 9999 \times \cdots \times\left(10^{2^{n}}-1\right)
$$
the sum of the digits in decimal notation. | 9\times2^{n} |
26,162 | 7. In $\square A B C D$, $A B=4, B C=2, \angle D A B$ $=60^{\circ}$, a point $P$ on side $B C$ and a point $Q$ on the extension of $D C$ satisfy $S_{\triangle B P Q}=\frac{\sqrt{3}}{32}$. Then the minimum value of $\overrightarrow{A P} \cdot \overrightarrow{B Q}$ is $\qquad$ | \frac{97}{16} |
26,172 | 8.3. In the city, there are four jewelers to whom the tsar sent 13 bags of gold. The first bag contained one gold ingot, the second - two, the third - three, ..., the
thirteenth - 13 gold ingots. One of the bags was immediately lost somewhere, and
the remaining jewelers distributed them so that each received an equal number of gold ingots and an equal number of bags. In this process, the bag with one ingot went to the first jeweler, with three - to the second, with eleven - to the third. Determine which bags went to the fourth jeweler, if the ingots were not removed from the bags. | 2,9,10 |
26,173 | $1 \cdot 47$ Let $x^{2}-x+a$ divide $x^{13}+x+90$, determine the positive integer value of $a$.
(24th Putnam Mathematical Competition, 1963) | 2 |
26,195 | 4.5.4 * Find the largest constant $k$ such that for all real numbers $a, b, c, d$ in $[0,1]$, the inequality
$$
a^{2} b+b^{2} c+c^{2} d+d^{2} a+4 \geqslant k\left(a^{2}+b^{2}+c^{2}+d^{2}\right)
$$
holds. | 2 |
26,200 | $\left[\begin{array}{l}\text { Isosceles, Inscribed, and Circumscribed Trapezoids } \\ {[\quad \text { Auxiliary Similar Triangles }}\end{array}\right]$
The center of a circle with radius 6, which touches the sides $A B, B C$, and $C D$ of the isosceles trapezoid $A B C D$, lies on its larger base $A D$. The base $B C$ is equal to 4. Find the distance between the points where the circle touches the lateral sides $A B$ and $C D$ of this trapezoid. | \frac{36}{5} |
26,206 | (3) In the tetrahedron $P-ABC$, $\angle APB=\angle BPC=\angle CPA=90^{\circ}$, and the sum of the lengths of all edges is $S$. Then the maximum volume of this tetrahedron is $\qquad$. | \frac{S^{3}}{162(1+\sqrt{2})^{3}} |
26,208 | 1. Problem: Let $A B C D$ be a convex quadrilateral such that $A B+B C=2021$ and $A D=C D$. We are also given that
$$
\angle A B C=\angle C D A=90^{\circ}
$$
Determine the length of the diagonal $B D$. | \frac{2021}{\sqrt{2}} |
26,222 | 4- 47 Let $a, b$ be real numbers, and $x^{4}+a x^{3}+b x^{2}+a x+1=0$ has at least one real root. Try to find the minimum value that $a^{2}+b^{2}$ can take. | \frac{4}{5} |
26,228 | [
The ratio in which the bisector divides the side. [The ratio of the areas of triangles with a common base or common height]
In triangle $ABC$, the median $AD$ and the bisector $BE$ are perpendicular and intersect at point $F$. It is known that $S_{DEF}=5$. Find $S_{ABC}$.
# | 60 |
26,230 | 3. For what values of the parameter $a$ does the inequality $\left(a^{2}-6 a-7\right)|x|+(-a-19) \sqrt{x^{2}-9}>0$ have no solutions? Write the answer as an interval. If the set of answers consists of several intervals, list them separated by a semicolon. | [-1;7] |
26,233 | ## Task A-4.7.
By drawing lines parallel to each side, an equilateral triangle with side length $n$ is divided into $n^{2}$ equilateral triangles with side length 1. What is the maximum number of line segments of length 1 on the resulting grid that can be colored red so that no three red segments form an equilateral triangle? | n(n+1) |
26,241 | Example 3. Find the mass of the plate $D$ with surface density $\mu=x / y^{5}$, bounded by the curves
$$
\frac{x^{2}}{16}+y^{2}=1, \quad \frac{x^{2}}{16}+y^{2}=3, \quad y=\frac{x}{4}, \quad x=0 \quad\left(y \geq \frac{x}{4}, x \geq 0\right)
$$ | 4 |
26,247 | 17. [10] Let $p(x)=x^{2}-x+1$. Let $\alpha$ be a root of $p(p(p(p(x)))$. Find the value of
$$
(p(\alpha)-1) p(\alpha) p(p(\alpha)) p(p(p(\alpha))
$$ | -1 |
26,274 | 6. Given 9 points in space, where no 4 points are coplanar, connect several line segments between the 9 points so that there is no tetrahedron in the graph. How many triangles can there be at most in the graph? | 27 |
26,275 | 1. Given complex numbers $z$ and $\omega$ satisfy the following two conditions:
(1) $z+\omega+3=0$;
(2) $|z|, 2, |\omega|$ form an arithmetic sequence.
Is there a maximum value for $\cos (\arg z - \arg \omega)$? If so, find it. | \frac{1}{8} |
26,277 | In the following figure, $ABC$ is an isosceles triangle with $BA = BC$. Point $D$ is inside it such that $\angle ABD = 13^\circ$, $\angle ADB = 150^\circ$, and $\angle ACD = 30^\circ$. Additionally, $ADE$ is an equilateral triangle. Determine the value of the angle $\angle DBC$.
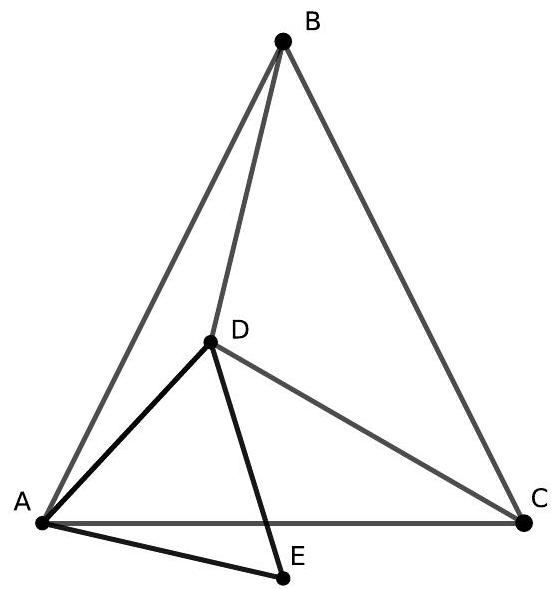 | 39 |
26,289 | 1. Find all values of $x$, for each of which one of the three given numbers $\log _{x^{2}}\left(x^{2}-3 x+2\right)$, $\log _{x^{2}} \frac{x^{2}}{x-2}$, and $\log _{x^{2}} \frac{x^{2}}{x-1}$ is equal to the sum of the other two. | 3 |
26,290 | 6. Given a positive integer $k$. If a sequence of subsets of the set of integers $\mathbf{Z}$, $I_{1} \supseteq I_{2} \supseteq \cdots \supseteq I_{k}$, satisfies that for $i=1,2, \cdots, k, 168$ $\in I_{i}$, and for any $x, y \in I_{i}$, we have $x-y \in I_{i}$ $\left(x, y\right.$ can be equal), then $\left(I_{1}, I_{2}, \cdots, I_{k}\right)$ is called a $k$-chain on $\mathbf{Z}$. How many $k$-chains are there on $\mathbf{Z}$? Please provide a reason. | \frac{(k+1)^{3}(k+2)(k+3)}{6} |
26,293 | 3. Determine the largest natural number $n$ for which there exist distinct sets $S_{1}, S_{2}, \ldots, S_{n}$ such that:
$1^{\circ}\left|S_{i} \cup S_{j}\right| \leqslant 2004$ for any two integers $1 \leqslant i, j \leqslant n$, and
$2^{\circ} S_{i} \cup S_{j} \cup S_{k}=\{1,2, \ldots, 2008\}$ for any three integers $1 \leqslant i<j<k \leqslant n$.
(Ivan Matic)
## SERBIAN MATHEMATICAL OLYMPIAD
competition of high school students in mathematics
Novi Sad, 14.04.2009.
## Second day | 32 |
26,299 | ## Problem Statement
Calculate the definite integral:
$$
\int_{-\arcsin (2 / \sqrt{5})}^{\pi / 4} \frac{2-\operatorname{tg} x}{(\sin x+3 \cos x)^{2}} d x
$$ | \frac{15}{4}-\ln4 |
26,300 | 10. In $\triangle A B C$, $A B=\sqrt{2}, A C=\sqrt{3}, \angle B A C=30^{\circ}, P$ is any point on the plane of $\triangle A B C$, then $\mu=\overrightarrow{P A} \cdot \overrightarrow{P B}+\overrightarrow{P B} \cdot \overrightarrow{P C}+\overrightarrow{P C} \cdot \overrightarrow{P A}$ has the minimum value of $\qquad$. | \frac{\sqrt{2}}{2}-\frac{5}{3} |
26,311 | 15. (16 points) Let $x_{1}, x_{2}, x_{3} \in [0,12]$,
$$
x_{1} x_{2} x_{3}=\left(\left(12-x_{1}\right)\left(12-x_{2}\right)\left(12-x_{3}\right)\right)^{2} \text {. }
$$
Find the maximum value of $f=x_{1} x_{2} x_{3}$. | 729 |
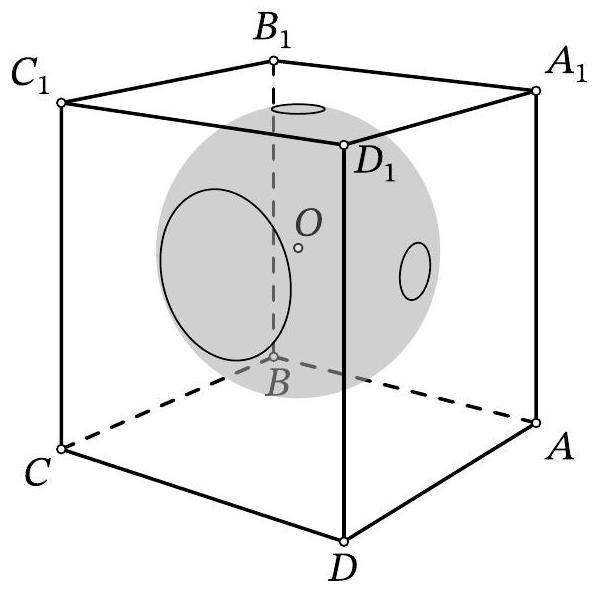
26,315 | Problem 11.6. Inside the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, there is the center $O$ of a sphere with radius 10. The sphere intersects the face $A A_{1} D_{1} D$ along a circle with radius 1, the face $A_{1} B_{1} C_{1} D_{1}$ along a circle with radius 1, and the face $C D D_{1} C_{1}$ along a circle with radius 3. Find the length of the segment $O D_{1}$.
 | 17 |
26,317 | 36*. A polyhedron is called regular if all its faces are regular and congruent polygons to each other and all its polyhedral angles are also regular and congruent to each other ${ }^{2}$. Investigate the possibility of constructing simple regular polyhedra with $n$-sided faces and $m$-sided angles and determine the possible number of their types, using the following considerations.
Divide the entire space into $f$ congruent regular $n$-sided angles with a common vertex $S$, with $m$ angles at each edge, and express the magnitudes of their dihedral angles in terms of $n$ and $f$. If a regular $n$-sided pyramid is constructed from the found magnitude of the dihedral angle, with the base being a regular $n$-sided polygon - a face of the desired polyhedron, then from such congruent pyramids, a regular polyhedron can be assembled (for example, a cube is assembled from six regular quadrilateral pyramids with a common vertex at the center of the cube). It can be proven that any regular polyhedron can be obtained by such a construction. (The last remark can be used without proof in solving this and the following problems.)
## 44 | 5 |
26,319 | Example 6 As shown in Figure $16-9$, in the tetrahedron $S-ABC$, $\triangle ABC$ is an equilateral triangle with a side length of 4, the plane $SAC \perp$ plane $ABC, SA=SC=2 \sqrt{3}, M, N$ are the midpoints of $AB, SB$ respectively.
(1) Find the size of the dihedral angle $N-CM-B$;
(2) Find the distance from point $B$ to the plane $CMN$. | \frac{4\sqrt{2}}{3} |
26,339 | 9. (16 points) Let the sequence $\left\{a_{n}\right\}$ satisfy:
$$
a_{0}=2, a_{1}=3, a_{2}=6 \text {, }
$$
and for $n \geqslant 3$, we have
$$
a_{n}=(n+4) a_{n-1}-4 n a_{n-2}+(4 n-8) a_{n-3} \text {. }
$$
Find the general term of $\left\{a_{n}\right\}$. | a_{n}=n!+2^{n} |
26,377 | # 8. Variant 1.
Consider the quadratic trinomial $P(x)=a x^{2}+b x+c$, which has distinct positive roots. Vasya wrote four numbers on the board: the roots of $P(x)$, as well as the roots of the trinomial $Q(x)=c x^{2}+b x+a$ multiplied by 4. What is the smallest integer value that the sum of the written numbers can have | 9 |
26,379 | The 29th question: In a class, there are $\mathrm{n}$ students, and any two are either friends or not friends, with the friendship being mutual. In this class, any $\mathrm{n}-1$ students can be arranged in a circle such that any two adjacent students in the circle are friends, but all $\mathrm{n}$ students cannot be arranged in such a circle. Find the minimum value of $\mathrm{n}$.
---
The 29th question: In a class, there are $\mathrm{n}$ students, and any two are either friends or not friends, with the friendship being mutual. In this class, any $\mathrm{n}-1$ students can be arranged in a circle such that any two adjacent students in the circle are friends, but all $\mathrm{n}$ students cannot be arranged in such a circle. Find the minimum value of $\mathrm{n}$. | 10 |
26,391 | Let $k$ be a positive integer. Each cell of a $3 k \times 3 k$ grid is colored either red or blue. A triple of cells $\left(C_{1}, C_{2}, C_{3}\right)$ is called a good cell group if $C_{1}$ and $C_{2}$ are in the same row, $C_{2}$ and $C_{3}$ are in the same column, and $C_{1}, C_{3}$ are colored blue, while $C_{2}$ is colored red. Find the maximum possible number of good cell groups. | 12k^{4} |
26,414 | 12. In the Cartesian coordinate system $x O y$, it is known that points $A_{1}(-2,0), A_{2}(2,0)$, and a moving point $P(x, y)$ satisfies the product of the slopes of lines $A_{1} P$ and $A_{2} P$ is $-\frac{3}{4}$. Let the trajectory of point $P$ be curve $C$.
(1) Find the equation of $C$;
(2) Suppose point $M$ is on the line $x=4$, and two lines passing through $M$ intersect $C$ at points $A, B$ and $P, Q$ respectively, and $|M A| \cdot|M B| = |M P| \cdot|M Q|$. Find the sum of the slopes of lines $A B$ and $P Q$. | 0 |
26,419 | Problem 7. Let's introduce the notation as shown in the figure. By extending the lateral sides, denote their point of intersection as $E$. The point of intersection of the diagonals is called $F$. Right triangles $B F C$ and $D F A$ are similar, and if the legs of the first are denoted as $x$ and $y$, then the corresponding legs of the second are $4 x$ and $4 y$.
The height of the trapezoid $h$ is composed of the heights of triangles $B F C$ and $A F D$:
$$
h=\frac{B F \cdot F C}{1}+\frac{A F \cdot F D}{4}=x y+\frac{4 x \cdot 4 y}{4}=5 x y
$$
The area of the trapezoid is $\frac{15}{16}$ of the area of triangle $A E D$. We get:
$$
\frac{1}{2} A C \cdot B D=\frac{15}{16} \cdot \frac{1}{2} \cdot A E \cdot E D \cdot \sin 60^{\circ}=\frac{15 \sqrt{3}}{64} \cdot \frac{4}{3} A B \cdot \frac{4}{3} C D=\frac{15 \sqrt{3}}{36} A B \cdot C D
$$
from which[^0]
$$
\frac{25}{2} x y=\frac{15 \sqrt{3}}{36} \sqrt{x^{2}+16 y^{2}} \cdot \sqrt{y^{2}+16 x^{2}}
$$
Considering that $x^{2}+y^{2}=1$, we find: $\frac{30}{\sqrt{3}} x y=\sqrt{1+15 y^{2}} \cdot \sqrt{1+15 x^{2}}$.
Performing obvious transformations:
$$
300 x^{2} y^{2}=1+15\left(x^{2}+y^{2}\right)+225 x^{2} y^{2} ; \quad 75 x^{2} y^{2}=16 ; \quad 5 x y=\frac{4}{\sqrt{3}}
$$ | \frac{4}{\sqrt{3}} |
26,425 | 15. In
the circle, fill in the natural numbers from 1 to 16 (each number must be used exactly once), so that the sum of the numbers in the 4 circles connected by the same straight line is equal. This is called an 8-order magic star, and this equal number is called the magic sum of the 8-order magic star. Therefore, the magic sum of the 8-order magic star is , and continue to complete the following 8-order magic star:
保留源文本的换行和格式,直接输出翻译结果。
(Note: The last sentence is a note in Chinese and is not part of the translated text. It is provided here for context.) | 34 |
26,432 | Russian problems Problem 62 A tangent to the inscribed circle of a triangle drawn parallel to one of the sides meets the other two sides at X and Y. What is the maximum length XY, if the triangle has perimeter p? | \frac{p}{8} |
26,481 | 4. (1989 21st Canadian Mathematical Olympiad) Given the numbers $1,2,2^{2}, \cdots, 2^{n-1}$ for any permutation $\sigma=\left(x_{1}\right.$, $\left.x_{2}, \cdots, x_{n}\right)$, define $S_{1}(\sigma)=x_{1}, S_{2}(\sigma)=x_{1}+x_{2}, S_{3}(\sigma)=x_{1}+x_{2}+x_{3}, \cdots, S_{n}(\sigma)=x_{1}+x_{2}+\cdots+x_{n}$, and let $Q(\sigma)=S_{1}(\sigma) \cdot S_{2}(\sigma) \cdot \cdots \cdot S_{n}(\sigma)$, find $\sum \frac{1}{Q(\sigma)}$ (the sum is taken over all permutations). | 2^{-\frac{n(n-1)}{2}} |
26,487 | B2. In a circle with radius $r$, we inscribe a deltoid, one side of which is twice as long as the other. Calculate the ratio of the areas of the inscribed deltoid and the circle. | \frac{8}{5\pi} |
26,497 | 8,9
In a parallelogram, the ratio of the sides and the ratio of the diagonals are the same and equal to $\frac{1}{2}$. From the vertex of the obtuse angle A, a height $A E$ is dropped to the larger side $C D$. Find the ratio $\frac{D E}{C E}$. | \frac{3}{5} |
26,532 | IMO 1973 Problem A3 a and b are real numbers for which the equation x 4 + ax 3 + bx 2 + ax + 1 = 0 has at least one real solution. Find the least possible value of a 2 + b 2 . | \frac{4}{5} |
26,551 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{\arccos \sqrt{2 / 3}} \frac{\tan x + 2}{\sin^2 x + 2 \cos^2 x - 3} \, dx
$$ | -\frac{\ln2+\sqrt{2}\pi}{4} |
26,562 | 3. Triangle $A B C$ with angle $\angle A B C=135^{\circ}$ is inscribed in circle $\omega$. The lines tangent to $\omega$ at points $A$ and $C$ intersect at point $D$. Find $\angle A B D$, given that $A B$ bisects segment $C D$. Answer: $90^{\circ}$
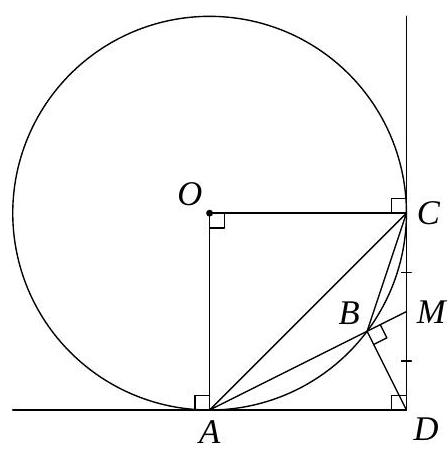 | 90 |
26,591 | 6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=75 \\
y^{2}+y z+z^{2}=49 \\
z^{2}+x z+x^{2}=124
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 70 |
26,594 | 3. [8] A semicircle with radius 2021 has diameter $A B$ and center $O$. Points $C$ and $D$ lie on the semicircle such that $\angle A O C<\angle A O D=90^{\circ}$. A circle of radius $r$ is inscribed in the sector bounded by $O A$ and $O C$ and is tangent to the semicircle at $E$. If $C D=C E$, compute $\lfloor r\rfloor$. | 673 |
26,598 | Example 22 (2003 China Western Mathematical Olympiad) Let $2n$ real numbers $a_{1}, a_{2}, \cdots, a_{2n}$ satisfy the condition
$$
\begin{array}{l}
\sum_{i=1}^{2n-1}\left(a_{i+1}-a_{i}\right)^{2}=1 . \\
\text { Find the maximum value of }\left(a_{n+1}+a_{n+2}+\cdots+a_{2n}\right)-\left(a_{1}+a_{2}+\cdots+a_{n}\right) \text { . }
\end{array}
$$ | \sqrt{\frac{n(2n^{2}+1)}{3}} |
26,613 | 1. In some cells of a $1 \times 2021$ strip, one chip is placed in each. For each empty cell, the number equal to the absolute difference between the number of chips to the left and to the right of this cell is written. It is known that all the written numbers are distinct and non-zero. What is the minimum number of chips that can be placed in the cells? | 1347 |
26,628 | Class $\mathbf{M}$.
In the class, there are 15 boys and 15 girls. On March 8, some boys called some girls to congratulate them on the holiday (no boy called the same girl twice). It turned out that the children could be uniquely divided into 15 pairs so that in each pair there was a boy who called the girl. What is the maximum number of calls that could have been made? | 120 |
26,646 | Example 13 (10th "Hope Cup" Invitational Competition Question) In the regular quadrilateral pyramid $O-A B C D$, $\angle A O B=30^{\circ}$, the dihedral angle formed by faces $O A B$ and $O B C$ is $\theta$, and $\cos \theta=a \sqrt{b}-c$, where $a, b, c \in \mathbf{N}$, and $b$ is not divisible by the square of any prime number, then $a+b+c=$ $\qquad$ | 14 |
26,660 | Example 9 (64th Putnam Mathematical Competition Problem) Find the minimum value of the following algebraic expression: $|\sin x+\cos x+\tan x+\cot x+\sec x+\csc x|$, where $x$ is a real number. | 2\sqrt{2}-1 |
26,686 | 3.52. A triangular pyramid is inscribed in a cone, with its lateral edges being pairwise perpendicular to each other. Find the angle between the slant height of the cone and its height. | \arcsin\frac{\sqrt{6}}{3} |
26,699 | 36th Putnam 1975 Problem B3 Let n be a fixed positive integer. Let S be any finite collection of at least n positive reals (not necessarily all distinct). Let f(S) = (∑ a∈S a) n , and let g(S) = the sum of all n-fold products of the elements of S (in other words, the nth symmetric function). Find sup S g(S)/f(S). Solution | \frac{1}{n!} |
26,706 | 7. Find all values of $a$ for each of which exactly one of the following two statements is true:
1) «The equation $\cos (\cos x)+\sin (\sin x)=a$ has exactly two roots on the interval $[0 ; \pi]$ »
2) «The equation $\sin ^{4} x+\cos ^{4} x+\sin 2 x=a$ has roots».
Answer: $\left[-\frac{1}{2} ; \cos 1\right) \cup\left(\frac{3}{2} ; 1+\sin 1\right)$. | [-\frac{1}{2};\cos1)\cup(\frac{3}{2};1+\sin1) |
26,712 | 21. (2004 China Western Mathematical Olympiad) Let $u$, $v$, $w$ be positive real numbers, satisfying the condition $u \sqrt{v w}+v \sqrt{w u}+w \sqrt{u v} \geqslant$ 1. Find the minimum value of $u+v+w$. | \sqrt{3} |
26,733 | 3. Equilateral $\triangle A B C$ and square $A B D E$ share a common side $A B$, the cosine of the dihedral angle $C-A B-D$ is $\frac{\sqrt{3}}{3}, M, N$ are the midpoints of $A C, B C$ respectively, then the cosine of the angle formed by $E M, A N$ is $\qquad$ . | \frac{1}{6} |
26,754 | ## Task A-1.6.
In triangle $A B C$, the measure of angle $\varangle A B C$ is $120^{\circ}$, and $|A B|=6$ and $|B C|=9$. Let points $P$ and $Q$ be on side $\overline{A C}$ such that triangle $B P Q$ is equilateral. Determine $|P Q|$. | \frac{18\sqrt{19}}{19} |
26,757 | 3. In a circle with radius $R$, determine the central angle corresponding to a circular segment with the following property: the chord of the segment is equal to the perimeter of the circle with the largest radius that is inscribed in it. | \alpha=2\arcsin\frac{4\pi}{4+\pi^{2}} |
26,770 | 5. An infinite sequence of real numbers $a_{1}, a_{2}, \ldots$ satisfies the recurrence
$$
a_{n+3}=a_{n+2}-2 a_{n+1}+a_{n}
$$
for every positive integer $n$. Given that $a_{1}=a_{3}=1$ and $a_{98}=a_{99}$, compute $a_{1}+a_{2}+\cdots+a_{100}$. | 3 |
26,780 | 10. For the ellipse $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$, the left and right foci are $F_{1}$ and $F_{2}$, respectively, and the right vertex is $A$. $P$ is any point on the ellipse $C$. It is known that the maximum value of $\overrightarrow{P F_{1}} \cdot \overrightarrow{P F_{2}}$ is 3, and the minimum value is 2.
(1) Find the equation of the ellipse $C$;
(2) If the line $l: y=k x+m$ intersects the ellipse $C$ at points $M$ and $N$ (where $M$ and $N$ are not the left or right vertices), and the circle with diameter $MN$ passes through point $A$. Prove that the line $l$ passes through a fixed point, and find the coordinates of this fixed point. | (\frac{2}{7},0) |
26,793 | Quadrilateral $ABCD$ is inscribed in a circle. It is known that $AC \perp BD$. Find the length of $BC$, if the distance from the center of the circle to side $AD$ is 2. | 4 |
26,794 | 6. Let $M$ be the midpoint of the height $D D_{1}$ of the regular tetrahedron $A B C D$. Then the dihedral angle $A-M B-C$ in radians is $\qquad$ | \frac{\pi}{2} |
26,800 | 3. Find the minimum value of the function $f(a, b)=(a-b)^{2}+\left(\sqrt{2-a^{2}}-\frac{9}{b}\right)^{2}$. | 8 |
26,806 | Example 5 Given that $\frac{z-1}{z+1}$ is a pure imaginary number, find $\min \left|z^{2}-z+2\right|$. | \frac{\sqrt{14}}{4} |
26,808 | 6 Given complex numbers $z_{1}$ and $z_{2}$ satisfy $\left|z_{2}\right|=4,4 z_{1}^{2}-2 z_{1} z_{2}+z_{2}^{2}=0$, then the maximum value of $\left|\left(z_{1}+1\right)^{2}\left(z_{1}-2\right)\right|$ is $\qquad$ . | 6\sqrt{6} |
26,814 | Putnam 1996 Problem A1 What is the smallest α such that two squares with total area 1 can always be placed inside a rectangle area α with sides parallel to those of the rectangle and with no overlap (of their interiors)? Solution | \frac{1}{2}(1+\sqrt{2}) |
26,834 | 19th CanMO 1987 Problem 2 Find all the ways in which the number 1987 can be written in another base as a three digit number with the digits having the same sum 25. | 19 |
26,838 | 7. Find the real solutions of the equation $\frac{2 x+2}{x^{2}+2 x+2}+x^{4}-8 x^{2}+17=0$.
(58th Moldova Mathematical Olympiad) | -2 |
26,843 | 2. The product of four different numbers, which are roots of the equations
$$
x^{2}+6 b x+c=0 \text{ and } x^{2}+6 c x+b=0
$$
is equal to 1. At least one of the numbers $\mathrm{b}$ and c is an integer. Find $\mathrm{b}+\mathrm{c}$ given that b and c are positive. | 2.5 |
26,846 | 6. Let $x_{1}$ and $x_{2}$ be the largest roots of the polynomials $f(x)=1-x-4 x^{2}+x^{4}$ and $g(x)=16-8 x-16 x^{2}+x^{4}$ respectively. Find $\frac{x_{1}}{x_{2}}$. Justify your solution.
# | 0.5 |
26,864 | 8.5. Girls stood in a circle, some of them wearing scarves. A circle is called correct if each girl without a scarf has a neighbor wearing a scarf. a) What is the minimum number of scarves in a correct circle of 25 girls? b) Prove that if in this correct circle of 25 girls there are more than 12 scarves, then some girls can take off their scarves, and the circle will still be correct. | 9 |
26,865 | 6. Given that the circumcenter of $\triangle A B C$ is $O$, and $3 \overrightarrow{O A}+4 \overrightarrow{O B}+5 \overrightarrow{O C}=\mathbf{0}$, then the value of $\cos \angle A B C$ is | \frac{\sqrt{5}}{5} |
26,895 | 19.7.17 ** Find the smallest integer greater than 2 that can be expressed both as the sum of the squares of two positive integers and as the sum of the cubes of two positive integers. Also prove that there are infinitely many positive integers that can be expressed both as the sum of the squares of two coprime positive integers and as the sum of the cubes of two coprime positive integers. | 65 |
26,899 | ## Subject I. (30 points)
Let the function $f: R \rightarrow(0, \infty), f(x)=\frac{21^{x}+1}{3^{x}+7^{x}}$.
a) Study the injectivity of the function;
b) Is the function f surjective?
c) What is the number of solutions to the equation $f(x)+f(-x)=1$?
Prof. Eugen Jecan, National College "Andrei Mureşanu" Dej | 0 |
26,907 | 2. In the tetrahedron $P-ABC$, $PA \perp$ plane $ABC$, $AC \perp BC$. If $AC=2$, the dihedral angle $P-BC-A$ is $60^{\circ}$, and the volume of the tetrahedron $P-ABC$ is $\frac{4 \sqrt{6}}{3}$, then the sine value of the angle formed by line $PB$ and plane $PAC$ is | \frac{\sqrt{3}}{3} |
26,924 | 1. Sei $A B C$ ein spitzwinkliges Dreieck mit $A B \neq B C$ und Umkreis $k$. Seien $P$ und $Q$ die Schnittpunkte von $k$ mit der Winkelhalbierenden beziehungsweise der Aussenwinkelhalbierenden von $\angle C B A$. Sei $D$ der Schnittpunkt von $A C$ und $P Q$. Bestimme das Verhältnis $A D: D C$.
## 1st solution: | 1 |
26,937 | II. (50 points)
Real numbers $a, b, c$ and a positive number $\lambda$ make $f(x)=x^{3}+a x^{2}+b x+c$ have 3 real roots $x_{1}, x_{2}$, $x_{3}$, and satisfy
(1) $x_{2}-x_{1}=\lambda$;
(2) $x_{3}>\frac{1}{2}\left(x_{1}+x_{2}\right)$.
Find the maximum value of $\frac{2 a^{3}+27 c-9 a b}{\lambda^{3}}$. | \frac{3\sqrt{3}}{2} |
26,958 | 6、$F_{1}, F_{2}$ are the two foci of the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$, and $P$ is a point on the ellipse. If the area of $\Delta P F_{1} F_{2}$ is $1$, $\tan \angle P F_{1} F_{2}=\frac{1}{2}$, and $\tan \angle P F_{2} F_{1}=-2$. Then $a=\frac{\sqrt{15}}{2}$. | \frac{\sqrt{15}}{2} |
26,959 | 2. A line $l$ is drawn through the right focus of the hyperbola $x^{2}-\frac{y^{2}}{2}=1$ intersecting the hyperbola at points $A$ and $B$. If a real number $\lambda$ makes $|A B|=\lambda$ such that there are exactly 3 lines $l$, then $\lambda=$ $\qquad$ . | 4 |
26,967 | 10. (40 points) Let $P(n)$ denote the product of the digits of a natural number $n$. For what largest natural number $k$ does there exist a natural number $n>10$ such that
$$
P(n)<P(2 n)<\ldots<P(k n) ?
$$ | 9 |
26,974 | On the plane, there is an angle of $60^{\circ}$. A circle touches one side of this angle, intersects the other side at points $A$ and $B$, and intersects the angle bisector at points $C$ and $D$. $A B = C D = \sqrt{6}$. Find the area of the circle bounded by this circle. | \pi\sqrt{3} |
26,980 | 1. $a, b$ are constants. If the parabola $C: y=\left(t^{2}+t+1\right) x^{2}-2(a+t)^{2} x+t^{2}+3 a t+b$ passes through the fixed point $P(1,0)$ for any real number $t$, when $t=$ $\qquad$, the chord intercepted by the parabola $C$ on the $x$-axis is the longest. | -1 |
26,988 | 7.57 Let $M$ be a finite set of points in the plane. For any two points $A$ and $B$ in $M$, there exists a third point $C$ such that $\triangle A B C$ is an equilateral triangle. Find the maximum number of elements in $M$. | 3 |
26,989 | 30. In square $ABCD$ with side length $4$, $M$ and $N$ are moving points on $AB$ and $CD$ respectively. If trapezoid $BCNM$ is folded along $MN$, point $B$ lands exactly on side $AD$. Then the minimum value of the area of trapezoid $BCNM$ is $\qquad$ | 6 |
26,993 | 3. $A B C D$ — a convex quadrilateral, where $A B=7, B C=4, A D=D C, \angle A B D=\angle D B C$. Point E is on segment $A B$ such that $\angle D E B=90^{\circ}$. Find the length of segment $A E$. (Spain, local phase, 2020-2021) | 1.5 |
27,042 | Example 10 Suppose the function for all $x>0$ has $f(x)>-\frac{1}{x}$ and is defined for all $x>0$, and satisfies:
(1) The function $f(x)$ is strictly increasing on $(0,+\infty)$;
(2) For all $x>0$, $f(x)>-\frac{1}{x}$;
(3) For all $x>0$, $f(x) f\left[f(x)+\frac{1}{x}\right]=1$. Find the function value $f(1)$. | \frac{1-\sqrt{5}}{2} |
27,063 | 12. Six positive integers $a, b, c, d, e, f$ are arranged in alphabetical order to form a sequence, where $a=1$. If a certain positive integer is greater than 1, then the number that is one less than this positive integer must appear to its left. For example, if $d>1$, then one of $a, b, c$ must be $d-1$. Examples: $1,1,2,1,3,2$ satisfies the condition; $1,2,3,1,4,1$ satisfies the condition; $1,2,2,4,3,2$ does not satisfy the condition. The number of different permutations that satisfy the condition is $\qquad$. | 203 |
27,068 | 9. (16 points) Given the bivariate function
$$
f(a, b)=\max _{x \in[-1,1]}\left\{\left|x^{2}-a x-b\right|\right\} \text {. }
$$
Find the minimum value of $f(a, b)$. | \frac{1}{2} |
27,084 | 153. The product of three prime numbers. A certain number is the product of three prime factors, the sum of the squares of which is 2331. There are 7560 numbers (including 1) less than this number and coprime with it. The sum of all divisors of this number (including 1 and the number itself) is 10560. Find this number. | 8987 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.