id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
29,170 | Problem 3.6. In a meeting between four UN countries, let's say $A, B, C$, and $D$, country $A$ has twice as many representatives as $B$, three times as many as $C$, and four times as many as $D$. It is intended to distribute the representatives at tables with the same number of people at each one. There is only one condition: in each table, any of the countries must be in a numerical minority compared to the other three combined. How many representatives should there be at each table, at a minimum? | 25 |
29,186 | ## Task 6 - 311236
Consider all pyramids $A B C S$ that satisfy the following conditions (1), (2), (3):
(1) The base $A B C$ of the pyramid has an area of 1.
(2) It holds that $A B=A C=S B=S C$.
(3) It holds that $B C=S A$.
Investigate whether among all pyramids that satisfy these conditions, there is one with the largest volume. If this is the case, determine the size of the angle $\angle B A C$ for such a pyramid. | 60 |
29,190 | 5. It is known that the polynomial $f(x)=8+32 x-12 x^{2}-4 x^{3}+x^{4}$ has 4 distinct real roots $\left\{x_{1}, x_{2}, x_{3}, x_{4}\right\}$. The polynomial of the form $g(x)=b_{0}+b_{1} x+b_{2} x^{2}+b_{3} x^{3}+x^{4}$ has roots $\left\{x_{1}^{2}, x_{2}^{2}, x_{3}^{2}, x_{4}^{2}\right\}$. Find the coefficient $b_{1}$ of the polynomial $g(x)$. | -1216 |
29,193 | Question 1 Find the smallest positive integer $n$ such that: for any $n$ points $A_{1}, A_{2}, \cdots, A_{n}$ taken on the circumference of $\odot O$, among the $\mathrm{C}_{n}^{2}$ angles $\angle A_{i} O A_{j}(1 \leqslant i<j \leqslant n)$, at least 2007 are not greater than $120^{\circ}$. | 91 |
29,194 | Example 3 Let $n$ be a positive integer,
$$
\begin{aligned}
S= & \{(x, y, z) \mid x, y, z \in\{0,1, \cdots, n\}, \\
& x+y+z>0\}
\end{aligned}
$$
is a set of $(n+1)^{3}-1$ points in three-dimensional space. Try to find the minimum number of planes whose union contains $S$ but does not contain $(0,0,0)$. | 3n |
29,210 | 8. In the Cartesian coordinate system $x O y$, there are 2018 circles: $\odot A_{1}, \odot A_{2}, \cdots, \odot A_{2018}$, where the center of $\odot A_{k}$ is $A_{k}\left(a_{k}, \frac{1}{4} a_{k}^{2}\right)$, and the radius is $\frac{1}{4} a_{k}^{2}(k=1, \cdots, 2018)$, here $a_{1}>\cdots>a_{2018}=\frac{1}{2018}$, and $\odot A_{k+1}$ is externally tangent to $\odot A_{k}$ $(k=1,2, \cdots, 2017)$, then $a_{1}=$ $\qquad$ | \frac{2}{2019} |
29,215 | 12.231. A rectangular parallelepiped is inscribed in a cylinder, with its diagonal forming angles $\alpha$ and $\beta$ with the adjacent sides of the base. Find the ratio of the volume of the parallelepiped to the volume of the cylinder. | \frac{4\cos\alpha\cos\beta}{\pi(\cos^{2}\alpha+\cos^{2}\beta)} |
29,227 | 4. Let $n \in \mathbf{Z}_{+}$. A volleyball team has $n$ male players and $n$ female players. Initially, each player is assigned to one of the positions numbered $1,2, \cdots, 2 n$, with only positions 1 and $n+1$ being outside the court. During the game, position swaps occur, and each swap involves moving the player in position $i(i=1,2, \cdots, 2 n)$ to position $i+1$, where position $2 n+1$ is the same as position 1. How many different initial allocation methods are there such that, regardless of how many rounds of swapping occur, at least $n-1$ female players are on the court? | 2^{n}(n!)^{2} |
29,231 | 9.1. Two spheres touch the plane of triangle $A B C$ at points $A$ and $B$ and are located on opposite sides of this plane. The sum of the radii of these spheres is 7, and the distance between their centers is 13. The center of a third sphere with radius 5 is at point $C$, and it touches each of the first two spheres externally. Find the radius of the circle circumscribed around triangle $A B C$. | \sqrt{30} |
29,275 | $$
\begin{array}{l}
a+b+c=5, a^{2}+b^{2}+c^{2}=15, \\
a^{3}+b^{3}+c^{3}=47 .
\end{array}
$$
$$
\text { Find }\left(a^{2}+a b+b^{2}\right)\left(b^{2}+b c+c^{2}\right)\left(c^{2}+c a+a^{2}\right)
$$
the value. | 625 |
29,278 | 6. Given the sequence $\left\{a_{n}\right\}$ satisfies
$$
a_{n+1}+(-1)^{n} a_{n}=2 n-1 \text {, }
$$
and the sum of the first 2019 terms of the sequence $\left\{a_{n}-n\right\}$ is 2019. Then the value of $a_{2020}$ is $\qquad$ .
6.1.
$$
\begin{array}{l}
\text { From } a_{n+1}+(-1)^{n} a_{n}=2 n-1 \\
\Rightarrow\left\{\begin{array}{l}
a_{2 n+1}+a_{2 n}=4 n-1, \\
a_{2 n}-a_{2 n-1}=4 n-3, \\
a_{2 n+2}-a_{2 n+1}=4 n+1
\end{array}\right. \\
\Rightarrow\left\{\begin{array}{l}
a_{2 n+1}+a_{2 n-1}=2, \\
a_{2 n+2}+a_{2 n}=8 n
\end{array}\right. \\
\Rightarrow a_{2 n-1}+a_{2 n}+a_{2 n+1}+a_{2 n+2}=8 n+2 \\
\Rightarrow\left(a_{2 n-1}-(2 n-1)\right)+\left(a_{2 n}-2 n\right)+a_{2 n+1}- \\
(2 n+1)+\left(a_{2 n+2}-(2 n+2)\right)=0 .
\end{array}
$$ | 1 |
29,286 | 12. The product of all elements of a finite set $S$ is called the "product number" of the number set $S$. Now, given the number set $M=$ $\left\{\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \cdots, \frac{1}{100}\right\}$, determine the sum of the "product numbers" of all even-numbered (2, 4, $\cdots$, 98) element subsets of $M$. | 24.255 |
29,294 | Around a circle with radius 3, an isosceles trapezoid $A B C D$ ($B C \| A D$) is described, the area of which is 48. The circle touches the sides $A B$ and $C D$ at points $K$ and $L$. Find $K L$.
# | 4.5 |
29,295 | 5. The bisectors $\mathrm{AD}$ and $\mathrm{BE}$ of triangle $\mathrm{ABC}$ intersect at point I. It turns out that the area of triangle ABI is equal to the area of quadrilateral CDIE. Find $AB$, if $CA=9, CB=4$. | 6 |
29,298 | In the drawing below, $ABC$ is a triangle with side lengths $AB=4 \, \text{cm}, AC=$ $6 \, \text{cm}$. Additionally, $\angle DAH=\angle HAB, \angle AHB=90^{\circ}$, and $M$ is the midpoint of $BC$. Find the length of the segment $MH$.
 | 1\, |
29,319 | 3.65. The height of a triangle divides the angle of the triangle in the ratio $2: 1$, and the base - into segments, the ratio of which (larger to smaller) is $k$. Find the sine of the smaller angle at the base and the permissible values of $k$. | \frac{1}{k-1} |
29,323 | 4. Let the ellipse $\Gamma: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ have an eccentricity of $\frac{\sqrt{3}}{2}$. A line with slope $k(k>0)$ is drawn through the left focus $F$, intersecting the ellipse $\Gamma$ at points $A$ and $B$. If $\overrightarrow{A F}=3 \overrightarrow{F B}$, then $k=$ $\qquad$ | \sqrt{2} |
29,353 | 3.87. The height of a regular truncated triangular pyramid is $H$ and is the mean proportional between the sides of the bases. The lateral edge makes an angle $\alpha$ with the base. Find the volume of the pyramid. | \frac{H^{3}\sqrt{3}}{4\sin^{2}\alpha} |
29,354 | 10,11
In a rectangular parallelepiped $A B C D A 1 B 1 C 1 D 1$ ( $A A 1|| B B 1 \| C C 1|| D D 1$ ), it is known that $A B=B C=2 a$, $A A 1=a$. A plane section passes through points $B 1$ and $D$ parallel to the line $A C$. Find the radius of the sphere that touches this section and the three faces of the parallelepiped with a common vertex $B$. | \frac{4-2\sqrt{2}}{3} |
29,360 | 8.5. In the parliament of the island state of Promenade-and-Tornado, only the indigenous inhabitants of the island can be elected, who are divided into knights and liars: knights always tell the truth, liars always lie. A secret ballot on 8.09.19 re-elected 2019 deputies. At the first meeting, all deputies were present: 2016 of them sat in the deputies' chairs, arranged in the hall in a rectangle $42 \times 48$, three - in the chairs of the chairman and his deputies in the presidium. During the meeting, each one stated that among his neighbors in the chair were only liars (neighbors - those who sit to the left, right, in front, behind, and diagonally: there can be from 3 to 8 in the hall and 1 or 2 in the presidium). Determine the minimum number of knights in the parliament. | 225 |
29,367 | 13. Let $x, y$ be non-zero real numbers, and satisfy $\frac{x \sin \frac{\pi}{5} + y \cos \frac{\pi}{5}}{x \cos \frac{\pi}{5} - y \sin \frac{\pi}{5}} = \tan \frac{9 \pi}{20}$.
(1) Find the value of $\frac{y}{x}$;
(2) In $\triangle ABC$, if $\tan C = \frac{y}{x}$, find the maximum value of $\sin 2A + 2 \cos B$. | \frac{3}{2} |
29,386 | Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x, y$
$$
f(f(x)+y)=2 x+f(-f(f(x))+f(y))
$$ | f(x)=x |
29,391 | 12.256. The base of the pyramid is a rectangle, where the angle between the diagonals is $\alpha$. One of the lateral edges is perpendicular to the base plane, and the largest edge forms an angle $\beta$ with the base plane. The radius of the sphere circumscribed around the pyramid is $R$. Find the volume of the pyramid. | \frac{2}{3}R^3\sin2\beta\cos\beta\sin\alpha |
29,403 | 3. Given that $A, B, C, D$ are points on a circle with radius 1, $\overrightarrow{A B}+2 \overrightarrow{A C}=\overrightarrow{A D}$, and $|A C|=1$. Then the area of quadrilateral $A B D C$ is $\qquad$. | \frac{3\sqrt{3}}{4} |
29,414 | 3. Given the seven-variable polynomial
$$
\begin{array}{l}
Q\left(x_{1}, x_{2}, \cdots, x_{7}\right) \\
=\left(x_{1}+x_{2}+\cdots+x_{7}\right)^{2}+2\left(x_{1}^{2}+x_{2}^{2}+\cdots+x_{7}^{2}\right)
\end{array}
$$
it can be expressed as the sum of seven squares of polynomials with non-negative integer coefficients, i.e.,
$$
\begin{array}{l}
Q\left(x_{1}, x_{2}, \cdots, x_{7}\right) \\
= P_{1}^{2}\left(x_{1}, x_{2}, \cdots, x_{7}\right)+ \\
P_{2}^{2}\left(x_{1}, x_{2}, \cdots, x_{7}\right)+\cdots+ \\
P_{7}^{2}\left(x_{1}, x_{2}, \cdots, x_{7}\right),
\end{array}
$$
where $P_{k}\left(x_{1}, x_{2}, \cdots, x_{7}\right)$ are polynomials with non-negative integer coefficients. Find all possible values of $P_{1}(1,1, \cdots, 1)$. | 3 |
29,428 | A week-old set's three-element subsets need to be colored such that if the intersection of two subsets is empty, then their colors differ. How many colors do we need at least? | 3 |
29,471 | $4 \cdot 212$ The river water is flowing, and at point $Q$ it flows into a still lake. A swimmer travels downstream from $P$ to $Q$, and then across the lake to $R$, taking a total of 3 hours. If he travels from $R$ to $Q$ and then to $P$, it takes a total of 6 hours. If the lake water also flows, with a speed equal to that of the river, then traveling from $P$ to $Q$ and then to $R$ would take $\frac{5}{2}$ hours. Under these conditions, how long would it take to travel from $R$ to $Q$ and then to $P$? | \frac{15}{2} |
29,476 | ## Task 3 - 060623
Given is an angle with the degree measure $\alpha=36^{\circ}$ (see figure).
Construct, using only a compass and straightedge, an angle whose degree measure is $99^{\circ}$!
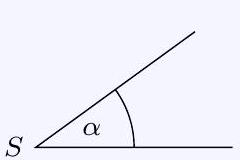 | 99 |
29,478 | 12. [7] $\triangle P N R$ has side lengths $P N=20, N R=18$, and $P R=19$. Consider a point $A$ on $P N . \triangle N R A$ is rotated about $R$ to $\triangle N^{\prime} R A^{\prime}$ so that $R, N^{\prime}$, and $P$ lie on the same line and $A A^{\prime}$ is perpendicular to $P R$. Find $\frac{P A}{A N}$. | \frac{19}{18} |
29,480 | 9.6. Two spheres touch the plane of triangle $A B C$ at points $B$ and $C$ and are located on opposite sides of this plane. The sum of the radii of these spheres is 12, and the distance between their centers is $4 \sqrt{29}$. The center of a third sphere with radius 8 is located at point $A$, and it touches each of the first two spheres externally. Find the radius of the circle circumscribed around triangle $A B C$. | 4\sqrt{5} |
29,491 | 3. For the ellipse $\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$, the right focus is $F$, and the right directrix is $l$. Points $P_{1}, P_{2}, \cdots, P_{24}$ are 24 points arranged in a counterclockwise order on the ellipse, where $P_{1}$ is the right vertex of the ellipse, and $\angle P_{1} F P_{2}=\angle P_{2} F P_{3}=\cdots=$ $\angle P_{23} F P_{24}=\angle P_{24} F P_{1}$. The sum of the reciprocals of the distances from these 24 points to $l$ is $\qquad$ | 6\sqrt{5} |
29,504 | Given a parallelepiped $A B C D A 1 B 1 C 1 D 1$. Points $M, L$, and $K$ are taken on the edges $A D, A 1 D 1$, and $B 1 C 1$ respectively, such that $B 1 K=\frac{1}{3} A 1 L, A M=\frac{1}{2} A 1 L$. It is known that $K L=2$. Find the length of the segment by which the plane $K L M$ intersects the parallelogram $A B C D$. | \frac{3}{2} |
29,511 | 6. In tetrahedron $ABCD$, $\triangle ABD$ is an equilateral triangle, $\angle BCD=90^{\circ}, BC=CD=1, AC=\sqrt{3}, E$ and $F$ are the midpoints of $BD$ and $AC$ respectively. Then the cosine of the angle formed by line $AE$ and $BF$ is $\qquad$ | \frac{\sqrt{2}}{3} |
29,518 | In quadrilateral $A B C D$, side $A B$ is equal to side $B C$, diagonal $A C$ is equal to side $C D$, and $\angle A C B = \angle A C D$. The radii of the circles inscribed in triangles $A C B$ and $A C D$ are in the ratio $3: 4$. Find the ratio of the areas of these triangles. | \frac{9}{14} |
29,526 | We say that two natural numbers form a perfect pair when the sum and the product of these two numbers are perfect squares. For example, 5 and 20 form a perfect pair, since $5+20=25=5^{2}$ and $5 \times 20=100=10^{2}$. Does 122 form a perfect pair with any other natural number? | 122\times121 |
29,531 | 37. Solve the equation $x^{4}-2 y^{4}-4 z^{4}-8 t^{4}=$ $=0$ in integers. | 0 |
29,545 | 13. Given three different prime numbers $p$, $q$, and $r$ that satisfy $p q r = 18 \underbrace{99 \ldots 9}_{n \uparrow 9} 62$, define $f(n)$ as the sum of the digits of the natural number $n$. Then $f(p) + f(q) + f(r) - f(p q r) =$ $\qquad$ | 8 |
29,546 | 9. (NET 2) ${ }^{\text {IMO4 }}$ Find all solutions in positive real numbers $x_{i}(i=$ $1,2,3,4,5)$ of the following system of inequalities:
$$
\begin{array}{l}
\left(x_{1}^{2}-x_{3} x_{5}\right)\left(x_{2}^{2}-x_{3} x_{5}\right) \leq 0, \\
\left(x_{2}^{2}-x_{4} x_{1}\right)\left(x_{3}^{2}-x_{4} x_{1}\right) \leq 0, \\
\left(x_{3}^{2}-x_{5} x_{2}\right)\left(x_{4}^{2}-x_{5} x_{2}\right) \leq 0 \\
\left(x_{4}^{2}-x_{1} x_{3}\right)\left(x_{5}^{2}-x_{1} x_{3}\right) \leq 0 \\
\left(x_{5}^{2}-x_{2} x_{4}\right)\left(x_{1}^{2}-x_{2} x_{4}\right) \leq 0 .
\end{array}
$$ | x_{1}=x_{2}=x_{3}=x_{4}=x_{5} |
29,578 | A regular octagon has sides alternating between 1 and $\sqrt{2}$. What is the area of the octagon? | 7 |
29,582 | 7. Let positive real numbers $x, y$ satisfy $x^{2}+y^{2}+\frac{1}{x}+\frac{1}{y}=\frac{27}{4}$. Then the minimum value of $P=\frac{15}{x}-\frac{3}{4 y}$ is | 6 |
29,600 | 33. Let $f: \mathbb{N} \rightarrow \mathbb{Q}$ be a function, where $\mathbb{N}$ denotes the set of natural numbers, and $\mathbb{Q}$ denotes the set of rational numbers. Suppose that $f(1)=\frac{3}{2}$, and
$$
f(x+y)=\left(1+\frac{y}{x+1}\right) f(x)+\left(1+\frac{x}{y+1}\right) f(y)+x^{2} y+x y+x y^{2}
$$
for all natural numbers $x, y$. Find the value of $f(20)$. | 4305 |
29,612 | 2. $48 n$ is the smallest positive integer that satisfies the following conditions:
(1) $n$ is a multiple of 75;
(2) $n$ has exactly 75 positive divisors (including 1 and itself). Find $\frac{n}{75}$. | 432 |
29,613 | Example 6 Let $n(n \geqslant 2)$ be a given positive integer. Find the smallest real number $\lambda(n)$, such that for any real numbers $x_{1}, x_{2}, \cdots, x_{n}$ satisfying $x_{1}+2 x_{2}+\cdots+n x_{n}=0$, we have
$$
\left(\sum_{i=1}^{n} x_{i}\right)^{2} \leqslant \lambda(n)\left(\sum_{i=1}^{n} x_{i}^{2}\right) .
$$ | \frac{n^{2}-n}{4n+2} |
29,615 | 1. For natural numbers $k, l, m$ it holds that
$$
\frac{k+m+k l m}{l m+1}=\frac{2051}{404}
$$
Determine all possible values of the product klm. | 2015 |
29,616 | . How many pairs $(m, n)$ of positive integers with $m<n$ fulfill the equation
$$
\frac{3}{2008}=\frac{1}{m}+\frac{1}{n} ?
$$
## Answer: 5. | 5 |
29,635 | 18th USAMO 1989 Problem 1 Let a n = 1 + 1/2 + 1/3 + ... + 1/n, b n = a 1 + a 2 + ... + a n , c n = b 1 /2 + b 2 /2 + ... + b n /(n+1). Find b 1988 and c 1988 in terms of a 1989 . | 1990a_{1989}-3978 |
29,649 | 10. Let $2 n$ real numbers $a_{1}, a_{2}, \cdots, a_{2 n}$ satisfy the condition $\sum_{i=1}^{2 n-1}\left(a_{i+1}-a_{i}\right)^{2}=1$, find the maximum value of $\left(a_{n+1}+a_{n+2}+\cdots+a_{2 n}\right)$ $-\left(a_{1}+a_{2}+\cdots+a_{n}\right)$. | \sqrt{\frac{n(2n^2+1)}{3}} |
29,650 | 14. Let $l, m$ be two skew lines, on $l$ there are three points $A, B, C$, and $A B=B C$. Draw perpendiculars from $A, B, C$ to $m$, denoted as $A D, B E, C F$, with feet of the perpendiculars being $D, E, F$ respectively. Given $A D=\sqrt{15}, B E=\frac{7}{2}$, $C F=\sqrt{10}$, find the distance between $l$ and $m$. | \sqrt{6} |
29,657 | 343. Let's write down the consecutive powers of the number 2:
$2,4,8,16,32,64,128,256,512,1024,2048,4096, \ldots$
It is easy to notice that the last digit in this sequence of numbers repeats periodically with a period of 4:
$$
2,4,8,6,2,4,8,6,2,4,8,6, \ldots
$$
Prove that the last 10 digits in this sequence of numbers, starting from some number, will also repeat periodically. Find the length of the period and the number in the sequence, starting from which the periodicity is observed. | 7812500 |
29,658 | 4. Given a right triangle $ABC$ with a right angle at $A$. On the leg $AC$, a point $D$ is marked such that $AD: DC = 1: 3$. Circles $\Gamma_{1}$ and $\Gamma_{2}$ are then constructed with centers at $A$ and $C$ respectively, passing through point $D$. $\Gamma_{2}$ intersects the hypotenuse at point $E$. Circle $\Gamma_{3}$ with center $B$ and radius $BE$ intersects $\Gamma_{1}$ inside the triangle at a point $F$ such that angle $AFB$ is a right angle. Find $BC$ if $AB = 5$.
(P. D. Mulyenko) | 13 |
29,671 | Example 12 (1998 Canadian Mathematical Olympiad) Find all real numbers $x$ such that
$$
x=\sqrt{x-\frac{1}{x}}+\sqrt{1-\frac{1}{x}}.
$$ | \frac{1+\sqrt{5}}{2} |
29,676 | ## Task B-1.7.
Quadrilateral $A B C D$ has exactly two right angles, at vertex $A$ and at vertex $C$. On the diagonal $\overline{A C}$, points $E$ and $F$ are the feet of the perpendiculars drawn from vertices $B$ and $D$ to $\overline{A C}$, respectively. If $|A E|=3,|B E|=5$ and $|C E|=7$, what is $|D F|$? | 4.2 |
29,678 | Thinking Question 2 Given the sequence $\left\{x_{n}\right\}$ satisfies $x_{n+2}=\frac{x_{n+1}^{2}-4}{x_{n}}$, and $x_{1}=6, x_{2}=4$, find the general term $x_{n}$. | x_{n}=8-2n |
29,683 | 9th Swedish 1969 Problem 4 Define g(x) as the largest value of |y 2 - xy| for y in [0, 1]. Find the minimum value of g (for real x). | 3-\sqrt{8} |
29,689 | 9. Given the function $f(x)=a \sin x-\frac{1}{2} \cos 2 x+a-\frac{3}{a}+\frac{1}{2}, a \in \mathbf{R}, a \neq 0$.
(1) If for any $x \in \mathbf{R}$, we have $f(x) \leqslant 0$, find the range of values for $a$;
(2) If $a \geqslant 2$, and there exists $x \in \mathbf{R}$ such that $f(x) \leqslant 0$, find the range of values for $a$. | [2,3] |
29,691 | 7. Let the volume of tetrahedron $ABCD$ be $V$, $E$ be the midpoint of edge $AD$, and point $F$ be on the extension of $AB$ such that $BF = AB$. The plane through points $C$, $E$, and $F$ intersects $BD$ at $G$. Then the volume of tetrahedron $CDGE$ is equal to $\qquad$. | \frac{V}{3} |
29,695 | Task 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1}$ with base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$ is inscribed in a sphere. Segment $C D$ is the diameter of this sphere, and point $K$ is the midpoint of edge $A A_{1}$. Find the volume of the prism if $C K=2 \sqrt{3}, D K=2 \sqrt{2}$. | 9\sqrt{2} |
29,699 | ## Subject III. (10 points)
Calculate: $I=\int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{(\arcsin x)^{2}}{\sqrt{1-x^{2}}+1+x} d x$
Prof. Ilie Diaconu, "Avram Iancu" Theoretical High School, Cluj-Napoca | \frac{\pi^{3}}{648} |
29,721 | 1. Determine all real numbers $s$ for which the equation
$$
4 x^{4}-20 x^{3}+s x^{2}+22 x-2=0
$$
has four distinct real roots, with the product of two of them being equal to -2. | 17 |
29,745 | 8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=12 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=28
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 16 |
29,750 | 11. If one side of the square $A B C D$ lies on the line $y=2 x-17$, and the other two vertices are on the parabola $y=x^{2}$, then the minimum value of the area of the square is $\qquad$ . | 80 |
29,763 | PROBLEM 4. Consider the sequence with the terms: $1,4,5,8,9,12,13,16,17,20, \ldots$
a) Write the next 2 terms of the sequence;
b) Determine the 2015th term of the sequence;
c) Calculate the sum of the terms less than or equal to 80 from the sequence.[^0]
## NATIONAL MATHEMATICS OLYMPIAD Local stage - 14.02. 2015 GRADING GUIDE - Grade 5 | 1620 |
29,764 | Find the smallest positive integer $n$, such that $x_{1}{ }^{3}+x_{2}{ }^{3}+\cdots+x_{n}{ }^{3}=2002^{2002}$ has integer solutions. | 4 |
29,768 | Problem 8.6. For quadrilateral $ABCD$, it is known that $AB=BD, \angle ABD=\angle DBC, \angle BCD=90^{\circ}$. A point $E$ is marked on segment $BC$ such that $AD=DE$. What is the length of segment $BD$, if it is known that $BE=7, EC=5$?
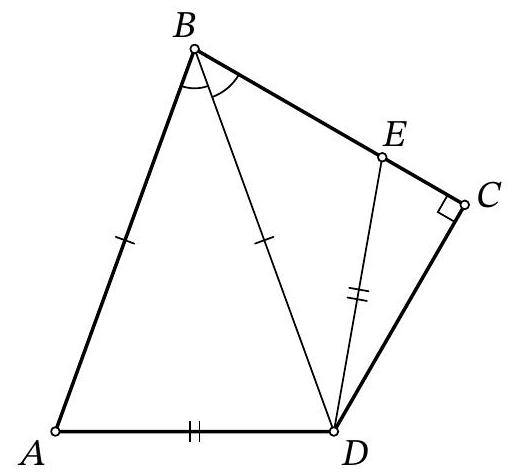 | 17 |
29,777 | [Example 3.4.6] Let $x_{1}, x_{2}, x_{3}, x_{4}$ be positive real numbers, and $x_{1}+x_{2}+x_{3}+x_{4}=$ $\pi$. Find the minimum value of the expression
$$
\begin{array}{l}
\left(2 \sin ^{2} x_{1}+\frac{1}{\sin ^{2} x_{1}}\right) \cdot\left(2 \sin ^{2} x_{2}+\frac{1}{\sin ^{2} x_{2}}\right) . \\
\left(2 \sin ^{2} x_{3}+\frac{1}{\sin ^{2} x_{3}}\right) \cdot\left(2 \sin ^{2} x_{4}+\frac{1}{\sin ^{2} x_{4}}\right)
\end{array}
$$ | 81 |
29,792 | 26. $[\mathbf{1 7}]$ For $1 \leq j \leq 2014$, define
$$
b_{j}=j^{2014} \prod_{i=1, i \neq j}^{2014}\left(i^{2014}-j^{2014}\right)
$$
where the product is over all $i \in\{1, \ldots, 2014\}$ except $i=j$. Evaluate
$$
\frac{1}{b_{1}}+\frac{1}{b_{2}}+\cdots+\frac{1}{b_{2014}} .
$$ | \frac{1}{2014!^{2014}} |
29,800 | Example 7 Let the sequence $a_{1}, a_{2}, a_{3}, \cdots$ satisfy: $a_{1}=1, a_{n+1}=\frac{1}{16}\left(1+4 a_{n}+\sqrt{1+24 a_{n}}\right), n=$ $1,2, \cdots$ Find the general term formula.
(1986 Federal Republic of Germany Olympiad Problem) | a_{n}=\frac{1}{3}+(\frac{1}{2})^{n}+\frac{1}{3}(\frac{1}{2})^{2n-1} |
29,811 | 4. $A$ and $B$ are playing a game on a $25 \times 25$ grid. At the beginning, $A$ can mark some cells. After marking is completed, they start taking turns to place gold coins on the grid, with $B$ going first. The rules for placing gold coins are as follows: (1) gold coins cannot be placed in marked cells; (2) once a gold coin is placed, no more gold coins can be placed in the same row or column; (3) if no more gold coins can be placed on the grid, the game ends. The player who places the last gold coin on the grid wins. How many cells does $A$ need to mark at the beginning of the game to ensure a win? (Assume both $A$ and $B$ use the best strategy) | 25 |
29,832 | 67. The perimeter of triangle $ABC$ is $2p$. What is the greatest value that the length of a segment tangent to the inscribed circle of $ABC$ and parallel to $BC$ can have? For which triangle (triangles) is this value achieved? | \frac{p}{4} |
29,845 | Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x$ and $y$,
$$
f(f(x)+f(f(y)))=2 x+f(f(y))-f(f(x))
$$ | f(x)=x |
29,858 | 3. In triangle $ABC (AB < AC)$, the interior bisector of angle $A$ intersects side $BC$ at point $D$ and the line parallel to $AB$ through $C$ at point $E$, and the median corresponding to side $BC$ intersects the same parallel line at point $N$. Let $M$ be the reflection of $A$ over $B$, $O$ be the midpoint of $[BC]$, and $\{P\}=MO \cap BN$. Find the value of the ratio $\frac{\mathcal{A}_{A P M}}{\mathcal{A}_{B M E}}$. | \frac{2}{3} |
29,863 | 10. (CZS 4) The square $A B C D$ is to be decomposed into $n$ triangles (nonoverlapping) all of whose angles are acute. Find the smallest integer $n$ for which there exists a solution to this problem and construct at
least one decomposition for this n. Answer whether it is possible to ask additionally that (at least) one of these triangles has a perimeter less than an arbitrarily given positive number. | 8 |
29,869 | 2.6. (GDR, 74). Solve the equation
$$
(x+2)^{4}-x^{4}=y^{3}
$$
in integers. | -1,0 |
29,895 | 17. Let $x$, $y$, $z$ be the lengths of the sides of a right triangle, with $z$ being the hypotenuse. When the inequality $x^{2}(y+z)+y^{2}(z+x)+z^{2}(x+y)>k x y z$ always holds, find the maximum value of the parameter $k$, and indicate when equality holds. | 2+3\sqrt{2} |
29,909 | Ex. 147. In a convex quadrilateral, the point of intersection of the diagonals divides each of them in the ratio $1: 2$. The quadrilateral formed by sequentially connecting the midpoints of the sides is a square with a side of 3. Find the perimeter of the original quadrilateral. | 4\sqrt{5}+6\sqrt{2} |
29,933 | The lateral edge of a regular quadrilateral pyramid is $b$, and the plane angle at the vertex is $\alpha$. Find the radius of the sphere circumscribed about the pyramid.
# | \frac{b}{2\sqrt{\cos\alpha}} |
29,945 | 8、Let $2 n$ real numbers $a_{1}, a_{2}, \mathrm{~L}, a_{2 n}$ satisfy the condition $\sum_{i=1}^{2 n-1}\left(a_{i+1}-a_{i}\right)^{2}=1$ then $\mu=\left(a_{n+1}+a_{n+2}+\mathrm{L}+a_{2 n}\right)-\left(a_{1}+a_{2}+\mathrm{L}+a_{n}\right)$ the maximum value is $\qquad$ | \sqrt{\frac{n(2n^{2}+1)}{3}} |
29,961 | Vasilev N.B.
A cherry, a sphere of radius $r$, is dropped into a round glass, the axial cross-section of which is the graph of the function $y=x^{4}$. For what largest $r$ will the sphere touch the lowest point of the bottom? (In other words, what is the maximum radius $r$ of a circle lying in the region $y \geq x^{4}$ and containing the origin?) | \frac{3\sqrt[3]{2}}{4} |
29,975 | [ Convex Polygons ]
Among all such numbers $n$, that any convex 100-gon can be represented as the intersection (i.e., common part) of $n$ triangles, find the smallest. | 50 |
29,976 | 91. On a long strip of paper, consecutive natural numbers $1, 2, 3, \cdots \cdots n$ are written in sequence. The long strip is cut into five segments, each containing some numbers (the digits of a single number will not be cut into different segments). The average of the numbers in these five segments are $1234, 345, 128, 19$, and $9.5$ (the order of these five numbers is scrambled). Therefore, $n=$ | 2014 |
29,977 | Example 11 Find the minimum value of the bivariate function $f(x, y)=(x-y)^{2}+\left(x+\frac{1}{y}+1\right)^{2}$.
(1998 "Hope Cup" Invitational Competition Question) | \frac{1}{2} |
29,998 | 8.3 On the side $BC$ of the rhombus $ABCD$, select a point $M$. From $M$, draw perpendiculars to the diagonals $BD$ and $AC$, which intersect the line $AD$ at points $P$ and $Q$, respectively. It is known that the lines $PB$, $QC$, and $AM$ intersect at the same point. What is the ratio $\frac{BM}{MC}$? | \frac{1}{2} |
30,005 | Solve the following system of equations:
$$
\begin{aligned}
x^{2}+7 y+2 & =2 z+4 \sqrt{7 x-3} \\
y^{2}+7 z+2 & =2 x+4 \sqrt{7 y-3} \\
z^{2}+7 x+2 & =2 y+4 \sqrt{7 z-3}
\end{aligned}
$$ | 1 |
30,027 | N22 (22-3, Netherlands) Given integers $m, n$ satisfying $m, n \in\{1,2, \cdots, 1981\}$ and $\left(n^{2}-m n-m^{2}\right)^{2}=1$, find the maximum value of $m^{2}+n^{2}$. | 3524578 |
30,028 | 8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=27 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=43
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 24 |
30,032 | 7. For any positive numbers $a, b, c$ satisfying $a+b+c=1$, it always holds that
$$
\begin{array}{l}
a^{2}+b^{2}+c^{2}+\lambda \sqrt{a b c} \leqslant 1 . \\
\text { Then } \lambda_{\text {max }}=
\end{array}
$$ | 2\sqrt{3} |
30,033 | In trapezoid $A B C D, A B$ is parallel to $D C$ and $\angle D A F=90^{\circ}$. Point $E$ is on $D C$ so that $E B=B C=C E$. Point $F$ is on $A B$ so that $D F$ is parallel to $E B$. In degrees, what is the measure of $\angle F D A$ ?
 | 30 |
30,044 | 6. On the edges of a trihedral angle with vertex at point $S$, there are points $M, N$, and $K$ such that $S M^{2}+S N^{2}+S K^{2} \leq 12$. Find the area of triangle $S M N$, given that the angle $M S N$ is $30^{\circ}$, and the volume of the pyramid $S M N K$ is maximally possible. | 1 |
30,048 | 5. It is known that in the pyramid $A B C D$ with vertex $D$, the sum $\angle A B D+\angle D B C=\pi$. Find the length of the segment $D L$, where $L$ is the base of the bisector $B L$ of triangle $A B C$, if it is known that
$$
A B=9, B C=6, A C=5, D B=1 .
$$ | 7 |
30,077 | Point $D$ is the midpoint of side $A C$ of triangle $A B C$. On side $B C$, a point $E$ is chosen such that $\angle B E A = \angle C E D$. Find the ratio $A E: D E$. | 2:1 |
30,082 | 7.2. Consider triangle $A B C$ with altitudes $B E$ and $C F$, where $E \in (A C)$ and $F \in (A B)$. Point $P$ lies on segment $(B E)$ such that $B P = A C$, and point $Q$ lies on the extension of segment $(C F)$, such that $F \in (C Q)$ and $C Q = A B$. Determine the measure of angle $Q A P$. | 90 |
30,090 | 3. Determine all pairs $(a, b)$ of real numbers for which the quadratic trinomials $P(x)=$ $=x^{2}+a x+b$ and $Q(x)=x^{2}+b x+a$ have the following property: each of the equations
$$
a P(x)+b Q(x)=0 \quad \text{and} \quad a Q(x)+b P(x)=0
$$
is a quadratic equation with a double root.
(Jaroslav Švrček) | (4,4) |
30,091 | If we add up the natural numbers from 1 to $n$, the sum in certain cases can be divisible by 10 raised to some positive integer power. What is the smallest $n$ for which the sum is divisible by ten thousand? | 9375 |
30,095 | 1. Given the sequence $\left\{a_{n}\right\}$ satisfies:
$$
a_{1}=1, a_{n}=5 a_{n-1}+3^{n-1}(n \geqslant 2) \text {. }
$$
Find $a_{n}$ and the highest power of 2 that divides $a_{k}\left(k=2^{2019}\right)$ | 2021 |
30,099 | PROBLEM 4. Let $A B C$ be a right-angled triangle at $A$ and $[B D,[C E$ its angle bisectors $(D \in A C$, $E \in A B)$. Denote by $I$ the intersection of lines $B D$ and $C E$ and by $F$, respectively $G$, the projections of points $D$ and $E$ onto line $B C$. Determine the measure of angle $F I G$.[^0]
## NATIONAL MATHEMATICS OLYMPIAD Local stage - 14.02. 2015 GRADING KEY - Grade 7 | 90 |
30,103 | (10 Given that the three lateral edges of a triangular pyramid are pairwise perpendicular, and the base area is 1, find the maximum volume of this triangular pyramid.
保留源文本的换行和格式,翻译结果如下:
(10 Given that the three lateral edges of a triangular pyramid are pairwise perpendicular, and the base area is 1, find the maximum volume of this triangular pyramid. | \frac{1}{3}\sqrt[4]{\frac{4}{27}} |
30,128 | 5. The subset $X$ of the set $\{00,01, \cdots, 98,99\}$ satisfies: in any infinite sequence of digits, there are two adjacent digits that form an element of $X$. What is the minimum number of elements that $X$ should contain?
(52nd Moscow Olympiad problem) | 55 |
30,146 | 5. Let $x, y, z \in \mathbf{R}_{+}$, satisfying $x+y+z=x y z$. Then the function
$$
\begin{array}{l}
f(x, y, z) \\
=x^{2}(y z-1)+y^{2}(z x-1)+z^{2}(x y-1)
\end{array}
$$
has the minimum value of . $\qquad$ | 18 |
30,153 | 65. Motorcycle with a sidecar. Atkins, Baldwin, and Clark decided to go on a trip. Their journey will be 52 km. Atkins has a motorcycle with a one-person sidecar. He needs to take one of his companions for some distance, drop him off to walk the rest of the way, return, pick up the other companion who started walking at the same time, and continue so that all three arrive at the destination at the same time. How can this be done?
The motorcycle's speed is 20 km/h, Baldwin can walk at a speed of 5 km/h, and Clark at 4 km/h. Of course, each one tries to move as quickly as possible and does not stop anywhere along the way.
The problem could be made more complex by introducing more passengers, but in our case, it is so simplified that even all distances are expressed in whole kilometers. | 5 |
30,188 | 10. (20 points) Given the sequence $\left\{a_{n}\right\}$ satisfies $a_{1}=1, a_{n+1}=\frac{a_{n}}{2}+2^{n-1} \cdot a_{n}^{2}\left(n \in \mathbf{N}^{*}\right)$. Let $S_{n}=$ $\sum_{i=1}^{n} \frac{1}{2^{n} a_{n}+1}$, find the value of $\lim _{n \rightarrow \infty} S_{n}$. | \frac{1}{2} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.