id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
28,261 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{2 \operatorname{arctan} \frac{1}{3}} \frac{\cos x d x}{(1-\sin x)(1+\cos x)}
$$ | -\frac{1}{3}-2\ln\frac{2}{3} |
28,262 | 8. Given triangle $A B C . \angle A=\alpha, \angle B=\beta$. Lines $O_{1} O_{2}, O_{2} O_{3}, O_{1} O_{3}$ are the bisectors of the external angles of triangle $A B C$, as shown in the figure. Point $\mathrm{O}$ is the center of the inscribed circle of triangle $A B C$. Find the angle between the lines $O_{1} O_{2}$ and $O O_{3}$.
# | 90 |
28,266 | 4. Given that point $P$ is on the curve $y=2 e^{x}$, and point $Q$ is on the curve $y=\ln \frac{x}{2}$, then the minimum value of $|P Q|$ is | \sqrt{2}(1+\ln2) |
28,267 | 91. In quadrilateral $A B C D$, given are $|A B|=a$, $|A D|=b$; sides $B C, C D$ and $A D$ touch a certain circle, the center of which is at the midpoint of $A B$. Find the side $|B C|$. | \frac{^2}{4b} |
28,270 | 5. The base of the pyramid $S A B C D$ is a rectangle $A B C D$, with the height being the edge $S A=25$. Point $P$ lies on the median $D M$ of the face $S C D$, point $Q$ lies on the diagonal $B D$, and the lines $A P$ and $S Q$ intersect. Find the length of $P Q$, if $B Q: Q D=3: 2$. | 10 |
28,285 | 6. Let's introduce the following notations: $a$ - the side of the base, $b$ - the lateral edge, $N$ - the midpoint of side $AB$, $M$ - the midpoint of side $AD$, $K$ - the midpoint of edge $SC$ of the regular quadrilateral pyramid $SABCD$.
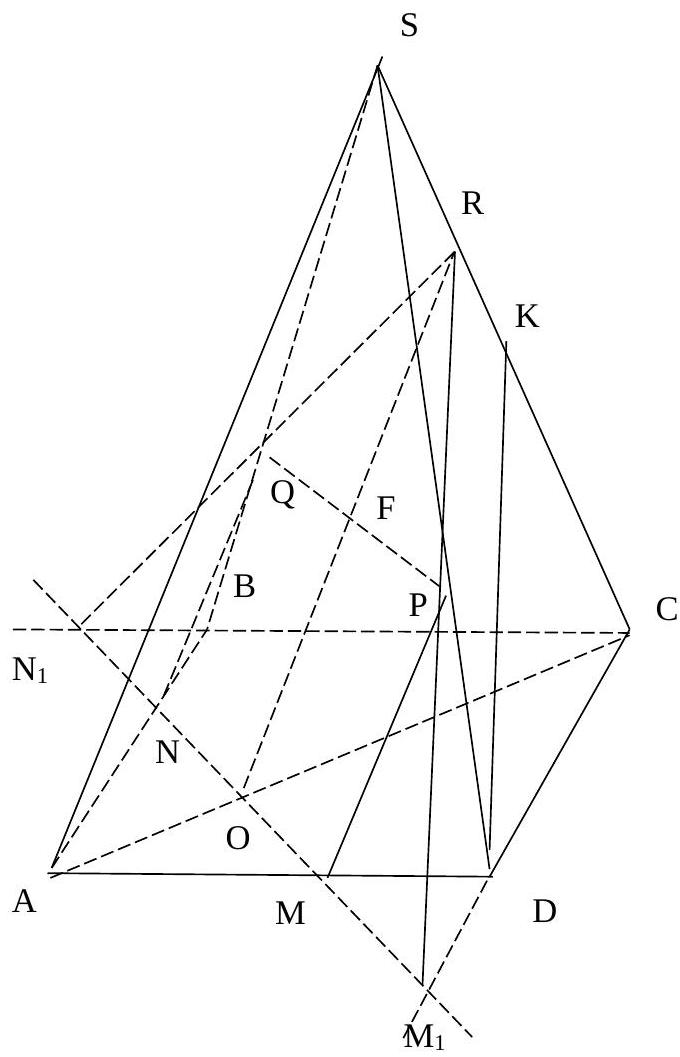
We construct the section of the pyramid $SABCD$ by a plane passing through points $N$ and $M$ and parallel to the median $DK$ of the lateral face $SDC$: through points $N$ and $M$ we draw the line $NM$ until it intersects with lines $BC$ and $CD$ at points $N_1$ and $M_1$ respectively; through point $M_1$ we draw a line parallel to the median $DK$, the points of intersection of this line with edges $SD$ and $SC$ are denoted as $P$ and $R$ respectively; we connect points $R$ and $N_1$; the point of intersection of $RN_1$ and $SB$ is denoted as $Q$; we connect $Q$ and $N$, $P$ and $M$. The section $NMPRQ$ is constructed. Let's find its area.
By the condition, $AM = MD = AN = NB = \frac{a}{2}$. Therefore, triangle $AMN$ is a right isosceles triangle and $MN = \frac{a}{\sqrt{2}}$. Note that triangles $MDM_1$ and $NBN_1$ are right triangles. They are equal to triangle $AMN$ by the leg and angle. Therefore, $M_1D = N_1B = \frac{a}{2}$. Consider the plane of the lateral face $SDC$. Since $M_1R \parallel DK$, then $\frac{RK}{CK} = \frac{M_1D}{CD} = \frac{1}{2}$. Then $RK = \frac{CK}{2} = \frac{b}{4}$, $SR = SK - RK = \frac{b}{4}$. Moreover, $PR \parallel DK$, $\frac{SP}{PD} = \frac{SR}{RK} = 1$. Therefore, $SP = PD = \frac{b}{2}$. Since $P$ is the midpoint of edge $SD$ and $M$ is the midpoint of base $AD$, then $PM$ is the midline of triangle $ADS$ and $PM = \frac{AS}{2} = \frac{b}{2}$, $PM \parallel AS$. Similarly, we can obtain that $QN = \frac{AS}{2} = \frac{b}{2}$, $QN \parallel AS$. Therefore, quadrilateral $PMQN$ is a parallelogram. We will prove that it is a rectangle. Indeed, the projection of $AC$ of edge $AS$ is the diagonal of the square $ABCD$. Therefore, $AC$ is perpendicular to the diagonal $BD$, and since $BD \parallel MN$, then $AC$ is perpendicular to $MN$. Hence, $AS$ is perpendicular to $MN$. Since $PM \parallel AS$, it follows that $PM$ is perpendicular to $MN$. Thus, the section $NMPRQ$ consists of a rectangle $PMQN$ with sides $MN = \frac{a}{\sqrt{2}}$ and $PM = \frac{b}{2}$ and an isosceles triangle $PQR$ with base $PQ = \frac{b}{2}$ and height $RF$. Let's find the area of the rectangle: $MN \cdot PM = \frac{ab}{2\sqrt{2}}$. Since $\frac{CR}{RS} = \frac{CO}{OA} = 3$, then $\frac{OR}{AS} = \frac{CO}{OA} = \frac{3}{4}$. From this, we get $OR = \frac{3b}{4}$, and $FR = \frac{3b}{4} - \frac{b}{2} = \frac{b}{4}$. Then the area of triangle $PQR$ is $\frac{1}{2} \cdot \frac{a}{\sqrt{2}} \cdot \frac{b}{4} = \frac{ab}{8\sqrt{2}}$. The area of the section $NMPRQ$ is: $\frac{ab}{2\sqrt{2}} + \frac{ab}{8\sqrt{2}} = \frac{5ab}{8\sqrt{2}} = \frac{5ab\sqrt{2}}{16}$. Substituting $a = 1$, $b = 2$, we find $S = \frac{5\sqrt{2}}{8}$. | \frac{5\sqrt{2}}{8} |
28,288 | Quadrilateral $ABCD$ with mutually perpendicular diagonals $AC$ and $BD$ is inscribed in a circle. Find its radius, if $AB=4, CD=2$.
# | \sqrt{5} |
28,297 | There are $n$ participants at a conference, each knowing at most $k$ languages. For every group of three participants, there are at least two who speak the same language. Find the smallest value of $n$ such that for any distribution of languages satisfying these properties, one can find a language spoken by at least three delegates. | 2k+3 |
28,298 | 6. In a match without ties, the game ends when one person wins 2 more games than the other, and the one with more wins is the winner. It is known that in the odd-numbered games, the probability of A winning is $\frac{3}{5}$; in the even-numbered games, the probability of B winning is $\frac{3}{5}$. Then the expected number of games played when the match ends is | \frac{25}{6} |
28,327 | 9. (1977 9th Canadian Mathematical Olympiad) Given a right circular cone with a base radius of $1 \mathrm{~cm}$ and a slant height of $3 \mathrm{~cm}$, $P$ is a point on the circumference of the base. The shortest path from $P$ around the cone back to $P$ is shown in Figure 313. What is the minimum distance from the vertex $V$ to this path? | \frac{3}{2} |
28,337 | 14. As shown in the figure, $D$ is a point inside $\triangle A B C$, and it satisfies $A B=C D=4$, $\angle A+\angle B D C=180^{\circ}$. Determine the maximum value of $S_{\triangle A B C}-S_{\triangle B D C}$. | 8 |
28,362 | GS. 4 Let $F$ be the number of integral solutions of $x^{2}+y^{2}+z^{2}+w^{2}=3(x+y+z+w)$. Find the value of $F$. | 208 |
28,416 | 24.3.13 Xuan Tai Given a positive integer $n$ greater than 2004, fill the numbers $1,2,3, \cdots, n^{2}$ into the squares of an $n \times n$ chessboard (consisting of $n$ rows and $n$ columns) such that each square contains exactly one number. If a square contains a number that is greater than the numbers in at least 2004 squares in its row and at least 2004 squares in its column, then this square is called a “super square”. Find the maximum number of “super squares” on the chessboard. | n(n-2004) |
28,420 | (4) A diameter $AB$ of a semicircle equals 2, and a perpendicular line to the plane of the circle is drawn through $A$. A point $S$ is taken on this perpendicular line such that $AS = AB$. $C$ is a moving point on the semicircle, and $M$ and $N$ are the projections of $A$ on $SB$ and $SC$, respectively. When the volume of the tetrahedron $S-AMN$ is maximized, the sine of the angle between $SC$ and the plane $ABC$ is $\qquad$. | \frac{\sqrt{3}}{2} |
28,422 | 16.15. (England, 68). Find the maximum number of points that can be placed on a sphere of radius 1 so that the distance between any two of them is: a) not less than $\sqrt{2} ;$ b) greater than $\sqrt{2}$. | 4 |
28,433 | Exercise 8. Let $a$ and $b$ be two real numbers. We define the sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ by $a_{0}=a, b_{0}=b$ and for all $n$ a natural number, $a_{n+1}=a_{n}+b_{n}$ and $b_{n+1}=a_{n} b_{n}$. Determine all pairs $(a, b)$ such that $\mathrm{a}_{2022}=\mathrm{a}_{0}$ and $\mathrm{b}_{2022}=\mathrm{b}_{0}$. | (,0) |
28,436 | 9. In $\triangle A B C$, $a=BC, b=CA, c=AB$. If $a^{2}+b^{2}=6, \cos (A-B) \cos C=\frac{2}{3}$, find the circumradius of $\triangle A B C$. | \frac{3\sqrt{10}}{10} |
28,457 | 15. Given $\angle B A C=90^{\circ}$, quadrilateral $A D E F$ is a square with side length 1, find the maximum value of $\frac{1}{A B}+\frac{1}{B C}+\frac{1}{C A}$. | 1+\frac{\sqrt{2}}{4} |
28,481 | SUBIECTUL II Let the sequence $\left(I_{n}\right)_{n \geq 1}$ with the general term:
$$
I_{n}=\int_{0}^{\frac{\pi}{4}} e^{n x}\left(\operatorname{tg}^{n-1} x+\operatorname{tg}^{n} x+\operatorname{tg}^{n+1} x\right) d x, n \geq 1
$$
## www.edums.ro
Calculate: $\lim _{n \rightarrow \infty} n\left(\sqrt[n^{2}]{n I_{n}}-1\right)$. | \frac{\pi}{4} |
28,488 | 107. Misunderstanding. An American reader asked me to find a number composed of any number of digits, for which division by 2 can be performed by moving the last digit to the front. Apparently, this problem arose for him after he became acquainted with a previously misstated problem. If it were required to move the first digit to the end, the answer would be the number 315789473684210526, and from this, it would be easy to find a solution starting with any digit. But if it is required to move the digit from the end to the front, there is no solution for the divisor 2. However, there is a solution for the divisor 3. Could you find it? | 428571 |
28,492 | 5. In triangle $A B C, \angle A=45^{\circ}$ and $M$ is the midpoint of $\overline{B C}$. $\overline{A M}$ intersects the circumcircle of $A B C$ for the second time at $D$, and $A M=2 M D$. Find $\cos \angle A O D$, where $O$ is the circumcenter of $A B C$. | -\frac{1}{8} |
28,499 | 3. Place a regular tetrahedron with volume 1 inside a cube, then the minimum volume of this cube is $\qquad$ | 3 |
28,519 | 8. [35] Let $A B C$ be an acute triangle with circumcenter $O$ such that $A B=4, A C=5$, and $B C=6$. Let $D$ be the foot of the altitude from $A$ to $B C$, and $E$ be the intersection of $A O$ with $B C$. Suppose that $X$ is on $B C$ between $D$ and $E$ such that there is a point $Y$ on $A D$ satisfying $X Y \| A O$ and $Y O \perp A X$. Determine the length of $B X$. | \frac{96}{41} |
28,531 | 8. In tetrahedron $ABCD$, $\triangle ABD$ is an equilateral triangle, $\angle BCD=90^{\circ}$, $BC=CD=1$, $AC=\sqrt{3}$, $E, F$ are the midpoints of $BD, AC$ respectively, then the cosine value of the angle formed by line $AE$ and $BF$ is $\qquad$ | \frac{\sqrt{2}}{3} |
28,537 | Problem 10. Points $M, N$, and $K$ are located on the lateral edges $A A_{1}, B B_{1}$, and $C C_{1}$ of the triangular prism $A B C A_{1} B_{1} C_{1}$ such that $A M: A A_{1}=1: 2, B N: B B_{1}=1: 3, C K: C C_{1}=1: 4$. Point $P$ belongs to the prism. Find the maximum possible value of the volume of the pyramid $M N K P$, if the volume of the prism is 16. | 4 |
28,541 | Solve the equation $5 x^{3}+11 y^{3}+13 z^{3}=0$ in integers.
# | (0,0,0) |
28,547 | 10. (15 points) From the 2015 positive integers 1, 2,
$\cdots, 2015$, select $k$ numbers such that the sum of any two different numbers is not a multiple of 50. Find the maximum value of $k$. | 977 |
28,585 | ## Task 1.
Determine all functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ such that for all $x, y \in \mathbb{Z}$,
$$
f(x y + f(y)) = f(x) f(y) + y
$$ | f(x)=x |
28,589 | Problem 4. Point $O$ is the center of the circumcircle of triangle $ABC$ with sides $BC=5$ and $AB=4$. Find the length of side $AC$ if the length of the vector $3 \overrightarrow{OA}-4 \overrightarrow{OB}+\overrightarrow{OC}$ is 10. | 8 |
28,591 | 9. (This question is worth 14 points) Find the smallest positive integer $n$, such that for any positive integer $k \geq n$, in the set $M=\{1,2, \cdots, k\}$ of the first $k$ positive integers, for any $x \in M$, there always exists another number $y \in M(y \neq x)$, such that $x+y$ is a perfect square. | 7 |
28,610 | Example 2. Investigate the stability of the solution of the degenerate equation for the equation
$$
\varepsilon \frac{d x}{d t}=x\left(e^{x}-2\right)
$$ | 0 |
28,618 | 12.263. The height of a regular truncated triangular pyramid is $H$ and is the mean proportional between the sides of the bases. The lateral edge makes an angle $\alpha$ with the base. Find the volume of the pyramid. | \frac{H^{3}\sqrt{3}}{4\sin^{2}\alpha} |
28,639 | 13. 6:10 ** Given the parabola $y^{2}=4 a x(0<a<1)$ with focus $F$, a circle is drawn above the $x$-axis with center $A(a+4,0)$ and radius $|A F|$, intersecting the parabola at two different points $M$ and $N$. Let $P$ be the midpoint of $M N$.
(1) Find the value of $|M F|+|N F|$;
(2) Does there exist a value of $a$ such that $|M F|, |P F|, |N F|$ form an arithmetic sequence? If so, find the value of $a$; if not, explain why. | 8 |
28,646 | Example 5 Solve the system of simultaneous equations
$$
\left\{\begin{array}{l}
x+y+z=3, \\
x^{2}+y^{2}+z^{2}=3, \\
x^{5}+y^{5}+z^{5}=3 .
\end{array}\right.
$$
Find all real or complex roots.
(2nd USA Mathematical Olympiad) | 1 |
28,652 | Let $\mathcal{P}$ be a regular 17 -gon; we draw in the $\left(\begin{array}{c}17 \\ 2\end{array}\right)$ diagonals and sides of $\mathcal{P}$ and paint each side or diagonal one of eight different colors. Suppose that there is no triangle (with vertices among vertices of $\mathcal{P}$ ) whose three edges all have the same color. What is the maximum possible number of triangles, all of whose edges have different colors? | 544 |
28,653 | 15.22. What is the smallest number of tetrahedra into which a cube can be cut? | 5 |
28,659 | Anna and Berta are playing a game where they take marbles from the table in turns. Anna makes the first move. If at the beginning of a turn there are $n \geq 1$ marbles on the table, then the player whose turn it is takes $k$ marbles, where $k \geq 1$ is either an even number with $k \leq \frac{n}{2}$ or an odd number with $\frac{n}{2} \leq k \leq n$. A player wins the game if they take the last marble from the table.
Determine the smallest number $N \geq 100000$, such that Berta can enforce a win if there are exactly $N$ marbles on the table at the start.
(Gerhard Woeginger)
Figure 2: Solution 3 | 131070 |
28,666 | II. (50 points) For all $a, b, c \in \mathbf{R}^{+}$, find the minimum value of $f(a, b, c)=\frac{a}{\sqrt{a^{2}+8 b c}}+\frac{b}{\sqrt{b^{2}+8 a c}}+\frac{c}{\sqrt{c^{2}+8 a b}}$. | 1 |
28,688 | 11 Given $f(x)=\frac{a x+1}{3 x-1}$, the equation $f(x)=-4 x+8$ has two distinct positive roots, and one root is three times the other. The first $n$ terms of the arithmetic sequences $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ have sums $S_{n}$ and $T_{n}$, respectively, and $\frac{S_{n}}{T_{n}}=f(n)(n=1,2,3, \cdots)$.
(1) Let $g(n)=\frac{a_{n}}{b_{n}}(n=1,2,3, \cdots)$, find the maximum value of $g(n)$;
(2) If $a_{1}=\frac{5}{2}$, and the common difference of the sequence $\left\{b_{n}\right\}$ is 3, investigate whether there are equal terms in the sequences $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$. If there are, find the general term formula of the sequence $\left\{c_{n}\right\}$ formed by these equal terms arranged in ascending order; if not, explain the reason. | \frac{5}{2} |
28,692 | VII.4. In trapezoid ABCD, diagonal AC is perpendicular to leg BC and is the angle bisector of the angle at vertex A. Calculate the length of the base AB, if $\triangle \mathrm{ABC}=60^{\circ}$, and the perimeter of the trapezoid is $\mathbf{25 cm}$. | 10 |
28,696 | 6. What is the smallest area that a right triangle can have, if its hypotenuse lies on the tangent to the graph of the function $y=\sqrt{x-3}$, one of its legs lies on the $y$-axis, and one of its vertices coincides with the point of tangency
points) | 4 |
28,703 | Example 5 There are $n$ people, and it is known that any 2 of them make at most one phone call. The total number of phone calls made among any $n-2$ of them is equal, and it is $3^{k}$ ($k$ is a positive integer). Find all possible values of $n$.
untranslated text remains the same in terms of line breaks and formatting. | 5 |
28,705 | 6. Given that the line $l$ passes through the left focus $F$ of the ellipse $C: \frac{x^{2}}{2}+y^{2}=1$ and intersects the ellipse $C$ at points $A, B$, and $O$ is the origin. If $O A \perp O B$, then the distance from point $O$ to the line $A B$ is $\qquad$ . | \frac{\sqrt{6}}{3} |
28,716 | 1. Find all values of $x$, for each of which one of the three given numbers $\log _{x^{2}}\left(x^{2}-7 x+10\right)$, $\log _{x^{2}} \frac{x^{2}}{x-2}$, and $\log _{x^{2}} \frac{x^{2}}{x-5}$ is equal to the sum of the other two. | 6 |
28,719 | 10. In quadrilateral $A B C D$, $A B=B C=C D=$ $26, A D=30 \sqrt{3}, A C$ intersects $B D$ at point $O, \angle A O B=$ $60^{\circ}$. Then $S_{\text {quadrilateral } A B C D}=$ $\qquad$ | 506\sqrt{3} |
28,723 | 3. [30] Find the number of ordered pairs $(A, B)$ such that the following conditions hold:
- $A$ and $B$ are disjoint subsets of $\{1,2, \ldots, 50\}$.
- $|A|=|B|=25$
- The median of $B$ is 1 more than the median of $A$. | \binom{24}{12}^2 |
28,734 | Example 5 As shown in Figure 3-9, in $\triangle A B C$, $\angle A=60^{\circ}, A B>A C$, point $O$ is the circumcenter, the two altitudes $B E, C F$ intersect at point $H$, points $M, N$ are on segments $B H, H F$ respectively, and satisfy $B M=C N$. Find the value of $\frac{M H+N H}{O H}$.
(2002 National High School League Question) | \sqrt{3} |
28,735 | Example 4 As shown in Figure 7, in the quadrilateral pyramid $P-ABCD$, $PA \perp$ base $ABCD$, $BC=CD=2$, $AC=4$, $\angle ACB=\angle ACD=\frac{\pi}{3}$, $F$ is the midpoint of $PC$, and $AF \perp PB$.
Figure 7
Find (1) the length of $PA$;
(2) the sine value of the dihedral angle $B-AF-D$. ${ }^{[4]}$ | \frac{\sqrt{63}}{8} |
28,736 | 12.117. The base of a pyramid inscribed in a cone is a quadrilateral with adjacent sides equal in pairs, and the angle between one pair of adjacent sides is $\alpha$. Find the ratio of the volume of the pyramid to the volume of the cone. | \frac{2\sin\alpha}{\pi} |
28,739 | 9. (16 points) In $\triangle A B C$, $\overrightarrow{A B} \cdot \overrightarrow{A C}+2 \overrightarrow{B A} \cdot \overrightarrow{B C}=3 \overrightarrow{C A} \cdot \overrightarrow{C B}$.
Find the maximum value of $\sin C$. | \frac{\sqrt{7}}{3} |
28,741 | 11.081. A cone with base radius $R$ is inscribed in an arbitrary pyramid, where the perimeter of the base of the pyramid is $2 p$. Determine the ratio of the volumes and the ratio of the lateral surface areas of the cone and the pyramid. | \frac{\piR}{p} |
28,747 | 15. Fill in the circles with the natural numbers from 1 to 16 (each number must be used exactly once), so that the sum of the numbers in the 4 circles connected by the same straight line is equal. This is called an 8th-order magic star, and this equal number is called the magic sum of the 8th-order magic star. Therefore, the magic sum of the 8th-order magic star is $\qquad$, and continue to complete the following 8th-order magic star.
Fill in the circles with the natural numbers from 1 to 16 (each number must be used exactly once), so that the sum of the numbers in the 4 circles connected by the same straight line is equal. This is called an 8th-order magic star, and this equal number is called the magic sum of the 8th-order magic star. Therefore, the magic sum of the 8th-order magic star is $\qquad$, and continue to complete the following 8th-order magic star. | 34 |
28,751 | 6. Find all real solutions of the system of equations
$$
\left\{\begin{array}{l}
\frac{1}{x}=\frac{32}{y^{5}}+\frac{48}{y^{3}}+\frac{17}{y}-15 \\
\frac{1}{y}=\frac{32}{z^{5}}+\frac{48}{z^{3}}+\frac{17}{z}-15 \\
\frac{1}{z}=\frac{32}{x^{5}}+\frac{48}{x^{3}}+\frac{17}{x}-15
\end{array}\right.
$$
(A. B. Vladimirov) | 2 |
28,762 | (9) Let the function $f(x)=\frac{x^{2}+n}{x^{2}+x+1}\left(n \in \mathbf{N}^{*}\right)$ have a maximum value of $a_{n}$ and a minimum value of $b_{n}$, then $a_{n}-b_{n}=$ | \frac{4}{3}\sqrt{n^{2}-n+1} |
28,774 | 8. Given a hyperbola $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ with an eccentricity of $\frac{\sqrt{6}}{2}$, the left and right foci are $F_{1}, F_{2}$, and $P$ is a point on the hyperbola. Let $R, r$ be the circumradius and inradius of $\triangle P F_{1} F_{2}$. If $\angle F_{1} P F_{2}=60^{\circ}$, then $\frac{R}{r}=$ $\qquad$ . | 2\sqrt{2}+2 |
28,782 | 15. Let the quadratic function $f(x)=a x^{2}+b x+c(a, b, c \in \mathbf{R}, a \neq 0)$ satisfy the following conditions:
(1) For $x \in \mathbf{R}$, $f(x-4)=f(2-x)$, and $f(x) \geqslant x$;
(2) For $x \in(0,2)$, $f(x) \leqslant\left(\frac{x+1}{2}\right)^{2}$;
(3) The minimum value of $f(x)$ on $\mathbf{R}$ is 0.
Find the largest $m(m>1)$ such that there exists $t \in \mathbf{R}$, for any $x \in[1, m]$, $f(x+t) \leqslant x$. | 9 |
28,783 | 3. Find the smallest distance from the point with coordinates $(10 ; 5 ; 10)$ to a point whose coordinates are positive and satisfy the inequality $(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \geq 9 \sqrt{1-(2 x+y)^{2}}$. In your answer, write the square of the found distance. | 115.2 |
28,784 | 2.4. (SRP, 81). Solve the equation
$$
x^{6}+3 x^{3}+1=y^{4}
$$
in integers. | 0,\1 |
28,791 | 11. In the Cartesian coordinate system $x O y$, for the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$, the right focus is $F(c, 0)$. If there exists a line $l$ passing through point $F$ intersecting the ellipse at points $A, B$, such that $O A \perp O B$. Find the range of the eccentricity $e=\frac{c}{a}$ of the ellipse. | [\frac{\sqrt{5}-1}{2},1) |
28,796 | 7. Let $P$ be an endpoint of a chord passing through one focus of an ellipse and perpendicular to the focal axis. If the normal line at point $P$ passes through one endpoint of the minor axis, find the eccentricity of the ellipse. | \sqrt{\frac{1}{2}(\sqrt{5}-1)} |
28,824 | 7. Let $\triangle A B C$ be an acute-angled triangle with the lengths of the sides opposite to its internal angles being $a$, $b$, and $c$ respectively. If $2 a^{2}=2 b^{2}+c^{2}$, then the minimum value of $\tan A+\tan B+\tan C$ is $\qquad$. | 6 |
28,825 | Example 1. Find the approximate value of the smallest characteristic number of the kernel by the Ritz method
$$
K(x, t)=x t ; \quad a=0, b=1
$$ | 3 |
28,829 | K2) Let $n$ be a natural number. A volleyball team consisting of $n$ women and $n$ men lines up for a game. Each team member occupies one of the positions $1,2, \ldots, 2 n$, whereby exactly positions 1 and $n+1$ are outside the court. During the game, all team members rotate, switching from position $i$ to position $i+1$ (or from $2 n$ to 1). How many possibilities are there for the starting line-up so that there are always at least $n-1$ women on the pitch, no matter how often the team rotates?
Note: Two starting line-ups are different if at least one team member occupies a different position. | (n!)^{2}\cdot2^{n} |
28,836 | 10. Let $a_{1}, a_{2}, a_{3}, a_{4}$ be 4 rational numbers such that
$$
\left\{a_{i} a_{j} \mid 1 \leqslant i<j \leqslant 4\right\}=\left\{-24,-2,-\frac{3}{2},-\frac{1}{8}, 1,3\right\},
$$
Find the value of $a_{1}+a_{2}+a_{3}+a_{4}$. | \frac{9}{4} |
28,844 | 8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=27 \\
y^{2}+y z+z^{2}=25 \\
z^{2}+x z+x^{2}=52
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 30 |
28,858 | 5. Two circles $k_{1}$, $k_{2}$ with radius $\frac{1}{2} r$ are inscribed in a circle $k$ with radius $r$, and they touch each other. Circle $l$ touches circles $k_{1}$, $k_{2}$ externally and has an internal touch with circle $k$. Circle $m$ has an external touch with circles $k_{2}$ and $l$ and an internal touch with circle $k$. Calculate the radii of circles $l$ and $m$. | \frac{1}{6}r |
28,888 | 7. There are a total of 10040 numbers written on the blackboard, including 2006 ones, 2007 twos, 2008 threes, 2009 fours, and 2010 fives. Each operation involves erasing 4 different numbers and writing the fifth type of number (for example, erasing 1, 2, 3, and 4 each once and writing one 5; or erasing 2, 3, 4, and 5 each once and writing one 1, etc.). If after a finite number of operations, there are exactly two numbers left on the blackboard, what is the product of these two numbers? | 8 |
28,903 | 12. A. As shown in Figure 5, in rectangle \(ABCD\), \(AB = a\), \(BC = b\), and \(a < b\). A line through the center \(O\) of rectangle \(ABCD\) intersects segments \(BC\) and \(DA\) at points \(E\) and \(F\), respectively. The quadrilateral \(ECDF\) is folded along \(EF\) to the plane of quadrilateral \(BEFA\), such that point \(C\) coincides with point \(A\), resulting in quadrilateral \(EFGA\).
Figure 5
(1) Prove that the area of pentagon \(ABEFG\) is \(\frac{a(3b^2 - a^2)}{4b}\);
(2) If \(a = 1\) and \(b\) is a positive integer, find the minimum value of the area of pentagon \(ABEFG\). | \frac{11}{8} |
28,913 | a) João found a way to arrange the numbers $\{1,2,3, \ldots, 16\}$ on a $4 \times 4$ board so that the sum of the numbers in each row, each column, and each diagonal is always the same. One of the possibilities is shown in the example below.
| 4 | 6 | 9 | 15 |
| :---: | :---: | :---: | :---: |
| 13 | 11 | 8 | 2 |
| 16 | 10 | 5 | 3 |
| 1 | 7 | 12 | 14 |
Find another example of distributing these 16 numbers that satisfies the same conditions.
b) Verify that in any possible distribution, the sum of the numbers in each row and column is always 34.
c) João has now created a new type of board with other positive numbers. The product of the numbers in each row, each column, and each diagonal is always the same. What is the value of the number $4H$?
| $1/2$ | 32 | $A$ | $B$ |
| :---: | :---: | :---: | :---: |
| $C$ | 2 | 8 | 2 |
| 4 | 1 | $D$ | $E$ |
| $F$ | $G$ | $H$ | 16 | | 4H=1 |
28,916 | Problem 8. In triangle $A B C$, side $A B=40$. The center $I$ of the inscribed circle divides the bisector $A L$ in the ratio $5: 3$, counting from the vertex. Find the radius of the circumscribed circle around triangle $A B C$, if the radius of the inscribed circle is 15. | 42.5 |
28,926 | Zhendarov R.G.
On the lateral sides $AB$ and $BC$ of an isosceles triangle $ABC$, points $K$ and $L$ are taken respectively, such that $AK + LC = KL$. From the midpoint $M$ of segment $KL$, a line parallel to $BC$ is drawn, and this line intersects side $AC$ at point $N$. Find the measure of angle $KNL$. | 90 |
28,927 | ## Problem Statement
Calculate the volumes of bodies bounded by the surfaces.
$$
\frac{x^{2}}{9}+\frac{y^{2}}{25}-\frac{z^{2}}{100}=-1, z=20
$$ | 200\pi |
28,943 | 7. In the triangle $A B C, A B=8, B C=7$ and $C A=6$. Let $E$ be the point on $B C$ such that $\angle B A E=3 \angle E A C$. Find $4 A E^{2}$. | 135 |
28,952 | 3. Given triangle $\mathrm{ABC}: \mathrm{BK}, \mathrm{CL}$ - angle bisectors, M - the point of their intersection. It turns out that triangle $\mathrm{AMC}$ is isosceles, one of whose angles is 150 degrees. Find what the perimeter of triangle $\mathrm{ABC}$ can be, if it is known that $\mathrm{BK}=4-2 \sqrt{3}$. | 4 |
28,955 | 9. Given that $O$ is the circumcenter of $\triangle A B C$, and $3 \overrightarrow{O A}+4 \overrightarrow{O B}+5 \overrightarrow{O C}=\overrightarrow{0}$, find the value of $\cos \angle B A C$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | \frac{\sqrt{10}}{10} |
28,969 | 2A. Below are recorded 2020 real numbers. The sum of each number in the sequence and the reciprocal of the next number is equal to 1. The product of all the numbers is equal to 2020. Which numbers are recorded at the first and last position in the sequence? | -2020 |
28,973 | Example 18 (1985 Poland-Austria Joint Competition Problem) Let $x, y, z, w$ be four real numbers, not all zero, find the maximum value of $S=$ $\frac{x y+2 y z+z w}{x^{2}+y^{2}+z^{2}+w^{2}}$. | \frac{\sqrt{2}+1}{2} |
28,977 | Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
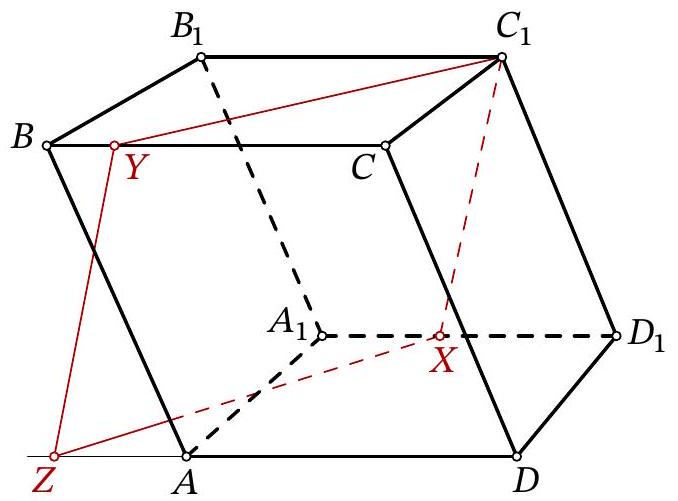 | 20 |
28,984 | We placed a cube in the center of a potter's wheel, with each of its faces inscribed with a natural number. Just before we spun the wheel, we could see three faces of the cube and thus only three numbers from our position. Their sum was 42. After rotating the potter's wheel by $90^{\circ}$, we observed from the same position three faces with numbers summing to 34, and after another $90^{\circ}$ rotation, we saw three numbers summing to 53 from the same spot.
1. Determine the sum of the three numbers we will see from our position after the wheel is rotated by another $90^{\circ}$.
2. The cube was lying on a face with the number 6 throughout the entire process. Determine the maximum possible sum of all six numbers on the cube.
(L. Šimůnek)
Hint. Focus on the relationship between the numbers on mutually parallel side faces. | 100 |
28,992 | 2.47 Among the positive integers less than 10000, how many integers \( x \) are there such that \( 2^x - x^2 \) is divisible by 7?
(6th Moscow Mathematical Olympiad, 1940) | 2857 |
28,993 | 5. let $a$ and $b$ be fixed positive numbers. Depending on $a$ and $b$, find the smallest possible value of the sum
$$
\frac{x^{2}}{(a y+b z)(a z+b y)}+\frac{y^{2}}{(a z+b x)(a x+b z)}+\frac{z^{2}}{(a x+b y)(a y+b x)}
$$
where $x, y, z$ are positive real numbers.
## Solution | \frac{3}{(+b)^{2}} |
29,002 | 2. (7p) Consider the positive real numbers $a, b, c, d$, such that $a b c d=1$. Calculate
$$
E=\frac{7+a}{1+a+a b+a b c}+\frac{7+b}{1+b+b c+b c d}+\frac{7+c}{1+c+c d+c d a}+\frac{7+d}{1+d+d a+d a b}
$$
GM11/2015 | 8 |
29,003 | 4. In a right triangle $ABC$ with angle $\angle A=60^{\circ}$, a point $N$ is marked on the hypotenuse $AB$, and the midpoint of segment $CN$ is marked as point $K$. It turns out that $AK=AC$. The medians of triangle $BCN$ intersect at point $M$. Find the angle between the lines $AM$ and $CN$. | 60 |
29,007 | 5. Let $A B C D$ be a convex trapezoid such that $\angle D A B=\angle A B C=90^{\circ}, D A=2, A B=3$, and $B C=8$. Let $\omega$ be a circle passing through $A$ and tangent to segment $\overline{C D}$ at point $T$. Suppose that the center of $\omega$ lies on line $B C$. Compute $C T$. | 4\sqrt{5}-\sqrt{7} |
29,017 | [ Properties and characteristics of an isosceles triangle. ]
In trapezoid $ABCD$ ($AD$ is the larger base), diagonal $AC$ is perpendicular to side $CD$ and bisects angle $BAD$. It is known that $\angle CDA = 60^\circ$, and the perimeter of the trapezoid is 2. Find $AD$. | \frac{4}{5} |
29,045 | 15.7. (NBR, 68). Inside the tetrahedron $A B C D$ is a point $O$ such that the lines $A O, B O, C O, D O$ intersect the faces $B C D, A C D, A B D, A B C$ of the tetrahedron at points $A_{1}, B_{1}$, $C_{1}, D_{1}$ respectively, and the ratios
$$
\frac{A O}{A_{1} O}, \frac{B O}{B_{1} O}, \frac{C O}{C_{1} O}, \frac{D O}{D_{1} O}
$$
are all equal to the same number. Find all possible values that this number can take. | 3 |
29,052 | Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive numbers whose sum is 1. Let
$$
s=\max \left(\frac{x_{1}}{1+x_{1}}, \frac{x_{2}}{1+x_{1}+x_{2}}, \cdots, \frac{x_{n}}{1+x_{1}+\cdots+x_{n}}\right)
$$
What is the smallest possible value of $s$? For which $x_{1}, x_{2}, \ldots, x_{n}$ does it attain this value? | 1-\sqrt[n]{\frac{1}{2}} |
29,055 | Example 3 (2003 Hungarian Mathematical Competition) Given the circumradius of $\triangle A B C$ is $R$, if $\frac{a \cos \alpha+b \cos \beta+c \cos \gamma}{a \sin \beta+b \sin \gamma+c \sin \alpha}=$ $\frac{a+b+c}{9 R}$, where $a, b, c$, are the lengths of the three sides of $\triangle A B C$; $\alpha, \beta, \gamma$ are the degrees of $\angle A, \angle B, \angle C$ respectively. Find $\alpha, \beta, \gamma$. | \alpha=\beta=\gamma=60 |
29,060 | 60. Given $\triangle A B C$. On the ray $B A$, take a point $D$ such that $|B D|=|B A|+|A C|$. Let $K$ and $M$ be two points on the rays $B A$ and $B C$ respectively such that the area of $\triangle B D M$ is equal to the area of $\triangle B C K$. Find $\widehat{B K M}$, if $\widehat{B A C}=\alpha$. | \alpha/2 |
29,061 | 5. [25] Thaddeus is given a $2013 \times 2013$ array of integers each between 1 and 2013 , inclusive. He is allowed two operations:
1. Choose a row, and subtract 1 from each entry.
2. Chooses a column, and add 1 to each entry.
He would like to get an array where all integers are divisible by 2013. On how many arrays is this possible? | 2013^{4025} |
29,068 | 1. Given the positive real numbers $x_{1}, x_{2}, x_{3}$, and $x_{4}$ such that
$$
x_{1}+x_{2}+x_{3}+x_{4}=1
$$
Let $s$ be the largest of the numbers
$$
\frac{x_{1}}{1+x_{1}}, \frac{x_{2}}{1+x_{1}+x_{2}}, \frac{x_{3}}{1+x_{1}+x_{2}+x_{3}}, \frac{x_{4}}{1+x_{1}+x_{2}+x_{3}+x_{4}}
$$
What is the smallest value that $s$ can achieve? | 1-\frac{1}{\sqrt[4]{2}} |
29,073 | 11.168. The base of the pyramid is a rectangle with an area of $S$. Two lateral faces are perpendicular to the base plane, while the other two are inclined to it at angles of 30 and $60^{\circ}$. Find the volume of the pyramid. | \frac{S\sqrt{S}}{3} |
29,078 | Example 11 The set of all positive integers can be divided into two disjoint subsets of positive integers $\{f(1), f(2), \cdots, f(n), \cdots\},\{g(1), g(2), \cdots, g(n), \cdots\}$, where $f(1)<f(2)<\cdots<f(n)<\cdots g(1)<$ $g(2)<\cdots<g(n)<\cdots$ and $g(n)=f[f(n)]+1(n \geqslant 1)$. Find $f(240)$. | 388 |
29,083 | 12. 2. $17^{\star \star}$ In $\triangle A B C$, $\angle C=90^{\circ}, \angle B=30^{\circ}, A C=2, M$ is the midpoint of $A B$. If $\triangle A C M$ is folded along $C M$ so that the distance between points $A$ and $B$ is $2 \sqrt{2}$, the volume of the tetrahedron $A-B C M$ is . $\qquad$ | \frac{2\sqrt{2}}{3} |
29,101 | 10. (20 points) Let $x, y, z \in \mathbf{R}$ and $x+y+z=0$.
If $\left(x^{2}+y^{2}+z^{2}\right)^{3} \geqslant m x^{2} y^{2} z^{2}$
always holds, find the maximum value of the real number $m$. | 54 |
29,106 | Task 7. On a circle, there are 25 non-overlapping arcs, and on each of them, two arbitrary prime numbers are written. The sum of the numbers on each arc is not less than the product of the numbers on the arc following it in a clockwise direction. What can the sum of all the numbers be? | 100 |
29,120 | At the base of a quadrilateral pyramid lies a rhombus $A B C D$, in which $\angle B A D=60^{\circ}$. It is known that $S A=S C$, $S D=S B=A B$. A point $E$ is taken on the edge $D C$ such that the area of triangle $B S E$ is the smallest among the areas of all sections of the pyramid containing the segment $B S$ and intersecting the segment $D C$. Find the ratio $D E: E C$. | \frac{2}{3} |
29,127 | $\left.\begin{array}{ll}\text { [Sine Theorem } \\ \text { [Inscribed, circumscribed, and exscribed circles; their radii] }\end{array}\right]$
A circle of radius $r$ passes through vertices $A$ and $B$ of triangle $ABC$ and intersects side $BC$ at point $D$. Find the radius of the circle passing through points $A, D$, and $C$, if $AB=c$ and $AC=b$. | \frac{}{} |
29,136 | 1. a) (3p) Determine the minimum of the expression $E(a)=(a+2)\left(a^{2}-6 a+16\right)$, where $a \in[0,+\infty)$.
b) (4p) Prove that for any positive real numbers $a, b, c \in[0,+\infty)$, with $a+b+c=6$, the inequality holds: $\frac{1}{a^{2}-6 a+16}+\frac{1}{b^{2}-6 b+16}+\frac{1}{c^{2}-6 c+16} \leq \frac{3}{8}$. Specify the case of equality.
Dan Popescu, Suceava | 32 |
29,137 | 5. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point $(50 ; 30)$. Find the number of such squares. | 930 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.