id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
63,240 | \left.\begin{array}{l}{[\text { Arithmetic. Mental calculation, etc. }]} \\ {[\text { Arithmetic progression }}\end{array}\right]
When little Clive approached his grandfather's cuckoo clock, it was 12:05.
Clive started turning the minute hand until the hour hand returned to its original position. How many "cuckoos" did his grandfather count during this time from the next room? | 78 |
56,125 | 49**. (Cayley's Problem). How many convex $k$-gons are there, all vertices of which coincide with the vertices of a given convex $n$-gon, and all sides are its diagonals? | \frac{n(n-k-1)!}{k!(n-2k)!} |
23,199 | In the figure below, $A B C D$ and $E F G H$ are rectangles with parallel sides. Given that $A E=10$, $B F=20$, and $D H=30$, determine the length of segment $C G$.
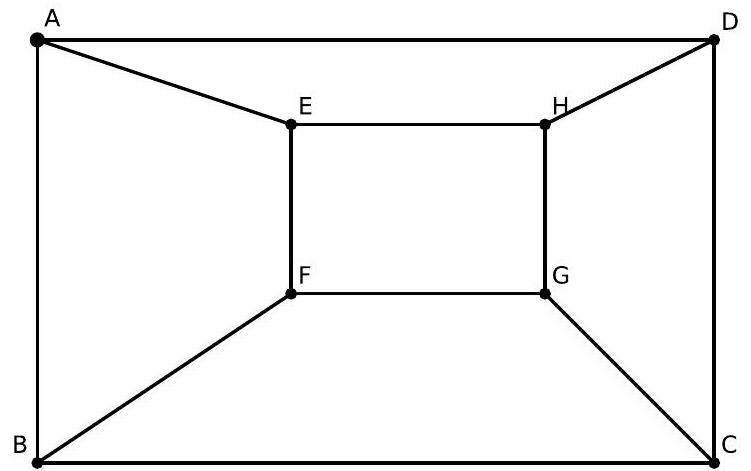 | 20\sqrt{3} |
15,402 | $\left[\begin{array}{l}\text { Pythagorean Theorem (direct and inverse) }\end{array}\right]$
[Area of a triangle (using two sides and the angle between them).]
Right triangles $A B C$ and $A B D$ have a common hypotenuse $A B=5$. Points $C$ and $D$ are located on opposite sides of the line passing through points $A$ and $B, B C=B D=3$. Point $E$ lies on $A C, E C=1$. Point $F$ lies on $A D, F D=2$. Find the area of the pentagon $E C B D F$. | \dfrac{228}{25} |
53,101 | Problem 7.1. Inside a large square, there is a small square, the corresponding sides of which are parallel. The distances between some sides of the squares are marked on the diagram. By how much is the perimeter of the large square greater than the perimeter of the small square?
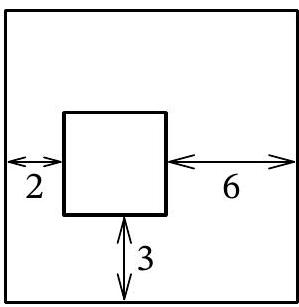 | 32 |
66,697 | B1. Find all quadruples of non-zero digits $a, b$, $c$ and $d$, for which $\overline{a b 20}-\overline{13 c d}=\overline{c d a b}$. | (6,7,5,3) |
53,016 | 1. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all $x \in \mathbb{R}$, $f(x) \leqslant x$ and for all $x, y \in \mathbb{R}$, $f(x+y) \leqslant f(x)+f(y)$. | f(x)=x |
13,478 | Compute
$$
\sum_{k=0}^{100}\left\lfloor\frac{2^{100}}{2^{50}+2^{k}}\right\rfloor .
$$
(Here, if \( x \) is a real number, then \( \lfloor x \rfloor \) denotes the largest integer less than or equal to \( x \).) | 101 \cdot 2^{49} - 50 |
19,570 | In a right square pyramid $O-ABCD$, $\angle AOB=30^{\circ}$, the dihedral angle between plane $OAB$ and plane $OBC$ is $\theta$, and $\cos \theta = a \sqrt{b} - c$, where $a, b, c \in \mathbf{N}$, and $b$ is not divisible by the square of any prime number. Find $a+b+c=$ _______. | 14 |
69,100 | A square is inscribed in an equilateral triangle, with each vertex of the square on the perimeter of the triangle. One side of the square cuts off a smaller equilateral triangle; into this, we again inscribe a square in the same manner, and so on. What fraction of the triangle is covered by the infinite sequence of squares? | \frac{3-\sqrt{3}}{2} |
55,402 | 10-6. The places of cyclists in the race are determined by the sum of the times on all stages: the first place goes to the rider with the smallest total time,..., the last place goes to the rider with the largest total time. There were 500 cyclists, the race took place over 15 stages, and there were no cyclists with the same times either on the stages or in the total time over all stages. Vasya always finished seventh. What is the lowest place (i.e., the place with the highest number) he could have taken? | 91 |
8,396 | Find all values that the expression
$$
3 \arcsin{x} - 2 \arccos{y}
$$
can take under the condition \(x^{2} + y^{2} = 1\). | \left[ -\dfrac{5\pi}{2}, \dfrac{\pi}{2} \right] |
58,924 | 9.3. Will the equation $x^{2019}+2 x^{2018}+3 x^{2017}+\cdots+2019 x+2020=0$ have integer roots | No |
7,123 | 9.3. Inside a semicircle of radius 12, there are a circle of radius 6 and a small semicircle, each touching the others pairwise, as shown in the figure. Find the radius of the small semicircle. | 4 |
58,665 | (*) We call $I$ the set of points in the plane such that their abscissa and ordinate are irrational numbers, and $R$ the set of points whose both coordinates are rational. How many points of $R$ at most can lie on a circle of irrational radius whose center belongs to $I$? | 2 |
27,240 | 11.5. The lateral faces of the pentagonal pyramid $S A B C D E$ are acute-angled triangles. We will call a lateral edge of the pyramid good if it is equal to the height of the opposite lateral face, drawn from the vertex of the pyramid (for example, the edge $S A$ is good if it is equal to the height of the triangle $S C D$, drawn from the vertex $S$). What is the maximum number of good edges that the pyramid can have? | 2 |
61,761 | 1. (1 mark) Let $n$ be a positive integer such that no matter how $10^{n}$ is expressed as the product of two positive integers, at least one of these two integers contains the digit 0 . Find the smallest possible value of $n$.
(1 分) 設 $n$ 是滿足以下條件的正整數:無論怎樣將 $10^{n}$ 分解為兩個正整數的積, 其中一個數必包含“ 0 ”這數字。求 $n$ 的最小可能值。 | 8 |
8,032 | ## Task 1 - 050721
At the Rostock public transport companies, you can buy tram tickets for adults at the following prices:
(1) A ticket from the ticket machine for 0.20 MDN
(2) A card with 6 fare sections for 1.00 MDN
(3) A block of 50 tickets for 7.50 MDN (The validity period is unlimited)
(4) A monthly pass for unlimited rides for 10.00 MDN
What is the minimum number of trips (per month) for which the monthly pass is the cheapest option for a person? | 67 |
63,884 | 4. Find all real numbers that satisfy the equation $\sqrt{x^{2}-p}+2 \sqrt{x^{2}-1}=x$, where $p$ is a parameter. | \frac{4-p}{\sqrt{8(2-p)}} |
6,984 | Through the point with coordinates $(2,2)$, lines (including two parallel to the coordinate axes) are drawn, which divide the plane into angles of $18^{\circ}$. Find the sum of the x-coordinates of the points of intersection of these lines with the line $y = 2016 - x$. | 10080 |
62,116 | 5. On the table, there are 7 clean sheets of paper. Every minute, Vasya chooses any 4 of them and draws one star on each of the chosen sheets. Vasya wants to end up with a different number of stars on each sheet (that is, there should be no two sheets with the same number of stars drawn on them). What is the minimum total number of stars he will have to draw to achieve this? | 28 |
53,348 | Problem 9.7. Two parallel lines are drawn through points $A(0 ; 14)$ and $B(0 ; 4)$. The first line, passing through point $A$, intersects the hyperbola $y=\frac{1}{x}$ at points $K$ and $L$. The second line, passing through point $B$, intersects the hyperbola $y=\frac{1}{x}$ at points $M$ and $N$.
What is $\frac{A L-A K}{B N-B M}$ ?
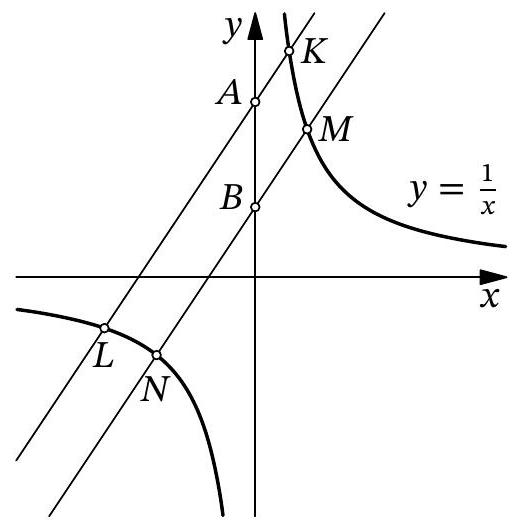 | 3.5 |
22,875 | Find the smallest natural number that cannot be represented in the form \(\frac{2^{a} - 2^{b}}{2^{c} - 2^{d}}\), where \(a, b, c, d\) are natural numbers. | 11 |
12,983 | There are \( n \geq 2 \) coins, each with a different positive integer value. Call an integer \( m \) sticky if some subset of these \( n \) coins have a total value \( m \). We call the entire set of coins a stick if all the sticky numbers form a consecutive range of integers. Compute the minimum total value of a stick across all sticks containing a coin of value 100. | 199 |
19,134 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{7} \frac{\sqrt{x+25}}{(x+25)^{2} \sqrt{x+1}} d x
$$ | \dfrac{1}{40} |
11,928 |
Through the center \( O \) of an equilateral triangle \( ABC \) with side length \( a \) runs a line \( A_1 B_1 \) which cuts segments \( x \) and \( y \) from sides \( AC \) and \( BC \) respectively, where \( x = AB_1 \) and \( y = BA_1 \). Prove that these segments satisfy the equation:
\[ 3xy - 2a(x + y) + a^2 = 0. \] | 3xy - 2a(x + y) + a^2 = 0 |
24,566 | Given the sets
$$
\begin{array}{l}
A=\{(x, y) \mid |x| + |y| = a, a > 0\}, \\
B=\{(x, y) \mid |xy| + 1 = |x| + |y|\}
\end{array}
$$
If $A \cap B$ forms the vertices of a regular octagon in the plane, find the value of $a$. | \sqrt{2} |
18,893 | Let $X$ be a point of intersection of circles $w_{1}$ and $w_{2}$ such that $X$ and $B$ lie on opposite sides of line $AC$. Prove that the point $X$ then lies on the altitude $BH$ of triangle $ABC$. | X \text{ lies on the altitude } BH |
25,011 | A group of adventurers is showing their loot. It is known that exactly 5 adventurers have rubies; exactly 11 have emeralds; exactly 10 have sapphires; exactly 6 have diamonds. Additionally, it is known that:
- If an adventurer has diamonds, then they have either emeralds or sapphires (but not both simultaneously);
- If an adventurer has emeralds, then they have either rubies or diamonds (but not both simultaneously).
What is the minimum number of adventurers that can be in such a group? | 16 |
19,228 | Prove that \( e^{z} e^{w} = e^{z+w} \) for any complex numbers \( z \) and \( w \). | e^{z} e^{w} = e^{z+w} |
61,014 | 3. The robot moves along straight segments, making turns of 90 degrees to the right or left every minute (neglect the time for turning). The robot travels 10 meters per minute. What is the minimum distance from the starting position that the robot can be after 9 minutes, if it did not turn during the first minute?
# | 10 |
68,206 | 6. (10 points) As shown in the figure, a rectangular block with dimensions $15 \mathrm{~cm}, 5 \mathrm{~cm}, 4 \mathrm{~cm}$ has a smaller rectangular block with dimensions $y \mathrm{~cm}, 5 \mathrm{~cm}, x \mathrm{~cm}$ (where $x, y$ are integers) cut out from it. The remaining volume is $120 \mathrm{~cm}^{3}$. What is $x+y=$ $\qquad$ . | 15 |
54,642 | 1. (3 points) The left figure below is the recently discovered Archimedes' "Stomachion" puzzle, dividing a square into 14 polygonal pieces: After research, experts found that these 14 pieces can be correctly drawn on a square with a side length of $12 \mathrm{~cm}$, as shown in the figure. Question: The area of the gray piece is $\qquad$ square centimeters. | 12 |
14,964 | In an isosceles trapezoid, the angle at the base is $50^{\circ}$, and the angle between the diagonals, adjacent to the lateral side, is $40^{\circ}$. Where is the center of the circumscribed circle located, inside or outside the trapezoid? | outside |
64,875 | A3. What is the largest integer for which each pair of consecutive digits is a square? | 81649 |
4,601 | It is allowed to multiply the number written on the board by 5 or to rearrange its digits (putting zero in the first position is not allowed). Is it possible to obtain the 100-digit number $222 \ldots 2225$ from the number 1 using these operations? | \text{No} |
53,656 | 4. Determine all polynomials $P(x)$ that for every real number $x$ satisfy the equation
$$
P(2 x)=8 P(x)+(x-2)^{2} .
$$ | P(x)=^{3}-\frac{1}{4}x^{2}+\frac{2}{3}x-\frac{4}{7} |
13,634 | A passenger train traveling from $A$ to $B$ has a speed of $60 \mathrm{~km} / \mathrm{h}$. The train, which departs later, is a fast train with a speed of $120 \mathrm{~km} / \mathrm{h}$ and must catch up to the passenger train at $B$. After covering $2 / 3$ of its journey, the passenger train continues at half its original speed and is caught by the fast train 80 kilometers before $B$. How far is $A$ from $B$? | 360 |
9,490 | From point $A$ to point $B$, which are 10 km apart, a car left at 7:00. After traveling $\frac{2}{3}$ of the way, the car passed point $C$, from which at that moment a cyclist left for point $A$. As soon as the car arrived at $B$, a bus immediately left from there in the opposite direction and arrived at $A$ at 9:00. How many kilometers from $B$ did the bus catch up with the cyclist, if the cyclist arrived at point $A$ at 10:00, and the speed of each participant was constant?
| 6 |
65,421 | One, (40 points) Let $S$ be a set of positive integers with the property: for any $x \in S$, the arithmetic mean of the remaining numbers in $S$ after removing $x$ is a positive integer, and it satisfies $1 \in S$, 2016 is the maximum element of $S$. Find the maximum value of $|S|$. | 32 |
22,469 | In triangle \(ABC\), the known angles are \(\angle B = 30^\circ\) and \(\angle A = 90^\circ\). On side \(AC\), there is a point \(K\), and on side \(BC\), there are points \(L\) and \(M\) such that \(KL = KM\) (point \(L\) lies on segment \(BM\)).
Find the length of segment \(LM\), given that \(AK = 4\), \(BL = 31\), and \(MC = 3\). | 14 |
20,789 | Find the largest real number \( p \) such that all three roots of the equation below are positive integers:
\[
5x^{3} - 5(p+1)x^{2} + (71p-1)x + 1 = 66p .
\] | 76 |
63,524 | 2. (1993 National High School Competition Question) There are 900 three-digit numbers, $100, 101, \cdots, 999$. When printing these three-digit numbers on cards, for example, 198 looks like 861 when flipped, while some cards do not, such as 531 which looks like IE9 when flipped. Therefore, some cards can be used for two numbers, thus the maximum number of cards that can be saved is $\qquad$. | 34 |
26,077 | On a particular street in Waterloo, there are exactly 14 houses, each numbered with an integer between 500 and 599, inclusive. The 14 house numbers form an arithmetic sequence in which 7 terms are even and 7 terms are odd. One of the houses is numbered 555 and none of the remaining 13 numbers has two equal digits. What is the smallest of the 14 house numbers?
(An arithmetic sequence is a sequence in which each term after the first is obtained from the previous term by adding a constant. For example, 3, 5, 7, 9 is an arithmetic sequence with four terms.) | 506 |
9,973 | A cube painted in black and white colors with each face as one square was placed on a square of a chessboard and rolled over it in such a way that the cube landed on every square exactly once. Is it possible to paint the cube and roll it across the board in such a way that each time the color of the square and the face of the cube touching it match? | \text{No} |
2,171 | B1. We consider numbers of two or more digits where none of the digits is 0. We call such a number thirteenish if every two adjacent digits form a multiple of 13. For example, 139 is thirteenish because $13=1 \times 13$ and $39=3 \times 13$.
How many thirteenish numbers of five digits are there? | 6 |
56,527 | A right-angled triangle with integer side lengths has one side with length 605 . This side is neither the shortest side nor the longest side of the triangle. What is the maximum possible length of the shortest side of this triangle? | 528 |
62,787 | $P$ and $Q$ are points on the semicircular arc with diameter $AB$. $R$ is a point on the radius $OB$, such that $O P R \angle = O Q R \angle = 10^{\circ}$. If $P O A \angle = 40^{\circ}$, what is the measure of $Q O B \angle$? | 20 |
53,498 | 1.39. A point $O$ inside a convex quadrilateral of area $S$ is reflected symmetrically with respect to the midpoints of its sides. Find the area of the quadrilateral with vertices at the resulting points.
## §4. Auxiliary Congruent Triangles
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly. | 2S |
58,493 | 1. (2 points) In trapezoid $A B C D$ with bases $A D=20$ and $B C=10$, circles constructed on sides $A B, B C$, and $C D$ as diameters intersect at one point. The length of diagonal $A C$ is 18. Find the length of $B D$. | 24 |
58,900 | 3. There are 5 rooms $A, B, C, D, E$ arranged in a circular pattern, with the number of people living in them being $17, 9, 14, 16, 4$ respectively. Now, adjustments are to be made so that the number of people in each room is the same, and it is stipulated that people can only move to the adjacent left or right room. How many people should each room move to the left or right so that the total number of people moved is minimized? | 11 |
67,589 | ## Task B-3.6.
A rectangle is given with side lengths $a$ and $b$, where $a = \frac{4}{7} b$. Determine the probability that a randomly selected point within the given rectangle is closer to the shorter side and is less than $\frac{a}{8}$ away from it. | \frac{1}{8} |
10,124 | Given a triangular prism $O-ABC$ with the three perpendicular edges $OA$, $OB$, $OC$, point $P$ is any point within the base $\triangle ABC$, and $\alpha, \beta, \gamma$ are the angles between $OP$ and the three lateral faces respectively. Prove that $\frac{\pi}{2} < \alpha + \beta + \gamma \leq 3 \arcsin \frac{\sqrt{3}}{3}$. | \frac{\pi}{2} < \alpha + \beta + \gamma \leq 3 \arcsin \frac{\sqrt{3}}{3} |
68,747 | 24.1.3 ** In a finite sequence of real numbers, the sum of any 3 consecutive terms is negative, and the sum of any 4 consecutive terms is positive. Find the maximum number of terms \( r \) in this sequence. | 5 |
54,321 | 6. 8 girls and 25 boys stand in a circle, with at least two boys standing between any two girls. Therefore, there are $\qquad$ different arrangements (arrangements that coincide by just rotating the circle are considered the same). | \frac{16!25!}{9!} |
53,115 | How many ways can 8 mutually non-attacking rooks be placed on the $9 \times 9$ chessboard (shown here) so that all 8 rooks are on squares of the same colour?
[Two rooks are said to be attacking each other if they are placed in the same row or column of the board.] | 40320 |
4,794 | The rank of a rational number \( q \) is the unique \( k \) for which \( q = \frac{1}{a_1} + \cdots + \frac{1}{a_k} \), where each \( a_i \) is the smallest positive integer such that \( q \geq \frac{1}{a_1} + \cdots + \frac{1}{a_i} \). Let \( q \) be the largest rational number less than \( \frac{1}{4} \) with rank 3, and suppose the expression for \( q \) is \( \frac{1}{a_1} + \frac{1}{a_2} + \frac{1}{a_3} \). Find the ordered triple \( \left(a_1, a_2, a_3\right) \). | (5, 21, 421) |
52,833 | 2. Determine whether the number $N=7 \times 9 \times 13+2020 \times 2018 \times 2014$ is prime or composite. Justify your answer. | Composite |
28,951 | 5th USAMO 1976 Problem 4 A tetrahedron ABCD has edges of total length 1. The angles at A (BAC etc) are all 90 o . Find the maximum volume of the tetrahedron. Solution | \frac{5\sqrt{2}-7}{162} |
57,829 | 20. For any positive integer $n$, let $f(n)$ denote the index of the highest power of 2 which divides $n!$, e.g. $f(10)=8$ since $10!=2^{8} \times 3^{4} \times 5^{2} \times 7$. Find the value of $f(1)+f(2)+\cdots+f(1023)$.
(3 marks)
對於任何正整數 $n$, 設 $f(n)$ 為可整除 $n$ ! 的 2 的最高乘冪的指數。例如:因為 $10!=2^{8} \times 3^{4} \times 5^{2} \times 7$, 所以 $f(10)=8$ 。求 $f(1)+f(2)+\cdots+f(1023)$ 的值。 | 518656 |
11,273 | For any continuous real-valued function $f$ defined on the interval $[0,1],$ let \[\mu(f)=\int_0^1f(x)\,dx,\text{Var}(f)=\int_0^1(f(x)-\mu(f))^2\,dx, M(f)=\max_{0\le x\le 1}|f(x)|.\] Show that if $f$ and $g$ are continuous real-valued functions defined on the interval $[0,1],$ then \[\text{Var}(fg)\le 2\text{Var}(f)M(g)^2+2\text{Var}(g)M(f)^2.\] | \text{Var}(fg)\le 2\text{Var}(f)M(g)^2+2\text{Var}(g)M(f)^2 |
56,843 | A man had seven married sons. Before his death, he distributed his oxen among his family members. The eldest son received a certain number of oxen, and his wife received one-ninth of the remainder. The second son received one more ox than his elder brother, and his wife also received one-ninth of the remainder. The third son similarly received one more ox than the second son, and his wife also received one-ninth of the remainder, and so on for the rest of his sons and their wives. In this way, each family received the same number of oxen. How many oxen did the man have? | 56 |
21,618 | Let \(\mathcal{C}\) be the hyperbola \(y^{2}-x^{2}=1\). Given a point \(P_{0}\) on the \(x\)-axis, we construct a sequence of points \((P_{n})\) on the \(x\)-axis in the following manner: let \(\ell_{n}\) be the line with slope 1 passing through \(P_{n}\), then \(P_{n+1}\) is the orthogonal projection of the point of intersection of \(\ell_{n}\) and \(\mathcal{C}\) onto the \(x\)-axis. (If \(P_{n}=0\), then the sequence simply terminates.)
Let \(N\) be the number of starting positions \(P_{0}\) on the \(x\)-axis such that \(P_{0}=P_{2008}\). Determine the remainder of \(N\) when divided by 2008. | 254 |
4,180 | We are distributing some identical candies into three non-empty piles such that the number of candies in each pile is different. How many candies do we have if the number of different possible groupings is exactly one more than the number of candies?
We have a certain number of identical candies, and we need to distribute them into three non-empty piles in such a way that the number of candies in each pile is different. If the number of different possible groupings is exactly one more than the number of candies, how many candies do we have? | 18 |
9,121 | 7.3. From the highway, four roads sequentially lead to four villages A, B, C, D. It is known that the route by road/highway/road from A to B is 9 km, from A to C - 13 km, from B to C - 8 km, from B to D - 14 km. Find the length of the route by road/highway/road from A to D. Explain your answer. | 19 |
52,610 | Example 2. Factorize in the set of real numbers $R$:
$$
a^{4}-14 a^{2}+25
$$ | (a+1+\sqrt{6})(a+1-\sqrt{6})(a-1+\sqrt{6})(a-1-\sqrt{6}) |
64,230 | 18. There were 36 participants in a party, some of whom shook hands with each other, such that any two participants shook hands with each other at most once. Each participant then recorded the number of handshakes made, and it was found that no two participants with the same number of handshakes made had shaken hands with each other. Find the maximum total number of handshakes in the party. (When two participants shook hand with each other this will be counted as one handshake.)
(2 marks)
某次聚會共有 36 人參加, 當中有些人曾經互相握手, 而每兩人之間握手最多一次。事後每人均記錄了自己的握手次數, 並發現握手次數相同的人之間均沒有互相握手。求聚會中握手總次數的最大可能值(兩人互相握手時算作一次)。
(2 分) | 546 |
28,510 | Problem 8.3. In triangle $ABC$, the sides $AC=14$ and $AB=6$ are known. A circle with center $O$, constructed on side $AC$ as the diameter, intersects side $BC$ at point $K$. It turns out that $\angle BAK = \angle ACB$. Find the area of triangle $BOC$.
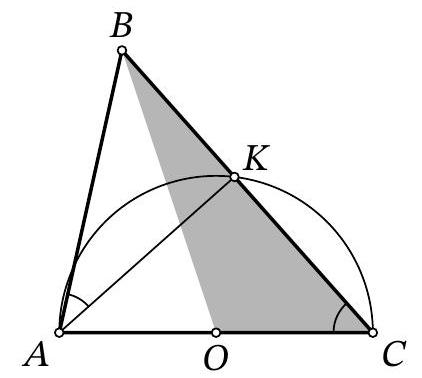 | 21 |
4,784 | There are 94 safes and 94 keys. Each key can open only one safe, and each safe can be opened by only one key. We place randomly one key into each safe. 92 safes are then randomly chosen, and then locked. What is the probability that we can open all the safes with the two keys in the two remaining safes?
(Once a safe is opened, the key inside the safe can be used to open another safe.) | \dfrac{1}{47} |
7,329 | Given sets \( A = \{(x, y) \mid y = a x + 2\} \) and \( B = \{(x, y) \mid y = |x+1| \} \), and that \( A \cap B \) is a singleton set, determine the range of values for the real number \( a \). | (-\infty, -1] \cup [1, \infty) |
16,104 | Through a point \(A\) outside a circle, two tangents \(A T_{1}\) and \(A T_{2}\) are drawn to the circle. From an arbitrary point \(M\) on the circle, three rays \(M M_{1}, M T_{1}, M T_{2}\) are drawn, forming angles \(\varepsilon, \varphi, \psi\) with the tangent to the circle at point \(M\), respectively \((M_{1}\) being the second intersection point of the line \(AM\) with the circle\)). Prove that the mentioned angles are related by the equation:
\[
\operatorname{ctg} \varepsilon = \frac{1}{2} (\operatorname{ctg} \varphi + \operatorname{ctg} \psi)
\] | \operatorname{ctg} \varepsilon = \frac{1}{2} (\operatorname{ctg} \varphi + \operatorname{ctg} \psi) |
55,155 | Given 10 points on a plane. We draw the perpendicular bisectors of the segments determined by them. In how many points can these lines intersect at most? | 750 |
59,990 | ## Condition of the problem
Calculate the definite integral:
$$
\int_{0}^{2 \operatorname{arctan} \frac{1}{2}} \frac{1+\sin x}{(1-\sin x)^{2}} d x
$$ | \frac{26}{3} |
16,774 | Two identical cylindrical vessels are connected at the bottom level by a small section of pipe with a valve. While the valve was closed, water was poured into the first vessel and oil into the second vessel so that the level of the liquids was the same and equal to $h=40$ cm. At what level will the water in the first vessel be when the valve is opened? The density of water is 1000 kg/m\(^3\) and the density of oil is 700 kg/m\(^3\). Neglect the volume of the connecting pipe. Provide the answer in centimeters. | 34 |
29,280 | Question 71: Positive real numbers $x, y$ satisfy the following conditions: there exist $a \in[0, x], b \in[0, y]$, such that $a^{2}+y^{2}=2$, $b^{2}+x^{2}=1, a x+b y=1$, then the maximum value of $x+y$ is $\qquad$ _. | \sqrt{5} |
62,100 | [ Counting in two ways ] $[\quad$ Trees $]$
A travel agency ran a promotion: "Buy a trip to Egypt, bring four friends who also buy a trip, and get the cost of your trip back." During the promotion, 13 buyers came on their own, and the rest were brought by friends. Some of them brought exactly four new customers, while the other 100 did not bring anyone. How many tourists went to the Land of the Pyramids for free? | 29 |
26,749 | B5. Simon has 2017 blue blocks numbered from 1 to 2017. He also has 2017 yellow blocks numbered from 1 to 2017. Simon wants to arrange his 4034 blocks in a row. He wants to do so in such a way that for every $k=1,2, \ldots, 2017$ the following conditions are met:
- to the left of the blue block with number $k$ there are $k$ or more yellow blocks;
- to the right of the yellow block with number $k$ there are $k$ or fewer blue blocks.
Determine all possible numbers of the 1000th block from the left in the row.
## C-problems
For the C-problems, not only the answer is important; your reasoning and the way of solving it must also be clearly written down. Solve each C-problem on a separate sheet of paper. Each correctly worked out C-problem is worth 10 points. Partial solutions can also earn points. Therefore, write everything clearly and submit your scratch paper (for each problem!) as well. | 500 |
18,828 | Example 4.22. Find the general solution of the equation
$$
y^{\prime \prime}+6 y^{\prime}+9 y=14 e^{-3 x} .
$$ | y = \left( C_1 + C_2 x + 7x^2 \right) e^{-3x} |
3,935 | Given several points and vectors $\overrightarrow{A B}$ for some pairs (A, B) of these points, such that the number of vectors starting at each point is equal to the number of vectors ending at that point. Prove that the sum of all the chosen vectors is $\overrightarrow{0}$. | \overrightarrow{0} |
65,191 | Let $\theta$ be a constant number such that $0\leq \theta \leq \pi.$
Evaluate
\[ \int_0^{2\pi} \sin 8x|\sin (x-\theta)|\ dx. \] | -\frac{4}{63} \sin 8\theta |
31,416 | Problem 2. Determine the perimeter of the scalene triangle $\mathrm{ABC}$ knowing that
$$
p^{2} \cdot \overrightarrow{G I}=(4 p-b-c) \cdot \overrightarrow{A I}+(4 p-c-a) \cdot \overrightarrow{B I}+(4 p-a-b) \cdot \overrightarrow{C I}
$$
where $\mathrm{G}$ is the centroid of $\triangle \mathrm{ABC}$, I is the incenter of $\triangle \mathrm{ABC}$, and $p$ is the semiperimeter of $\triangle \mathrm{ABC}$. | 12 |
28,189 | 4. In an acute-angled triangle $A B C$, the altitudes $A A_{1}, B B_{1}$, and $C C_{1}$ are dropped. A point $T$ is chosen on the plane such that the lines $T A$ and $T B$ are tangents to the circumcircle of triangle $A B C$, and point $O$ is the center of this circle. The perpendicular dropped from point $T$ to the line $A_{1} B_{1}$ intersects the line $C C_{1}$ at point $K$, and the line passing through point $C_{1}$ parallel to $O K$ intersects the segment $C O$ at point $L$. Find the angle $\angle C L A_{1}$. | 90 |
66,991 | 2. Plot on the plane $(x ; y)$ the set of points satisfying the equation $\left|16+6 x-x^{2}-y^{2}\right|+|6 x|=16+12 x-x^{2}-y^{2}$, and find the area of the resulting figure. | 25\pi-25\arcsin0.8+12 |
51,097 | 7. A rectangle $A B C D$ with a diagonal of length $20 \text{ cm}$ is circumscribed by a circle. The side $\overline{C D}$ of the rectangle $A B C D$ is the base of an isosceles triangle whose third vertex $E$ is on the shorter arc determined by the chord $\overline{C D}$ of the circle circumscribed around the rectangle. What is the length of the side $\overline{A D}$ of the rectangle if the area of the rectangle $A B C D$ is equal to the area of triangle DCE?
SCHOOL/CITY COMPETITION IN MATHEMATICS21st January 2016.8th grade-elementary school
Problems worth 6 points: | 4 |
10,951 | Two circles \(\mathcal{C}_{1}\) and \(\mathcal{C}_{2}\) intersect in \(P\) and \(Q\). A line through \(P\) intersects \(\mathcal{C}_{1}\) and \(\mathcal{C}_{2}\) again in \(A\) and \(B\), respectively, and \(X\) is the midpoint of \(AB\). The line through \(Q\) and \(X\) intersects \(\mathcal{C}_{1}\) and \(\mathcal{C}_{2}\) again in \(Y\) and \(Z\), respectively. Prove that \(X\) is the midpoint of \(YZ\). | X \text{ is the midpoint of } YZ |
58,926 | 14. Fill in the blanks with 1 and 10, using each number only once. It is required that the number in $\square$ equals the difference (larger minus smaller) of the two numbers above it to the left and right, and the number in $\mathrm{O}$ equals the sum of the two numbers above it to the left and right. Find: the value of $A$.
Fill in the blanks with 1 and 10, using each number only once. It is required that the number in $\square$ equals the difference (larger minus smaller) of the two numbers above it to the left and right, and the number in $\mathrm{O}$ equals the sum of the two numbers above it to the left and right. Find: the value of $A$. | 9 |
62,322 | Example 4 Given that $\alpha$ is an acute angle, $\beta$ is an obtuse angle, and $\sec (\alpha-2 \beta) 、 \sec \alpha 、 \sec (\alpha+2 \beta)$ form an arithmetic sequence, find the value of $\frac{\cos \alpha}{\cos \beta}$. | -\sqrt{2} |
5,415 |
Lesha did not hesitate to calculate the sum
$$
9+99+999+\ldots+\underbrace{9 \ldots 9}_{2017}
$$
and wrote it on the board. How many times does the digit 1 appear in the final result? | 2013 |
56,022 | Consider the $4\times4$ array of $16$ dots, shown below.
[asy]
size(2cm);
dot((0,0));
dot((1,0));
dot((2,0));
dot((3,0));
dot((0,1));
dot((1,1));
dot((2,1));
dot((3,1));
dot((0,2));
dot((1,2));
dot((2,2));
dot((3,2));
dot((0,3));
dot((1,3));
dot((2,3));
dot((3,3));
[/asy]
Counting the number of squares whose vertices are among the $16$ dots and whose sides are parallel to the sides of the grid, we find that there are nine $1\times1$ squares, four $2\times2$ squares, and one $3\times3$ square, for a total of $14$ squares. We delete a number of these dots. What is the minimum number of dots that must be deleted so that each of the $14$ squares is missing at least one vertex? | 4 |
9,520 | Prove: If \(a, b, n\) are natural numbers and \(a^{n} \mid b\), then \(a^{n+1} \mid (a+1)^{b} - 1\). | a^{n+1} \mid (a+1)^{b} - 1 |
156 | Let \( G \) be a graph such that the average degree of its vertices is at least \( \tilde{\mathrm{A}}(1 / 2 + c) n \), with \( c > 0 \). Show that \( G \) contains at least \( c \binom{n}{3} \) triangles. | c \binom{n}{3} |
52,108 | 10.5. A circle is inscribed with 103 numbers. It is known that among any five consecutive numbers, there are at least two positive numbers. What is the minimum number of positive numbers that can be among these 103 written numbers? | 42 |
62,421 | 3.2. Two identical cylindrical vessels are connected at the bottom by a small-section pipe with a valve. While the valve was closed, water was poured into the first vessel, and oil into the second, so that the level of the liquids was the same and equal to \( h = 40 \, \text{cm} \). At what level will the water stabilize in the first vessel if the valve is opened? The density of water is 1000 kg \(/ \text{m}^3\), and the density of oil is 700 kg \(/ \text{m}^3\). Neglect the volume of the connecting pipe. Provide the answer in centimeters. | 34 |
57,217 | Example 9 If positive integers $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$ satisfy
$$
x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=x_{1} x_{2} x_{3} x_{4} x_{5} \text {, }
$$
find the maximum value of $x_{5}$. | 5 |
64,048 | 10.2. Find all values of the parameter $a$ for which the equation $|x+a|=\frac{1}{x}$ has exactly two roots. | -2 |
51,710 | 4. On a plane, an infinite number of parallel lines are drawn, each separated from the next by a distance of 1. A circle with a diameter of 1 is randomly thrown onto the plane. Find the probability that a line intersecting the circle divides it into parts such that the ratio of the areas (of the smaller to the larger part) does not exceed the number \((2 \pi - 3 \sqrt{3}) : (10 \pi + 3 \sqrt{3})\). | \frac{2-\sqrt{3}}{2} |
66,120 | 5. In a $7 \times 7$ unit square grid, there are 64 grid points, and there are many squares with these grid points as vertices. How many different values can the areas of these squares have?
(21st Jiangsu Province Junior High School Mathematics Competition) | 18 |
29,694 | Example 13. Calculate the circulation of the vector field given in spherical coordinates: $2=r \mathbf{e}_{r}+(R+r) \sin \theta \mathbf{e}_{\varphi}$, along the circle $L:\{r=$ $\left.R, \theta=\frac{\pi}{2}\right\}$ in the direction of increasing angle $\varphi$ directly and using Stokes' theorem. | 4\piR^{2} |
64,366 | Task B-1.2. In triangle $\triangle A B C$, the measures of the angles at vertex $A$ and vertex $B$ are $\alpha=38^{\circ}$ and $\beta=52^{\circ}$, respectively. Calculate the measure of the angle formed by the external angle bisector at vertex $B$ and the line on which side $\overline{A C}$ lies. | 26 |
67,767 | 17. Happy Sums (from 8th grade, 4 points). In the "Happy Sum" lottery, there are $N$ balls numbered from 1 to $N$. During the main draw, 10 balls are randomly drawn. During the additional draw, 8 balls are randomly selected from the same set of balls. The sum of the numbers on the drawn balls in each draw is announced as the happy sum, and players who predicted this sum win a prize.
Can it be that events $A$ "the happy sum in the main draw is 63" and $B$ "the happy sum in the additional draw is 44" are equally likely? If yes, under what condition? | 18 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.