id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
56,979 | 3. Let's call a natural number an almost palindrome if it can be transformed into a palindrome by changing one of its digits. How many nine-digit almost palindromes exist? (20 points) | 3240000 |
14,923 | 19. Determine the largest prime number less than 5000 of the form $a^{n}-1$, where $a$ and $n$ are positive integers, and $n$ is greater than 1 . | 127 |
67,982 | David has a collection of 40 rocks, 30 stones, 20 minerals and 10 gemstones. An operation consists of removing three objects, no two of the same type. What is the maximum number of operations he can possibly perform?
[i]Ray Li[/i] | 30 |
59,979 | 12. 8 girls and 25 boys stand in a circle, with at least two boys standing between any two girls. Therefore, there are $\qquad$ different arrangements (arrangements that can be made identical by rotating the circle are considered the same). | \frac{16!\cdot25!}{9!} |
63,629 | 8. If a positive integer $n$ makes the equation $x^{3}+y^{3}=z^{n}$ have positive integer solutions $(x, y, z)$, then $n$ is called a "good number". Then, the number of good numbers not exceeding 2,019 is $\qquad$ . | 1346 |
64,903 | ## Task Condition
Find the derivative.
$$
y=3 x-\ln \left(1+\sqrt{1-e^{6 x}}\right)-e^{-3 x} \cdot \arcsin \left(e^{3 x}\right)
$$ | 3e^{-3x}\cdot\arcsin(e^{3x}) |
62,935 | 14. (15 points) Math Competition, 8 fill-in-the-blank questions, 4 points for each correct answer, 0 points for each incorrect answer; 6 short-answer questions, 7 points for each correct answer, 0 points for each incorrect answer, 400 participants, what is the minimum number of people who have the same total score? | 8 |
1,752 | ## Task Condition
Find the derivative.
$$
y=\frac{1}{2} \cdot \operatorname{arctan} \frac{e^{x}-3}{2}
$$ | \dfrac{e^x}{4 + (e^x - 3)^2} |
734 | A $5 \mathrm{~cm}$ by $5 \mathrm{~cm}$ pegboard and a $10 \mathrm{~cm}$ by $10 \mathrm{~cm}$ pegboard each have holes at the intersection of invisible horizontal and vertical lines that occur in $1 \mathrm{~cm}$ intervals from each edge. Pegs are placed into the holes on the two main diagonals of both pegboards. The $5 \mathrm{~cm}$ by $5 \mathrm{~cm}$ pegboard is shown; it has 16 holes. The 8 shaded holes have pegs, and the 8 unshaded holes do not. How many empty holes does the $10 \mathrm{~cm}$ by $10 \mathrm{~cm}$ pegboard have?
 | 64 |
55,375 | [
The ratio in which the bisector divides the side
] Similarity
[The ratio of the areas of triangles with a common base or common height] Class In triangle $A B C$, the bisectors $C F$ and $A D$ are drawn. Find the ratio $S_{A F D}: S_{A B C}$, if $A B: A C: B C=21: 28: 20$.
# | 1:4 |
56,968 | How to connect 50 cities with the smallest number of air routes so that you can travel from any city to any other, making no more than two transfers?
# | 49 |
60,208 | 9.2 In the fishing, 11 experienced fishermen and $n$ children participated. Together they caught $n^{2}+$ $5 n+22$ fish, with all experienced fishermen catching the same amount, and all children catching the same amount, but each 10 less than an experienced fisherman. Who was there more of at the fishing - experienced fishermen or children? | 11 |
25,099 | 7.5. Vasya had 101 real coins. One of them was replaced with a fake one (it differs in weight, but it is unknown whether it is lighter or heavier than a real coin). Vasya wants to find as many real coins as possible in one weighing on a balance scale without weights. What should he do and how many real coins will he be able to find? | 50 |
24,711 | In triangle \(ABC\), angle \(C\) is \(60^\circ\) and the radius of the circumcircle of this triangle is \(2\sqrt{3}\).
A point \(D\) is taken on the side \(AB\) such that \(AD = 2DB\) and \(CD = 2\sqrt{2}\). Find the area of triangle \(ABC\). | 3\sqrt{2} |
59,843 | At the New Year's school party in the city of Lzheretsark, 301 students came. Some of them always tell the truth, while the rest always lie. Each of the 200 students said: "If I leave the hall, then among the remaining students, the majority will be liars." Each of the other students stated: "If I leave the hall, then among the remaining students, there will be twice as many liars as those who tell the truth." How many liars were at the party? | 151 |
448 | 14.Can there be two lucky tickets among ten consecutive tickets? A ticket is considered lucky if the sums of its first three and last three digits are equal. | Yes |
52,546 | 15. Given that $f$ is a real-valued function on the set of all real numbers such that for any real numbers $a$ and $b$,
$$
\mathrm{f}(a \mathrm{f}(b))=a b
$$
Find the value of $\mathrm{f}(2011)$. | 2011 |
64,084 | 1. On an island, there are 10 people, some of whom are honest people who always tell the truth, and others are liars who always lie. Each of them has thought of a real number (not necessarily an integer). Then, the first person says: “My number is greater than 1.” The second person says: “My number is greater than 2.” ... The tenth person says: “My number is greater than 10.” Afterwards, these ten people stand in a line in some order and say one by one: “My number is less than 1.” “My number is less than 2.” ... “My number is less than 10.” (Each person says exactly one sentence) How many honest people can there be at most among these people? | 9 |
12,619 | Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x$ and $y$,
$$
f(f(x+1)+y-1)=f(x)+y
$$
## Solutions to the exercises | f(x) = x |
24,959 | Find the measure of angle \( B \widehat{A} D \), given that \( D \widehat{A C}=39^{\circ} \), \( A B = A C \), and \( A D = B D \). | 47^{\circ} |
14,703 | There are 2021 points placed on a circle. Kostya marks a point, then marks the next point to the right, then marks the point to the right skipping one, then the point to the right skipping two, and so on. On which move will a point be marked for the second time? | 67 |
56,198 | 2. For which natural numbers $n$ will there exist a natural number $k$ such that the number $2 k^{2}+k+2018$ is divisible by $n$ ! (as usual, $n$ ! denotes the product of all natural numbers not exceeding $n$, for example, $4!=1 \cdot 2 \cdot 3 \cdot 4) ?$ | 1,2,3,4 |
65,227 | 14. Given that $c$ is a positive integer not exceeding 2017, and there exist positive integers $a$ and $b$ such that
$$
2^{a} \times 5^{b}=\left(a^{3}+a^{2}+a+1\right) c \text {. }
$$
Find the maximum value of $c$. | 1000 |
24,381 | What is the largest integer \( n \) such that
$$
\frac{\sqrt{7}+2 \sqrt{n}}{2 \sqrt{7}-\sqrt{n}}
$$
is an integer? | 343 |
51,184 | 18. In how many different ways can we rearrange the twelve integers 1 to 12 on the face of a clock so that the sum of any three adjacent integers after the rearrangement is divisible by 3 ?
(2 marks)
有多少種不同的方法可把鐘面上 1 至 12 等 12 個整數重新排列, 使得排列後任意三個相鄰的整數之和皆可被 3 整除?
(2分) | 82944 |
67,581 | Find the number of $4$-digit numbers (in base $10$) having non-zero digits and which are divisible by $4$ but not by $8$. | 729 |
23,809 | In parallelogram $ABCD$ , let $O$ be the intersection of diagonals $\overline{AC}$ and $\overline{BD}$ . Angles $CAB$ and $DBC$ are each twice as large as angle $DBA$ , and angle $ACB$ is $r$ times as large as angle $AOB$ . Find $\lfloor 1000r \rfloor$ | 777 |
63,681 | In the acute triangle $ABC$, $\angle BAC = 60^\circ$. The circle constructed on the side $BC$ as a diameter intersects the side $AB$ at $D$ and the side $AC$ at $E$. Determine the ratio of the area of the quadrilateral $BDEC$ to the area of triangle $ABC$.
---
The translation is provided as requested, maintaining the original formatting and structure. | \frac{3}{4} |
19,032 | Given positive real numbers \(x, y, z\) such that \(x + y + z = 3\), show that \(\sqrt{x} + \sqrt{y} + \sqrt{z} \geq xy + yz + zx\). | \sqrt{x} + \sqrt{y} + \sqrt{z} \geq xy + yz + zx |
50,905 | 11.4. Given a cube $A B C D A_{1} B_{1} C_{1} D_{1}$ with edge length a. The ends of the segment intersecting edge $C_{1} D_{1}$ lie on the lines $A A_{1}$ and $B C$. What is the minimum length that this segment can have | 3a |
16,799 | Let \( F \) be the number of integral solutions of \( x^{2}+y^{2}+z^{2}+w^{2}=3(x+y+z+w) \). Find the value of \( F \). | 208 |
65,047 | 19. In a magical country, there are only two types of people, type $\mathrm{A}$ people who only tell the truth, and type $\mathrm{B}$ people who only tell lies. One day, 2014 citizens of this country lined up, and each one said: “There are more type $\mathbf{B}$ people behind me than type $\mathbf{A}$ people in front of me.” Therefore, among these 2014 citizens, there are _— type A people. | 1007 |
1,147 | On graph paper, a "corner" of 3 cells was colored, after which the following operation was repeated 100 times: color all cells adjacent (by side) to any of the already colored cells. How many cells in total (including the cells of the original corner) were colored? | 20503 |
57,461 | A bag of coconuts is to be shared among five children and a monkey. One of the five children, without the others knowing, divided the coconuts in the bag into five equal parts. This way, he got one coconut as a remainder, which he gave to the monkey, and then left with one-fifth of the coconuts. The second child also divided the remaining coconuts into five equal parts, and he too got one as a remainder, which he gave to the monkey, and left with one-fifth of the coconuts. The other three children did the same. Finally, the five children came together and divided the remaining coconuts into five equal parts, and once again got one coconut as a remainder, which they gave to the monkey.
What is the minimum number of coconuts that were originally in the bag? | 15621 |
59,557 | 16. Bridges. (From 9th grade, 3 points) Along the southern shore of an endless sea, there stretches an archipelago of an infinite number of islands. The islands are connected by an infinite chain of bridges, and each island is connected by a bridge to the shore. In the event of a strong earthquake, each bridge independently of the others is destroyed with a probability of $p=0.5$. What is the probability that after a strong earthquake, one can cross from the first island to the shore using the surviving bridges? | \frac{2}{3} |
33,935 | 9.2. On a line, there are blue and red points, with no fewer than 5 red points. It is known that on any segment with endpoints at red points, containing a red point inside, there are at least 4 blue points. And on any segment with endpoints at blue points, containing 3 blue points inside, there are at least 2 red points. What is the maximum number of blue points that can be on a segment with endpoints at red points, not containing other red points? | 4 |
23,191 | Given \( x, y, z \in \mathbf{R} \) with \( 0 < z < y < x < \frac{\pi}{2} \), prove that:
\[ \frac{\pi}{2} + 2 \sin x \cdot \cos y + 2 \sin y \cdot \cos z > \sin 2x + \sin 2y + \sin 2z. \] | \frac{\pi}{2} + 2 \sin x \cdot \cos y + 2 \sin y \cdot \cos z > \sin 2x + \sin 2y + \sin 2z |
53,705 | 2. Let $a_{1}, a_{2}, \ldots$ be a sequence of integers defined by $a_{1}=3, a_{2}=3$, and
$$
a_{n+2}=a_{n+1} a_{n}-a_{n+1}-a_{n}+2
$$
for all $n \geq 1$. Find the remainder when $a_{2020}$ is divided by 22 . | 11 |
517 | Points \( A, B, C, D \) are on the same circle, and \( BC = CD = 4 \). Let \( E \) be the intersection of \( AC \) and \( BD \), with \( AE = 6 \). If the lengths of segments \( BE \) and \( DE \) are both integers, what is the length of \( BD \)? | 7 |
33,551 | Question 95, Given 0 as the circumcenter of $\triangle A B C$, satisfying $\overrightarrow{C O}=t \cdot \overrightarrow{C A}+\left(\frac{1}{2}-\frac{3 t}{4}\right) \cdot \overrightarrow{C B}(t \in R \backslash\{0\})$, if $|A B|=3$, try to find the maximum value of the area of $\triangle A B C$. | 9 |
51,098 | One hundred musicians are planning to organize a festival with several concerts. In each concert, while some of the one hundred musicians play on stage, the others remain in the audience assisting to the players. What is the least number of concerts so that each of the musicians has the chance to listen to each and every one of the other musicians on stage? | 9 |
67,285 | Example 2 Find the range of $y=\sqrt{x^{2}-2 x+5}-$ $\sqrt{x^{2}-6 x+13}$. | (-2,2) |
19,904 | Example 3. Find the integral $\int \sin ^{4} x d x$. | \dfrac{3}{8}x - \dfrac{1}{4} \sin 2x + \dfrac{1}{32} \sin 4x + C |
11,218 | A guard has detained an outsider and wants to expel him. The outsider then stated that he made a bet with his friends for 100 coins that the guard would not expel him (if the guard expels him, the outsider pays his friends 100 coins; otherwise, his friends pay him 100 coins). The outsider, deciding to buy off the guard, offered him to name a sum. What is the maximum number of coins the guard can demand so that the outsider, guided only by his own benefit, will definitely pay the guard? | 199 |
24,042 | Let \( f: \mathbb{R} \rightarrow \mathbb{R} \) be a differentiable function such that \( f(0) = 0 \), \( f(1) = 1 \), and \( |f'(x)| \leq 2 \) for all real numbers \( x \). If \( a \) and \( b \) are real numbers such that the set of possible values of \( \int_{0}^{1} f(x) \, dx \) is the open interval \( (a, b) \), determine \( b - a \). | \dfrac{3}{4} |
10,588 | A numerical sequence is defined by the conditions: \( a_{1}=1 \), \( a_{n+1}=a_{n}+\left \lfloor \sqrt{a_{n}} \right \rfloor \).
How many perfect squares are among the first terms of this sequence that do not exceed 1,000,000? | 10 |
66,161 | 7. $\left[\left(\frac{1+\sqrt{5}}{2}\right)^{2009}\right]$ when divided by 7 leaves a remainder of
The above text is translated into English, please keep the original text's line breaks and format, and output the translation result directly. | 6 |
30,986 | 7.4. Find the volume of a regular triangular pyramid, the midpoint of the height of which is at a distance of 2 and $\sqrt{7}$ from the lateral face and the lateral edge, respectively. Round your answer to two decimal places if necessary. | 112\sqrt{7} |
6,384 | Determine all functions from $\mathbb{Z}$ to $\mathbb{Z}$ satisfying:
$$
\forall(x, y) \in \mathbb{Z}^{2}, f(x+y)=f(x)+f(y)+2
$$ | f(x) = ax - 2 |
30,713 | The height of the isosceles trapezoid $ABCD$ with bases $AD$ and $BC$ is $4 \sqrt{3}$, the diagonals of the trapezoid intersect at point $O, \angle AOD=120^{\circ}$. Find the midline of the trapezoid. | 12 |
31,030 | Example 4 Let the natural number $n \geqslant 5, n$ different natural numbers $a_{1}, a_{2}, \cdots, a_{n}$ have the following property: for any two different non-empty subsets $A$ and $B$ of the set $S=$ $\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, the sum of all numbers in $A$ and the sum of all numbers in $B$ will not be equal. Under the above conditions, find the maximum value of $\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}$. (1994 Shanghai Competition Problem) | 2-\frac{1}{2^{n-1}} |
12,567 | Given that $M$ is the midpoint of the minor arc $\overparen{AC}$ and $B$ is any point on the arc $\overparen{AM}$, construct $MD \perp BC$ at point $D$. Prove:
$$
BD = \frac{1}{2}(BC - AB).
$$ | BD = \frac{1}{2}(BC - AB) |
27,107 | 6. A circle, the center of which lies on the line $y=b$, intersects the parabola $y=\frac{3}{4} x^{2}$ at least at three points; one of these points is the origin, and two of the remaining points lie on the line $y=\frac{3}{4} x+b$. Find all values of $b$ for which the described configuration is possible. | \frac{25}{12} |
59,600 | 337. Find the condition under which the numbers $a, b, c$ would be the $p$-th, $n$-th, $k$-th terms of the same arithmetic progression. | (n-k)+b(k-p)+(p-n)=0 |
16,729 | There are 8 balls, each labeled with a number: $2, 3, 4, 5, 6, 7, 8, 9$. In how many ways can the balls be placed into three boxes such that no box contains both a number and one of its divisors? | 432 |
62,075 | 4. Add three digits after 764 to make the resulting six-digit number divisible by 8, 9, and 11. | 764280 |
54,360 | 31. Let $x$ and $y$ be positive integers such that $27 x+35 y \leq 945$. Find the largest possible value of $x y$. | 234 |
52,601 | 8. The number of different shapes of ellipses with eccentricity $e=\log _{p} q$ (where $p, q$ are positive integers not exceeding 9) is
保留了源文本的换行和格式。 | 26 |
32,688 | If there exists a positive integer $m$ such that $m!$ ends with exactly $n$ zeros, then the positive integer $n$ is called a "factorial tail". How many numbers less than 1992 are not "factorial tails"? | 396 |
989 | 1. Given $n>2$ natural numbers, among which there are no three equal, and the sum of any two of them is a prime number. What is the largest possible value of $n$? | 3 |
21,482 | Given sets \( M = \left\{ x \mid x^{2} - 9 > 0 \right\} \) and \( N = \left\{ x \in \mathbf{Z} \mid x^{2} - 8x + a < 0 \right\} \). If the number of subsets of \( M \cap N \) is 4, then the range of the real number \( a \) is \(\qquad\). | [12, 15) |
50,397 | 2. In an acute triangle, the interior angles $A, B$ satisfy $\tan A-\frac{1}{\sin 2 A}=\tan B$ and $\cos ^{2} \frac{B}{2}=\frac{\sqrt{6}}{3}$, then $\sin 2 A=$ | \frac{2\sqrt{6}-3}{3} |
55,052 | 5. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point ( $60 ; 45$ ). Find the number of such squares. | 2070 |
65,376 | 6-152 Find all functions $f$ from the set of real numbers to the set of real numbers that satisfy the following conditions:
(1) $f(x)$ is strictly increasing;
(2) For all real numbers $x, f(x) + g(x) = 2x$, where $g(x)$ is the inverse function of $f(x)$. | f(x)=x+ |
19,182 | 10th Irish 1997 Problem A3 Find all polynomials p(x) such that (x-16) p(2x) = (16x-16) p(x). | (x-2)(x-4)(x-8)(x-16) |
64,101 | 27. 9 racing cars have different speeds, and they need to compete to determine who is faster, but there are no timing tools, so they can only race on the track to see who comes first, and each time a maximum of 3 cars can race. Therefore, the minimum number of races needed to guarantee selecting the 2 fastest cars is $\qquad$. | 5 |
10,711 | Given a sequence \( A = (a_1, a_2, \cdots, a_{10}) \) that satisfies the following four conditions:
1. \( a_1, a_2, \cdots, a_{10} \) is a permutation of \{1, 2, \cdots, 10\};
2. \( a_1 < a_2, a_3 < a_4, a_5 < a_6, a_7 < a_8, a_9 < a_{10} \);
3. \( a_2 > a_3, a_4 > a_5, a_6 > a_7, a_8 > a_9 \);
4. There does not exist \( 1 \leq i < j < k \leq 10 \) such that \( a_i < a_k < a_j \).
Find the number of such sequences \( A \). | 42 |
51,263 | Example 1. The following numbers are all approximate numbers obtained by rounding. Find their absolute error bounds and relative error bounds:
$$
\begin{array}{l}
\text { (1) } \mathrm{a}_{1} \approx 12.5, \quad(2) \mathrm{a}_{2} \approx 1.25 \times 10^{4}, \\
\text { (3) } \mathrm{a}_{3} \approx 0.0125
\end{array}
$$ | 0.4\% |
31,074 | 2. In the cells of an $11 \times 11$ square, zeros and ones are arranged in such a way that in any figure of four cells in the shape of $\square$, the sum of the numbers is odd. (The figure can be rotated and flipped). What is the minimum number of ones that can be in such an arrangement? | 25 |
56,565 | 39th Putnam 1978 Problem B1 A convex octagon inscribed in a circle has 4 consecutive sides length 3 and the remaining sides length 2. Find its area. | 13+12\sqrt{2} |
61,912 | 42nd Putnam 1981 Problem B1 Evaluate lim n→∞ 1/n 5 ∑ (5 r 4 - 18 r 2 s 2 + 5 s 4 ), where the sum is over all r, s satisfying 0 < r, s ≤ n. Solution | -1 |
9,917 | 1021. Among all rectangular parallelepipeds having a given volume $\mathrm{V}$, find the one with the smallest total surface area. | \sqrt[3]{V} |
3,390 | A river flows at a constant speed. Piers A and B are located upstream and downstream respectively, with a distance of 200 kilometers between them. Two boats, A and B, depart simultaneously from piers A and B, traveling towards each other. After meeting, they continue to their respective destinations, immediately return, and meet again for the second time. If the time interval between the two meetings is 4 hours, and the still water speeds of boats A and B are 36 km/h and 64 km/h respectively, what is the speed of the current in km/h? | 14 |
29,125 | 14. In the quadrilateral pyramid $P-ABCD$, the side face $PAD$ is an equilateral triangle, and it is perpendicular to the base $ABCD$. The base $ABCD$ is a rhombus with a side length of 2, and $\angle BAD=60^{\circ}$. $N$ is the midpoint of $PB$, and the section $DAN$ intersects $PC$ at $M$. Find the size of the dihedral angle $P-AD-M$. | 45 |
7,915 | In an isosceles trapezoid $ABCD$ with bases $AD$ and $BC(AD > BC)$, the side length is 20 cm, and the angle $\angle BAC$ is $45^\circ$. Let $O$ be the center of the circumscribed circle around $ABCD$. It turns out that lines $OD$ and $AB$ are perpendicular. Find the length of the base $AD$ of the trapezoid. | 10(\sqrt{6} + \sqrt{2}) |
12,625 | The function \( f(x)=\frac{1}{3} x^{3}+\frac{1}{2} b x^{2}+c x+d \) has both a local maximum and a local minimum in the interval \( (0,2) \). Determine the range of values of \( c^{2}+2 b c+4 c \). ___ . | (0,1) |
56,465 | ## Angle Bisectors, Concurrency Problem $\underline{115562}$ topics: [Area of a Triangle (using semiperimeter and radius of inscribed or exscribed circle [ Inscribed, circumscribed, and exscribed circles; their radii
A circle with center $O$, inscribed in triangle $A B C$, touches its sides $A B$ and $A C$ at points $M$ and $N$. A circle with center $Q$ is inscribed in triangle $A M N$. Find $O Q$, if $A B=13, B C=15$ and $A C=14$.
# | 4 |
61,768 | 9. (15 points) As shown in the figure, two squares $A B F E$ and $C D E F$ with side lengths of 6 are combined to form rectangle $A B C D$. $G$ is the midpoint of $D E$. Connect $B G$ and it intersects $E F$ at $H$. Find the area of pentagon $C D G H F$ in the figure. | 33 |
68,686 | ## angle between the tangent and the chord [Angles subtended by equal arcs and equal chords]
A circle touches the sides $A C$ and $B C$ of triangle $A B C$ at points $A$ and $B$ respectively. On the arc of this circle, lying inside the triangle, there is a point $K$ such that the distances from it to the sides $A C$ and $B C$ are 6 and 24, respectively. Find the distance from point $K$ to the side $A B$. | 12 |
26,435 | Ex. 19. In triangle $ABC$, points $M$ and $N$ are chosen on sides $AB$ and $AC$. It is known that $\angle ABC=70^{\circ}, \angle ACB=50^{\circ}, \angle ABN=20^{\circ}$, $\angle ACM=10^{\circ}$. Find $\angle NMC$.
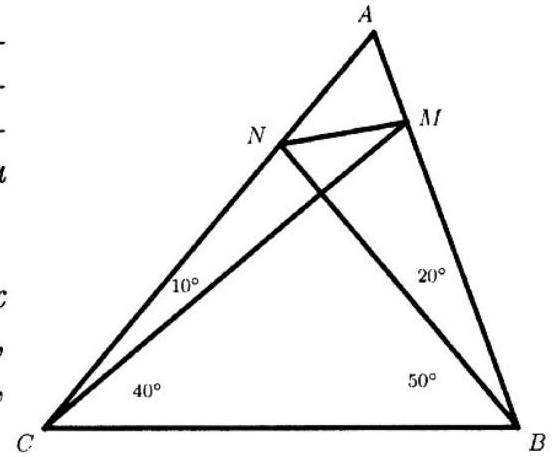
## Generalized Sine Theorem
The length of a chord is equal to the product of the diameter of the circle and the sine of half the angular length of the arc whose ends the chord connects
$$
d=2 R \sin \frac{\varphi}{2}
$$
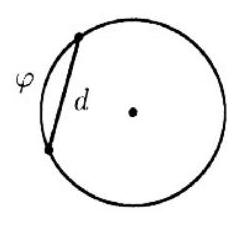 | 30 |
68,560 | Example 17 As shown in Figure 1.4.19, a semicircle is constructed inside trapezoid $ABCD$, tangent to the upper base and the two non-parallel sides, with its diameter lying on the lower base. If $AB=2, CD=3$, find the length of the lower base $BC$.
untranslated text remains the same as the original, only the content within the example has been translated. | 5 |
10,618 | A quadrilateral \(A B C D\) is inscribed in a circle with radius 6 and center at point \(O\). Its diagonals \(A C\) and \(B D\) are mutually perpendicular and intersect at point \(K\). Points \(E\) and \(F\) are the midpoints of \(A C\) and \(B D\), respectively. The segment \(O K\) is equal to 5, and the area of the quadrilateral \(O E K F\) is 12. Find the area of the quadrilateral \(A B C D\). | 12\sqrt{15} |
59,564 | ЕЕооокимов M.A. Anya calls a date beautiful if all 6 digits in its notation are different. For example, 19.04.23 is a beautiful date, while 19.02.23 and 01.06.23 are not. How many beautiful dates are there in 2023? | 30 |
59,415 | Problem 10.1. In each cell of a $5 \times 5$ table, a natural number is written in invisible ink. It is known that the sum of all the numbers is 200, and the sum of three numbers located inside any $1 \times 3$ rectangle is 23. What is the central number in the table?
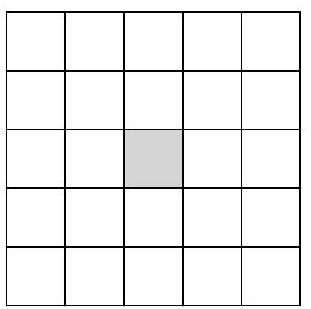 | 16 |
5,248 | In triangle \(ABC\) with \(BC = 4\) and \(AB = 2\sqrt{19}\), it is known that the center of the circle passing through the midpoints of the sides of the triangle lies on the bisector of angle \(C\). Find \(AC\). | 10 |
60,722 | 3. (3 points) Anya, Vanya, Danya, and Tanya were collecting apples. It turned out that each of them collected a whole percentage of the total number of apples collected, and all these numbers were different and greater than zero. Then Tanya, who collected the most apples, ate her apples. After this, it turned out that each of the children still had a whole percentage, but now of the remaining number of apples. What is the minimum number of apples that could have been collected?
Answer: 20 : for example $2+3+5+10$ | 20 |
68,379 | 5. Let planar vectors $\boldsymbol{\alpha}, \boldsymbol{\beta}$ satisfy $|\boldsymbol{\alpha}+2 \boldsymbol{\beta}|=3,|2 \boldsymbol{\alpha}+3 \boldsymbol{\beta}|=4$, then the minimum value of $\boldsymbol{\alpha} \cdot \boldsymbol{\beta}$ is | -170 |
25,260 | 3. Inside the circle $\omega$ are located intersecting at points $K$ and $L$ circles $\omega_{1}$ and $\omega_{2}$, touching the circle $\omega$ at points $M$ and $N$. It turned out that points $K, M$, and $N$ lie on the same line. Find the radius of the circle $\omega$, if the radii of the circles $\omega_{1}$ and $\omega_{2}$ are 3 and 5, respectively. | 8 |
50,382 | ## Task 6 - 190936
For suitable natural numbers $n$, there are polyhedra with $n$ vertices and fewer than $n$ faces. For example, for $n=8$, a cuboid is such a polyhedron, as it has exactly 8 vertices and is bounded by exactly 6 planar faces (rectangles).
Investigate whether there exists a natural number $N$ such that for every natural number $n \geq N$, there is a polyhedron with $n$ vertices that is bounded by fewer than $n$ planar faces!
If this is the case, determine the smallest natural number $N$ with this property! | 6 |
65,890 | 5. Call two vertices of a simple polygon "visible" to each other if and only if they are adjacent or the line segment connecting them lies entirely inside the polygon (except for the endpoints which lie on the boundary). If there exists a simple polygon with $n$ vertices, where each vertex is visible to exactly four other vertices, find all possible values of the positive integer $n$.
Note: A simple polygon is one that has no holes and does not intersect itself. | 5 |
61,795 | ## Task Condition
Find the derivative of the specified order.
$$
y=\frac{\log _{2} x}{x^{3}}, y^{\prime \prime \prime}=?
$$ | \frac{47-60\lnx}{\ln2\cdotx^{6}} |
3,398 | In an isosceles trapezoid \(M N K L\) with bases \(ML\) and \(NK\), the diagonals are perpendicular to the sides \(MN\) and \(KL\), and they intersect at an angle of \(22.5^\circ\). Find the height of the trapezoid if the length \(NQ = 3\), where \(Q\) is the midpoint of the longer base. | \dfrac{3\sqrt{2 - \sqrt{2}}}{2} |
64,125 | 13) (10 points) If there exist $n$ real numbers $x_{1}, x_{2}, \cdots, x_{n}$ satisfying $x_{1}+2 x_{2}+\cdots+$ $n x_{n}=2009$, and $x_{1}+x_{2}+\cdots+x_{n}=0$, where $x_{i}= \pm 7, i=1,2, \cdots$,
$n$. Determine the minimum value of $n$. | 34 |
55,521 | 13. Let $\left\{a_{n}\right\}$ be a geometric sequence with the sum of the first $n$ terms $S_{n}=2^{n}+r$ (where $r$ is a constant). Let $b_{n}=2\left(1+\log _{2} a_{n}\right)\left(n \in \mathbf{Z}_{+}\right)$.
(1) Find the sum of the first $n$ terms $T_{n}$ of the sequence $\left\{a_{n} b_{n}\right\}$;
(2) If for any positive integer $n$, we have
$$
\frac{1+b_{1}}{b_{1}} \cdot \frac{1+b_{2}}{b_{2}} \cdots \cdots \frac{1+b_{n}}{b_{n}} \geqslant k \sqrt{n+1} \text {, }
$$
find the maximum value of the real number $k$. | \frac{3\sqrt{2}}{4} |
56,483 | 136. Twenty-four. In one book it was written: “Write the number 24 using three identical digits, different from 8. (There are two solutions to this problem.)”
The book also provided two answers: $22+2=24$ and $3^{3}-3=24$. Readers familiar with the old puzzle “Four Fours” and similar puzzles might ask why there are only the two solutions given above. Can you find more? | 24 |
17,251 | In a circle with center $O$, the diameter $A B$ is extended to $C$ such that $B C = \frac{1}{2} \cdot A B = \frac{r}{2}$. A tangent line $s$ is drawn at point $B$, and from an arbitrary point $M$ on this tangent $s$, another tangent $M D$ to the circle is drawn. Show that $\angle B M C = \frac{1}{3} \angle D M C$. | \angle BMC = \frac{1}{3} \angle DMC |
31,271 | 9.8. In an acute-angled triangle $A B C$, the bisector $B L$ is drawn. The circumcircle of triangle $A B L$ intersects side $B C$ at point $D$. It turns out that point $S$, symmetric to point $C$ with respect to the line $D L$, lies on side $A B$ and does not coincide with its endpoints. What values can $\angle A B C$ take?
(B. Obukhov, zhori) | 60 |
60,115 | King Arthur's bodyguards held a knightly tournament. At the end of the tournament, it turned out that the king could find a third one for any two bodyguards who participated, who had defeated both of them. What is the minimum number of bodyguards who participated in the tournament? | 7 |
52,496 | 9. (3 points) The following is a 3x3 grid, where the characters 【Hua, Luo, Geng, Bei, Shu, Xue, Jing, Ying, Sai】 represent nine different digits from 1 to 9, and these nine numbers meet the following three conditions:
(1) The sum of the four numbers in each "square" is equal.
(2) Hua $\times$ Hua $=$ Ying $\times$ Ying + Sai $\times$ Sai.
(3) Shu > Xue
According to the above conditions, the product of the three numbers represented by 【Hua, Bei, Sai】 is $\qquad$ | 120 |
6,942 | Max repeatedly throws a fair coin in a hurricane. For each throw, there is a $4\%$ chance that the coin gets blown away. He records the number of heads $H$ and the number of tails $T$ before the coin is lost. (If the coin is blown away on a toss, no result is recorded for that toss.) What is the expected value of $|H-T|$ ?
*Proposed by Krit Boonsiriseth.* | \dfrac{24}{7} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.