id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
58,870 | 2. In the triangular pyramid $SABC$, points $\boldsymbol{D}$, $\boldsymbol{E}$, and $\boldsymbol{F}$ are chosen on the edges $SA$, $SB$, and $SC$ respectively, such that the area of triangle $\boldsymbol{ABE}$ is $1/3$ of the area of triangle $\boldsymbol{AES}$, the area of triangle $\boldsymbol{BCF}$ is $1/4$ of the area of triangle $BFS$, and the area of triangle $ACD$ is $1/5$ of the area of triangle DCS. Find the ratio of the volumes of pyramids SDEF and $SABC$. (14 points). | 0.5 |
58,731 | $A$ bets with $B$ that in a group of 7 people, at least one individual was born on a Sunday. $A$ bets 10 Forints against $B$'s 5 Forints.
a) Who has the advantage in this bet?
b) How many people must the group consist of at least, so that even a 1 Forint bet by $B$ would be disadvantageous for $B$? | 16 |
51,339 | $2 \cdot 45$ A sequence of integers that is monotonically increasing, if its first term is odd, the second term is even, the third term is odd, the fourth term is even, $\cdots$, and so on, is called an alternating sequence. The empty set is also considered an alternating sequence. Let $A(n)$ denote the number of alternating sequences, where the integers are all taken from the set $\{1,2, \cdots, n\}$. Clearly, $A(1)=2, A(2)=3$. Find $A(20)$, and prove your conclusion. | 17711 |
17,692 | Given \( a = 19911991 \cdots \cdots 1991 \) (a repeated sequence of 1991), what is the remainder when \( a \) is divided by 13? | 8 |
13,541 | Let \( a \) and \( b \) be real numbers, and consider the function \( f(x) = x^{3} + a x^{2} + b x \). If there exist three real numbers \( x_{1}, x_{2}, x_{3} \) such that \( x_{1} + 1 \leqslant x_{2} \leqslant x_{3} - 1 \), and \( f(x_{1}) = f(x_{2}) = f(x_{3}) \), find the minimum value of \( |a| + 2|b| \). | \sqrt{3} |
11,040 | In the complex plane, the complex numbers \( z_1, z_2, z_3 \) satisfy:
\[
z_{1}=\lambda z_{2}(\lambda<0),\left|z_{1}-z_{2}\right|=13,
\]
\[
\left|z_{1}\right|^{2}+\left|z_{3}\right|^{2}+\left|z_{1} z_{3}\right|=144,
\]
\[
\left|z_{2}\right|^{2}+\left|z_{3}\right|^{2}-\left|z_{2} z_{3}\right|=25 .
\]
Then \( \left|z_{3}\right| = \) | \dfrac{40\sqrt{3}}{13} |
56,295 | 11. Let $S(k)$ denote the sum of all the digits in the decimal representation of a positive integer $k$. Let $n$ be the smallest positive integer satisfying the condition $S(n)+S(n+1)=$ param1. As the answer to the problem, write down a five-digit number such that its first two digits coincide with the first two digits of $n$ and its last three digits coincide with the last three digits of $n$. For example, if $\mathrm{n}=1234567890$, then the answer must be 12890.
| param1 | Answer |
| :---: | :---: |
| 2016 | 59989 |
| 664 | 49989 |
| 1580 | 39989 |
| 4000 | 79989 |
## Condition
Let $S(k)$ denote the sum of all the digits in the decimal representation of a positive integer $k$. Let $n$ be the smallest positive integer such that $S(n)+S(n+1)=2016$. As the answer to the problem, write down a five-digit number such that its first two digits coincide with the first two digits of $n$ and its last three digits coincide with the last three digits of $n$. For example, if $\mathrm{n}=1234567890$, then the answer must be 12890.
## Answer.
59989
## Solution
If the number $n$ does not end in 9, then $S(n+1)=S(n)+1$, and the sum $S(n)+S(n+1)$ is odd, which means it cannot equal 2016. Therefore, the number $n$ must end in 9. If it ends in one 9, then $S(n+1)=S(n)-8$, and thus $S(n)=1012$. The smallest number with such a sum of digits is 599...989 (the total number of 9s is 111). If the number of 9s at the end of $n$ is not less than two, then by similar reasoning, the sum $S(n)$ will be larger, and the number $n$ will also be larger. Therefore, the answer is 59989.
12. Let $A C$ be the largest side of triangle $A B C$. Points $K$ and $M$ are chosen on side $A C$ such that $A M=A B$ and $C K=C B$. It is given that the radius of the circumcircle of triangle $K B M$ equals param1, and the radius of the incircle of triangle $A B C$ equals param2. Find the length of $B T$ squared if $T$ is the point where the incircle of $A B C$ touches its side $B C$.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 7 | 5 | 24 |
| 8 | 5 | 39 |
| 9 | 7 | 32 |
| 11 | 8 | 57 |
| 13 | 9 | 88 |
## Condition
Let $A C$ be the largest side of triangle $A B C$. Points $K$ and $M$ are chosen on side $A C$ such that $A M=A B$ and $C K=C B$. It is given that the radius of the circumcircle of triangle $K B M$ equals 7, and the radius of the incircle of triangle $A B C$ equals 5. Find the length of $B T$ squared if $T$ is the point where the incircle of $A B C$ touches its side $B C$.
## Answer.
24 | 24 |
67,130 | 3. On the number line, points with coordinates $1, 2, \cdots, 2006$ are called "marked points". A frog starts from point 1, and after 2006 jumps, it visits all the marked points and returns to the starting point. What is the maximum length of the path the frog can jump? Explain your reasoning.
(2006, Shandong Province Junior High School Mathematics Competition) | 2 \times 1003^2 |
55,059 | C6. I have four identical black beads and four identical white beads. Carefully explain how many different bracelets I can make using all the beads. | 8 |
66,705 | 1. Find all positive roots of the equation $x^{x}+x^{1-x}=x+1$.
# | 1 |
65,508 | 9.3. There are 12 matches, each 2 cm long. Can a polygon with an area of 16 cm $^{2}$ be formed from them? (The matches cannot be broken, and all matches must be used.) | 16 |
32,184 | 4. Find the largest constant $k$, such that for all real numbers $a, b, c, d$ in $[0,1]$, the inequality $a^{2} b+b^{2} c+c^{2} d+d^{2} a+4 \geqslant k\left(a^{3}+b^{3}+c^{3}+d^{3}\right)$ holds. | 2 |
53,051 | p1. Consider the sequence of positive integers $2, 3, 5, 6, 7, 8, 10, 11 ...$. which are not perfect squares. Calculate the $2019$-th term of the sequence.
p2. In a triangle $ABC$, let $D$ be the midpoint of side $BC$ and $E$ be the midpoint of segment $AD$. Lines $AC$ and $BE$ intersect at $F$. Show that $3AF = AC$.
p3. Find all positive integers $n$ such that $n! + 2019$ is a square perfect.
p4. In a party, there is a certain group of people, none of whom has more than $3$ friends in this. However, if two people are not friends at least they have a friend in this party. What is the largest possible number of people in the party? | 2064 |
2,777 | 10.3. Solve in $\mathbb{R}$ the equation $\sqrt{8 x^{2}+10 x-3}-\sqrt{8 x+12}=3+\sqrt{4 x+8}-\sqrt{4 x^{2}+7 x-2}$. | 2 |
62,803 | 9.6 Calculate the following product, accurate to within 0.00001:
$$
\left(1-\frac{1}{10}\right)\left(1-\frac{1}{10^{2}}\right) \cdots\left(1-\frac{1}{10^{99}}\right) .
$$ | 0.89001 |
62,593 | Problem 1
Find the largest integer $k$ having the following property: for any real numbers $x_{1}, x_{2}, \ldots, x_{2024}$ such that
$$
x_{1}^{2}=\left(x_{1}+x_{2}\right)^{2}=\cdots=\left(x_{1}+x_{2}+\cdots+x_{2024}\right)^{2}
$$
there are at least $k$ of them that are all equal. | 675 |
9,256 | In a $5 \times 5$ grid, place 6 crosses such that each row and each column contains at least one cross. How many ways can this be done? | 4200 |
12,421 | 20. Patrick asks SpongeBob: "What is your lucky number?" SpongeBob says: "There is a sequence of numbers: $0,1,3,8$, $21,55,144,377,987, \cdots \cdots$ Starting from the third number, each number multiplied by 3 is exactly equal to the sum of the numbers immediately before and after it. My lucky number is the remainder when the 2020th number in this sequence is divided by 6." So, SpongeBob's lucky number is $\qquad$ . (If it is divisible, then the remainder is 0) | 2 |
56,632 | Problem 1. Petya was given several physics problems and several math problems for homework. All the problems solved by Petya constitute $5 \%$ of the total number of physics problems and $20 \%$ of the total number of math problems. What percentage of the total number of problems did Petya solve? | 4 |
19,905 | 3. Person A and Person B go to a discount store to buy goods. It is known that both bought the same number of items, and the unit price of each item is only 8 yuan and 9 yuan. If the total amount spent by both on the goods is 172 yuan, then the number of items with a unit price of 9 yuan is $\qquad$ pieces.
Person A and Person B go to a discount store to buy goods,
it is known that both bought
the same number of items, and the unit price of each
item is only 8 yuan and 9 yuan. If the total amount spent by both on the goods is
172 yuan, then the number of items with a unit price of 9 yuan is $\qquad$ pieces. | 12 |
3,658 | Example 6. Find the general solution of the equation
$$
y^{\prime \prime}-3 y^{\prime}=x^{2}
$$ | y = C_1 + C_2 e^{3x} - \dfrac{x^3}{9} - \dfrac{x^2}{9} - \dfrac{2x}{27} |
29,089 | (12) Let the acute triangle $ABC$ have internal angles $A, B, C$ opposite to sides $a, b, c$ respectively, and $\sin A = 2a \sin B$, with the circumradius of $\triangle ABC$ being $\frac{\sqrt{3}}{6}$. Then the range of the perimeter of $\triangle ABC$ is . $\qquad$ | (\frac{1+\sqrt{3}}{2},\frac{3}{2}] |
12,209 | The circles $\odot O_{1}$ and $\odot O_{2}$ have radii $R_{1}$ and $R_{2}$ respectively and are externally tangent. Line $AB$ is tangent to $\odot O_{1}$ and $\odot O_{2}$ at points $A$ and $B$ respectively. Line $CD$ is perpendicular to $AB$ at point $D$, and the distance $CD$ is $d$. Prove that:
$$
\frac{1}{R_{1}}+\frac{1}{R_{2}}=\frac{2}{d}.
$$ | \dfrac{1}{R_{1}} + \dfrac{1}{R_{2}} = \dfrac{2}{d} |
8,855 | A convex 2011-sided polygon is drawn on the board. Peter sequentially draws diagonals inside the polygon such that each newly drawn diagonal intersects at most one of the previously drawn diagonals at internal points. What is the maximum number of diagonals Peter can draw? | 4016 |
57,649 | 7. Given complex numbers $z_{1}, z_{2}, z_{3}$ satisfy:
$$
\begin{array}{l}
\left|z_{1}\right| \leqslant 1,\left|z_{2}\right| \leqslant 2, \\
\left|2 z_{3}-z_{1}-z_{2}\right| \leqslant\left|z_{1}-z_{2}\right| .
\end{array}
$$
Then the maximum value of $\left|z_{3}\right|$ is $\qquad$ | \sqrt{5} |
66,769 | [ Decimal numeral system ]
Find the largest number in which each digit, starting from the third, is equal to the sum of the two preceding digits.
# | 10112358 |
14,230 | Circle \( \odot O \) is internally tangent to circle \( \odot O' \) at point \( A \). The radii of the two circles are \( r \) and \( r' \) respectively. Line \( BC \) is perpendicular to line \( OO' \) and intersects the two circles at points \( B \) and \( C \) respectively. The radius of the circumcircle of triangle \( ABC \) is \( R \). Prove that \( R^2 = rr' \). | R^2 = rr' |
34,748 | 12.050. A plane is drawn through vertex $C$ of the base of a regular triangular pyramid $S A B C$ perpendicular to the lateral edge $S A$. This plane forms an angle with the base plane, the cosine of which is $2 / 3$. Find the cosine of the angle between two lateral faces. | \frac{1}{7} |
28,254 | 10.1. It is known that the quadratic equations in $x$, $2017 x^{2} + p x + q = 0$ and $u p x^{2} + q x + 2017 = 0$ (where $p$ and $q$ are given real numbers) have one common root. Find all possible values of this common root and prove that there are no others. | 1 |
50,767 | 4. Given the set $=\left\{x \mid x=a_{0}+a_{1} \times 8+a_{2} \times 8^{2}+a_{3} \times 8^{3}\right\}$, where $a_{i} \in\{0,1,2,3,4,5,6,7\}, i=0,1,2,3$
and $a_{3} \neq 0$, if positive integers $m, n \in A$, satisfy $m+n=2018$, and $m>n$, then the number of positive integers $m$ that meet the condition is
$\qquad$ | 497 |
65,331 | $8.57 \log _{3} \log _{4} \frac{4 x-1}{x+1}-\log _{\frac{1}{3}} \log _{\frac{1}{4}} \frac{x+1}{4 x-1}<0$. | (\frac{2}{3},\infty) |
1,159 | Example 1 (kp. $1^{\circ}$ ). Find $\int \sin 5 x \cos 7 x d x$. | -\dfrac{1}{24}\cos 12x + \dfrac{1}{4}\cos 2x + C |
63,465 | 11. In the Cartesian coordinate system $x O y$, the circle $\odot M$ with center $M(0,1)$ intersects the parabola $y=x^{2}$ at four points $A$, $B$, $C$, and $D$ in sequence.
(1) Find the range of the radius $r$ of $\odot M$;
(2) Find the maximum area of quadrilateral $A B C D$ (accurate to $10^{-4}$). | 1.0887 |
52,871 | 1. Use $A$, $B$, and $C$ to form a permutation of length $n$ (with $n$ letters), but it is not required that all three letters appear in the permutation. If no two $A$s are adjacent, how many such permutations are there? | a_{n}=\frac{(2+\sqrt{3})(1+\sqrt{3})^{n}}{2\sqrt{3}}+\frac{(-2+\sqrt{3})(1-\sqrt{3})^{n}}{2\sqrt{3}} |
60,542 | 1. Let's say that three mutually distinct natural numbers form a sum triplet if the sum of the first two of them equals the third number. Determine the maximum number of sum triplets that can be found in a set of twenty natural numbers. | 90 |
24,544 | Given a fixed integer \( n \) where \( n \geq 2 \):
a) Determine the smallest constant \( c \) such that the inequality \(\sum_{1 \leq i < j \leq n} x_i x_j (x_i^2 + x_j^2) \leq c \left( \sum_{i=1}^n x_i \right)^4\) holds for all nonnegative real numbers \( x_1, x_2, \ldots, x_n \geq 0 \).
b) For this constant \( c \), determine the necessary and sufficient conditions for equality to hold. | \dfrac{1}{8} |
3,638 | Given a circle centered at $O$ with a point $A$ on it and a line $d$ passing through $O$. A secant line starting from $A$ intersects the circle at $B$ and intersects $d$ at $D$. Prove that if the secant rotates around $A$, the circle passing through the points $O, B, D$, besides $O$, always passes through another fixed point. | A' |
16,643 | 4. Given $a_{0}=-1, a_{1}=1, a_{n}=2 a_{n-1}+3 a_{n-2}+3^{n}(n \geqslant 3)$, find $a_{n}$. | \dfrac{3^{n+1}(4n - 3) - 7(-1)^n}{16} |
53,711 | On a sheet of paper, Emanuelle draws two circles of radius 1 that are tangent at one point. Then, she draws a third circle of radius $1-\sqrt{2}$ that tangentially touches the previous two externally, as shown in the figure below.
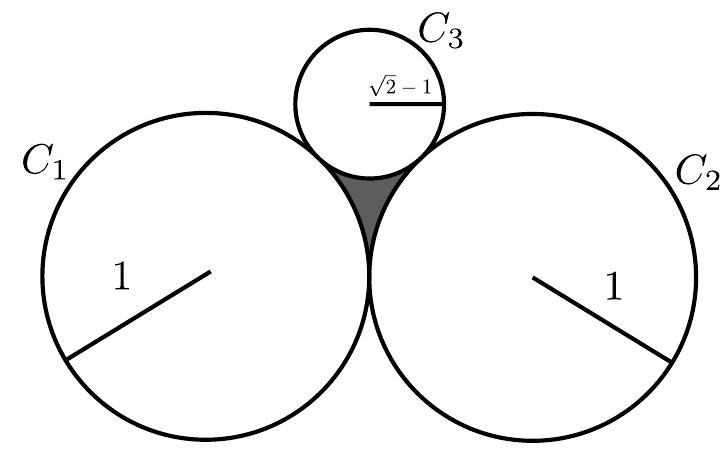
Emanuelle calculates the area of the region bounded and exterior to the three circles, which is shown in gray in the figure above. What value did she find?
# | 1-\pi\frac{(2-\sqrt{2})}{2} |
62,212 | ## Task A-4.5.
In a certain school, students can learn two classical languages: Latin and Greek. Out of 100 students, 50 study Latin, 40 study Greek, and 20 study both languages. If we randomly select two students, what is the probability that at least one of them studies Latin and at least one of them studies Greek? | \frac{239}{495} |
15,941 | The height of a cone is 20, the radius of the base is 25. Find the area of the cross-section, passing through the vertex, if its distance from the center of the base of the cone is 12. | 500 |
10,788 | 7. In $\triangle A B C, \tan \angle C A B=\frac{22}{7}$ and the altitude from $A$ to $B C$ divides $B C$ into segments of lengths 3 and 17. Find the area of $\triangle A B C$.
(1 mark)
在 $\triangle A B C$ 中, $\tan \angle C A B=\frac{22}{7}$, 且從 $A$ 到 $B C$ 的高把 $B C$ 分成長度 3 和 17 的兩段。求 $\triangle A B C$ 的面積。
(1分) | 110 |
59,288 | 8. (10 points) From 1 to 1000, the maximum number of numbers that can be selected such that the difference between any two of these numbers does not divide their sum is $\qquad$. | 334 |
17,199 | Example 2 If $z \in \mathbf{C}$, satisfies $3 z^{6}+2 \mathrm{i} z^{5}-2 z-3 \mathrm{i}=0$, find $|z|$. | 1 |
11,738 | Let $ABC$ be an acute-angled triangle with $AC < AB$ and circumradius $R$. Point $D$ is the foot of the altitude through vertex $A$. Point $T$ lies on line $AD$ such that $AT = 2R$ and $D$ is between $A$ and $T$.
Let $S$ denote the center of the circumcircle arc $BC$ that does not contain $A$.
Show that $\angle AST = 90^\circ$. | 90^\circ |
32,518 | 6. Let the two foci of the ellipse $\Gamma$ be $F_{1}, F_{2}$, and a line passing through point $F_{1}$ intersects $\Gamma$ at points $P, Q$. If $\left|P F_{2}\right|=\left|F_{1} F_{2}\right|$, and $3\left|P F_{1}\right|=4\left|Q F_{1}\right|$, then the ratio of the minor axis to the major axis of the ellipse $\Gamma$ is $\qquad$. | \frac{2\sqrt{6}}{7} |
3,216 | Let \( n \) be a positive integer. Consider the set
\[
S = \left\{\left(x_{1}, x_{2}, \cdots, x_{k}\right) \mid x_{1}, x_{2}, \cdots, x_{k} \in \{0, 1, \cdots, n\}, x_{1} + x_{2} + \cdots + x_{k} > 0 \right\}
\]
which consists of \((n+1)^{k} - 1\) points in \( k \)-dimensional space. Find the minimum number of hyperplanes whose union contains \( S \) but does not include the point \((0, 0, \cdots, 0)\). | nk |
34,172 | Problem 9.3. Find the least number of colors with the following property: the integers $1,2 \ldots, 2004$ can be colored such that there are no integers $a<b<c$ of the same color for which $a$ divides $b$ and $b$ divides $c$.
Alexander Ivanov | 6 |
61,956 | ## Task B-1.7.
Two right triangles $P S T$ and $R S T$ have a common hypotenuse $\overline{S T}$. Vertices $P$ and $R$ are on the same side of the hypotenuse $\overline{S T}$. The legs $\overline{P T}$ and $\overline{R S}$ intersect at point $Q$. If $|P S|=6 \mathrm{~cm},|P T|=17 \mathrm{~cm}$ and $|R T|=1 \mathrm{~cm}$, what is the area of triangle $Q S T$? | \frac{39}{5} |
26,104 | 5. Let $K$ be the incenter of $\triangle A B C$, and let points $C_{1}, B_{1}$ be the midpoints of sides $A B, A C$, respectively. Line $A C$ intersects $C_{1} K$ at point $B_{2}$, and line $A B$ intersects $B_{1} K$ at point $C_{2}$. If $S_{\triangle A B_{2} c_{2}}=S_{\triangle A B C}$, find $\angle C A B$. | 60 |
55,896 | $4 \cdot 247$ Find all positive integers $n$ such that the following equation has an integer solution.
$$
x^{n}+(2+x)^{n}+(2-x)^{n}=0 \text {. }
$$ | 1 |
17,589 | In $\triangle ABC$, $AF$ is the angle bisector of $\angle BAC$, and $BF$ is perpendicular to $AF$ at $F$. A circle with diameter $AC$ intersects $BC$ at $D$ and intersects $AF$ at $E$. Point $M$ is the midpoint of $BC$. Prove that points $M$, $F$, $D$, and $E$ are concyclic. | M, F, D, E \text{ are concyclic} |
29,700 | ## Problem 4
Determine the triples of non-zero natural numbers $(x, y, z)$ that satisfy the equation $x^{4}+y^{4}=2 z^{2}$, and the numbers $x$ and $y$ are coprime. | (1,1,1) |
10,168 | Let $M=\left\{1,2, \cdots, 2^{m} n\right\}$ (where $m$ and $n$ are positive integers) be a set consisting of continuous $2^{m}n$ positive integers. Find the minimum value of the positive integer $k$ such that any $k$-element subset of $M$ contains $m+1$ numbers $a_1, a_2, \cdots, a_{m+1}$ that satisfy $a_i$ divides $a_{i+1}$ for $i=1,2, \cdots, m$. | (2^m -1)n +1 |
22,409 | In trapezoid \(ABCD\), the side \(AB\) is perpendicular to the base \(BC\). A circle passes through points \(C\) and \(D\) and is tangent to line \(AB\) at point \(E\).
Find the distance from point \(E\) to line \(CD\), if \(AD = 4\) and \(BC = 3\). | 2\sqrt{3} |
23,630 | Find the value of \(\tan \left(\tan^{-1} \frac{1}{2} + \tan^{-1} \frac{1}{2 \times 2^2} + \tan^{-1} \frac{1}{2 \times 3^2} + \cdots + \tan^{-1} \frac{1}{2 \times 2009^2}\right)\). | \dfrac{2009}{2010} |
31,372 | 8. Let $A B C$ be a triangle with circumradius $R=17$ and inradius $r=7$. Find the maximum possible value of $\sin \frac{A}{2}$. | \frac{17+\sqrt{51}}{34} |
54,199 | In a $4 \times 4$ chessboard composed of 16 small squares, 8 of the small squares are to be colored black, such that each row and each column has exactly 2 black squares. There are $\qquad$ different ways to do this. | 90 |
11,219 | 155 birds sit on a circle centered at O. Birds at points A and B are mutually visible if and only if the angle ∠AOB is less than or equal to 10 degrees. Multiple birds may sit at the same point. What is the smallest possible number of mutually visible pairs of birds? | 270 |
51,425 | 5. Given the sequence $\left\{a_{n}\right\}$ satisfies:
$$
a_{0}=\sqrt{6}, a_{n+1}=\left[a_{n}\right]+\frac{1}{\left\{a_{n}\right\}} \text {, }
$$
where, $[a]$ denotes the greatest integer not exceeding the real number $a$, and $\{a\}=a-[a]$. Then $a_{2020}=$ $\qquad$ . | 6060+\sqrt{6} |
65,664 | Two players take turns breaking a $6 \times 8$ chocolate bar. On a turn, a player is allowed to make a straight break of any of the pieces along a groove. The player who cannot make a move loses. Who will win this game? | 1 |
25,033 | In a country with 15 cities, some of which are connected by airlines belonging to three different companies, it is known that even if any one of the airlines ceases operations, it will still be possible to travel between any two cities (possibly with transfers) using the remaining two companies' flights. What is the minimum number of airline routes in the country? | 21 |
54,217 | Three people are playing table tennis, with the player who loses a game giving way to the player who did not participate in it. In the end, it turned out that the first player played 10 games, the second - 21. How many games did the third player play? | 11 |
13,903 | Vojta wanted to add several three-digit natural numbers using a calculator. On the first attempt, he got a result of 2224. To check, he summed the numbers again and got 2198. He calculated it once more and this time got a sum of 2204. It turned out that the last three-digit number was troublesome—Vojta failed to press one of its digits hard enough each time, resulting in entering a two-digit number instead of a three-digit number into the calculator. No other errors occurred during the addition. What is the correct sum of Vojta's numbers? | 2324 |
11,813 | Given a sequence \( \left\{a_n\right\} \) that satisfies \( a_n=\left[(2+\sqrt{5})^n+\frac{1}{2^n}\right] \) for \( n \in \mathbf{N}^* \), where \([x]\) represents the greatest integer less than or equal to the real number \( x \). Let \( C \) be a real number such that for any positive integer \( n \), the following holds:
\[ \sum_{k=1}^{n} \frac{1}{a_k a_{k+2}} \leqslant C \]
Find the minimum value of \( C \). | \dfrac{1}{288} |
52,337 | 1. Given a convex quadrilateral $A B C D$ in which $\angle B A C=20^{\circ}, \angle C A D=60^{\circ}$, $\angle A D B=50^{\circ}$, and $\angle B D C=10^{\circ}$. Find $\angle A C B$. | 80 |
50,668 | 11.5. Find all numbers $a$ such that for any natural $n$ the number $a n(n+2)(n+3)(n+4)$ is an integer.
(O. Podlipsky) | \frac{k}{6} |
62,449 | 2. In an equilateral triangle $ABC$, points $A_{1}$ and $A_{2}$ are chosen on side $BC$ such that $B A_{1}=A_{1} A_{2}=A_{2} C$. On side $AC$, a point $B_{1}$ is chosen such that $A B_{1}: B_{1}C=1: 2$. Find the sum of the angles $\angle A A_{1} B_{1}+\angle A A_{2} B_{1}$. | 30 |
34,371 | 8,9 |
In triangle $A B C$, it is known that $\angle B A C=75^{\circ}, A B=1, A C=\sqrt{6}$. A point $M$ is chosen on side $B C$, such that $\angle$ ВАМ $=30^{\circ}$. Line $A M$ intersects the circumcircle of triangle $A B C$ at point $N$, different from $A$. Find $A N$. | 2 |
835 | 5 Mathematical Induction
Mathematical induction can be used to solve function problems on the set of natural numbers.
Example 6 Find all functions $f: Z_{+} \rightarrow Z_{+}$, such that for any positive integer $n$, we have
$$
f(f(f(n)))+f(f(n))+f(n)=3 n \text {. }
$$
(2008, Dutch National Team Selection Exam) | f(n) = n |
68,145 | 2. Given that the modulus of the complex number $z$ is 1, if $z=z_{1}$ and $z=z_{2}$ when $|z+1+\mathrm{i}|$ respectively attain the maximum and minimum values, then $z_{1}-z_{2}=$ $\qquad$ . | \sqrt{2}+\sqrt{2}\mathrm{i} |
17,462 | Two cars leave points A and B simultaneously and meet at 12 PM. If the speed of the first car is doubled while keeping the speed of the second car the same, the meeting will occur 56 minutes earlier. If the speed of the second car is doubled while keeping the speed of the first car the same, they will meet 65 minutes earlier. Determine the meeting time if the speeds of both cars were doubled. | 10:29 |
68,304 | Suppose that the real numbers $a_{1},a_{2},...,a_{2002}$ satisfying
$\frac{a_{1}}{2}+\frac{a_{2}}{3}+...+\frac{a_{2002}}{2003}=\frac{4}{3}$
$\frac{a_{1}}{3}+\frac{a_{2}}{4}+...+\frac{a_{2002}}{2004}=\frac{4}{5}$
$...$
$\frac{a_{1}}{2003}+\frac{a_{2}}{2004}+...+\frac{a_{2002}}{4004}=\frac{4}{4005}$
Evaluate the sum $\frac{a_{1}}{3}+\frac{a_{2}}{5}+...+\frac{a_{2002}}{4005}$. | 1 - \frac{1}{4005^2} |
14,196 | A board $ n \times n$ ( $n \ge 3$ ) is divided into $n^2$ unit squares. Integers from $O$ to $n$ included, are written down: one integer in each unit square, in such a way that the sums of integers in each $2\times 2$ square of the board are different. Find all $n$ for which such boards exist. | n = 3, 4, 5, 6 |
32,641 | 18. Collinear points $A, B$, and $C$ are given in the Cartesian plane such that $A=(a, 0)$ lies along the $x$-axis, $B$ lies along the line $y=x, C$ lies along the line $y=2 x$, and $A B / B C=2$. If $D=(a, a)$, the circumcircle of triangle $A D C$ intersects $y=x$ again at $E$, and ray $A E$ intersects $y=2 x$ at $F$, evaluate $A E / E F$. | 7 |
58,848 | A cylindrical tank has radius $10 \mathrm{~m}$ and length $30 \mathrm{~m}$. The tank is lying on its side on a flat surface and is filled with water to a depth of $5 \mathrm{~m}$. Water is added to the tank and the depth of the water increases from $5 \mathrm{~m}$ to $10+5 \sqrt{2} \mathrm{~m}$. If the volume of water added to the tank, in $\mathrm{m}^{3}$, can be written as $a \pi+b+c \sqrt{p}$ for
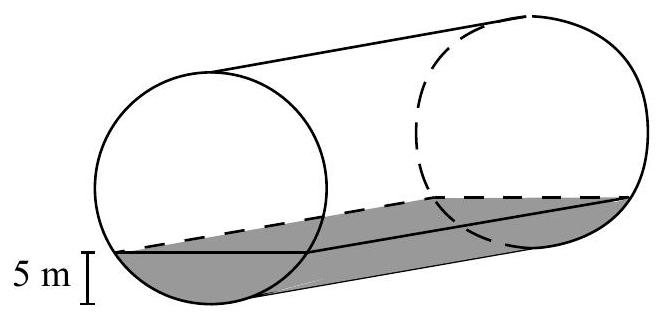
some integers $a, b, c$ and prime number $p$, determine the quadruple $(a, b, c, p)$. | (1250,1500,750,3) |
60,506 | 3. In how many ways can a $3 \times 3$ table be filled with elements of the set $\{10,3,2018\}$ such that the sum of the numbers in each row, each column, and both diagonals is divisible by 3? | 27 |
52,545 | 4. Let $n=\overline{a b c}$ be a three-digit number, where $a, b, c$ are the lengths of the sides that can form an isosceles (including equilateral) triangle. The number of such three-digit numbers $n$ is $\qquad$.
untranslated part: $\qquad$ | 165 |
66,982 | 5. There are 19 children with ages ranging from $1 \sim 19$ years old standing in a circle. Record the difference in ages between each pair of adjacent children. The maximum possible sum of these 19 differences is . $\qquad$ | 180 |
67,680 | 3. The numbers $x, y, z$ satisfy the relations $\sin (x+y+z)=\frac{9}{41}$ and $\cos x \cos y \cos z=\frac{5}{41}$. Find $\operatorname{tg} x \operatorname{tg} y+\operatorname{tg} y \operatorname{tg} z+\operatorname{tg} z \operatorname{tg} x$.
If there are multiple possible answers, write them in any order separated by a semicolon. | -7;9 |
68,796 | 87. The natural numbers $1,2,3,4,5 \cdots \cdots$ are arranged in sequence, and the multiples of 2 and 3 are crossed out, with all multiples of 7 being retained. The 2007th remaining number is $\qquad$. | 4683 |
31,680 | Problem 8.6. In a $3 \times 3$ table, real numbers are arranged. It turns out that the product of the numbers in any row and any column is 10, and the product of the numbers in any $2 \times 2$ square is 3. Find the number in the central cell. | 0.00081 |
32,315 | A circle intersecting the lateral sides $A C$ and $C B$ of an isosceles triangle $A C B$ at points $P$ and $Q$, respectively, is circumscribed around triangle $A B Q$. Segments $A Q$ and $B P$ intersect at point $D$ such that $A Q: A D=4$ : 3. Find the area of triangle $D Q B$ if the area of triangle $P Q C$ is 3. | \frac{9}{2} |
68,538 | $6 \cdot 54$ Find the constant $c$ such that the function
$$
f(x)=\operatorname{arctg} \frac{2-2 x}{1+4 x}+c
$$
is an odd function on the interval $\left(-\frac{1}{4}, \frac{1}{4}\right)$. | -\operatorname{arctg}2 |
54,683 | 5. How many natural numbers from 1 to 2015 inclusive have a sum of digits that is a multiple of 5? | 402 |
63,276 | # 3.1. Condition:
The number 4597 is displayed on the computer screen. In one move, it is allowed to swap any two adjacent digits, but after this, 100 is subtracted from the resulting number. What is the largest number that can be obtained by making no more than two moves? | 8357 |
57,008 | The integers $ 1,2,...,n$ are placed in order so that each value is either strictly bigger than all the preceding values or is strictly smaller than all preceding values. In how many ways can this be done? | 2^{n-1} |
52,101 | Five football teams held a tournament - each team played against each other once. 3 points were awarded for a win, 1 point for a draw, and no points for a loss. Four teams scored 1, 2, 5, and 7 points respectively. How many points did the fifth team score?
# | 12 |
20,069 |
On a large one-way street, there are two traffic lights one after the other; each traffic light is set up so that the time interval when it shows a green light is two-thirds of the total operating time of the traffic light. A motorist noticed that when he drives through the first traffic light during the green light at his usual speed, in 3 out of 4 cases, the second traffic light does not stop him. Suppose now that the motorist passes the first traffic light during the red light. What is the probability that the second traffic light will also be red? | \dfrac{1}{2} |
65,997 | Given 10 numbers - one one and nine zeros. It is allowed to choose two numbers and replace each of them with their arithmetic mean.
What is the smallest number that can end up in the place of the one?
# | \frac{1}{512} |
31,756 | (9) In tetrahedron $ABCD$, face $ABC$ and face $BCD$ form a dihedral angle of $60^{\circ}$, the projection of vertex $A$ onto face $BCD$ is the orthocenter $H$ of $\triangle BCD$, $G$ is the centroid of $\triangle ABC$, if $AH=4$, $AB=AC$, then $GH=$ $\qquad$ | \frac{4}{9}\sqrt{21} |
53,741 | A round table has a diameter of 1.40 meters.
For a party, the table is expanded by adding three planks, each 40 cm wide, as shown in the figure. If each person at the table should have 60 cm of space, how many guests can sit at the table?
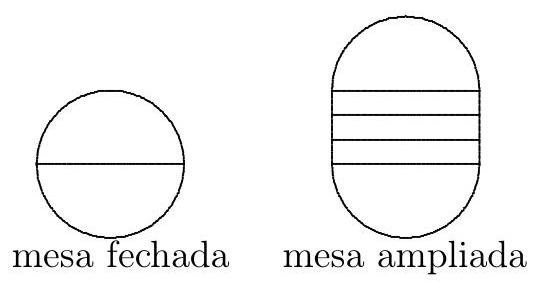 | 11 |
65,002 | 4.1. The product of several (not necessarily distinct) prime numbers is 10 times greater than their sum. Find these numbers. | {2,3,5,5} |
59,452 | $\left[\begin{array}{ll}{[\text { Decimal numeral system }}\end{array}\right]$
From $A$ to $B 999$ km. Along the road, there are kilometer markers indicating the distances to $A$ and to $B$:
$0|999,1| 998, \ldots, 999 \mid 0$.
How many of them have only two different digits? | 40 |
30,143 | 11.201 The lateral edges of a triangular pyramid are of equal length and equal to $a$. Of the three planar angles formed by these edges at the apex of the pyramid, two contain $45^{\circ}$, and the third contains $60^{\circ}$. Determine the volume of the pyramid. | \frac{^3}{12} |
24,266 | Let \( R \) be a semicircle with diameter \( XY \). A trapezoid \( ABCD \) in which \( AB \) is parallel to \( CD \) is circumscribed about \( R \) such that \( AB \) contains \( XY \). If \( AD = 4 \), \( CD = 5 \), and \( BC = 6 \), determine \( AB \). | 10 |
60,001 | Test: Given that $a$ is a natural number, a quadratic trinomial with integer coefficients and $a$ as the leading coefficient has two distinct positive roots less than 1. Find the minimum value of $a$.
---
The above text translated into English, preserving the original text's line breaks and format. | 5 |
66,408 | Think about question 2: In the complex plane, points $A$ and $B$ correspond to the complex numbers $z_{1}=2$, $z_{2}=-3$, respectively. Point $P$ corresponds to the complex number $z$, and the principal value of the argument of $\frac{z-z_{1}}{z-z_{2}}$ is $\varphi$. When point $P$ moves on the upper semicircle with the origin as the center and a radius of 1 (excluding the two endpoints), find the minimum value of $\varphi$. | \pi-\arctan\frac{5\sqrt{6}}{12} |
55,448 | 5. There is a method of setting a six-digit password: the first 2 digits are the last 2 digits of the birth year, the middle 2 digits are the birth month, and the last 2 digits are the birth date. For example, if born on April 23, 1998, the six-digit password is set as 980423. The number of possible passwords set in this way is $\qquad$ kinds. | 36525 |
53,632 | Exercise 3. Let $x, y, z$ be non-zero real numbers such that $x+y+z=0$. Suppose that
$$
\frac{x}{y}+\frac{y}{z}+\frac{z}{x}=\frac{x}{z}+\frac{z}{y}+\frac{y}{x}+1
$$
Determine the value of $\frac{x}{y}+\frac{y}{z}+\frac{z}{x}$. | -1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.