id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
67,343 | 4. Given in $\triangle A B C$, $\angle A=120^{\circ}$, let vector $\alpha=\frac{\overrightarrow{B A}}{|\overrightarrow{B A}| \cos A}+\frac{\overrightarrow{B C}}{|\overrightarrow{B C}| \cos C}, \beta=$ $\frac{\overrightarrow{C A}}{|\overrightarrow{C A}| \cos A}+\frac{\overrightarrow{C B}}{|\overrightarrow{C B}| \cos B}$, then the angle between $\alpha$ and $\beta$ is -. $\qquad$ | 60 |
52,299 | # Problem 4. (3 points)
On the side $B C$ of triangle $A B C$, points $A_{1}$ and $A_{2}$ are marked such that $B A_{1}=6, A_{1} A_{2}=8$, $C A_{2}=4$. On the side $A C$, points $B_{1}$ and $B_{2}$ are marked such that $A B_{1}=9, C B_{2}=6$. Segments $A A_{1}$ and $B B_{1}$ intersect at point $K$, and $A A_{2}$ and $B B_{2}$ intersect at point $L$. Points $K, L$ and $C$ lie on the same line. Find $B_{1} B_{2}$. | 12 |
67,503 | 373. Cutting a Cube. In a mathematical journal, the following question and answer appeared.
Question: "A carpenter wants to cut a wooden cube with a side of 3 inches into 27 cubes with a side of 1 inch. He can easily do this by making 6 cuts while keeping the pieces together so they don't fall apart. What is the minimum number of cuts if the carpenter is allowed to rearrange the pieces in any way during the cutting process $?$"
Answer: "The minimum number of cuts is 6, since it takes 6 cuts, one for each face, to separate the inner cube."
Now, suppose the inner cube is missing. What is the minimum number of cuts in this case if the pieces can be rearranged in any way during the cutting process $?$ | 6 |
32,979 | Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
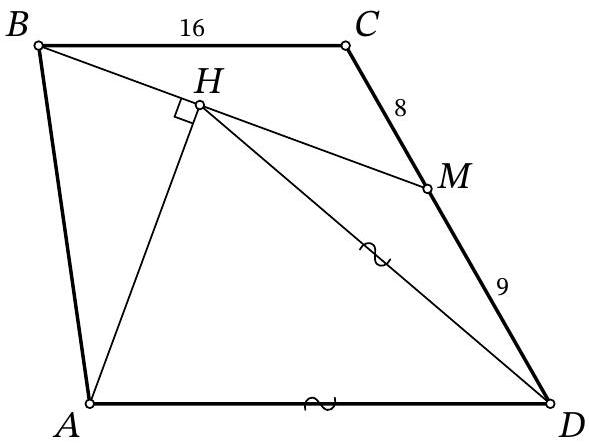 | 18 |
34,345 | Kirienko D:
Sasha and Masha each thought of a natural number and told them to Vasya. Vasya wrote the sum of the numbers on one sheet of paper and their product on another, then hid one of the sheets and showed the other (which had the number 2002 written on it) to Sasha and Masha. Seeing this number, Sasha said that he did not know what number Masha had thought of. Hearing this, Masha said that she did not know what number Sasha had thought of. What number did Masha think of? | 1001 |
17,798 | In the city of Omsk, a metro line was built in a straight line. On this same line is the house where Nikita and Yegor live. Every morning, they simultaneously leave the house for their lessons, after which Yegor runs to the nearest metro station at a speed of 12 km/h, while Nikita walks along the metro line to another station at a speed of 6 km/h. Despite this, Nikita always manages to reach his lesson on time, whereas Yegor does not, even though he doesn't delay anywhere. Find the maximum possible speed of the metro trains, given that it is constant and an integer. (Assume the school is located directly at a certain metro station, distinct from the given ones). | 23 |
68,497 | 3. In $\triangle A B C$, the sides opposite to $\angle A, \angle B, \angle C$ are $a, b, c$ respectively. If
$$
a^{2}+2\left(b^{2}+c^{2}\right)=2 \sqrt{2} \text {, }
$$
then the maximum value of the area of $\triangle A B C$ is $\qquad$ . | \frac{1}{4} |
32,569 | 2. Let positive numbers $a, b, c, x, y, z$ satisfy $c y + b z = a, a z + c x = b, b x + a y = c$, find the minimum value of the function $f(x, y, z)=$
$\frac{x^{2}}{1+x}+\frac{y^{2}}{1+y}+\frac{z^{2}}{1+z}$. | \frac{1}{2} |
52,355 | 4-2. A circle touches the sides of an angle at points $A$ and $B$. The distance from a point $C$ lying on the circle to the line $A B$ is 6. Find the sum of the distances from point $C$ to the sides of the angle, given that one of these distances is 5 more than the other. | 13 |
52,846 | 69 If $11 z^{10}+10 i z^{9}+10 i z-11=0$, then $|z|=$
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
However, the translation is already provided in the response, so there's no need for further action. The text is a mathematical problem asking for the magnitude of $z$ given a specific polynomial equation. If you need further assistance with solving the problem or have any other requests, feel free to let me know! | 1 |
28,755 | 6. For any positive integers $x, y, z$, if $x \mid y^{3}$, $y \mid z^{3}$, $z \mid x^{3}$, and $x y z \mid (x+y+z)^{n}$, find the smallest positive integer $n$ that satisfies the condition. | 13 |
56,782 | # Problem 4. (3 points)
Petya wrote the number 11234567 on the board, and then all the numbers obtained from it by rearranging the digits, in ascending order. What was the position of the number $46753211$? | 12240 |
10,261 | G3.3 In Figure $1, \angle A=60^{\circ}, \angle B=\angle D=90^{\circ} . B C=2, C D=3$ and $A B=x$, find the value of $x$. | \dfrac{8\sqrt{3}}{3} |
21,632 | 50. How many divisors does the integer
$$
N=a^{\alpha} \cdot b^{\beta} \cdot c^{\gamma} \ldots l^{\lambda}
$$
have, where $a, b, c, \ldots l$ are prime numbers and $\alpha, \beta, \gamma, \ldots \lambda$ are any integers? | (\alpha + 1)(\beta + 1)(\gamma + 1) \cdots (\lambda + 1) |
14,885 | There are several contestants participating in a math competition. Some of the contestants know each other, and any two contestants who do not know each other have exactly two mutual acquaintances. It is known that contestant $A$ and contestant $B$ know each other, but they have no mutual acquaintances. Prove that they have the same number of acquaintances. | A \text{ and } B \text{ have the same number of acquaintances.} |
13,973 | 35*. What is the greatest number of rays in space that form pairwise obtuse angles? | 4 |
60,323 | 5. Given the function $f(x)$
$=\log _{a}\left(a x^{2}-x+\frac{1}{2}\right)$ is always positive on the interval $[1,2]$, then the range of the real number $a$ is $\qquad$ | (\frac{1}{2},\frac{5}{8})\cup(\frac{3}{2},+\infty) |
53,396 | How many positive integers between 1 and 1988 can be expressed in the form
$$
[x]+[2 x]+[4 x]+[8 x]
$$
for some real number $x$? | 1061 |
28,671 | 9. Let $A B C D$ be a regular tetrahedron with side length 1 . Let $X$ be the point in triangle $B C D$ such that $[X B C]=2[X B D]=4[X C D]$, where $[\varpi]$ denotes the area of figure $\varpi$. Let $Y$ lie on segment $A X$ such that $2 A Y=Y X$. Let $M$ be the midpoint of $B D$. Let $Z$ be a point on segment $A M$ such that the lines $Y Z$ and $B C$ intersect at some point. Find $\frac{A Z}{Z M}$. | \frac{4}{7} |
64,060 | 4. In a box, there is a large batch of flowers of six types mixed together. Vasya randomly takes flowers one by one from the box. As soon as he collects 5 flowers of the same type, he makes a bouquet and sells it. What is the minimum number of flowers he needs to take to guarantee selling 10 bouquets? | 70 |
51,450 | 8. Let $a_{1}, a_{2}, \cdots, a_{21}$ be a permutation of $1,2, \cdots, 21$, satisfying
$$
\left|a_{20}-a_{21}\right| \geqslant\left|a_{19}-a_{21}\right| \geqslant\left|a_{18}-a_{21}\right| \geqslant \cdots \geqslant\left|a_{1}-a_{21}\right| \text {. }
$$
The number of such permutations is $\qquad$ | 3070 |
63,889 | Question 150: Four spheres with a radius of 1 are pairwise externally tangent. Then the volume of the circumscribed regular tetrahedron is $\qquad$ . | \frac{\sqrt{3}(6+\sqrt{6})^{3}}{27} |
27,211 | 10. (20 points) Let the left vertex of the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ be $A$, and the right focus be $F(c, 0)$, and $2b$, $a$, $c$ form a geometric sequence. A line passing through point $F$ intersects the ellipse at points $M$ and $N$, and the lines $AM$ and $AN$ intersect the right directrix at points $P$ and $Q$, respectively. Find the size of $\angle P F Q$. | 90 |
21,566 | What is the largest possible remainder that is obtained when a two-digit number is divided by the sum of its digits? | 15 |
67,848 | 88. A five-digit number $\overline{a b c d e}$, where each digit is unique, is a multiple of 9, and $\overline{a b c d}$ is a multiple of 4. The smallest $\overline{a b c d e}$ is $\qquad$ | 10287 |
68,001 | ## Task B-1.5.
Three friends Marta, Iva, and Ana love to travel. Marta has visited 20 countries, Iva has visited $90\%$ more countries than Marta, and Ana has visited 13 fewer countries than Iva. Ana has visited $40\%$ of the countries Marta has visited, and Iva has visited one-fifth of the countries Ana has visited and half of the countries Marta has visited. The number of countries visited by all three friends is 16 times smaller than the total number of countries they have visited. How many countries have they visited in total? | 64 |
26,844 | Task 2. Lёnya has cards with digits from 1 to 7. How many ways are there to glue them into two three-digit numbers (one card will not be used) so that their product is divisible by 81, and their sum is divisible by 9? | 36 |
57,542 | Example 1.11. Find $\int \frac{\sin ^{3} x}{\cos ^{5} x} d x$. | \frac{1}{4\cos^{4}x}-\frac{1}{2\cos^{2}x}+C |
26,981 | 3. Circle $\omega_{1}$ with center $O$ intersects circle $\omega_{2}$, which passes through point $O$, at points $K$ and $L$. A line through point $O$ intersects circle $\omega_{2}$ again at point $A$. Segment $OA$ intersects circle $\omega_{1}$ at point $B$. Find the ratio of the distances from point $B$ to the lines $A L$ and $K L$. | 1:1 |
18,429 | Given that $A_k = \frac {k(k - 1)}2\cos\frac {k(k - 1)\pi}2,$ find $|A_{19} + A_{20} + \cdots + A_{98}|.$
Please give the answer directly without any intermediate steps. | 40 |
31,323 | 10. (20 points) Let the line $y=2 \sqrt{2} x+2 \sqrt{3}$ intersect the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ at points $A$ and $B$, with the origin of coordinates being $O$. If $\angle A O B=90^{\circ}$ and $A B=\frac{12 \sqrt{11}}{17}$, find the equation of the ellipse. | \frac{x^{2}}{4}+\frac{y^{2}}{2}=1 |
25,329 | 2. Determine the maximum possible value of the expression
$$
\frac{a_{1} a_{2} \ldots a_{n}}{\left(1+a_{1}\right)\left(a_{1}+a_{2}\right) \ldots\left(a_{n-1}+a_{n}\right)\left(a_{n}+2^{n+1}\right)}
$$
where $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ are positive real numbers. | \frac{1}{3^{n+1}} |
68,674 | 7.4. A biologist sequentially placed 150 beetles into ten jars. Moreover, in each subsequent jar, he placed more beetles than in the previous one. The number of beetles in the first jar is no less than half the number of beetles in the tenth jar. How many beetles are in the sixth jar? | 16 |
60,676 | Example (11)
If three circles with radius $r^{\prime}\left(r^{\prime}<r\right)$ can cover $\odot(O, r)$, how large does $r^{\prime}$ need to be at least? | \frac{\sqrt{3}}{2}r |
63,229 | Exercise 6. A set of $\mathrm{n}$ cells in an $\mathrm{n} \times \mathrm{n}$ grid is said to be distributed if it never includes two cells in the same row or column. In how many ways can one color some (possibly none) cells of an $\mathrm{n} \times \mathrm{n}$ grid so that all distributed sets contain the same number of colored cells? | 2^{n+1}-2 |
6,480 | The difference between the longest and shortest diagonals of the regular n-gon equals its side. Find all possible n. | 9 |
17,645 | The positive integer \( N \) has six digits in increasing order. For example, 124689 is such a number. However, unlike 124689, three of the digits of \( N \) are 3, 4, and 5, and \( N \) is a multiple of 6. How many possible six-digit integers \( N \) are there? | 3 |
55,484 | 10. (7 points) In the repeating decimal 0.2017, if the sum of all digits from the $m$-th digit to the $n$-th digit after the decimal point is 2017, when $m$ takes the minimum value, $n=$ $\qquad$
| 808 |
52,936 | Petr glued 17 dice into a snake (as shown in the picture). He always glued the sides with the same number of dots. Then he examined the snake from all sides and correctly calculated the total number of dots on its surface. What did he get? (The sum of the dots on opposite sides of a die is 7.)
(S. Bodláková, M. Dillingerová)
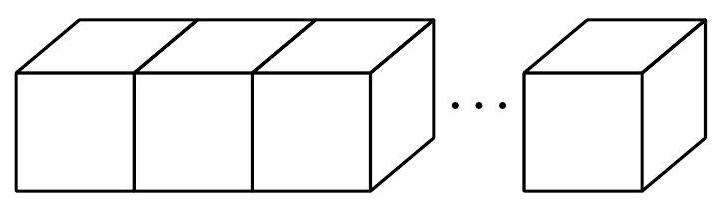 | 245 |
14,170 | 2. Vasya constructed a robot, but he messed up the program, so the robot makes random moves that somehow always lead it to the right point.
A move is a one-kilometer displacement either north (N), east (E), south (S), or west (W).
The robot reached its goal in 22 moves:
# EENENNWNENESEEEEESSSWN.
How many moves would the robot need if it did not make any extra moves? | 10 |
62,117 | 5. How many even six-digit numbers exist, in the notation of which identical digits do not stand next to each other | 265721 |
28,071 | Example 8 Find the odd prime $p$ that satisfies the following condition: there exists a permutation $b_{1}, b_{2}, \cdots, b_{p-1}$ of $1,2, \cdots, p-1$, such that $1^{b_{1}}, 2^{b_{2}}, \cdots,(p-1)^{b_{p-1}}$ forms a reduced residue system modulo $p$. | 3 |
52,889 | 76. A barrel water company originally sells a barrel of water for 20 yuan, and now is holding a promotional activity, “Buy 10 barrels and get a 40 yuan voucher, with a chain gift”, meaning that for every 10 barrels of water purchased (10 barrels can be bought with cash, vouchers, or a combination of both), a 40 yuan voucher is given; for every 20 barrels of water, an 80 yuan voucher is given, and so on. Xiaomei's family spent 1000 yuan and can get back the maximum of $\qquad$ barrels of water. | 62 |
54,167 | 1. The numbers $x, y, z \neq 0$ are such that $\frac{x^{2}+y^{2}-z^{2}}{2 x y}+\frac{y^{2}+z^{2}-x^{2}}{2 y z}+\frac{z^{2}+x^{2}-y^{2}}{2 x z}=1$.
What values can the expression
$$
\left(\frac{x^{2}+y^{2}-z^{2}}{2 x y}\right)^{2016}+\left(\frac{y^{2}+z^{2}-x^{2}}{2 y z}\right)^{2016}+\left(\frac{z^{2}+x^{2}-y^{2}}{2 x z}\right)^{2016} ?
$$
take? | 3 |
34,758 | Sine Theorem [ Two tangents drawn from one point ]
One of the angles of a triangle is $\frac{3 \pi}{4}$, the radius of the inscribed circle is 4, and the perimeter of the triangle is $16(6+\sqrt{2})$. Find the radius of the circle circumscribed around this triangle. | 26\sqrt{2}+4 |
27,543 | 4. Let $A B C$ be an acute triangle, $\mathcal{K}$ a circle with diameter $A B$, $E$ and $F$ the intersections of the circle with sides $A C$ and $B C$, and $P$ the intersection of the tangents to the circle $\mathcal{K}$ at points $E$ and $F$. Calculate the ratio of the radii of the circumcircles of triangles $A B C$ and $E F P$. | 2 |
3,410 | 5. Garden workers need to dig holes at equal distances along the edge of a circular flower bed with a circumference of 300 meters. They started digging holes every 3 meters along the edge of the flower bed. When they had dug 30 holes, they received instructions from their superiors to change to planting trees every 5 meters. How many more holes do they need to dig to complete the task? | 54 |
61,208 | 7. [6] Rachel has two indistinguishable tokens, and places them on the first and second square of a $1 \times 6$ grid of squares, She can move the pieces in two ways:
- If a token has free square in front of it, then she can move this token one square to the right
- If the square immediately to the right of a token is occupied by the other token, then she can "leapfrog" the first token; she moves the first token two squares to the right, over the other token, so that it is on the square immediately to the right of the other token.
If a token reaches the 6th square, then it cannot move forward any more, and Rachel must move the other one until it reaches the 5 th square. How many different sequences of moves for the tokens can Rachel make so that the two tokens end up on the 5 th square and the 6 th square? | 42 |
67,173 | Jana had to calculate the product of two six-digit numbers for her homework. When copying from the board, she omitted one digit from one of the numbers, and instead of a six-digit number, she wrote only 85522. When she got home, she realized her mistake. However, she remembered that the number she had copied incorrectly was divisible by three. She decided to try to determine what the original number could have been.
Determine how many such six-digit numbers exist.
(M. Dillingerová) | 13 |
28,707 | 10. (20 points) Let $a_{1}, a_{2}, a_{3}, a_{4}$ be four rational numbers such that
$$
\left\{a_{i} a_{j} \mid 1 \leqslant i<j \leqslant 4\right\}=\left\{-24,-2,-\frac{3}{2},-\frac{1}{8}, 1,3\right\} .
$$
Find the value of $a_{1}+a_{2}+a_{3}+a_{4}$. | \\frac{9}{4} |
33,296 | 10. (20 points) Given the hyperbola $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$, points $B$ and $F$ are the right vertex and right focus of the hyperbola $C$, respectively, and $O$ is the origin. Point $A$ is on the positive $x$-axis and satisfies $|O A|,|O B|,|O F|$ forming a geometric sequence. A line $l$ is drawn from point $F$ perpendicular to the asymptotes of the hyperbola $C$ in the first and third quadrants, with the foot of the perpendicular being $P$.
(1) Prove: $\overrightarrow{P A} \cdot \overrightarrow{O P}=\overrightarrow{P A} \cdot \overrightarrow{F P}$;
(2) Let $a=1, b=2$, and the line $l$ intersects the left and right branches of the hyperbola $C$ at points $D$ and $E$, respectively. Find the value of $\frac{|D F|}{|D E|}$. | \frac{3}{2} |
50,343 | $\left.\begin{array}{l}\left.\text { [ } \begin{array}{l}\text { Rebus } \\ \text { [Divisibility of numbers. General properties }\end{array}\right] \\ \text { [ Decimal system } \\ \text { [ Case enumeration }\end{array}\right]$
Which digits can stand in place of the letters in the example $A B \cdot C=D E$, if different letters represent different digits and the digits are written from left to right in ascending order? | 13\cdot6=78 |
29,617 | 12. Let three distinct complex numbers $z_{1}, z_{2}, z_{3}$ satisfy the equation $4 z_{1}^{2}+5 z_{2}^{2}+5 z_{3}^{2}=4 z_{1} z_{2}+6 z_{2} z_{3}+4 z_{3} z_{1}$. Denote the lengths of the sides of the triangle formed by $z_{1}, z_{2}, z_{3}$ on the complex plane, in ascending order, as $a, b, c$, then $a: b: c=$ $\qquad$. | 2:\sqrt{5}:\sqrt{5} |
63,073 | 23. A person is climbing a staircase with a total of $n$ steps. If it is stipulated that he can only climb 1 step or 3 steps at a time, how many different ways are there to climb the stairs? | \sum_{k=0}^{\lfloor\frac{n}{3}\rfloor}\binom{n-2k}{k} |
66,400 | 4. In an isosceles trapezoid $A B C D (B C \| A D)$, angles $A B D$ and $D B C$ are $135^{\circ}$ and $15^{\circ}$ respectively, and $B D=\sqrt{6}$. Find the perimeter of the trapezoid. | 9-\sqrt{3} |
60,891 | 10. Let $a>1$ be a positive real number, and $n \geqslant 2$ be a natural number, and the equation $[a x]=x$ has exactly $n$ distinct solutions, then the range of values for $a$ is . $\qquad$ | [1+\frac{1}{n},1+\frac{1}{n-1}) |
3,374 | Let $\omega = \cos\frac{2\pi}{7} + i \cdot \sin\frac{2\pi}{7},$ where $i = \sqrt{-1}.$ Find the value of the product \[\prod_{k=0}^6 \left(\omega^{3k} + \omega^k + 1\right).\]
Please give the answer directly without any intermediate steps. | 24 |
66,117 | Task No. 1.1
## Condition:
Five friends - Masha, Nastya, Irina, Olya, and Anya - meet in the park every day after buying ice cream from the shop around the corner. One day, the girls had a conversation.
Irina: I was the first in line!
Olya: No one was after me.
Anya: Only one person was after me.
Masha: There were five people in front of me.
Nastya: I was standing next to Irina.
The girls are friends, so they don't lie to each other. How many people were between Masha and Nastya? | 3 |
59,747 | Example 3. A region is divided into five administrative areas as shown in the figure. There are 4 colors available to color the map, with the requirement that adjacent areas must not use the same color. How many different coloring methods are there? | 72 |
6,015 | 11.7. The area of the surface of a spherical segment is $S$ (the spherical part of its surface is meant). What is the greatest possible volume of such a segment? | \dfrac{S^{3/2}}{3\sqrt{2\pi}} |
62,103 | ## Task 14/88
We are looking for the smallest number $n \in N$, for which both the cross sum $q(n)$ and the cross sum $q(n+1)$ of the successor $n+1$ are divisible by 11. | 2899999 |
7,977 | Let $A B C$ be a triangle with an inscribed circle centered at $I$. The inscribed circle is tangent to $B C, C A,$ and $A B$ at points $D, E,$ and $F$ respectively. Let $P$ be on the same side of $E F$ as $A$ such that $\widehat{P E F}=\widehat{A B C}$ and $\widehat{P F E}=\widehat{A C B}$.
Show that $P, I,$ and $D$ are collinear. | P, I, D \text{ are collinear} |
57,173 | Let $ABC$ be a triangle, $M$ the midpoint of $BC$, and $N$ one-third of the way along $AC$ from $C$. The line $(MN)$ intersects $(AB)$ at $P$. Determine the position of $P$ relative to $A$ and $B$. | \frac{PA}{PB}=2 |
54,905 | 7. 5 people participate in 4 groups, each group has two people, and each person must participate in at least one group. Then, the number of different groupings is
$\qquad$ kinds. | 135 |
24,623 | An airline company is planning to introduce a network of connections between the ten different airports of Sawubonia. The airports are ranked by priority from first to last (with no ties). We call such a network *feasible* if it satisfies the following conditions:
- All connections operate in both directions
- If there is a direct connection between two airports A and B, and C has higher priority than B, then there must also be a direct connection between A and C.
Some of the airports may not be served, and even the empty network (no connections at all) is allowed. How many feasible networks are there? | 512 |
56,052 | 5. Person A and Person B start walking towards each other at a constant speed from points $A$ and $B$ respectively, and they meet for the first time at a point 700 meters from $A$; then they continue to walk, with A reaching $B$ and B reaching $A$, and both immediately turning back, meeting for the second time at a point 400 meters from $B$. Then the distance between $A$ and $B$ is meters. | 1700 |
9,025 | How many ways are there to win tic-tac-toe in \(\mathbb{R}^{n}\)? That is, how many lines pass through three of the lattice points \((a_{1}, \ldots, a_{n})\) in \(\mathbb{R}^{n}\) with each coordinate \(a_{i}\) in \(\{1,2,3\}\)? Express your answer in terms of \(n\). | \dfrac{5^n - 3^n}{2} |
33,962 | Problem 8.7. Given an isosceles triangle $ABC$, where $AB = AC$ and $\angle ABC = 53^{\circ}$. Point $K$ is such that $C$ is the midpoint of segment $AK$. Point $M$ is chosen such that:
- $B$ and $M$ are on the same side of line $AC$;
- $KM = AB$
- angle $MAK$ is the maximum possible.
How many degrees does angle $BAM$ measure?
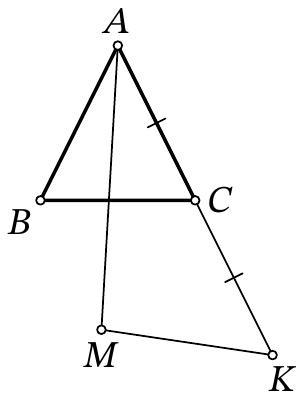 | 44 |
26,167 | Example 22 (2001 Guangdong College Entrance Examination Question) In the quadrilateral pyramid $S-ABCD$ with a right trapezoid base, $\angle ABC=$ $90^{\circ}, SA \perp$ plane $ABCD, SA=AB=BC=1, AD=\frac{1}{2}$, find the tangent of the dihedral angle formed by faces $SCD$ and $SBA$. | \frac{\sqrt{2}}{2} |
52,276 | Let $P$ be an arbitrary interior point of the equilateral triangle $ABC$. Let the feet of the perpendiculars from $P$ to the sides $BC$, $CA$, and $AB$ be $D$, $E$, and $F$ respectively. Determine the value of the ratio
$$
\frac{P D+P E+P F}{B D+C E+A F}
$$ | \frac{\sqrt{3}}{3} |
64,293 | 8 Let $A_{1}, A_{2}, \cdots, A_{8}$ be any 8 points taken on a plane, and for any directed line $l$ on the plane, let the projections of $A_{1}, A_{2}, \cdots, A_{8}$ on this line be $P_{1}, P_{2}, \cdots, P_{8}$. If these 8 projections are pairwise distinct, they are arranged in sequence according to the direction of line $l$ as $P_{i_{1}}$, $P_{i_{2}}, \cdots, P_{i_{8}}$. Thus, a permutation $i_{1}, i_{2}, \cdots, i_{8}$ of 1, $2, \cdots, 8$ is obtained (in the figure, this permutation is $2,1,8$, $3,7,4,6,5$). Let the number of different permutations obtained by projecting these 8 points onto all directed lines on the plane be $N_{8}=N\left(A_{1}, A_{2}, \cdots, A_{8}\right)$. Try to find the maximum value of $N_{8}$. (Provided by Su Chun) | 56 |
20,325 | 12. If $\sec \alpha \sqrt{1+\tan ^{2} \alpha}+\tan \alpha \sqrt{\csc ^{2} \alpha-1}=\tan ^{2} \alpha$, determine the sign of the product $\sin (\cos \alpha) \cdot \cos (\sin \alpha)$. | positive |
31,548 | 45th Putnam 1984 Problem A4 A convex pentagon inscribed in a circle radius 1 has two perpendicular diagonals which intersect inside the pentagon. What is the maximum area the pentagon can have? Solution | 1+\frac{3\sqrt{3}}{4} |
52,194 | Which numbers have the property that their last two digits are the same as the last two digits of their square? | 00,01,25,76 |
5,915 | Positive integers $(p,a,b,c)$ called *good quadruple* if
a) $p $ is odd prime,
b) $a,b,c $ are distinct ,
c) $ab+1,bc+1$ and $ca+1$ are divisible by $p $ .
Prove that for all good quadruple $p+2\le \frac {a+b+c}{3} $ , and show the equality case. | p + 2 \le \frac{a + b + c}{3} |
63,202 | Example 8 Let the three-digit number $n=\overline{a b c}$, if the lengths of the sides of a triangle can be formed with $a, b, c$ as an isosceles (including equilateral) triangle, then the number of such three-digit numbers $n$ is $\qquad$.
(2004 National High School League Question, originally a multiple-choice question) | 165 |
8,787 | A bag of rice takes Liu Bei 5 days to finish eating alone, and Guan Yu 3 days to finish eating alone. A bag of wheat takes Guan Yu 5 days to finish eating alone, and Zhang Fei 4 days to finish eating alone. Liu Bei's daily food consumption is $\qquad$% less than Zhang Fei's daily food consumption. | 52 |
10,397 | 3. An electronic flea can jump from one circle to an adjacent circle with each step. Now, a red flea starts from the circle marked with the number "0" and jumps 1991 steps in a clockwise direction, landing in one circle. A black flea also starts from the circle marked with the number "0", but it jumps 1949 steps in a counterclockwise direction, landing in another circle. What is the product of the numbers in these two circles? | 77 |
64,712 | (10) Given that $F_{1}$ and $F_{2}$ are the left and right foci of the hyperbola $C: x^{2}-y^{2}=1$, and point $P$ is on $C$. If the area of $\triangle P F_{1} F_{2}$ is $\sqrt{3}$, find $\angle F_{1} P F_{2}$. | 60 |
32,229 | Example 7 Let $P$ and $Q$ be points on the parabola $y^{2}=x$ and the circle $(x-3)^{2}+y^{2}=1$ respectively. Find $|P Q|_{\text {min }}$. | \frac{\sqrt{11}}{2}-1 |
59,726 | Fins all ordered triples $ \left(a,b,c\right)$ of positive integers such that $ abc \plus{} ab \plus{} c \equal{} a^3$. | (a, a - 1, a) |
16,336 | Find the polynomials with integer coefficients $P$ such that:
$$
\forall n, n \text { divides } P\left(2^{n}\right)
$$ | 0 |
61,712 | Sharygin I.F.
On the side $AB$ of triangle $ABC$, a square is constructed externally with center $O$. Points $M$ and $N$ are the midpoints of sides $AC$ and $BC$ respectively, and the lengths of these sides are $a$ and $b$ respectively. Find the maximum of the sum $OM + ON$ as the angle $ACB$ changes. | \frac{1+\sqrt{2}}{2}(+b) |
32,821 | 5. What is the smallest number of different numbers that can be chosen so that each chosen number is equal to the sum of some three other different chosen numbers?
---
Note: The translation maintains the original text's formatting and line breaks. | 7 |
1,029 | Given positive numbers $a_1$ and $b_1$ , consider the sequences defined by
\[a_{n+1}=a_n+\frac{1}{b_n},\quad b_{n+1}=b_n+\frac{1}{a_n}\quad (n \ge 1)\]
Prove that $a_{25}+b_{25} \geq 10\sqrt{2}$ . | 10\sqrt{2} |
15,391 | In an isosceles trapezoid, there are two circles. One of them has a radius of 1 and is inscribed in the trapezoid, while the other circle touches two sides of the trapezoid and the first circle. The distance from the vertex of the angle formed by the two sides of the trapezoid, which touch the second circle, to the point where the circles touch is twice the diameter of the second circle. Find the area of the trapezoid. | \dfrac{9\sqrt{2}}{2} |
62,208 | 12. Place 1 sphere with a radius of 2 between two inclined planes whose lines of intersection are on a horizontal plane, with the angles between these planes and the horizontal plane being $60^{\circ}$ and $30^{\circ}$, respectively. Then the distance from the center of the sphere to the horizontal plane is $\qquad$ | \sqrt{3}+1 |
4,704 | Given a sequence \(\{a_n\}\) that satisfies:
\[ a_1 = \sqrt{3}, \quad a_{n+1} = \lfloor a_n \rfloor + \frac{1}{\{a_n\}}, \]
where \(\lfloor a_n \rfloor\) and \(\{a_n\}\) denote the integer part and the fractional part of the positive number \(a_n\), respectively. Find \(a_{2015}\). | 3021 + \sqrt{3} |
62,003 | Adam is playing Minesweeper on a $9\times9$ grid of squares, where exactly $\frac13$ (or 27) of the squares are mines (generated uniformly at random over all such boards). Every time he clicks on a square, it is either a mine, in which case he loses, or it shows a number saying how many of the (up to eight) adjacent squares are mines.
First, he clicks the square directly above the center square, which shows the number $4$. Next, he clicks the square directly below the center square, which shows the number $1$. What is the probability that the center square is a mine?
[i]Proposed by Adam Bertelli[/i] | \frac{88}{379} |
61,529 | 3+ [Mutual Position of Two Circles]
In a regular $n$-gon ( $n \geq 3$ ), the midpoints of all sides and diagonals are marked.
What is the maximum number of marked points that can lie on one circle? | n |
22,770 | ## Problem 4
Determine the primitives of the function $f:[0, \pi] \rightarrow \mathbf{R}$, which is primitive-able, and satisfies the relation $f(x) \sin x - f(\pi - x) = \cos^2 x, \forall x \in [0, \pi]$. | -x + \cos x + C |
56,353 | 9. Let $M=\{1,2, \cdots, 2005\}, A$ be a subset of $M$ and satisfy the condition: if $x \in A$ then $15 x \notin A$, then the maximum number of elements in $A$ is $\qquad$ | 1880 |
53,551 | 5. Given that $\triangle A B C$ is an equilateral triangle with side length 5, and $P$ is a point inside it such that $P A=4, P B=3$. Then the length of $P C$ is $\qquad$. | \sqrt{25-12 \sqrt{3}} |
28,303 | 2. Positive numbers $a, b, c$ are such that $a+b+c=3$. Find the minimum value of the expression
$$
A=\frac{a^{3}+b^{3}}{8 a b+9-c^{2}}+\frac{b^{3}+c^{3}}{8 b c+9-a^{2}}+\frac{c^{3}+a^{3}}{8 c a+9-b^{2}}
$$ | \frac{3}{8} |
64,817 | 2. Thirty beads (blue and green) were laid out in a circle. For 26 beads, the neighboring one was blue, and for 20 beads, the neighboring one was green. How many blue beads were there? | 18 |
68,338 | What is the minimum number of planes determined by $6$ points in space which are not all coplanar, and among which no three are collinear? | 11 |
4,192 | Find the number of permutations \(a_1, a_2, \ldots, a_{10}\) of the numbers \(1, 2, \ldots, 10\) such that \(a_{i+1}\) is not less than \(a_i - 1\) for \(i = 1, 2, \ldots, 9\). | 512 |
65,050 | 4. Which digit must be substituted instead of the star so that the following large number is divisible by 7 ?
$$
\underbrace{66 \cdots 66}_{2023} \times \underbrace{55 \cdots 55}_{2023}
$$ | 6 |
21,294 | ## Task 3 - 050713
The driver of a car registered in the GDR fled the scene after a traffic accident. After questioning several witnesses, the following information was obtained about the police registration number of the car:
a) The two letters of the license plate were AB or AD.
b) The two front digits were the same and different from the last two digits.
c) The number formed by the last two digits was 69 or 96.
What is the maximum possible number of cars that can meet these conditions? | 32 |
31,210 | On the sides of triangle $ABC$, points $D, E, F, G$ are given, as shown in the figure. It is given that quadrilateral $DEFG$ is a rhombus and segments $AD, DE$, and $EB$ are congruent.
Determine the measure of angle $ACB$.
(I. Jančigová)
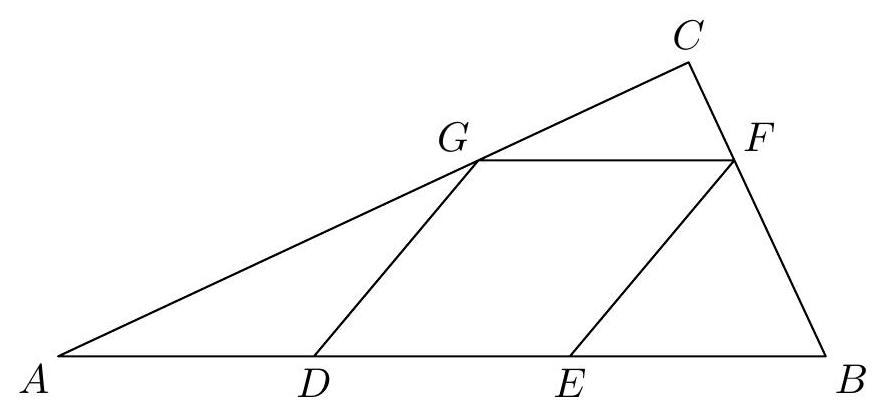
Hint. What is the relative position of lines $AC$ and $DF$? | 90 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.