id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
52,475 | Task 2. Find the number of ways to color all natural numbers from 1 to 20 in blue and red such that both colors are used and the product of all red numbers is coprime with the product of all blue numbers. | 62 |
58,194 | Bogdanov I.I.
In the language of the AU tribe, there are two letters - "a" and "u". Some sequences of these letters are words, and each word has no fewer than one and no more than 13 letters. It is known that if you write down any two words in a row, the resulting sequence of letters will not be a word. Find the maximum possible number of words in such a language. | 2^{14}-2^{7} |
26,516 | 10. Let positive real numbers $a, b, c$ satisfy $a^{2}+4 b^{2}+9 c^{2}=4 b+12 c-2$, find the minimum value of $\frac{1}{a}+\frac{2}{b}+\frac{3}{c}$. | 6 |
2,186 | In the rectangular coordinate plane, the number of integer points (i.e., points with both integer x and y coordinates) that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
y \leqslant 3x \\
y \geqslant \frac{1}{3}x \\
x + y \leqslant 100
\end{array}\right.
$$
is ______. | 2551 |
17,164 | The fraction
\[\dfrac1{99^2}=0.\overline{b_{n-1}b_{n-2}\ldots b_2b_1b_0},\]
where $n$ is the length of the period of the repeating decimal expansion. What is the sum $b_0+b_1+\cdots+b_{n-1}$ | 883 |
30,567 | 3. In the city of Gentle-city, there live 19 gentlemen, any two of whom are either friends or enemies. At some point, each gentleman asked each of his friends to send a hate card to each of his enemies (gentleman A asks gentleman B to send a card to all enemies of gentleman B). Each gentleman fulfilled all the requests, and he sent each of his enemies as many cards as he was asked to. What is the maximum number of cards that could have been sent? | 1538 |
32,860 | 5. Given the number $5300 \ldots 0035$ (100 zeros). It is required to replace some two zeros with non-zero digits so that after the replacement, the resulting number is divisible by 495. In how many ways can this be done? | 22100 |
10,328 | There are $N$ prime numbers written on a board (not necessarily distinct). It turns out that the sum of any three numbers on the board is also a prime number. What is the largest possible value of $N$? | 4 |
24,452 | sequence of positive integers with $a_1=1$ and $a_9+a_{10}=646$ is formed so that the first three terms are in geometric progression , the second, third, and fourth terms are in arithmetic progression , and, in general, for all $n\ge1,$ the terms $a_{2n-1}, a_{2n}, a_{2n+1}$ are in geometric progression, and the terms $a_{2n}, a_{2n+1},$ and $a_{2n+2}$ are in arithmetic progression. Let $a_n$ be the greatest term in this sequence that is less than $1000$ . Find $n+a_n.$ | 973 |
19,199 | In the triangle $ABC$, let $AA_1$, $BB_1$, and $CC_1$ be the angle bisectors intersecting at point $O$. Prove that $8 \leq \frac{AO}{A_1O} \cdot \frac{BO}{B_1O} \cdot \frac{CO}{C_1O} \leq \frac{4R}{r}$, where $R$ denotes the circumradius and $r$ denotes the inradius. | 8 \leq \frac{AO}{A_1O} \cdot \frac{BO}{B_1O} \cdot \frac{CO}{C_1O} \leq \frac{4R}{r} |
939 | Find the smallest positive integer $n$ such that in any two-coloring of a complete graph $K_{n}$ with $n$ vertices, there always exist $m$ edges of the same color that are pairwise disjoint. | 3m - 1 |
25,023 | Given real numbers \( a, b, c \) and a positive number \( \lambda \) such that the polynomial \( f(x) = x^3 + a x^2 + b x + c \) has three real roots \( x_1, x_2, x_3 \), and the conditions \( x_2 - x_1 = \lambda \) and \( x_3 > \frac{1}{2}(x_1 + x_2) \) are satisfied, find the maximum value of \( \frac{2 a^3 + 27 c - 9 a b}{\lambda^3} \). | \dfrac{3\sqrt{3}}{2} |
50,539 | How many positive integers of at most $n$ digits are there whose square ends in the same $n$ digits (possibly with some leading zeros)? | 3 |
55,593 | What is the maximum number of interior angles greater than $180^{\circ}$ that a 2006-sided polygon can have?
The translation maintains the original text's line breaks and format. | 2003 |
1,259 | In triangle \( ABC \) with \( AB = 8 \) and \( AC = 10 \), the incenter \( I \) is reflected across side \( AB \) to point \( X \) and across side \( AC \) to point \( Y \). Given that segment \( XY \) bisects \( AI \), compute \( BC^2 \). (The incenter \( I \) is the center of the inscribed circle of triangle \( ABC \).) | 84 |
52,742 | Solve the following equation:
$$
8^{x}+27^{x}+64^{x}+125^{x}=24^{x}+30^{x}+40^{x}+60^{x} .
$$ | 0 |
17,624 | Several points were marked on a line. After that, two more points were placed between each pair of neighboring points, and then the same procedure (with the entire set of points) was repeated once more. Could there be 82 points on the line as a result? | Yes |
12,895 | The town of Hamlet has $3$ people for each horse, $4$ sheep for each cow, and $3$ ducks for each person. Which of the following could not possibly be the total number of people, horses, sheep, cows, and ducks in Hamlet? | 47 |
34,599 | Given the convex pentagon $A B C D E$, each of its sides and diagonals must be drawn in either red or blue so that for any triangle formed by three of its vertices, both colors appear on its perimeter. In how many ways can this be done? | 12 |
10,035 | In an isosceles triangle \( \triangle ABC \), points \( E \) and \( F \) are taken on the sides \( AB \) and \( AC \) respectively, such that \( AE = CF \). If \( BC = 2 \), prove that \( EF \geq 1 \). | EF \geq 1 |
21,844 | Luis wrote the sequence of natural numbers, that is,
$$
1,2,3,4,5,6,7,8,9,10,11,12, \ldots
$$
When did he write the digit 3 for the $25^{\mathrm{th}}$ time? | 131 |
59,485 | A set contains 4 numbers. The six sums of two elements of this set are 189, 320, 287, 264, $x$ and $y$. Find the largest possible value for $x+y$.
# | 761 |
33,000 | 39. Aladdin used the magic lamp to summon the genie, who said to Aladdin: “You can choose some numbers from the natural numbers 1, 2, 3, 4, 5, $\qquad$ 2019, 2020 such that the sum of any two numbers is not an integer multiple of their difference. The number of numbers you choose, I will give you that many gold coins.” Therefore, the maximum number of gold coins Aladdin can get is $\qquad$. | 674 |
9,312 | Example 7. Find the linear function that maps the triangle with vertices at points $0,1, i$ in the $z$-plane to a similar triangle with vertices $1+i, 0,2$ in the $w$-plane. | (1 + i)(1 - z) |
33,267 | 13. It is given that $k$ is a positive integer not exceeding 99. There are no natural numbers $x$ and $y$ such that $x^{2}-k y^{2}=8$. Find the difference between the maximum and minimum possible values of $k$. | 96 |
8,144 | Example 5. Integrate the differential equation $y^{\prime}=\frac{x \sqrt{1+x^{2}}+1}{\sqrt{1+x^{2}}\left(y+e^{y}\right)}$ and also find the particular solution that satisfies the Cauchy condition: $x_{0}=2, y_{0}=1$. | \frac{1}{2}y^2 + e^y = \frac{1}{2}x^2 + \ln\left(x + \sqrt{1 + x^2}\right) + e - \frac{3}{2} - \ln\left(2 + \sqrt{5}\right) |
24,054 | Consider the two hands of an analog clock, each of which moves with constant angular velocity. Certain positions of these hands are possible (e.g. the hour hand halfway between the 5 and 6 and the minute hand exactly at the 6), while others are impossible (e.g. the hour hand exactly at the 5 and the minute hand exactly at the 6). How many different positions are there that would remain possible if the hour and minute hands were switched? | 143 |
8,669 | Given an isosceles triangle $ABC$ ($AB = BC$). Point $E$ is marked on ray $BA$ beyond point $A$, and point $D$ is marked on side $BC$. It is known that
$$
\angle ADC = \angle AEC = 60^\circ, \quad AD = CE = 13.
$$
Find the length of segment $AE$ if $DC = 9$. | 4 |
64,465 | 3. Solve the inequality:
$$
\frac{2|2 x-1|+2}{3}+\frac{6}{1+|2 x-1|} \leq 4-\sqrt{16 x^{4}-8 x^{2}+1}
$$ | -0.5 |
3,054 | Let $ABCD$ be a convex quadrilateral with $AC \perp BD$ , and let $P$ be the intersection of $AC$ and $BD$ . Suppose that the distance from $P$ to $AB$ is $99$ , the distance from $P$ to $BC$ is $63$ , and the distance from $P$ to $CD$ is $77$ . What is the distance from $P$ to $AD$ ? | 231 |
54,485 | a) Calculate the sum of the squares of the roots of the equation $(x+2)(x-1)(x-3)=2$.
b) Prove that the following equation cannot have all real roots:
$$
x^{10}-2 x^{9}+5 x^{8}+a x^{7}-b x^{6}+c x^{5}+d x^{4}+e x^{3}+f x^{2}+g x+h=0 .
$$ | 14 |
62,536 | 1. Find the value of the expression $(\ldots(((2 * 3) * 4) * 5) * \ldots) * 1995$, where $x * y=\frac{x+y}{1+x y}$.
(Macedonia) | \frac{998\cdot1995-1}{998\cdot1995+1} |
53,015 | In how many ways can the nine digits from 1 to 9 be placed in a $3 \times 3$ grid so that the sums of the rows and the sums of the columns are all equal? | 72 |
941 | Find all values of the parameter \(a\) for which the equation \(x^{2} + 2x + 2|x + 1| = a\) has exactly two roots. | a > -1 |
4,182 | Exercise 11. Find all functions $\mathrm{f}$ from $\mathbb{R}$ to $\mathbb{R}$ such that for every pair $(x, y)$ of real numbers:
$$
f(f(x))+f(f(y))=2 y+f(x-y)
$$ | f(x) = x |
9,436 | Vertices $A$ and $B$ of the prism $ABC A_1 B_1 C_1$ lie on the axis of the cylinder, and the other vertices lie on the lateral surface of the cylinder. Find the dihedral angle with edge $AB$ in this prism. | 120^\circ |
457 | Two brothers sold a flock of sheep that belonged to both of them, receiving as many rubles for each sheep as there were sheep in the flock. The brothers divided the money received as follows: first the elder brother took ten rubles from the total amount, then the second brother took ten rubles, after which the first brother took another ten rubles, and so on. The younger brother lacked ten rubles in the end, so he took all the remaining small change, and in addition, to make the division fair, the elder brother gave the younger brother his pocket knife. What was the value of the pocket knife? | 2 |
66,549 | 4. (7 points) On the plane, there is a square $A B C D$ with side length 1 and a point $X$ (see the figure). It is known that $X A=\sqrt{5}, X C=\sqrt{7}$. What is $X B$?
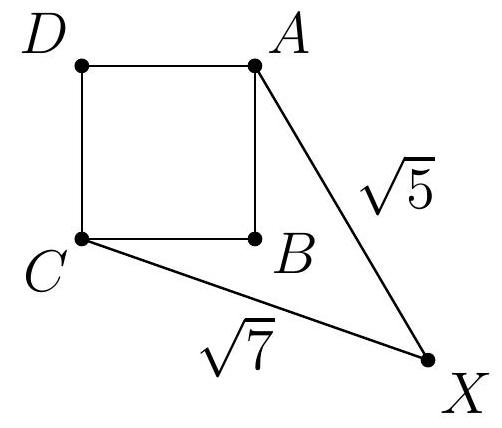 | \sqrt{6-\sqrt{10}} |
34,641 | 6.2. There are 7 safes and 7 codes for them, but it is unknown which code belongs to which safe. What is the minimum number of attempts required to guarantee matching the codes to the safes? | 21 |
62,163 | Example 13 Given that the domain of the function $f(x)$ is $[0,1]$, and it satisfies the following conditions:
( I ) For any $x \in[0,1]$, we always have $f(x) \geqslant 3$;
( II ) $f(1)=4$;
(III) If $x_{1} \geqslant 0, x_{2} \geqslant 0, x_{1}+x_{2} \leqslant 1$, then $f\left(x_{1}+x_{2}\right) \geqslant f\left(x_{1}\right)+f\left(x_{2}\right)-3$.
(1) Try to find the value of $f(0)$;
(2) Try to find the maximum value of the function $f(x)$;
(3) Try to prove: When $x \in\left(\frac{1}{3}, 1\right]$, $f(x)<3 x+3$; When $x \in\left(\frac{1}{3^{n+1}}, \frac{1}{3^{n}}\right]\left(n \in \mathbf{N}^{*}\right)$, $f(x)<3 x+3$. | 4 |
3,815 | ## Task Condition
Find the derivative.
$$
y=\frac{\operatorname{ctg} x+x}{1-x \cdot \operatorname{ctg} x}
$$ | -\dfrac{x^2 \csc^2 x}{(1 - x \cot x)^2} |
4,078 | 6. Let $k$ be a real number, in the Cartesian coordinate system $x O y$ there are two point sets $A=\left\{(x, y) \mid x^{2}+y^{2}=\right.$ $2(x+y)\}$ and $B=\{(x, y) \mid k x-y+k+3 \geqslant 0\}$. If $A \cap B$ is a singleton set, then the value of $k$ is $\qquad$ | -2 - \sqrt{3} |
50,798 | 4. In how many ways can a bamboo trunk (a non-uniform natural material) 4 m long be sawn into three parts, the lengths of which are multiples of 1 dm, and from which a triangle can be formed?
(12 points) | 171 |
65,743 | ## Problem 2
Consider the sequence $\left(x_{n}\right) \mathrm{n} \geq 1$ of positive real numbers with $\lim _{n \rightarrow \infty} \mathrm{x}_{\mathrm{n}}=0$.
Calculate:
$\lim _{n \rightarrow \infty} \frac{\sqrt{x_{1}^{2}-x_{1} x_{2}+x_{2}^{2}}+\sqrt{x_{2}^{2}-x_{2} x_{3}+x_{3}^{2}}+\cdots+\sqrt{x_{n}^{2}-x_{n} x_{1}+x_{1}^{2}}}{n}$
GMB 4/2012 | 0 |
25,377 | 9,10,11 |
| :---: | :---: | :---: |
| | Division with remainder | |
| | Product rule | |
| | Cooperative algorithms Evaluation + example | |
Authors: Knyaz K.A., Leontyeva O.
A magician and an assistant are going to perform the following trick. A spectator writes a sequence of $N$ digits on a board. The assistant then covers two adjacent digits with a black circle. The magician then enters and his task is to guess both covered digits (and the order in which they are arranged). For what smallest $N$ can the magician and the assistant agree on a strategy to ensure the trick always succeeds? | 101 |
541 | The year 2009 has the following property: by rearranging the digits of the number 2009, it is not possible to obtain a smaller four-digit number (numbers do not start with zero). In which year will this property occur again for the first time? | 2022 |
32,279 | Among the fractions with positive denominators less than 1001, which one has the smallest difference from $\frac{123}{1001}$? | \frac{94}{765} |
18,587 | For positive real numbers $s$ , let $\tau(s)$ denote the set of all obtuse triangles that have area $s$ and two sides with lengths $4$ and $10$ . The set of all $s$ for which $\tau(s)$ is nonempty, but all triangles in $\tau(s)$ are congruent, is an interval $[a,b)$ . Find $a^2+b^2$ | 736 |
33,478 | 3. Variant 1.
The height $A H$ and the bisector $C L$ of triangle $A B C$ intersect at point $O$. Find the angle $B A C$, if it is known that the difference between the angle $C O H$ and half the angle $A B C$ is $46^{\circ}$. | 92 |
58,053 | On the Island of Misfortune with a population of 96 people, the government decided to carry out five reforms. Each reform is opposed by exactly half of all citizens. A citizen will go to a rally if they are dissatisfied with more than half of all the reforms. What is the maximum number of people the government can expect at the rally? | 80 |
23,586 | Given a parabola \(C\) with the center of ellipse \(E\) as its focus, the parabola \(C\) passes through the two foci of the ellipse \(E\), and intersects the ellipse \(E\) at exactly three points. Find the eccentricity of the ellipse \(E\). | \dfrac{2\sqrt{5}}{5} |
64,068 | Satisfy $m n \geqslant 0, m^{3}+n^{3}+99 m n=33^{3}$ the historical integer pairs $(m, n)$ are $\qquad$ pairs. | 35 |
7,707 | Sally has five red cards numbered $1$ through $5$ and four blue cards numbered $3$ through $6$ . She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards? | 12 |
53,045 | 16. If an internal point of some $n$-sided prism is connected to all its vertices, then we obtain $n$ quadrilateral pyramids with a common vertex at this point, the bases of which are the lateral faces of the prism. Find the ratio of the sum of the volumes of these pyramids to the volume of the given prism. | \frac{2}{3} |
20,840 | What is the largest possible area of the orthogonal projection of a $3 \times 4 \times 12$ rectangular prism? | 12\sqrt{26} |
23,457 | Cover each rational number in the interval $(0,1]$ that can be written as $\frac{a}{b}$, where $\operatorname{gcd}(a, b)=1$, with the interval
$$
\left[\frac{a}{b} - \frac{1}{4b^2}, \frac{a}{b} + \frac{1}{4b^2}\right].
$$
Prove that the number $\frac{\sqrt{2}}{2}$ is not covered. | \frac{\sqrt{2}}{2} |
53,949 | Bogdanov I.I.
In the language of the AU tribe, there are two letters - "a" and "u". Some sequences of these letters are words, and each word has no fewer than one and no more than 13 letters. It is known that if you write down any two words in a row, the resulting sequence of letters will not be a word. Find the maximum possible number of words in such a language.
# | 16256 |
55,187 | Let's find a 6-digit number that is a perfect square and remains the same when the order of its digits is reversed. | 698896 |
13,612 | Given positive numbers \(a, b, c\) such that \(a + b + c = 13\). Find the minimum value of \(\frac{a^{2} + b^{3} + c^{4} + 2019}{10b + 123c + 26}\). | 4 |
26,438 | Let $l, m$ be two skew lines, on $l$ there are three points $A, B, C$, and $A B=B C$. Draw perpendiculars from $A, B, C$ to $m$, denoted as $A D, B E, C F$, with feet of the perpendiculars being $D, E, F$ respectively. Given $A D=\sqrt{15}, B E=\frac{7}{2}, C F=\sqrt{10}$. Find the distance between $l$ and $m$. | \sqrt{6} |
33,375 | The fifteenth question: Given a positive integer $n \geq 2$, find the largest positive real number $\lambda(n)$, such that for any real numbers $x_{1}, x_{2}, \cdots, x_{n}$, not all positive, we have $\prod_{i=1}^{n}\left(x_{i}^{2}-x_{i}+1\right) \geq \lambda(n) \cdot\left(\left(\prod_{i=1}^{n} x_{i}\right)^{2}-\prod_{i=1}^{n} x_{i}+1\right)$. | (\frac{3}{4})^{n-1} |
52,753 | Let $M$ be a finite set of numbers. It is known that among any three of its elements, there are two whose sum belongs to $M$.
What is the maximum number of elements that can be in $M$? | 7 |
55,492 | Which is the smallest positive odd number that has as many divisors as 360? | 3465 |
53,320 | When Paulo turned 15, he invited 43 friends to a party. The cake was in the shape of a regular 15-sided polygon and had 15 candles on it. The candles were placed in such a way that no three candles were in a straight line. Paulo divided the cake into triangular pieces where each cut connected two candles or connected a candle to a vertex. Moreover, no cut crossed another already made. Explain why, by doing this, Paulo was able to give a piece of cake to each of his guests, but he himself was left without any.
# | 43 |
58,856 | 1. In a certain triangle, the sum of the tangents of the angles turned out to be 2016. Estimate (at least to the nearest degree) the magnitude of the largest of its angles. | 90 |
66,190 | 7.54 Suppose the radius of the small circle is $\frac{r}{2}$, and the radius of the large circle is $r$. How many small circles are needed at minimum to completely cover the area of the large circle? | 7 |
13,250 | Let's find the polynomial $p(x)$ of the lowest degree that satisfies the following conditions:
a) the coefficients of $p(x)$ are integers,
b) $p(x)$ can be factored into the product of linear polynomials,
c) the roots of $p(x)$ are integers,
d) $p(0)=-1$,
e) $p(3)=128$. | (x - 1)(x + 1)^3 |
54,109 | 11. In the temple, there is an ancient scale. For objects weighing less than 1000 grams, the scale shows their correct weight; for objects weighing 1000 grams or more, the scale shows a random number greater than or equal to 1000. Xiao Ming has five items, each weighing less than 1000 grams, which we will denote as $\mathrm{P}$, $\mathrm{Q}$, $\mathrm{R}$, $\mathrm{S}$, and $\mathrm{T}$ for their weights. When these five items are paired and weighed on the scale, the following results are obtained: $Q+S=1200$ (grams), $R+T=2100$ (grams), $Q+T=800$ (grams), $Q+R=900$ (grams), $P+T=700$ (grams). What is the order of the weights of these five items from heaviest to lightest? | S,R,T,Q,P |
57,706 | Let $M$ - be a finite set of numbers. It is known that among any three of its elements, there will be two whose sum belongs to $M$.
What is the maximum number of elements that can be in $M$? | 7 |
64,594 | A.Y. of evnin
2000 people registered on a new website. Each of them invited 1000 people to be their friends. Two people are considered friends if and only if each of them invited the other to be a friend. What is the minimum number of pairs of friends that could have formed? | 1000 |
56,894 | 5.7. In an isosceles triangle \(ABC\) with lateral sides \(AB = BC\), the angle \(ABC\) is \(80^\circ\). Inside the triangle, a point \(O\) is taken such that the angle \(OAC\) is \(10^\circ\) and the angle \(OCA\) is \(30^\circ\). Find the angle \(AOB\). | 70 |
16,240 | Find all functions \( f: S \rightarrow S \) such that
\[ f(x + f(y) + x f(y)) = y + f(x) + y f(x) \]
for all \( x \) and \( y \) in \( S \), and \( f(x) / x \) is strictly increasing for \(-1<x<0\) and for \(0<x\). | -\dfrac{x}{x + 1} |
55,782 | 6. The solution set of the inequality
$$
x^{6}+3 x^{5}+5 x^{4}+3 x^{3}-2 x^{2}-1<0
$$
is $\qquad$ . | (\frac{-1-\sqrt{5}}{2},\frac{-1+\sqrt{5}}{2}) |
57,659 | 7. Let the incircle of equilateral triangle $ABC$ have a radius of 2, with the center at $I$. If point $P$ satisfies $PI=1$, then the maximum value of the ratio of the areas of $\triangle APB$ to $\triangle APC$ is $\qquad$
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | \frac{3+\sqrt{5}}{2} |
31,547 | We inscribe a sphere in an equilateral cone, to which we lay an tangent plane parallel to the base of the cone. We then inscribe another sphere in the resulting cone, and so on. Determine the sum of the volumes of the spheres if this procedure is continued to infinity. The slant height of the cone is $l=2$. | \frac{2\pi\sqrt{3}}{13} |
15,453 | An ant starts at vertex \( A \) of a cube \( ABCD-EFGH \). Each time, it crawls with equal probability to one of the three neighboring vertices. What is the probability that the ant is back at vertex \( A \) after six moves? | \dfrac{61}{243} |
19,587 | On the blackboard, there is a multiplication example of two three-digit numbers. If the multiplication sign is replaced with a 0, we get a seven-digit number that is an integer multiple of the product. By how much exactly? | 73 |
60,033 | Problem 5. Small Island and Big Island have a rectangular shape and are divided into rectangular counties. In each county, a road is laid along one of the diagonals. On each island, these roads form a closed path that does not pass through any point more than once. Here is how Small Island is organized, with a total of 6 counties (see Fig. 1). Draw how Big Island might be organized if it has an odd number of counties. How many counties did you get?
[7 points] (A. V. Shapovalov)
Fig. 1
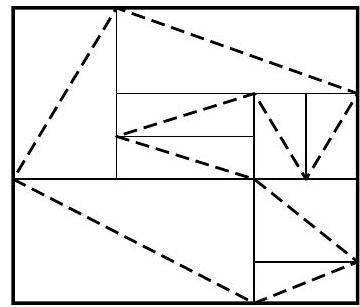
Fig. 2 | 9 |
5,450 | Let the heights of a triangle be denoted by \( m_a, m_b, \) and \( m_c \) and the semiperimeter by \( s \). Prove that
$$
m_{a}^{2}+m_{b}^{2}+m_{c}^{2} \leq s^{2}
$$ | m_{a}^{2}+m_{b}^{2}+m_{c}^{2} \leq s^{2} |
55,100 | -、(Full marks 10 points) There are two decks of playing cards, each deck arranged in such a way that the first two cards are the Big Joker and the Small Joker, followed by the four suits of Spades, Hearts, Diamonds, and Clubs, with each suit arranged in the order of $1,2,3$, $\cdots, J, Q, K$. Someone stacks the two decks of cards in the above order, then discards the first card, places the second card at the bottom, discards the third card, places the fourth card at the bottom, …, and continues this process until only one card remains. What is the last remaining card? | 6 \text{ of Diamonds} |
60,320 | 34th Eötvös 1930 Problem 2 A straight line is drawn on an 8 x 8 chessboard. What is the largest possible number of the unit squares with interior points on the line? | 15 |
4,769 | Let \( P \in \mathbb{R}[X] \). Show that
$$
(\forall x \in \mathbb{R}, P(x) \geqslant 0) \Leftrightarrow \left(\exists(A, B) \in(\mathbb{R}[X])^{2}, P = A^{2} + B^{2}\right) .
$$ | (\forall x \in \mathbb{R}, P(x) \geqslant 0) \Leftrightarrow \left(\exists(A, B) \in(\mathbb{R}[X])^{2}, P = A^{2} + B^{2}\right) |
63,674 | Problem 2. For what least $n$ do there exist $n$ numbers from the interval $(-1 ; 1)$ such that their sum is 0 and the sum of their squares is 40? | 42 |
63,451 | 12. Select 3 cards from five number cards $0,4,6,7,8$ to form a two-digit number, then a total of $\qquad$ different three-digit numbers can be formed (Note: Cards can be flipped). | 78 |
27,112 | In a line, there are 2020 white stones and one black stone. A possible operation is as follows: choose a black stone that is not at the edge and change the color of its neighboring stones. Find all possible initial positions for the black stone such that it is possible to color all the stones black with a finite number of operations. | 1011 |
18,136 | Prove that if the midline of a quadrilateral passes through the intersection point of the diagonals and is bisected by this point, then the quadrilateral is a parallelogram. | \text{The quadrilateral is a parallelogram.} |
33,999 | 27. N8 (IRN) Let $p$ be a prime number and let $A$ be a set of positive integers that satisfies the following conditions:
(i) the set of prime divisors of the elements in $A$ consists of $p-1$ elements;
(ii) for any nonempty subset of $A$, the product of its elements is not a perfect $p$ th power.
What is the largest possible number of elements in $A$ ? | (p-1)^2 |
32,427 | 18. Let $A, B, C$ be the three angles of a triangle. Let $L$ be the maximum value of
$$
\sin 3 A+\sin 3 B+\sin 3 C \text {. }
$$
Determine $\lfloor 10 L\rfloor$. | 25 |
28,168 | A7. Let $n>1$ be an integer. In the space, consider the set
$$
S=\{(x, y, z) \mid x, y, z \in\{0,1, \ldots, n\}, x+y+z>0\} .
$$
Find the smallest number of planes that jointly contain all $(n+1)^{3}-1$ points of $S$ but none of them passes through the origin. | 3n |
13,360 | Find the number of integer pairs \((m, n)\) that satisfy \(mn \geq 0\) and \(m^3 + n^3 + 99mn = 33^3\). | 35 |
63,182 | G1.4 Using numbers: $1,2,3,4,5,6$ to form a six-digit number: $A B C D E F$ such that $A$ is divisible by $1, A B$ is divisible by $2, A B C$ is divisible by $3, A B C D$ is divisible by $4, A B C D E$ is divisible by $5, A B C D E F$ is divisible by 6 . Find the greatest value of $A$. | 3 |
66,507 | 15. (Fuzhou City 28th High School Mathematics Competition Question) $f(x)$ is a function defined on $(-\infty,+\infty)$ that is odd, and $f(1+x)+f(1-x)=f(1)$, $f(x)$ is a decreasing function on $[0,1]$, then $-f\left(\frac{10}{3}\right), f\left(-2+\frac{\sqrt{2}}{2}\right), f\left(\frac{9}{2}\right)$ arranged from smallest to largest is $\qquad$. | f(-2+\frac{\sqrt{2}}{2})<-f(\frac{10}{3})<f(\frac{9}{2}) |
54,049 | Example 6 In isosceles $\triangle A B C$, $\angle B=\angle C=40^{\circ}$, extend $A B$ to point $D$, such that $A D=B C$. Find the degree measure of $\angle B C D$. | 10^{\circ} |
55,496 | [ Two pairs of similar triangles ]
Points $M$ and $N$ are on the lateral sides $A B$ and $C D$ of trapezoid $A B C D$, line $M N$ is parallel to $A D$, and segment $M N$ is divided into three equal parts by the diagonals of the trapezoid. Find the length of segment $M N$, if $A D=a, B C=b$, and the point of intersection of the diagonals of the trapezoid lies inside quadrilateral $M B C N$. | \frac{3ab}{+2b} |
57,195 | B1. The diagram shows the distribution of bronze, silver, and gold medals at a competition.
(a) What is the value of $x$? (see image)
(b) Write the ratio of gold, silver, and bronze medals in the smallest possible natural numbers.
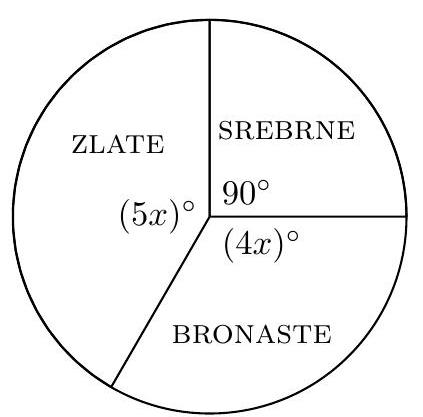
(c) At the competition, 84 medals were awarded. How many bronze, how many silver, and how many gold medals were awarded?
(d) How many grams does a bronze medal weigh if it has the shape of a cylinder with a diameter of $7 \mathrm{~cm}$ and a height of 3 $\mathrm{mm}$? The density of bronze is $8700 \frac{\mathrm{kg}}{\mathrm{m}^{3}}$. | 100 |
2,663 | For the inequality \(\lg \left(20-5 x^{2}\right)>\lg (a-x)+1\) in terms of \(x\) to have a unique integer solution of 1, determine the range of the real number \(a\). | [2, \frac{5}{2}) |
22,249 | A triangular array of numbers has a first row consisting of the odd integers $1,3,5,\ldots,99$ in increasing order. Each row below the first has one fewer entry than the row above it, and the bottom row has a single entry. Each entry in any row after the top row equals the sum of the two entries diagonally above it in the row immediately above it. How many entries in the array are multiples of $67$ ?
Please give the answer directly without any intermediate steps. | 17 |
66,326 | 12.070. The lateral edges of a regular triangular pyramid are pairwise perpendicular. Find the angle between a lateral face and the plane of the base. | \arccos\frac{\sqrt{3}}{3} |
31,847 | 10. (20 points) For a positive integer $n$ and a real number $x (0 \leqslant x < n)$, define
$$
f(n, x)=(1-\{x\}) \mathrm{C}_{n}^{[x]}+\{x\} \mathrm{C}_{n}^{[x]+1},
$$
where $[x]$ denotes the greatest integer not exceeding the real number $x$, and $\{x\}=x-[x]$. If integers $m, n \geqslant 2$ satisfy
$$
f\left(m, \frac{1}{n}\right)+f\left(m, \frac{2}{n}\right)+\cdots+f\left(m, \frac{m n-1}{n}\right)=123,
$$
find the value of $f\left(n, \frac{1}{m}\right)+f\left(n, \frac{2}{m}\right)+\cdots+f\left(n, \frac{m n-1}{m}\right)$. | 74 |
4,877 | One side of a rectangle is $1 \mathrm{~cm}$. It is divided into four smaller rectangles by two perpendicular lines, such that the areas of three of the smaller rectangles are not less than $1 \mathrm{~cm}^{2}$, and the area of the fourth rectangle is not less than $2 \mathrm{~cm}^{2}$. What is the minimum length of the other side of the original rectangle? | 3 + 2\sqrt{2} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.