id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
26,416 | Problem 4. Let $\triangle A^{\prime} B^{\prime} C$ be the image of $\triangle A B C$ under a rotation with center $C$. Denote by $M, E$ and $F$ the midpoints of the segments $B A^{\prime}, A C$ and $B^{\prime} C$, respectively. If $A C \neq B C$ and $E M=F M$, find $\Varangle E M F$.
Ivailo Kortezov | 60 |
24,713 | Given the linear function \( y = ax + b \) and the hyperbolic function \( y = \frac{k}{x} \) (where \( k > 0 \)) intersect at points \( A \) and \( B \), with \( O \) being the origin. If the triangle \( \triangle OAB \) is an equilateral triangle with an area of \( \frac{2\sqrt{3}}{3} \), find the value of \( k \). | \dfrac{2}{3} |
55,865 | 10. A positive integer $n$ is called "flippant" if $n$ does not end in 0 (when written in decimal notation) and, moreover, $n$ and the number obtained by reversing the digits of $n$ are both divisible by 7 . How many flippant integers are there between 10 and 1000 ? | 17 |
22,612 | Prove: If a polynomial with real coefficients \( P(x) \) takes only non-negative values for all \( x \in \mathbb{R} \), then it can be expressed as
$$
P(x) = \left[Q_{1}(x)\right]^{2} + \cdots + \left[Q_{n}(x)\right]^{2},
$$
where \( Q_{1}(x), \cdots, Q_{n}(x) \) are polynomials with real coefficients. | P(x) = \left[Q_{1}(x)\right]^{2} + \cdots + \left[Q_{n}(x)\right]^{2} |
22,028 | Let \(ABC\) be an isosceles triangle with \(AB = AC\), and let \(P\) be a point moving along the side \(BC\). Drop the perpendiculars \(PX\) and \(PY\) from \(P\) to the sides \(AB\) and \(AC\). Prove that the sum \(PX + PY\) remains constant as \(P\) moves. | PX + PY \text{ is constant.} |
59,734 | 10. The last two digits of the integer $\left[\frac{10^{93}}{10^{31}+3}\right]$ are $\qquad$ . (Write the tens digit first, followed by the units digit, where $[x]$ denotes the greatest integer less than or equal to $x$) | 8 |
29,482 | Let's find all sequences of integers $a_{1}<a_{2}<\cdots<a_{n}<\ldots$ such that:
- for every positive integer $n$, $a_{2 n}=a_{n}+n$
- if $a_{n}$ is a prime number, then $n$ is also a prime number. | a_{n}=n |
31,462 | # Task 8.5
On the Island of Liars and Knights, a circular arrangement is called correct if each person standing in the circle can say that among their two neighbors, there is a representative of their tribe. Once, 2019 natives formed a correct arrangement in a circle. A liar approached them and said: "Now we can also form a correct arrangement in a circle together." How many knights could there have been in the initial arrangement?
## Number of points 7 | 1346 |
55,690 | 3. Find all prime numbers of the form 1010101...0101 (i.e., whose decimal representation consists of the digit 1 followed by a block "01" repeated an arbitrary number of times). | 101 |
65,561 | 4. a) Determine the geometric place of the midpoints of the chords of a circle $C$, which lie on lines passing through a given point.
b) Perform a discussion. | (x-\frac{}{2})^{2}+(y-\frac{b}{2})^{2}=\frac{^{2}+b^{2}}{4} |
54,113 | ## Task 12/78
When asked how old he is, someone answers that in the year $x^{2}$ he was exactly $x$ years old. In which year was he born? | 1892 |
30,774 | The base $A D$ of a trapezoid $A B C D$ measures $30 \mathrm{~cm}$. Suppose there is a point $E$ on $A D$ such that the triangles $\triangle A B E, \triangle B C E$ and $\triangle C D E$ have equal perimeters. Determine the length of $B C$. | 15 |
55,242 | [level. $B$. .
There are 1000 candies lined up. First, Vasya ate the ninth candy from the left, and then he ate every seventh candy, moving to the right. After that, Petya ate the seventh candy from the left among the remaining candies, and then he ate every ninth candy, also moving to the right. How many candies are left after this?
# | 763 |
158 | There are 12 stages in a racing tournament and $n$ participants. After each stage, all participants receive points $a_{k}$ based on their position $k$ ($a_{k}$ are natural numbers, and $a_{1}>a_{2}>\ldots>a_{n}$). For what is the smallest $n$ such that the tournament organizer can choose numbers $a_{1}, \ldots, a_{n}$ so that after the penultimate stage, at least two participants will still have a chance to take first place, regardless of the possible distribution of positions? | 13 |
25,007 | Let $ABC$ be a triangle with area $5$ and $BC = 10.$ Let $E$ and $F$ be the midpoints of sides $AC$ and $AB$ respectively, and let $BE$ and $CF$ intersect at $G.$ Suppose that quadrilateral $AEGF$ can be inscribed in a circle. Determine the value of $AB^2+AC^2.$ *Proposed by Ray Li* | 200 |
32,863 | Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
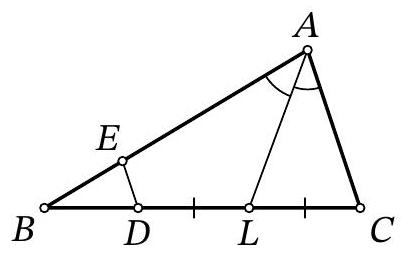 | 3 |
28,638 | 4. Let $A L, B M, C N$ be the medians of triangle $A B C$, intersecting at point $K$. It is known that a circle can be circumscribed around quadrilateral $C L K M$, and $A B=2$. Find the length of the median $C N$. | \sqrt{3} |
66,969 | 18. A five-digit number $\overline{A B C D E}$ is a multiple of 2014, and $\overline{C D E}$ has exactly 16 factors. What is the minimum value of $\overline{A B C D E}$? | 24168 |
25,973 | \section*{Problem 5 - 131035}
Given a circle \(k\) with diameter \(A B\) of length \(d\). In this circle, there are two circles \(k_{1}\) and \(k_{2}\) such that they touch \(k\) from the inside at points \(A\) and \(B\) respectively, and touch each other from the outside at a point \(M\), so that \(A M + M B = A B\) holds. Here, \(A M \geq M B\).
The area of the colored region is equal to the difference between the area of \(k\) and the sum of the areas of \(k_{1}\) and \(k_{2}\).
Determine the length of \(A M\) for which the area of this colored region is maximized!
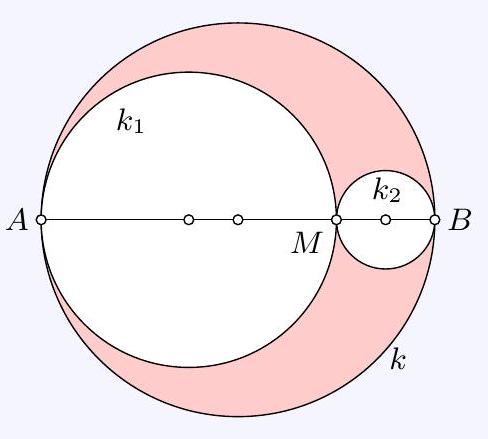 | \frac{}{2} |
27,947 | 10. As shown in the figure, given the parabola $y^{2}=2 p x(p>0)$ with focus $F$ and directrix $l$, a line through point $F$ intersects the parabola at points $A, B$, and $|A B|=3 p$. Let the projections of points $A, B$ on $l$ be $A^{\prime}, B^{\prime}$, respectively. If a point $M$ is randomly thrown into the quadrilateral $A A^{\prime} B^{\prime} B$, the probability that point $M$ falls within $\triangle F A^{\prime} B^{\prime}$ is | \frac{1}{3} |
31,289 | 6. The base of the pyramid $S A B C$ is an isosceles triangle $A B C$, with $A B = B C = 3$, and $A C = 5$. The height of the pyramid $S A B C$ is the segment $S O$, where $O$ is the intersection point of the line passing through vertex $B$ parallel to side $A C$ and the line passing through $C$ perpendicular to side $A C$. Find the distance from the center of the inscribed circle of triangle $A B C$ to the plane containing the lateral face $B S C$, if the height of the pyramid is $7 / 12$. | \frac{35\sqrt{11}}{396} |
24,703 | circle of radius 1 is randomly placed in a 15-by-36 rectangle $ABCD$ so that the circle lies completely within the rectangle. Given that the probability that the circle will not touch diagonal $AC$ is $m/n,$ where $m$ and $n$ are relatively prime positive integers. Find $m + n.$ | 817 |
3,640 | B4. For the second round of the Math Olympiad, 999 students are invited. Melanie prepares invitation letters in the order of participant numbers: $1,2,3, \ldots$ For some values of $n \geqslant 100$, she notices the following: the number of participant numbers from $1$ to $n$ that end in a 5 is exactly equal to the number formed by the last two digits of $n$.
For how many values of $n$ (with $100 \leqslant n<1000$) does this hold? | 9 |
1,191 | From the vertices of a convex quadrilateral, perpendiculars are dropped onto the diagonals. Prove that the quadrilateral formed by the bases of the perpendiculars is similar to the original quadrilateral. | \text{The quadrilateral formed by the bases of the perpendiculars is similar to the original quadrilateral.} |
8,728 | Let \( S \) be any point on the circumscribed circle of \( \triangle PQR \). Then the feet of the perpendiculars from \( S \) to the three sides of the triangle lie on the same straight line. Denote this line by \( l(S, PQR) \). Suppose that the hexagon \( ABCDEF \) is inscribed in a circle. Show that the four lines \( l(A, BDF) \), \( l(B, ACE) \), \( l(D, ABF) \), and \( l(E, ABC) \) intersect at one point if and only if \( CDEF \) is a rectangle. | CDEF \text{ is a rectangle} |
16,525 | In the quadrilateral \(ABCD\), diagonals \(AC\) and \(BD\) intersect at point \(K\). Points \(L\) and \(M\) are the midpoints of sides \(BC\) and \(AD\), respectively. Segment \(LM\) contains point \(K\). The quadrilateral \(ABCD\) is such that a circle can be inscribed in it. Find the radius of this circle, given that \(AB = 3\), \(AC = \sqrt{13}\), and \(LK: KM = 1: 3\). | \dfrac{3}{2} |
68,677 | Example 7 Let $x=(15+\sqrt{220})^{19}+(15+\sqrt{200})^{22}$. Find the unit digit of the number $x$.
| 9 |
20,184 | In a certain competition, there are $a$ contestants and $b$ judges, where $b \geq 3$ and $b$ is an odd number. Each judge's decision for each contestant can only be "pass" or "fail". It is known that any two judges have at most $k$ contestants for whom they have the same decision. Prove that $\frac{k}{a} \geq \frac{b-1}{2b}$. | \dfrac{k}{a} \geq \dfrac{b-1}{2b} |
7,744 | Prove that \( \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \ldots + \frac{1}{n^2} < 1 \) | \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \ldots + \frac{1}{n^2} < 1 |
34,651 | 10.2.7 Find all positive pairs $a, b$ that satisfy: there exists a right triangle $\triangle CDE$ and points $A$, $B$ on its hypotenuse $DE$, such that $\overrightarrow{DA}=\overrightarrow{AB}=\overrightarrow{BE}$, and $AC=a$, $BC=b$. | \frac{1}{2}<\frac{}{b}<2 |
6,568 | In triangle \(ABC\) with angle \(\angle B=120^{\circ}\), angle bisectors \(AA_1\), \(BB_1\), and \(CC_1\) are drawn. Segment \(A_1B_1\) intersects angle bisector \(CC_1\) at point \(M\). Find the measure of angle \(\angle B_1BM\) in degrees. | 30 |
64,580 | 28. It is given that $a, b, c$ and $d$ are four positive prime numbers such that the product of these four prime numbers is equal to the sum of 55 consecutive positive integers. Find the smallest possible value of $a+b+c+d$. (Remark: The four numbers $a, b, c, d$ are not necessarily distinct.) | 28 |
23,836 | In a regular tetrahedron \( ABCD \) with side length \( \sqrt{2} \), it is known that \( \overrightarrow{AP} = \frac{1}{2} \overrightarrow{AB} \), \( \overrightarrow{AQ} = \frac{1}{3} \overrightarrow{AC} \), and \( \overrightarrow{AR} = \frac{1}{4} \overrightarrow{AD} \). If point \( K \) is the centroid of \( \triangle BCD \), then what is the volume of the tetrahedron \( KPQR \)? | \dfrac{1}{36} |
54,547 | 11. String 6 red balls, 1 white ball, and 8 yellow balls into a necklace, then the number of possible arrangements is $\qquad$ (balls of the same color are indistinguishable). | 1519 |
51,303 | 7. Let $a_{1}, a_{2}, \cdots, a_{21}$ be a permutation of $1,2, \cdots, 21$, satisfying
$$
\left|a_{20}-a_{21}\right| \geqslant\left|a_{19}-a_{21}\right| \geqslant\left|a_{18}-a_{21}\right| \geqslant \cdots \geqslant\left|a_{1}-a_{21}\right| \text {. }
$$
The number of such permutations is $\qquad$ . | 3070 |
33,070 | 190. Among the numbers of the form $36^{k}-5^{l}$, where $k$ and $l$ are natural numbers, find the smallest in absolute value. Prove that the found number is indeed the smallest. | 11 |
5,729 | Given a trapezoid \(ABCD\) with bases \(AB\) and \(CD\), and angles \(\angle C = 30^\circ\) and \(\angle D = 80^\circ\). Find \(\angle ACB\), given that \(DB\) is the bisector of \(\angle D\). | 10^\circ |
54,927 | In an acute triangle $ABC$ , the bisector of angle $\angle A$ intersects the circumscribed circle of the triangle $ABC$ at the point $W$. From point $W$ , a parallel is drawn to the side $AB$, which intersects this circle at the point $F \ne W$. Describe the construction of the triangle $ABC$, if given are the segments $FA$ , $FW$ and $\angle FAC$.
(Andrey Mostovy) | ABC |
25,354 | Let's calculate the volume of the tetrahedron that can be circumscribed around four mutually tangent, equal-radius spheres.
(Kövi Imre, teacher at the Fógymnasium, Iglón). | \frac{r^{3}}{3}(2\sqrt{3}+\sqrt{2})^{3} |
66,840 | For the polynomial
$$
p(x)=985 x^{2021}+211 x^{2020}-211 \text {, }
$$
let its 2021 complex roots be $x_{1}, x_{2}, \cdots, x_{2021}$. Then
$$
\sum_{k=1}^{2021} \frac{1}{x_{k}^{2}+1}=
$$
$\qquad$ | 2021 |
61,405 | 3. (3 points) Find the distance between the curves $y=e^{3 x+5}$ and $y=(\ln x-5) / 3$.
---
The text has been translated while preserving the original formatting and line breaks. | \sqrt{2}(2+\frac{\ln3}{3}) |
63,258 | 3. In $\triangle A B C$, $\angle B=\frac{\pi}{3}$, point $D$ is on side $A B$, $B D=1, A C=\sqrt{3}, D A=D C$. Then $\angle D C A=$ $\qquad$ | \frac{\pi}{6} |
69,090 | 8 Given a positive integer $n(\geqslant 2)$, find the minimum value of $|X|$, such that for any $n$ two-element subsets $B_{1}, B_{2}, \cdots, B_{n}$ of the set $X$, there exists a subset $Y$ of $X$ satisfying:
(1) $|Y|=n$;
(2) For $i=1,2, \cdots, n$, we have $\left|Y \cap B_{i}\right| \leqslant 1$.
Here $|A|$ denotes the number of elements in the finite set $A$. (Leng Gangsong) | 2n-1 |
1,703 | King Arthur's bodyguards had a knight tournament. At the end of the tournament, it was revealed that for any two bodyguards, there is a third one who defeated both of them. What is the minimum number of bodyguards who participated in the tournament? | 7 |
59,179 | # 8.3. Condition:
On an island, there are two tribes: knights, who always tell the truth, and liars, who always lie. Four islanders lined up, each 1 meter apart from each other.
- The leftmost in the row said: "My fellow tribesman in this row stands 1 meter away from me."
- The second from the left said: "My fellow tribesman in this row stands 2 meters away from me."
It is known that there are two knights and two liars in the row. What distances could the third and fourth islanders from the left have named? List all possible options.
## Options for matching:
Third islander $\quad 1$ m
Fourth islander $\quad 2$ m
$3 \mathrm{M}$
$4 \mathrm{M}$
# | 1 |
10,544 | A ray emanating from the vertex \( A \) of the triangle \( ABC \) intersects the side \( BC \) at \( X \) and the circumcircle of \( ABC \) at \( Y \). Prove that \(\frac{1}{AX}+\frac{1}{XY} \geq \frac{4}{BC} \). | \dfrac{1}{AX} + \dfrac{1}{XY} \geq \dfrac{4}{BC} |
53,072 | Solve the following system of equations:
$$
\left\{\begin{array}{l}
x \cdot(y+z) \cdot(x+y+z)=1170 \\
y \cdot(z+x) \cdot(x+y+z)=1008 \\
z \cdot(x+y) \cdot(x+y+z)=1458
\end{array}\right.
$$ | x=5,y=4,z=9 |
62,650 | How many 3-term geometric sequences $a$, $b$, $c$ are there where $a$, $b$, and $c$ are positive integers with $a < b < c$ and $c = 8000$? | 39 |
34,058 | 5. Given a circle $s$ with center $O$ and diameter $A B=4 \text{~cm}$.
a) Construct three tangents to this circle, two of which are at points $A$ and $B$, and the third such that the segment $C D$ between the first two tangents is $5 \text{~cm}$ long.
b) Determine $\Varangle C O D$.
c) Determine the area of the figure bounded by the constructed tangents and the given circle. | 10-2\pi |
61,593 | 36. Find the prime number $p$, given that the number $13 p+1$ is a perfect cube. | 211 |
23,079 | The pentagon ABCDE is inscribed in a circle with the angles ordered such that ∠A ≤ ∠B ≤ ∠C ≤ ∠D ≤ ∠E. Show that ∠C > π/2 and that this is the best possible lower bound. | \angle C > \frac{\pi}{2} |
63,445 | 3. Alice has six segments of different lengths. Five of them have lengths $6,7,8,9$ and 11. Any three of them can form a triangle. What integer values can the length of the fifth segment take? If there are multiple possible answers, write them in any order separated by a semicolon. | 10;12 |
20,032 | Let \( U \) and \( V \) be independent random variables, where \( U \) is uniformly distributed on the interval \( [0, 1] \), and \( \{u\} \) denotes the fractional part of the number \( u \). Show that the random variable \( \{U + V\} \) is uniformly distributed on \( [0, 1] \) and is independent of \( V \). | \{U + V\} \text{ is uniformly distributed on } [0, 1] \text{ and independent of } V |
57,900 | Problem 7.5. On an island, there live knights who always tell the truth, and liars who always lie. One day, 35 inhabitants of the island sat down at 7 tables, with 5 people at each table. Each of these 35 inhabitants was asked: "Are there more than three tables where at least 3 knights are sitting?"
(a) (1 point) What is the maximum number of inhabitants who could have answered "Yes"?
(b) (3 points) What is the maximum number of inhabitants who could have answered "No"? | 23 |
66,722 | $1 \cdot 49$ integers $1,2, \cdots, n$ are arranged in a permutation such that each number is either greater than all the numbers before it, or less than all the numbers before it. How many such permutations are there? | 2^{n-1} |
53,839 | 8. The number $a$ is a root of the equation $x^{11}+x^{7}+x^{3}=1$. Indicate all natural values of $n$ for which the equality $a^{4}+a^{3}=a^{n}+1$ holds. | 15 |
18,108 | In the image, squares $ABCD, EFCA, GHC E$, and $IJHE$ are illustrated. Points $S, B$, $F$, and $G$ are centers of these squares, respectively. The segment $AC$ is $1 \text{ cm}$ long.
Determine the area of triangle $IJS$.
(Hint: The area of the triangle is half the area of some rectangle.) | 3 |
57,145 | 3.12 In the first grade, more than 100 students took exams in Chinese, English, and mathematics. Among them, 92 passed the Chinese exam, 75 passed the English exam, and 65 passed the mathematics exam; 65 passed both Chinese and English exams, 54 passed both Chinese and mathematics exams, and 45 passed both English and mathematics exams. Find the number of students who passed all three subjects.
---
The problem can be solved using the principle of inclusion-exclusion. Let's denote:
- \( A \) as the set of students who passed the Chinese exam,
- \( B \) as the set of students who passed the English exam,
- \( C \) as the set of students who passed the mathematics exam.
We are given:
- \( |A| = 92 \)
- \( |B| = 75 \)
- \( |C| = 65 \)
- \( |A \cap B| = 65 \)
- \( |A \cap C| = 54 \)
- \( |B \cap C| = 45 \)
We need to find \( |A \cap B \cap C| \), the number of students who passed all three subjects.
Using the principle of inclusion-exclusion for three sets, we have:
\[
|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|
\]
We know that the total number of students is more than 100, so:
\[
|A \cup B \cup C| > 100
\]
Substituting the given values:
\[
|A \cup B \cup C| = 92 + 75 + 65 - 65 - 54 - 45 + |A \cap B \cap C|
\]
\[
|A \cup B \cup C| = 168 - 164 + |A \cap B \cap C|
\]
\[
|A \cup B \cup C| = 4 + |A \cap B \cap C|
\]
Since \( |A \cup B \cup C| > 100 \):
\[
4 + |A \cap B \cap C| > 100
\]
\[
|A \cap B \cap C| > 96
\]
Since \( |A \cap B \cap C| \) must be an integer, the smallest possible value is 97. Therefore, the number of students who passed all three subjects is:
\[
\boxed{97}
\] | 97 |
62,843 | 1. Consider the function $f:(-1, \infty) \rightarrow \mathbb{R}, f(x)=\frac{\sqrt{x^{2}+1}}{x+1}$.
a) Calculate $f^{\prime}(x), x>-1$.
b) Calculate $\int_{0}^{1} \frac{x^{2}+3 x}{(x+1)^{2} \sqrt{x^{2}+1}} d x$. | \ln(1+\sqrt{2})+\frac{\sqrt{2}}{2}-1 |
29,020 | 6. Circle $k_{1}$ with a radius of 8 cm lies inside circle $k$. Both circles intersect circle $k_{2}$ with a radius of 15 cm, as shown in the figure. What is the radius of $k$ if the shaded area inside $k$ but outside $k_{1}$ is equal to the total shaded area inside $k_{2}$?
 | 17 |
14,104 | Let \( a_{1}, a_{2}, \ldots, a_{n} \) be integers whose greatest common divisor is 1. Let \( S \) be a set of integers with the following properties:
(a) \( a_{i} \in S \) for \( i=1, \ldots, n \).
(b) \( a_{i} - a_{j} \in S \) for \( i, j = 1, \ldots, n \), not necessarily distinct.
(c) If \( x, y \in S \) and \( x + y \in S \), then \( x - y \in S \) too.
Prove that \( S = \mathbb{Z} \). | S = \mathbb{Z} |
3,426 | In a chess tournament, a team of schoolchildren and a team of students, each consisting of 15 participants, compete against each other. During the tournament, each schoolchild must play with each student exactly once, with the condition that everyone can play at most once per day. Different numbers of games could be played on different days.
At some point in the tournament, the organizer noticed that there is exactly one way to schedule the next day with 15 games and $N$ ways to schedule the next day with just 1 game (the order of games in the schedule does not matter, only who plays with whom matters). Find the maximum possible value of $N$. | 120 |
17,321 | We suppose that $AB=1$, and that the oblique segments form an angle of $45^{\circ}$ with respect to $(AB)$. There are $n$ vertices above $(AB)$.
What is the length of the broken line? | \sqrt{2} |
27,931 | 19. Find the minimum value of
$$
\sqrt{x^{2}+(20-y)^{2}}+\sqrt{y^{2}+(21-z)^{2}}+\sqrt{z^{2}+(20-w)^{2}}+\sqrt{w^{2}+(21-x)^{2}} .
$$ | 58 |
23,647 | A capacitor with a capacitance of $C_{1} = 20 \mu$F is charged to a voltage $U_{1} = 20$ V. A second capacitor with a capacitance of $C_{2} = 5 \mu$F is charged to a voltage $U_{2} = 5$ V. The capacitors are connected with opposite-charged plates. Determine the voltage that will be established across the plates. | 15 |
22,570 | In triangle \(ABC\), the side lengths are given as \( |AB| = 12 \), \( |BC| = 13 \), and \( |CA| = 15 \). Point \(M\) is taken on side \(AC\) such that the radii of the inscribed circles in triangles \(ABM\) and \(BCM\) are equal. Find the ratio \( |AM| : |MC| \). | \dfrac{22}{23} |
61,903 | 10.098. A line parallel to the base of a triangle divides it into parts whose areas are in the ratio of $2: 1$. In what ratio, counting from the vertex, does it divide the lateral sides? | (\sqrt{6}+2):1or(\sqrt{3}+1):2 |
51,445 | 3. In a quadratic trinomial, the second coefficient and the constant term were swapped, after which the result was added to the original trinomial. This resulted in a third quadratic trinomial, which turned out to have a single root. What can this root be equal to? If there are multiple correct answers, list them separated by a semicolon. | 0;-2 |
21,561 | Given the ellipse \( C: \frac{x^{2}}{4}+y^{2}=1 \) with the upper vertex \( M \) and the lower vertex \( N \), \( T(t, 2) (t \neq 0) \) is a point on the line \( y=2 \). The lines \( TM \) and \( TN \), passing through point \( T \), intersect the ellipse \( C \) at points \( E \) and \( F \), respectively. If the area of triangle \( TMN \) is \( k \) times the area of triangle \( TEF \), find the value of \( t \) that maximizes \( k \). | \pm 2\sqrt{3} |
4,472 | From a point \( P \) located on the hypotenuse \( AB \) of an isosceles right triangle \( \triangle ABC \), perpendiculars are drawn to the legs. These perpendiculars divide \( \triangle ABC \) into three parts - two triangles and a rectangle. Could the area of each of these parts be less than \(\frac{4}{9}\) of the area of the original triangle? | No |
56,962 | 3. As shown in Figure 2, in rhombus $A B C D$, the distances from vertex $A$ to sides $B C$ and $C D$ are $A E$ and $A F$, both equal to $5$, and $E F=6$. Therefore, the side length of rhombus $A B C D$ is $\qquad$ | \frac{125}{24} |
26,382 | Example. Given a positive integer $n \geqslant 2, x_{1}, x_{2}, \cdots, x_{n} \in \mathbf{R}^{+}$ and $x_{1}+x_{2}+\cdots+x_{n}=\pi$, find the minimum value of $\left(\sin x_{1}+\frac{1}{\sin x_{1}}\right)\left(\sin x_{2}+\frac{1}{\sin x_{2}}\right) \cdots\left(\sin x_{n}+\frac{1}{\sin x_{n}}\right)$. | (\sin\frac{\pi}{n}+\frac{1}{\sin\frac{\pi}{n}})^{n} |
2,370 | Let \( f(x) = \frac{1010x + 1009}{1009x + 1010} \), and define \( f^{(1)}(x) = f(x) \), \( f^{(i)}(x) = f(f^{(i-1)}(x)) \) for \( i = 2, 3, \cdots \). Determine \( f^{(n)}(x) \). | \dfrac{(2019^n + 1)x + 2019^n - 1}{(2019^n - 1)x + 2019^n + 1} |
7,762 | In an isosceles trapezoid \(ABCD\) with lateral sides \(AB\) and \(CD\) both equal to 10, perpendiculars \(BH\) and \(DK\) are drawn from vertices \(B\) and \(D\) to the diagonal \(AC\). It is known that the bases of the perpendiculars lie on segment \(AC\) and \(AH : AK : AC = 5 : 14 : 15\). Find the area of trapezoid \(ABCD\). | 180 |
24,511 | Five friends sat in a movie theater in a row containing $5$ seats, numbered $1$ to $5$ from left to right. (The directions "left" and "right" are from the point of view of the people as they sit in the seats.) During the movie Ada went to the lobby to get some popcorn. When she returned, she found that Bea had moved two seats to the right, Ceci had moved one seat to the left, and Dee and Edie had switched seats, leaving an end seat for Ada. In which seat had Ada been sitting before she got up? | 2 |
3,480 | Nine skiers started sequentially and covered the distance, each at their own constant speed. Could it be that each skier participated in exactly four overtakes? (In each overtake, exactly two skiers are involved - the one who overtakes and the one who is being overtaken.) | No |
27,928 | 6. In a convex quadrilateral $ABCD$, angles $A$ and $C$ are both 100°. Points $X$ and $Y$ are chosen on sides $AB$ and $BC$ respectively such that $AX = CY$. It turns out that line $YD$ is parallel to the bisector of angle $ABC$. Find angle $AXY$. (A. Kuznetsov, S. Berlov) | 80 |
21,872 | \section*{Problem 5 - 331035}
Determine all pairs \((m ; n)\) of positive integers \(m\) and \(n\) for which
\[
\frac{m^{2}}{m+1}+\frac{n^{2}}{n+1}
\]
is an integer. | (1, 1) |
15,062 | Given the sequence $\left\{a_{n}\right\}$ satisfying: $a_{0}=1, a_{1}=2, a_{n}=a_{n-1}+\frac{1}{a_{n-1}}$ for $n=1,2,3, \ldots$, prove that $63 < a_{2004} < 78$. | 63 < a_{2004} < 78 |
60,721 | 5. In a football tournament where each team played against each other once, teams A, B, C, D, and E participated. For a win, a team received 3 points, for a draw 1 point, and for a loss 0 points. In the end, it turned out that teams A, B, C, D, and E each had 7 points. What is the maximum number of points that team $\mathrm{E}$ could have? | 7 |
67,246 | Example 7. $\rho^{2}=a \cos 2 \varphi$. Find the orthogonal trajectories of the family of lemniscates | \rho^{2}=C\sin2\varphi |
311 | Mr. Guo has a cake to divide among 4 or 5 children. He cuts the cake into several pieces, each of varying sizes. Regardless of whether there are 4 or 5 children, they can each take some pieces so that everyone gets an equal amount. How many pieces does Mr. Guo need to cut the cake into at least? | 8 |
62,600 | 3. The numbers $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$ satisfy the condition $x_{1}^{2}+\ldots+x_{n}^{2}+y_{1}^{2}+\ldots+y_{n}^{2} \leqslant 1$. Find the maximum value of the expression
$$
A=\left(3\left(x_{1}+\ldots+x_{n}\right)-5\left(y_{1}+\ldots+y_{n}\right)\right) \cdot\left(5\left(x_{1}+\ldots+x_{n}\right)+3\left(y_{1}+\ldots+y_{n}\right)\right)
$$ | 17n |
27,673 | Example 4 The 10 complex roots of the equation $x^{10}+(13 x-1)^{10}=0$ are $r_{1}, \overline{r_{1}}, r_{2}, \overline{r_{2}}, r_{3}, \overline{r_{3}}, r_{4}$, $\overline{r_{4}}, r_{5}, \overline{r_{5}}$. Find the value of the algebraic expression $\frac{1}{r_{1} \overline{r_{1}}}+\frac{1}{r_{2} \overline{r_{2}}}+\cdots+\frac{1}{r_{5} \overline{r_{5}}}$. | 850 |
23,283 | A magician and their assistant plan to perform a trick. The spectator writes a sequence of $N$ digits on a board. The magician's assistant then covers two adjacent digits with a black dot. Next, the magician enters and has to guess both covered digits (including the order in which they are arranged). What is the smallest $N$ for which the magician and the assistant can arrange the trick so that the magician can always correctly guess the covered digits? | 101 |
60,498 | Example 4. Calculate: $\frac{3.6 \times 11.74 \times 138.4}{6 \times 2437}$.
(6 is an exact number) | 0.40 |
50,718 | ## Task 1 - 250611
On a $(3 \times 3)$-board, three game pieces are to be placed such that they do not threaten each other. A game piece is to threaten exactly those fields that lie in the same horizontal or the same vertical row as it does.
a) Draw all possible positions of the required kind for three such game pieces!
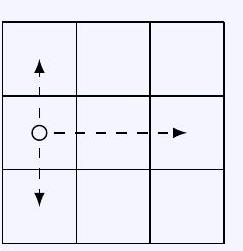
b) How many different positions are there if two positions are considered different if and only if one cannot be obtained from the other by rotating around the center field? | 2 |
61,592 | 7. Let the pair of positive integers $(x, y)$ satisfy $\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}=\frac{1}{\sqrt{20}}$. Then $xy$ has $\qquad$ different possible values. | 2 |
32,596 | 3. Triangle $A B C$ with angle $\angle A B C=135^{\circ}$ is inscribed in circle $\omega$. The lines tangent to $\omega$ at points $A$ and $C$ intersect at point $D$. Find $\angle A B D$, given that $A B$ bisects segment $C D$. Answer: $90^{\circ}$
 | 90 |
61,862 | 11. As shown in Figure 3, the vertex of the parabola $y=x^{2}$ is the origin $O$, and two perpendicular lines are drawn through $O$ intersecting the parabola $y=x^{2}$ at points $P$ and $Q$, respectively. Connect $P Q$.
(1) When $P Q \parallel x$-axis, find the distance from point $O$ to $P Q$; (2) Find the maximum distance from point $O$ to $P Q$. | 1 |
53,281 | A room is built in the shape of the region between two semicircles with the same center and parallel diameters. The farthest distance between two points with a clear line of sight is $12$m. What is the area (in $m^2$) of the room?
[img]https://cdn.artofproblemsolving.com/attachments/b/c/d2b2fc9fa9cca27dc9d692a1bb3089ba792063.png[/img] | 18\pi |
20,812 | Let $S^{}_{}$ be a subset of $\{1,2,3^{}_{},\ldots,1989\}$ such that no two members of $S^{}_{}$ differ by $4^{}_{}$ or $7^{}_{}$ . What is the largest number of elements $S^{}_{}$ can have?
Please give the answer directly without any intermediate steps. | 905 |
53,853 | 6. The set of positive integers $k$ that make $\left(x^{2}-1\right)^{2 k}+\left(x^{2}+2 x\right)^{2 k}+(2 x+1)^{2 k}=2\left(1+x+x^{2}\right)^{2 k}$ true for all real numbers $x$ is $\qquad$ | {1,2} |
67,620 | 10.300. The side of a regular triangle is equal to $a$. Determine the area of the part of the triangle that lies outside a circle of radius $a / 3$, the center of which coincides with the center of the triangle. | \frac{^{2}(3\sqrt{3}-\pi)}{18} |
56,308 | Example. Find the circulation of the vector field
$$
\vec{a}=\frac{y}{3} \vec{i} + 3 - 3 x \vec{j} + x \vec{k}
$$
along the closed contour $\Gamma$
$$
\left\{\begin{array}{l}
x=2 \cos t \\
y=2 \sin t \\
z=1-2 \cos t-2 \sin t
\end{array} t \in[0,2 \pi]\right.
$$ | -\frac{52\pi}{3} |
18,489 | Example 6. Factorize in the set of real numbers $R$:
$$
(x+1)(x+2)(x+3)(x+6)-3 x^{2}
$$ | (x + 4 - \sqrt{10})(x + 4 + \sqrt{10})(x^2 + 4x + 6) |
56,911 | 18. Peppa Pig observes the clock at home, finding that within a day, between 0 o'clock and 24 o'clock, the hour and minute hands form a $35^{\circ}$ angle $\qquad$ times. | 44 |
60,524 | 4. 100 balls of the same mass move along a trough towards a metal wall with the same speed. After colliding with the wall, a ball bounces off it with the same speed. Upon collision of two balls, they scatter with the same speed. (The balls move only along the trough). Find the total number of collisions between the balls. | 4950 |
56,822 | 11. Given the quadratic function $f(x)=x^{2}+a x+b(a, b \in \mathbf{R})$ has two distinct zeros, if $f\left(x^{2}+2 x-1\right)$ $=0$ has four distinct roots $x_{1}<x_{2}<x_{3}<x_{4}$, and $x_{1}, x_{2}, x_{3}, x_{4}$ form an arithmetic sequence, find the range of $a-b$. | (-\infty,\frac{25}{9}] |
55,181 | 30.7. Find the number of real roots of the equation
$$
4 \cos (2007 a)=2007 a \text {. }
$$ | 3 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.