id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
6,619 | A semicircular sponge with a diameter of $20 \text{ cm}$ is used to wipe a corner of a room's floor such that the ends of the diameter continuously touch the two walls forming a right angle. What area does the sponge wipe? | 100\pi |
63,665 | $\left.\begin{array}{l}\text { [Inscribed angle, subtending the diameter]} \\ {\left[\begin{array}{l}\text { Auxiliary similar triangles }\end{array}\right]} \\ {[\text { Pythagorean Theorem (direct and inverse). }} \\ {[\text { Trapezoids (other). }}\end{array}\right]$
Given trapezoid $ABCD$, where angle $BAD$ is a right angle. A circle is constructed on side $AB$ as its diameter, intersecting diagonal $BD$ at point $M$. It is known that $AB=3$, $AD=4$, and $BC=1$. Find the angle $CAM$. | \arcsin\frac{1}{\sqrt{10}} |
5,500 | Inside a semicircle with a radius of 12, there is a circle with a radius of 6 and a small semicircle, all pairwise tangent to each other, as shown in the diagram. Find the radius of the small semicircle. | 4 |
33,612 | Problem 4. Given is $\triangle A B C$ with the angle bisector of the angle at vertex $A$, $A L(L \in B C)$. The point $M \in A C$ is such that $M L \| A B$. Let $\beta^{\prime}$ be the exterior angle at vertex $B$ of $\triangle A B C$ and $\measuredangle A C B: \beta^{\prime}=5: 11$.
a) Determine the ratio $\measuredangle C A B$ : $\measuredangle A C B$.
b) If $\measuredangle A L B=80^{\circ}$, determine $\measuredangle A L M$. | 30 |
67,916 | 6. Jack Sparrow needed to distribute 150 piastres into 10 purses. After placing a certain number of piastres in the first purse, he put more in each subsequent purse than in the previous one. As a result, it turned out that the number of piastres in the first purse was not less than half the number of piastres in the last purse. How many piastres are in the 6th purse? | 16 |
11,042 | The numbers \(1, 2, 3, \ldots, 400\) are written on 400 cards. Two players, \(A\) and \(B\), play the following game:
1. In the first step, \(A\) takes 200 cards for themselves.
2. \(B\) then takes 100 cards from both the remaining 200 cards and the 200 cards that \(A\) has, totaling 200 cards for themselves, and leaves the remaining 200 cards for \(A\).
3. In the next step, \(A\) takes 100 cards from both players' cards, totaling 200 cards for themselves, leaving the remaining 200 cards for \(B\).
This process continues until \(B\) completes the 200th step. At the end, the sums of the numbers on the cards held by \(A\) and \(B\) are calculated as \(C_A\) and \(C_B\) respectively. Then, player \(A\) pays player \(B\) the difference \(C_B - C_A\).
What is the maximum difference that \(B\) can achieve if both players play optimally? | 20000 |
51,452 | 27. The number of five-digit numbers that are multiples of 4 and whose sum of digits is 40 is $\qquad$.
untranslated part: $\qwen$ (Note: This part is not translatable as it is a placeholder or variable in the original text.)
For the purpose of a complete translation, the final answer should look like this:
27. The number of five-digit numbers that are multiples of 4 and whose sum of digits is 40 is $\qquad$. | 20 |
67,986 | 3. Find all integer solutions to the equation $\sqrt{n+1}-\sqrt{n}=(\sqrt{2}-1)^{2021}$. | \frac{1}{4}((\sqrt{2}+1)^{2021}-(\sqrt{2}-1)^{2021})^{2} |
7,836 | Given three arbitrary points \(A\), \(B\), and \(C\), with \(BC = a\), \(CA = b\), and \(AB = c\), find the minimum value of \(y = \frac{c}{a + b} + \frac{b}{c} \). | \sqrt{2} - \dfrac{1}{2} |
51,960 | 2.48 Find all sets of distinct positive integers (at least 2) such that the sum of the numbers equals their product. | {1,2,3} |
67,628 | 4. It is known that the numbers EGGPLANT and FROG are divisible by 3. What is the remainder when the number CLAN is divided by 3? (Letters represent digits, the same letters represent the same digits, different letters represent different digits).
Answer: 0 | 0 |
24,760 |
Given positive real numbers \( a, b, c, d \) that satisfy the equalities
\[ a^{2}+d^{2}-ad = b^{2}+c^{2}+bc \quad \text{and} \quad a^{2}+b^{2} = c^{2}+d^{2}, \]
find all possible values of the expression \( \frac{ab+cd}{ad+bc} \). | \dfrac{\sqrt{3}}{2} |
10,443 | One hundred mathematicians attending an international combinatorial conference are being accommodated in a hotel where the rooms are numbered from 1 to 100. The reception plans to assign the mathematicians to rooms according to their arrival order and their corresponding room numbers. However, the first guest forgets the instruction and randomly chooses a room. The receptionist then instructs the subsequent guests to take the room corresponding to their arrival number sequentially and, if that room is occupied, to choose any free room that they like. In how many different ways could the guests occupy the rooms? | 2^{99} |
16,884 | Let \( n \geq 2 \) be a fixed integer. Find the least constant \( C \) such that the inequality
\[ \sum_{i<j} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right) \leq C\left(\sum_{i} x_{i}\right)^{4} \]
holds for every \( x_{1}, \ldots, x_{n} \geq 0 \) (the sum on the left consists of \(\binom{n}{2}\) summands). For this constant \( \bar{C} \), characterize the instances of equality. | \dfrac{1}{8} |
34,578 | 3. $f(x)$ is an odd function, $g(x)$ is an even function, and $f(x)+g(x)+f(x) g(x)=\left(e^{x}+\sin x\right) \cdot \cos x$, then $f(x)$ has $\qquad$ zeros in $[0,4 \pi)$. | 5 |
25,298 | 1st Swedish 1961 Problem 3 For which n is it possible to put n identical candles in a candlestick and to light them as follows. For i = 1, 2, ... , n, exactly i candles are lit on day i and burn for exactly one hour. At the end of day n, all n candles must be burnt out. State a possible rule for deciding which candles to light on day i. | n |
8,620 | Select three different digits from $0, 1, \cdots, 9$ to form a four-digit number (one of the digits may appear twice), such as 5224. How many such four-digit numbers are there? | 3888 |
23,338 | We color a $98 \times 98$ checkerboard in the style of a chessboard. A move consists of selecting a rectangle made up of small squares and inverting their colors. What is the minimum number of moves required to make the entire checkerboard monochromatic? | 98 |
62,562 | 71. A sheep is tied to a vertex of an equilateral triangular fence with a side length of 5 meters, the rope is 7 meters long. If the sheep can only walk outside the fence, the area that the sheep can reach is $\qquad$ square meters. ( $\pi$ is taken as 3.14) | 136.59 |
29,205 | 3. The $n$th term of a sequence is the first non-zero digit of the decimal expansion of $\frac{1}{\sqrt{n}}$. How many of the first one million terms of the sequence are equal to 1 ? | 757576 |
29,879 | Find all triplets of strictly positive integers $(x, y, z)$ such that
$$
(x+y)^{2}+3 x+y+1=z^{2} .
$$ | (x,x,2x+1) |
59,316 | Paint three faces of an $8 \times 8$ cube red and three faces blue (requiring that any three faces sharing a common vertex cannot all be the same color), then cut it into 512 $1 \times 1 \times 1$ small cubes. Among these 512 small cubes, there are $\qquad$ small cubes that have both red and blue faces. | 56 |
66,574 | Task 8. For what values of the parameter $a$ does the equation
$$
5^{x^{2}-6 a x+9 a^{2}}=a x^{2}-6 a^{2} x+9 a^{3}+a^{2}-6 a+6
$$
have exactly one solution? | 1 |
21,834 | Five people stand in a line, each wearing a different hat numbered $1, 2, 3, 4, 5$. Each person can only see the hats of the people in front of them. Xiao Wang cannot see any hats; Xiao Zha can only see hat $4$; Xiao Tian does not see hat $3$, but can see hat $1$; Xiao Yan can see three hats, but not hat $3$; Xiao Wei can see hat $3$ and hat $2$. What number hat is Xiao Wei wearing? | 5 |
60,160 | 15. For a complex number $z$, find the minimum value of $u=|z|+|z-i|+|z-\sqrt{3}|$. | \sqrt{7} |
64,763 | I. (25 points) The Xiguang Factory glasses workshop has received a batch of tasks, requiring the processing of 6000 Type A parts and 2000 Type B parts. This workshop has 214 workers, and each of them can process 3 Type B parts in the time it takes to process 5 Type A parts. These workers are to be divided into two groups, with both groups working simultaneously, each group processing one type of part. To complete this batch of tasks in the shortest time, how should the workers be divided? | 137 |
17,361 | Prove that \( S = \frac{a^2 + d^2 - b^2 - c^2}{4} \tan A \quad (\text{if } A \neq 90^\circ) \). | S = \dfrac{a^2 + d^2 - b^2 - c^2}{4} \tan A |
9,005 |
Find all pairs \((\alpha, \beta)\) of positive real numbers with the following properties:
(a) For all positive real numbers \(x, y, z, w\) it holds that
\[
x + y^2 + z^3 + w^6 \geq \alpha (xyzw)^\beta
\]
(b) There is a quadruple \((x, y, z, w)\) of positive real numbers such that equality holds in (a). | (2^{4/3} \cdot 3^{1/4}, \frac{1}{2}) |
1,009 | Let \( x_{1} > 0 \) and \( a > 0 \), and define the sequence \( x_{n+1} = \left( x_{n} + \frac{a}{x_{n}} \right) \) for \( n \geqslant 1 \). Calculate the limit \( \lim_{n \rightarrow \infty} x_{n} \). | \sqrt{a} |
1,381 |
A group of one hundred friends, including Petya and Vasya, live in several cities. Petya found the distance from his city to the city of each of the other 99 friends and summed these 99 distances, obtaining a total of 1000 km. What is the maximum possible total distance that Vasya could obtain using the same method? Assume cities are points on a plane and if two friends live in the same city, the distance between their cities is considered to be zero. | 99000 |
52,507 | $3.416 \cos \frac{\pi}{33} \cdot \cos \frac{2 \pi}{33} \cdot \cos \frac{4 \pi}{33} \cdot \cos \frac{8 \pi}{33} \cdot \cos \frac{16 \pi}{33}=\frac{1}{32}$. | \frac{1}{32} |
67,162 | 10. Let the function $f(x)=\frac{(x+1)^{2}+\ln \left(\sqrt{x^{2}+1}+x\right)}{x^{2}+1}$ have a maximum value of $M$ and a minimum value of $N$. Determine the value of $M+N$. | 2 |
63,493 | Kaiibhanov A.K:
The audience has the shape of a regular hexagon with a side of 3 m. In each corner, a snoremeter is installed, determining the number of sleeping students at a distance not exceeding 3 m. How many sleeping students are there in total in the audience, if the sum of the snoremeter readings is 7?
# | 3 |
51,090 | Example 4. As shown in the figure, points $A, B, C, D$ lie on the same circle, and $BC=DC=4, AE=6$. The lengths of segments $BE$ and $DE$ are both positive integers. What is the length of $BD$? (1988
National Junior High School Mathematics Competition) | 7 |
9,239 | Let \( l \) and \( m \) be two skew lines. On line \( l \), there are three points \( A \), \( B \), and \( C \) such that \( A B = B C \). From points \( A \), \( B \), and \( C \), perpendiculars \( A D \), \( B E \), and \( C F \) are drawn to line \( m \) with feet at \( D \), \( E \), and \( F \) respectively. Given \( A D = \sqrt{15} \), \( B E = \frac{7}{2} \), and \( C F = \sqrt{10} \), find the distance between \( l \) and \( m \). | \sqrt{6} |
52,310 | 7. Highway (from 7th grade, 3 points). A highway running from west to east intersects with $n$ equal roads, numbered from 1 to $n$ in order. Cars travel on these roads from south to north and from north to south. The probability that a car will approach the highway from each of these roads is $\frac{1}{n}$. Similarly, the probability that a car will turn off the highway onto each of these roads is $\frac{1}{n}$. The road by which a car leaves the highway is independent of the road by which it entered the highway.
which the car leaves the highway, is independent of the road by which it entered the highway.
Find the probability that a random car that has entered the highway will pass the $k$-th intersection (either drive through it or turn at it). | \frac{2kn-2k^{2}+2k-1}{n^{2}} |
18,289 | For the polynomial
\[ p(x) = 985 x^{2021} + 211 x^{2020} - 211, \]
let its 2021 complex roots be \( x_1, x_2, \cdots, x_{2021} \). Calculate
\[ \sum_{k=1}^{2021} \frac{1}{x_{k}^{2} + 1} = \]
| 2021 |
12,334 | Given a geometric sequence $\{a_{n}\}$ that satisfies $\lim_{n \rightarrow +\infty} \sum_{i=1}^{n} a_{4} = 4$ and $\lim_{n \rightarrow +\infty} \sum_{i=1}^{n} a_{i}^{2} = 8$, determine the common ratio $q$. | \dfrac{1}{3} |
32,687 | 15. Given the function $f(x)=\frac{4 \mathrm{e}^{x-1}}{x+1}+x^{2}-3 a x+a^{2}-1$, if there exists $x_{0}>0$, such that $f\left(x_{0}\right) \leqslant 0$, find the minimum possible value of the real number $a$. | 1 |
58,164 | 1. In the field of real numbers, solve the equation
$$
\sqrt{2}(\sin t+\cos t)=\tan^{3} t+\cot^{3} t .
$$ | \frac{1}{4}\pi+2k\pi |
52,643 | 2. Given $a, b \in \mathbf{R}$, the circle $C_{1}: x^{2}+y^{2}-2 x+4 y-b^{2}+5=0$ intersects with $C_{2}: x^{2}+y^{2}-2(a-6) x-2 a y$ $+2 a^{2}-12 a+27=0$ at two distinct points $A\left(x_{1}, y_{1}\right), B\left(x_{2}, y_{2}\right)$, and $\frac{y_{1}+y_{2}}{x_{1}+x_{2}}+\frac{x_{1}-x_{2}}{y_{1}-y_{2}}$ $=0$, then $a=$ $\qquad$ | 4 |
53,577 | 5. As shown in Figure 1, the vertices of $\triangle O A B$ are $O(0,0)$, $A(2,1)$, and $B(10,1)$. The line $C D \perp x$-axis and bisects the area of $\triangle O A B$. If the coordinates of point $D$ are $(x, 0)$, then the value of $x$ is . $\qquad$ | 10-2\sqrt{10} |
15,926 | Given \( A + B + C = 180^\circ \) and \(\frac{\sin A + \sin B + \sin C}{\cos A + \cos B + \cos C} = 1\), find the value of \(\frac{\cos 2A + \cos 2B + \cos 2C}{\cos A + \cos B + \cos C}\). | 2 |
22,316 | For any \( n \in \mathbf{N}^{*} \), prove that: \(\frac{2}{3} n \sqrt{n}<\sum_{k=1}^{n} \sqrt{k}<\left(\frac{4 n+3}{6}\right) \sqrt{n}\). | \frac{2}{3} n \sqrt{n}<\sum_{k=1}^{n} \sqrt{k}<\left(\frac{4 n+3}{6}\right) \sqrt{n} |
67,040 | 7. In the Cartesian coordinate system $x O y$, $P$ is a moving point on the ellipse $\frac{y^{2}}{4}+\frac{x^{2}}{3}=1$, and the coordinates of points $A, B$ are $(1,1),(0,-1)$, respectively. Then the maximum value of $|P A|+|P B|$ is $\qquad$. | 5 |
66,430 | 6. Answer: 1) $S_{1}=\frac{3 \sqrt{3}}{2}$ 2) $S_{2}=6 \sqrt{6}$
Option 0
In a cube $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with edge $a$, a section is made by a plane parallel to the plane $B D A^{\prime}$ and at a distance $b$ from it. Find the area of the section. | S_{1}=\frac{\sqrt{3}}{2}(-b\sqrt{3})^{2} |
53,329 | A marble is placed on each $33$ unit square of a $10*10$ chessboard. After that, the number of marbles in the same row or column with that square is written on each of the remaining empty unit squares. What is the maximum sum of the numbers written on the board?
| 438 |
19,140 | Let $A$ and $B$ be two subsets of the set $\{1,2, \ldots, 20\}$, where $A \cap B = \varnothing$, and if $n \in A$, then $2n + 2 \in B$. Let $M(A)$ denote the sum of the elements of $A$. The maximum value of $M(A)$ is: | 39 |
2,539 | Given a tetrahedron with six edge lengths \(a, b, c, d, e, f\) and surface area \(S\), prove that \(S \leq \frac{\sqrt{3}}{6}\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}+f^{2}\right)\). | S \leq \frac{\sqrt{3}}{6}\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}+f^{2}\right) |
5,703 | Tam created the mosaic shown using a regular hexagon, squares, and equilateral triangles. If the side length of the hexagon is \( 20 \text{ cm} \), what is the outside perimeter of the mosaic? | 240 |
67,380 | The number $S$ is the result of the following sum: $1 + 10 + 19 + 28 + 37 +...+ 10^{2013}$
If one writes down the number $S$, how often does the digit `$5$' occur in the result? | 4022 |
5,607 | A regular hexagon is drawn on the plane with a side length of 1. Using only a ruler, construct a segment whose length is $\sqrt{7}$. | \sqrt{7} |
33,315 | 6. Given $f(x)=x^{3}+b x^{2}+c x+d$ is an increasing function on $(-\infty, 0)$, and a decreasing function on $[0,2]$, and the equation $f(x)=0$ has three roots, which are $\alpha, 2, \beta$, then the range of $|\alpha-\beta|$ is | [3,+\infty) |
32,213 | [ Properties of bisectors, concurrency ] [ The ratio in which the bisector divides the side $]$ [ Properties of bisectors, concurrency ]
In triangle $A B C$, points $M$ and $N$ are marked on sides $A B$ and $B C$ respectively, such that $B M=B N$. A line is drawn through point $M$ perpendicular to $B C$, and a line through point $N$ perpendicular to $A B$. These lines intersect at point $O$. The extension of segment $B O$ intersects side $A C$ at point $P$ and divides it into segments $A P=5$ and $P C=4$. Find the length of segment $B P$, given that $B C=6$. | 5 |
21,026 | There is a five-digit odd positive integer \( x \). By changing all 2s in \( x \) to 5s and all 5s in \( x \) to 2s, while keeping all other digits unchanged, we obtain a new five-digit number \( y \). If \( x \) and \( y \) satisfy the equation \( y = 2(x+1) \), then \( x \) is ________. | 29995 |
7,967 | Find the smallest positive integer \( n \) such that, if there are initially \( 2n \) townspeople and 1 goon, then the probability that the townspeople win is greater than 50%. | 3 |
52,501 | 7. There are less than 100 cells in a row, and at the beginning, only the cells at both ends contain a chess piece each. Several students take turns placing chess pieces in the cells. Each person places one piece at a time, and it must be placed in the middle of two adjacent cells that already contain pieces (for example, if the 3rd and 7th cells from left to right contain pieces, and the 4th, 5th, and 6th cells do not, a piece can be placed in the 5th cell; but if the 4th and 7th cells contain pieces, and the 5th and 6th cells do not, neither the 5th nor the 6th cell can be used). Each of these students placed 9 pieces, resulting in each cell containing exactly one piece. How many students are there? $\qquad$ | 7 |
65,434 | 3 ( A square with an area of 24 has a rectangle inscribed in it such that one vertex of the rectangle lies on each side of the square. The sides of the rectangle are in the ratio $1: 3$.
Find the area of the rectangle.
# | 9 |
15,802 | Calculate the areas of the figures bounded by the lines given in polar coordinates.
$$
r = 4 \cos 4 \phi
$$ | 8\pi |
744 | 5.19 It is known that 1982 people attended a gathering, and among any 4 people, at least 1 person knows the other 3. How many people at least know all the attendees at this gathering? | 1979 |
33,665 | Tokarev S.I.
Find all such pairs of prime numbers $p$ and $q$ that $p^{3}-q^{5}=(p+q)^{2}$. | p=7,q=3 |
54,156 | 11.1. Petya wrote ten natural numbers on the board, none of which are equal. It is known that among these ten numbers, three can be chosen that are divisible by 5. It is also known that among the ten numbers written, four can be chosen that are divisible by 4. Can the sum of all the numbers written on the board be less than $75$?
(P. Kozhevnikov) | 71 |
61,854 | Find the total number of triples of integers $(x,y,n)$ satisfying the equation $\tfrac 1x+\tfrac 1y=\tfrac1{n^2}$, where $n$ is either $2012$ or $2013$. | 338 |
10,921 | Given \(a, b, c, x, y, z \in \mathbf{R}_{+}\) satisfying the equations:
\[
cy + bz = a, \quad az + cx = b, \quad bx + ay = c,
\]
find the minimum value of the function
\[
f(x, y, z) = \frac{x^2}{1 + x} + \frac{y^2}{1 + y} + \frac{z^2}{1 + z}.
\] | \dfrac{1}{2} |
31,605 | 3. In $\triangle A B C$, $B C=a, C A=b, A B=c$. If $2 a^{2}+b^{2}+c^{2}=4$, then the maximum value of the area of $\triangle A B C$ is $\qquad$ (Provided by Li Hongchang) | \frac{\sqrt{5}}{5} |
21,328 | For positive real numbers $a, b, c, d,$ satisfying the following conditions: $a(c^2 - 1)=b(b^2+c^2)$ and $d \leq 1$ , prove that : $d(a \sqrt{1-d^2} + b^2 \sqrt{1+d^2}) \leq \frac{(a+b)c}{2}$ | \frac{(a + b)c}{2} |
15,484 | Consider a circle of radius \( R \) centered at the origin on the Cartesian plane. Specify at least one value of \( R \) for which there are exactly 32 integer points (a point is called an integer point if both its x-coordinate and y-coordinate are integers) lying on this circle. | \sqrt{1105} |
53,090 | There are three equal-radius, tangent circles. What is the area of the lobe between the circles if the radius of each circle is $r$? | r^{2}(\sqrt{3}-\frac{\pi}{2}) |
54,200 | 4. To build a batch of identical houses with a total area of $2500 \mathrm{~m}^{2}$, the cost of a $a \mathrm{~m}^{2}$ house is the sum of material cost $100 p_{1} a^{\frac{3}{2}}$ yuan, construction cost $100 p_{2} a$ yuan, and other various expenses $100 p_{3} a^{\frac{1}{2}}$ yuan, where the numbers $p_{1} 、 p_{2} 、 p_{3}$ are three consecutive terms of a geometric sequence, their sum is 21, and their product is 64. If 63 such houses are built, the material cost will be less than the sum of the construction cost and other various expenses. To minimize the total cost, what is the maximum number of houses that can be built? | 156 |
63,939 | 7. Given planar vectors $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}$ satisfying $|\boldsymbol{a}|=|\boldsymbol{b}|=1,|\boldsymbol{c}|=5$, and $\boldsymbol{a} \cdot \boldsymbol{c}=3, \boldsymbol{b} \cdot \boldsymbol{c}=4$, then for any real number $t, z=|c-t a-b|$ the minimum value is $\qquad$. | 3 |
7,354 | The circumcircle of acute $\triangle ABC$ has center $O$ . The line passing through point $O$ perpendicular to $\overline{OB}$ intersects lines $AB$ and $BC$ at $P$ and $Q$ , respectively. Also $AB=5$ , $BC=4$ , $BQ=4.5$ , and $BP=\frac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .
Please give the answer directly without any intermediate steps. | 23 |
513 | On the diagonal of a unit cube, points \( M \) and \( N \) are taken, and on a skew diagonal of a face, points \( P \) and \( Q \) are taken. It is known that \( M N = \frac{1}{2} \) and \( P Q = \frac{1}{3} \). Find the volume of the tetrahedron \( M N P Q \). | \dfrac{\sqrt{6}}{216} |
62,059 | 15. In how many ways can a million be factored into three factors? Factorizations that differ only in the order of the factors are considered the same. | 139 |
3,750 | ## Task 1 - 090521
Six equally sized dice are stacked on a table as shown in the image. The number on the top face is 1.
Determine the sum of the numbers on the hidden faces of these dice!
Note that the sum of the numbers on opposite faces of each die is always 7.
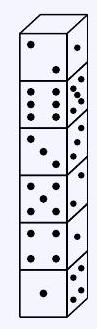 | 41 |
31,355 | 11.3. On one main diagonal and all edges of a cube, directions are chosen. What is the smallest length that the sum of the resulting 13 vectors can have, if the edge length is 1, and the length of the main diagonal is $\sqrt{3}$. | \sqrt{3} |
26,412 | 8.4. For all triples $(x, y, z)$ satisfying the system
$$
\left\{\begin{array}{l}
\sqrt{3} \cos x=\operatorname{ctg} y \\
2 \cos y=\operatorname{tg} z \\
\cos z=2 \operatorname{ctg} x
\end{array}\right.
$$
find the smallest value of the expression $\sin x+\sin z$. | -\frac{7\sqrt{2}}{6} |
14,620 | Find the maximum value of the parameter \( b \) for which the inequality \( b \sqrt{b}\left(x^{2}-10 x+25\right)+\frac{\sqrt{b}}{\left(x^{2}-10 x+25\right)} \leq \frac{1}{5} \cdot \sqrt[4]{b^{3}} \cdot \left| \sin \frac{\pi x}{10} \right| \) has at least one solution. | \dfrac{1}{10000} |
55,926 | [Parallel lines, properties and signs. Transversals]
Points $M$ and $N$ are located on the lateral sides $A B$ and $C D$ of trapezoid $A B C D$, respectively, such that $M N \| A D$. It is known that the area of trapezoid $M B C N$ is to the area of trapezoid $A M N D$ as $2: 3$. Find $M N$, if $B C = a, A D = b$. | \sqrt{\frac{3a^2+2b^2}{5}} |
67,829 | 3. (3 points) Find the distance between the curves $y=e^{3 x+7}$ and $y=(\ln x-7) / 3$.
---
The text has been translated while preserving the original formatting and line breaks. | \sqrt{2}(\frac{8+\ln3}{3}) |
57,813 | 3. As shown in Figure 4, in $\triangle A B C$, $\angle C=90^{\circ}, D$ is a point on side $B C$, $\angle A D C=3 \angle B A D, B D=9$, $D C=5$. Then $A B=$ | 21 |
1,046 | 3 [ Central symmetry helps solve the problem]
What is the maximum number of pawns that can be placed on a chessboard (no more than one pawn per square), if:
1) a pawn cannot be placed on the e4 square;
2) no two pawns can stand on squares that are symmetric relative to the e4 square?
# | 39 |
20,909 | 17. Two thirds in addition (to the unknown), $\frac{1}{3}$ in subtraction, 10 remains (i.e., two thirds of the unknown are added to it, and one third is subtracted from the resulting sum. The remainder is 10). | 9 |
6,805 | $ABCD$ is a right trapezoid with bases $AD=4$ and $BC=3$. $AB \perp BC$. A circle passing through $C$ and $D$ is tangent to $AB$ at point $E$. Find the distance from point $E$ to line $CD$. | 2\sqrt{3} |
18,692 | Given $n$ distinct positive numbers $a_{1}, a_{2}, \cdots, a_{n}$, form all possible sums using 1 to $n$ of them as addends. Prove that among these sums, there are at least $\frac{1}{2} n(n+1)$ distinct sums. | \frac{1}{2}n(n+1) |
64,865 | 8. A small bug crawls on the surface of a regular octahedron,
each second it moves from one vertex to one of the four adjacent vertices with equal probability. Then the probability that the bug returns to the initial position at the 8th second is $\qquad$ . | \frac{43}{256} |
62,234 | A number is called special if it does not contain the digit zero and, in addition, the sum of its digits is equal to twice the first digit. For example, the number 8161 is special because:
- none of its digits is zero;
- the sum of all its digits is $8+1+6+1=16$;
- the double of its first digit is $8 \times 2=16$.
a) Is there a special number with five digits that is even? Why or why not? If it exists, give an example.
b) What is the smallest special number with four digits?
c) What is the largest special number?
d) What is the largest special number that has all distinct digits? | 9621 |
55,937 | Exercise 5. Let $x, y, z$ be strictly positive real numbers such that
$$
x+\frac{y}{z}=y+\frac{z}{x}=z+\frac{x}{y}=2
$$
Determine all possible values that the number $x+y+z$ can take. | 3 |
28,151 | 145. In a regular hexagonal pyramid, the center of the circumscribed sphere lies on the surface of the inscribed sphere. Find the ratio of the radii of the circumscribed and inscribed spheres. | \frac{3+\sqrt{21}}{3} |
63,659 | 8.5. Vasya wrote a set of different natural numbers on the board, each of which does not exceed 2023. It turned out that for any two written numbers $a$ and $b$, the number $a+b$ is not divisible by $a-b$. What is the maximum number of numbers Vasya could have written? | 675 |
15,496 | The 200-digit number \( M \) is composed of 200 ones. What is the sum of the digits of the product \( M \times 2013 \)? | 1200 |
53,633 | 6. In the Cartesian coordinate plane $x O y$, the area of the region determined by the system of inequalities
$$
\left\{\begin{array}{l}
|x| \leqslant 2, \\
|y| \leqslant 2, \\
|| x|-| y|| \leqslant 1
\end{array}\right.
$$
is $\qquad$ | 12 |
8,207 | $\begin{array}{l}\text { 9. } \frac{1-2 \log _{6} 5 \cdot \log _{10} 3 \cdot \log _{15} 2}{\log _{6} 5 \cdot \log _{10} 3+\log _{10} 3 \cdot \log _{15} 2+\log _{15} 2 \cdot \log _{6} 5} \\ =\end{array}$ | 1 |
62,683 | 23. The sequence $\left(x_{n}\right)_{n-1}^{\infty}$ is defined recursively by
$$
x_{n+1}=\frac{x_{n}+(2-\sqrt{3})}{1-x_{n}(2-\sqrt{3})}
$$
with $x_{1}=1$. Determine the value of $x_{1001}-x_{401}$. | 0 |
3,042 | In triangle \( \triangle A B C \), let \( A D, B E, C F \) be the three altitudes, and \( D, E, F \) the feet of these altitudes, respectively. From points \( A, B, \) and \( C \), lines \( A K \perp E F \) at \( K \), \( B L \perp F D \) at \( L \), and \( C N \perp D E \) at \( N \) are drawn. Prove that the lines \( A K, B L, \) and \( C N \) intersect at a single point. | O |
20,000 | Find the range of the function \(f(x) = \frac{1}{g\left(\frac{64 g\left(16 g\left(\log_{2} x\right)\right)}{5}\right)}\), where \(g(x) = \sqrt[5]{x} + \frac{1}{\sqrt[5]{x}}\). | \left[ -\dfrac{2}{5}, 0 \right) \cup \left( 0, \dfrac{2}{5} \right] |
21,175 | Find the smallest natural number $n$ such that if $p$ is a prime number and $n$ is divisible by $p-1$, then $n$ is also divisible by $p$. | 1806 |
14,330 | If a positive integer cannot be written as the difference of two square numbers, then the integer is called a "cute" integer. For example, 1, 2, and 4 are the first three "cute" integers. Find the \(2010^{\text{th}}\) "cute" integer. | 8030 |
3,610 | ## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \sqrt{n^{3}+8}\left(\sqrt{n^{3}+2}-\sqrt{n^{3}-1}\right)$ | \dfrac{3}{2} |
25,894 | (7) Let a fixed point $P$ outside the plane $\alpha$ be at a distance $h$ from $\alpha$, and let three moving points $A$, $B$, and $C$ on $\alpha$ be at distances $a$, $b$, and $c$ from $P$ respectively, with $\angle PBA = 90^{\circ}$. Then the maximum area of $\triangle ABC$ is $\qquad$ (expressed in terms of $a$, $b$, $c$, and $h$). | \frac{1}{2}\sqrt{^{2}-b^{2}}(\sqrt{b^{2}-^{2}}+\sqrt{^{2}-^{2}}) |
58,691 | 2. Given $a, b, c > 0$, find the maximum value of the expression
$$
A=\frac{a^{2}(b+c)+b^{2}(c+a)+c^{2}(a+b)}{a^{3}+b^{3}+c^{3}-2 a b c}
$$ | 6 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.