id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
100,458 | \section*{Task 1 - V11231}
In a large state-owned enterprise in the electrical industry, 12,000 units of a certain semi-finished product are annually procured from a supplier at a price of 1.00 DM per unit. The orders were previously placed twice a year, on January 1 and July 1.
The administrative costs for each order (issuing and sending the order, monitoring the delivery date, invoice review, booking, etc.) amount to 30.00 DM. The storage costs (space costs, administration, "shrinkage" due to spoilage and damage, etc.) amount to 20% of the value of the average inventory. The costs for ordering and storage were therefore:
2 orders ... 60.00 DM
Storage costs 20% of the average inventory (3000 units), i.e., 20% of 3000.00 DM, which is 600.00 DM
Total 660.00 DM
In a production meeting, it is suggested to reduce costs by ordering the quantity needed for each quarter (3000 units) four times a year.
a) How high are the costs according to this suggestion?
b) For how many orders do the lowest costs occur? How high are the costs in this case?
Hint: The term "Deutsche Mark" was only changed to "Mark der Deutschen Notenbank" (MDN) in 1964 in East Germany, and subsequently to "Mark" in 1968. | 380 |
100,526 | Problem 4. Ana can run a circular track three times in 8 minutes. Maria can run the same track twice in 5 minutes. If Ana and Maria start running at the same time from the start, what is the total number of laps they will run before they meet again at the start for the first time? How many times has each of them run the track when they meet again at the start for the first time? | 31 |
100,534 | ## Task 2
Draw two line segments:
the 1st line segment $\overline{A B}=8 \mathrm{~cm}$, the 2nd line segment $\overline{C D}$ should be $2 \mathrm{~cm}$ shorter than the line segment $\overline{A B}$! | 6 |
100,581 | Problem 1. After $\frac{1}{4}$ of the gasoline was poured out from the barrel, and then another $10\%$ of the total amount in the barrel, 26 liters of gasoline remained. How many liters of gasoline were there in the barrel at the beginning? | 40 |
100,617 | Task 4. Before and after the number 10, write one digit each so that the resulting number is divisible by 36 and the quotient of that number divided by 36 is a number written with different digits from the given number. | 9108 |
100,620 | 2. Solve the equation in the set of prime numbers
$$
3 p^{2}+3 p=166+q
$$ | 7 |
100,691 | 4. Seven coworkers (Maria, Iskra, Lile, Petre, Mile, Todor, and Kosta) have lunch together in three restaurants ($P, Q$, and $R$).
Maria goes to a restaurant only on Wednesday.
Iskra and Mile can never be in the same restaurant at the same time.
Lile does not go to a restaurant if Maria does not go.
Petre and Kosta will not go to the same restaurant together unless Iskra goes.
Mile does not go to restaurant $Q$.
If six of the coworkers have lunch together on Wednesday in one of the restaurants, which coworker will be absent?
What is the maximum number of coworkers that can have lunch together on Tuesday? | 4 |
100,702 | 5. Aneta and Viktor are playing a game. The game starts with Aneta saying a number from 1 to 7. Then Viktor adds that number to another number from 1 to 7 and says the sum. Aneta, in turn, adds the number Viktor said to another number from 1 to 7 and says the sum, and this process alternates until one of them says the number 100. The winner is the one who first says the number 100. Can Aneta, as the player who starts the game, ensure a sure victory, and how? | 4 |
100,720 | A $5 \mathrm{~m} \times 5 \mathrm{~m}$ flat square roof receives $6 \mathrm{~mm}$ of rainfall. All of this water (and no other water) drains into an empty rain barrel. The rain barrel is in the shape of a cylinder with a diameter of $0.5 \mathrm{~m}$ and a height of $1 \mathrm{~m}$. Rounded to the nearest tenth of a percent, what percentage of the barrel will be full of water? | 76.4 |
100,765 | 1. Marco thought of a six-digit number, whose digit in the ten-thousands place is 5. Then, he moved the digit 5 to the units place, the order of the other digits remained unchanged, and he got a number that is four times smaller than the thought number. What number did Marco think of? | 512820 |
100,796 | Figure $A B C D E F$ has $A B=8, B C=15$, and $E F=5$, as shown. Determine the perimeter of $A B C D E F$.
 | 56 |
24,182 | Given the quadrilateral \(ABCD\), it is known that \(\angle BAC = \angle CAD = 60^\circ\) and \(AB + AD = AC\). It is also known that \(\angle ACD = 23^\circ\). What is the measure, in degrees, of \(\angle ABC\)? | 83 |
56,411 | 7th Junior Balkan 2003 Problem 2 A 1 , A 2 , ... , A n are points in the plane, so that if we take the points in any order B 1 , B 2 , ... , B n , then the broken line B 1 B 2 ...B n does not intersect itself. What is the largest possible value of n? | 4 |
66,197 | 18. Three-digit number $\overline{a b c}(a, b, c$ are distinct), $a$ is the least common multiple of $a, b, c$, $b$ is the greatest common divisor of $a, b, c$, $c$ equals the number of divisors of $a$, such three-digit numbers have $\qquad$ in total. | 3 |
66,388 | ## Task 3 - 260733
Let $ABC$ be an acute-angled triangle; its circumcircle $k$ has the center $M$. The ray from $A$ through $M$ intersects $k$ at $D$, the ray from $B$ through $M$ intersects $k$ at $E$, the ray from $C$ through $M$ intersects $k$ at $F$.
Determine the ratio of the areas of the hexagon $A F B D C E$ and the triangle $A B C$! | 2:1 |
31,330 | 8. Given that $n$ is a positive integer. Find the smallest positive integer $k$ such that in a $2 n \times 2 n$ grid, marking $k$ cells ensures there is a unique way to tile the $2 n \times 2 n$ grid with $1 \times 2$ and $2 \times 1$ dominoes, and no domino contains two marked cells. | 2n |
51,775 | 10.5. Find all numbers $a$ such that for any natural $n$ the number $a n(n+2)(n+3)(n+4)$ is an integer.
(O. Podlipsky) | \frac{k}{6} |
13,402 | The vertices of the triangle \( ABC \) are lattice points and there is no smaller triangle similar to \( ABC \) with its vertices at lattice points. Show that the circumcenter of \( ABC \) is not a lattice point. | \text{The circumcenter of } ABC \text{ is not a lattice point.} |
6,560 | A square is inscribed in an equilateral triangle such that each vertex of the square touches the perimeter of the triangle. One side of the square intersects and forms a smaller equilateral triangle within which we inscribe another square in the same manner, and this process continues infinitely. What fraction of the equilateral triangle's area is covered by the infinite series of squares? | \dfrac{3 - \sqrt{3}}{2} |
22,606 | Task 1. What is greater: 1 or $\frac{21}{64}+\frac{51}{154}+\frac{71}{214} ?$ | 1 |
5,878 | Given numbers \(a, b, c\) satisfy \(a b c+a+c-b\). Then the maximum value of the algebraic expression \(\frac{1}{1+a^{2}}-\frac{1}{1+b^{2}}+\frac{1}{1+c^{2}}\) is | \dfrac{5}{4} |
54,061 | 8. (10 points) In a plane, there are 5 points, among which no 3 points are collinear. Connecting line segments with these points as endpoints, apart from these 5 points, these line segments have at least $\qquad$ intersection points. | 1 |
66,008 | On a circle of radius 1, a point $O$ is marked, and from it, a notch is made to the right with a radius of $l$. From the resulting point $O_{1}$, another notch is made in the same direction with the same radius, and this is repeated 1968 times. After this, the circle is cut at all 1968 notches, resulting in 1968 arcs. How many different lengths of arcs can be obtained in this way? | 3 |
62,524 | 6.1. A cube lies on a plane. Each face is marked with 1 to 6 points such that the sum of points on opposite faces is always 7. The cube is rolled over the plane as shown in the picture. How many points will be on the top face of the cube when it lands on the last cell?
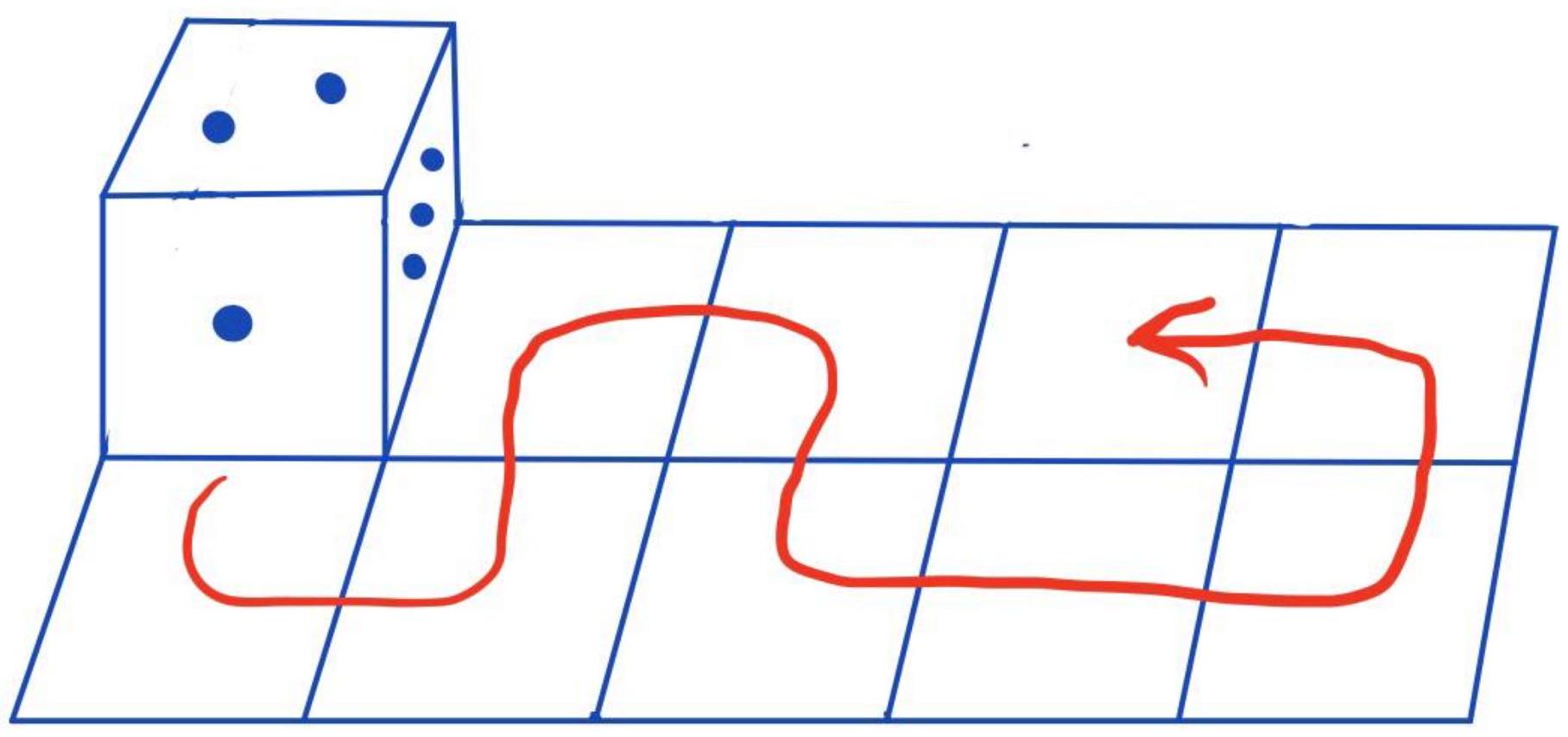 | 5 |
19,837 | Suppose a virus enters a culture consisting of $n$ bacteria and immediately infects one of the bacteria; after one minute, 2 viruses are released from the infected bacterium and, during this time, all other bacteria divide exactly once. (Each bacterium divides into two new bacteria.) Subsequently, every free virus immediately infects one of the bacteria (each bacterium is infected by only one virus), and within one minute $2$ viruses are produced in each infected bacterium, while the rest of the bacteria continue to divide.
Will the bacterial culture be eradicated, and if so, how much time will it take? | n |
5,945 | Given \(0 < a < 1\) and \(x^{2} + y = 0\), prove \(\log_{a}\left(a^{x} + a^{y}\right) \leq \log_{a} 2 + \frac{1}{8}\). | \log_{a}\left(a^{x} + a^{y}\right) \leq \log_{a} 2 + \frac{1}{8} |
248 | A teacher wanted to write an arithmetic problem on the board:
\[ 1.05 + 1.15 + 1.25 + 1.4 + 1.5 + 1.6 + 1.75 + 1.85 + 1.95 = ? \]
but accidentally forgot to write one decimal point. After that, Kolya went to the board, correctly performed all the calculations, and obtained an integer as the result. What is that integer? | 27 |
34,650 | 2. Find all triples of positive integers $(a, b, c)$ such that $a^{3}+b^{3}+c^{3}=(a b c)^{2}$. | (1,2,3) |
55,029 | 2. Given $A, B, C$ are any three points on a plane, and $BC=a, CA=b, AB=c, y=$ $\frac{c}{a+b}+\frac{b}{c}$, the minimum value of $y$ is . $\qquad$ | \sqrt{2}-\frac{1}{2} |
52,020 | 11. Let $A$ be an $n$-element subset of the set $\{1,2, \cdots, 2017\}$, and any two numbers in $A$ are neither coprime nor have a divisibility relationship. Find the maximum value of $n$. | 504 |
54,404 | 47. As shown in the figure, $A B / / C D / / E F / / G H, A E / / D G$, point $C$ is on $A E$, point $F$ is on $D G$. Let the number of angles equal to $\angle \alpha$ be $m$ (excluding $\angle \alpha$ itself), and the number of angles supplementary to $\angle \beta$ be $n$. If $\alpha \neq \beta$, then the value of $m+n$ is $\qquad$. | 11 |
15,213 | 4. Points $A, B, C, D$ lie on the circumference of a circle, and $B C=D C=4, A E=6$, the lengths of segments $B E$ and $D E$ are both integers, find the length of $B D$.
| 7 |
5,283 | 130 trees are planted in a circle: birches and lindens (both types are present). Each tree has a sign that reads: "Two different trees are growing nearby." It is known that the sign is false on all lindens and exactly on one birch. How many birches could have been planted? Specify all possible options. | 87 |
8,020 | Let points \( A_{1}, A_{2}, A_{3}, A_{4}, A_{5} \) be located on the unit sphere. Find the maximum value of \( \min \left\{A_{i} A_{j} \mid 1 \leq i < j \leq 5 \right\} \) and determine all cases where this maximum value is achieved. | \sqrt{2} |
24,995 | In the quadrilateral \(ABCD\), diagonals \(AC\) and \(BD\) intersect at point \(K\). Points \(L\) and \(M\) are the midpoints of sides \(BC\) and \(AD\), respectively. Segment \(LM\) contains point \(K\). The quadrilateral \(ABCD\) is such that a circle can be inscribed in it. Find the radius of this circle, given that \(AB = 3\), \(AC = \sqrt{13}\), and \(LK: KM = 1: 3\). | \dfrac{3}{2} |
26,087 | \left.\begin{array}{l}{[\quad \text { Law of Sines }} \\ {\left[\begin{array}{l}\text { Angle between a tangent and a chord }]\end{array}\right]}\end{array}\right]
In triangle $ABC$, angle $\angle B$ is equal to $\frac{\pi}{6}$. A circle with a radius of 2 cm is drawn through points $A$ and $B$, tangent to line $AC$ at point $A$. A circle with a radius of 3 cm is drawn through points $B$ and $C$, tangent to line $AC$ at point $C$. Find the length of side $AC$. | \sqrt{6} |
530 | Let $a,$ $b,$ $c,$ $d$ be real numbers such that
\begin{align*}
a + b + c + d &= 6, \\
a^2 + b^2 + c^2 + d^2 &= 12.
\end{align*}Let $m$ and $M$ denote minimum and maximum values of
\[4(a^3 + b^3 + c^3 + d^3) - (a^4 + b^4 + c^4 + d^4),\]respectively. Find $m + M.$ | 84 |
63,314 | Example 7.13 Find the number of first-class circular permutations made from 2 $a$s, 2 $b$s, 2 $c$s. | 16 |
66,954 | Example 1. Using the method of tangents, find the real root of the equation $x^{3}+x-3=0$. | 1.213412 |
64,038 | Example 4 Refer to Figure 1.13.3, in $\triangle A B C$, $A D, B E, C F$ intersect at $P, A P=P D=6$, $B P=9, P E=3, C F=20$, find $S_{\triangle A B C}$. | 108 |
13,912 | Given point \( A \) is a point inside a unit circle centered at \( O \), satisfying \( |\overrightarrow{OA}| = \frac{1}{2} \). Points \( B \) and \( C \) are any two points on the unit circle \( O \). Determine the range of values for \( \overrightarrow{AC} \cdot \overrightarrow{BC} \). | \left[ -\dfrac{1}{8}, 3 \right] |
13,368 | As shown in the figure, given that \(PA\) and \(PB\) are two tangents to circle \(\odot O\), and \(PCD\) is a secant line of \(\odot O\). Let \(E\) be the intersection of \(AB\) and \(PD\). Prove that:
$$
\frac{PC}{PD}=\frac{CE}{DE}.
$$ | \frac{PC}{PD} = \frac{CE}{DE} |
4,337 | A reconnaissance plane flies in a circle with center at point $A$. The radius of the circle is $10 \mathrm{kм}$, and the plane's speed is $1000 \mathrm{км/ч}$. At a certain moment, a missile is launched from point $A$, which has the same speed as the plane and is guided such that it always lies on the line connecting the plane with point A. How long after launch will the missile catch up with the plane? | \dfrac{\pi}{200} |
66,882 | 3. Given a cube and 12 colors. Find the number of ways to paint the faces of this cube using these colors (each face in one color) such that adjacent faces are of different colors. Colorings that differ by a rotation are considered different. | 987360 |
60,819 | 18.4.3 $\star \star$ A positive integer $n$ is not divisible by $2$ or $3$, and there do not exist non-negative integers $a$, $b$ such that $\left|2^{a}-3^{b}\right|=n$. Find the minimum value of $n$. | 35 |
32,332 | 3. A room is built in the shape of the region between two semicircles with the same center and parallel diameters. The farthest distance between two points with a clear line of sight is $12 \mathrm{~m}$. What is the area (in $\mathrm{m}^{2}$ ) of the room? | 18\pi |
51,286 | Determine all polynomials $P$ satisfying the following equation for all real $x$:
$$
\left(x^{2}-6 x+8\right) P(x)=\left(x^{2}+2 x\right) P(x-2)
$$ | P(x)=x^{2}(x^{2}-4) |
19,333 | In the sequence $\left\{x_{n}\right\}$, where $x_{0}=x_{1}=1$, $x_{2}=3$, and $x_{n} = 4 x_{n-1} - 2 x_{n-2} - 3 x_{n-3}$ for $n \geqslant 3$, prove that $x_{n} > \frac{3}{2}\left(1 + 3^{n-2}\right)$. | x_n > \frac{3}{2}\left(1 + 3^{n-2}\right) |
55,716 | The sum of three positive numbers is 1, and none of the numbers is greater than twice any other. What is the minimum of the product of the three numbers? | \frac{1}{32} |
59,710 | Tokorevev. S.
Among 2000 indistinguishable balls, half are aluminum with a mass of 10 g, and the rest are duralumin with a mass of 9.9 g. It is required to separate the balls into two piles such that the masses of the piles are different, but the number of balls in them is the same. What is the smallest number of weighings on a balance scale without weights that can achieve this? | 1 |
61,258 | . Let $ABC$ be a right triangle at $C$. We denote by $M$ the midpoint of $[AB]$ and by $H$ the foot of the altitude from $C$. Given that $CH=1$ and $CM=2$, determine the angle $\widehat{CAB}$. | 15 |
53,548 | 2. There is a cube fixed on legs, and six different paints. In how many ways can all the faces of the cube be painted (each in one color, not all paints have to be used) so that adjacent faces (having a common edge) are of different colors? (16 points) | 4080 |
9,136 | In a circle, two perpendicular chords $KM$ and $LN$ are drawn. It is known that lines $KL$ and $MN$ are parallel, and two sides of the quadrilateral $KLMN$ are equal to 2. Find the radius of the circle. | \sqrt{2} |
60,264 | In the star $A B C D E$ of the given figure, it is known that $G \widehat{B} F=20^{\circ}$ and $G \widehat{H} I=$ $130^{\circ}$. What is the value of the angle $J \widehat{E} I$ ?
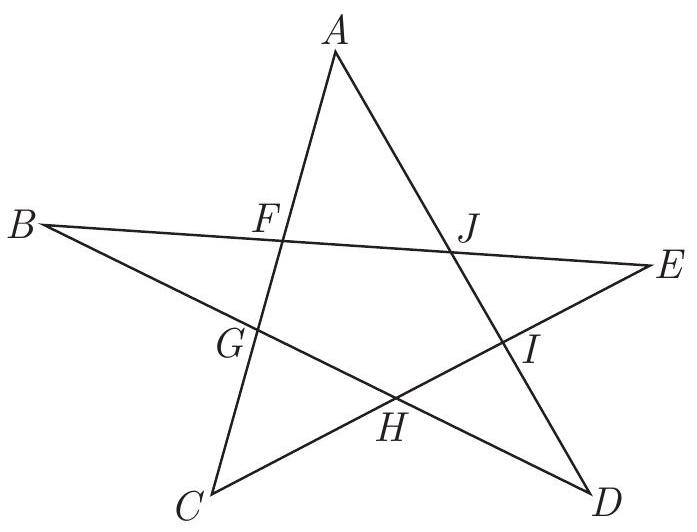 | 30 |
32,376 | 4. Find all pairs $(a, b)$ for which the set of solutions to the inequality $\log _{2014}(2 x+a)>x^{2}-2 x-b \quad$ coincides with the interval $(1 ; 2)$. | =-\frac{4024}{2013},b=\log_{2014}(\frac{2013}{4028}) |
16,382 | 2. For a rectangle, the sum of two sides is 11, and the sum of three sides is 19.5. Find the product of all possible different values of the perimeter of such a rectangle. | 15400 |
11,909 | 1. According to the problem, Sasha makes one step in 1 second, while Dan makes one step in $\frac{6}{7}$ seconds. Therefore, after 6 seconds, both Sasha and Dan will have made an integer number of steps, specifically, Sasha will have made 6 steps, and Dan will have made 7 steps. Consequently, we need to consider moments of time that are multiples of 6 seconds, i.e., $t=6k, k=1,2, \ldots$. Since Sasha's step length is 0.4 meters and Dan's step length is 0.6 meters, in $t=6k$ seconds, Sasha will have walked $6 \cdot k \cdot 0.4 = 2.4k$ meters, and Dan will have walked $7 \cdot k \cdot 0.6 = 4.2k$ meters. The distance between Sasha and Dan on the road at such moments of time is:
$$
d(k)=|200-2.4k|+|300-4.2k|.
$$
Consider the function $d(x), x \in \mathbb{R}$. For $x \leq x_{1}=\frac{300}{4.2}=71.42 \ldots$
$$
d(x)=200-2.4x+300-4.2x=500-6.6x
$$
For $x_{1} \leq x \leq x_{2}=\frac{200}{2.4}=83$,(3)
$$
d(x)=200-2.4x-300+4.2x=1.8x-100
$$
For $x \geq x_{2}$
$$
d(x)=-200+2.4x-300+4.2x=6.6x-500
$$
We have obtained that for $x \leq x_{1}$ the function $d(x)$ is decreasing, and for $x \geq x_{1}$ it is increasing. This means that at the point $x=x_{1}$ the function $d(x)$ attains its minimum value. To find the minimum of the function $d(k)$, consider the nearest integer values of $k$ to $x=x_{1}$: $k_{1}=\left[x_{1}\right]=71$ and $k_{2}=\left[x_{1}\right]+1=72$. Calculate $d(71)=500-6.6 \cdot 71=31.4$ and $d(72)=1.8 \cdot 72-100=29.6$. Therefore, the smallest possible distance between Sasha and Dan is 29.6 meters. Since this distance is achieved at $k=72$, the number of steps Sasha has taken by this time is $6 \cdot 72=432$, and the number of steps Dan has taken is $7 \cdot 72=504$. | 29.6 |
4,995 | Given a regular tetrahedral prism $P-ABCD$ where the base edge length is equal to the height, point $G$ is the centroid of the face $\triangle PBC$. Find the sine of the angle between the line $AG$ and the base $ABCD$. | \dfrac{\sqrt{38}}{19} |
25,946 | Example 4 (2003 China National Training Team) In $\triangle ABC$, $AC > AB$, $P$ is the intersection of the perpendicular bisector of $BC$ and the internal angle bisector of $\angle A$. Draw $PX \perp AB$, intersecting the extension of $AB$ at point $X$, and $PY \perp AC$ intersecting $AC$ at point $Y$, $Z$ is the intersection of $XY$ and $BC$. Find the value of $\frac{BZ}{ZC}$. | 1 |
18,312 | ## Task 2 - 330522
Rolf is looking for four-digit numbers in which no two digits are the same. The difference between the tens and the hundreds digit should be 3, and the difference between the hundreds and the thousands digit should be 4.
When calculating these differences, the order of the two digits involved should not matter.
How many four-digit numbers of the desired type are there in total?
Explain why there cannot be more than the number you have specified! | 112 |
23,631 | The center of the circle inscribed in a trapezoid is at distances of 5 and 12 from the ends of one of the non-parallel sides. Find the length of this side. | 13 |
28,139 | 5. Let $p$ be a prime number. How many colors are needed at minimum to place tokens on a square $p \times p$ board, each token being colored with one of these colors, so that each field of the board has exactly one token and there are no two tokens of the same color that attack each other? Two tokens attack each other if they are on the same row, column, or if the line connecting them is parallel to one of the diagonals of the square. | p |
16,501 | In the sequence \(\left\{a_{n}\right\}\),
\[
a_{0}=a \quad (a \in \mathbf{Z}_{+}), \quad a_{n+1}=\frac{a_{n}^{2}}{a_{n}+1}.
\]
Find the largest integer not exceeding \(a_{n}\) when \(0 \leqslant n \leqslant \frac{a}{2}+1\). | a - n |
59,760 | 3. (7 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $14$, and $\sin \alpha = \frac{\sqrt{33}}{7}$? | 16 |
54,430 | 2. Given numbers $x, y, z \in\left[0, \frac{\pi}{2}\right]$. Find the minimum value of the expression
$$
A=\cos (x-y)+\cos (y-z)+\cos (z-x)
$$ | 1 |
51,137 | 7. (10 points) A sequence of numbers $a_{1}, a_{2}, \cdots, a_{n} \cdots$, let $S(a_{i})$ be the sum of all digits of $a_{i}$, for example, $S(22)=2+2=4$. If $a_{1}=2017, a_{2}=22, a_{n}=S(a_{n-1})+S(a_{n-2})$, then $a_{2017}$ equals $\qquad$ | 10 |
10,628 | In a certain state, license plate numbers are composed of 6 digits (from the digits 0-9). The state mandates that any two license plate numbers must differ by at least two digits (for example, 027592 and 020592 cannot both be used). Determine the maximum number of distinct license plate numbers possible, and provide a proof. (19th US Mathematical Olympiad, 1990) | 100000 |
61,916 | 6. (10 points) As shown in the figure, the area of $\triangle A B C$ is 100 square centimeters, and the area of $\triangle A B D$ is 72 square centimeters. $M$ is the midpoint of side $C D$, $\angle M H B=90^{\circ}$, and it is known that $A B=20$ centimeters. Then the length of $M H$ is $\qquad$ centimeters. | 8.6 |
15,817 | In a country with 15 cities, some of which are connected by airlines belonging to three different companies, it is known that even if any one of the airlines ceases operations, it will still be possible to travel between any two cities (possibly with transfers) using the remaining two companies' flights. What is the minimum number of airline routes in the country? | 21 |
61,636 | 9. In a $4 \times 4$ table, place 4 chess pieces such that each row, each column, and each diagonal contains exactly 1 piece. How many ways are there to do this?
Place the above text in English, preserving the original text's line breaks and format, and output the translation result directly. | 8 |
31,953 | 8.8. (Austria - PDR, 79). For each value of $n \in \mathbf{N}$, find the greatest value of $k \in \mathbf{Z}^{+}$, for which the number $\left[(3+\sqrt{11})^{2 n-1}\right]$ is divisible by $2^{k}$. | n |
52,449 | 8. Given the sequence $\left\{a_{n}\right\}$ with the first term being 2, and satisfying
$$
6 S_{n}=3 a_{n+1}+4^{n}-1 \text {. }
$$
Then the maximum value of $S_{n}$ is $\qquad$ | 35 |
24,836 | There are four cards, each with a number on both sides. The first card has 0 and 1, the other three cards have 2 and 3, 4 and 5, and 7 and 8 respectively. If any three cards are selected and arranged in a row, how many different three-digit numbers can be formed? | 168 |
9,977 | ## Problem Statement
Calculate the volumes of the bodies bounded by the surfaces.
$$
\frac{x^{2}}{16}+\frac{y^{2}}{9}+\frac{z^{2}}{16}=1, z=2, z=0
$$ | 22\pi |
16,885 | The ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ (where $a > b > 0$) has foci $F_{1}$ and $F_{2}$ located on the left and right ends respectively, and a point $P$ on the ellipse which does not coincide with the major axis vertices. Points $I$ and $G$ are the incenter and centroid of $\triangle P F_{1} F_{2}$ respectively. Given that for any point $\boldsymbol{P}$, $\boldsymbol{I}$, and $\boldsymbol{G}$ are always perpendicular to the $\boldsymbol{x}$-axis, find the eccentricity of the ellipse. | \dfrac{1}{3} |
24,398 | For each integer $n\geq 2$ , let $S_n$ be the sum of all products $jk$ , where $j$ and $k$ are integers and $1\leq j<k\leq n$ . What is the sum of the 10 least values of $n$ such that $S_n$ is divisible by $3$ | 197 |
25,034 | Let $m$ be the number of solutions in positive integers to the equation $4x+3y+2z=2009$ , and let $n$ be the number of solutions in positive integers to the equation $4x+3y+2z=2000$ . Find the remainder when $m-n$ is divided by $1000$ | 0 |
33,100 | 11. (6 points) Natural numbers $1,2,3, \cdots$ are written down consecutively to form a number $123456789101112 \cdots$. When a certain number is reached, the formed number is exactly divisible by 72 for the first time. This number is $\qquad$ _. $\qquad$ | 36 |
27,053 | 7. Triangles $A B C$ and $A B D$ are inscribed in a semicircle with diameter $A B=5$. The perpendicular from $D$ to $A B$ intersects segment $A C$ at point $Q$, ray $B C$ at point $R$, and segment $A B$ at point $P$. It is known that $P R=27 / 10$, and $P Q=5 / 6$. Find the length of segment $D P$. If necessary, round the answer to the hundredths.
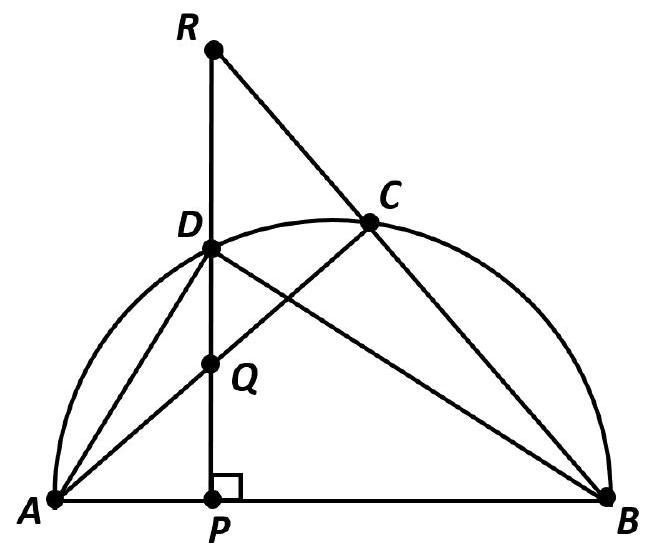 | 1.5 |
8,697 | $\left[\begin{array}{l}{\left[\begin{array}{l}\text { Tangent circles } \\ {\left[\text { Right triangle with an angle of } 30^{\circ}\right.}\end{array}\right]}\end{array}\right]$
In an equilateral triangle, a circle is inscribed. Three smaller circles are tangent to this circle and the sides of the triangle. Find the side of the triangle if the radius of the smaller circle is $r$. | 6\sqrt{3}r |
2,896 | Let \( S \) be a set of 2017 distinct points in the plane. Let \( R \) be the radius of the smallest circle containing all points in \( S \) on either the interior or boundary. Also, let \( D \) be the longest distance between two of the points in \( S \). Let \( a, b \) be real numbers such that \( a \leq \frac{D}{R} \leq b \) for all possible sets \( S \), where \( a \) is as large as possible and \( b \) is as small as possible. Find the pair \( (a, b) \). | (\sqrt{3}, 2) |
55,178 | 1. By deleting three consecutive numbers from the set of natural numbers from 1 to 2021, it has been observed that the arithmetic mean of the remaining numbers is a natural number. Determine the numbers that were deleted. | 1010,1011,1012 |
27,024 | 8. Find the smallest real number $m$, such that for any positive integers $a, b, c$ satisfying $a+b+c=1$, the inequality $m\left(a^{3}+b^{3}+c^{3}\right) \geqslant 6\left(a^{2}+b^{2}+c^{2}\right)+1$ holds.
(2006 China Southeast Mathematical Olympiad) | 27 |
63,072 | In which acute-angled triangle is the value of $\operatorname{tg} \alpha \cdot \operatorname{tg} \beta \cdot \operatorname{tg} \gamma$ the smallest? | \sqrt{27} |
61,058 | 6. Given that $A, B, C$ are any three points, $BC=a, CA=b, AB=c$, then the minimum value of $y=\frac{c}{a+b}+\frac{b}{c}$ is | \sqrt{2}-\frac{1}{2} |
5,861 | Let $\omega_{1}$ and $\omega_{2}$ be two circles such that $\omega_{1}$ is internally tangent to $\omega_{2}$ at point $A$. Let $P$ be a point on the circle $\omega_{2}$. The tangents to $\omega_{1}$ from point $P$ are tangent to $\omega_{1}$ at two points $X$ and $Y$ and intersect the circle $\omega_{2}$ at two points $Q$ and $R$. Show that $\widehat{Q A R}=2 \widehat{X A Y}$. | \widehat{Q A R} = 2 \widehat{X A Y} |
3,983 |
Given: $1-\frac{1}{6+\frac{1}{6+\frac{1}{6}}}=\frac{1}{\mathrm{~A}+\frac{1}{\mathrm{~B}+\frac{1}{1}}}$ where $A, B$, and $C$ are distinct natural numbers greater than 0, then $(A+B) \div C=$ | 1 |
53,433 | 23. The birth date of Albert Einstein is 14 March 1879. If we denote Monday by 1, Tuesday by 2, Wednesday by 3, Thursday by 4, Friday by 5, Saturday by 6 and Sunday by 7, which day of the week was Albert Einstein born? Give your answer as an integer from 1 to 7 . | 5 |
9,598 | There are two pieces of wood, one rectangular and one cylindrical, with the same height and a volume ratio of 1:1. If the rectangular wood is processed into the largest possible cylinder and the cylindrical wood is processed into the largest possible rectangular prism, what is the ratio of the volume of the cylinder to the volume of the rectangular prism? $\qquad$. | \dfrac{\pi^2}{8} |
55,182 | 4. Given $\arcsin x<\arccos x<\operatorname{arccot} x$, the range of real number $x$ is $\qquad$ | (0,\frac{\sqrt{2}}{2}) |
64,760 | A sequence of numbers $1, 4, 7, 10, \cdots, 697, 700$ follows the rule: the first number is 1, and each subsequent number is 3 more than the previous one, up to 700. If all these numbers are multiplied together, find the number of trailing zeros in the resulting product (for example, the number of trailing zeros in 12003000 is 3). | 60 |
60,011 | Knop K.A.
The re-attestation of the Council of Sages happens as follows: the king lines them up in a single column and puts a cap on each one, either white, blue, or red. All sages can see the colors of the caps of all the sages in front of them, but they cannot see the color of their own cap or those of the sages behind them. Once a minute, one of the sages must shout out one of the three colors (each sage shouts out a color only once).
After this process is completed, the king will execute each sage who shouted out a color different from the color of their cap.
On the eve of the re-attestation, all one hundred members of the Council of Sages agreed and came up with a plan to minimize the number of executions. How many of them are guaranteed to avoid execution? | 99 |
67,034 | What is the last non-zero digit of the product of the first hundred natural numbers?
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly. | 4 |
50,613 | 3. Problem: Find all real numbers $x$ and $y$ such that
$$
\begin{aligned}
x^{2}+y^{2} & =2, \\
\frac{x^{2}}{2-y}+\frac{y^{2}}{2-x} & =2 .
\end{aligned}
$$ | 1 |
17,074 | Let $S(n)$ be the sum of the digits of an integer $n$. For example, $S(327)=3+2+7=12$. Find the value of
$$
A=S(1)-S(2)+S(3)-S(4)+\ldots-S(2016)+S(2017)
$$ | 1009 |
64,182 | Example 2 For any natural number $k$, if $k$ is even, divide it by 2, if $k$ is odd, add 1 to it, this is called one operation. Let the number of numbers that become 1 after exactly $n$ operations be $a_{n}$, try to find $a_{15}$. | 610 |
12,564 | For all positive real numbers \(a, b, c\), show that
$$
\left(a^{2} b+b^{2} c+c^{2} a\right)\left(a b^{2}+b c^{2}+c a^{2}\right) \geqslant 9 a^{2} b^{2} c^{2}
$$ | \left(a^{2} b + b^{2} c + c^{2} a\right)\left(a b^{2} + b c^{2} + c a^{2}\right) \geqslant 9 a^{2} b^{2} c^{2} |
58,915 | In triangle $ABC$, the angle at vertex $B$ is $120^{\circ}$. The angle bisector of this angle intersects side $AC$ at point $P$. The external angle bisector from vertex $C$ intersects the line of side $AB$ at point $Q$, and segment $PQ$ intersects side $BC$ at point $R$. What is the measure of angle $PRA$? | 30 |
27,575 | 10.45 Let $S(n)$ denote the sum of the digits of the natural number $n$.
(1) Does there exist a natural number $n$ such that $n + S(n) = 1980$?
(2) Prove that among any two consecutive natural numbers, one can be expressed in the form $n + S(n)$, where $n$ is some natural number.
(14th All-Soviet Union Mathematical Olympiad, 1980) | 1962 |
33,113 | 13. Given the ellipse $C: \frac{x^{2}}{24}+\frac{y^{2}}{16}=1$, the line $l: \frac{x}{12}+\frac{y}{8}=1$, and a point $P$ on $l$, the ray $O P$ intersects the ellipse at point $R$. Another point $Q$ lies on $O P$ such that $|O Q| \cdot|O P|=|O R|^{2}$. Find the equation of the trajectory of point $Q$ as point $P$ moves along $l$; and identify what type of curve the trajectory is. | \frac{(x-1)^{2}}{\frac{5}{2}}+\frac{(y-1)^{2}}{\frac{5}{3}}=1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.