id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
97,714 | 4. Two students, A and B, are selecting courses from five subjects. They have exactly one course in common, and A selects more courses than B. The number of ways A and B can select courses to meet the above conditions is $\qquad$
翻译完成,保留了原文的换行和格式。 | 155 |
97,807 | 29. The sequence $7,17,177,1777,17777, \cdots \cdots$ The digit in the hundreds place of the sum of the first 10 numbers is | 6 |
97,819 | 9. $\tan 20^{\circ} \csc 60^{\circ}\left(\csc 10^{\circ}-1\right)=$ | 2 |
97,842 | 79. A company has 100 shareholders, and any 66 of them hold no less than $50 \%$ of the total shares. Find the maximum shareholding percentage of the shareholder who owns the most shares in the company. | 25 |
97,859 | 5. The inequality $\left|f^{\prime}(0)\right| \leq A$ holds for all quadratic functions $f(x)$ satisfying $|f(x)| \leq 1(0 \leq x \leq 1)$, then the minimum value of the real number $\boldsymbol{A}$ is $\qquad$ | 8 |
97,885 | 4・174 Find the integer solutions of the following equation
$$
\left[\frac{x}{1!}\right]+\left[\frac{x}{2!}\right]+\cdots+\left[\frac{x}{10!}\right]=1001
$$ | 584 |
97,913 | 8. (3 points) Five judges score a gymnast. If the highest score is removed, the average score is 9.46. If the lowest score is removed, the average score is 9.66. How many more points is the highest score than the lowest score?
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 0.8 |
97,937 | 25. Real numbers $x, y, z$ satisfy $x \geqslant y \geqslant z \geqslant 0$, and $6 x+5 y+4 z=120$, then the sum of the maximum and minimum values of $x+y+z$ is $\qquad$. | 44 |
97,943 | 19. Using the digits $0, 1, 2$ and a decimal point, you can form $\qquad$ different decimals. All three digits must be used, and 0 cannot be placed at the end. | 6 |
97,995 | 23. The Youth Palace has three interest groups: A, B, and C. Among them, 68 people are not in group A, 52 people are not in group B, and groups A and B together have 60 people. How many people are in group B? $\qquad$ people. | 38 |
97,998 | 10. Given that $m, n$ are constants, and the parabola $C: y=\left(t^{2}+t+\right.$ 1) $x^{2}-2(m+t)^{2} x+\left(t^{2}+3 m t+n\right)$, passes through the point $P(1,0)$ for any $t \in \mathbf{R}$.
( I ) Find the values of $m, n$;
(II) For what value of $t$ is the length of the chord intercepted by the parabola $C$ on the $x$-axis maximized? What is the maximum value? | 2 |
98,026 | 41. Given that the two-digit number $\overline{a b}$ and $\overline{b a}$ differ by 45, find the number of $\overline{a b}$ that satisfy the condition. | 8 |
98,074 | 9. As shown in the figure, quadrilaterals $A C D E$ and $C B F G$ are both squares, $A B=10$, point $P$ is the midpoint of $E F$, then the area of $\triangle P A B$ is | 25 |
98,104 | 3. (5 points) 190 is expressed as the sum of 10 consecutive even numbers, the largest of which is
Express the above text in English, keeping the original text's line breaks and format, and output the translation result directly. | 28 |
98,113 | 46. At 8:00 AM, Xiao Zhang departs from location A to location B at a speed of 60 kilometers per hour. At 9:00 AM, Xiao Wang departs from location B to location A. After reaching location B, Xiao Zhang immediately returns along the same route and both arrive at location A exactly at 12:00 PM. How far from location A did the two meet? $\qquad$ kilometers. | 96 |
98,142 | 2. Traditional Tetris blocks are made up of 4 squares joined together, forming 7 different shapes (shapes that can overlap after rotation in the same plane are considered the same). Using 5 squares to form new Tetris blocks, the maximum number of different shapes that can be formed is $\qquad$.
保留源文本的换行和格式,直接输出翻译结果。 | 18 |
98,149 | Example 7 In a certain region, the electricity price last year was 0.80 yuan/(kW・h), and the annual electricity consumption was $a$ kW・h. This year, the plan is to reduce the electricity price to between 0.55 yuan/(kW - h) and 0.75 yuan/(kW - h), while the user's expected electricity price is 0.40 yuan/(kW・h).
After calculation, the additional electricity consumption after the price reduction is inversely proportional to the difference between the actual electricity price and the user's expected electricity price (the proportionality constant is $k$), and the cost of electricity in the region is 0.30 yuan/(kW・h).
(1) Write the function relationship between the power department's revenue $y$ and the actual electricity price $x$ after the electricity price is reduced this year;
(2) Let $k=0.2 a$, what is the minimum electricity price that can still ensure that the power department's revenue increases by at least 20% compared to last year. | 0.60 |
98,155 | 11. (15 points) Four people, A, B, C, and D, share 2013 candies. A gets 10 more than twice what B gets, 18 more than three times what C gets, and 55 less than five times what D gets. How many candies does A get?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。 | 990 |
98,214 | 34. Taiyi Zhenren and Shen Gongbao competed for the position of Golden Immortal, making their disciples Nezha and Ao Bing take the same exam. After one incense stick, both of them finished all the questions. Nezha got $\frac{1}{3}$ of the questions wrong, and Ao Bing got 6 questions wrong. Taiyi Zhenren said: “The questions you both got wrong account for $\frac{1}{5}$ of all the questions.”
Shen Gongbao said: “Fortunately, the questions you both got right exceeded half of all the questions.”
Smart students, calculate how many questions Nezha and Ao Bing both got right. $\qquad$ questions. | 20 |
98,263 | 10. Read the following text, then answer the questions that follow.
Pythagorean Theorem: In a right-angled triangle, the sum of the squares of the two legs $a, b$ equals the square of the hypotenuse $c$, i.e., $a^{2}+b^{2}=c^{2}$.
Converse of the Pythagorean Theorem: If the three sides of a triangle $a, b, c$ satisfy $a^{2}+b^{2}=c^{2}$, then the triangle is a right-angled triangle.
Using the theorems above, determine how many right-angled triangles are among the following four triangles.
(1) The lengths of the three sides of the triangle are $3,4,5$.
(2) The lengths of the three sides of the triangle are $3 \frac{11}{13}, 9 \frac{3}{13}, 10$.
(3) The heights on the three sides of the triangle are $156,65,60$.
(4) The heights on the three sides of the triangle are $5,12,13$. | 3 |
98,271 | 3. Find the smallest prime $p$ such that $(p, N)=1$, where $N$ is the number of all $\left(a_{0}, a_{1}, \cdots, a_{2012}\right)$ satisfying the following conditions:
(1) $\left(a_{0}, a_{1}, \cdots, a_{2012}\right)$ is a permutation of $0,1, \cdots, 2012$;
(2) For any positive divisor $m$ of 2013 and all $n(0 \leqslant n<n+m \leqslant 2012)$, $m \mid\left(a_{n+m}-a_{n}\right)$. | 67 |
98,293 | 7. (10 points) There are 10 cards each of the numbers “3”, “4”, and “5”. From these, any 8 cards are selected so that their sum is 27. Then, the maximum number of cards that can be “3” is $\qquad$.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。 | 6 |
98,300 | 28. As shown in the figure, $\angle D A C=2 x, \angle A C B=4 x, \angle A B C=3 x, A D=B C, \angle B A D=$ | 18 |
98,322 | 71. As shown in the figure, several paths are laid out in a square plaza with a side length of 24 meters. The width of the paths is 4 meters, and the green part is planted with grass. What is the planting area of the grass in square meters?
Translating the text into English while preserving the original text's line breaks and format, the result is as follows:
71. As shown in the figure, several paths are laid out in a square plaza with a side length of 24 meters. The width of the paths is 4 meters, and the green part is planted with grass. What is the planting area of the grass in square meters? | 400 |
98,338 | 27. Given that $a, b, c, d, e$ are five distinct integers, and $a+b+c+d+e=9$, let the integer solution of the equation $(x-a)(x-b)(x-c)(x-d)(x-e)=2009$ be $P$, then $P=$ $\qquad$ | 10 |
98,348 | Example 3 Given real numbers $x_{1}, x_{2}, \cdots, x_{10}$ satisfy $\sum_{i=1}^{10}\left|x_{i}-1\right| \leqslant 4, \sum_{i=1}^{10}\left|x_{i}-2\right| \leqslant 6$. Find the average value $\bar{x}$ of $x_{1}, x_{2}, \cdots, x_{10}$. (2012, Zhejiang Province High School Mathematics Competition) | 1.4 |
98,376 | 98. The sum of all simplest proper fractions with 105 as the denominator is
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 24 |
98,454 | 3. In a planar convex quadrilateral $ABCD$, $M$ and $N$ are the midpoints of sides $AD$ and $BC$, respectively. If $|\overrightarrow{AB}|=2, |\overrightarrow{MN}|=\frac{3}{2}$, $\overrightarrow{MN} \cdot (\overrightarrow{AD}-\overrightarrow{BC})=\frac{3}{2}$, then $\overrightarrow{AB} \cdot \overrightarrow{CD}=$ . $\qquad$ | -2 |
98,496 | [Example 3.5.6] Given that $p$ is a prime number, $r$ is the remainder when $p$ is divided by 210. If $r$ is a composite number and can be expressed as the sum of two perfect squares, find $r$.
保留源文本的换行和格式,直接输出翻译结果。 | 169 |
98,500 | 67. As shown in the figure, in trapezoid $A B C D$, $A D / / B C, \angle A=90^{\circ}$, point $E$ is on $A B$, if $A E=42, B E=28$, $B C=70, \angle D C E=45^{\circ}$, then the length of $D E$ is $\qquad$ | 58 |
98,503 | 2. The solution set of the equation $\log _{5}\left(3^{x}+4^{x}\right)=\log _{4}\left(5^{x}-3^{x}\right)$ is | 2 |
98,575 | 36th Putnam 1975 Problem B1 Let G be the group { (m, n) : m, n are integers } with the operation (a, b) + (c, d) = (a + c, b + d). Let H be the smallest subgroup containing (3, 8), (4, -1) and (5, 4). Let H ab be the smallest subgroup containing (0, a) and (1, b). Find a > 0 such that H ab = H. Solution | 7 |
98,627 | 12th Irish 1999 Problem A5 The sequence u 0 , u 1 , u 2 , ... is defined as follows. u 0 = 0, u 1 = 1, and u n+1 is the smallest integer > u n such that there is no arithmetic progression u i , u j , u n+1 with i < j < n+1. Find u 100 . | 981 |
98,647 | 3. [5] Dragoons take up $1 \times 1$ squares in the plane with sides parallel to the coordinate axes such that the interiors of the squares do not intersect. A dragoon can fire at another dragoon if the difference in the $x$-coordinates of their centers and the difference in the $y$-coordinates of their centers are both at most 6 , regardless of any dragoons in between. For example, a dragoon centered at $(4,5)$ can fire at a dragoon centered at the origin, but a dragoon centered at $(7,0)$ can not. A dragoon cannot fire at itself. What is the maximum number of dragoons that can fire at a single dragoon simultaneously? | 168 |
98,722 | 1. [5] A regular 2022-gon has perimeter 6.28. To the nearest positive integer, compute the area of the 2022-gon. | 3 |
98,849 | I1.1 Let $P$ be the unit digit of $3^{2003} \times 5^{2002} \times 7^{2001}$. Find the value of $P$.
I1.2 If the equation $\left(x^{2}-x-1\right)^{x+P-1}=1$ has $Q$ integral solutions, find the value of $Q$.
I1.3 Let $x, y$ be real numbers and $x y=1$.
If the minimum value of $\frac{1}{x^{4}}+\frac{1}{Q y^{4}}$ is $R$, find the value of $R$.
11.4 Let $x_{R}, x_{R+1}, \ldots, x_{K}(K>R)$ be $K-R+1$ distinct positive integers and $x_{R}+x_{R+1}+\ldots+x_{K}=2003$ If $S$ is the maximum possible value of $K$, find the value of $S$. (Reference: 2004 HI4) | 62 |
98,867 | G4.4 Let $[x]$ be the largest integer not greater than $x$, for example, $[2.5]=2$.
If $a=1+\frac{1}{2^{2}}+\frac{1}{3^{2}}+\cdots+\frac{1}{2004^{2}}$ and $S=[a]$, find the value of $a$. | 1 |
98,869 | G1.4 Let $a$ be an integer. If the inequality $|x+1|<a-1.5$ has no integral solution, find the greatest value of $a$. | 1 |
98,953 | If a sequence $\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ of positive integers (where $n$ is a positive integer) has the property that the last digit of $a_{k}$ is the same as the first digit of $a_{k+1}$ (here $k=1,2, \ldots, n$ and we define $\left.a_{n+1}=a_{1}\right)$, then the sequence is said to be a 'dragon sequence'. For example, $\{414\},\{208,82\}$ and $\{1,17,73,321\}$ are all 'dragon sequences'. At least how many two-digit numbers must be chosen at random to ensure that a 'dragon sequence' can be formed among some of the chosen numbers?
(2 marks)
If a sequence $\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ (where $n$ is a positive integer) of positive integers has the property that the last digit of $a_{k}$ is the same as the first digit of $a_{k+1}$ (here $k=1,2, \ldots, n$, and we define $a_{n+1}=a_{1}$), then the sequence is called a 'dragon sequence'. For example, \{414\}, \{208,82\}, and $\{1,17,73,321\}$ are all 'dragon sequences'. At least how many two-digit numbers must be chosen at random to ensure that a 'dragon sequence' can be formed among some of the chosen numbers?
(2 marks) | 46 |
98,954 | 19. For $0 \leq x \leq 1$ and positive integer $n$, let $f_{0}(x)=|1-2 x|$ and $f_{n}(x)=f_{0}\left(f_{n-1}(x)\right)$. How many solutions are there to the equation $f_{10}(x)=x$ in the range $0 \leq x \leq 1$ ?
對於 $0 \leq x \leq 1$ 和正整數 $n$, 設 $f_{0}(x)=|1-2 x|$ 和 $f_{n}(x)=f_{0}\left(f_{n-1}(x)\right)$ 。那麼方程 $f_{10}(x)=x$ 在 $0 \leq x \leq 1$ 區間內有多少個解? | 2048 |
99,060 | 8. Find the largest three-digit integer for which the product of its digits is 3 times the sum of its digits. | 951 |
99,115 | 22. (CZS 3) ${ }^{\mathrm{IMO2}}$ Find all positive integers $x$ for which $p(x)=x^{2}-10 x-22$, where $p(x)$ denotes the product of the digits of $x$. | 12 |
99,142 | 23. Consider the 800 -digit integer
$$
234523452345 \cdots 2345 .
$$
The first $m$ digits and the last $n$ digits of the above integer are crossed out so that the sum of the remaining digits is 2345 . Find the value of $m+n$. | 130 |
99,209 | 33. Find the largest positive integer $n$ such that $\sqrt{n-100}+\sqrt{n+100}$ is a rational number. | 2501 |
99,246 | B4. a) How many different pizzas can you make if you have four different toppings and each pizza must have at least two toppings?
b) An ice cream shop offers 9 different ice cream flavors. A group of children came to the ice cream shop and each of them bought two scoops. No child chose scoops of the same flavor, and all possible flavor combinations were chosen. How many children bought ice cream?
c) During the Christmas season, Jana ate 100 cookies in five days. Each day she ate 6 more cookies than the previous day. How many cookies did she eat on the first day?
## Solutions to Problems and Scoring
A contestant who arrives at the solution by any correct method (even if not anticipated by the scoring) receives all possible points.
A correct method is one that
- sensibly takes into account the wording of the problem,
- leads to the solution of the problem,
- is mathematically correct and complete.
A contestant who has only partially solved the problem, from otherwise correct steps in solving but does not show the path to the final solution of the problem, cannot receive more than half of the possible points.
## PART I
The correct answers are recorded in the table. A correct answer by the contestant is scored with 2 points, an incorrect answer with -1 point, and a blank field in the table with 0 points.
| Problem | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Answer | $\mathrm{D}$ | $\mathrm{B}$ | $\mathrm{C}$ | $\mathrm{D}$ | $\mathrm{D}$ | $\mathrm{B}$ | $\mathrm{D}$ | $\mathrm{C}$ | $\mathrm{B}$ | $\mathrm{E}$ | | 11 |
99,271 | 4. Calculate
$$
\lfloor\underbrace{\sqrt{2017+\sqrt{2017+\cdots+\sqrt{2017+\sqrt{2017}}}}}_{2017 \text{ square roots }}\rfloor
$$
(With $\lfloor x\rfloor$ we denote the greatest integer not greater than $x$.) | 45 |
99,274 | 2. Five students are competing in a 10 km race. It is known that after 5 km, the first was Ace, the second Bojan, the third Vuk, the fourth Goran, and the fifth Dejan, while at the end, the first was Vuk, the second Dejan, the third Ace, the fourth Goran, and the fifth Bojan. How many different rankings were there at least during this race? (Rankings where some students are tied are not considered, and it is assumed that two overtakes do not occur at the same time.) | 7 |
99,279 | 4. Dana je pravokotna mreža velikosti $7 \times 9$ (glej sliko). V spodnjem levem vozlišču mreže je kolonija mravelj, v zgornjem desnem vozlišču pa je njihovo mravljišče. V vseh ostalih vozliččih mreže je po eno zrno riža. Vsaka mravlja iz kolonije se na poti do mravljišča sprehaja po povezavah mreže, vendar le v smereh desno ali navzgor. Na svoji poti pobere vsa zrna riža, na katera naleti, in ko pride do mravljišča, tam tudi ostane. Najmanj koliko mravelj bi moralo biti v koloniji, da bi lahko pobrale vsa zrna riža?

9
## 59th Mathematical Competition for High School Students in Slovenia
Kranj, April 18, 2015
## Problems for 2nd Year
Solve the problems independently. You have 210 minutes to solve them.

The use of notes, literature, or a pocket calculator is not allowed. | 8 |
99,285 | 5. The master and his assistant received 197200 SIT for the completed work. The master's daily wage is $56.5\%$ higher than the assistant's daily wage. How much did each earn if the master worked for 20 days and the assistant for 18 days? Write down your answer.
Solve each problem independently on the attached paper, and each problem on its own page.
Do not sign the sheets, write only your code.
Write your answers with a pen clearly and neatly. Each problem's solution will be graded from 0 to 6 points.
## You have $120 \mathrm{~min}$ for solving.
THE NATIONAL COMPETITION COMMITTEE WISHES YOU GREAT SUCCESS.
6th national mathematics competition for students of secondary technical and vocational schools Kranj, April 22, 2006
## PROBLEMS FOR 2nd GRADE | 72000 |
99,291 | 4. Find the smallest number $n>4$ for which there exists a set of $n$ people such that any two who know each other have no common acquaintances, and any two who do not know each other have exactly two common acquaintances. (Acquaintance is a symmetric relation: if $A$ knows $B, A \neq B$, then $B$ also knows $A$.)
(Bulgarian) | 16 |
99,314 | 43. In a right triangle $ABC$, the bisector $CL$ is drawn. It is known that point $L$ is equidistant from the vertex of the right angle $B$ and the midpoint of the hypotenuse $AC$. Find the angle $BAC$. | 30 |
99,331 | 20. Let $A$ be the sum of all non-negative integers $n$ satisfying
$$
\left\lfloor\frac{n}{27}\right\rfloor=\left\lfloor\frac{n}{28}\right\rfloor .
$$
Determine $A$. | 95004 |
99,359 | B3. The diagram shows the distribution of bronze, silver, and gold medals at a competition.
(a) What is the value of $x$? (see image)
(b) Write the ratio of gold, silver, and bronze medals in the smallest possible natural numbers.

(c) At the competition, 84 medals were awarded. How many bronze, how many silver, and how many gold medals were awarded?
(d) How many grams does a bronze medal weigh if it has the shape of a cylinder with a diameter of $7 \mathrm{~cm}$ and a height of 3 $\mathrm{mm}$? The density of bronze is $8700 \frac{\mathrm{kg}}{\mathrm{m}^{3}}$.
## 21st Mathematics Knowledge Competition for Vocational School Students National Competition, May 15, 2021
## Problems for 3rd Year
Time for solving: 90 minutes. In section A, we will award two points for a correct answer, while we will deduct half a point for an incorrect answer. Enter the answers for section A in the left table. In section B, we will award up to seven points for a correct answer.
 | 100 |
99,366 | 3. Determine all prime numbers $p$ for which $\frac{p^{2}-p-2}{2}$ is a cube of a natural number. | 127 |
99,385 | B3 A log in the shape of a cylinder is charred to the maximum possible brown with a square cross-section. What percentage is waste?
(7 points) | 36.3 |
99,389 | 1. Jaka thought of a trimest number $x$, which in $\mathrm{v}$ notation has different non-zero digits. Then he wrote down all other trimest numbers that he could write using the digits of the number $x$. Determine all possible numbers $x$, if the sum of the numbers on the list is 3434. | 784 |
99,449 | King Arthur has 50 knights sitting at the Round Table, and he wants to send 15 of them to investigate the Holy Grail. In how many ways can he do this if he does not want to select adjacent knights? | 4639918800 |
99,453 | The road from city $A$ to city $B$ has an uphill, a flat, and a downhill section. A pedestrian walked from $A$ to $B$ in 2.3 hours and returned in 2.6 hours. On the uphill, they walked at 3 km/h, on the flat section at 4 km/h, and on the downhill at 6 km/h. What can we determine about the length of the $A B$ road section? What can we determine if the pedestrian only walked at 5 km/h on the downhill?
---
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 9.8 |
99,467 | What is the maximum number of acute angles that can be in an $n$-sided convex polygon? | 3 |
99,474 | A bus had a utilization ratio of $322.5 \mathrm{~kg} /$ passenger on its route, meaning that out of the empty bus's weight, this much was attributed to one passenger. On the return trip, 18 more passengers boarded the bus, improving the ratio to $187.5 \mathrm{~kg} /$ passenger. What will the ratio be if 7 more passengers board, and thus all available seats are filled? | 161.25 |
99,541 | In how many ways can a thousand be written as the sum of consecutive integers? | 8 |
99,565 | What weights can be measured on a balance with weights of $1,3,9,27$ grams? Generalize the problem!
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 40 |
99,566 | A regular triangle is rotated in a positive direction around its center, first by $3^{\circ}$, then by $9^{\circ}$, and then by $27^{\circ}$, and in the $k$-th step by $3^{k}$ degrees. How many different positions can the triangle take as a result of these rotations? | 4 |
99,591 | If we increase the sides of an isosceles right triangle by $4 \mathrm{~cm}$, then the area of the triangle increases by $112 \mathrm{~cm}^{2}$. What are the sides of the original triangle? | 26 |
99,625 | A capital of $4\%$ accrues interest for 2 years and 5 months. How long will it take for this capital to accrue the same amount of interest at $3 \frac{3}{4}\%$?
untranslated portion:
Valamely tőke $4 \%$ mellett 2 évig és 5 hónapig kamatozik. Mennyi idő alatt hajt e tôke $3 \frac{3}{4} \%$ mellett ugyanannyi kamatot?
translated portion:
A capital of $4\%$ accrues interest for 2 years and 5 months. How long will it take for this capital to accrue the same amount of interest at $3 \frac{3}{4}\%$? | 2 |
99,627 | How many zeros does the number end with, which is equal to the product of the first 10000 numbers?
Translate the above text back into Hungarian, please keep the original text's line breaks and format, output the translation result directly.
| 2499 |
99,635 | A hectoliter barrel is full of wine; from it, 1 liter of liquid flows out within 24 hours, which is replaced by 1 liter of water flowing in during the same time. After how much time will the content of the barrel be half wine and half water? | 69 |
99,705 | Someone wanted to gift 6 liters of wine from a 12-liter jug that is full of wine. However, they only have a 7-liter and a 5-liter jug for measuring. How can they fill the 7-liter jug with 6 liters of wine? | 6 |
99,732 | Someone in 1860 placed 100,000 frt at 5% interest for the purpose of building and maintaining an orphanage for 100 orphans at some point. When can the construction and opening of the orphanage take place if the construction and equipment costs are 100,000 frt, the staff of the orphanage costs 3,960 frt per year, and the maintenance of one orphan costs 200 frt? | 1896 |
99,823 | ## Subject 4.
Ana, Barbu, and Cristi together have an amount of money less than 100 lei, and each of them has more than 5 lei. Ana and Barbu together have three times more than Cristi, and Barbu and Cristi together have three times more than Ana. Find the largest and smallest amounts of money that the three children can have.
## Note: All subjects are mandatory
Time allowed: 2 hours
## MATHEMATICS OLYMPIAD LOCAL STAGE JANUARY 18, 2014
## GRADE 5 Scoring Guidelines | 24 |
99,841 | ## Subject I
Determine $x, y, z \geq 0$ such that:
$$
\left\{\begin{array}{c}
\sqrt{x}+\sqrt{y}+\sqrt{z}=3 \sqrt{2} \\
2^{x^{2}+y}+2^{y^{2}+z}+2^{z^{2}+x}=192
\end{array}\right.
$$ | 2 |
99,905 | 3. Let points $A, B, C$ be collinear in this order, and the rays $(B D$ and $(B E$ be in the same half-plane determined by the line $A C$ such that $(B D$ and $(B E$ are perpendicular. What values can the measure of the angle formed by the bisectors of angles $\varangle A B E$ and $\varangle D B C$ take? | 135 |
99,907 | 1. a) (3p) Factorize the number $4 n^{4}+1, n \in \mathbb{N}^{*}$.
b) (4p) Determine the integer part of the number $A=\frac{4}{5}+\frac{8}{65}+\frac{12}{325}+\ldots+\frac{4 n}{4 n^{4}+1}, n \in \mathbb{N}^{*}$.
Gazeta Matematică Nr. 10/2014 | 0 |
99,909 | 1. (7p) Determine the number $\overline{a b}$ for which $\frac{\overline{a,(b)}+\overline{b,(a)}}{a+b}=\frac{a+b}{3 a}$.
GM12/2015 | 37 |
99,923 | 2. A natural number is called " $p$ lucky" if it has $p$ digits and is divisible by $p$.
a) What is the smallest "13 lucky" number? (Justify your answer)
b) What is the largest "13 lucky" number? (Justify your answer) | 9999999999990 |
99,932 | ## Subject IV.
Determine the natural numbers of the form $\overline{a b c}$ that satisfy the relation $\overline{a b} \cdot\left(b^{2}+c^{2}\right)=2014$
Mathematical Gazette
## Note.
All problems are mandatory.
Each problem is worth 7 points.
Time allowed: 2 hours.
Proposers: Todoran Nicoleta, Seceleanu Daniela, Ginta Florica.
## MURES COUNTY SCHOOL INSPECTORATE
## S.S.M.R - MURES BRANCH Mathematics Olympiad Local phase 14.02.2014 5th Grade Grading Rubric | 195 |
99,937 | ## 181. Math Puzzle $6 / 80$
A gasoline car consumes 10.5 l of gasoline per $100 \mathrm{~km}$. It is known that the energy efficiency of a gasoline engine is 24 percent, while that of a diesel engine is 38 percent.
How much fuel would the car consume if it were powered by a diesel engine of the same performance and driving style? | 6.6 |
99,945 | ## Task 1 - 020521
During the autumn holidays, many high school students participated in the harvest. Each of the 1200 students in a city district collected an average of 8 dt of potatoes daily. The students worked for 4 days.
a) How many potatoes were collected in total by the students of this city district? (Specify in dt)
b) How many families can be supplied with potatoes from this stock if the annual requirement per family is $250 \mathrm{~kg}$? | 15360 |
99,981 | ## 188. Math Puzzle $1 / 81$
A service car (passenger car) was driven $1992 \mathrm{~km}$ in one month; of this, $379 \mathrm{~km}$ was city driving. The fuel consumption limit is eleven liters per $100 \mathrm{~km}$ for city driving and ten liters per $100 \mathrm{~km}$ for long-distance driving.
At the beginning of the month, there were still 20 l of fuel in the tank, and an additional 190.4 l were added. At the end of the month, there were still $30 \mathrm{l}$ in the tank.
How much fuel did the driver save compared to the limit through exemplary driving? | 22.59 |
99,984 | 4. a) On a circle, the natural numbers from 1 to 20 are written in order in a clockwise direction. By a step, we mean to swap the positions of any two of the 20 numbers written on the circle. What is the minimum number of steps required to rearrange these numbers successively in the counterclockwise direction?
b) What is the answer to the question in a) if 21 numbers are written on the circle in a clockwise direction from 1 to 21?
## MATHEMATICS OLYMPIAD SECTOR STAGE, 21.02.2016 5th GRADE SOLUTIONS AND ORIENTATIVE SCORING GUIDELINES
Note: Each problem is scored from 0 to 7 points. Only integer scores are given. Any other solution is assimilated according to the scoring guidelines. | 10 |
100,018 | ## Task 2 - 200612
From the financial records of a health resort, it was evident that a total of $21 \mathrm{~kg}$ of butter was consumed for 25 vacationers who were catered to for 14 days.
Calculate how many kg of butter must be provided in total for 30 people who are to be catered to for 6 days, assuming that each person consumes the same amount of butter per day as in the given example! | 10.8 |
100,027 | ## Subject (3).
a) Determine the set $M=\{(x, y) \in \mathbb{Z} \times \mathbb{Z} \mid 5 x+7 y=1\}$.
b) Determine the largest natural number $n$ that cannot be written in the form $n=5 x+7 y$, where $x, y \in \mathbb{N}$. Justify your answer.
Maria Pop, Cluj | 23 |
100,069 | 2. Let $n_{1}, n_{2} \in \mathbb{R}$ and $f\left(n_{1}\right)=f\left(n_{2}\right)$. Then
$6 n_{1}+5=(f \circ f)\left(n_{1}\right)=f\left(f\left(n_{1}\right)\right)=f\left(f\left(n_{2}\right)\right)=(f \circ f)\left(n_{2}\right)=6 n_{2}+5 \Rightarrow n_{1}=n_{2}$
In the given relation, we substitute $n$ with $f(n)$ and obtain
$(f \circ f)(f(n))=6 f(n)+5, f(6 n+5)=6 f(n)+5$
$n=15 \Rightarrow f(95)=11$
$n=95 \Rightarrow f(575)=71$
$n=575 \Rightarrow f(3455)=431$ | 431 |
100,071 | ## Task 16/66
In the newspaper "Neues Deutschland" on June 29, 1965, the following note was found:
When a small animal keeper in Christdorff in the district of Wittstock slaughtered a chicken a few days ago, it provided not only the Sunday roast but also a sum of cash as an addition. In the chicken's stomach, 17 coins were found, totaling 34 Pfennig ...
Assuming it was coins currently in circulation. Which coins were they and in what quantities? | 1 |
100,105 | ## Task 1 - 050811
A student had attached the following overview of participation in the 1st stage of the 4th Olympiad of Young Mathematicians of the GDR to the wall newspaper:
Class 8a: Out of 33 students, 20 participated, which is approximately 60.6 percent.
Class 8b: Out of 32 students, 21 participated, which is approximately 65.6 percent.
Class 8c: Out of 27 students, 19 participated, which is approximately 70.4 percent.
The students of these classes are tasked with determining the overall percentage of participation of the 8th grade students. Some students calculate the arithmetic mean of the percentages, while others calculate the quotient of the total number of participants and the total number of students in these classes, multiplied by 100.
a) How large is the difference that results from the two calculations?
b) Which students have calculated the percentage in the correct way? | 0.31 |
100,115 | ## Aufgabe 3 - 290713
Rolf sagt an seinem Geburtstag, dem 1. September 1989:
"Die Quersumme der Jahreszahl meines Geburtsjahres ist zugleich auch das in Jahren gerechnete Alter, das ich heute erreiche."
Untersuche, ob es genau ein Jahr als Rolfs Geburtsjahr gibt, für das seine Aussage zutrifft! Ist das der Fall, so gib dieses Geburtsjahr an!
| 1971 |
100,143 | ## Task 5 - 030725
In a box, there are 70 balls, namely 20 red, 20 green, 20 yellow, and the rest are black or white. Brigitte is supposed to take out as many balls from this box in the dark so that among them, there are certainly at least 10 balls of the same color.
How many balls does she have to take out at least? Justify your answer! | 38 |
100,153 | ## Task 1 - V00901
The sum of two numbers is 20, and the sum of their squares is 202. Solve the problem mathematically. | 911 |
100,155 | ## Task 2 - 340632
The letters of a word can be rearranged into a different order. Each such sequence of letters is also called a "word," even if it does not make sense in the German language. What is important is that each letter appears exactly as many times as in the original word.
For example, the following words can be formed from the word TAL:
$$
A L T, \quad A T L, \quad L A T, \quad L T A, \quad T A L, \quad T L A
$$
They are listed here in alphabetical order (for example, ATL comes before LAT because the first letter A of ATL appears earlier in the alphabet than the first letter L of LTA; the second letter decides the order between LAT and LTA, etc.).
As you can see, the word TAL is in the 5th position in this list.
(a) List all the words that can be formed from the word LAND (the word LAND should also be included)!
(b) If the words in (a) are listed alphabetically, at which position does the word LAND appear?
(c) How many words can be formed from the word UMLAND? (Again, UMLAND should be included.)
(d) At which position does the word UMLAND appear when the words from (c) are listed alphabetically? | 686 |
100,169 | ## Task 1 - 290811
On a bottle of standard 40 percent acetic acid, the following instructions are given: "The contents of this bottle ( $200 \mathrm{ml}$ ), mixed with $800 \mathrm{ml}$ of water, yield a ten percent vinegar."
Is this correct? | 8 |
100,227 | ## Task 2 - 060812
From cow's milk, $21 \%$ of the mass can be obtained as cream. From cream, butter is produced, and the mass of butter is $23 \%$ of the cream mass.
Determine the smallest amount of cow's milk that is sufficient to produce exactly $1 \mathrm{~kg}$ of butter under the given conditions!
The milk quantity should be given in kg and expressed as a decimal, rounded to one decimal place to ensure that the amount is sufficient to produce $1 \mathrm{~kg}$ of butter. | 20.8 |
100,243 | \section*{Problem 13 - V01213}
In triangle \(A B C\), the angle \(\gamma\) is to be calculated, given that:
\[
\sin \gamma=\sqrt{2} \cdot \cos \frac{\alpha+\beta}{2}
\] | 90 |
100,275 | ## Task 3
Inge buys 2 notebooks for 8 Pfennig each. Her friend needs twice as many notebooks. They pay together and put a 1 DM coin on the counter.
a) How many notebooks do the girls buy and how much do they pay for them?
b) How much money does the saleswoman give them back? | 52 |
100,302 | ## Task 3 - 290823
Let $A B C D E F G H$ be a cube with an arbitrary edge length (see figure).
a) Determine the size of the angle $\angle D E B$!
b) Prove that the angles $\angle A H B$ and $\angle B E C$ have the same size!
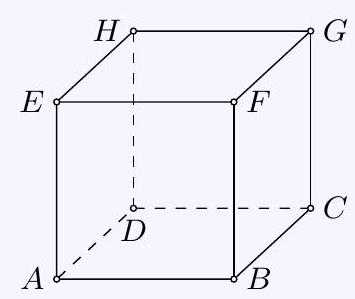 | 60 |
100,329 | ## Task 1
The members of a youth brigade helped to prepare apartments for elderly citizens. The value amounted to 1200 Marks. They helped with cable installation. This value amounted to 2100 Marks. In the operation, they saved materials. This value amounted to 1500 Marks.
How many Marks did the youth brigade bill for? | 4800 |
100,360 | ## Task 2
Sven is saving for a bicycle. It costs 330 marks. If he has saved six times as much money as he already has, he can buy the bike.
How much money has Sven already saved? | 55 |
100,392 | ## Task 4 - 270834
Let $\overparen{A B} M$ be a sector of a circle, where the length $r=\overline{M A}=\overline{M B}$ is given and the central angle $\angle A M B$ is $60^{\circ}$. A line $g$, which is parallel to $A B$ and intersects the segments $M A$ and $M B$ at points $C$ and $D$ respectively, is known to have the property that the perimeter $u_{1}$ of triangle $M C D$ is equal to the perimeter $u_{2}$ of the figure $\widehat{A B D C}$ (see figure).
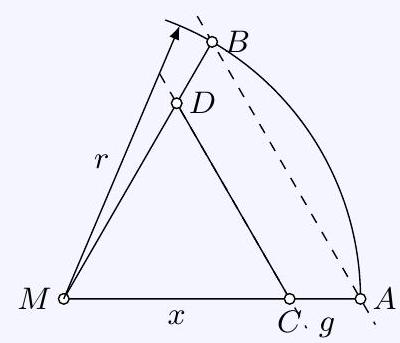
a) Determine the length $x=\overline{M C}$ in dependence on $r$ under this condition!
b) The length $r$ is measured with an accuracy that gives $r=6.7 \mathrm{~cm}$ to one decimal place. Furthermore, for the calculation, it is used that $\pi=3.14$ to two decimal places.
Prove that from this, the length $x$ (in centimeters) can be determined to one decimal place by calculating bounds! What is this length $x$? | 5.1 |
100,398 | \section*{Exercise 1 - 281021}
The smallest positive natural number is sought, whose digit representation (in the decimal system) consists only of the digits 0 and 1 and which is divisible by 450. | 11111111100 |
100,408 | ## Aufgabe 4 $8258-4123 \quad 4831-1210 \quad 7725+5+38+756$
| 8524 |
100,415 | ## Task 2
Katja has 6 coins in her pocket. Could it be a total of 27 pennies? Justify your answer! | 27 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.