id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
92,795 | ## Task Condition
Approximately calculate using the differential.
$y=\sqrt[3]{x}, x=8,24$ | 2.02 |
92,797 | 719. Find all numbers of the form $222 \ldots 2$ that can be represented as the sum of two perfect squares. | 2 |
92,833 | 9.1 $\quad A_{x}^{2} C_{x}^{x-1}=48$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
9.1 $\quad A_{x}^{2} C_{x}^{x-1}=48$. | 4 |
92,847 | 13.322. Bees, when processing flower nectar into honey, remove a significant portion of the water. Studies have shown that nectar usually contains about $70 \%$ water, while the honey obtained from it contains only $17 \%$ water. How many kilograms of nectar do bees need to process to obtain 1 kg of honey? | 2.77 |
92,865 | 2.254. $\left(\frac{x+2 y}{8 y^{3}\left(x^{2}+2 x y+2 y^{2}\right)}-\frac{(x-2 y): 8 y^{2}}{x^{2}-2 x y+2 y^{2}}\right)+\left(\frac{y^{-2}}{4 x^{2}-8 y^{2}}-\frac{1}{4 x^{2} y^{2}+8 y^{4}}\right)$ $x=\sqrt[4]{6}, \quad y=\sqrt[8]{2}$. | 3 |
92,878 | 9.9 How many three-digit numbers can be formed from the digits 1, 2, $3,4,5,6?$ | 216 |
92,886 | 2.282. $\left(\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{1-x}{\sqrt{1-x^{2}}-1+x}\right) \cdot\left(\sqrt{\frac{1}{x^{2}}-1}-\frac{1}{x}\right)=0<x<1$. | -1 |
92,927 | 10.007. An isosceles trapezoid with a side length of 17 cm is circumscribed around a circle with a diameter of 15 cm. Find the bases of the trapezoid. | 9 |
93,014 | 13.370. A schoolboy is re-sticking all his stamps into a new album. If he sticks 20 stamps on one page, the album will not be enough, but if he sticks 23 stamps on a page, at least one page will remain empty. If the schoolboy is given another such album, with 21 stamps on each page, he will have a total of 500 stamps. How many pages are in the album? | 12 |
93,032 | 10.013. Given a triangle with sides 12, 15, and \(18 \, \text{cm}\). A circle is drawn that touches both smaller sides and has its center on the larger side. Find the segments into which the center of the circle divides the larger side of the triangle. | 8 |
93,043 | Shapovalov A.V.
Petya liked the puzzle, he decided to glue it together and hang it on the wall. In one minute, he glued together two pieces (initial or previously glued). As a result, the entire puzzle was assembled into one complete picture in 2 hours. How long would it take to assemble the picture if Petya glued together three pieces per minute instead?
# | 60 |
93,088 | [Sum of angles in a triangle. Theorem of the exterior angle.] Counting in two ways
In a square, 20 points were marked and connected by non-intersecting segments to each other and to the vertices of the square, such that the square was divided into triangles. How many triangles were formed? | 42 |
93,150 | The figure shows a track scheme for karting. The start and finish are at point $A$, and the karting driver can make as many laps as they want, returning to the starting point.
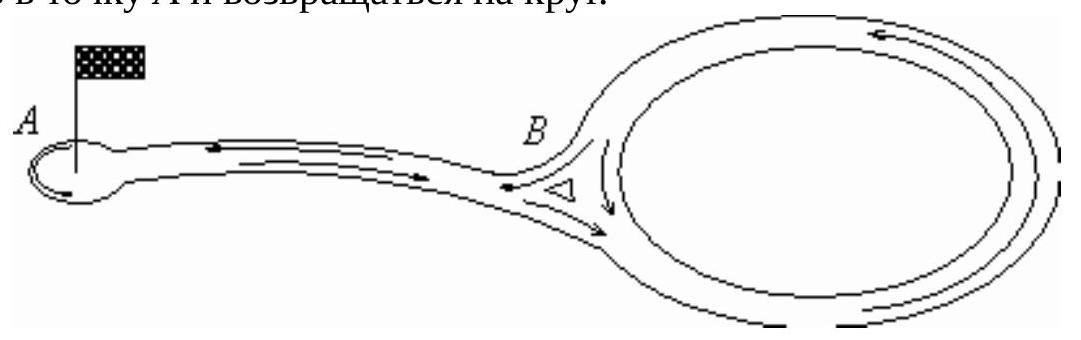
The young driver Yura spends one minute on the path from $A$ to $B$ or back. Yura also spends one minute on the loop. The loop can only be driven counterclockwise (arrows indicate possible directions of movement). Yura does not turn back halfway and does not stop. The race duration is 10 minutes. Find the number of possible different routes (sequences of passing sections). # | 34 |
93,258 | Let's call a natural number "remarkable" if it is the smallest among natural numbers with the same sum of digits as it has. What is the sum of the digits of the two thousand and first remarkable number?
# | 2001 |
93,282 | Shapovalov A.V.
What is the maximum number of white and black chips that can be placed on a chessboard so that in each row and each column there are exactly twice as many white chips as black ones? | 48 |
93,299 | 2In one move, you are allowed to either double the number or erase its last digit. Is it possible to get from the number 458 to the number 14 in several moves?
# | 14 |
93,422 | 10,11
A triangular pyramid $A B C D$ intersects with plane $P$ at a quadrilateral $E F G H$ such that vertices $E$ and $F$ lie on edges $A B$ and $A C$. It is known that plane $P$ is parallel to edges $A D$ and $B C$, the ratio of segment $E A$ to segment $E B$ is 2, and edges $A D$ and $B C$ are equal. Find the ratio $E F: E H$. | 2 |
93,484 | $[$ Extremal properties (other) $]$
What is the maximum number of cells on an $8 \times 8$ chessboard that can be cut by a single straight line? # | 15 |
93,489 | 10,11 Find the volume of a rectangular parallelepiped, the areas of the diagonal sections of which are equal to $\sqrt{13}, 2 \sqrt{10}$ and $3 \sqrt{5}$ | 6 |
93,512 | 86486 Topics [ Decimal Number System ]
Let's call a natural number "remarkable" if it is the smallest among natural numbers with the same digit sum as it has. What is the sum of the digits of the two thousand and first remarkable number?
# | 2001 |
93,554 | $[$ [Arithmetic. Mental calculation, etc.] $]$
Authors: Gaityerri G.A., Grierenko D.:
2002 is a palindrome year, which means it reads the same backward as forward. The previous palindrome year was 11 years earlier (1991). What is the maximum number of non-palindrome years that can occur consecutively (between 1000 and 9999 years)? | 109 |
93,625 | [ [Divisibility of numbers. General properties]
Authors: Binkov A.d,, Raskina I.v.
Several whole heads of cheese were stored in the warehouse. At night, rats came and ate 10 heads, and all of them ate equally. Several rats got sick from overeating. The remaining seven rats the next night finished off the remaining cheese, but each rat was able to eat only half as much cheese as the night before. How much cheese was originally in the warehouse?
# | 11 |
93,628 | [ Arithmetic operations. Numerical identities ]
30 with three identical digits. Write the number 30 in the form of four different expressions, each with three identical digits. The digits can be connected with operation signs.
# | 30 |
93,682 | 2 [ Inequalities problems. Case analysis ]
Sasha invited Petya to visit, saying that he lives in the 10th entrance in apartment No. 333, but forgot to mention the floor. Approaching the building, Petya noticed that the building is nine-story. Which floor should he go to? (The number of apartments on each floor is the same, apartment numbers in the building start from one.)
# | 3 |
93,685 | [ Periodicity and Aperiodicity $]$ [ Classical Combinatorics (other)]
In an old manor, the house is surrounded by tall trees - pines, spruces, and birches. There are a total of 96 trees. These trees have a strange property: of the two trees growing two apart from any conifer, one is coniferous and the other is deciduous, and of the two trees growing four apart from any conifer, one is coniferous and the other is deciduous. How many birches are planted around the house? | 32 |
93,691 | [ Residue arithmetic (other).]
How many zeros does the number $9^{999}+1$ end with?
# | 1 |
93,729 | Tokkymov M.A.
Find the smallest natural number that starts with 2016 (in decimal notation) and is divisible by 2017.
# | 20161932 |
93,757 | The sum of the three smallest distinct divisors of some number $A$ is 8. How many zeros can the number $A$ end with?
# | 1 |
93,762 | [ Text problems (miscellaneous) ] [Arithmetic. Mental calculation, etc.]
In response to a question about the age of his children, the mathematician answered:
- My wife and I have three children. When our first child was born, the total age of the family members was 45 years, a year ago, when the third child was born - 70 years, and the current total age of the children is 14 years.
How old is each child, given that all family members have their birthdays on the same day? # | 8 |
93,774 | $[\underline{\text { equations in integers }}]$
Solve the equation $\underbrace{\sqrt{n+\sqrt{n+\ldots \sqrt{n}}}}_{1964 \text { times }}=m$ in integers
# | 0 |
93,892 | a) Show a way to separate all the numbers from 1 to 16 into four sets with four numbers each, so that each set has the same sum.
b) Show that there are at least 1024 ways to write the numbers from 1 to 16 in each of the cells of a $4 \times 4$ board so that the sum of the numbers in each row is equal. | 1024 |
93,896 | On planet $X$, there are 100 alien countries in conflict with each other. To prevent a world war, these countries organize themselves into military alliance groups for mutual protection. We know that the alliances follow these rules:
1) No alliance contains more than 50 countries.
2) Any two countries belong to at least one alliance.
a) Is it possible for a country to participate in fewer than three military alliances?
b) What is the minimum number of alliances possible for these two conditions to be satisfied? | 6 |
93,938 | a) José learned a method for calculating the product of two numbers more quickly based on factorization:
$$
(n-k)(n+k)=n^{2}-k^{2}
$$
To calculate 23 $\cdot 17$, he chooses $n=20, k=3$ and calculates:
$$
23 \cdot 17=20^{2}-3^{2}=400-9=391
$$
Determine, without using a calculator, the value of $\sqrt{1001 \cdot 1003+1}$.
b) Verify that $(n(n+3)+1)^{2}=n(n+1)(n+2)(n+3)+1$.
c) Determine, without using a calculator, the value of:
$$
\sqrt{(2014)(2015)(2016)(2017)+1}
$$ | 4062239 |
94,017 | Analyzing the 4-digit natural numbers:
a) How many of them have all different digits?
b) How many have the digit 1 exactly once and all different digits?
c) How many have the digit 1? | 3168 |
94,082 | 4. For non-negative real numbers $a, b, c$ it holds that $a+b+c=1$. Find the greatest and the smallest possible value of the expression
$$
(a+b)^{2}+(b+c)^{2}+(c+a)^{2} .
$$ | 2 |
94,091 | 3. Determine the smallest natural number $n$, for which the following holds: If some natural number has at least $n$ three-digit multiples, then 840 is one of them.
(Michal Rolínek) | 101 |
94,102 | a) Consider the $4 \times 4$ board shown in the following figure. The letters and numbers have been placed to help locate the small squares. For example, the square $A 1$ is in the top-left corner and the $D 4$ is in the bottom-right corner.
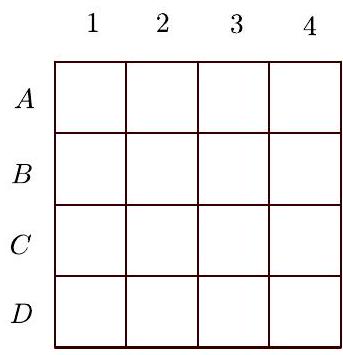
Show a way to choose 12 squares such that exactly 3 squares are chosen in each row and each column.
b) Determine the number of different ways to choose 12 squares on the $4 \times 4$ board such that exactly 3 squares are chosen in each row and each column.
c) Consider an $8 \times 8$ board with a similar identification of rows and columns as the previous board, but colored alternately black and white.
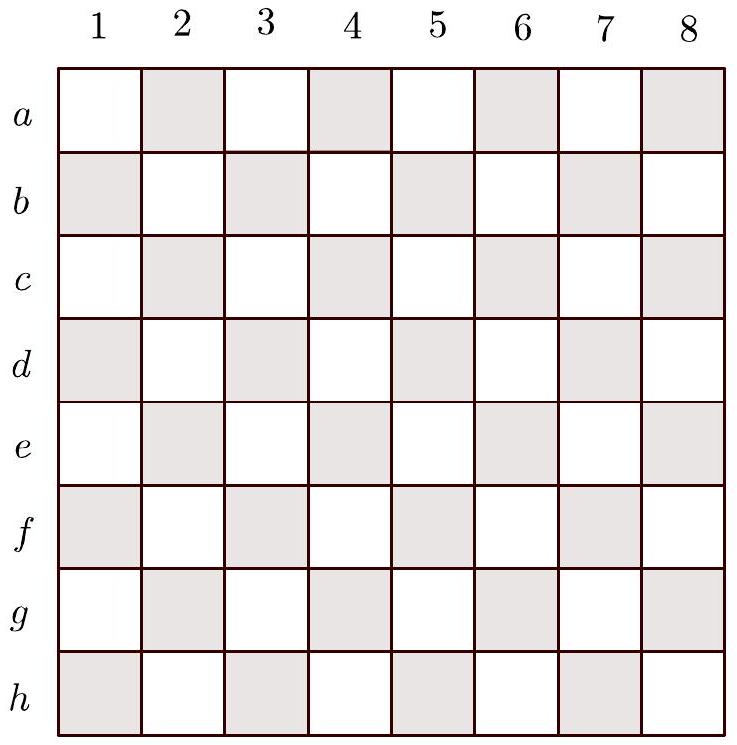
Determine the number of ways to choose 56 squares from the board such that all the black squares are chosen and exactly 7 squares are chosen in each row and each column. | 576 |
94,166 | Martin decided to spend all his savings on sweets. He found out that he could buy three lollipops and $3 \mathrm{dl}$ of cola or $18 \mathrm{dkg}$ of yogurt-covered raisins or $12 \mathrm{dkg}$ of yogurt-covered raisins and half a liter of cola. In the end, he bought one lollipop and 6 dl of cola. How many grams of yogurt-covered raisins did he still have left?
(Bednářová) | 60 |
94,284 | On each cell of a $9 \times 9$ grid, there is a chip. At a certain signal, each chip jumps to one of the cells touching diagonally the one it is in. Find the minimum number of empty cells after this move. | 9 |
94,289 | A group of students consists of 5 boys and 4 girls. We want to form a team of three students chosen from the students in this group.
a) What is the number of possible teams?
b) Is it true that less than $5 \%$ of the possible teams are made up entirely of girls? | 84 |
94,312 | Solve the equation $x^{4}-3 x^{3}+4 x^{2}-3 x+1=0$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly. | 1 |
94,320 | Study the sequence defined by $\mathfrak{u}_{0}=0$ and $\mathfrak{u}_{n+1}=\sqrt{12+\mathfrak{u}_{n}}$ for all $\mathfrak{n} \in \mathbb{N}$.
Regarding the second type of equations:
Definition 2.11. Let $\left(u_{n}\right)$ be a real sequence. We say it satisfies a recurrence equation of order $\mathbf{k}$ (linear) if there exists $k \in \mathbb{N}^{*}$ and real numbers $a_{0}, \cdots, a_{k-1}$ such that for all natural numbers $n$,
$$
u_{n+k}+a_{k-1} u_{n+k-1}+\cdots+a_{0} u_{n}=0
$$
Definition 2.12. The equation $X^{k}+a_{k-1} X^{k-1}+\cdots+a_{0}=0$ is called the characteristic equation.
Example 2.13. For an arithmetic sequence with common difference $a, u_{n+1}-u_{n}=u_{n+2}-u_{n+1}=a$, so $u_{n+2}-2 u_{n+1}+u_{n}=0$ is a recurrence equation satisfied by $u_{n}$.
For a geometric sequence with common ratio $a, u_{n+1}-a u_{n}=0$.
An arithmetico-geometric sequence satisfies a relation of the form: $\mathfrak{u}_{n+1}=a u_{n}+b$, and we obtain the recurrence equation $u_{n+2}-(a+1) u_{n+1}+a u_{n}=0$.
The general solution of such a recurrence equation (whose proof is unnecessary and tedious in our context) uses the concept of polynomials, discussed in the following section. Let's focus on orders 1 and 2 here.
Proposition 2.14. If for all $n \in \mathbb{N}, u_{n+1}-a u_{n}=0$, then $u_{n}=u_{0} a^{n}$.
Proposition 2.15. If for all $n \in \mathbb{N}, u_{n+2}+a_{1} u_{n+1}+a_{0} u_{n}=0$, we solve the quadratic characteristic equation $X^{2}+a_{1} X+a_{0}=0$.
- If it has two distinct solutions $r_{1}$ and $r_{2}$, then: $u_{n}=c_{1} r_{1}^{n}+c_{2} r_{2}^{n}$, where $c_{1}$ and $c_{2}$ are determined using, for example, the values of $\mathfrak{u}_{0}$ and $\mathfrak{u}_{1}$.
- If it has a double root $r$, then: $\mathfrak{u}_{n}=(a n+b) r^{n}$, and again $\mathfrak{u}_{0}$ and $\mathfrak{u}_{1}$ allow us to determine $a$ and $b$.
Would you be able to find in the previous property where the arithmetic, geometric, and arithmetico-geometric sequences are hidden?
Example 2.16. A geometric sequence corresponds to a recurrence equation of order 1. An arithmetic sequence corresponds to a recurrence equation of order 2 with 1 as a double root.
An arithmetico-geometric sequence with common ratio $a$ corresponds to a recurrence equation of order 2 whose solutions are 1 and $a$.
So much promising theory only calls out more strongly for exercises allowing us to apply these new knowledge victoriously. | 4 |
94,334 | A sheet of paper is torn into 3 pieces. Then, one of these pieces is torn again into 3 pieces, and so on. Can we obtain, at some point, a total of 503 pieces? 2020 pieces | 503 |
94,363 | Let $0 \leqslant a, b, c \leqslant 1$. Show that $\frac{a}{b c+1}+\frac{b}{a c+1}+\frac{c}{a b+1} \leqslant 2$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly. | 2 |
94,364 | Find all integers $n \geqslant 1$ such that $n$ divides $2^{n}-1$. | 1 |
94,557 | ## 1. Squares
The image shows four figures composed of black and yellow squares. If we continue to draw figures in the same way, how many black and yellow squares in total does the 22nd figure in the sequence consist of?

Result: $\quad 925$ | 925 |
94,589 | ## Task B-3.4.
How many solutions does the equation $\frac{1}{2} \sin 2 x + 1 = \sin x + \cos x$ have on the interval $[0, 2020 \pi]$? | 2021 |
94,607 | ## Task A-1.2.
Determine the smallest value that the expression
$$
a^{2}+b^{2}+|a b-1|+|a b-4|
$$
can take for some real numbers $a$ and $b$. | 5 |
94,646 | ## 6. Trokut i kutovi
U trokutu $A B C$ veličina najvećeg kuta iznosi $118^{\circ}$. Na produžetku najdulje stranice $\overline{A B}$ preko vrha $A$ odabrana je točka $X$ takva da je $|A X|=|A C|$, a na produžetku preko vrha $B$ točka $Y$ takva da je $|B Y|=|B C|$. Kolika je veličina kuta $\Varangle X C Y$ u kutnim stupnjevima?
Rezultat: 149
| 149 |
94,647 | ## Task B-3.2.
Determine all even natural numbers $n$ for which
$$
\left|\log _{0.5} 20^{\cos \pi}+\log _{0.5} 30^{\cos 2 \pi}+\log _{0.5} 42^{\cos 3 \pi}+\cdots+\log _{0.5}\left(n^{2}+7 n+12\right)^{\cos n \pi}\right|=1
$$ | 4 |
94,659 | 【Question 14】
As shown in the figure, in rectangle $A B C D$, $A B=6, B C=8$. After folding rectangle $A B C D$ along $C E$, point $D$ lands on point $F$ on diagonal $A C$. What is the area of trapezoid $A B C E$? $\qquad$ | 39 |
94,660 | ## Task A-4.5.
Given are 100 points arranged in 10 rows and 10 columns. Each point is either red or blue. A point is in a corner if it is at the end of both a row and a column, and on the edge if it is at the end of a row or a column, but not both. Two points are adjacent if they are in the same row or column, with no other points between them. Each pair of adjacent points is connected by a line of red, blue, or green color, such that each red line connects two red points, each blue line connects two blue points, and each green line connects one red and one blue point. It is known that there are 52 red points in total, of which 16 are on the edge and two are in the corners. It is also known that there are a total of 98 green lines.
Determine the total number of blue lines. | 37 |
94,661 | ## 4. Magic Square
In each cell of the table in the picture, one of the numbers $1,2,3,4,5,6$, 7, 8, and 9 is written. The sums of the three numbers in the cells of each row and each column are equal. In the central cell of the table, the number 3 is located. Let $A$ be the sum of the numbers in the cells marked with a circle, and $B$ be the sum of the numbers in the cells marked with a triangle. What is the value of $A \cdot B$?
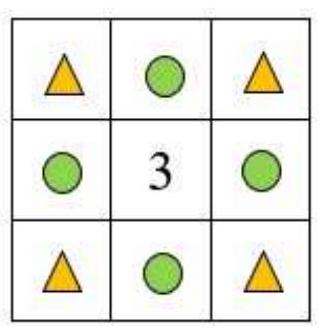
## Result: $\quad 432$ | 432 |
94,724 | 6. (10 points) Car A and Car B depart from City A to City B, which is 300 kilometers away. It is known that Car A departs 1 hour later than Car B, but arrives 1 hour earlier at City B. Then, Car A catches up with Car B at a distance of $\qquad$ kilometers from City B. | 150 |
94,767 | 6. Given real numbers $a, b, c$ satisfy $a b c \geq 1, a+b+c \geq 0$, then the minimum value of $a^{3}+b^{3}+c^{3}$ is . $\qquad$ | 3 |
94,798 | 3. Arrange the numbers in the set $\left\{2^{x}+2^{y} \mid x, y\right.$ are non-negative integers, $\left.x<y\right\}$ in ascending order, then the 60th number is $\qquad$ (answer with a number). | 2064 |
94,807 | 11. (10 points) Above are the building blocks with one star, two stars, and three stars as shown in figures $(a)$, $(b)$, and $(c)$. There are 5 blocks with one star, 2 blocks with two stars, and 1 block with three stars. If several of these blocks are used to form a strip of five stars, how many different ways can this be done? (Figure $(d)$ is one of the possible arrangements). | 13 |
94,812 | Example 12 (2001 National High School Competition Question) In the six regions of a regular hexagon, ornamental plants are to be planted (as shown in Figure 12-2). The requirement is that the same type of plant is planted in the same region, and different types of plants are planted in adjacent regions. Given 4 different types of plants to choose from, how many planting schemes are there? | 732 |
94,910 | B2. A stone general is a chess piece that moves one square diagonally upward on each move; that is, it may move from the coordinate $(a, b)$ to either of the coordinates $(a-1, b+1)$ or $(a+1, b+1)$. How many ways are there for a stone general to move from $(5,1)$ to $(4,8)$ in seven moves on a standard 8 by 8 chessboard? | 35 |
94,922 | 3. If the real number $x$ satisfies $\arcsin x>\arccos x$, then the range of the expression
$$
f(x)=\sqrt{2 x^{2}-x+3}+2^{\sqrt{x^{2}-x}}
$$
is $\qquad$ | 3 |
94,932 | 10. As shown in the figure, in the rectangular plate $ABCD$, $AB=3, BC=2$, with the edge $AD$ standing vertically on the ground. There is another vertical rod $MN$ on the ground, such that $NE$ is the perpendicular bisector of $AB$, with $E$ being the foot of the perpendicular, $NE=3$, $MN=5$. There is a point light source at point $M$. Then the area of the projection of the rectangular plate on the ground is $\qquad$. | 8 |
94,933 | 22. Mei Yangyang is coloring a ball. She divides the ball into 4 identical sections, each to be painted with one color, which can be chosen from red or blue. Mei Yangyang has $\qquad$ different ways to color the ball. | 6 |
94,944 | 7. Given $z=\frac{(4-3 \mathrm{i})^{2}(-1-\sqrt{3 \mathrm{i}})^{10}}{(1+\mathrm{i})^{12}}$, then $|z|=$ | 400 |
94,948 | 12. When $s$ and $t$ take all real values, the minimum value that $(s+5-3|\cos t|)^{2}+(s-2|\sin t|)^{2}$ can reach is $\qquad$ | 2 |
94,994 | 39. As shown in the figure, in $\triangle A B C$, $\angle B=2 \angle C, A D \perp B C$ at $D, M$ is the midpoint of $B C, A B=10$, then the length of $D M$ is $\qquad$ . | 5 |
95,001 | 4. (8 points) Count the number of triangles in the figure: $\qquad$ triangles.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 8 |
95,017 | 97. Li Ping went to the supermarket and bought three kinds of snacks he likes, with unit prices of 17 yuan, 8 yuan, and 5 yuan, respectively, and spent a total of 55 yuan. Then Li Ping has
$\qquad$ different ways to buy them. | 2 |
95,019 | 80. The number of right-angled triangles with a perimeter of 6 and an integer area is $\qquad$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly. | 1 |
95,033 | 10. Li Yun is sitting by the window in a train traveling at a speed of 60 kilometers per hour, and he sees a freight train with 30 carriages coming towards him. When the front of the freight train passes his window, he starts timing, and when the last carriage passes his window, the recorded time is 18 seconds. It is known that the length of each freight carriage is 15.8 meters, the spacing between carriages is 1.2 meters, and the length of the freight train's front is 10 meters. What is the speed of the freight train? | 44 |
95,048 | 1. Xiaohong lives on the fourth floor. She needs 2 minutes to go from the ground floor to the second floor. So, how many minutes does she need to go from the ground floor to the fourth floor? | 6 |
95,170 | 71. The cube and its surface development are shown below, where five faces are marked with numbers. Then the face shaded in the cube is marked with the number in the development diagram is $\qquad$
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly. | 5 |
95,175 | 7. For any positive integer $n$, let $f_{1}(n)$ denote the square of the sum of the digits plus $r+1$, where $r$ is the integer satisfying $n=3 q+$ $r(q$ is an integer $), 0 \leqslant r \leqslant 3$. For $k \geqslant 2$, let $f_{k}(n)=f_{1}\left[f_{k-1}(n)\right]$, then $f_{2001}(2345)=$ $\qquad$ ,$f_{2001}(2001)=$ $\qquad$ . | 10 |
95,211 | 55. Let $x, y$ be positive integers, and let $\sqrt{x-116}+\sqrt{x+100}=y$, then the maximum value of $y$ is | 108 |
95,234 | 9. The natural number 2015 can be expressed as the sum of $\qquad$ consecutive odd numbers. | 31 |
95,269 | 7. In the figure below, there are three scales. By observing the first two scales, we can find that 5 " $\boldsymbol{\Delta}$ " and 3 " $\bigcirc$ " weigh the same, and 1 " " weighs the same as 1 " $\boldsymbol{\Delta}$ " plus 2 " $\boldsymbol{\square}$ ". Therefore, 1 " $\boldsymbol{\Delta}$ " plus 1 " 0 " weighs the same as $\qquad$ " $\square$ ".
保留源文本的换行和格式,直接输出翻译结果如下:
7. In the figure below, there are three scales. By observing the first two scales, we can find that 5 " $\boldsymbol{\Delta}$ " and 3 " $\bigcirc$ " weigh the same, and 1 " " weighs the same as 1 " $\boldsymbol{\Delta}$ " plus 2 " $\boldsymbol{\square}$ ". Therefore, 1 " $\boldsymbol{\Delta}$ " plus 1 " 0 " weighs the same as $\qquad$ " $\square$ ". | 3 |
95,333 | 5. Wolf Gray and its brothers caught many sheep. If each wolf gets 3 sheep, there will be 2 sheep left over; if each wolf gets 8 sheep, there will be 8 sheep short. So, including Wolf Gray, there are
wolves sharing
sheep. | 2 |
95,343 | 78. As shown in the figure, in rectangle $A B C D$, $A B=20 \text{ cm}, B C=10 \text{ cm}$. If points $M$, $N$ are taken on $A C$, $A B$ respectively, such that the value of $B M+M N$ is minimized, what is this minimum value in $\text{cm}$? | 16 |
95,345 | 10. The area of the large regular hexagon in the figure is 2022, then the area of the shaded part is | 1011 |
95,346 | Example 3: Team A and Team B each send out 7 players to participate in a Go team match according to a pre-arranged order. Both sides start with the No. 1 players competing. The loser is eliminated, and the winner then competes with the No. 2 player of the losing side... until all players of one side are eliminated. The other side wins. This forms a match process. How many different match processes can occur? | 3432 |
95,354 | 10. (6 points) A few hundred years ago, Columbus discovered the New World in America, and the four digits of that year are all different, their sum equals 16. If the tens digit is increased by 1, then the tens digit is exactly 5 times the units digit, so Columbus discovered the New World in America in the year $\qquad$.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。 | 1492 |
95,358 | 11. In the cube $A B C D-A_{1} B_{1} C_{1} D_{1}$, the measure of the dihedral angle $A-B D_{1}-A_{1}$ is | 60 |
95,383 | 2. In the Cartesian coordinate system, the area of the region formed by points $(x, y)$ satisfying $|x|+|y|+|x-2| \leqslant 4$ is
$\qquad$ (Supplied by An Zhenping) | 12 |
95,415 | 60. In a plane, there are 7 lines, among which three lines are pairwise parallel, and three lines intersect at a single point $A$. The maximum number of intersection points formed by these 7 lines is $\qquad$.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。 | 16 |
95,466 | 8. (1963 24th Putnam Mathematical Competition) Suppose $x^{2}-x+a$ divides $x^{13}+x+90$, determine the value of the positive integer $a$.
untranslated text remains the same as the source text. | 2 |
95,479 | 9、A、 、 、 $\mathrm{C} 、 \mathrm{D} 、 \mathrm{E}$ are all single digits, and $\overline{D E}=A+B+C$. Given that $\overline{A B C}+\overline{B C A}+\overline{C A B}+\overline{D E}=2016, \overline{D E A B C}$ is maximized as $\qquad$ - | 18981 |
95,497 | Example 4-11 The side chain of methane $\mathrm{CH}_{4}$ is , if the 4 H bonds are replaced by one of $\mathrm{H}, \mathrm{Cl}, \mathrm{CH}_{3}, \mathrm{C}_{2} \mathrm{H}_{5}$, how many different chemical structures are there? | 36 |
95,547 | 7. (10 points) A natural number $A$ is written twice in a row (for example, 12 is written as 1212) to form a new number $B$. If $B$ is a multiple of 2016, then the smallest $A$ is $\qquad$
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
Note: The last sentence is a repetition of the instruction and should not be included in the translated text. Here is the final version:
7. (10 points) A natural number $A$ is written twice in a row (for example, 12 is written as 1212) to form a new number $B$. If $B$ is a multiple of 2016, then the smallest $A$ is $\qquad$ | 288 |
95,552 | 63. A museum has 7 exhibition rooms in a row. The guard starts walking into the first room, then to the second... and after reaching the seventh room, he turns back, walking to the sixth room, then to the fifth... Each time he enters a room, he toggles the light switch. If all 7 rooms are initially lit, how many rooms will still be lit after he has walked into 100 rooms?
If initially all 7 rooms are lit, then after he has walked into 100 rooms, there will be $\qquad$ rooms still lit. | 3 |
95,579 | 1. Positive real numbers $a, b, c$ satisfy $\ln (a b), \ln (a c), \ln (b c)$ form an arithmetic sequence, and $4(a+c)=17 b$, then all possible values of $\frac{c}{a}$ are $\qquad$ . | 16 |
95,591 | 1. Calculate: $123456789 \times 8+9=$ | 987654321 |
95,597 | 79. A company sells color TVs at the original price, making a profit of 60 yuan per unit. Now, the TVs are sold at a reduced price, resulting in the sales volume doubling, and the total profit increasing by 0.5 times. How much did the price of each color TV decrease? $\qquad$ yuan.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。 | 15 |
95,624 | 18. Four distinct natural numbers multiplied together give a product of 2022. The sum of these four natural numbers is
untranslated part:
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
Note: The note is not part of the translation but is provided to explain that the untranslated part was not included in the translation. | 343 |
95,661 | 3. If $x^{4}+16 x=12$, then $x^{2}+2 x+4=$
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 6 |
95,717 | 4. How many positive odd numbers can divide 510510?
untranslated text remains unchanged:
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。 | 64 |
95,749 | Draw $* \star$ three circles, each with a radius of 3, and centers at $(14,92)$, $(17,76)$, and $(19,84)$. Draw a line through the point $(17,76)$ such that the sum of the areas of the parts of these three circles on one side of the line equals the sum of the areas of the parts of these three circles on the other side of the line. Find the absolute value of the slope of this line. | 24 |
95,755 | 12・147 Find the smallest prime that cannot be expressed as $\left|3^{a}-2^{b}\right|$, where $a$ and $b$ are non-negative integers.
(China National Team Selection Exam, 1995) | 41 |
95,817 | 6. According to the arrangement rules of the table below, 2020 will appear $\qquad$ times.
1st Column 2nd Column 3rd Column 4th Column 5th Column
\begin{tabular}{llllll}
1st Row & 1 & 2 & 3 & 4 & 5 \\
2nd Row & 2 & 4 & 6 & 8 & 10 \\
3rd Row & 3 & 6 & 9 & 12 & 15 \\
4th Row & 4 & 8 & 12 & 16 & 20
\end{tabular} | 12 |
95,836 | 8. As shown in the figure, in $\triangle A B C$, $\angle C B D=30^{\circ}, \angle D B A=40^{\circ}, \angle D A B=20^{\circ}, \angle C A D=50^{\circ}$, then $\angle B C D=$ $\qquad$ . | 10 |
95,840 | 6. A company has $n$ employees, and it is known that every two of these $n$ employees can ensure that there are at least three days in a week when one works while the other does not (these days do not have to be the same employee working, and employees can choose not to work the entire week). Find the maximum value of $n$.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
Note: The last sentence is a repetition of the instruction and should not be included in the final translation. Here is the corrected output:
6. A company has $n$ employees, and it is known that every two of these $n$ employees can ensure that there are at least three days in a week when one works while the other does not (these days do not have to be the same employee working, and employees can choose not to work the entire week). Find the maximum value of $n$. | 16 |
95,847 | 24. In the $O$ and $\triangle$ below, fill in $1, 2, 3, 4, 5, 6$, such that each $\triangle$ contains a number equal to the sum of the numbers in the two adjacent $O$s. The number 1 is already filled in, so what is the number at the "?" place? $\qquad$ _.
| 6 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.