id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
66,121 | Task B-2.4. Dundo and Maro were competing by giving each other unusual math problems. Thus, Maro was given the task to calculate the exact value of the cosine of an angle of $36^{\circ}$. He was not allowed to use any tools except paper and a pencil for writing and calculating.
It's impossible, Maro thought, until Dundo drew a few isosceles triangles, at least one of whose angles measured $36^{\circ}$. Maro observed one of the triangles and quickly calculated $\cos 36^{\circ}$. What value did Maro get and how did he do it? | \frac{1+\sqrt{5}}{4} |
66,128 | [Inscribed quadrilateral with perpendicular diagonals]
$A B C D$ is an inscribed quadrilateral with perpendicular diagonals. $O$ is the center of the circumscribed circle of quadrilateral $A B C D$. $P$ is the point of intersection of the diagonals.
Find the sum of the squares of the diagonals, given the length of the segment $O P$ and the radius of the circle $R$. | 8R^2-4OP^2 |
66,158 | 10. From any point $P$ on the parabola $y^{2}=2 x$, draw a perpendicular to its directrix $l$, with the foot of the perpendicular being $Q$. The line connecting the vertex $O$ and $P$ and the line connecting the focus $F$ and $Q$ intersect at point $R$. Then the equation of the locus of point $R$ is | y^{2}=-2x^{2}+x |
66,170 | 5. A five-digit number $\overline{a b c d e}$, from the five digits, any two digits are taken to form a two-digit number (maintaining the original order of the digits in the five-digit number), there are 10 such two-digit numbers: $33, 37, 37, 37, 38, 73, 77, 78, 83, 87$, then $\overline{a b c d e}=$ $\qquad$ - | 37837 |
66,178 | 14. The function $f(x)$ defined on $\mathbf{R}$ satisfies $\left\{\begin{array}{l}f(x+2016) \leqslant f(x)+2016, \\ f(x+2017) \geqslant f(x)+2017,\end{array}\right.$ and $f(1)=2$. Let $a_{n}=f(n)\left(n \in \mathbf{N}^{*}\right)$, then $a_{2018}=$ $\qquad$ | 2019 |
66,215 | Jimmy runs a successful pizza shop. In the middle of a busy day, he realizes that he is running low on ingredients. Each pizza must have 1 lb of dough, $\frac14$ lb of cheese, $\frac16$ lb of sauce, and $\frac13$ lb of toppings, which include pepperonis, mushrooms, olives, and sausages. Given that Jimmy currently has 200 lbs of dough, 20 lbs of cheese, 20 lbs of sauce, 15 lbs of pepperonis, 5 lbs of mushrooms, 5 lbs of olives, and 10 lbs of sausages, what is the maximum number of pizzas that JImmy can make? | 80 |
66,217 | $:$ Tolinho A.K.
How many different ways are there to break down the number 2004 into natural addends that are approximately equal? There can be one or several addends. Numbers are considered approximately equal if their difference is no more than 1. Ways that differ only in the order of the addends are considered the same. | 2004 |
66,224 | Evaluate $ \int_{ \minus{} 1}^ {a^2} \frac {1}{x^2 \plus{} a^2}\ dx\ (a > 0).$
You may not use $ \tan ^{ \minus{} 1} x$ or Complex Integral here. | \frac{\pi}{2a} |
66,316 | Example 1 Color each vertex of a square pyramid with one color, and make the endpoints of the same edge have different colors. If only 5 colors are available, then the total number of different coloring methods is $\qquad$
(1995, National High School Mathematics Competition)
The modified solution better illustrates the principle of multiplication. | 420 |
66,331 | Let's inscribe a right circular cylinder of the largest possible volume in a given right circular cone. What percentage of the cone's volume is the volume of the cylinder? (The base of the inscribed cylinder lies in the base of the cone, and the other circle of the cylinder is a plane section of the cone.) | 44\frac{4}{9} |
66,350 | 2. Which three-digit numbers are more numerous: those in which all digits have the same parity, or those in which adjacent digits have different parity | 225 |
66,371 | ## Task A-4.2.
Determine all ordered pairs $(p, n)$, where $p$ is a prime and $n$ is a natural number, for which
$$
1+p+p^{2}+p^{3}+\cdots+p^{n}=2801
$$ | (7,4) |
66,382 | 5. In the number $2 * 0 * 1 * 6 * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can repeat) so that the resulting 11-digit number is divisible by 12. In how many ways can this be done? | 1296 |
66,383 | 7. Let $f(m)$ be the product of the digits of the positive integer $m$. Find the positive integer solutions to the equation $f(m)=m^{2}-10 m-36$. | 13 |
66,389 | 16. Nine consecutive positive integers are arranged in an increasing sequence $a_{1}, a_{2}, \cdots, a_{9}$. If $a_{1}+a_{3}+a_{5}+a_{7}+a_{9}$ is a perfect square, and $a_{2}+a_{4}+a_{6}+a_{8}$ is a perfect cube, then the minimum value of $a_{1}+a_{2}+\cdots+a_{9}$ is | 18000 |
66,406 | Consider the collection of all 5-digit numbers whose sum of digits is 43. One of these numbers is chosen at random. What is the probability that it is a multiple of 11?
# | \frac{1}{5} |
66,412 | (20 (12 points) Given the function $f(x)=\frac{2 x+3}{3 x}$, the sequence $\left\{a_{n}\right\}$ satisfies $a_{1}=1, a_{n+1}=$ $f\left(\frac{1}{a_{n}}\right), n \in \mathbf{N}^{*}$.
(1) Find the general term formula of the sequence $\left\{a_{n}\right\}$;
(2) Let $T_{n}=a_{1} a_{2}-a_{2} a_{3}+a_{3} a_{4}-a_{4} a_{5}+\cdots-a_{2 n} a_{2 n+1}$, find $T_{n}$. | -\frac{4}{9}(2n^{2}+3n) |
66,418 | 110 If $x, y$ satisfy $4 x^{2}=8-y^{2}$, then the minimum value of $\sqrt{x^{2}+(y-3)^{2}}+\sqrt{(x-2)^{2}+(y-1)^{2}}$ is $\qquad$ | 2\sqrt{2} |
66,420 | 162 On the Cartesian plane, a point whose both coordinates are integers is called an integer point. For some integer point $P$ and some positive number $d$, there are exactly $k(>0)$ different integer points, each at a distance $d$ from $P$. Denote the range of $k$ values as $\left\{k_{1}, k_{2}, \cdots\right\}$, where $0<k_{1}<k_{2}<\cdots$, then $k_{2}=$ $\qquad$ | 8 |
66,425 | Example 3 The function $f(x)$ is defined on the set of real numbers, and for all real numbers $x$ it satisfies the equations: $f(2+x)=f(2-x)$ and $f(7+x)=f(7-x)$. Suppose $x=0$ is a root of $f(x)=0$, and let $N$ be the number of roots of $f(x)=0$ in the interval $-1000 \leqslant x \leqslant 1000$. Find the minimum value of $N$. | 401 |
66,438 | 92. 50 chess pieces are arranged in a circle, and numbers $1, 2, 3, \cdots \cdots$ 50 are sequentially marked on the chess pieces in a clockwise direction. Then, in a clockwise direction, every other chess piece is removed until only one chess piece remains. If the number of the remaining chess piece is 42, then the first chess piece to be taken away is $\qquad$ number chess piece. | 7 |
66,449 | 4. If 6 pieces of $1 \times 2$ paper are used to cover a $3 \times 4$ grid, the number of different ways to cover it is. | 11 |
66,480 | 13. (15 points) As shown in the figure, in the isosceles right triangle $A B C$, $\angle A=90^{\circ}, A B=A C=1$, rectangle $E H G F$ is inside triangle $A B C$, and $G, H$ are on side $B C$. Find the maximum area of rectangle $E H G F$. | \frac{1}{4} |
66,485 | $3+$ [ Law of Sines
In an isosceles trapezoid, the bases are given as $a=21, b=9$ and the height $h=8$. Find the radius of the circumscribed circle.
# | \frac{85}{8} |
66,506 | 20. Let $a$ and $b$ be real numbers such that $17\left(a^{2}+b^{2}\right)-30 a b-16=0$. Find the maximum value of $\sqrt{16 a^{2}+4 b^{2}-16 a b-12 a+6 b+9}$.
(2 marks)
設 $a$ 、 $b$ 為實數 , 使得 $17\left(a^{2}+b^{2}\right)-30 a b-16=0$ 。 求 $\sqrt{16 a^{2}+4 b^{2}-16 a b-12 a+6 b+9}$ 的最大值。 | 7 |
66,515 | 3 [ Angles subtended by equal arcs and equal chords]
In a convex quadrilateral $A B C D$, it is known that $\angle C B D=58^{\circ}, \angle A B D=44^{\circ}, \angle A D C=78^{\circ}$. Find the angle $C A D$. | 58 |
66,525 | For example, there are 18 admission tickets to be distributed among four classes, A, B, C, and D, with the requirement that Class A gets at least 1 ticket but no more than 5 tickets, Class B gets at least 1 ticket but no more than 6 tickets, Class C gets at least 2 tickets but no more than 7 tickets, and Class D gets at least 4 tickets but no more than 10 tickets. How many different ways are there to distribute the tickets? | 140 |
66,527 | 4. (20 points) For two perpendicular lines $a$ and $b$ on a plane, $(a, b)$ is called a "perpendicular pair", and both $a$ and $b$ belong to this "perpendicular pair". How many "perpendicular pairs" can be formed at most when there are twenty lines on the plane? | 100 |
66,567 | The article in the fifth issue of our journal in 1983, titled "A Simple Method for Compiling Radical Equations," states that the equation
$$
\sqrt{5 \mathrm{x}-1}+\sqrt{2 \mathrm{x}}=3 \mathrm{x}-1
$$
"will produce a quartic equation after squaring twice, which may be quite troublesome to solve." In fact, this equation can be solved using a simpler method. | x=2 |
66,577 | $\quad$ Inscribed and Circumscribed Circles [ Trigonometric Ratios in a Right Triangle
A regular hexagon $A B C D E K$ is inscribed in a circle of radius $3+2 \sqrt{3}$. Find the radius of the circle inscribed in triangle $B C D$.
# | \frac{3}{2} |
66,586 | 5.18. In parallelogram $A B C D$, point $K$ is the midpoint of side $B C$, and point $M$ is the midpoint of side $C D$. Find $A D$, if $A K=6$ cm, $A M=3$ cm, and $\angle K A M=60^{\circ}$. | 4 |
66,601 | In the class, there are 30 students: excellent students, C-grade students, and D-grade students. Excellent students always answer questions correctly, D-grade students always make mistakes, and C-grade students answer the questions given to them strictly in turn, alternating between correct and incorrect answers. All students were asked three questions: "Are you an excellent student?", "Are you a C-grade student?", and "Are you a D-grade student?". 19 students answered "Yes" to the first question, 12 to the second, and 9 to the third. How many C-grade students are there in this class? | 20 |
66,632 | 5. Given that the diameter $A B$ of circle $O$ divides the circle into upper and lower semicircles, and points $C, D$ are on the upper and lower semicircles respectively (neither coinciding with points $A, B$), if $A C=2, A D=1$, then $\overrightarrow{A B} \cdot \overrightarrow{D C}=$ $\qquad$ . | 3 |
66,635 | 3. (10 points) In a $3 \times 3$ grid (each cell is a $1 \times 1$ square), place two identical pieces, with at most one piece per cell. There are $\qquad$ different ways to place the pieces. (If two placements can be made to coincide by rotation, they are considered the same placement). | 10 |
66,645 | 3.283. $\cos \left(270^{\circ}-2 \alpha\right) \operatorname{ctg}\left(30^{\circ}-2 \alpha\right) \operatorname{tg}\left(240^{\circ}-2 \alpha\right)(2 \cos 4 \alpha-1)$. | -\sin6\alpha |
66,647 | The difference between the cube and the square of a number is in the form $a b c a b c$ (in the decimal system). Which number is this? | 78 |
66,651 | 3. Find the largest natural number $\mathrm{n}$, for which the system of inequalities
$1<x<2, 2<x^{2}<3, \ldots, n<x^{n}<n+1$
has a solution. (6 points) | 4 |
66,669 | 8. Variant 1.
A line parallel to the leg $A C$ of the right triangle $A B C$ intersects the leg $B C$ at point $K$, and the hypotenuse $A B$ at point $N$. On the leg $A C$, a point $M$ is chosen such that $M K=M N$. Find the ratio $\frac{A M}{M C}$, if $\frac{B K}{B C}=14$. | 7 |
66,679 | 16. Given the function $y=3 x+\sqrt{x^{2}-2 x}$, find the range of this function. | (-\infty,3-2\sqrt{2}]\cup[6,+\infty) |
66,681 | 9. Let $f(x)$ be an odd function defined on $\mathbf{R}$. If for any real number $x$, $f(x+2)=-f(x)$, and when $x \in[0,1]$, $f(x)=2 x$, then $f(10 \sqrt{3})=$ $\qquad$ | 36-20\sqrt{3} |
66,682 | I want the necessary and sufficient condition for the fraction
$$
\frac{a_{1} x^{2}+b_{1} x+c_{1}}{a_{2} x^{2}+b_{2} x+c_{2}}
$$
to be a constant value for all values of $x$. | \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} |
66,684 | [ Divisibility of numbers. General properties ]
Find the smallest natural $n$ for which $(n+1)(n+2)(n+3)(n+4)$ is divisible by 1000. | 121 |
66,702 | ## Problem Statement
Find the second-order derivative $y_{x x}^{\prime \prime}$ of the function given parametrically.
$$
\left\{\begin{array}{l}
x=\frac{\cos t}{1+2 \cos t} \\
y=\frac{\sin t}{1+2 \cos t}
\end{array}\right.
$$ | -\frac{(1+2\cos)^{3}}{\sin^{3}} |
66,706 | 8,9
The side of a cell on a grid paper is 1. A rectangle with sides $m$ and $n$ is constructed along the grid lines.
Can a closed broken line be drawn within the rectangle along the grid lines that passes exactly once through each grid node located inside or on the boundary of the rectangle? If so, what is its length? | (n+1)(+1) |
66,718 | In trapezoid $ABCD$ with $AD\parallel BC$, $AB=6$, $AD=9$, and $BD=12$. If $\angle ABD=\angle DCB$, find the perimeter of the trapezoid. | 39 |
66,727 | 8.2 Sergey arranged several (more than two) pairwise distinct real numbers in a circle so that each number turned out to be equal to the product of its neighbors. How many numbers could Sergey have arranged? | 6 |
66,744 | 8. Calculate:
$$
\sum_{k=1}^{2014}\left[\frac{-3+\sqrt{8 k+1}}{4}\right]=
$$
$\qquad$
where, $[x]$ denotes the greatest integer not exceeding the real number $x$. | 40115 |
66,752 | 3. Let the function $f(x)=\frac{(x+1)^{2}+\sin x}{x^{2}+1}$ have the maximum value and minimum value as $M$ and $N$, respectively. Then $M+N=$ $\qquad$ | 2 |
66,755 | 15.26. Into how many parts do the planes of the faces divide the space a) of a cube; b) of a tetrahedron? | 15 |
66,757 | Avor: frankin 5.
A natural number $\$ \mathrm{k} \$$ is called interesting if the product of the first $\$ \mathrm{k} \$$ prime numbers is divisible by $\$ \mathrm{k} \$$ (for example, the product of the first two prime numbers is $2 \cdot 3=6$, and 2 is an interesting number).
What is the maximum number of interesting numbers that can occur consecutively? | 3 |
66,758 | 3. A sequence of numbers, the first three numbers are $1, 9, 9$, and each subsequent number is the remainder of the sum of the three preceding numbers divided by 3. What is the 1999th number in this sequence? | 0 |
66,778 | [ Algebra and arithmetic (miscellaneous).] $[$ Sequences (miscellaneous) ]
Find the value of the expression $1!* 3-2!* 4+3!* 5-4!* 6+\ldots-2000!* 2002+2001!$. | 1 |
66,787 | Task 2 - 040912 At the school sports day, Christian (C), Bernd (B), Alfred (A), and Dieter (D) had qualified for the final 100 m race. Based on their preliminary run times, it was expected that they would finish in the order $C B A D$. However, neither the position of any runner nor any pair of directly consecutive runners was correctly predicted. The physical education teacher expected the order to be $A D B C$. This was a good guess; because two runners did come in at the expected positions.
In what order did the runners finish the race? | DABC |
66,793 | Four consecutive three-digit numbers are divided respectively by four consecutive two-digit numbers. What minimum number of different remainders can be obtained?
[i](A. Golovanov)[/i] | 1 |
66,795 | 9. (16 points) Find the sum of all elements in the set
$$
\begin{aligned}
M= & \left\{a \left\lvert\, a=\frac{x+y+z}{t}\right., 3^{x}+3^{y}+3^{z}=3^{t},\right. \\
& x 、 y 、 z 、 t 、 a \in \mathbf{Z}\}
\end{aligned}
$$ | 12 |
66,802 | 10. When $x, y, z$ are positive numbers, the maximum value of $\frac{4 x z+y z}{x^{2}+y^{2}+z^{2}}$ is . $\qquad$ | \frac{\sqrt{17}}{2} |
66,812 | 5.3. Find the angle $C$ of triangle $ABC$, if the distance from vertex $C$ to the orthocenter of the triangle is equal to the radius of the circumscribed circle. | 60 |
66,821 | 2. The password consists of four different digits, the sum of which is 27. How many password options exist | 72 |
66,828 | # 9. Solution.
1st method. An elementary outcome in the random experiment is a triplet of positions where the children in green caps stand. Consider the event $A$ "all three green caps are together." This event is favorable in 9 elementary outcomes. The event $B$ "two green caps are together, and the third is separate" is favorable in 45 elementary outcomes (9 ways to choose two adjacent places, and the third place must be one of the 5 places not adjacent to the already chosen ones). The total number of ways to choose a triplet is $C_{9}^{3}=84$. Then the probability of the event "some two green caps are together" is $\mathrm{P}(A)+\mathrm{P}(B)=\frac{54}{84}=\frac{9}{14}$, and the desired probability is $1-\mathrm{P}(A)-\mathrm{P}(B)=\frac{5}{14}$.
2nd method. Number the children in green caps and form pairs "green-red" such that a red cap is placed to the right of each green cap. To the right of the first green cap, any of the six red caps can be placed, to the right of the second, one of the five remaining, and to the right of the third, one of the four remaining red caps. This results in three pairs "green-red" and three separate red caps. There are exactly $6 \cdot 5 \cdot 4=120$ such groupings. Arrange these pairs and separate caps (a total of six elements) in a circle. This can be done in 5! ways, and no two green caps will be adjacent, as a red cap is located to the right of each green cap.
The total number of ways to arrange 9 children in a circle is 8!.
Thus, the desired probability is $\frac{120 \cdot 5!}{8!}=\frac{120}{8 \cdot 7 \cdot 6}=\frac{5}{14}$.
3rd method is similar to the 2nd method from the first variant. Other methods of solution are also possible. | \frac{5}{14} |
66,851 | 1348. Calculate the integral $\int_{0}^{6}\left(x^{2}+3\right) d \bar{x}$ using the Newton-Leibniz formula and approximate formulas of rectangles and trapezoids, dividing the interval of integration into 6 equal parts $(n=6)$. Find the absolute and relative errors of the results obtained by the approximate formulas. | 90 |
66,859 | 816. The correlation function $K_{x}\left(t_{1}, t_{3}\right)=$ $=\cos \omega t_{1} \cos \omega t_{2}$ of the random function $X(t)$ is given. Find: a) the correlation function; b) the variance of the integral $Y(t)=$ $=\int_{0}^{1} X(s) \mathrm{d} s$. | \frac{\sin^{2}\omega}{\omega^{2}} |
66,860 | 9.3. The inscribed circle of triangle $A B C$ with center $O$ touches the sides $A B, B C$ and $A C$ at points $M, N$ and $K$ respectively. It turns out that angle $A O C$ is four times the angle $M K N$. Find angle $B$. | 108 |
66,862 | 3 [ Auxiliary similar triangles
A circle of radius 1 touches a circle of radius 3 at point $C$. A line passing through point $C$ intersects the smaller circle at point $A$ and the larger circle at point $B$. Find $A C$, if $A B=2 \sqrt{5}$.
# | \frac{\sqrt{5}}{2} |
66,867 | What part of the area of an isosceles trapezoid $K L M N (K L \| M N)$ is formed by the area of triangle $A B C$, where $A$ is the midpoint of the base $K L$, $B$ is the midpoint of the base $M N$, and $C$ is the midpoint of the side $K N$? | \frac{1}{4} |
66,877 | 1. (5 points) Find the degree measure of the angle
$$
\delta=\arccos \left(\left(\sin 2905^{\circ}+\sin 2906^{\circ}+\cdots+\sin 6505^{\circ}\right)^{\cos } 2880^{\circ}+\cos 2881^{\circ}+\cdots+\cos 6480^{\circ}\right)
$$ | 65 |
66,895 | 4.1. Through the vertex $A$ of the parallelogram $A B C D$, a line is drawn intersecting the diagonal $B D$, the side $C D$, and the line $B C$ at points $E, F$, and $G$ respectively. Find the ratio $B E: E D$, if $F G: F E=4$. Round your answer to the nearest hundredth if necessary. | 2.24 |
66,917 | 477*. What is the greatest common divisor of all numbers $7^{n+2}+8^{2 n+1}(n \in N)$? | 57 |
66,921 | A square and an equilateral triangle have the property that the area of each is the perimeter of the other. What is the area of the square? | 12\sqrt[3]{4} |
66,928 | 5. Let $p(x)=2 x^{3}-3 x^{2}+1$. How many squares of integers are among the numbers $p(1), p(2), \ldots$, $p(2016) ?$
# | 32 |
66,930 | Lyla and Isabelle run on a circular track both starting at point $P$. Lyla runs at a constant speed in the clockwise direction. Isabelle also runs in the clockwise direction at a constant speed $25 \%$ faster than Lyla. Lyla starts running first and Isabelle starts running when Lyla has completed one third of one lap. When Isabelle passes Lyla for the fifth time, how many times has Lyla returned to point $P$ ? | 17 |
66,940 | 8. Petya suggests Vasya play the following game. Petya gives Vasya two boxes of candies. Each of the two boxes contains chocolate candies and caramels. In total, there are 25 candies in both boxes. Petya suggests Vasya take one candy from each box. If both candies turn out to be chocolate, Vasya wins. Otherwise, Petya wins. The probability that Vasya will get two caramels is 0.54. Who has a higher chance of winning? | Petya |
66,951 | 2.035. $\left(\frac{a+2}{\sqrt{2 a}}-\frac{a}{\sqrt{2 a}+2}+\frac{2}{a-\sqrt{2 a}}\right) \cdot \frac{\sqrt{a}-\sqrt{2}}{a+2}$. | \frac{1}{\sqrt{}+\sqrt{2}} |
66,957 | Determine the number of ways to serve $n$ foods in the cafeteria, knowing that apples are taken in groups of 3, yogurts come in pairs, and one is allowed at most 2 pieces of bread and one bowl of cereal due to a change in provider. | n+1 |
66,962 | 9.3. In parallelogram $A B C D$, diagonal $A C$ is twice the length of side $A B$. A point $K$ is chosen on side $B C$ such that $\angle K D B = \angle B D A$. Find the ratio $B K: K C$. | 2:1 |
66,977 | 4. As shown in Figure $4, B D$ and $C E$ are altitudes of acute $\triangle A B C$, $\angle A B C=60^{\circ}$, $A E=8, B E=4$, and $P$ is a moving point on side $B C$. Then the minimum value of $P D+P E$ is $\qquad$. | \frac{20\sqrt{7}}{7} |
66,990 | 6. Given 4 spheres with a radius of 1, each pair of which are externally tangent, then the edge length of the circumscribed regular tetrahedron of the geometric body formed by these 4 spheres is | 2\sqrt{6}+2 |
66,997 | In the city of records and curiosities, they built a pyramid from cubes. In the top layer, there is one cube, and the number of cubes in each layer increases by two as you move downward (the top layers of the structure are shown in the image).
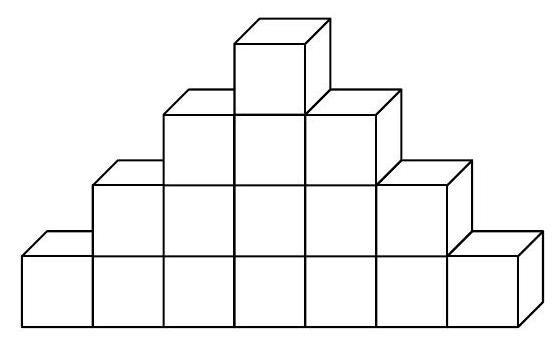
The first, i.e., the bottom layer, is black, the second is gray, the third is white, the fourth is black again, the fifth is gray, the sixth is white, and the colors alternate regularly up to the top layer.
Determine how many layers the pyramid has, given that 55 more black cubes were used than white ones.
(L. Simünek) | 41 |
67,002 | 7. As shown in the figure, in rectangle $A B C D$, $A B=3, A D=4, E$ is a point on $A B$, and $A E=1$. Now, $\triangle B C E$ is folded along $C E$ so that the projection of point $B$ on plane $A E C D$ falls on $A D$. Then, the volume of the pyramid $B-A E C D$ is $\qquad$ . | \frac{4\sqrt{3}}{3} |
67,007 | XXI OM - I - Problem 10
Find the largest natural number $ k $ with the following property: there exist $ k $ different subsets of an $ n $-element set, such that any two of them have a non-empty intersection. | 2^{n-1} |
67,032 | 4. Red, blue, green, and white four dice, each die's six faces have numbers $1,2,3,4,5,6$. Throwing these four dice simultaneously so that the product of the numbers facing up on the four dice equals 36, there are $\qquad$ possible ways. | 48 |
67,066 | 4. How many even five-digit numbers are there that are not divisible by 3 and do not contain the digit 9? | 19440 |
67,078 | 8. For a regular 2017-gon $A_{1} A_{2} \cdots A_{2017}$ inscribed in the unit circle $O$, if any two distinct vertices $A_{i}, A_{j}$ are chosen, then the probability that $\overrightarrow{O A_{i}} \cdot \overrightarrow{O A_{j}}>\frac{1}{2}$ is $\qquad$. | \frac{1}{3} |
67,084 | $$
\begin{array}{l}
\text { 6. Given } x, y \in \mathbf{R}, \\
z_{1}=x+(y+2) \mathrm{i}, \\
z_{2}=(x-2)+y \mathrm{i}, \\
\left|z_{1}\right|+\left|z_{2}\right|=4 .
\end{array}
$$
Then the maximum value of $|x+y|$ is | 2\sqrt{2} |
67,096 | Task 2. (10 points) Simplify the expression $2+22+222+\ldots+\underbrace{222 . . .2}_{2021}$. | \frac{20\cdot10^{2021}-36398}{81} |
67,117 | 1. In $\triangle A B C$, the sides opposite to angles $A, B, C$ are $a, b, c$ respectively. If the sizes of angles $A, B, C$ form a geometric sequence, and $b^{2}-a^{2}=a c$, then the radian measure of angle $B$ is equal to | \frac{2\pi}{7} |
67,123 | Example 5. Let's find all values of $a$ for which the system
$$
\left\{\begin{array}{l}
2^{b x}+(a+1) b y^{2}=a^{2} \\
(a-1) x^{3}+y^{3}=1
\end{array}\right.
$$
has at least one solution for any value of $b,(a, b, x, y \in \mathbf{R})$. | -1 |
67,138 | 9. Use three rectangles to form a larger rectangle (without gaps or overlaps), where two of the rectangles are $3 \mathrm{~cm} \times 8 \mathrm{~cm}$ and $2 \mathrm{~cm} \times 5 \mathrm{~cm}$, respectively. The dimensions of the third rectangle can be $\qquad$ kinds. | 4 |
67,166 | 3A. Determine the smallest natural number $n$ such that the proportion
$$
h_{a}: h_{b}: h_{c}=n:(n+1):(n+2)
$$
holds, where $h_{a}, h_{b}, h_{c}$ are the lengths of the altitudes in triangle $ABC$. | 2 |
67,185 | 8. The number of positive integer solutions $(x, y, z)$ to the equation $x+y+z=2010$ that satisfy $x \leqslant y \leqslant z$ is $\qquad$ . | 336675 |
67,208 | 3B. Given a parallelogram $A B C D$. The bisector of $\angle D A B$ intersects side $D C$ at point $L$, and diagonal $B D$ at point $K$, such that $\overline{D K}: \overline{K B}=3: 4$. Calculate the length of segment $L C$, if the perimeter of the parallelogram is 28. | 2 |
67,214 | B3. Two right triangles $\triangle A X Y$ and $\triangle B X Y$ have a common hypotenuse $X Y$ and side lengths (in units) $A X=5, A Y=10$, and $B Y=2$. Sides $A Y$ and $B X$ intersect at $P$. Determine the area (in square units) of $\triangle P X Y$. | \frac{25}{3} |
67,229 | 3. A school is hosting a Mathematics Culture Festival. According to statistics, there were more than 980 (no less than 980, less than 990) students visiting the school that day. Each student visits for a period of time and then leaves (and does not return). If, regardless of how these students arrange their visit times, we can always find $k$ students such that either all $k$ students are in the school at the same time, or at no time are any two of them in the school at the same time. What is the maximum value of $k$? | 32 |
67,230 | Let $A_{n}$ be the area outside a regular $n$-gon of side length 1 but inside its circumscribed circle, let $B_{n}$ be the area inside the $n$-gon but outside its inscribed circle. Find the limit as $n$ tends to infinity of $\frac{A_{n}}{B_{n}}$.
Then $A_{n}=\pi\left(\frac{1}{2} \csc \frac{\pi}{n}\right)^{2}-\frac{n}{4} \cot \frac{\pi}{n}$, and $B_{n}=\frac{n}{4} \cot \frac{\pi}{n}-\pi\left(\frac{1}{2} \cot \frac{\pi}{n}\right)^{2}$, so $\frac{A_{n}}{B_{n}}=\frac{\pi\left(\csc \frac{\pi}{n}\right)^{2}-n \cot \frac{\pi}{n}}{n \cot \frac{\pi}{n}-\pi\left(\cot \frac{\pi}{n}\right)^{2}}$. Let $s$ denote $\sin \frac{\pi}{n}$ and $c$ denote $\cos \frac{\pi}{n}$. Multiply numerator and denominator by $s^{2}$ to get $\frac{A_{n}}{B_{n}}=\frac{\pi-n c s}{n c s-\pi c^{2}}$. Now use Taylor series to replace $s$ by $\frac{\pi}{n}-\frac{\left(\frac{\pi}{n}\right)^{3}}{6}+\ldots$ and $c$ by $1-\frac{\left(\frac{\pi}{n}\right)^{2}}{2}+\ldots$. By l'Hôpital's rule it will suffice to take just enough terms so that the highest power of $n$ in the numerator and denominator is determined, and that turns out to be $n^{-2}$ in each case. In particular, we get the limit $\frac{A_{n}}{B_{n}}=\frac{\pi-n \frac{\pi}{n}+n \frac{2}{3}\left(\frac{\pi}{n}\right)^{3}+\ldots}{n \frac{\pi}{n}-n \frac{2}{3}\left(\frac{\pi}{n}\right)^{3}-\pi+\pi\left(\frac{\pi}{n}\right)^{2}+\ldots}=\frac{\frac{2}{3} \frac{\pi^{3}}{n^{2}}+\ldots}{\frac{1}{3} \frac{\pi^{3}}{n^{2}}+\ldots} \rightarrow \mathbf{2}$ | 2 |
67,251 | Task 2. Determine all positive integers $n$ for which there exist positive integers $a_{1}, a_{2}, \ldots, a_{n}$ such that
$$
a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}=6 n
$$
and
$$
\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}=2+\frac{1}{n}
$$ | 3 |
67,267 | 6.31 Team A and Team B each send out 7 players to participate in a Go relay match according to a pre-arranged order. Both sides start with the No. 1 player competing, the loser is eliminated, and the winner then competes with the No. 2 player from the losing side, $\cdots$, until all players from one side are eliminated, and the other side wins, forming a match process. How many different possible match processes are there? | 3432 |
67,271 | $3+$ [Properties and characteristics of an isosceles triangle.]
On each side of a square, one point was taken. It turned out that these points are the vertices of a rectangle, the sides of which are parallel to the diagonals of the square. Find the perimeter of the rectangle if the diagonal of the square is 6.
# | 12 |
67,296 | 28. [14] Compute the nearest integer to
$$
100 \sum_{n=1}^{\infty} 3^{n} \sin ^{3}\left(\frac{\pi}{3^{n}}\right)
$$ | 236 |
67,323 | 5. Egor wrote a number on the board and encrypted it according to the rules of letter puzzles (different letters correspond to different digits, the same letters correspond to the same digits). The result was the word "GUATEMALA". How many different numbers could Egor have initially written if his number was divisible by 25? | 18480 |
67,337 | 3. In the cells of a $3 \times 3$ square, the numbers $1,2,3, \ldots, 9$ are arranged. It is known that any two consecutive numbers are located in adjacent (by side) cells. Which number can be in the central cell if the sum of the numbers in the corner cells is $18?$ | 7 |
67,362 | What is the largest possible value of $|a_1 - 1| + |a_2-2|+...+ |a_n- n|$ where $a_1, a_2,..., a_n$ is a permutation of $1,2,..., n$? | \left\lfloor \frac{n^2}{2} \right\rfloor |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.