id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
63,671 | Does the following limit exist? If so, determine it.
$$
\lim _{x \rightarrow 0} x \cdot\left[\frac{1}{x}\right]
$$ | 1 |
63,677 | Example 2 Given the sequence $\left\{a_{n}\right\}$,
$$
a_{1}=a_{2}=a_{3}=1, a_{n+3} a_{n}=a_{n+1} a_{n+2}+1 \text {. }
$$
Find $a_{2 n+3} a_{2 n-1}-a_{2 n+1}^{2}$. | 2 |
63,705 | ## 259. Math Puzzle 12/86
We are looking for a specific number that ends in 2. If you move this last digit to the front of the number, the number doubles.
What is the number? | 105263157894736842 |
63,712 | 7 In the Cartesian coordinate system $x O y$, the graph of the function $f(x)=a \sin a x+\cos a x$ $(a>0)$ over an interval of the smallest positive period length and the graph of the function $g(x)=$ $\sqrt{a^{2}+1}$ enclose a closed figure whose area is $\qquad$ | \frac{2\pi}{}\sqrt{^{2}+1} |
63,715 | Suggestion: Show that triangle BEC is isosceles.
Facts that Help: The sum of the measures of the interior angles of a triangle is equal to $180^{\circ}$.
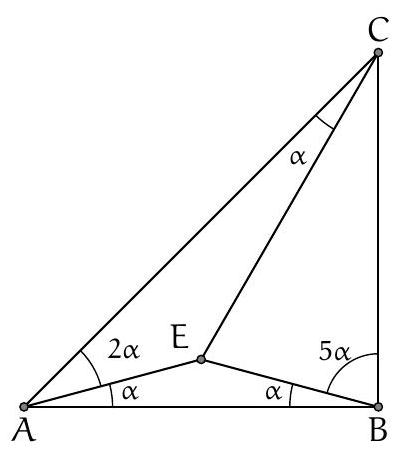
Inside a triangle $ABC$, a point $E$ is taken such that $AE = BE$ and $AB = EC$. If $A \hat{B E} = \alpha = E \hat{C A}$, $E \hat{A} C = 2 \alpha$ and $E \hat{B C} = 5 \alpha$, determine $\alpha$.
## | 15 |
63,718 | Exercise 10. Let $A B C D$ be a square and $E$ a point on the segment $[B D]$ such that $E B=A B$. We define the point $F$ as the intersection of the lines $(C E)$ and $(A D)$. Find the value of the angle $\widehat{F E A}$. | 45 |
63,723 | 14. [9] You have a $2 \times 3$ grid filled with integers between 1 and 9 . The numbers in each row and column are distinct, the first row sums to 23 , and the columns sum to 14,16 , and 17 respectively.
\begin{tabular}{c|c|c|c|}
& 14 & 16 & 17 \\
\hline 23 & $a$ & $b$ & $c$ \\
\hline & $x$ & $y$ & $z$ \\
\hline
\end{tabular}
What is $x+2 y+3 z$ ? | 49 |
63,724 | 3. Given the parabola $C: y^{2}=2 p x(p>0)$ and points $A(a, 0), A^{\prime}(-a, 0)(t>0)$. A line passing through point $A^{\prime}$ intersects the parabola at points $P, Q$. Then the sum of the slopes of lines $A P, A Q$ is $k_{A P}+k_{A Q}=$ $\qquad$ | 0 |
63,726 | Example 6 Given that for all real numbers $x$, the inequality $\left[\left(\log _{3} m\right)^{2}-\log _{3}\left(27 m^{2}\right)\right] x^{2}-\left(\log _{3} m-3\right) x-1<0$ always holds, find the range of real numbers $m$. | (3^{-\frac{1}{5}},27] |
63,736 | Let's find the largest number $A$ for which the following statement is true.
No matter how we choose seven real numbers between 1 and $A$, there will always be two of them for which the ratio $h$ satisfies $\frac{1}{2} \leqq h \leqq 2$. | 64 |
63,744 | 9 Given that the function $f(x)$ is defined on $\mathbf{R}$, and satisfies: (1) $f(x)$ is an even function; (2) For any $x \in \mathbf{R}$, $f(x+4)=f(x)$, and when $x \in[0,2]$, $f(x)=x+2$. Then the distance between the two closest intersection points of the line $y=4$ and the graph of the function $f(x)$ is $\qquad$ | 4 |
63,779 | # Problem 8.3
## Condition:
Given triangle $\mathrm{ABC}$, where $2 \mathrm{BC}=\mathrm{AC}$ and angle $\mathrm{C}=46^{\circ}$. On the ray $\mathrm{BC}$, segment $\mathrm{CM}=$ CB is marked. Then, from point M, a perpendicular is drawn to the line containing the median of triangle $\mathrm{ABC}$, drawn from vertex $\mathrm{B}$, and the intersection point is N. What is the measure of angle CMN? Express your answer in degrees. | 23 |
63,813 | A $2 \times 3$ rectangle and a $3 \times 4$ rectangle are contained within a square without overlapping at any point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square?
$\textbf{(A) } 16\qquad \textbf{(B) } 25\qquad \textbf{(C) } 36\qquad \textbf{(D) } 49\qquad \textbf{(E) } 64$ | 25 |
63,820 | 4. In triangle $A B C$, the median $B M$ was drawn. It turned out that $A B=2 B M$ and $\angle M B A=40^{\circ}$. Find $\angle C B A$.
# | 110 |
63,842 | Exercise 13. For any real number $x$, we denote $\lfloor x\rfloor$ as the greatest integer less than or equal to $x$, and we call the fractional part of $x$ the number $\langle x\rangle$ defined as $\langle x\rangle=x-\lfloor x\rfloor$. How many real numbers $x$ satisfy $1 \leqslant x \leqslant 10$ and $\langle x\rangle^{2}=\left\langle x^{2}\right\rangle$? | 91 |
63,843 | (5) Now arrange for 7 students to participate in 5 sports events, requiring that students A and B cannot participate in the same event, each event must have participants, and each person can only participate in one event. The number of different arrangements that meet the above requirements is (answer in numbers) | 15000 |
63,864 | 9. Given non-negative real numbers $u, v, w$ satisfy $u+v+w=$ 2, then the range of $u^{2} v^{2}+v^{2} w^{2}+w^{2} u^{2}$ is $\qquad$ | [0,1] |
63,881 | Example 2 Color each vertex of a square pyramid with one color, and make the endpoints of the same edge have different colors. If only 5 colors are available, then the total number of different coloring methods is $\qquad$ | 420 |
63,887 | (4) Given the functions $f(x)=\frac{x^{3}+x^{-3}}{5}, g(x)=\frac{x^{3}-x^{-3}}{5}$.
(1) For what real number $m$ does the equation $f(x)=m$ have a solution?
(2) Prove that $f(x)$ is an odd function, and find the intervals of monotonicity for $f(x)$;
(3) Calculate $g(4)-5 f(2) g(2)$ and $g(9)-5 f(3) g(3)$, and from this, generalize an equation involving the functions $f(x)$ and $g(x)$ that holds for all non-zero real numbers $x$, and prove it. | (x^{2})-5f(x)(x)=0 |
63,891 | 65. As shown in the figure, the intersection points of the two pairs of opposite sides of quadrilateral $ABCD$ are $E$ and $F$, and the intersection point of the diagonals is $G$. By selecting three points from $A$, $B$, $C$, $D$, $E$, $F$, and $G$ as the vertices of a triangle, the number of triangles that can be formed is $\qquad$. | 29 |
63,901 | Call a $ 3$-digit number [i]geometric[/i] if it has $ 3$ distinct digits which, when read from left to right, form a geometric sequence. Find the difference between the largest and smallest geometric numbers. | 840 |
63,928 | 4. Find all natural numbers that have exactly six divisors, whose sum is 3500. | 1996 |
63,929 | * On the hyperbola $x y=1$, the point with the abscissa $\frac{n}{n+1}$ is $A_{n}$, and the point with the abscissa $\frac{n+1}{n}$ is $B_{n}(n \in \mathbf{N})$. The point with coordinates $(1,1)$ is denoted as $M$. Also, $P_{n}\left(x_{n}, y_{n}\right)$ is the circumcenter of $\triangle A_{n} B_{n} M$. When $n \rightarrow \infty$, find: the limit point coordinates $(a, b)$ of $P_{n}$, where $a=\lim _{n \rightarrow \infty} x_{n}, b=\lim _{n \rightarrow \infty} y_{n}$. | (2,2) |
63,937 | 10.80 Euler's conjecture was disproved by American mathematicians in 1960, who confirmed the existence of a positive integer $n$ such that $133^{5}+110^{5}+84^{5}+27^{5}=n^{5}$. Find the value of $n$.
(7th American Invitational Mathematics Examination, 1989) | 144 |
63,948 | 3. In the diagram, $O A B$ is a quarter circle, $O E$ and $C D$ are parallel, $B C$ and $E A$ are parallel, and $\angle B C D=$ $4 \times \angle O B C$.
What is the size of $\angle O B C$ ?
Quadrilateral $F C G E$ must be a parallelogram, as $O E$ is parallel to $C D$ and $B C$ is parallel to $E A$ (given in the question).
We have that $\angle B C D=\angle A E O=4 x^{\circ}$, as opposite angles in a parallelogram are equal and we are told in the question that $\angle B C D=4 \times \angle O B C$.
Triangle $O A E$ is isosceles as $O A=O E$ because both are radii of the quarter circle $O A B$, thus $\angle O A E=\angle A E O=$ $4 x^{\circ}$.
Also $\angle O C B=\angle O A E$, as $B C$ is parallel to $E A$ and hence they are corresponding angles.
As $O A B$ is a quarter circle then $\angle B O A=90^{\circ}$.
Considering the sum of the interior angles of the right-angled triangle $O C B$,
$$
180^{\circ}=90^{\circ}+4 x^{\circ}+x^{\circ}
$$
Finally, the previous equation simplifies to $90^{\circ}=5 x^{\circ}$ and so $\angle O B C=x^{\circ}=18^{\circ}$. | 18 |
63,962 | 8. Solve the equation $\log _{5}(3 x-4) \cdot \log _{5}(7 x-16) \cdot\left(3-\log _{5}\left(21 x^{2}-76 x+64\right)\right)=1$. | 3 |
63,967 | 6. As shown in the figure, in the cube $A B C D-A_{1} B_{1} C_{1} D_{1}$, $M, N$ are the midpoints of edges $A_{1} B_{1}, B B_{1}$ respectively. A section is made through points $D, M, N$ of the cube, and it is known that the section is a polygon $\Gamma$. Then, the cosine value of the interior angle of $\Gamma$ at vertex $D$ is $\qquad$ | \frac{4}{13} |
63,970 | 1. How many times in a day does the angle between the hour and minute hands equal exactly $19^{\circ}$? | 44 |
63,978 | ## Task Condition
Find the derivative.
$$
y=\operatorname{arctg} \frac{\sqrt{1-x}}{1-\sqrt{x}}
$$ | \frac{1}{4\sqrt{x(1-x)}} |
63,980 | 8. As shown in Figure 5, the area of rectangle $A B C D$ is $35 \mathrm{~cm}^{2}$, the area of shaded $\triangle A B E$ is $5 \mathrm{~cm}^{2}$, and the area of shaded $\triangle A D F$ is $7 \mathrm{~cm}^{2}$. What is the area of $\triangle A E F$ in square centimeters? | 15.5 |
63,984 | 4. Team A and Team B each send out 7 players to participate in a Go relay match in a pre-arranged order. Both sides start with their No. 1 players competing. The loser is eliminated, and the winner then competes with the No. 2 player of the losing side, ... until all players of one side are eliminated, and the other side wins, forming a match process. The total number of all possible match processes is $\qquad$ . | 3432 |
64,000 | 4. Find all prime numbers whose decimal representation has the form 101010 ... 101 (ones and zeros alternate). | 101 |
64,018 | 1. The number of proper subsets of the set $\left\{x \left\lvert\,-1 \leqslant \log _{\frac{1}{x}} 10<-\frac{1}{2}\right., x \in \mathbf{N}\right\}$ is | 2^{90}-1 |
64,021 | 3.449 $A=\operatorname{tg}\left(\arccos \frac{1}{\sqrt{1+a^{2}}}+\arccos \frac{a}{\sqrt{1+a^{2}}}\right) a<0$.
3.449 $A=\tan\left(\arccos \frac{1}{\sqrt{1+a^{2}}}+\arccos \frac{a}{\sqrt{1+a^{2}}}\right) a<0$. | \frac{1-^{2}}{2} |
64,044 | 3. (16 points) A chess player played 42 games and scored 30 points (1 point for each win, -0.5 points for each draw, 0 points for each loss). Find the difference between the number of his wins and the number of his losses. | 18 |
64,062 | Example 10. Solve the equation
$$
y^{\prime \prime \prime}-2 y^{\prime \prime}+2 y^{\prime}=4 \cos x \cos 3 x+6 \sin ^{2} x
$$ | C_{1}+(C_{2}\cosx+C_{3}\sinx)e^{x}+\frac{1}{65}(\cos4x-\frac{7}{4}\sin4x)+\frac{1}{10}(\frac{\sin2x}{2}-\cos2x)+\frac{3}{2}x |
64,065 | 3. We call integers composed of the digit 8 "lucky numbers", such as $8, 88, 888$, etc. A number obtained by adding 8 "lucky numbers" is called a "happy number", such as $8+8+8+8+8+8+88+88=224$. The number of "happy numbers" less than 1000 is $\qquad$. | 10 |
64,090 | PROBLEM 4. We say that a number of the form $\overline{0, a b c d e}$ has property $(P)$ if the digits $a, b, c, d, e$ belong to the set $\{4,6\}$.
a) Show that the solution to the equation $x+0,46646=1,1111$ has property $(P)$;
b) Determine how many different numbers of the form $\overline{0, a b c d e}$ have property $(P)$;
c) Show that from any 17 different numbers of the form $\overline{0, a b c d e}$ that have property $(P)$, two can be chosen whose sum is 1,1111 .[^0]
## NATIONAL MATHEMATICS OLYMPIAD Local stage - 5.03. 2016 GRADING GUIDE - 6th Grade | 32 |
64,123 | 21. A sequence of numbers is arranged according to the rule:
$$
1^{1}, 2^{2}, 3^{3}, 4^{4}, 5^{5}, 1^{6}, 2^{7}, 3^{8}, 4^{9}, 5^{10}, \cdots \cdots
$$
The bases cycle through $1 \sim 5$, and the exponents start from 1 and increase sequentially. Let the sum of the first $n$ numbers be denoted as $P(n)$. When $P(n)$ is a multiple of 10 for the first time, $n=$ $\qquad$ . | 37 |
64,131 | (5) In a regular tetrahedron $ABCD$, $AO \perp$ plane $BCD$, with the foot of the perpendicular being $O$. Let $M$ be a point on the line segment $AO$ such that $\angle BMC=90^{\circ}$. Then $\frac{AM}{MO}=$ $\qquad$ . | 1 |
64,138 | In the diagram, $A B$ is parallel to $C D$. Points $E$ and $F$ are on $A B$ and $C D$, respectively, so that $\angle F A B=30^{\circ}$ and $\angle A F E=\angle E F B=\angle B F D=x^{\circ}$. What is the value of $x$ ?
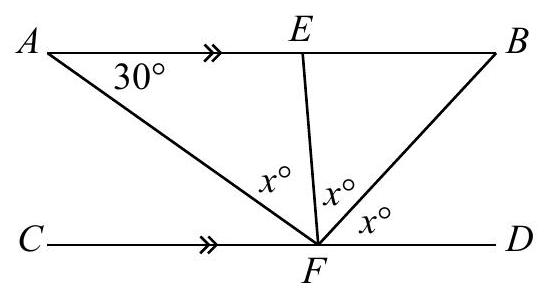 | 50 |
64,151 | 3. Given numbers $x_{1}, \ldots, x_{n} \in\left(0, \frac{\pi}{2}\right)$. Find the maximum value of the expression
$$
A=\frac{\cos ^{2} x_{1}+\ldots+\cos ^{2} x_{n}}{\sqrt{n}+\sqrt{\operatorname{ctg}^{4} x_{1}+\ldots+\operatorname{ctg}^{4} x_{n}}}
$$ | \frac{\sqrt{n}}{4} |
64,163 | I2.3 There are less than $4 Q$ students in a class. In a mathematics test, $\frac{1}{3}$ of the students got grade $A$, $\frac{1}{7}$ of the students got grade $B$, half of the students got grade $C$, and the rest failed. Given that $R$ students failed in the mathematics test, find the value of $R$. | 1 |
64,170 | 2. [20] Let $a, b$, and $c$ be complex numbers such that $|a|=|b|=|c|=|a+b+c|=1$. If $|a-b|=|a-c|$ and $b \neq c$, evaluate $|a+b||a+c|$. | 2 |
64,205 | Three. (50 points)
The sequence of real numbers $a_{1}, a_{2}, \cdots a_{n}, \cdots$, is defined by the following equation:
$$
a_{n+1}=2^{n}-3 a_{n}, n=0,1,2, \cdots \text {. }
$$
1. Find the expression for $a_{n}$ in terms of $a_{0}$ and $n$;
2. Find $a_{0}$ such that for any positive integer $n, a_{n+1}>a_{n}$. | a_{0}=\frac{1}{5} |
64,239 | 3. Given an acute-angled triangle $A B C$. A circle with diameter $B C$ intersects sides $A B$ and $A C$ at points $D$ and $E$ respectively. Tangents drawn to the circle at points $D$ and $E$ intersect at point $K$. Find the angle between the lines $A K$ and $B C$. | 90 |
64,246 | 7.191. $\log _{10} x+\log _{\sqrt{10}} x+\log _{\sqrt[3]{10}} x+\ldots+\log _{\sqrt[1]{10}} x=5.5$. | \sqrt[10]{10} |
64,247 | ## Task B-3.5.
Four cities on the map determine the vertices of a quadrilateral $A B C D$ to which a circle of radius $R$ can be circumscribed. The distance between cities $A$ and $C$ is $2 R$, and the distance between cities $A$ and $B$ is equal to the distance between cities $B$ and $C$. The ratio of the distance between cities $A$ and $D$ and the distance between cities $C$ and $D$ is $\sqrt{3}$. What is the distance between cities $B$ and $D$? | R\sqrt{2+\sqrt{3}} |
64,274 | Task 3. (Option 2)
Thirty clever students from 6a, 7a, 8a, 9a, and 10a grades were tasked with creating forty problems for the olympiad. Any two classmates came up with the same number of problems, while any two students from different grades came up with a different number of problems. How many people came up with just one problem? | 26 |
64,277 | 1. Given the set
$$
M=\{1,2, \cdots, 2020\},
$$
for any non-empty subset $A$ of $M, \lambda_{A}$ is the sum of the largest and smallest numbers in the set $A$. Then the arithmetic mean of all such $\lambda_{A}$ is $\qquad$ . | 2021 |
64,278 | 3. (17 points) In triangle $A B C$, a point $N$ is taken on side $A C$ such that $A N=N C$. Side $A B$ is twice as long as $B N$, and the angle between $A B$ and $B N$ is $50^{\circ}$. Find the angle $A B C$. | 115 |
64,284 | 5. The sum of the digits of the result of the calculation $\underbrace{99 \cdots 99}_{2021 \uparrow 9} \times \underbrace{99 \cdots 99}_{2020 \uparrow 9}$ is $\qquad$ | 18189 |
64,288 | Problem 9. The function $F$ is defined on the set of triples of integers and takes real values. It is known that for any four integers $a, b, c$ and $n$ the equalities $F(n a, n b, n c)=n \cdot F(a, b, c)$, $F(a+n, b+n, c+n)=F(a, b, c)+n$, $F(a, b, c)=F(c, b, a)$ hold. Find $F(58,59,60)$. | 59 |
64,321 | 6. Find the set of values of the function $f(x)=4 \cos \left(\frac{\pi}{3} \sin \left(x^{2}+6 x+10-\sin x\right)\right)$.
# | [2;4] |
64,339 | Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
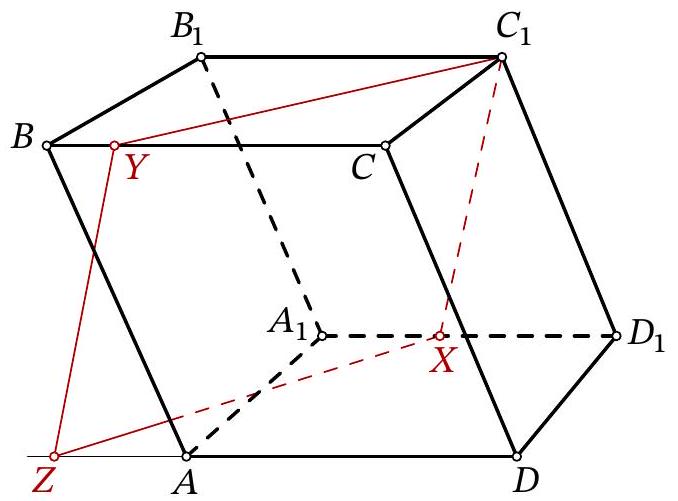 | 20 |
64,343 | We have 1000 unit-edged small cubes. From these, we want to create a hollow cube with a wall thickness of one unit. The small cubes can be glued together, but they cannot be cut. What is the maximum volume (external) cube we can make this way? | 2197 |
64,354 | 12. In the first quarter, Vasya had 5 math grades, with the most being fives. It turned out that the median of all grades was 4, and the arithmetic mean was 3.8. What grades could Vasya have had? | (2,3,4,5,5) |
64,359 | Five. (Full marks: 15 points) From the 91 natural numbers $1,2,3, \cdots, 90,91$, select $k$ numbers such that there must be two natural numbers $p, q$ satisfying $\frac{2}{3} \leqslant \frac{q}{p} \leqslant \frac{3}{2}$. Determine the minimum value of the natural number $k$, and explain your reasoning. | 10 |
64,377 | $7 \cdot 67$ Given 11 sets $M_{1}, M_{2}, \cdots, M_{11}$, where each set has exactly 5 elements and for all $i, j, 1 \leqslant i<j \leqslant 11$, there is $M_{i} \cap M_{j} \neq \varnothing$, find the minimum possible value of the maximum number of sets among these sets whose intersection is non-empty. | 4 |
64,382 | Problem 11.4. In a sports school, 55 people are training, each of whom is either a tennis player or a chess player. It is known that there are no four chess players who would have the same number of friends among the tennis players. What is the maximum number of chess players that can train in this school? | 42 |
64,401 | 456. Every evening, Uncle Chernomor appoints 9 or 10 out of 33 bogatyrs for duty, at his discretion. What is the smallest number of days after which it can happen that each of the bogatyrs has been on duty the same number of times? | 7 |
64,416 | 3. Let the pair of positive integers $(x, y)$ be such that $\frac{x^{2}+y^{2}}{11}$ is an integer, and satisfies the condition $\frac{x^{2}+y^{2}}{11} \leqslant 1991$. Find the number of such pairs of positive integers $(x, y)$ (when $a \neq b$, $(a, b)$ and $(b, a)$ are considered different pairs). | 131 |
64,431 | 20th APMC 1997 Problem 3 The 97 numbers 49/1, 49/2, 49/3, ... , 49/97 are written on a blackboard. We repeatedly pick two numbers a, b on the board and replace them by 2ab - a - b + 1 until only one number remains. What are the possible values of the final number? | 1 |
64,442 | 6. The range of the function $f(x)=\frac{x-x^{3}}{\left(1+x^{2}\right)^{2}}$ is $\qquad$ | [-\frac{1}{4},\frac{1}{4}] |
64,445 | 8.4 The sequence of numbers $\mathrm{a}_{1}, \mathrm{a}_{2}, \mathrm{a}_{3}, \ldots, \mathrm{a}_{\mathrm{n}}, \ldots$ satisfies the relations $\mathrm{a}_{\mathrm{n}}=\mathrm{a}_{\mathrm{n}-1} \cdot \mathrm{a}_{\mathrm{n}-3}$ for $\mathrm{n}=4,5,6, \ldots$ Find $\mathrm{a}_{2019}$ if it is known that $\mathrm{a}_{1}=1, \mathrm{a}_{2}=1$, $\mathrm{a}_{3}=-1$ | -1 |
64,485 | ## Task Condition
Find the derivative.
$$
y=\ln \left(x+\sqrt{x^{2}+1}\right)-\frac{\sqrt{1+x^{2}}}{x}
$$ | \frac{\sqrt{x^{2}+1}}{x^{2}} |
64,515 | 635. What exact square is equal to the product of four consecutive odd numbers? | 9 |
64,527 | 7. Express the polynomial in $x$
$$
f(x)=1-x+x^{2}-x^{3}+\cdots-x^{19}+x^{20}
$$
as a polynomial in $y$
$$
g(y)=a_{0}+a_{1} y+\cdots+a_{20} y^{20},
$$
where $y=x-4$. Then $a_{0}+a_{1}+\cdots+a_{20}=$
$\qquad$ | \frac{5^{21}+1}{6} |
64,529 | Problem 77. Find the sum of the squares of the sides of an inscribed quadrilateral with perpendicular diagonals in a circle of radius $R$.
---
Translated as requested, maintaining the original text's line breaks and format. | 8R^{2} |
64,537 | Determine the gcd of all numbers of the form
$$
(a-b)(b-c)(c-d)(d-a)(b-d)(a-c)
$$
where $a, b, c, d$ range over $\mathbb{Z}$. | 12 |
64,552 |
5. Determine the number of all coverings of a chessboard $3 \times 10$ by (nonoverlapping) pieces $2 \times 1$ which can be placed both horizontally and vertically.
(Stanislava Sojáková)
| 571 |
64,554 | 10.6. In an equilateral triangle $ABC$, a point $P$ is chosen such that $AP=10, BP=8, CP=6$. Find the area of this triangle.
# | 36+25\sqrt{3} |
64,577 | I am thinking of a non-negative number in the form of a fraction with an integer numerator and a denominator of 12. When I write it as a decimal number, it will have one digit before and one digit after the decimal point, and both of these digits will be non-zero. There are multiple numbers that have both of these properties. However, if I arrange them from smallest to largest, the one I am thinking of will be the second to last.
What number am I thinking of? | 8.5 |
64,647 | ## 265. Math Puzzle $6 / 87$
For a motorcycle, the optimal rotational speed of the engine shaft is $6000 \mathrm{U} / \mathrm{min}$.
What is the gear ratio of the rear axle to the engine shaft produced by the transmission if the optimal rotational speed results in a speed of $60 \mathrm{~km} / \mathrm{h}$?
The diameter of the rear wheel is $53 \mathrm{~cm}$ (circumference 1.67 m). | 1:10 |
64,660 | 7.4. Two cyclists set off simultaneously towards each other from points $A$ and $B$ and met 70 km from $A$. Continuing to move at the same speeds, they reached $A$ and $B$ and turned back. They met for the second time 90 km from $B$. Find the distance from $A$ to $B$. | 120 |
64,664 | A convex polyhedron has more faces than vertices. What is the minimum number of triangles among the faces? | 6 |
64,684 | [ Divisibility of numbers. General properties ]
The year of the current mathematics festival is divisible by its number: $2006: 17=118$.
a) Name the first number of the math festival for which this was also true.
b) Name the last number of the math festival for which this will also be true.
# | 1989 |
64,704 | Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x$ and $y$:
$$
f\left(x^{2022}+y\right)=f\left(x^{1747}+2 y\right)+f\left(x^{42}\right)
$$ | 0 |
64,721 | Three unit-radius circles pass through a common point. Their second intersection points are $A, B$, and $C$. What is the radius of the circle $ABC$? | 1 |
64,726 | 17. Three composite numbers $A, B, C$ are pairwise coprime, and $A \times B \times C=11011 \times 28$, then the maximum value of $A+B+C$ is . $\qquad$ | 1626 |
64,738 | 7. As shown in Figure 1, there is a solid metal sphere with a radius of 20. A circular hole with a radius of 12 is drilled along a certain diameter as the central axis, and the remaining part is melted and cast into a new solid sphere. What is the radius of the new sphere? $\qquad$ | 16 |
64,748 | Alice returned the rattle to its rightful owner, but a few days later, another brother broke the rattle again. This time, the raven did not come to scare the brothers, and they began to beat each other with all their might. Alice grabbed the broken rattle and ran out of the forest.
After some time, Alice met the White King and told him in detail everything that had happened.
- All of this is very, very interesting, - the King assured her. - The most remarkable thing about the whole story is that, although you know to whom you returned the rattle, we still do not know who the owner is, Tralala or Trulala.
- You are quite right, your majesty, - agreed Alice. - But what are we to do with the broken rattle?
- Nonsense, - said the King. - It's nothing for me to fix it again.
And true to his word, the White King repaired the rattle so skillfully that it became as good as new, and a few days later he returned it to Alice. With trepidation, Alice set off for the forest, fearing that the brothers were still fighting. But by this time, Tralala and Trulala had declared a truce, and Alice found one of them resting under a tree. Alice approached him and asked:
- Which of you does the rattle belong to?
He answered enigmatically:
- The true owner of the rattle lies today.
What are the chances that he was the true owner of the rattle? | 0 |
64,774 | Example 7 Let the sequence $\left\{a_{n}\right\}$ be such that $a_{1}=1, a_{n+1}=\frac{1}{16}\left(1+4 a_{n}+\sqrt{1+24 a_{n}}\right)$, find $a_{n}$. | a_{n}=\frac{1+3\times2^{n-1}+2^{2n-1}}{3\times2^{2n-1}} |
64,779 | 1. When $a^{3}-a-1=0$, $a+\sqrt{2}$ is a root of some polynomial with integer coefficients. Find the polynomial of the lowest degree with leading coefficient 1 that satisfies the above condition. | x^{6}-8x^{4}-2x^{3}+13x^{2}-10x-1 |
64,785 | 2. The quartic (4th-degree) polynomial $P(x)$ satisfies $P(1)=0$ and attains its maximum value of 3 at both $x=2$ and $x=3$. Compute $P(5)$. | -24 |
64,797 | [ [MT - line or segment]
Two wheels of radii $r_{1}$ and $r_{2}$ roll along a line $l$. Find the set of points of intersection $M$ of their common internal tangents.
# | \frac{2r_{1}r_{2}}{r_{1}+r_{2}} |
64,799 | For constant $k>1$, 2 points $X,\ Y$ move on the part of the first quadrant of the line, which passes through $A(1,\ 0)$ and is perpendicular to the $x$ axis, satisfying $AY=kAX$. Let a circle with radius 1 centered on the origin $O(0,\ 0)$ intersect with line segments $OX,\ OY$ at $P,\ Q$ respectively. Express the maximum area of $\triangle{OPQ}$ in terms of $k$.
[i]2011 Tokyo Institute of Technology entrance exam, Problem 3[/i] | \frac{1}{2} \left( \frac{k-1}{k+1} \right) |
64,802 | In a chess tournament, sports masters and candidates for masters are participating. What is the smallest number of people that can participate in this tournament if it is known that among them, masters are less than half, but more than $45 \%$.
# | 11 |
64,813 | 1. The irrational number $0.123456789101112 \ldots$ is formed by concatenating, in increasing order, all the positive integers. Find the sum of the first 2016 digits of this number after the decimal point. | 8499 |
64,824 | 155.
From the Middle Sanctuary, one can exit through four doors $\mathrm{X}, \mathrm{Y}, \mathrm{Z}$, and $\mathrm{W}$. At least one of them leads to the Inner Sanctuary. Those who exit through another door are devoured by a fire-breathing dragon.
In the Middle Sanctuary, during the trial, there are eight priests A, B, C, D, E, F, G, and H, each of whom is either a knight or a liar. The priests told our philosopher the following.
A: X is the door leading to the Inner Sanctuary.
B: At least one of the doors Y and Z leads to the Inner Sanctuary.
C: A and B are knights.
D: Both doors X and Y lead to the Inner Sanctuary.
E: Both doors X and Y lead to the Inner Sanctuary.
F: Either D or E is a knight.
G: If C is a knight, then F is a knight.
H: If G and I myself are knights, then A is a knight.
Which door should the philosopher choose? | X |
64,828 | Example 7 Given $a=\sqrt{5}-1$. Then the value of $2 a^{3}+7 a^{2}-2 a$ -12 is $\qquad$ [7]
(2010) "Mathematics Weekly" Cup National Junior High School Mathematics Competition) | 0 |
64,836 | 17. What is the smallest three-digit positive integer which can be written in the form $p q^{2} r$, where $p, q$ and $r$ are distinct primes? | 126 |
64,842 | 3. Two baby squirrels are located at points $A$ and $B$, and start jumping simultaneously along lines $A O$ and $B O$ towards point $O$ (after passing point $O$, each continues moving along its own line). The distance $A O=120$ meters, $B O=80$ meters, and the angle $A O B=60^{\circ}$. The baby squirrels have a constant and identical speed. What is the minimum distance between the baby squirrels during their movement? | 20\sqrt{3} |
64,846 | 10. Given that $\lambda$ is a positive real number, the sequence $\left\{a_{n}\right\}$ satisfies: $a_{1}=\frac{1}{3}, a_{n+1}=\frac{2 a_{n}^{2}}{4 a_{n}^{2}-2 a_{n}+1}, n=1,2,3, \cdots$. If for any $m \in \mathbf{N}^{*}$, we have $\sum_{k=1}^{m} a_{k}<\lambda$, find the minimum value of $\lambda$. | 1 |
64,857 | Example 17 Let $x, y \in \mathbf{R}$, find the minimum value of the function $f(x, y)=\sqrt{x^{2}+y^{2}}+\sqrt{(x-1)^{2}+(y-1)^{2}}+$ $\sqrt{(x+2)^{2}+(y+2)^{2}}$. | 3\sqrt{2} |
64,858 | 10. In $\triangle A B C$, $A B=A C, \angle A=80^{\circ}, D$ is a point inside the triangle, and $\angle D A B=\angle D B A=10^{\circ}$, find the degree measure of $\angle A C D$.
(Problem 432 from "Mathematics Teaching") | 30 |
64,887 | Example 8 Simplify $\tan \alpha \tan 2 \alpha+\tan 2 \alpha \tan 3 \alpha+\cdots+\tan (n-1) \alpha \tan n \alpha$. | \frac{\tann\alpha}{\tan\alpha}-n |
64,889 | 12.142. A triangle is inscribed in a circle of radius $R$, with its vertices dividing the circle into three parts in the ratio $2: 5: 17$. Find the area of the triangle. | \frac{R^{2}}{4} |
64,929 | 7. Given that $x, y, z$ are positive real numbers, satisfying $x+y+z=1$, if $\frac{a}{x y z}=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-2$, then the range of the real number $a$ is | (0,\frac{7}{27}] |
64,968 | 6. In a checkers tournament, students from 10th and 11th grades participated. Each player played against every other player once. A player received 2 points for a win, 1 point for a draw, and 0 points for a loss. There were 10 times more 11th graders than 10th graders, and together they scored 4.5 times more points than all the 10th graders. How many points did the most successful 10th grader score? | 20 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.