id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
67,371 | In the diagram, some of the hexagons are shaded. What fraction of all of the hexagons are shaded?
(A) $\frac{1}{2}$
(D) $\frac{1}{3}$
(B) $\frac{5}{9}$
(C) $\frac{4}{5}$
(E) $\frac{5}{6}$
 | \frac{5}{9} |
67,382 | Car A is traveling at 20 miles per hour. Car B is 1 mile behind, following at 30 miles per hour. A fast fly can move at 40 miles per hour. The fly begins on the front bumper of car B, and flies back and forth between the two cars. How many miles will the fly travel before it is crushed in the collision? | 4 |
67,392 | Find the integers $n \geqslant 1$ for which $n$ divides $2^{n}-1$. | 1 |
67,410 | 46th Putnam 1985 Problem B1 p(x) is a polynomial of degree 5 with 5 distinct integral roots. What is the smallest number of non-zero coefficients it can have? Give a possible set of roots for a polynomial achieving this minimum. Solution | 3 |
67,428 | 4. Person A and Person B are stacking pyramids with some spheres of radius 2. Person A stacks a square pyramid: composed of $n$ layers, with 1 sphere on the top layer, 4 spheres on the second layer, 9 spheres on the third layer, ... each sphere touching four spheres in the layer below. Person B stacks a triangular pyramid: composed of $n$ layers, with 1 sphere on the top layer, 3 spheres on the second layer, 6 spheres on the third layer, ... each sphere touching three spheres in the layer below. If Person A uses 2109 spheres, then Person B needs to use at least $\qquad$ spheres to ensure that his pyramid is taller than Person A's. | 816 |
67,460 | 22. Let $S$ be the set of points whose coordinates $x, y$ and $z$ are integers that satisfy $0 \leq x \leq 2,0 \leq y \leq 3$ and $0 \leq z \leq 4$. Two distinct points are randomly chosen from $S$. Find the probability that the midpoint of the two chosen points also belongs to $S$ ?
設 $S$ 爲座標 $x 、 y 、 z$ 皆臬整數, 且滿足 $0 \leq x \leq 2 、 0 \leq y \leq 3$ 和 $0 \leq z \leq 4$ 的點集。現從 $S$ 中隨意抽出兩個不同的點,求該兩點的中點亦屬於 $S$ 的概率。 | \frac{23}{177} |
67,468 | 4. In triangle $A B C$ with area 51 , points $D$ and $E$ trisect $A B$ and points $F$ and $G$ trisect $B C$. Find the largest possible area of quadrilateral $D E F G$. | 17 |
67,471 | Let $m=999 \ldots 99$ be the number formed by 77 digits all equal to 9 and let $n=777 \ldots 77$ be the number formed by 99 digits all equal to 7. What is the number of digits of $m \cdot n$? | 176 |
67,500 | 18. If $\frac{a(b-c)}{b(c-a)}=\frac{b(c-a)}{c(b-a)}=r$ and $r>0$, find $r$.
(2 marks)
若 $\frac{a(b-c)}{b(c-a)}=\frac{b(c-a)}{c(b-a)}=r$, 且 $r>0$, 求 $r$ 。 | \frac{\sqrt{5}-1}{2} |
67,504 | [ Thales' Theorem and the Proportional Segments Theorem ] The Midline of a Triangle
In triangle $A B C$, point $M$ is the midpoint of side $A C$, and point $P$ lies on side $B C$. Segment $A P$ intersects $B M$ at point $O$. It turns out that $B O = B P$.
Find the ratio $O M: P C$. | 1:2 |
67,506 | 8. Through a point $P$ on a sphere with radius 5, three mutually perpendicular chords $P A, P B$, and $P C$ are drawn such that $P A=2 P B$. Then the maximum value of $P A+P B+P C$ is $\qquad$ . | 2\sqrt{70} |
67,508 | 1. Consider a rectangular parallelepiped $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$, where $A B C D$ is the bottom face with the letters assigned in a clockwise direction, and $A, B, C$, and $D$ are directly below $A^{\prime}, B^{\prime}, C^{\prime}$, and $D^{\prime}$ respectively. The parallelepiped is divided into eight pieces by three planes that are orthogonal to each other and parallel to the faces of the parallelepiped. For each vertex $P$ of the parallelepiped, let $V_{P}$ denote the volume of the piece of the parallelepiped that contains $P$. Given that $V_{A}=40, V_{C}=300, V_{B^{\prime}}=360$ and $V_{C^{\prime}}=90$, what is the volume of the parallelepiped $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$? | 2015 |
67,514 | 201. Segments defining an equilateral triangle. Three segments of lengths 3, 4, and 5 cm connect an internal point \( P \) of an equilateral triangle to its vertices. What is the length of the side of this triangle?
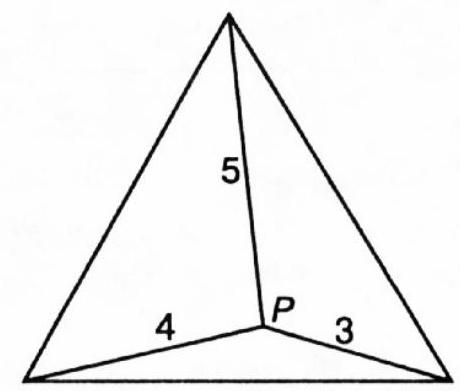 | 6.7664 |
67,527 | In a tournament with $55$ participants, one match is played at a time, with the loser dropping out. In each match, the numbers of wins so far of the two participants differ by not more than $1$. What is the maximal number of matches for the winner of the tournament? | 8 |
67,537 | Bakayev E.V.
Forty children were holding hands in a circle. Out of them, 22 were holding hands with a boy and 30 were holding hands with a girl. How many girls were in the circle?
# | 24 |
67,549 | Calculate the number of ways of choosing $4$ numbers from the set ${1,2,\cdots ,11}$ such that at least $2$ of the numbers are consecutive. | 260 |
67,551 | 5. Yesterday at the market, with one hundred tugriks you could buy 9 gingerbreads and 7 pastries (and even get some change), but today this amount is no longer enough. However, with the same one hundred tugriks today, you can buy two gingerbreads and 11 pastries (also with some change), but yesterday this amount would not have been enough. A gingerbread and a pastry cost a whole number of tugriks, and the price of each sweet changed by no more than one tugrik overnight. $A$ How much does one gingerbread cost today? | 5 |
67,561 | [ Symmetry helps solve the problem.] Rearrangement of areas $\quad]$
A point located inside an equilateral triangle is at distances of 5, 6, and 7 from its vertices. Find the area of the triangle. | \frac{55\sqrt{3}+36\sqrt{6}}{4} |
67,566 | 6. Draw a normal line (a normal line is a line passing through the point of tangency and perpendicular to the tangent line) at point $A$ on the parabola $y=x^{2}$, intersecting the parabola at another point $B$, and $O$ is the origin. When the area of $\triangle O A B$ is minimized, the y-coordinate of point $A$ is $\qquad$ (Liu Kaifeng) | \frac{-3+\sqrt{33}}{24} |
67,579 | (3) For a point $M(1,1)$ on the parabola $y=x^{2}$ as the right-angle vertex, construct two inscribed right-angled triangles $\triangle M A B$ and $\triangle M C D$ in the parabola, then the coordinates of the intersection point $E$ of line segments $A B$ and $C D$ are | (-1,2) |
67,638 | Problem 2. In a two-digit number, each digit was increased by 2 or by 4 (different digits could be increased by different numbers), as a result of which the number increased fourfold. What could the original number have been? Find all possible options and prove that there are no others. | 14 |
67,642 | The set $M$ consists of all 7-digit positive integers that (in decimal notation) contain each of the digits 1, 3, 4, 6, 7, 8, and 9 exactly once.
(a) Determine the smallest positive difference $d$ between two numbers in $M$.
(b) How many pairs $(x, y)$ with $x$ and $y$ from $M$ are there such that $x-y=d$?
Answer. a) The smallest possible difference is 9. b) There are 480 such number pairs. | 480 |
67,643 | 95. Three points $A, B$ and $C$ are taken at random on a circle. What is the probability that triangle $A B C$ will be acute? | \frac{1}{4} |
67,648 | $:$ Govanov A.S.
Petya and Vasya came up with ten polynomials of the fifth degree. Then Vasya sequentially called out natural numbers (starting from some number), and Petya substituted each called number into one of the polynomials of his choice and wrote down the obtained values on the board from left to right. It turned out that the numbers written on the board form an arithmetic progression (in this exact order). What is the maximum number of numbers Vasya could have called? | 50 |
67,650 | 3. Zhenya had 9 cards with numbers from 1 to 9. He lost the card with the number 7. Can the remaining 8 cards be arranged in a row so that any two adjacent cards form a number divisible by 7? | no |
67,713 | In an $n$-by-$m$ grid, $1$ row and $1$ column are colored blue, the rest of the cells are white. If precisely $\frac{1}{2010}$ of the cells in the grid are blue, how many values are possible for the ordered pair $(n,m)$ | 96 |
67,753 | 8. There are 9 different pastries and drinks placed at 9 positions around a round table. 6 gentlemen and 3 ladies are having breakfast together. The number of ways for the 3 ladies to sit such that no two of them are adjacent is $\qquad$ kinds. | 129600 |
67,790 | 9. In the Cartesian coordinate system, $F_{1}, F_{2}$ are the two foci of the hyperbola $\Gamma: \frac{x^{2}}{3}-y^{2}=1$. A point $P$ on $\Gamma$ satisfies $\overrightarrow{P F_{1}} \cdot \overrightarrow{P F_{2}}=1$. Find the sum of the distances from point $P$ to the two asymptotes of $\Gamma$. | \frac{3\sqrt{2}}{2} |
67,793 | 13. An ant crawls along the edges of a cube with side length 1 unit. Starting from one of the vertices, in each minute the ant travels from one vertex to an adjacent vertex. After crawling for 7 minutes, the ant is at a distance of $\sqrt{3}$ units from the starting point. Find the number of possible routes the ant has taken.
(2 marks)
An ant crawls along the edges of a cube with side length 1 unit. Starting from one of the vertices, in each minute the ant travels from one vertex to an adjacent vertex. After crawling for 7 minutes, the ant is at a distance of $\sqrt{3}$ units from the starting point. Find the number of possible routes the ant has taken. | 546 |
67,801 | ## Task A-4.3.
How many complex numbers $z$ satisfy the following two conditions:
$$
|z|=1, \quad \operatorname{Re}\left(z^{100}\right)=\operatorname{Im}\left(z^{200}\right) \quad ?
$$ | 400 |
67,835 | 16. Given a function $f(x)$ defined on $(0,+\infty)$ that satisfies: for any $x \in(0,+\infty)$, it always holds that
$$
f(2 x)=2 f(x) \text {; }
$$
when $x \in(1,2]$, $f(x)=2-x$.
The following conclusions are given:
(1) For any $m \in \mathbf{Z}$, $f\left(2^{m}\right)=0$;
(2) The range of the function $f(x)$ is $[0,+\infty)$;
(3) There exists $n \in \mathbf{Z}$ such that $f\left(2^{n}+1\right)=9$;
(4) The necessary and sufficient condition for "the function $f(x)$ is monotonically decreasing on the interval $(a, b)$" is "there exists $k \in \mathbf{Z}$ such that $(a, b) \subseteq\left(2^{k}, 2^{k+1}\right)$.
Among these, the sequence numbers of all correct conclusions are $\qquad$ | 1(2)(4) |
67,860 | Example. Find the flux of the vector field
$$
\vec{a}=-x \vec{i}+2 y \vec{j}+z \vec{k}
$$
through the part of the plane
$$
x+2 y+3 z=1
$$
located in the first octant (the normal forms an acute angle with the $O Z$ axis). | \frac{1}{18} |
67,881 | 3. Given that $E$ is a point on the extension of side $BC$ of square $ABCD$, and a square $AEFG$ is constructed with $AE$ as one side, such that points $A$ and $G$ are on the same side of $BE$. The extension of $BD$ intersects $AF$ at point $H$, with $HD=\sqrt{2}$ and $FH=5\sqrt{2}$. Then the length of $BE$ is $\qquad$ | 8 |
67,898 | 5. The midline of a trapezoid is 4. A line parallel to the bases of the trapezoid and dividing its area in half intersects the lateral sides at points $M$ and $N$. Find the smallest possible length of the segment $M N$. | 4 |
67,899 | 10.3.1. (12 points) The curve given by the equation $y=2^{p} x^{2}+5 p x-2^{p^{2}}$ intersects the $O x$ axis at points $A$ and $B$, and the $O y$ axis at point $C$. Find the sum of all values of the parameter $p$ for which the center of the circle circumscribed around triangle $A B C$ lies on the $O x$ axis. | -1 |
67,907 | 1.6.5 ** Find all functions \( f: \mathbf{N}^{*} \rightarrow \mathbf{N}^{*} \), such that for any \( x, y \in \mathbf{N}^{*} \), we have
$$
f(x+f(y))=f(x)+y .
$$ | f(x)=x |
67,911 | In the trapezoid $K L M N$, the base $K L$ has a length of $40 \mathrm{~cm}$ and the base $M N$ has a length of $16 \mathrm{~cm}$. Point $P$ lies on the segment $K L$ such that the segment $N P$ divides the trapezoid into two parts with equal areas.
Determine the length of the segment $K P$.
(L. Hozová)
Hint. Modify the shapes so that their areas can be more easily compared. | 28 |
67,936 | 4. Find the equation of a line $L$ such that the graph of the function
$$
y=x^{4}+4 x^{3}-26 x^{2}
$$
lies on one side of this line, having two common points with it. | 60x-225 |
67,938 | Example 4-13 The 6 faces of a cube are to be colored using red and blue. How many different coloring schemes are there? | 10 |
67,954 | 10. The area of square $A B C D$ is 9 square centimeters, and the area of square $E F G H$ is 64 square centimeters. As shown in the figure, side $B C$ lies on $E H$. Given that the area of triangle $A C G$ is 6.75 square centimeters, then the area of triangle $A B E$ is $\qquad$ square centimeters. | 2.25 |
67,965 | 2.148. $\frac{3+\sqrt{2}+\sqrt{3}}{3-\sqrt{2}-\sqrt{3}}$. | -\frac{(4+3\sqrt{2})(5+3\sqrt{3})}{2} |
67,989 | We regularly transport goods from city $A$ to city $B$, which is $183 \mathrm{~km}$ away. City $A$ is $33 \mathrm{~km}$ from the river, while city $B$ is built on the riverbank. The cost of transportation per km on the river is half that on land. Where should we build the road to minimize the transportation cost? | 11\sqrt{3} |
67,994 | Kevin colors three distinct squares in a $3\times 3$ grid red. Given that there exist two uncolored squares such that coloring one of them would create a horizontal or vertical red line, find the number of ways he could have colored the original three squares. | 36 |
68,010 | 3 . Divide the nine digits 1 - 9 into two groups: $1, 9, 8, 3$ and 2,
$4, 5, 6, 7$, and fill them into the following equation to make it true:
$$
\frac{\square \square}{\square \square}=\frac{O+O+O}{O+O} \text {. }
$$ | \frac{38}{19}=\frac{4+5+7}{2+6} |
68,016 | 10. Evaluate
$$
\int_{-\infty}^{\infty} \frac{1-x^{2}}{1+x^{4}} d x
$$ | 0 |
68,047 | 1. Determine a four-digit number that is a square of a natural number and where the first two digits and the last two digits are equal. | 7744 |
68,053 | 37. A mechanical beetle crawls along a square spiral on the ground. It starts from the lower left corner and crawls in the direction of the arrows, sequentially for $1 \mathrm{~cm}, 1 \mathrm{~cm}, 1 \mathrm{~cm}, 1 \mathrm{~cm}, 2 \mathrm{~cm}, 2 \mathrm{~cm}, 1 \mathrm{~cm}, 3 \mathrm{~cm}, 3 \mathrm{~cm}$, $\qquad$. It crawls $1 \mathrm{~cm}$ per second. How many seconds after departure does it just finish crawling the 100th line segment? | 1156 |
68,067 | 35. In $\triangle A B C$, $\angle A C B=90^{\circ}, \angle A=31^{\circ}$, with $C$ as the center, $\triangle A B C$ is rotated by an angle $\theta$ to $\triangle A_{1} B_{1} C$ (the shape and size of $\triangle A B C$ remain unchanged during the rotation), and point $B$ exactly falls on $A_{1} B_{1}$. Then the size of the rotation angle $\theta$ is $\qquad$ ${ }^{\circ}$. | 62 |
68,070 | 3. (5 points) In the figure, $ABCD$ and $DEFG$ are both squares. Given that $CE=14, AG=2$, the sum of the areas of the two squares is $\qquad$ .
| 100 |
68,082 | 13. 1. 3 * The vertices of $\triangle A B C$ are $A(0,0), B(0,420), C(560,0)$, and a die has its six faces marked with $A, A, B, B, C, C$. A point $P_{1}=(k, m)$ is taken inside $\triangle A B C$, and points $P_{2}, P_{3}, P_{4}, \cdots$ are generated according to the following rule: If $P_{n}$ is already determined, roll the die to get a mark $L, L \in\{A, B, C\}$, then $P_{n+1}$ is the midpoint of $P_{n} L$. Given $P_{7}=(14,92)$, find: the value of $k+m$. | 344 |
68,092 | 15. Fill in the circles with natural numbers from to $_{12}$ (each number must be used exactly once), so that the sum of the 4 numbers in the circles connected by the same straight line is equal. This is called a ${ }_{6}$-order magic star, and this equal number is called the magic sum of the ${ }_{6}$-order magic star. Then, the magic sum of the 6-order magic star is $\qquad$, and continue to complete the following $6_{6}$-order magic star:
```
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
```
Note: The last sentence is a note to the translator and should not be included in the translated text. Here is the final translated text:
```
15. Fill in the circles with natural numbers from to $_{12}$ (each number must be used exactly once), so that the sum of the 4 numbers in the circles connected by the same straight line is equal. This is called a ${ }_{6}$-order magic star, and this equal number is called the magic sum of the ${ }_{6}$-order magic star. Then, the magic sum of the 6-order magic star is $\qquad$, and continue to complete the following $6_{6}$-order magic star:
``` | 26 |
68,114 | How many distinct sums can be made from adding together exactly 8 numbers that are chosen from the set $\{ 1,4,7,10 \}$, where each number in the set is chosen at least once? (For example, one possible sum is $1+1+1+4+7+7+10+10=41$.) | 13 |
68,150 | 4. Let $A_{1} A_{2} \cdots A_{21}$ be a regular 21-sided polygon inscribed in a circle. Select $n$ different vertices from $A_{1}, A_{2}, \cdots, A_{21}$ and color them red, such that the distances between any two of these $n$ red points are all different. Then the maximum value of the positive integer $n$ is $\qquad$ . | 5 |
68,163 | How many ordered triplets $(a, b, c)$ of positive integers such that $30a + 50b + 70c \leq 343$. | 30 |
68,197 | [ Motion problems]
The road from home to school takes Petya 20 minutes. One day, on his way to school, he remembered that he had forgotten his pen at home. If he continues his journey at the same speed, he will arrive at school 3 minutes before the bell, but if he returns home for the pen, he will, walking at the same speed, be 7 minutes late for the start of the lesson. What part of the way had he walked before he remembered the pen? | \frac{1}{4} |
68,199 | ## Problem Statement
Calculate the lengths of the arcs of the curves given by the equations in polar coordinates.
$$
\rho=6(1+\sin \varphi),-\frac{\pi}{2} \leq \varphi \leq 0
$$ | 12(2-\sqrt{2}) |
68,231 | 1. In a computer game, a turtle moves across a grid on the computer screen, which contains 5 columns and 7 rows. Initially, it is located at the bottom-left corner of the screen - on the cell with coordinates $(0,0)$. If the program instructs the turtle to move off the screen, it reappears on the opposite side - for example, taking one step up from the cell $(3,6)$, the turtle will end up in the cell $(3,0)$. Where will the turtle be after executing the following program:
1) 1 step down; 2) 2 steps to the right; 3) 3 steps up; 4) 4 steps to the left; 5) 5 steps down; 6) 6 steps to the right; ... ; 2016) 2016 steps to the left; 2017) 2017 steps down? | (2,6) |
68,257 | 5. In a regular tetrahedron $S-ABC$, the edge length is $a$, and $E$, $F$ are the midpoints of $SA$ and $BC$ respectively. Find the angle formed by the skew lines $BE$ and $SF$.
In a regular tetrahedron $S-ABC$, the edge length is $a$, and $E$, $F$ are the midpoints of $SA$ and $BC$ respectively. Find the angle formed by the skew lines $BE$ and $SF$. | \arccos\frac{2}{3} |
68,263 | 1. Once in a physics and mathematics school, September was declared the month of information technology. Therefore, every Monday in September, there was 1 computer science lesson in each class, every Tuesday - 2 lessons, every Wednesday - 3 lessons, every Thursday - 4 lessons, and every Friday - 5 computer science lessons. Saturdays and Sundays were weekends in this school. On September 1st, there were ceremonial assemblies in the school, so there were no lessons. It is known that in total, 64 computer science lessons were held in each class throughout September. On which day of the week did September 1st fall that year? September has 30 days. | Wednesday |
68,265 | 8 If for all $\theta \in \mathbf{R}$, the modulus of the complex number $z=(a+\cos \theta)+(2 a-\sin \theta) \mathrm{i}$ does not exceed 2, then the range of the real number $a$ is $\qquad$. | [-\frac{\sqrt{5}}{5},\frac{\sqrt{5}}{5}] |
68,267 | 4. In trapezoid $A B C D$, $A D / / B C, E, F$ are points on $A B, C D$ respectively, $E F / / B C$ and $E F$ bisects the area of the trapezoid. If $A D=a, B C=b$, then the length of $E F$ is $\qquad$ | \sqrt{\frac{a^{2}+b^{2}}{2}} |
68,268 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{\frac{\pi}{2}} \frac{\sin x \, dx}{(1+\sin x)^{2}}
$$ | \frac{1}{3} |
68,281 | Example 8 Let $a, b, c \in \mathbf{R}^{+}$, and $a b c=1$, find the minimum value of $\frac{1}{2 a+1}+\frac{1}{2 b+1}+\frac{1}{2 c+1}$. | 1 |
68,288 | 3. On the diagonal $BD$ of square $ABCD$, take two points $E$ and $F$, such that the extension of $AE$ intersects side $BC$ at point $M$, and the extension of $AF$ intersects side $CD$ at point $N$, with $CM = CN$. If $BE = 3$, $EF = 4$, what is the length of the diagonal of this square? | 10 |
68,297 | 8. The real value range of the function $f(x)=\sqrt{\cos ^{2} x-\frac{3}{4}}+\sin x$ is | [-\frac{1}{2},\frac{\sqrt{2}}{2}] |
68,309 | 15. City $A$ has 4 suburban counties $(B, C, D, E)$, as shown in Figure 2. There are 5 colors available. How many different coloring methods are there such that no two adjacent areas share the same color, and each area is painted with only one color? | 420 |
68,312 | Ten test papers are to be prepared for the National Olympiad. Each paper has 4 problems, and no two papers have more than 1 problem in common. At least how many problems are needed? | n = 13 |
68,318 | In the figure below, how many ways are there to select two squares which do not share an edge?
[asy]
size(3cm);
for (int t = -2; t <= 2; t=t+1) { draw( shift((t,0))*unitsquare ) ; if (t!=0) draw( shift((0,t))*unitsquare ); }
[/asy]
[i]Proposed by Evan Chen[/i] | 28 |
68,319 | 5. After substituting $x=\cos \alpha, y=\sin \alpha$, the second equation is satisfied, and the first equation can be written as $\cos ^{15} 3 \alpha+\sin ^{16} 3 \alpha=1$. From the chain
$$
1=\cos ^{15} 3 \alpha+\sin ^{16} 3 \alpha \leqslant \cos ^{2} 3 \alpha+\sin ^{2} 3 \alpha=1
$$
it follows that $\cos ^{15} 3 \alpha=\cos ^{2} 3 \alpha$ and $\sin ^{16} 3 \alpha=\sin ^{2} 3 \alpha$. Therefore, either $3 \alpha=\pi / 2+\pi k$ or $3 \alpha=2 \pi k$, which means $\alpha=\frac{\pi}{6}+\frac{\pi k}{3}$ or $\alpha=\frac{2 \pi n}{3}$. This results in 9 pairs of solutions $(x, y)$:
$$
\left(\frac{\sqrt{3}}{2} ; \pm \frac{1}{2}\right) ;\left(-\frac{\sqrt{3}}{2} ; \pm \frac{1}{2}\right) ;\left(-\frac{1}{2} ; \pm \frac{\sqrt{3}}{2}\right) ;(0 ; \pm 1) ;(1 ; 0)
$$ | 9 |
68,332 | 4. If real numbers $x, y$ satisfy $x^{3}+y^{3}+3 x y=1$, then the minimum value of $x^{2}+y^{2}$ is $\qquad$ . | \frac{1}{2} |
68,341 | 15. From 11, 22, 33, 44, 55, 66, 77, 88, 99, select 7 numbers such that their sum is a multiple of 3, there are ( ) different ways. | 12 |
68,381 | ## Task 4 - 100924
A regular right triangular pyramid is a pyramid whose base is an equilateral triangle and whose foot of the height coincides with the centroid of the base. In the regular pyramid with vertices $A, B, C, D$ and apex $D$, the inclination angle between each of the three side faces and the base is $60^{\circ}$. The base has a side length of $a$.
Calculate the volume $V$ of this pyramid!
Note: If two planes have a common edge and $P$ is a point on this edge different from the endpoints, then the angle formed by two perpendicular segments erected at $P$ on the edge and lying in the two planes is equal to the inclination angle of the two planes to each other. | \frac{\sqrt{3}}{24}^{3} |
68,394 | 8. $x+y+z=1$, where $x \geqslant 0, y \geqslant 0, z \geqslant 0$, let $f(z)=(z-x)(z-y)$, then the range of $f(z)$ is $\qquad$ | [-\frac{1}{8},1] |
68,414 | 7. A die is rolled twice in succession, and the numbers obtained are $a$ and $b$ respectively. Then the probability $p=$ $\qquad$ that the cubic equation $x^{3}-(3 a+1) x^{2}+(3 a+2 b) x-2 b=0$ has three distinct real roots is $\qquad$ .(Answer with a number). | \frac{3}{4} |
68,427 | 4. If $[x]$ denotes the greatest integer not exceeding $x$, then $\left[\frac{1}{3}\right]+\left[\frac{2}{3}\right]+\left[\frac{2^{2}}{3}\right]+\cdots+\left[\frac{2^{1000}}{3}\right]=$ | \frac{1}{3}(2^{1001}-2)-500 |
68,435 | Problem condition
Find the derivative.
$y=6 \arcsin \frac{\sqrt{x}}{2}-\frac{6+x}{2} \cdot \sqrt{x(4-x)}$ | \frac{x^{2}-3}{\sqrt{x(4-x)}} |
68,440 | 7.1. Find the number of all integer solutions of the inequality $\sqrt{1-\sin \frac{\pi x}{4}-3 \cos \frac{\pi x}{2}}-\sqrt{6} \cdot \sin \frac{\pi x}{4} \geq 0$, belonging to the interval [1991; 2013]. | 8 |
68,441 | ## Problem Statement
Calculate the definite integral:
$$
\int_{\pi / 2}^{\pi} 2^{4} \cdot \sin ^{6} x \cos ^{2} x d x
$$ | \frac{5\pi}{16} |
68,488 | 8. Let the equation $x y z=900$ have all positive integer solutions $\left(x_{i}, y_{i}, z_{i}\right)(1 \leqslant i \leqslant n)$. Then $\sum_{k=1}^{n}\left(x_{k}+y_{k}+z_{k}\right)=$ | 22572 |
68,490 | (5) A bag contains one black ball and one white ball. Each time a ball is randomly drawn from the bag, the drawn ball is not returned, but another black ball is added instead. The probability of drawing a black ball on the $n$-th draw is $a=$ $\qquad$ . | 1-\frac{1}{2^{n}} |
68,491 | 3. Let the set $A=\{1,2, \cdots, n\}, X, Y$ be non-empty subsets of $A$ (allowing $X=Y$), the maximum element of $X$ and the minimum element of $Y$ are denoted as $\max X, \min Y$, respectively. Find the number of ordered pairs of sets $(X, Y)$ that satisfy $\max X>\min Y$. | 2^{2n}-(n+1)2^{n} |
68,495 | 13.3.6 ** Given $P(3,4)$ is a point inside the circle $x^{2}+y^{2}=64$, and two moving points $A$ and $B$ on the circumference of the circle satisfy $\angle A P B-\frac{\pi}{2}$. A rectangle $A P B Q$ is constructed with $A P$ and $B P$ as adjacent sides. Find the equation of the trajectory of point $Q$. | x^{2}+y^{2}=103 |
68,503 | 7.1. Mihai drew several right-angled triangles on the board, such that any two triangles do not have common points. In each of these triangles, Mihai drew the following important lines (segments): all angle bisectors, all medians, and the altitude to the hypotenuse. Counting, the total number of important lines drawn in all the triangles is 44. Determine how many right-angled isosceles triangles Mihai drew on the board. | 6 |
68,506 | 【Question 3】A natural number greater than 1 that can only be divided by 1 and itself, like $2,3,5,7$, is called a prime number. Decompose 2015 into the sum of 100 prime numbers, requiring that the largest prime number be as small as possible. What is this largest prime number? $\qquad$ - | 23 |
68,513 | 4. Let $[x]$ denote the greatest integer not exceeding $x$. Then the set $\{[x]+[2 x]+[3 x] \mid x \in R\} \mid\{1,2, \ldots, 100\}$ has
$\qquad$ elements. | 67 |
68,515 | 5. The numbers $1,2,3, \ldots, 16$ are written on slips of paper, one number per slip. Kosta, without looking, sequentially draws one slip at a time, until the product of the numbers written on any two of the drawn slips is a perfect square. What is the maximum number of slips Kosta can draw without the product of any two numbers written on the drawn slips being a perfect square? | 11 |
68,531 | Find the number of positive integers with three not necessarily distinct digits, $abc$, with $a \neq 0$ and $c \neq 0$ such that both $abc$ and $cba$ are multiples of $4$. | 40 |
68,533 | 5-2. Solve the inequality
$$
\sqrt{6 x-13}-\sqrt{3 x^{2}-13 x+13} \geqslant 3 x^{2}-19 x+26
$$
In your answer, specify the sum of all integer values of $x$ that satisfy the inequality. | 7 |
68,534 | 2.99 A set of numbers is called "simple" if it does not contain elements $x, y, z$ such that $x+y=z$. Given the set $\{1,2, \cdots, 2 n+1\}$. Find the maximum number of elements a simple subset can contain. | n+1 |
68,548 | 5. Filling a $3 \times 3$ table with numbers from 1 to 9 is called a magic square if each number is used exactly once, and the sums in each row, each column, and both diagonals are all equal. Determine how many different magic squares $3 \times 3$ exist. (Two magic squares are considered different if they have different numbers in at least one cell.)
## Third Grade - B Category | 8 |
68,549 | Let $ABC$ be a right triangle with right angle at $B$. Let $ACDE$ be a square drawn exterior to triangle $ABC$. If $M$ is the center of this square, find the measure of $\angle MBC$. | 45^\circ |
68,552 | $3+$ [ Law of Sines $\quad]$
Quadrilateral $A B C D$ is inscribed in a circle, $A C=a, B D=b, A B \perp C D$. Find the radius of the circle. | \frac{\sqrt{^{2}+b^{2}}}{2} |
68,557 | Example 2. Color the five vertices of a square pyramid so that the two endpoints of the same edge have different colors. If only 5 colors are available, how many different coloring methods are there? | 420 |
68,578 | 3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 12. In how many ways can this be done? | 5184 |
68,588 | $\left.\begin{array}{l}{[\text { Auxiliary equal triangles }} \\ \text { [ Congruent triangles. Criteria for congruence }]\end{array}\right]$
Given triangle $A B C$, where $A B=A C$ and $\angle A=80^{\circ}$. Inside triangle $A B C$, a point $M$ is taken such that $\angle M B C=30^{\circ}$, and $\angle M C B=10^{\circ}$. Find $\angle A M C$. | 70 |
68,602 | Example 2 Arrange all positive integers that are coprime with 105 in ascending order, and find the 1000th term of this sequence. | 2186 |
68,623 | 1. A line is drawn through the vertex $C$ of parallelogram $A B C D$ which intersects the rays $A B$ and $A D$ at points $K$ and $L$ respectively. Express the area $s$ of parallelogram $A B C D$ in terms of the areas $p$ and $q$ of triangles $BKC$ and $D C L$. | 2\sqrt{pq} |
68,630 | 16. Line-up. At the physical education teacher's whistle, all 10 boys and 7 girls lined up in a random order - wherever they managed to get. Find the mathematical expectation of the quantity "The number of girls standing to the left of all boys." | \frac{7}{11} |
68,688 | Problem 5. (5 points) In how many different ways can the number 2004 be represented as a sum of natural numbers (one or several) that are approximately equal? Two numbers are called approximately equal if their difference is no more than 1. Sums that differ only in the order of the addends are considered the same. | 2004 |
68,691 | 9. Revenues from 09.2019 to 12.2019 will be:
$$
(55000+45000+10000+17400) * 4=509600 \text { rubles }
$$
Expenses from 09.2019 to 11.2019 will be:
$$
(40000+20000+5000+2000+2000) * 4=276000 \text { rubles }
$$
By 12.31.2019, the family will have saved $1147240+521600-276000=1340840$ rubles and will be able to buy a car. | 1340840 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.