id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
68,746 | Solve the following system of equations:
$$
\begin{aligned}
& x+2 \sqrt{y}=2 \\
& 2 \sqrt{x}+y=2
\end{aligned}
$$ | 4-2\sqrt{3} |
68,761 | 12. Let real numbers $x, y, z$ satisfy $xy \neq 0, x+y \neq 0$. Find
$$
\left(\frac{y+z}{x}+2\right)^{2}+\left(\frac{z}{y}+2\right)^{2}+\left(\frac{z}{x+y}-1\right)^{2}
$$
the minimum value. | 5 |
68,776 | 4. Given a positive integer $n \geqslant 2$. Let integers $a_{0}, a_{1}, \cdots$, $a_{n}$ satisfy $0=a_{0}<a_{1}<\cdots<a_{n}=2 n-1$. Find the minimum possible number of elements in the set $\left\{a_{i}+a_{j} \mid 0 \leqslant i \leqslant j \leqslant n\right\}$. | 3n |
68,784 | 7. The maximum value of the function $y=\frac{3-\sin x}{2-\cos x}$ is $\qquad$ | \frac{6+2\sqrt{3}}{3} |
68,799 | 2. Find all prime numbers $p$ for which the polynomial
$$
q(x)=2 x^{3}-2 p x^{2}+(1-p) x+p
$$
has at least one rational root. | 2 |
68,805 | Pr i mer 7. For the normal operation of the car base, there should be no less than eight cars on the line, and there are ten of them. The probability of each car not coming out on the line is 0.1. Find the probability of the normal operation of the car base for the next day. | 0.9298 |
68,843 | 7. (10 points) For a natural number $N$, if at least eight of the nine natural numbers from $1$ to $9$ can divide $N$, then $N$ is called an "Eight Immortals Number". Among the natural numbers greater than 2000, the smallest "Eight Immortals Number" is | 2016 |
68,851 | Variant 11.3.1. The polynomial $G(x)$ with real coefficients takes the value 2022 at exactly five different points $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. It is known that the graph of the function $y=G(x)$ is symmetric with respect to the line $x=-8$.
(a) (2 points) Find $x_{1}+x_{3}+x_{5}$.
(b) (2 points) What is the smallest degree that $G(x)$ can have? | 6 |
68,862 | Three candles can burn for $30$, $40$, and $50$ minutes respectively (but they are not lit at the same time). It is known that the three candles are burning simultaneously for 10 minutes, and only one candle is burning for 20 minutes. Then, the time when exactly two candles are burning simultaneously is $\qquad$ minutes. | 35 |
68,865 | 3. $\left(2 \sin 36^{\circ} \cdot 2 \sin 72^{\circ}\right)^{2}=$ | 5 |
68,871 | 5. (8 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $8$ and $\cos \alpha = \frac{3}{4}$? | 12 |
68,884 | 1. The graphs of a quadratic trinomial with a positive leading coefficient 2 and its derivative intersect at the vertex of the parabola with abscissa $x_{0}$ and at another point with abscissa $x_{1}$. Find the total area of both regions bounded by the graphs of the trinomial, its derivative, and the line symmetric to the line $x=x_{1}$ with respect to the line $x=x_{0}$ (see figure).
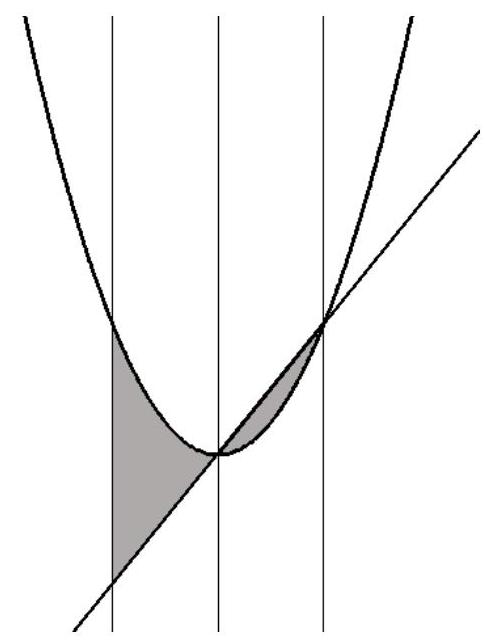 | 16 |
68,890 | 7.1. People stand in a circle - liars who always lie, and ryiars who always tell the truth. And each of them said that among the people standing next to them, there are as many liars as ryiars. How many people are there in total if there are 48 ryiars? | 72 |
68,914 | ## Task Condition
Based on the definition of the derivative, find $f^{\prime}(0)$:
$$
f(x)=\left\{\begin{array}{c}
\frac{2^{\operatorname{tg} x}-2^{\sin x}}{x^{2}}, x \neq 0 \\
0, x=0
\end{array}\right.
$$ | \ln\sqrt{2} |
68,921 | 1. Scientific organization of labor. There are logs of two types: 6 meters and 7 meters long. They need to be sawn into 1-meter logs. Which logs are more profitable to saw? | 6 |
68,937 | A coin is flipped until either $F F F$ or $F I F$ appears in three consecutive flips (where $F$ represents heads and $I$ represents tails). What is the probability that $F F F$ appears before $F I F$? | \frac{2}{5} |
68,945 | 10.1. Propose a word problem that reduces to solving the inequality
$$
\frac{11}{x+1.5}+\frac{8}{x} \geqslant \frac{12}{x+2}+2
$$
Write the problem statement, its solution, and the answer.
Example of the required problem. Points A and B are connected by two roads: one is 19 km long, and the other is 12 km long. At 12:00, a pedestrian left point A on the longer road and walked the first 11 km at a constant speed, and then, getting tired, walked the remaining distance to point B at an average speed 1.5 km/h slower. At 14:00, a second pedestrian left point A on the shorter road and walked the entire distance at an average speed 0.5 km/h faster than the first pedestrian initially walked. What was the average speed at which the first pedestrian walked the last 8 km of the journey, if it is known that he arrived at point B no earlier than the second pedestrian?
Brief solution. If \( x \) is the required average speed of the first pedestrian (in km/h) on the second part of the journey, then \( x+1.5 \) is his speed on the first part, and \( (x+1.5)+0.5=x+2 \) is the average speed of the second pedestrian. Then, by calculating the time each pedestrian spent on the journey, we obtain the required inequality. Since by the problem's condition \( x > 0 \), both sides of the inequality can be multiplied by the quantity \( x(x+1.5)(x+2) > 0 \), then we get \( 11x(x+2) + 8(x+1.5)(x+2) \geqslant 12x(x+1.5) + 2x(x+1.5)(x+2) \), or, after transformations, \( (x-4)(x+1)(x+3) \leqslant 0 \). Therefore, \( 0 < x \leqslant 4 \), and all found values of \( x \) satisfy the problem's condition. | 4 |
68,955 | 3. From two points $A$ and $B$, the distance between which is 300 km, two cars set off simultaneously. The speed of the car that set off from $A$ is 40 km/h. Determine the speed of the second car, given that after two hours the distance between the cars was 100 km. | 60 |
68,966 | 1. By replacing every $*$ in the expression $1 * 2 * 3 * 4 * 5 * \cdots * 2019 * 2020$ with a plus or minus sign ( + or - ), a long arithmetic expression is formed. Place the plus and minus signs in such a way that the result is the smallest possible positive number (greater than 0).
What is this result? | 2 |
68,978 | 3. Given a periodic sequence $\left\{x_{n}\right\}$ satisfying $x_{n}=\mid x_{n-1}-$ $x_{n-2} \mid(n \geqslant 3)$, if $x_{1}=1, x_{2}=a \geqslant 0$, then when the period of the sequence is the smallest, find the sum of the first 2008 terms of the sequence. | 1339 |
68,985 | Exercise 9. Let $A B C$ be an isosceles triangle at $A$. Let $M$ be the midpoint of the segment $[B C]$. Let $D$ be the symmetric point of $M$ with respect to the segment $[A C]$. We denote $x$ as the angle $\widehat{B A C}$. Determine, in terms of $x$, the value of the angle $\widehat{M D C}$. | \frac{x}{2} |
68,987 | Task 1. (5 points) Find $\frac{a^{12}-729}{27 a^{6}}$, if $\frac{a^{2}}{3}-\frac{3}{a^{2}}=6$. | 234 |
68,989 | ## Task A-4.5.
In a room, there are $n$ boxes of heights $1,2,3, \ldots, n$ that need to be arranged in some order against a wall. Cat Fiko can jump from one box to the next if the next box is lower (regardless of how much lower) than the one he is on, or if it is at most 1 higher than the one he is currently on. In how many ways can the boxes be arranged so that Fiko can start from the first box in the row and jump sequentially to each subsequent box? | 2^{n-1} |
68,991 | 29. The figure below shows a triangle $\mathrm{ABC}$ where $\mathrm{AB}=\mathrm{AC} . \mathrm{D}$ and $\mathrm{E}$ are points on sides $A B$ and $A C$, respectively, such that $A B=4 D B$ and $A C=4 A E$. If the area of the quadrilateral BCED is $52 \mathrm{~cm}^{2}$ and the area of the triangle $A D E$ is $x \mathrm{~cm}^{2}$, find $x$. | 12 |
69,012 | The graphs $y=2 \cos 3 x+1$ and $y=-\cos 2 x$ intersect at many points. Two of these points, $P$ and $Q$, have $x$-coordinates between $\frac{17 \pi}{4}$ and $\frac{21 \pi}{4}$. The line through $P$ and $Q$ intersects the $x$-axis at $B$ and the $y$-axis at $A$. If $O$ is the origin, what is the area of $\triangle B O A ?$ | \frac{361\pi}{8} |
69,047 | Find the smallest positive integer $n$ such that a cube with sides of length $n$ can be divided up into exactly $2007$ smaller cubes, each of whose sides is of integer length. | n = 13 |
69,063 | Problem 7.3. (15 points) Several boxes are stored in a warehouse. It is known that there are no more than 60 boxes, and each of them contains either 59 apples or 60 oranges. After a box with a certain number of oranges was brought to the warehouse, the number of fruits in the warehouse became equal. What is the smallest number of oranges that could have been in the brought box? | 30 |
69,097 | 2. If $x \neq 0$, then the maximum value of $\frac{\sqrt{1+x^{2}+x^{4}}-\sqrt{1+x^{4}}}{x}$ is | \sqrt{3}-\sqrt{2} |
69,106 | 9. (2000 Shanghai Competition Problem) Let $a_{1} a_{2} a_{3} a_{4} a_{5}$ be a permutation of $1,2,3,4,5$, satisfying that for any $1 \leqslant i \leqslant 4$, $a_{1} a_{2} a_{3} \cdots a_{i}$ is not any permutation of $1,2, \cdots, i$. Find the number of such permutations. | 71 |
69,107 | Problem 7.8. On a rectangular sheet of paper, a picture in the shape of a "cross" was drawn from two rectangles $A B C D$ and $E F G H$, the sides of which are parallel to the edges of the sheet. It is known that $A B=9, B C=5, E F=3, F G=10$. Find the area of the quadrilateral $A F C H$.
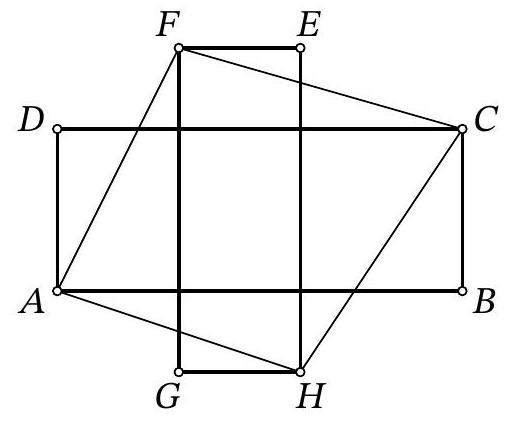 | 52.5 |
69,116 | ## Task B-4.5.
On a square tile of dimensions $8 \times 8$, a field in the second row and third column is colored. Let $A$ be the number of squares $k \times k, k \in\{1,2, \ldots, 8\}$ that contain the colored field, and $B$ be the number of squares that do not contain the colored field. Determine the ratio $\frac{A}{B}$.
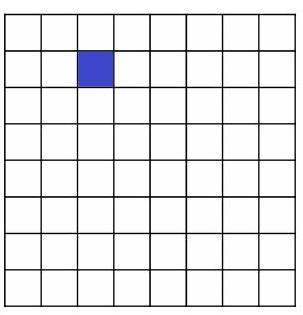 | \frac{1}{5} |
69,129 | Franklin 5.
A convex $n$-gon $P$, where $n>3$, is cut into equal triangles by diagonals that do not intersect inside it.
What are the possible values of $n$, if the $n$-gon is cyclic? | 4 |
69,147 | G8.2 If the area of the equilateral triangle $P Q R$ is $6+b \sqrt{3}$, find the value of $b$. | 4 |
69,193 | 1. Customers of the online store "Ali-Express" live in five houses located at the vertices of a convex pentagon. One order was placed by residents of the first house, two orders by residents of the second house, and so on, with four orders from the residents of the fourth house. However, the residents of the last fifth house made 10 orders. The store manager is thinking about where to deliver all the orders so that the total distance traveled by all customers to pick up their items is minimized. Help him solve this problem and justify the result. | 5 |
69,268 | 1.1. On the Island of Knights and Liars, knights always tell the truth, while liars always lie. One day, a traveler interviewed seven residents of the island.
- I am a knight, - said the first.
- Yes, he is a knight, - said the second.
- Among the first two, there are no less than 50% liars, - said the third.
- Among the first three, there are no less than 65% liars, - said the fourth.
- Among the first four, there are no less than 50% knights, - said the fifth.
- Among the first five, there are no less than 40% liars, - said the sixth.
- Among the first six, there are no less than 65% knights, - said the seventh.
Determine how many knights there are among them in reality. | 5 |
69,285 | 5. The length of the diagonal $AC$ of the rhombus $ABCD$ with an acute angle at vertex $A$ is 20. Points $M$ and $N$ on sides $DA$ and $DC$ are the bases of the heights of the rhombus dropped from vertex $B$. The height $BM$ intersects the diagonal $AC$ at point $P$ such that $AP: PC=3: 4$. Find the length of the segment $MN$. | 5 |
69,330 | 2. On the side AC of triangle ABC with an angle of 120 degrees at vertex B, points D and E are marked such that $AD = AB$ and $CE = CB$. A perpendicular $DF$ is dropped from point D to the line BE. Find the ratio $BD / DF$. | 2 |
69,472 | 3. Among all six-digit natural numbers, the digits of which are arranged in ascending order (from left to right), numbers containing the digit 1 and not containing this digit are considered. Which numbers are more and by how many? | 28 |
69,502 | 1. In the "Sweet Tooth" store, they are thinking of what promotion to announce before March 8. Manager Vasya suggests reducing the price of a box of candies by $20 \%$ and hopes to sell twice as much of the product as usual. Deputy Director Kolya says that it would be more profitable to increase the price of the same box of candies by a third and announce a promotion "buy two, get one free," in which case sales will remain the same (not counting the free items). In whose version of the promotion will the revenue be higher? In the answer, write how much more revenue there will be if the usual revenue from selling boxes of candies is 10000? | 6000 |
69,668 | 3. Let's call a four-digit number accompanying the year $\overline{20 a b}$ if it also ends in $\overline{a b}$ and, in addition, is divisible by $\overline{a b}$ (a two-digit number), for example, the number 4623 accompanies the year 2023. How many numbers accompany the year $2022?$ | 9 |
69,768 | # Task № 6.4
## Condition:
Given triangle ABC. The median BM is perpendicular to the bisector $\mathrm{AL}$, and $\mathrm{LM}=4$. Find BL. | 4 |
69,776 | # Problem 1. (1 point)
Anton was selling rabbits, the same number each day. On the first day, 20% of all the rabbits were bought by Old Lady #1, 1/4 of the remaining rabbits were taken by Man #1, after which an unknown person X purchased some rabbits, and Anton was left with 7 rabbits. On the second day, 25% of all the rabbits were bought by Old Lady #2, 1/3 of the remaining rabbits were taken by Man #2, after which the unknown person X purchased twice as many rabbits as on the first day, and Anton was left with no rabbits. How many rabbits did the unknown person X buy on the first day? | 5 |
69,790 | # 6. Problem 6"
Consider an alphabet of 2 letters. A word is any finite combination of letters. We will call a word unpronounceable if it contains more than two identical letters in a row. How many unpronounceable words of 7 letters exist? Points for the problem: 8 .
# | 86 |
69,799 | 8.4. In triangle $A B C$, points $E$ and $D$ are on sides $A B$ and $B C$ respectively, such that segments $A D$ and $C E$ are equal, $\angle B A D=\angle E C A$ and $\angle A D C=\angle B E C$. Find the angles of the triangle. | 60 |
69,803 | 1. A $6 \times 6$ table is filled with numbers. Numbers in adjacent cells (sharing a side) differ by exactly a factor of two. One of the cells contains the number 1. What is the maximum number that can be in this table? | 1024 |
69,821 | 3. Given a regular 11-gon. In how many ways can 3 diagonals be drawn in it so that every two of them intersect (inside the 11-gon)? | 462 |
69,826 | # Problem 7. (3 points)
Given a triangle $ABC$. An inscribed circle is tangent to sides $AB, AC, BC$ at points $C_{1}$,
$B_{1}, A_{1}$ respectively. Find the radius of the excircle $w$ that is tangent to side $AB$ at point $D$, the extension of side $BC$ at point $E$, and the extension of side $AC$ at point $G$. It is known that $CE=6$, the radius of the inscribed circle is $1$, and $CB_{1}=1$. | 6 |
69,834 | # Problem 6. (3 points)
In how many ways can the number 1500 be represented as the product of three natural numbers (variants where the multipliers are the same but differ in order are considered the same)?
# | 32 |
69,871 | 3. Given two quadratic equations with the leading coefficient 1. The difference between the roots of the first is 17, the difference between the roots of the second is 31. What is the greatest value that the difference between the roots of the sum of these equations can take? | 25 |
69,898 | Problem 3. Two numbers $x$ and $y$ are randomly chosen from the interval $(0,1)$. What is the probability that $\left[\log _{2} x\right]=\left[\log _{2} y\right]$? If necessary, round your answer to 0.01. The notation $[a]$ represents the greatest integer not exceeding $a$. | 0.33 |
69,907 | 10.4. On the side $A C$ of triangle $A B C$, a point $M$ is taken. It turns out that $A M=B M+M C$ and $\angle B M A=\angle M B C+\angle B A C$. Find $\angle B M A$. | 60 |
70,092 | Example 3. Compare the number $a$ with one, if
$$
a=0.99999^{1.00001} \cdot 1.00001^{0.99999} .
$$ | 1 |
70,105 | Example 2. Let $y \neq-1$. We set,
$$
x_{1}=\frac{y-1}{y+1}, \quad x_{2}=\frac{x_{1}-1}{x_{1}+1}, \quad x_{3}=\frac{x_{2}-1}{x_{2}+1}, \ldots
$$
What is $y$ if $x_{1978}=-\frac{1}{3}$? | 3 |
70,115 | 1. A certain ancient Greek was born on January 7, 40 BC, and died on January 7, 40 AD. How many years did he live? | 79 |
70,138 | 26. The amount of scrap metal collected by one class is expressed as a three-digit number. If the first digit 9 of this number is moved to the end, the resulting number represents the kilograms of scrap metal collected by another class. It is known that one class collected 216 kg more than the other. How much scrap metal did each class collect? | 975 |
70,163 | 17. How many natural numbers $N \leqslant 1000000$ exist such that $N$ is divisible by $[\sqrt{N}]$? | 2998 |
70,189 | 63. Four friends bought a football together. The first one contributed 2 p. 30 k., the second - a third of the amount contributed by the others, the third - a quarter of the amount contributed by the others, and the fourth - a fifth of the amount contributed by the others. Determine the cost of the purchase and the amount contributed by each boy. | 6 |
70,204 | 66. Do there exist two consecutive natural numbers, the quotient of which is an integer? | 12 |
70,238 | 16. What is the maximum number of numbers that can be chosen from the set $1,2,3, \ldots, 1985$ such that the difference between any two of the chosen numbers is not a prime number? | 497 |
70,324 | 85. The Fly and the Cars. The length of the road is 300 km. Car $A$ starts at one end of the road at noon and moves at a constant speed of 50 km/h. At the same time, at the other end of the road, car $B$ starts at a constant speed of 100 km/h and a fly, flying at 150 km/h. Upon meeting car $A$, the fly turns and flies towards $B$.
1) When will the fly meet $B$?
2) If, upon meeting $B$, the fly turned, flew towards $A$, met him, turned again, and continued flying back and forth between $A$ and $B$ until they collided, when would the cars crush the fly? | 2 |
70,340 | 191. Three Shepherds. When the Crackhams approached a large city, they had to stop because a flock of sheep was moving along the road, followed by a herd of bulls, and then the shepherds were driving a herd of horses. The Crackhams realized that it was market day in the city today. George, taking advantage of the opportunity, came up with the following puzzle.
Three shepherds driving their herds met on a highway. Jack said to Jim:
- If I give you 6 pigs for one horse, then your herd will have twice as many heads as mine.
And Dan remarked to Jack:
- If I give you 14 sheep for one horse, then your herd will have three times as many heads as mine.
Jim, in turn, said to Dan:
- And if I give you 4 cows for one horse, then your herd will be six times larger than mine.
The deals did not go through, but could you still tell how many heads of livestock there were in the three herds. | 39 |
70,373 | 10.3. Can two digits be appended to the number 277 so that the resulting number is divisible by any number from 2 to 12? | 27720 |
70,396 | Ex. 37. In an isosceles triangle $ABC (AB=BC)$, the bisectors $AM$ and $BK$ intersect at point $O$. The areas of triangles $BOM$ and $COM$ are 25 and 30, respectively. Find the area of triangle $ABC$. | 176 |
70,453 | In the TV series "The Secret of Santa Barbara", 20 characters are involved. In each episode, one of the following events occurs: a certain character learns the Secret, a certain character learns that someone knows the Secret, a certain character learns that someone does not know the Secret. What is the maximum number of episodes the series can last? | 780 |
70,702 | [ Evenness and Oddness ]
On five cards, natural numbers from 1 to 5 are written. Leshа and Dima took two cards each, without looking, and hid the remaining card without looking as well. After examining his cards, Leshа told Dima: "I know that the sum of the numbers on your cards is even!"; and he was right. What numbers are written on Leshа's cards?
# | 24 |
70,727 | Kazicinat T. T.
Grisha has 5000 rubles. In the store, chocolate bunnies are sold at 45 rubles each. To carry the bunnies home, Grisha will have to buy several bags at 30 rubles each. No more than 30 chocolate bunnies can fit in one bag. Grisha bought the maximum possible number of bunnies and enough bags to carry all the bunnies. How much money does Grisha have left? | 20 |
70,879 | Determine the last digit of the product of all even natural numbers less than 100 that are not multiples of ten.
(M. Volfová) | 6 |
70,917 | Exercise 7. Let $A B C$ be a triangle. We denote $|A B C|$ as its area. Let $P$ be an interior point of the triangle such that $\frac{|A B C|}{|P A B|}=\frac{|A B C|}{|P A C|}=10$. Let $M$ be the point on $[A B]$ such that $(P M)$ is parallel to $(A C)$, and $N$ the point on $[A C]$ such that $(P N)$ is parallel to $(A B)$. Determine $\frac{|A B C|}{|P M A N|}$. | 50 |
70,920 | Find all integers $n$ such that $4 n^{4}+1$ is a prime number. | 1 |
71,003 | A spider has 8 identical socks and 8 identical shoes. In how many different orders can she put them on, knowing that, obviously, on each leg, she must put the shoe after the sock? | 81729648000 |
71,077 | A3 A number can be modified according to the following two game rules:
- it can be multiplied by 3,
- 1 can be added to it.
Using one of these two rules once is called a move.
You start with the number 0. What is the minimum number of moves it takes you to reach 2000? | 14 |
71,095 | ## Task A-2.2.
Each of the numbers $x_{1}, x_{2}, \ldots, x_{2014}$ can be $-1, 0$ or 1. What is the smallest possible value of the sum of all products $x_{i} x_{j}$ for $1 \leqslant i<j \leqslant 2014$? | -1007 |
71,184 | 5. The Monkey King distributed 75 peaches among some baby monkeys, among which there must be one baby monkey that received 5 or more peaches. The maximum number of baby monkeys is $\qquad$.
| 18 |
71,185 | 【Example 7】How many five-digit numbers are divisible by 3 and contain the digit 6? How many of these have 6 as the units digit? | 3000 |
71,324 | 10. There is a four-digit number. By rearranging the digits (none of which are 0) of this four-digit number, the largest new number obtained is 5562 greater than the original number, and the smallest new number is 2700 less than the original number. What is the original four-digit number? $\qquad$ | 4179 |
71,332 | 6. Given $A=\{1,-1, \mathrm{i},-\mathrm{i}\}$ (i is the imaginary unit), $f(x)$ is a function with domain and range both being $A$, for any $x, y \in A$, there is $f(x y)=f(x) f(y)$. Then the number of functions $f(x)$ that satisfy the condition is $\qquad$.
| 2 |
71,355 | 9. In the Cartesian coordinate system $x O y$, the moving line $l$ is always tangent to the graph of the function $y=\frac{6-4 \sqrt{2}}{x}$, $l$ intersects the $x$-axis at point $A$, and the $y$-axis at point $B$. Then the minimum perimeter of the right triangle $\triangle A O B$ is $\qquad$ | 4 |
71,445 | 8. From the ten digits 0 to 9, form three three-digit numbers such that the sum of these three numbers equals 2020. What is the digit that was not selected? $\qquad$ . | 5 |
71,494 | 1. If the set of real numbers
$$
A=\{2 x, 3 y\} \text { and } B=\{6, x y\}
$$
have exactly one common element, then the product of all elements in $A \cup B$ is $\qquad$ . | 0 |
71,513 | 9. (10 points) Let $P$ be a square number. If $q-2$ and $q+2$ are both prime numbers, then $q$ is called a $P$-type square number. For example:
9 is a $P$-type square number. What is the largest $P$-type square number less than 1000? | 441 |
71,517 | (1) Let $|X|$ denote the number of elements in the set $X$. If finite sets $A, B, C$ satisfy $|A \cup B|=20,|B \cup C|=30,|C \cup A|=40$, then the maximum possible value of $|A \cap B \cap C|$ is $\qquad$ . | 10 |
71,606 | 22. The math prodigy Gauss was an expert in number theory, and his elementary school teacher once tested him with the following problem: from the digits $1,2,3,4,5,6,7,8,9$, choose any 3 digits to form a three-digit number. Among the numbers formed, the number of three-digit numbers that can be divided by 4 is $\qquad$. | 112 |
71,637 | 60. A natural number has exactly 48 divisors, and among them, there are 10 consecutive natural numbers. What is the minimum value of this number? $\qquad$ . | 2520 |
71,660 | 74. The NBA Finals are between the Los Angeles Lakers and the Boston Celtics, with a 7-game, 4-win series, meaning the first team to win 4 games will be the champion. The games are divided into home and away matches. Due to the Los Angeles Lakers' better regular-season record, the 1st, 2nd, 6th, and 7th games are played in Los Angeles, while the 3rd, 4th, and 5th games are played in Boston. Ultimately, the Lakers won the championship on their home court. Therefore, the number of possible win-loss outcomes during the series is $\qquad$ kinds. | 30 |
71,710 | 10. (12 points) There are a total of 62 large and small boxes. Small boxes weigh 5 per ton, and large boxes weigh 3 per ton. Now, these boxes need to be transported using a truck. If large boxes are loaded first, after all the large boxes are loaded, the truck can still fit 15 small boxes. If small boxes are loaded first, after all the small boxes are loaded, the truck can still fit 15 large boxes. How many of these boxes are large? $\qquad$ | 27 |
71,808 | 16. Given $S=(a-b)^{2}+\left(2-a-\frac{9}{b}\right)^{2}$, where $a$ is a real number, and $b$ is a positive real number, then the minimum value of $S$ | 8 |
71,874 | Example 1 If a positive integer has 21 positive divisors, what is the smallest such positive integer?
Analysis We use the unique factorization theorem to handle this.
| 576 |
71,942 | 27. (5 points)
Piggy is playing the game "Candy Crush". On the blackboard, there are 100 natural numbers from 1 to 100. How many numbers does Piggy need to erase at least, so that the product of the remaining numbers ends with the digit 5? | 50 |
72,002 | 75. Archaeologists have determined using remote sensing and geophysical exploration methods that the underground palace of the Mausoleum of the First Qin Emperor is 35 meters deep, 170 meters long from east to west, and 145 meters wide from north to south, forming a rectangular shape. If the earth and stone from above the underground palace were used to build a cylindrical column with a diameter of 20 meters, then the height of this column would be $\qquad$ meters (take $\pi$ as 3.14, and round the result to 2 decimal places). | 2747.61 |
72,007 | 5. $3333 \times 5555+6 \times 4444 \times 2222=$ | 77762223 |
72,033 | 8. (3 points) Xiao Li and Xiao Hua are competing in a stair-climbing race. When Xiao Li reaches the 5th floor, Xiao Hua is exactly at the 3rd floor. According to this calculation, when Xiao Li reaches the 25th floor, Xiao Hua will be at the $\qquad$ floor. | 13 |
72,034 | 2. Each beach volleyball match has four players on the court. In a beach volleyball tournament, it is known that $n$ players have played a total of $n$ matches, and any two players have played at least one match together. Find the maximum value of $n$.
| 13 |
72,056 | 8. There are 11 cups with their mouths facing up. Each operation involves flipping 7 of these cups over. At least $\qquad$ operations are needed to achieve a situation where 6 cups have their mouths facing up and 5 cups have their mouths facing down. | 3 |
72,065 | 66. Trees are planted on both sides of a road, with one tree every 10 meters (no trees at the ends of the road). The road is 240 meters long in total, and a total of $\qquad$ trees need to be planted. | 46 |
72,067 | 60. Four primary school students, A, B, C, and D, stand in a horizontal line, holding a total of 35 flowers. It is known that the students standing to the right of A are holding 16 flowers in total, the students standing to the right of C are holding 4 flowers in total, and the students standing to the right of D are holding 25 flowers in total. The student with the most flowers is holding $\qquad$ flowers. | 12 |
72,075 | 2. The set $M=\left\{x \in \mathbb{R} \mid x^{3}-3 a^{2} x+2 a^{3}=0, a \in \mathbb{R}, a \neq 0\right\}$ has how many non-empty subsets? | 3 |
72,080 | 10.9 A two-digit number divided by its reverse yields a quotient that is exactly equal to the remainder. Find this two-digit number.
(China Beijing Junior High School Grade 2 Mathematics Competition, 1991) | 52 |
72,086 | 10. Given that $b, c$ are integers, and $c<2000$. If the two roots of the quadratic equation $x^{2}-b x+c=0$ have real parts both greater than 1, then the number of all $(b, c)$ pairs is $\qquad$ . | 1995003 |
72,179 | 54. There are 2, 2, 3, and 3 small flags of red, yellow, blue, and white, respectively. Any three flags are taken out and arranged in a row to represent a signal. In total, $\qquad$ different signals can be represented. | 62 |
72,329 | 23. A natural number is divided by $3, 5, 7, 11, 13$, respectively, the sum of the quotients is 185, and the sum of the remainders is 8 (if divisible, the remainder is recorded as 0), this natural number is $\qquad$ . | 221 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.