id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
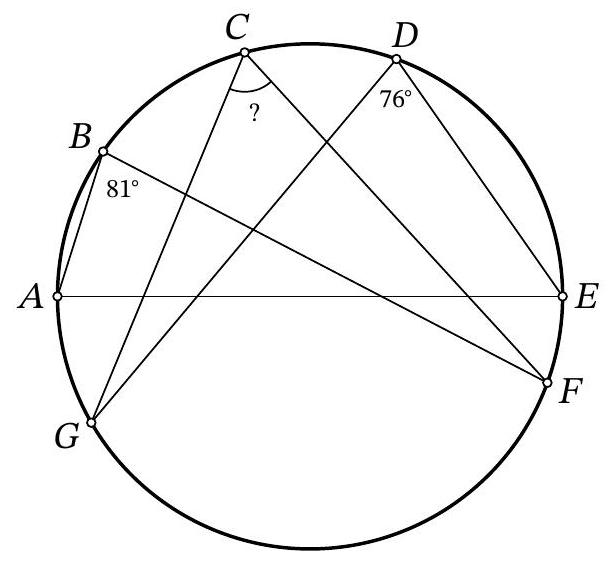
61,015 | Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
 | 67 |
61,016 | 8. (10 points) In the expression $(x+y+z)^{2036}+(x-y-z)^{2036}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained? | 1038361 |
61,049 | 10. Let the sequence $\left\{a_{n}\right\}$ have the sum of the first $n$ terms $S_{n}$ satisfying: $S_{n}+a_{n}=\frac{n-1}{n(n+1)}, n=1,2, \cdots$, then the general term $a_{n}=$ . $\qquad$ | a_{n}=(\frac{1}{2})^{n}-\frac{1}{n(n+1)} |
61,077 | 10. (12 points) There are now two animals, mice and rabbits, which grow in the following ways: every month, the number of mice doubles from the previous month, and the number of rabbits becomes the sum of the numbers from the previous two months (the second month and the first month have the same number). For example: in the first month, there are 2 mice and 2 rabbits, in the second month, there are 4 mice and 2 rabbits, in the third month, there are 8 mice and 4 rabbits. Now we know that in the 7th month, there is one more rabbit than mice. Then, in the first month, the minimum number of rabbits is $\qquad$. | 5 |
61,087 | 15. Given the function $f(x)=a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}$
$\left(n \in \mathbf{N}_{+}\right), a_{1}, a_{2}, \cdots, a_{n}$ are terms of a sequence. If $f(1)=n^{2}+1$, (1) find the general term formula of the sequence $\left\{a_{n}\right\}$; (2) find $\lim _{n \rightarrow \infty}\left(1-\frac{1}{a_{n}}\right)^{n}$. | e^{-\frac{1}{2}} |
61,094 | ## [
[ Quadrilateral Pyramid ]
Edge $P A$ of the pyramid $P A B C$ is perpendicular to the base plane $A B C$ and equals 1. In triangle $A B C$, the angle at vertex $A$ is a right angle, and each of the legs $A B$ and $A C$ equals 2. Points $M$ and $N$ are the midpoints of $A C$ and $B C$ respectively. Find the radius of the sphere inscribed in the pyramid PMNC.
# | \frac{1}{\sqrt{2}+2+\sqrt{6}} |
61,098 | 14 、Using "10, 1, $ \times , \div$ and adding () to calculate $6, 8, 8, 9$, to make the result 24, for example $9 \times 8 - 8 \times 6 = 24$, please write another expression _.
Please write another expression _. | (8+8)\times9\div6=24 |
61,106 | Problem 9.3. To 30 palm trees in different parts of an uninhabited island, a sign is nailed.
- On 15 of them, it is written: "Exactly under 15 signs, treasure is buried."
- On 8 of them, it is written: "Exactly under 8 signs, treasure is buried."
- On 4 of them, it is written: "Exactly under 4 signs, treasure is buried."
- On 3 of them, it is written: "Exactly under 3 signs, treasure is buried."
It is known that only the signs under which there is no treasure are true.
Under what minimum number of signs can the treasure be buried? | 15 |
61,122 | 1. Can five identical rectangles with a perimeter of 10 be arranged to form one rectangle with a perimeter of 22? | Yes |
61,141 | \section*{Problem 6B - 111246B}
As the "distance" between two functions \(f\) and \(g\), which are defined in the same interval, denote the largest of all values \(|f(x)-g(x)|\) that occur in this interval, provided such a largest value exists.
Let the functions \(f\) and \(g\) be given in the interval \(-2 \leq x \leq 2\) by \(f(x)=2-|x|\) and \(g(x)=-a x^{2}+2\) (where \(a\) is a positive real number), respectively.
Investigate whether there is a value of \(a\) for which the "distance" between \(f\) and \(g\) is as small as possible. If such an \(a\) exists, give all such values of \(a\). | \frac{1}{4}(1+\sqrt{2}) |
61,146 | 7. There are $n$ different positive integers, each one not greater than 2013 , with the property that the sum of any three of them is divisible by 39 . Find the greatest value of $n$.
(1 mark)
現有 $n$ 個互不相同且每一個都不大於 2013 的正整數, 且當中任意三個之和均可被 39 整除。求 $n$ 的最大值。 | 52 |
61,147 | Thales' Theorem and the Proportional Segments Theorem [The ratio of the areas of triangles with a common base or common height]
In triangle $ABC$, a point $K$ is taken on side $AB$, such that $AK: BK=1: 2$, and a point $L$ is taken on side $BC$, such that $CL: BL=2: 1$. $Q$ is the point of intersection of lines $AL$ and $CK$. Find the area of triangle $ABC$, given that $S_{BQC}=1$. | \frac{7}{4} |
61,173 | B2. How many four-digit numbers are there with the following properties:
- the second digit is the average of the first digit and the third digit,
- the third digit is the average of the second digit and the fourth digit? (A number does not start with the digit 0.) | 30 |
61,188 | 8. (10 points) In the expression $(x+y+z)^{2020}+(x-y-z)^{2020}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained? | 1022121 |
61,201 | 25. One day, the owner put more than 60 identical chess pieces into some identical boxes, with only one box being empty. The mischievous Tom cat took one piece from each of the boxes that had pieces and put them into the empty box. The clever Jerry mouse rearranged the boxes, and as a result, the position of each box and the number of pieces in each box looked the same as before. Therefore, there are $\qquad$ boxes. | 12 |
61,203 | 5. Scott stacks golfballs to make a pyramid. The first layer, or base, of the pyramid is a square of golfballs and rests on a flat table. Each golfball, above the first layer, rests in a pocket formed by four golfballs in the layer below (as shown in Figure 1). Each layer, including the first layer, is completely filled. For example, golfballs can be stacked into a pyramid with 3 levels, as shown in Figure 2. The four triangular faces of the pyramid in Figure 2 include a total of exactly 13 different golfballs. Scott makes a pyramid in which the four triangular faces include a total of exactly 145 different golfballs. How many layers does this pyramid have? | 9 |
61,214 | ## Task B-2.7.
Determine the area of the set of points defined by the solutions of the inequalities $\operatorname{Im} z \geqslant|\operatorname{Re} z-1|,|z-1| \leqslant 1$ in the complex plane. | \frac{\pi}{4} |
61,241 | ## Task B-2.1.
If $a=\sqrt{\sqrt{3}-\sqrt{2}}(\sqrt{\sqrt{3}-1}+\sqrt{\sqrt{3}+1}), b=\sqrt{\sqrt{3}+\sqrt{2}}(\sqrt{\sqrt{3}-1}-\sqrt{\sqrt{3}+1})$, what is $a+b$? | 0 |
61,246 | ## Problem Statement
Find the second-order derivative $y_{x x}^{\prime \prime}$ of the function given parametrically.
$\left\{\begin{array}{l}x=\cos t+\sin t \\ y=\sin 2 t\end{array}\right.$ | 2 |
61,265 | 3. Given the sequence $\left\{a_{n}\right\}$ satisfies: $a_{1}=1, a_{2}=2, a_{2 k+1}=\frac{a_{2 k}^{2}}{a_{2 k-1}}$, and $a_{2 k+2}=2 a_{2 k+1}-a_{2 k}\left(k \in \mathbf{N}^{*}\right)$, then the last two digits of $a_{2022}$ are | 32 |
61,267 | 1. Determine the number of all infinite arithmetic sequences of integers that have both numbers 1 and 2005 among their first ten terms. | 68 |
61,286 | Let $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers. Consider the $2^{n}-1$ (non-empty) sums formed from these. How many of these can be positive? | 2^{n-1} |
61,307 | 21. As shown in the figure, through a point inside the triangle, three lines parallel to the three sides are drawn, dividing $\triangle A B C$ into 3 triangles and 3 quadrilaterals. If the areas of the 3 triangles are 1, 4, 9, then the area of $\triangle A B C$ is $\qquad$ | 36 |
61,315 | $2 \cdot 111$ two-digit number set $\{00,01, \cdots, 98,99\}$ has a subset $X$ with the following property: in any infinite sequence of digits, there are two adjacent digits that form an element of $X$. How many elements does $X$ have at minimum? | 55 |
61,319 | 11.32. The area of a trapezoid is 1. What is the smallest value that the largest diagonal of this trapezoid can have? | \sqrt{2} |
61,329 | Exercise 2. Let $A B C$ be an isosceles triangle at $A$. Let $M$ be the midpoint of the segment $[B C]$. Let $D$ be the symmetric point of $M$ with respect to the segment $[A C]$. We denote $x$ as the angle $\widehat{B A C}$. Determine, in terms of $x$, the value of the angle $\widehat{M D C}$. | \frac{x}{2} |
61,331 | 3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 18 minutes?
 | 2584 |
61,332 | ## Task 2 - 010912
In ballistics, the term "mean precision" $p_{m}$ is frequently used. If $p_{m}$ is taken as the radius of a circle, then about 20 percent of all hits lie within this circle. All hits are captured by a circle with a radius that is approximately $4 \frac{1}{2}$ times larger. Western military experts currently estimate a mean precision (for rockets) of $p_{m}=0.5$ percent of the range. Later, they aim to achieve values of $p_{m}=0.1$ percent and in the distant future even $p_{m}=0.05$ percent.
a) How large would the radius of the 20 percent circle and that of the circle containing all hits be for these values if the range is $12500 \mathrm{~km}$?
b) What mean precision $p_{m}$ did the Soviet Union achieve, considering that the radius of the circle containing all hits in the tests conducted in October 1961 was less than $1 \mathrm{~km}$? | 0.0018 |
61,347 | 2. Find the largest positive integer $n$, such that $n^{2}+2000 n$ is a perfect square. | 249001 |
61,348 | I2.4 Determine the unit digit, $\delta$, of $\left(\left(\gamma^{\gamma}\right)^{\gamma}\right)^{\gamma}$. | 7 |
61,366 | Problem 2. Experimenters Glafira and Gavriil placed a triangle made of thin wire with sides of 30 mm, 40 mm, and 50 mm on a white flat surface. This wire is covered with millions of mysterious microorganisms. The scientists found that when an electric current is applied to the wire, these microorganisms begin to move chaotically on this surface in different directions at an approximate speed of $\frac{1}{6}$ mm/sec. As they move, the surface along their path is stained red. Find the area of the stained surface after 1 minute of current application. Round it to the nearest whole number of square millimeters. | 2114 |
61,371 | 8. (10 points) In the expression $(x+y+z)^{2028}+(x-y-z)^{2028}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained? | 1030225 |
61,379 | 116 The four vertices of a regular tetrahedron are $A, B, C, D$, with edge length $1, P \in AB, Q \in CD$, then the range of the distance between points $P, Q$ is $\qquad$ . | [\frac{\sqrt{2}}{2},1] |
61,386 | $\left[\begin{array}{l}\text { Combinations and Permutations } \\ {\left[\begin{array}{l}\text { Partitions into Pairs and Groups; Bijections }]\end{array}\right]}\end{array}\right]$
There are 20 people - 10 boys and 10 girls. How many ways are there to form a company in which there would be an equal number of boys and girls? | 184756 |
61,401 | 3. Someone wrote down two numbers $5^{2020}$ and $2^{2020}$ in a row. How many digits will the resulting number contain? | 2021 |
61,410 | The Princeton University Band plays a setlist of 8 distinct songs, 3 of which are tiring to play. If the Band can't play any two tiring songs in a row, how many ways can the band play its 8 songs? | 14400 |
61,431 | 【Question 11】
Xiao Ling is reading an interesting storybook. Every day she reads twice the number of pages she has read in the previous days, and on the sixth day, she read $\frac{1}{9}$ of the book. On which day did Xiao Ling finish reading the book? | 8 |
61,455 | 【Question 7】
Among the 95 numbers $1^{2}, 2^{2}, 3^{2}, \cdots, 95^{2}$, the numbers with an odd digit in the tens place are $\qquad$ in total. | 19 |
61,457 | 3. A non-empty finite set of numbers is called a trivial set if the sum of the squares of all its elements is odd.
Let the set $A=\{1,2, \cdots, 2017\}$. Then the number of trivial sets among all proper subsets of $A$ is $\qquad$ (powers of numbers are allowed in the answer). | 2^{2016}-1 |
61,470 | 7. (4 points) Given a triangle $A B C$, where $A B=2, B C=8, A C=8$. From point $B$, a bisector is drawn which intersects the circumcircle of this triangle at point $D$. Find the value of $D I$, where $I$ is the center of the inscribed circle of triangle $A B C$. | \frac{16}{3} |
61,475 | A trapezoid's diagonals are perpendicular, its height is 4 units, and one of its diagonals is 5 units. What is the area of the trapezoid? | \frac{50}{3} |
61,484 | Task 3. Determine the smallest four-digit number that is divisible by 9, if the product of its digits is equal to 180. | 1566 |
61,489 | 3. From a point $P$ inside $\triangle A B C$, perpendiculars are drawn to the sides $B C, C A, A B$, with the feet of the perpendiculars being $D, E, F$ respectively. Semi-circles are constructed outwardly on $A F, B F$, $B D, C D, C E, A E$ as diameters. As shown in the figure, the areas of these six semi-circles are denoted as $S_{1}, S_{2}$, $S_{3}, S_{4}, S_{5}, S_{6}$, respectively. If $S_{5}-S_{6}=2, S_{1}-S_{2}=1$, then $S_{4}-S_{3}=$ $\qquad$ | 3 |
61,496 | 8. The solution set of the inequality $-2<\sqrt{x^{2}-2 x+4}-\sqrt{x^{2}-10 x+28}<2$ is | (3-\sqrt{2},3+\sqrt{2}) |
61,504 | $\underline{\text { Chernyaev N.L. }}$
Ten children were given 100 spaghetti noodles each in their plates. The children did not want to eat and started playing. In one move, one of the children transfers one noodle from their plate to each of the other children. After what minimum number of moves can all the children have a different number of noodles in their plates? | 45 |
61,514 | 12.3. Can we select such digits $a, b, c$, so that the numbers $\overline{a b}$, $\overline{b a}, \overline{b c}, \overline{c b}, \overline{c a}, \overline{a c}$ are prime?
$$
(6-7 \text { grade })
$$ | 1,3,7 |
61,519 | How many (non-degenerate) triangles with integer side lengths and a perimeter of 100 exist?
# | 208 |
61,530 | 2. 50 businessmen - Japanese, Koreans, and Chinese - are sitting at a round table. It is known that between any two nearest Japanese, there are as many Chinese as there are Koreans at the table. How many Chinese can there be at the table?
## Answer: 32. | 32 |
61,578 | 10. The distance between Port A and Port B does not exceed 5000 kilometers. Today, three ships depart from Port A to Port B at midnight simultaneously. Assuming the three ships sail at a constant speed for 24 hours a day, the first ship arrives at midnight several days later, the second ship arrives at 18:00 several days after that, and the third ship arrives at 8:00 a few days after the second ship. If the first ship travels 300 kilometers per day, the second ship travels 240 kilometers per day, and the third ship travels 180 kilometers per day, what is the actual distance between Port A and Port B in kilometers, and how long did each of the three ships travel? | 3300 |
61,606 | # Problem № 7 (10 points)
A person and his faithful dog started moving along the perimeter of a block from point A at the same time $t_{0}=0$ min. The person moved with a constant speed clockwise, while the dog ran with a constant speed counterclockwise (see fig.). It is known that they met for the first time after $t_{1}=1$ min from the start of the movement. This meeting occurred at point $B$. Given that they continued to move in the same direction and at the same speed after this, determine at what moment in time they will next be at point $B$ simultaneously. Note that $A B=C D=100$ m, $B C=A D=300$ m.
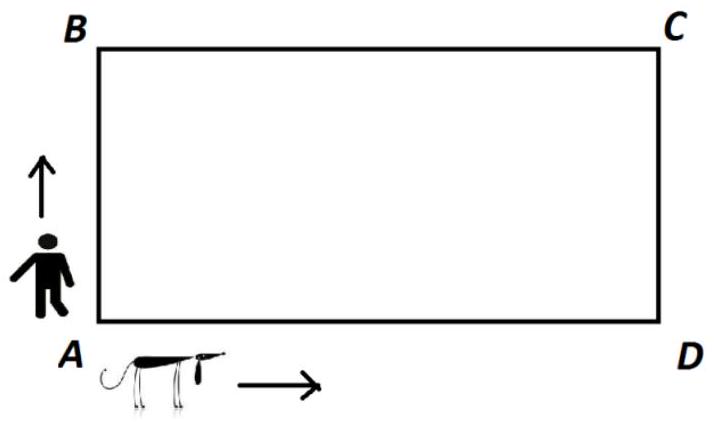 | 9 |
61,641 | [
How many times in a day do the hour and minute hands of a correctly running clock form an angle of $90^{\circ}$?
# | 44 |
61,677 | 8. Let the complex numbers be $z_{1}=-3-\sqrt{3} \mathrm{i}, z_{2}=\sqrt{3}+\mathrm{i}, z=\sqrt{3} \sin \theta+\mathrm{i}(\sqrt{3} \cos \theta+2)$, then the minimum value of $\left|z-z_{1}\right|+\left|z-z_{2}\right|$ is $\qquad$. | 2(\sqrt{3}+1) |
61,680 | [ Inscribed angle, based on the diameter ] Sine Theorem
[ Sine Theorem $\quad$]
Diagonal $B D$ of quadrilateral $A B C D$ is the diameter of the circle circumscribed around this quadrilateral. Find diagonal $A C$, if $B D=2, A B=1, \angle A B D: \angle D B C=4: 3$. | \frac{\sqrt{2}+\sqrt{6}}{2} |
61,695 | 20. From the 10 natural numbers 0 to 9, select 4 different numbers such that the sum of the selected 4 numbers is a multiple of 3. There are $\qquad$ ways to do this. | 72 |
61,698 | The diagonals of the trapezoid are 3 and 5, and the segment connecting the midpoints of the bases is 2. Find the area of the trapezoid.
# | 6 |
61,699 | (3) Let the function $f(x)=x^{2}+x+m\left(m \in \mathbf{R}^{+}\right)$, if $f(t)<0$, then your judgment on the existence of zeros of the function $y=f(x)$ in the interval $(t, t+1)$ is $\qquad$ . | 1 |
61,704 | ## Problem Statement
Calculate the lengths of the arcs of the curves given by equations in a rectangular coordinate system.
$$
y=2-e^{x}, \ln \sqrt{3} \leq x \leq \ln \sqrt{8}
$$ | 1+\frac{1}{2}\ln\frac{3}{2} |
61,711 | 7. A pocket contains five equally sized small balls, of which two are red, two are white, and one is black. The probability that the colors of two adjacent balls are different when the five balls are drawn in sequence is $\qquad$ (answer with a number).
| \frac{2}{5} |
61,713 | 8. Find the smallest positive integer $k$ such that the equation $2 x y-3 x-5 y=k$ has an odd number of positive integral solutions.
(1 mark)
求最小的正整數 $k$, 使方程 $2 x y-3 x-5 y=k$ 的正整數解數目為奇數。 | 5 |
61,733 | 8. Solve the equation $\frac{3}{\log _{2} x}=4 x-5$.
Answer: 2.
Solution: The function $y=\log _{2} x$ is increasing, therefore $y=\frac{3}{\log _{2} x}$ is a decreasing function. On the other hand, the function $y=4 x-5$ is increasing, therefore, the given equation has no more than one root. By trial, we find that $x=2$ is a solution to the equation. | 2 |
61,754 | D/2 Given a positive integer $N$ (written in base 10), define its integer substrings to be integers that are equal to strings of one or more consecutive digits from $N$, including $N$ itself. For example, the integer substrings of 3208 are $3,2,0,8,32,20,320,208$, and 3208 . (The substring 08 is omitted from this list because it is the same integer as the substring 8 , which is already listed.)
What is the greatest integer $N$ such that no integer substring of $N$ is a multiple of 9 ? (Note: 0 is a multiple of 9 .) | 88,888,888 |
61,759 | ## Problem Statement
Calculate the lengths of the arcs of the curves given by equations in a rectangular coordinate system.
$$
y=e^{x}+6, \ln \sqrt{8} \leq x \leq \ln \sqrt{15}
$$ | 1+\frac{1}{2}\ln\frac{6}{5} |
61,764 | 97. Let's calculate the area of the figure bounded by the lines
$$
y=1, y=0, y=\log _{2} x \text { and } x=0
$$ | \frac{1}{\ln2} |
61,772 | 2. Based on $AC$ of the isosceles triangle $ABC$, a point $E$ is taken, and on the lateral sides $AB$ and $BC$ - points $K$ and $M$ such that $KE$ is parallel to $BC$ and $EM$ is parallel to $AB$. What part of the area of triangle $\mathrm{ABC}$ is occupied by the area of triangle $KEM$, if $\mathbf{BM}: \mathbf{EM}=2: 3 ?$ | \frac{6}{25} |
61,775 | 3.2.29 ** Let the sequence of positive numbers $\left\{a_{n}\right\}$ satisfy: $a_{0}=1, a_{n}=a_{n+1}+a_{n+2}, n=0,1,2, \cdots$. Find $a_{1}$. | \frac{\sqrt{5}-1}{2} |
61,798 | $2 \cdot 60$ number $1978^{n}$ and $1978^{m}$ have the same last three digits, try to find the positive integers $m$ and $n$, where $n>m \geqslant 1$, such that $m+n$ takes the minimum value. | 106 |
61,812 | 3. A cherry, a sphere of radius $r$, is dropped into a round glass, the axial cross-section of which is the graph of the function $y=x^{4}$. For what largest $r$ will the sphere touch the lowest point of the bottom? (In other words, what is the maximum radius $r$ of a circle lying in the region $y \geqslant x^{4}$ and containing the origin?) | \frac{3\sqrt[3]{2}}{4} |
61,815 | The $4$ code words
$$\square * \otimes \,\,\,\, \oplus \rhd \bullet \,\,\,\, * \square \bullet \,\,\,\, \otimes \oslash \oplus$$
they are in some order
$$AMO \,\,\,\, SUR \,\,\,\, REO \,\,\,\, MAS$$
Decrypt $$\otimes \oslash \square * \oplus \rhd \square \bullet \otimes $$ | \text{SUMAREMOS} |
61,818 | Calculate $\frac{\pi}{\sqrt{2}}$ to three decimal places. | 2.221 |
61,831 | 6. What is the maximum number of natural numbers not exceeding 2016 that can be marked so that the product of any two marked numbers is a perfect square? | 44 |
61,837 | Let $n$ be an integer. Express $A_{n}=a^{n}+a^{-n}$ in terms of $A_{1}=A$ and $n$.
---
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | A_{n}=\frac{1}{2^{n}}{(A+\sqrt{A^{2}-4})^{n}+(A-\sqrt{A^{2}-4})^{n}} |
61,851 | 3.2.7 * Let the sequence $\left\{a_{n}\right\}$ satisfy $a_{1}=3, a_{2}=8, a_{n+2}=2 a_{n+1}+2 a_{n}, n=1,2, \cdots$. Find the general term $a_{n}$ of the sequence $\left\{a_{n}\right\}$. | a_{n}=\frac{2+\sqrt{3}}{2\sqrt{3}}(1+\sqrt{3})^{n}+\frac{\sqrt{3}-2}{2\sqrt{3}}(1-\sqrt{3})^{n} |
61,860 | 9. If the sum of the digits of a natural number $a$ equals 7, then $a$ is called a "lucky number". Arrange all "lucky numbers" in ascending order as $a_{1}, a_{2}, a_{3}, \cdots$. If $a_{n}=2005$, then $a_{5 n}=$ $\qquad$. | 52000 |
61,881 | 22 、A triangle with a perimeter of 36 has three sides that are all composite numbers, then the number of such triangles is. $\qquad$ | 9 |
61,911 | 3. The base edge of a square pyramid is $26 \mathrm{~cm}$, and the adjacent lateral faces form a $120^{\circ}$ angle with each other. What is the height of the pyramid? | 13 |
61,927 | 9. As shown in the figure, $AB$ is the diameter of the unit circle. Take any point $D$ on $AB$, and construct $DC \perp AB$, intersecting the circumference at $C$. If the coordinates of point $D$ are $(x, 0)$, then when $x \in$ $\qquad$, segments $AD$, $BD$, and $CD$ can form an acute triangle. | (2-\sqrt{5},\sqrt{5}-2) |
61,943 | ## Task 19/76
In a dice game with 6 dice, only those throws should be evaluated where at least one 1 or at least one 5 or at least 3 of the same (any) numbers appear.
What is the probability that no evaluation takes place? | \frac{5}{162} |
61,973 | 2. The range of the function $y=\sqrt{3 x+6}+\sqrt{8-x}$ is $\qquad$ | [\sqrt{10},2\sqrt{10}] |
61,984 | Example 6 There are 10 sets of test papers, each set containing 4 questions, and at most one question is the same between any two sets. Among these test papers, what is the minimum number of different questions?
(2005, Taiwan Mathematical Olympiad) | 13 |
62,011 | 4.1. A smooth sphere with a radius of 1 cm was dipped in red paint and launched between two perfectly smooth concentric spheres with radii of 4 cm and 6 cm, respectively (this sphere ended up outside the smaller sphere but inside the larger one). Upon touching both spheres, the sphere leaves a red trail. During its movement, the sphere traveled along a closed path, resulting in a red-contoured area on the smaller sphere with an area of 37 square cm. Find the area of the region bounded by the red contour on the larger sphere. Provide the answer in square centimeters, rounding to the nearest hundredth if necessary. | 83.25 |
62,015 | 6. Let $r, s, t$ be integers, and the set $\left\{a \mid a=2^{r}+2^{s}+2^{t}, 0 \leqslant t<s<r\right\}$ consists of numbers that form the sequence $\left\{a_{n}\right\}: 7,11,13,14, \cdots$, then $a_{36}=$ $\qquad$ | 131 |
62,017 | 11.6. Calculate $\lim _{n \rightarrow \infty}\left(\sum_{k=0}^{n} C_{2 n}^{2 k} 61^{k}\right) /\left(\sum_{k=0}^{n-1} C_{2 n}^{2 k+1} 61^{k}\right)$. | \sqrt{61} |
62,023 | 6. Joker and Harley Quinn plan to earn money by mining cryptocurrencies. For mining, they chose Ethereum (Ethereum) as one of the most stable and promising currencies. For this, they bought a system unit for 9499 rubles and two video cards for 20990 rubles each. The power consumption of the system unit is 120 W, and each video card consumes 185 W. The mining speed on one video card is 23 million hashes per second, allowing them to earn 0.00630 Ethereum per day on one video card. 1 Ethereum equals 27790.37 rubles. How many days will it take for the heroes' investments to pay off, considering the cost of electricity at 5.38 rubles per 1 kWh? (20 points)
# | 179.44 |
62,025 | Example 7 In $\triangle A B C$, $\angle A B C=50^{\circ}, \angle A C B=20^{\circ}, N$ is a point inside $\triangle A B C$, $\angle N A B=40^{\circ}$. $\angle N B C=30^{\circ}$. Find the degree measure of $\angle N C B$. | 10 |
62,028 | 4. Let $S$ be the set of integers that can be written in the form $50 m+3 n$ where $m$ and $n$ are non-negative integers. For example 3, 50, 53 are all in $S$. Find the sum of all positive integers not in $S$. | 2009 |
62,037 | Variant 134. a) $36+8 \pi$ cm or $23+3 \sqrt{41}+8 \pi$ cm; b) not always.
Evaluation criteria: 20 points - correct (not necessarily the same as above) solution and correct answer; $\mathbf{1 5}$ points - mostly correct solution and correct answer, but there are defects (for example: comparison of numbers in the last part of the solution is not performed or is performed incorrectly; it is not proven that the sum of the lengths of the arcs is equal to the length of the circumference); 10 points - the solution is mostly correct, but contains computational errors; 5 points - only one of the two cases is considered, and the solution and answer (for this case) are completely correct.
## Problem 4 (Variant 131).
When studying the operation of a new type of heat engine working cyclically, it was found that for part of the period it receives heat, with the absolute value of the heat supply power expressed by the law: $P_{1}(t)=P_{0} \frac{\sin \omega t}{100+\sin t^{2}}, 0<t<\frac{\pi}{\omega}$. The gas performs work, developing mechanical power $P_{2}(t)=3 P_{0} \frac{\sin (2 \omega t)}{100+\sin (2 t)^{2}}, 0<t<\frac{\pi}{2 \omega}$. The work done on the gas by external bodies is $2 / 3$ of the magnitude of the work done by the gas. Determine the efficiency of the engine. | \frac{1}{2} |
62,047 | ## Problem Statement
Calculate the lengths of the arcs of the curves given by equations in a rectangular coordinate system.
$$
y=\ln \frac{5}{2 x}, \sqrt{3} \leq x \leq \sqrt{8}
$$ | 1+\frac{1}{2}\ln\frac{3}{2} |
62,080 | In the triangle $ABC$, we divided each side into $p$ equal parts, where $p$ is a prime number. Then, from each side, we connected one of the division points to the opposite vertex of the triangle in such a way that these three lines intersect at a single point. Determine the possible values of $p$. | 2 |
62,108 | 6.26 For a positive integer $k$, there exist positive integers $n$ and $m$ such that $\frac{1}{n^{2}}+\frac{1}{m^{2}}=\frac{k}{n^{2}+m^{2}}$. Find all positive integers $k$.
(Hungarian Mathematical Olympiad, 1984) | 4 |
62,141 | 16. Two cars are driving on a highway, 100 meters apart, both traveling at 60 kilometers per hour. The highway has different speed points (the speed points are far apart). After each car passes the first speed point, their speed immediately increases to 80 kilometers per hour; after passing the second speed point, their speed immediately increases to 100 kilometers per hour; after passing the third speed point, their speed immediately increases to 120 kilometers per hour. After both cars have passed the third speed point, how far apart are the two cars in meters? | 200 |
62,142 | 5. Let the function $f(x)=x-\ln (a x+2 a+1)+2$. If for any $x \geqslant-2$, $f(x) \geqslant 0$ always holds, then the range of the real number $a$ is $\qquad$ . | [0,1] |
62,159 | In an isosceles right triangle, one of the legs is 36 units. Starting from the right-angle vertex on one of the legs, we draw an infinite sequence of equilateral triangles, each touching the next, such that the third vertex of each inscribed triangle always lies on the hypotenuse, and the sides opposite these vertices fill the leg. Determine the sum of the areas of the equilateral triangles. | 324 |
62,160 | ## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{\sqrt{n^{3}+1}-\sqrt{n-1}}{\sqrt[3]{n^{3}+1}-\sqrt{n-1}}$ | \infty |
62,166 | 76. In $\triangle A B C$, $C P=\frac{1}{3} B C, C Q=\frac{1}{4} A C, B Q$ intersects $A P$ at point $N$. If the area of $\triangle A B C$ is 12, find the area of $\triangle A B N$. | \frac{72}{11} |
62,169 | # Task 11.3. (12 points)
How many distinct roots does the equation $f(f(f(x)))=1$ have, if $f(x)=x-\frac{2}{x}$. | 8 |
62,173 | 4. Given real numbers $x, y$ satisfy
$\frac{x^{2}}{3}+y^{2}=1$, then the range of $P=|2 x+y-4|+|4-x-2 y|$ is $\qquad$ | [2,14] |
62,192 | 10. As shown in the right figure, there are six circles at the vertices of four small triangles. If six prime numbers are filled in these circles, their sum is 20, and the sum of the numbers at the three vertices of each small triangle is equal. What is the product of these six prime numbers? | 900 |
62,199 | 7.3. A cube is placed on a table. Can 8 numbers; $1,2, \ldots, 8$, be placed at its vertices so that the following two conditions are met: 1) if the two numbers at the ends of each vertical edge are added, then all four sums are the same; 2) the sum of the numbers on the top face is equal to the sum of the numbers on the bottom face? | Yes |
62,232 | 3.1. A transgalactic ship has encountered an amazing meteorite stream. Some of the meteorites are flying along a straight line, one after another, at equal speeds and at equal distances from each other. Another part is flying in the same way but along another straight line parallel to the first, at the same speeds but in the opposite direction, and at the same distance from each other. The ship is flying parallel to these lines. Astronaut Gavrila noted that the ship meets meteorites flying towards the ship every 7 s, and meteorites flying in the same direction as the ship every 13 s. He wondered how often meteorites would fly past him if the ship were to stand still. It seemed to him that he should take the arithmetic mean of the two given times. Is Gavrila right? If yes, write down this arithmetic mean in the answer. If not, specify the correct time in seconds, rounded to tenths. | 9.1 |
62,238 | ## Task Condition
Find the derivative of the specified order.
$$
y=(5 x-1) \ln ^{2} x, y^{\prime \prime \prime}=?
$$ | \frac{6-2(5x+2)\lnx}{x^{3}} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.