id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
58,225 | 8. Xiao Li and Old Li drive from cities Jia and Yi, respectively, at the same time towards each other, and they agree to meet in city Bing (as shown in the figure below). It is known that the distance between Jia and Bing is $\frac{3}{5}$ of the distance between Yi and Bing. Xiao Li averages 72 kilometers per hour, and Old Li averages 108 kilometers per hour. When Xiao Li arrives at city Bing 15 minutes later, Old Li just arrives. The distance between Jia and Yi is kilometers.
---
The translation maintains the original text's format and line breaks. | 432 |
58,237 | How many values of $x\in\left[ 1,3 \right]$ are there, for which $x^2$ has the same decimal part as $x$? | 7 |
58,251 | 1.45. In a circle of radius $R$, two parallel chords are drawn on opposite sides of the center, one of which subtends an arc of $60^{\circ}$, the other an arc of $120^{\circ}$. Find the area of the part of the circle enclosed between the chords. | 0.5R^{2}(\pi+\sqrt{3}) |
58,256 | (Try to find the number of real numbers $a$ such that for each $a$, the cubic equation $x^{3}=a x+a+1$ has an even root satisfying $|x|<1000$. (Xiong Bin))
---
The above text has been translated into English, preserving the original text's line breaks and format. | 999 |
58,264 | 20. Let $x$ be a non-zero real number such that $\sqrt[5]{x^{3}+20 x}=\sqrt[3]{x^{5}-20 x}$. Find the product of all possible values of $x$.
(2 marks)
Let $x$ be a non-zero real number such that $\sqrt[5]{x^{3}+20 x}=\sqrt[3]{x^{5}-20 x}$. Find the product of all possible values of $x$.
(2 marks) | -5 |
58,279 | 1. In a game, three types of tokens are used, each with a different value expressed in denars. The value of each token is a natural number. Bojan, Ace, and Sasha each have at least one token of each type. Bojan has 4 tokens with a total value of 28 denars, Ace has 5 tokens with a total value of 21 denars, and Sasha has 3 tokens. What is the total value of Sasha's tokens? | 17 |
58,282 | ## Task A-4.5.
Determine the last three digits of the number $21^{2021}$. | 421 |
58,305 | Problem 3.5. Vanya wrote the number 1347 on the board.
- Look! - noticed Petya. - In this number, each of the last two digits is equal to the sum of the two preceding ones.
- Exactly! - agreed Vasya.
- Can you write the largest four-digit number like this?
Help Vasya complete Petya's task. | 9099 |
58,320 | A function $f$ is defined for all real numbers and satisfies \[f(2 + x) = f(2 - x)\qquad\text{and}\qquad f(7 + x) = f(7 - x)\] for all real $x$. If $x = 0$ is a root of $f(x) = 0$, what is the least number of roots $f(x) = 0$ must have in the interval $-1000 \le x \le 1000$? | 401 |
58,327 | 16. The central garden is composed of five equally sized squares, and a fence surrounds the garden, with a perimeter of 96 meters. The area of the central garden is $\qquad$ square meters. | 320 |
58,344 | Three dice with faces numbered 1 through 6 are stacked as shown. Seven of the eighteen faces are visible, leaving eleven faces hidden (back, bottom, between). The total number of dots NOT visible in this view is | 41 |
58,351 | 9. (6 points) In isosceles $\triangle A B C$, the ratio of the measures of two interior angles is 1:2. Then, the largest angle in $\triangle A B C$ can be $\qquad$ degrees. | 90 |
58,360 | At least how many moves must a knight make to get from one corner of a chessboard to the opposite corner? | 6 |
58,365 | 8. The King's Path (from 7th grade, 2 points). A chess king is on the a1 square of a chessboard and wants to move to the h8 square, moving right, up, or diagonally up-right. In how many ways can he do this? | 48639 |
58,367 | Let $ABCD$ be a parallelogram. Let $E$ be the midpoint of $AB$ and $F$ be the midpoint of $CD$. Points $P$ and $Q$ are on segments $EF$ and $CF$, respectively, such that $A, P$, and $Q$ are collinear. Given that $EP = 5$, $P F = 3$, and $QF = 12$, find $CQ$. | 8 |
58,368 | 6. The numbers $112,121,123,153,243,313$, and 322 are among the rows, columns, and diagonals of a $3 \times 3$ square grid of digits (rows and diagonals read left-to-right, and columns read top-to-bottom). What 3-digit number completes the list?
Solution:
524 | 524 |
58,371 | For 10 positive integers $x$, let $m=\left[\frac{x}{2}\right]+\left[\frac{x}{2^{2}}\right]+\left[\frac{x}{2^{3}}\right]+\cdots+\left[\frac{x}{2^{k}}\right]$, where $k$ is the smallest integer satisfying $2^{k} \geqslant x$, and the symbol $[x]$ represents the greatest integer not exceeding $x$. The difference between $x$ and $m$, i.e., $x-m$, is called the "deficiency number" of the positive integer $x$. (For example, when $x=100$,
\[
\begin{aligned}
m & =\left[\frac{100}{2}\right]+\left[\frac{100}{2^{2}}\right]+\left[\frac{100}{2^{3}}\right]+\left[\frac{100}{2^{4}}\right]+\left[\frac{100}{2^{5}}\right]+\left[\frac{100}{2^{6}}\right]+\left[\frac{100}{2^{7}}\right] \\
& =50+25+12+6+3+1+0=97,
\end{aligned}
\]
$x-m=100-97=3$, so the "deficiency number" of the number 100 is 3. ) Then the smallest positive integer $x$ whose "deficiency number" is 9 is $\qquad$ | 511 |
58,372 | 35. (1985 American Mathematical Invitation Contest) Let the four vertices of a regular tetrahedron be $A, B, C, D$, with each edge length being 1 meter. A small insect starts from point $A$ and moves according to the following rule: at each vertex, it chooses one of the three edges connected to that vertex with equal probability, and crawls all the way to the end of the chosen edge. Suppose the probability that the insect is exactly at vertex $A$ after crawling 7 meters is $p=\frac{n}{729}$. Find the value of $n$. | 182 |
58,383 | Example 4 (to $4^{\circ}$ ). Find $\int \sin ^{2} x \cos ^{4} x d x$. | \frac{1}{16}(x-\frac{1}{12}\sin6x+\frac{1}{4}\sin2x-\frac{1}{4}\sin4x)+C |
58,405 | ## 163. The Court.
In the language of the tribe inhabiting the island located not far from the island of zombies, the words "bal" and "da" mean "yes" and "no," but words that sound the same do not necessarily have the same meaning. Some of the island's inhabitants answer questions with "bal" and "da," while others, breaking an ancient taboo, prefer to speak English (and answer with "yes" and "no").
For some unexplained reasons, all members of any family on this island are of the same type. In particular, any two brothers are either both zombies or both humans.
One of the island's natives has been accused of treason. Given the particular importance of the case, it was decided to call Inspector Craig from London. The three main witnesses, A, B, and C, were natives of the island. The following excerpt is taken from the court transcript. The questioning of the witnesses is conducted by Inspector Craig.
Question (to witness A). Is the defendant not guilty? Answer (from witness A). Bal.
Question (to witness B). What does "bal" mean?
Answer (from witness B). "Bal" means "yes."
Question (to witness C). Are witnesses A and B brothers?
Answer (from witness C). No.
Second question (to witness C). Is the defendant not guilty?
Answer (from witness C). Yes.
Is the defendant guilty or not guilty? | notguilty |
58,425 | Example 1 Find integers $a, b, c$, such that they satisfy the condition:
$$
a^{2}+b^{2}+c^{2}+3 < a b + 3 b + 2 c \text{. }
$$ | =1,b=2,=1 |
58,444 | 1. Given 5000 cards, on which natural numbers from 1 to 5000 are written (each card has exactly one number, and the numbers do not repeat). It is required to choose two cards such that the sum of the numbers written on them is divisible by 100. In how many ways can this be done? | 124950 |
58,465 | 2. The solution set of the inequality $\sqrt{x-x^{2}}+\sqrt{4 x-x^{2}} \geqslant 2$ is $\qquad$ . | \left\{\frac{4}{5}\right\} |
58,466 | 28.3. On the sides $B C$ and $C D$ of the square $A B C D$, points $K$ and $M$ are chosen such that the perimeter of triangle $K M C$ is equal to twice the side length of the square $A B C D$. Find the angle $K A M$.
$$
(7-10 \text { grades })
$$ | 45 |
58,471 | 6. Given $\sin \alpha+\sin (\alpha+\beta)+\cos (\alpha+\beta)=\sqrt{3}, \beta \in\left[\frac{\pi}{4}, \pi\right]$, then $\beta=$ | \frac{\pi}{4} |
58,473 | In trapezoid $A B C D(B C \| A D)$, it is known that $A D=3 \cdot B C$. A line intersects the lateral sides of the trapezoid at points $M$ and $N, A M: M B=3: 5, C N: N D=2: 7$. Find the ratio of the areas of quadrilaterals $M B C N$ and $A M N D$.
# | \frac{9}{23} |
58,479 | 7. The diagram shows a triangle $A B C$ with area $12 \mathrm{~cm}^{2}$. The sides of the triangle are extended to points $P, Q, R, S, T$ and $U$ as shown so that $P A=A B=B S, Q A=A C=C T$ and $R B=B C=C U$.
What is the area (in $\mathrm{cm}^{2}$ ) of hexagon $P Q R S T U$ ? | 156 |
58,481 | 10.195. The circle touches two adjacent sides of the square and divides each of the other two sides into segments equal to 2 and 23 cm. Find the radius of the circle. | 17 |
58,517 | ## Task Condition
Find the derivative of the specified order.
$$
y=\left(x^{2}+3\right) \ln (x-3), y^{IV}=?
$$ | \frac{-2x^{2}+24x-126}{(x-3)^{4}} |
58,519 | Example 12 In a convex hexagon $A B C D E F$, $\angle A=\angle B=\angle C=$ $\angle D=\angle E=\angle F$, and $A B+B C=11, F A-C D=3$, find $B C+D E$. | 14 |
58,529 | 22. $[$ 12] Sandra the Maverick has 5 pairs of shoes in a drawer, each pair a different color. Every day for 5 days, Sandra takes two shoes out and throws them out the window. If they are the same color, she treats herself to a practice problem from a past HMMT. What is the expected value (average number) of practice problems she gets to do? | \frac{5}{9} |
58,551 | 3. $[x]$ represents the integer part of $x$, for example $[1.67]=1,[3]=3$. If $[x+0.40]+[x+0.41]+[x+0.42]+\cdots+[x+0.99]=400$, then $[x+0.11]+[x+0.12]+[x+0.13]+\cdots+[x+1.28]=$ | 777 |
58,581 | Problem 11.6. Inside the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, there is the center $O$ of a sphere with radius 10. The sphere intersects the face $A A_{1} D_{1} D$ along a circle with radius 1, the face $A_{1} B_{1} C_{1} D_{1}$ along a circle with radius 1, and the face $C D D_{1} C_{1}$ along a circle with radius 3. Find the length of the segment $O D_{1}$.
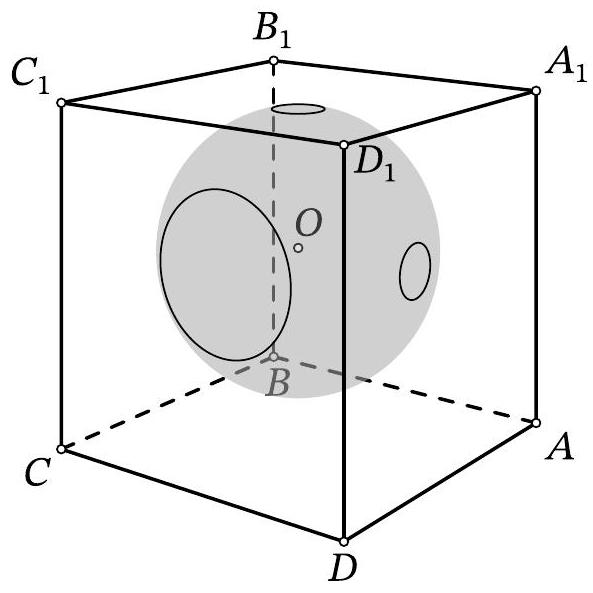 | 17 |
58,597 | 12. A small ball with a radius of 1 can move freely in all directions inside a regular tetrahedron container with an internal edge length of $4 \sqrt{6}$. The area of the container's inner wall that the ball can never touch is $\qquad$. | 72\sqrt{3} |
58,610 | 14.21. How many four-digit numbers (from 0001 to 9999) exist where the sum of the first two digits is equal to the sum of the last two digits? | 669 |
58,612 | 3. Let $[x]$ denote the greatest integer not exceeding the real number $x$. Set $A=\left[\frac{7}{8}\right]+\left[\frac{7^{2}}{8}\right]+\cdots+\left[\frac{7^{2016}}{8}\right]$. Then the remainder when $A$ is divided by 50 is $\qquad$ . | 42 |
58,630 | 9. (6 points) Three mice found a pile of peanuts and agreed to come and share them equally the next day. The next day, the first mouse arrived the earliest. He found that the peanuts could not be divided equally, so he ate one, and the remaining could be divided into 3 equal parts, and he took one part. The second and third mice came one after another, encountering the same problem, and took the same method, each eating one and then dividing the remaining peanuts into three parts, taking one part. So, what is the minimum number of peanuts in this pile? | 25 |
58,631 | Ilya Muromets meets the three-headed Zmei Gorynych. And the battle begins. Every minute Ilya cuts off one of Zmei's heads. With a probability of $1 / 4$, two new heads grow in place of the severed one, with a probability of $1 / 3$ - only one new head, and with a probability of $5 / 12$ - no heads at all. The Zmei is considered defeated if he has no heads left. Find the probability that Ilya will eventually defeat the Zmei. | 1 |
58,644 | What fraction of the Earth's volume lies above the $45$ degrees north parallel? You may assume the Earth is a perfect sphere. The volume in question is the smaller piece that we would get if the sphere were sliced into two pieces by a plane. | \frac{8-5\sqrt{2}}{16} |
58,697 | 6. If $x^{3}-3 \sqrt{2} x^{2}+6 x-2 \sqrt{2}-8=0$, find the value of $x^{5}-41 x^{2}+2012$.
(1 mark) If $x^{3}-3 \sqrt{2} x^{2}+6 x-2 \sqrt{2}-8=0$, find the value of $x^{5}-41 x^{2}+2012$. | 1998 |
58,709 | In how many ways can $1999^{1999}$ be written as the sum of consecutive natural numbers? | 2000 |
58,735 | 5 In the number array shown in the figure, the three numbers in each row form an arithmetic sequence, and the three numbers in each column also form an arithmetic sequences. If $a_{22}=2$, then the sum of all these 9 numbers is $\qquad$ | 18 |
58,736 | [Sum of angles in a triangle. Theorem about the exterior angle. ] [ Lengths of sides, heights, medians, and angle bisectors ]
In triangle $A B C \angle A=40^{\circ}, \angle B=20^{\circ}$, and $A B-B C=4$. Find the length of the angle bisector of angle $C$. | 4 |
58,738 | We attached three rods (whose thickness can be neglected) pairwise perpendicularly to each other at a common point at one of their ends. The lengths of the rods are 1, 2, and 3. We placed the resulting structure on the table so that the free ends of the rods touch the table surface. Determine the exact height at which the attachment point is above the table.
We attached three rods (whose thickness can be neglected) pairwise perpendicularly to each other at a common point at one of their ends. The lengths of the rods are 1, 2, and 3. We placed the resulting structure on the table so that the free ends of the rods touch the table surface. Determine the exact height at which the attachment point is above the table. | \frac{6}{7} |
58,740 | 10. (5 points) The New Year's party has a total of 8 programs, including 3 non-singing programs. When arranging the program list, it is stipulated that non-singing programs should not be adjacent, and the first and last programs must be singing programs. Therefore, there are $\qquad$ different ways to arrange the program list. | 2880 |
58,766 | 6. (3 points) Find the total length of intervals on the number line where the inequalities $x<1$ and $\sin \log _{2} x<0$ are satisfied. | \frac{2^{\pi}}{1+2^{\pi}} |
58,767 | 2. The circle with the diameter of the two foci of the ellipse intersects the ellipse at four different points. Connecting these four intersection points and the two foci in sequence forms a regular hexagon. Then the eccentricity of this ellipse is $\qquad$ | \sqrt{3}-1 |
58,774 | 1. Given the function $F$ applied to a four-digit positive integer $\overline{a b c d}$ yields the integer $F(\overline{a b c d})=a^{4}+b^{3}+c^{2}+d^{1}$. For example, $F(2019)=2^{4}+0^{3}+1^{2}+9^{1}=26$.
Then $F(2019)-F(2018)+$
$$
F(2017)-\cdots-F(2000)=
$$
$\qquad$ | 10 |
58,778 | 4. Given the set $S=\{1,2, \cdots, 2005\}, A \subseteq S, A$ such that the sum of any two numbers in $A$ is not divisible by 117, find the maximum value of $|A|$.
untranslated text remains the same as requested. However, if you need any further assistance or a different translation, feel free to let me know! | 1003 |
58,803 | 4. There are four positive numbers, one of which is $\frac{1}{2}$. If any two numbers are taken from these four, among the remaining two numbers, there must be one number such that the sum of these three numbers is 1. Then these four numbers are | \frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{2} |
58,812 | Mice have built an underground house consisting of chambers and tunnels:
- each tunnel leads from one chamber to another (i.e., none are dead ends),
- from each chamber, exactly three tunnels lead to three different chambers,
- from each chamber, one can reach any other chamber via tunnels,
- the house has exactly one tunnel such that its collapse would divide the house into two separate parts.
What is the minimum number of chambers the mouse house could have? Sketch how the chambers could be connected.
(K. Jasenčáková)
Hint. Start with the critical tunnel. | 10 |
58,829 | 4. Variant 1.
In the number, two digits were swapped, and as a result, it increased by more than 3 times. The resulting number is 8453719. Find the original number. | 1453789 |
58,853 | 6. 2 teachers are taking 30 students across a river by boat, but there is only one small boat that can carry 8 people (no boatman). Each time they cross the river, 2 teachers are needed to act as boatmen. To get everyone across, the boat must make at least $\qquad$ trips. (A round trip counts as 2 trips) | 9 |
58,857 | Let real numbers $a, b, c, x$ satisfy
$$
a \cos ^{2} x+b \cos x+c=0 .
$$
Try to give a quadratic equation that $\cos 2 x$ satisfies in terms of $a, b, c$. Compare these two equations in the case of $a=4, b=2, c=-1$. | 4\cos^{2}2x+2\cos2x-1=0 |
58,858 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{1} \frac{x^{4} \cdot d x}{\left(2-x^{2}\right)^{3 / 2}}
$$ | \frac{5}{2}-\frac{3\pi}{4} |
58,865 | Example. Evaluate the double integral
$$
\iint_{D} \frac{x}{y^{5}} d x d y
$$
where the region $D$ is defined by the inequalities
$$
1 \leq \frac{x^{2}}{16}+y^{2} \leq 3, \quad y \geq \frac{x}{4}, \quad x \geq 0
$$ | 4 |
58,891 | 8. In an acute-angled triangle $ABC$, a point $Q$ is chosen on side $AC$ such that $AQ: QC = 1: 2$.
From point $Q$, perpendiculars $QM$ and $QK$ are dropped to sides $AB$ and $BC$ respectively. It is given that $BM: MA = 4: 1, BK = KC$. Find $MK: AC$. | \frac{2}{\sqrt{10}} |
58,894 | 5. Determine the sum of all four-digit numbers in which every two consecutive digits form a square of a natural number. (For example, 164 is such a three-digit number because 16 and 64 are squares of the numbers 4 and 8).
## Tasks worth 10 points: | 13462 |
58,935 | ## Task 2 - 340622
The gardens of the Kniffel family and the Knobel family are both square-shaped and adjoin each other as shown in Figure a.
The area of Kniffel's garden is 1225 square meters, and the area of Knobel's garden is 625 square meters.
a) What is the width $A D$ or $E F$ of the gardens?
b) The Kniffel family gives a piece of their garden to the Knobel family. After this, both gardens have the same area. How large is this area?
c) Figure b shows the new division. By what length $G H$ has Knobel's garden become longer?
a)
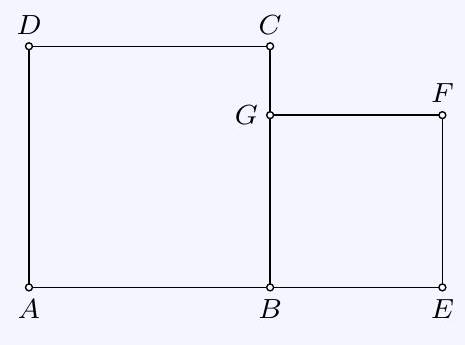
b)
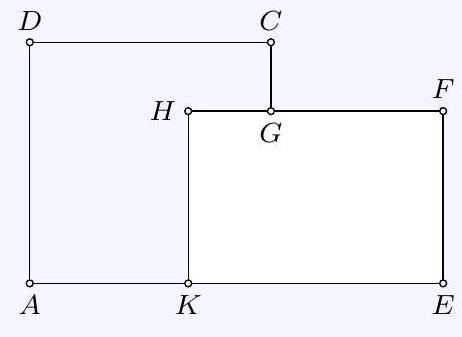 | 12\, |
58,955 | 4. Given a moving large circle $\odot O$ that is externally tangent to a fixed small circle $\odot O_{1}$ with radius 3 at point $P, AB$ is the external common tangent of the two circles, with $A$ and $B$ being the points of tangency. A line $l$ parallel to $AB$ is tangent to $\odot O_{1}$ at point $C$ and intersects $\odot O$ at points $D$ and $E$. Then $C D \cdot C E=$ $\qquad$ | 36 |
58,962 | 5. The number of non-empty subsets of the set $\{1,2, \cdots, 2016\}$ whose elements sum to an odd number is $\qquad$ | 2^{2015} |
58,964 | 4. Each cell of a $2 \times 13$ table is to be colored with exactly one of four colors. In how many ways can this be done so that no two adjacent cells are colored the same? (We consider two cells to be adjacent if they share a common side.)
(Jaroslav Švrček) | 12\cdot7^{12} |
58,965 | 5. Tanya was sequentially writing down numbers of the form $n^{7}-1$ for natural numbers $n=2,3, \ldots$ and noticed that for $n=8$ the resulting number is divisible by 337. For what smallest $n>1$ will she get a number divisible by $2022?$ | 79 |
58,977 | The figure shows a track scheme for karting. The start and finish are at point $A$, and the karting driver can make as many laps as they want, returning to the starting point.
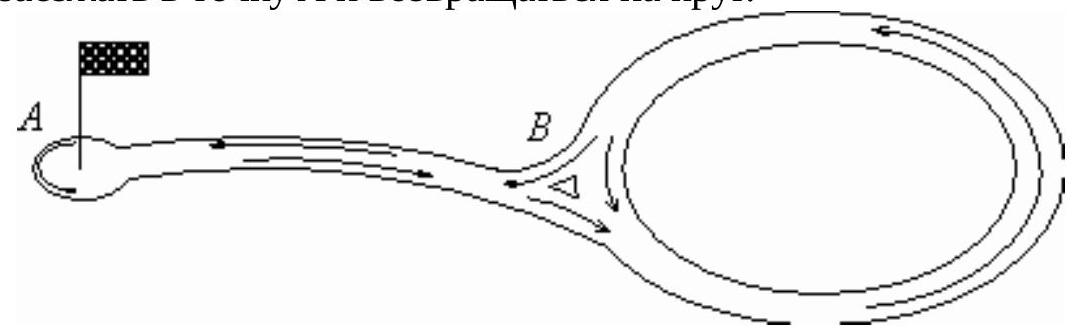
The young driver Yura spends one minute on the path from $A$ to $B$ or back. Yura also spends one minute on the loop. The loop can only be driven counterclockwise (arrows indicate possible directions of movement). Yura does not turn back halfway and does not stop. The race duration is 10 minutes. Find the number of possible different routes (sequences of passing sections). # | 34 |
58,980 | Example 2 Let the parabola
$$
y=x^{2}+(2 a+1) x+2 a+\frac{5}{4}
$$
intersect the $x$-axis at only one point.
(1) Find the value of $a$;
(2) Find the value of $a^{18}+323 a^{-6}$.
(1998, National Junior High School Mathematics Competition) | 5796 |
58,985 | 6. [5] We say " $s$ grows to $r$ " if there exists some integer $n>0$ such that $s^{n}=r$. Call a real number $r$ "sparse" if there are only finitely many real numbers $s$ that grow to $r$. Find all real numbers that are sparse. | -1,0,1 |
58,989 | 2 Positive integers $a_{1}, a_{2}, \cdots, a_{2006}$ (which can be the same) such that $\frac{a_{1}}{a_{2}}$, $\frac{a_{2}}{a_{3}}, \cdots, \frac{a_{2005}}{a_{2006}}$ are all distinct. How many different numbers are there at least among $a_{1}, a_{2}, \cdots, a_{2006}$? (Provided by Yonggao Chen) | 46 |
59,007 | Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
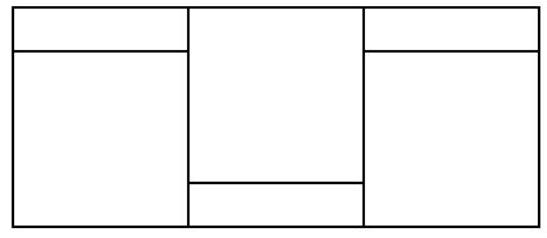 | 52 |
59,046 | 11.6. What is the minimum value of the ratio of the volumes of a cone and a cylinder circumscribed about the same sphere? | \frac{4}{3} |
59,050 | ## SUBJECT 2
Find the cardinality of the set:
$$
A=\left\{\overline{a b c} / \frac{a \sqrt{2}}{\sqrt{1}+\sqrt{2}+\sqrt{3}}-\frac{b \sqrt{3}}{\sqrt{1}+\sqrt{3}+\sqrt{4}}-\frac{2 c \sqrt{8}}{\sqrt{4}+\sqrt{8}+\sqrt{12}}=\frac{-3}{\sqrt{2}} ; a \neq b \neq c\right\}
$$
Prof. Nicolae Jurubiță | 4 |
59,060 | Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
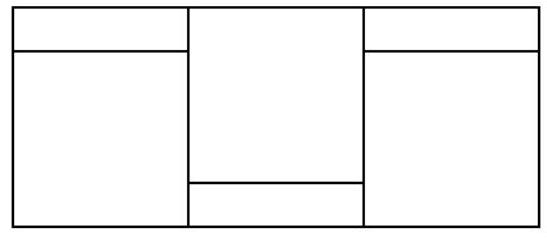 | 52 |
59,072 | Using the digits $0,1,5,6,7,9$,
a) how many 6-digit numbers can be formed where at least one digit is repeated?
b) how many 6-digit numbers can be formed that consist entirely of different digits and are not divisible by 4? | 504 |
59,081 | [ Auxiliary similar triangles ]
Given an equilateral triangle $A B C$. Point $K$ is the midpoint of side $A B$, point $M$ lies on side $B C$, and $B M: M C=1: 3$. A point $P$ is chosen on side $A C$ such that the perimeter of triangle $P K M$ is the smallest possible. In what ratio does point $P$ divide side $A C$? | 2:3 |
59,107 | 20. Let $x, y$ be acute angles such that $\sin y=2005 \cos (x+y) \sin x$. Find the greatest possible value of $\tan y$.
(3 marks)
Let $x, y$ be acute angles such that $\sin y=2005 \cos (x+y) \sin x$. Find the greatest possible value of $\tan y$. | \frac{2005\sqrt{2006}}{4012} |
59,111 | 3. From the eight numbers $-3,-2,-1,0,1,2,3,4$, any three different numbers are taken as the coefficients of the quadratic function $f(x)=a x^{2}+b x+c(a \neq 0)$. If the graph of the quadratic function passes through the origin, and its vertex is in the first quadrant or the third quadrant, how many such quadratic functions are there? $\qquad$ | 24 |
59,113 | 66 If the parabola $C_{m}: y=x^{2}-m x+m+1$ intersects the line segment $A B$ with endpoints $A(0,4), B(4,0)$ at exactly two points, then the range of values for $m$ is $\qquad$ . | [3,\frac{17}{3}] |
59,161 | 5. Given the functions
$$
f(x)=\cos \pi x, g(x)=2^{x} a-\frac{1}{2}(a \neq 0) .
$$
If there exist $x_{1} 、 x_{2} \in[0,1]$, such that $f\left(x_{1}\right)=g\left(x_{2}\right)$ holds, then the range of the real number $a$ is . | [-\frac{1}{2},0)\cup(0,\frac{3}{2}] |
59,182 | 9.3. Find the value of the expression $x-\sqrt{2022 x}+2023$,
if $x-\sqrt{\frac{2022}{x}}=2023$. | 2024 |
59,200 | Example 1 The numbers 1447, 1005, and 1231 have certain common points, that is, each number is a four-digit number starting with 1, and in each four-digit number, exactly two digits are the same. How many such four-digit numbers are there? | 432 |
59,236 | 2. From the 4040 integers ranging from -2020 to 2019, choose 3 numbers to multiply. Let the smallest result be $m$, and the largest result be $n$. Then $\frac{m}{n}=$ $\qquad$ . (The result should be expressed as a simplified fraction) | -\frac{2018}{2019} |
59,256 | 4. Let the roots of the equation $x^{4}+5 x^{3}+6 x^{2}+5 x+1=0$ in the complex number range be $x_{1}, x_{2}, x_{3}, x_{4}$. Then $x_{1}^{3}+x_{2}^{3}+x_{3}^{3}$ $+x_{4}^{3}=$ $\qquad$ . | -50 |
59,268 | \section*{Problem 1 - 111241}
All real numbers \(x\) are to be specified for which the expression
\[
\frac{2 x}{|x-3|-5}+\frac{1}{x+2}
\]
exists, and among these, all \(x\) are to be determined that satisfy the following inequality (2):
\[
\frac{2 x}{|x-3|-5}+\frac{1}{x+2} \geq 1
\] | x\in(-2,-\frac{1}{3}]\cup(8,\infty) |
59,314 | Shapovalov A.V.
55 boxers participated in a tournament with a "loser leaves" system. The fights proceeded sequentially. It is known that in each match, the number of previous victories of the participants differed by no more than 1. What is the maximum number of fights the tournament winner could have conducted? | 8 |
59,317 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{\arcsin \sqrt{3 / 7}} \frac{\tan^{2} x \, dx}{3 \sin ^{2} x + 4 \cos ^{2} x - 7}
$$ | -\frac{\sqrt{3}}{8}+\frac{\sqrt{3}\pi}{32} |
59,335 | [ Properties of medians. The centroid of a triangle.] [ The ratio of the areas of similar triangles $]$
The area of triangle $A B C$ is $S$. Find the area of the triangle whose sides are equal to the medians of triangle $A B C$. | \frac{3S}{4} |
59,338 | 88 In the Cartesian coordinate system $x O y$, the area of the figure formed by points whose coordinates satisfy the condition $\left(x^{2}+y^{2}+2 x+2 y\right)\left(4-x^{2}-y^{2}\right) \geqslant$ 0 is | 2\pi+4 |
59,387 | 8. For any subset $S \subseteq\{1,2, \ldots, 15\}$, a number $n$ is called an "anchor" for $S$ if $n$ and $n+|S|$ are both members of $S$, where $|S|$ denotes the number of members of $S$. Find the average number of anchors over all possible subsets $S \subseteq\{1,2, \ldots, 15\}$. | \frac{13}{8} |
59,388 | 3. The letters of the word MATHEMATICS are rearranged to form distinct strings of the same 11 letters. What proportion of these strings do not contain the string MATH? | \frac{491}{495} |
59,390 | 1. [3] Find the number of integers between 1 and 200 inclusive whose distinct prime divisors sum to 16 . (For example, the sum of the distinct prime divisors of 12 is $2+3=5$.) | 6 |
59,417 | On side $A B$ of triangle $A B C$, a point $K$ is marked. Segment $C K$ intersects the median $A M$ of the triangle at point $P$. It turns out that $A K = A P$.
Find the ratio $B K: P M$. | 2 |
59,430 | The sum of non-negative numbers $x_{1}, x_{2}, \ldots, x_{10}$ is 1. Find the maximum possible value of the sum $x_{1} x_{2}+$ $x_{2} x_{3}+\ldots+x_{9} x_{10}$ | 0.25 |
59,432 | 1. In a regular quadrilateral pyramid $P-ABCD$, all four lateral faces are equilateral triangles. Let the dihedral angle between a lateral face and the base be $\theta$, then $\tan \theta=$ $\qquad$ | \sqrt{2} |
59,442 | Problem 5. There are 4 numbers, not all of which are the same. If you take any two of them, the ratio of the sum of these two numbers to the sum of the other two numbers will be equal to the same value k. Find the value of k. Provide at least one set of four numbers that satisfy the condition. Describe all possible sets of such numbers and determine how many there are. | -1 |
59,457 | From Zlatoust to Miass, a "GAZ", a "MAZ", and a "KamAZ" set off simultaneously. The "KamAZ", upon reaching Miass, immediately turned back and met the "MAZ" 18 km from Miass, and the "GAZ" - 25 km from Miass. The "MAZ", upon reaching Miass, also immediately turned back and met the "GAZ" 8 km from Miass. What is the distance from Zlatoust to Miass? | 60 |
59,470 | For how many integers $n$ is $\frac{2 n^{3}-12 n^{2}-2 n+12}{n^{2}+5 n-6}$ equal to an integer? | 32 |
59,482 | 24. Find the number of 7-digit integers formed by some or all of the five digits, namely, $0,1,2,3$, and 4 , such that these integers contain none of the three blocks 22,33 and 44 . | 29776 |
59,497 | Problem 5. Milan and Aleksandar had a large box of chocolate candies, which they were to divide in the following way: First, Milan took 1 candy, and Aleksandar took two candies, then Milan took three, and Aleksandar took four candies, and so on, each taking one more candy alternately.
When the number of candies left in the box was less than the required number, the friend whose turn it was took all the remaining candies. How many candies were there in the box at the beginning, if Milan was the last to take candies and ended up with 101 candies. | 211 |
59,505 | (2) Define $b-a$ as the "length" of the set $\{x \mid a \leqslant x \leqslant b\}$. Let $M=$ $\left\{x \left\lvert\, m \leqslant x \leqslant m+\frac{3}{4}\right.\right\}, N=\left\{x \left\lvert\, n-\frac{1}{3} \leqslant x \leqslant n\right.\right\}$, and both $M$ and $N$ are subsets of the set $\{x \mid 0 \leqslant x \leqslant 1\}$. Then the minimum "length" of the set $M \cap N$ is $\qquad$. | \frac{1}{12} |
59,515 | Solve the following equation:
$$
\frac{x+a+b}{x+a}=\frac{x+a-b}{x-a}-\frac{a^{2}+b^{2}}{x^{2}-a^{2}}
$$ | -\frac{+b}{2} |
59,565 | Problem 4
Find all integers $n \geqslant 0$ such that $20 n+2$ divides $2023 n+210$.
## $\S$ | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.