id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
59,566 | ## Task B-4.4.
Points $A, B$, and $C$ are the vertices of a triangle. On side $\overline{A B}$, 6 points are marked, on side $\overline{B C}$, 7 points are marked, and on side $\overline{C A}$, 8 points are marked. The vertices of the triangle are not among the marked points. How many different quadrilaterals can we determine whose vertices are the marked points? | 4347 |
59,594 | Problem 7.8. On a rectangular sheet of paper, a picture in the shape of a "cross" was drawn from two rectangles $A B C D$ and $E F G H$, the sides of which are parallel to the edges of the sheet. It is known that $A B=9, B C=5, E F=3, F G=10$. Find the area of the quadrilateral $A F C H$.
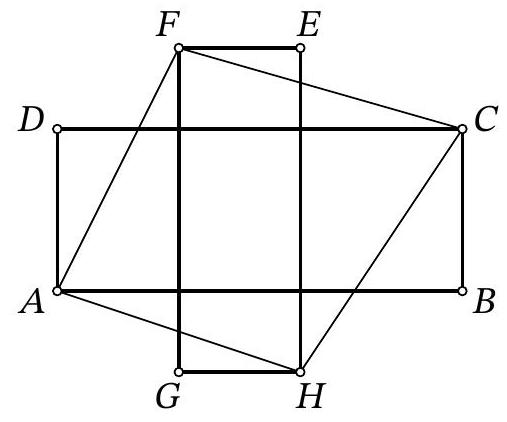 | 52.5 |
59,599 | 15th Irish 2002 Problem A1 The triangle ABC has a, b, c = 29, 21, 20 respectively. The points D, E lie on the segment BC with BD = 8, DE = 12, EC = 9. Find ∠DAE. | 45 |
59,605 | Problem 9.7. Two parallel lines are drawn through points $A(0 ; 14)$ and $B(0 ; 4)$. The first line, passing through point $A$, intersects the hyperbola $y=\frac{1}{x}$ at points $K$ and $L$. The second line, passing through point $B$, intersects the hyperbola $y=\frac{1}{x}$ at points $M$ and $N$.
What is $\frac{A L-A K}{B N-B M}$ ?
 | 3.5 |
59,608 | ## Task Condition
Find the derivative.
$y=(2+3 x) \sqrt{x-1}-\frac{3}{2} \operatorname{arctg} \sqrt{x-1}$ | \frac{18x^{2}-8x-3}{4x\sqrt{x-1}} |
59,610 | 11.2. In the quarry, there are 120 granite slabs weighing 7 tons each and 80 slabs weighing 9 tons each. A railway platform can load up to 40 tons. What is the minimum number of platforms required to transport all the slabs? | 40 |
59,625 | G3.4 Spilt the numbers $1,2, \ldots, 10$ into two groups and let $P_{1}$ be the product of the first group and $P_{2}$ the product of the second group. If $P_{1}$ is a multiple of $P_{2}$, find the minimum value of $\frac{P_{1}}{P_{2}}$. | 7 |
59,626 | 1. Among the integers $1,2, \cdots, 2011$, the number of integers that can be expressed in the form $[x[x]]$ is $\qquad$, where $[x]$ denotes the greatest integer not exceeding the real number $x$. | 990 |
59,629 | ## Task Condition
Find the derivative.
$y=5 x-\ln \left(1+\sqrt{1-e^{10 x}}\right)-e^{-5 x} \cdot \arcsin \left(e^{5 x}\right)$ | 5e^{-5x}\cdot\arcsin(e^{5x}) |
59,632 | 10.4. Given the function $f(x)=\sqrt{x^{2}-x}$. Find the domain of the function $y=f(f(x))$. | (-\infty,\frac{1-\sqrt{5}}{2}]\cup{0}\cup{1}\cup[\frac{1+\sqrt{5}}{2},+\infty) |
59,653 | Example 1 Allocate 24 volunteer slots to 3 schools. Each school must receive at least one slot and the number of slots each school receives must be different. The number of allocation methods is $\qquad$ . ${ }^{[2]}$
(2008, National High School Mathematics Competition) | 222 |
59,691 | 5. (10 points) The distance from home to work is $s=3 \kappa$ km. At the moment Ivan left work, his favorite dog ran out of the house towards him. They met at a distance of a quarter of the entire path from work. The dog instantly turned around and ran back home. Upon reaching home, he instantly turned around again and ran towards his owner, and so on. Assuming Ivan and his dog move at constant speeds, determine the distance the dog will have run by the time Ivan gets home. | 9\kappa |
59,697 | 5. Find all prime numbers whose decimal representation has the form 101010 ... 101 (ones and zeros alternate). | 101 |
59,722 | Four. (15 points) The number of elements in set $S$ is denoted as $|S|$, and the number of subsets of set $S$ is denoted as $n(S)$. Given three non-empty finite sets $A$, $B$, and $C$ that satisfy the condition:
$$
\begin{array}{l}
|A|=|B|=2019, \\
n(A)+n(B)+n(C)=n(A \cup B \cup C) .
\end{array}
$$
Determine the maximum value of $|A \cap B \cap C|$, and briefly describe the reasoning process. | 2018 |
59,723 | 1.2. Given an equilateral triangle $A B C$. Point $D$ is such that $\angle B D C=90^{\circ}$ and $D$ and $A$ lie in different half-planes relative to the line $B C$. Point $M$ is the midpoint of side $A B$. Find the angle $B D M$. | 30 |
59,732 | [Pythagorean Theorem (direct and inverse) $]$ Law of Cosines $\quad]$
A circle inscribed in a right triangle with legs of 6 and 8 touches the hypotenuse at point $M$. Find the distance from point $M$ to the vertex of the right angle. | 2\sqrt{\frac{29}{5}} |
59,754 | The cities of Coco da Selva and Quixajuba are connected by a bus line. Buses leave Coco da Selva for Quixajuba every hour, with the first one departing at midnight on the dot. Buses leave Quixajuba for Coco da Selva every hour, with the first one departing at half past midnight. The bus journey takes exactly 5 hours.
If a bus leaves Coco da Selva at noon, how many buses coming from Quixajuba does it encounter during the journey?
Figure 21.2
Figure 21.3
Figure 21.4 | 10 |
59,758 | 34. Find the smallest positive integer $n$ such that $n(n+1)(n+2)$ is divisible by 247 . | 37 |
59,788 | 59. Determine the value of
$$
1 \cdot 2-2 \cdot 3+3 \cdot 4-4 \cdot 5+\cdots+2001 \cdot 2002
$$ | 2004002 |
59,827 | 10.389 In an isosceles triangle $A B C \quad A B=B C=25$ cm and $A C=14$ cm. Calculate the radius of the circle that touches $B C$ at point $D$, the foot of the altitude $A D$, and passes through the midpoint of $A C$. | \frac{175}{48} |
59,868 | Prokop constructed a triangle $ABC$, where the interior angle at vertex $A$ was greater than $60^{\circ}$ and the interior angle at vertex $B$ was less than $60^{\circ}$. Jirka drew a point $D$ in the half-plane defined by the line $AB$ and point $C$, such that triangle $ABD$ was equilateral. Then, the boys found that triangles $ACD$ and $BCD$ were isosceles with the main vertex at $D$.
Determine the measure of angle $ACB$.
(E. Semerádová)
Hint. Find the relationships between the interior angles of the mentioned triangles. | 30 |
59,895 | 14. Let $x$ be the smaller of the two solutions of the equation $x^{2}-4 x+2=0$. What are the first three digits after the decimal point in the base 10 representation of the number
$$
x+x^{2}+x^{3}+\cdots+x^{2009} ?
$$ | 414 |
59,896 | 6. Given $f(x)=\sqrt{a x^{2}+2 b x}$, there exists at least one positive number $b$, such that the domain and range of $f(x)$ are the same. Then the value of the real number $a$ that satisfies the condition is $\qquad$ . | 0or-4 |
59,899 | Task 3. Find all functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ that satisfy
$$
f(-f(x)-f(y))=1-x-y
$$
for all $x, y \in \mathbb{Z}$. | f(x)=x-1 |
59,905 | 23. The sum of 2000 positive integers is 2020, then among these 2000 numbers, at most $\qquad$ of them can be the same.
| 1999 |
59,924 | ## Task 17/88
Determine all three-digit natural numbers $n$ that are equal to five times their cross product! | 175 |
59,926 | Example 8. Find the Wronskian determinant for the functions: $y_{1}(x)=\sin x$,
$$
y_{2}(x)=\sin \left(x+\frac{\pi}{8}\right), y_{3}(x)=\sin \left(x-\frac{\pi}{8}\right)
$$ | 0 |
59,970 | 4. Let $x$, $y$, $z$ be the lengths of the line segments connecting the midpoints of the opposite edges of the tetrahedron $P-ABC$. If the sum of the squares of the six edges of the tetrahedron is 300, then $x^{2}+y^{2}+z^{2}=$ $\qquad$ . | 75 |
60,028 | [ Combinations and Permutations ] $[$ Polygons (other) ]
In a convex polygon with an odd number of vertices, equal to $2 n+1$, two random diagonals are chosen independently of each other.
Find the probability that these diagonals intersect inside the polygon. | \frac{n(2n-1)}{3(2n^{2}-n-2)} |
60,044 | A triangle, two of whose sides are 3 and 4 , is inscribed in a circle. Find the minimal possible radius of the circle. | 2 |
60,053 | Problem 3
Let $n$ be an integer greater than or equal to 1. Find, in terms of $n$, the smallest integer $k \geqslant 2$ such that, among $k$ real numbers, there necessarily exist two whose difference, in absolute value, is either strictly less than $1 / n$ or strictly greater than $n$.
## § | n^{2}+2 |
60,080 | 15. (6 points) A car and a truck start from locations $A$ and $B$ respectively at the same time, heading towards each other. It is known that the car's speed is twice that of the truck. The car arrives at point $C$ on the way at 8:30, and the truck arrives at point $C$ at 15:00 on the same day. The two vehicles do not stop when they reach point $C$ and continue to move forward. The time when the two vehicles meet is $\qquad$. | 10:40 |
60,090 | 6. In the Cartesian coordinate system, the "rectilinear distance" between points $P\left(x_{1}, y_{1}\right)$ and $Q\left(x_{2}, y_{2}\right)$ is defined as
$$
d(P, Q)=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right| \text {. }
$$
If point $C(x, y)$ has equal rectilinear distances to $A(1,3)$ and $B(6,9)$, where the real numbers $x$ and $y$ satisfy $0 \leqslant x, y \leqslant 10$, then the sum of the lengths of all loci of points $C$ that satisfy the condition is $\qquad$ . | 5(\sqrt{2}+1) |
60,123 | 3. If the expansion of $(a+2 b)^{n}$ has three consecutive terms whose binomial coefficients form an arithmetic sequence, then the largest three-digit positive integer $n$ is $\qquad$ . | 959 |
60,128 | 2. determine the largest natural number $n$ so that
$$
4^{995}+4^{1500}+4^{n}
$$
is a square number. | 2004 |
60,129 | 4. In the cells of a $3 \times 3$ square, the numbers $0,1,2, \ldots, 8$ are arranged. It is known that any two consecutive numbers are located in adjacent (by side) cells. Which number can be in the central cell if the sum of the numbers in the corner cells is 18? | 2 |
60,137 | 3. Among all possible four-digit numbers formed using the digits $1,9,9,0$, for each such four-digit number and a natural number $n$, their sum when divided by 7 does not leave a remainder of 1. List all such natural numbers $n$ in descending order.
$$
n_{1}<n_{2}<n_{3}<n_{4}<\cdots \cdots,
$$
Find: the value of $n_{1}$. | 4 |
60,150 | 5,6,7 |
Giuseppe has a sheet of plywood measuring $22 \times 15$. Giuseppe wants to cut as many rectangular blanks of size $3 \times 5$ as possible from it. How can he do this? | 22 |
60,170 | 6. (2006 National Winter Camp) Positive integers $a_{1}, a_{2}, \cdots$, $a_{2006}$ (which can be the same) such that $\frac{a_{1}}{a_{2}}, \frac{a_{2}}{a_{3}}, \cdots, \frac{a_{2005}}{a_{2006}}$ are all distinct. How many different numbers are there at least among $a_{1}, a_{2}, \cdots, a_{2006}$? | 46 |
60,197 | 14. A regular 201-sided polygon is inscribed inside a circle of center $C$. Triangles are drawn by connecting any three of the 201 vertices of the polygon. How many of these triangles have the point $C$ lying inside the triangle?
14. 一個正 201 邊形內接於一個以 $C$ 為圓心的圓形內。把多邊形 201 個頂點中的任意三個頂點連起, 可以組成不同的三角形。有多少個這樣的三角形, 將 $C$ 點包含在其內部?
(2 分) | 338350 |
60,214 | 8. Count the number of triangles with positive area whose vertices are points whose $(x, y)$-coordinates lie in the set $\{(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\}$. | 76 |
60,226 | 4. Given a cube. $A, B$ and $C$ are the midpoints of its edges (see figure). What is the angle $ABC$?
Answer. $120^{\circ}$. | 120 |
60,229 | 8. $(8,9)$ It is known that the number $\frac{(2+\sqrt{3})^{4}+(2-\sqrt{3})^{4}}{(2+\sqrt{3})^{6}+(2-\sqrt{3})^{6}}$ is rational. Write this number as an irreducible fraction. | \frac{97}{1351} |
60,236 | 8. [25] A regular 12-sided polygon is inscribed in a circle of radius 1. How many chords of the circle that join two of the vertices of the 12-gon have lengths whose squares are rational? (No proof is necessary.) | 42 |
60,252 | # Task 7. (14 points)
In a certain company, no two employees have jobs of the same difficulty, and no two employees receive the same salary. On April 1, each employee made two statements:
(a) There will not be 12 employees with more difficult jobs.
(b) At least 30 employees have a higher salary. How many employees are in the company if some employees told the truth twice, and the rest lied twice.
# | 42 |
60,258 | 4. Kuzya the flea can make jumps from each vertex of a regular tetrahedron \(ABCD\) to the three adjacent vertices, with the choice of these vertices being random and equally probable. Kuzya started jumping from vertex \(A\) and, after 2018 jumps, ended up at vertex \(C\). What is the probability that this could happen? | \frac{3^{2018}-1}{4\cdot3^{2018}} |
60,286 | Bangladesh National Mathematical Olympiad 2016 Higher Secondary
[b][u]Problem 5:[/u][/b]
Suppose there are $m$ Martians and $n$ Earthlings at an intergalactic peace conference. To ensure the Martians stay peaceful at the conference, we must make sure that no two Martians sit together, such that between any two Martians there is always at least one Earthling.
(a) Suppose all $m + n$ Martians and Earthlings are seated in a line. How many ways can the Earthlings and Martians be seated in a line?
(b) Suppose now that the $m+n$ Martians and Earthlings are seated around a circular round-table. How many ways can the Earthlings and Martians be seated around the round-table? | (n-1)! \times \binom{n}{m} \times m! |
60,332 | 3.247. $\left(1-\operatorname{ctg}^{2}\left(\frac{3}{2} \pi-2 \alpha\right)\right) \sin ^{2}\left(\frac{\pi}{2}+2 \alpha\right) \operatorname{tg}\left(\frac{5}{4} \pi-2 \alpha\right)+\cos \left(4 \alpha-\frac{\pi}{2}\right)$. | 1 |
60,346 | 4.1.1. (12 points) From point $A$ to point $B$, a bus and a cyclist departed simultaneously at 13:00. After arriving at point $B$, the bus, without stopping, headed back and met the cyclist at point $C$ at 13:10. Upon returning to point $A$, the bus again, without stopping, headed to point $B$ and caught up with the cyclist at point $D$, which is located $\frac{2}{3}$ km from point $C$. Find the speed of the bus (in km/h), if the distance between points $A$ and $B$ is 4 km, and the speeds of the bus and the cyclist are constant. | 40 |
60,364 | Example 8 Find the last 3 digits of $1 \times 3 \times 5 \times 7 \times \cdots \times 2005$. | 375 |
60,398 | Proposition 1 Use $m(m \geqslant 2)$ different colors to color $n(n \geqslant 2)$ interconnected regions $A_{1}, A_{2}, \cdots, A_{n}$ in Figure 1, and any two adjacent regions must be colored differently. Then the number of different coloring schemes is
$$
a_{n}=(-1)^{n}(m-1)+(m-1)^{n} \text {. }
$$ | a_{n}=(-1)^{n}(-1)+(-1)^{n} |
60,403 | Problem 6.6. Several oranges (not necessarily of equal weight) were picked from a tree. When they were weighed, it turned out that the weight of any three oranges taken together is less than $5 \%$ of the total weight of the remaining oranges. What is the smallest number of oranges that could have been picked? | 64 |
60,414 | 1. The function
$$
f(x)=(\sin x-1)(\cos x-1)(x \in \mathbf{R})
$$
has the range $\qquad$ . | [0,\frac{3+2\sqrt{2}}{2}] |
60,418 | 14.28. In how many different ways can 1000000 be represented as a product of three natural numbers? Products that differ only in the order of the factors are considered the same.
## 14.5. Inequalities for binomial coefficients | 139 |
60,420 | A deck of playing cards is laid out on the table (for example, in a row). On top of each card, a card from another deck is placed. Some cards may have matched. Find:
a) the expected value of the number of matches;
b) the variance of the number of matches.
# | 1 |
60,511 |
6. How many integers $m$ satisfy both the following properties:
(i) $1 \leq m \leq 5000$; (ii) $[\sqrt{m}]=[\sqrt{m+125}]$ ?
(Here $[x]$ denotes the largest integer not exceeding $x$, for any real number $x$.)
| 72 |
60,522 | 3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 75. In how many ways can this be done? | 2592 |
60,529 | 5. From 30 people with distinct ages, select two groups, the first with 12 people and the second with 15 people, such that the oldest person in the first group is younger than the youngest person in the second group. How many ways are there to select these groups? | 4060 |
60,535 | 3. A three-stage launch vehicle consists of stages in the form of cylinders. All these cylinders are similar to each other. The length of the middle stage is two times less than the sum of the lengths of the first and third stages. In the fueled state, the mass of the middle stage is $13 / 6$ times less than the total mass of the fueled first and third stages. Find the ratio of the lengths of the first and third stages. The masses of the engines, instruments, and the stages' shells can be neglected. | \frac{7}{5} |
60,546 | Let's find all the square numbers with at most four digits that are equal to one and a half times a cube number! | 0324 |
60,555 | 11. Stephanie enjoys swimming. She goes for a swim on a particular date if, and only if, the day, month (where January is replaced by '01' through to December by '12') and year are all of the same parity (that is they are all odd, or all are even). On how many days will she go for a swim in the two-year period between January 1st of one year and December 31st of the following year inclusive? | 183 |
60,566 | 2. Master Wang needs to process a batch of parts. If he processes 20 parts per day, he can complete the task 1 day ahead of the original plan. After working for 4 days, due to improved technology, he processes 5 more parts per day than before. As a result, he completes the task 3 days ahead of the original plan. How many parts are there in total? (10 points) | 280 |
60,575 | We roll a die 30 times. Determine the probability, to 8 decimal places, that among the numbers rolled there will be a six, and that before the first six, neither a five nor a four appears. | 0.33333333 |
60,580 | 3. Let $[x]$ denote the greatest integer not exceeding the real number $x$. Set $A=\left[\frac{7}{8}\right]+\left[\frac{7^{2}}{8}\right]+\cdots+\left[\frac{7^{2016}}{8}\right]$, then the remainder when $A$ is divided by 50 is . $\qquad$ | 42 |
60,594 | 9.4. In the country, there are 20 cities. An airline wants to organize two-way flights between them so that from any city, it is possible to reach any other city with no more than $k$ transfers. At the same time, the number of air routes from any city should not exceed four. What is the smallest $k$ for which this is possible?
## 9th grade
## Second day | 2 |
60,617 | 2. Given $a^{2}+b^{2}+c^{2}=1$, then the range of $a b+b c+a c$ is | [-\frac{1}{2},1] |
60,641 | 21. 2.9 * Color the vertices of the $n$-sided pyramid $S-A_{1} A_{2} \cdots A_{n}$, with each vertex being a different color from its adjacent vertices on the same edge. Given $n+1$ colors to use, how many different coloring methods are there? (When $n=4$, this is a problem from the 1995 National High School Competition in China) | (n+1)[(n-1)^{n}+(-1)^{n}(n-1)] |
60,658 | ## Problem 1
Determine the smallest sum of the digits of the number $3 n^{2}+n+1$, where $n \in \mathbb{N}, n \geq 2$. | 3 |
60,662 | ## Task Condition
Write the canonical equations of the line.
$6 x-7 y-z-2=0$
$x+7 y-4 z-5=0$ | \frac{x-1}{35}=\frac{y-\frac{4}{7}}{23}=\frac{z}{49} |
60,664 | 1. Solve the equation
$$
\sqrt{x^{2}+x}+\sqrt{1+\frac{1}{x^{2}}}=\sqrt{x+3}
$$
in the set of real numbers. | -1 |
60,669 | 【Question 29】
How many five-digit numbers are divisible by 3 and have at least one digit as '3'? | 12504 |
60,683 | Let $a_1\in (0,1)$ and $(a_n)_{n\ge 1}$ a sequence of real numbers defined by $a_{n+1}=a_n(1-a_n^2),\ (\forall)n\ge 1$. Evaluate $\lim_{n\to \infty} a_n\sqrt{n}$. | \frac{\sqrt{2}}{2} |
60,688 | ## Task Condition
Find the derivative.
$y=2 x-\ln \left(1+\sqrt{1-e^{4 x}}\right)-e^{-2 x} \cdot \arcsin \left(e^{2 x}\right)$ | 2e^{-2x}\cdot\arcsin(e^{2x}) |
60,702 | 5. Let the set $I=\{0,1,2, \cdots, 22\}, A=\{(a, b, c, d) \mid a, b, c, d \in I, a+d \equiv 1(\bmod 23)$, and $a d-b c \equiv 0$ $(\bmod 23)\}$, then the number of elements in set $A$ is | 552 |
60,724 | 2. Determine the number of all quadratic polynomials $P(x)$ with integer coefficients such that for every real number $x$ the following holds:
$$
x^{2}+2 x-2023<P(x)<2 x^{2} \text {. }
$$
(Ján Mazák, Michal Rolínek) | 4042 |
60,728 | 577. a) From a sample of size $n$, extracted from a normal general population with a known standard deviation $\sigma$, the sample mean $\bar{x}$ has been found. At a significance level $\alpha$, it is required to find the power function of the test criterion for testing the null hypothesis $H_{0}: a=a_{0}$ about the equality of the general mean $a$ to the hypothetical value $a_{0}$ under the alternative hypothesis $H_{1}: a=a_{1} \neq a_{0}$.
**Solution. The alternative hypothesis has the form** $a \neq a_{0}$, therefore the critical region is two-sided. Using rule 1, we find the critical point $u_{\text {cr }}$ from the equality $\Phi\left(u_{\text {cr }}\right)=(1-\alpha) / 2$. Consequently, the two-sided critical region is defined by the inequality $|U|>u_{\mathrm{cr}}$, or in more detail
$$
\left|\frac{\left(\bar{x}-a_{0}\right)}{\sigma / \sqrt{n}}\right|>u_{\mathrm{cr}}
$$
We will find the power of the considered criterion, i.e., the probability of the criterion falling into the critical region assuming that the alternative hypothesis $a=a_{1} \neq a_{0}$ is true:
$$
1-\beta=P\left(\left|\frac{x-a_{0}}{\sigma / \sqrt{n}}\right|>u_{\mathrm{cr}} ; \quad a=a_{1}\right)
$$
Transform the expression under the modulus sign:
$$
\frac{\bar{x}-a_{0}}{\sigma / \sqrt{n}}=\frac{\bar{x}-a_{1}}{\sigma / \sqrt{n}}+\frac{a_{1}-a_{0}}{\sigma / \sqrt{n}}=b+\lambda
$$
where $b=\frac{\bar{x}-a_{1}}{\sigma / \sqrt{n}}, \lambda=\frac{a_{1}-a_{0}}{\sigma / \sqrt{n}}$. Using these relations, we get
$$
\begin{gathered}
1-\beta=P\left(|b+\lambda|>u_{\mathrm{cr}}\right)=P\left(b+\lambda>u_{\mathrm{cr}}\right)+P\left(b+\lambda<-u_{\mathrm{cr}}\right)= \\
=P\left(b>u_{\mathrm{cr}}-\lambda\right)+P\left(b<-u_{\mathrm{cr}}-\lambda\right)= \\
=\left[1-P\left(b<u_{\mathrm{cr}}-\lambda\right)\right]+P\left(b<-u_{\mathrm{cr}}-\lambda\right)= \\
=\left[1-\Phi\left(u_{\mathrm{cr}}-\lambda\right)\right]+\Phi\left(-u_{\mathrm{cr}}-\lambda\right)=1-\Phi\left(u_{\mathrm{cr}}-\lambda\right)-\Phi\left(u_{\mathrm{cr}}+\lambda\right) .
\end{gathered}
$$
Thus, the power of the two-sided criterion at $a=a_{1}$ is
$$
1-\beta=1-\left[\Phi\left(u_{\mathrm{cr}}-\lambda\right)+\Phi\left(u_{\mathrm{cr}}+\lambda\right)\right]
$$
where $\lambda=\left(a_{1}-a_{0}\right) \sqrt{n} / \sigma$.
Each value of $a_{1}$ corresponds to a certain power value, so the power of the criterion is a function of $a_{1}$; denote it by $\pi_{2}\left(a_{1}\right)$.
Thus, the sought power of the two-sided criterion is
$$
\pi_{2}\left(a_{1}\right)=1-\left[\Phi\left(u_{\mathrm{cr}}-\lambda\right)+\Phi\left(u_{\mathrm{cr}}+\lambda\right)\right]
$$
where $\Phi(x)$ is the Laplace function, $\lambda=\left(a_{1}-a_{0}\right) \sqrt{n} / \sigma, u_{\text {cr }}$ is found from the equality $\Phi\left(u_{\text {cr }}\right)=(1-\alpha) / 2$.
b) From a sample of size $n=16$, extracted from a normal general population with a known standard deviation $\sigma=5$, at a significance level of 0.05, the null hypothesis $H_{0}: a=a_{0}=20$ about the equality of the general mean $a$ to the hypothetical value $a_{0}=20$ is tested under the alternative hypothesis $H_{1}: a \neq 20$. Find the power of the two-sided criterion for testing the considered hypothesis for the hypothetical value of the general mean $a_{1}=24$. | 0.8925 |
60,734 | 5. If $\sqrt{3-a}-\sqrt{a+1}>\frac{1}{2}$ always holds, then the range of values for $a$ is $\qquad$ . | [-1,1-\frac{\sqrt{31}}{8}) |
60,747 | 1. The sequence $(a_{n})$ is defined by $a_{1}=1, a_{2}=\sqrt{19}$ and $a_{n+1}+a_{n}+a_{n-1}=3 n, n \geq 2$.
Calculate $a_{2011}$. | 2011 |
60,752 | 7. Given positive numbers $a, b$ satisfy $2 a+b=1$, then the maximum value of $4 a^{2}+b^{2}+4 \sqrt{a b}$ is $\qquad$ | \frac{1}{2}+\sqrt{2} |
60,764 | A four-digit number, which is a perfect square of a number, has its first two and last two digits equal; find this number. | 7744 |
60,780 | Consider polynomial functions $ax^2 -bx +c$ with integer coefficients which have two distinct zeros in the open interval $(0,1).$ Exhibit with proof the least positive integer value of $a$ for which such a polynomial exists. | 5 |
60,798 | Let $x_{1}, x_{2}, \ldots, x_{n}$ be non-negative numbers whose sum is 1.
How large can
$$
x_{1} x_{2}+x_{2} x_{3}+\ldots+x_{n-2} x_{n-1}+x_{n-1} x_{n}
$$
be? | \frac{1}{4} |
60,810 | 17th Mexico 2003 Problem B1 The quadrilateral ABCD has AB parallel to CD. P is on the side AB and Q on the side CD such that AP/PB = DQ/CQ. M is the intersection of AQ and DP, and N is the intersection of PC and QB. Find MN in terms of AB and CD. | MN=\frac{AB\cdotCD}{AB+CD} |
60,825 | ## Task B-4.1.
If in each term of the binomial expansion $(x-y)^{n}, n \geqslant 2, x, y \neq 0$, we substitute $x=672 y$, the sum of the third and fourth terms will be equal to 0. Determine the 2018th term in the expansion of this binomial. | -1356096y^{2018} |
60,831 | 5.1. Alina travels to school by bus. The bus runs on a schedule every 15 minutes. It always takes the girl the same number of minutes to get to the bus stop. If she leaves home at 8:20, she will be at school at 8:57, but if she leaves home at 8:21, she will be late for school. Classes start at 9:00. How many minutes will Alina be late for school if she leaves home at 8:23? | 12 |
60,835 | Problem 1
Let $u_{0}, u_{1}, u_{2}, \ldots$ be integers such that
$\triangleright u_{0}=100$;
$\triangleright$ for all $k \geqslant 0$, the inequality $u_{k+2} \geqslant 2+u_{k}$ is satisfied;
$\triangleright$ for all $\ell \geqslant 0$, the inequality $u_{\ell+5} \leqslant 5+u_{\ell}$ is satisfied.
Find all possible values for the integer $u_{2023}$.
## $\S$ | 2123 |
60,845 | Problem 4. Find all solutions to the puzzle
$$
\mathrm{G}+\mathrm{OH}+\mathrm{OH}+\mathrm{OH}+\mathrm{OH}+\mathrm{OH}+\mathrm{OH}+\mathrm{OH}+\mathrm{OH}=\mathrm{Mb} .
$$
(Same letters encode the same digits, different letters encode different digits.)
[5 points] (D. E. Schnol) | 0+12+12+12+12+12+12+12+12=96 |
60,846 | 1. A motorcyclist set out from point $A$ with an initial speed of 90 km/h, uniformly increasing his speed (that is, over equal time intervals, his speed increases by the same amount). After three hours, the motorcyclist arrived at point $B$, passing through $C$ along the way. After that, he turned around and, still uniformly increasing his speed, headed back. Two hours later, he passed point $C$ again at a speed of 110 km/h and continued on to $A$. Find the distance between points $A$ and $C$. | 76 |
60,854 | Which two-digit (integer) number is equal to the product of the sum and difference of its digits? | 48 |
60,864 | Carla wrote on the blackboard the integers from 1 to 21. Diana wants to erase some of them so that the product of the remaining numbers is a perfect square.
a) Show that Diana must necessarily erase the numbers 11, 13, 17, and 19 to achieve her goal.
b) What is the minimum number of numbers that Diana must erase to achieve her goal?
# | 5 |
60,866 | Four, As shown in the figure, points $M, N$ are on the sides $B C$, $C D$ of square $A B C D$, respectively. It is known that the perimeter of $\triangle M C N$ is equal to half the perimeter of square $A B C D$. Find $\angle M A N$ | 45^{\circ} |
60,873 | 1. As shown in the figure, $\angle A C B=90^{\circ}, A C=B C, A D \perp C E$, $B E \perp C E$, with the feet of the perpendiculars being $D, E$ respectively. Given $A D=8$, $B E=3$, then $D E=$ $\qquad$ | 5 |
60,884 | 3.4. A transgalactic ship has encountered an amazing meteorite stream. Some of the meteorites are flying along a straight line, one after another, at equal speeds and at equal distances from each other. Another part is flying the same way but along another straight line parallel to the first, at the same speeds but in the opposite direction, and at the same distance from each other. The ship is flying parallel to these lines. Astronaut Gavrila noted that the ship meets meteorites flying towards the ship every 7 s, and meteorites flying in the same direction as the ship every 13 s. He wondered how often meteorites would fly past him if the ship were to stand still. It seemed to him that he should take the arithmetic mean of the two given times. Is Gavrila right? If yes, write down this arithmetic mean in the answer. If not, specify the correct time in seconds, rounded to tenths. | 9.1 |
60,903 | 2. $7+77+777+\cdots+\underbrace{777 \cdots 77}_{2021 \text { 7s }}$ The last four digits of the calculation result are
The calculation result of the above expression is to find the last four digits. | 4847 |
60,904 | 8. Let $p_{k}=1+\frac{1}{k}-\frac{1}{k^{2}}-\frac{1}{k^{3}}$, where $k$ is a positive integer. Find the least positive integer $n$ such that the product $p_{2} p_{3} \ldots p_{n}$ exceeds 2010 . | 8038 |
60,914 | 2. Given $f(x)=\frac{1}{x^{2}}+\frac{1}{x^{4}}$, if $f(a-2)<f(2 a+1)$ holds, then the range of values for $a$ is | (-3,-\frac{1}{2})\cup(-\frac{1}{2},\frac{1}{3}) |
60,949 | 13. Given the function $f(x)=2 \sin ^{2}\left(\frac{\pi}{4}+x\right)-\sqrt{3} \cos 2 x-1, x \in\left[\frac{\pi}{4}, \frac{\pi}{2}\right]$.
(1) Find the interval where $f(x)$ is monotonically increasing;
(2) If the inequality $|f(x)-m|<2$ holds for all $x \in\left[\frac{\pi}{4}, \frac{\pi}{2}\right]$, find the range of the real number $m$. | (0,3) |
60,956 | 3. [5] How many six-digit multiples of 27 have only 3,6 , or 9 as their digits? | 51 |
60,978 | A cooperative has 5 sites with the following known distances (the distances are understood to be between the entrances of the sites): From Almás, Bárkány is 2 km away, from there Cseresznye is $1650 \mathrm{~m}$ away. From Cseresznye to Dinnye, the distance is 8 and a half km, and from there to Epres, it is 3 and $3 / 4 \mathrm{~km}$. Finally, from Epres to Almás, it is 1100 m. How far is it from Epres to Bárkány? | 3100 |
60,988 | 6. Given $x \in[0,3]$, then the maximum value of $\frac{\sqrt{2 x^{3}+7 x^{2}+6 x}}{x^{2}+4 x+3}$ is $\qquad$ | \frac{1}{2} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.