id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
55,303 | 24. The witch's 10 boxes contain $0,1,2,3,4,5,6,7,8,9$ pearls respectively. The merchant needs to select 4 of these boxes and distribute the pearls in the boxes equally among his three daughters. The merchant has $\qquad$ different ways to choose. | 72 |
55,330 | 3. How many ordered pairs of integers $(a, b)$ satisfy all of the following inequalities?
$$
\begin{array}{l}
a^{2}+b^{2}<16 \\
a^{2}+b^{2}<8 a \\
a^{2}+b^{2}<8 b
\end{array}
$$ | 6 |
55,348 | 2. Let $n(A)$ denote the number of subsets of $A$. Given $|A|=|B|=100, n(A)+$ $n(B)+n(C)=n(A \cup B \cup C)$. Find the minimum value of $|A \cap B \cap C|$. | 97 |
55,355 | 1. In trapezoid $A B C D, A D$ is parallel to $B C . \angle A=\angle D=45^{\circ}$, while $\angle B=\angle C=135^{\circ}$. If $A B=6$ and the area of $A B C D$ is 30 , find $B C$. | 2\sqrt{2} |
55,371 | 8. Let the integer pair $(m, n)$ satisfy $\frac{m^{2}+m n+n^{2}}{m+2 n}=\frac{13}{3}$. Then $m+2 n=$ $\qquad$ . | 9 |
55,381 | Test Question D: The sum of four positive numbers is 4, and the sum of their squares is 8. Determine the maximum value of the largest of these four numbers.
Restate it as: Let \( a \geqslant b \geqslant c \geqslant d > 0 \), and satisfy
\[
a+b+c+d=4, \quad a^{2}+b^{2}+c^{2}+d^{2}=8,
\]
Find \(\max a=\) ? | 1+\sqrt{3} |
55,386 | [ The product of the lengths of the chord segments and the lengths of the secant segments ]
On a line, points $A, B, C$, and $D$ are arranged in the given order. It is known that $B C = 3, A B = 2 \cdot C D$. A circle is drawn through points $A$ and $C$, and another circle is drawn through points $B$ and $D$. Their common chord intersects segment $B C$ at point $K$. Find $B K$.
# | 2 |
55,398 | 3. Three consecutive terms of a geometric progression with a common ratio $q$ were used as coefficients of a quadratic trinomial, with the middle term being the leading coefficient. For what largest integer $q$ will the resulting trinomial have two distinct roots regardless of how the other two coefficients are arranged? | -1 |
55,413 | 7. Given the circle $x^{2}+y^{2}=1$ and the line $y=2 x+m$ intersect at $A$ and $B$, and $O A$ and $O B$ form angles $\alpha, \beta$ with the positive direction of the $x$-axis, then $\sin (\alpha+\beta)=$ $\qquad$ | -\frac{4}{5} |
55,417 | Example 4 For all $a, b, c \in \mathbf{R}^{+}$, find the minimum value of $f(a, b, c)=\frac{a}{\sqrt{a^{2}+8 b c}}+\frac{b}{\sqrt{b^{2}+8 a c}}+\frac{c}{\sqrt{c^{2}+8 a b}}$. | 1 |
55,431 | * An ellipse on the $x y$ plane, with foci at $(9,20)$ and $(49,55)$, and tangent to the $x$-axis. Find the length of the major axis. | 85 |
55,436 | 7,8,9 |
What is the maximum number of kings that can be placed on a chessboard so that no two of them attack each other
# | 16 |
55,494 | Emília's tree grows according to the following rule: two weeks after a branch appears, that branch produces a new branch every week, and the original branch continues to grow. After five weeks, the tree has five branches, as shown in the figure. How many branches, including the main branch, will the tree have at the end of eight weeks?
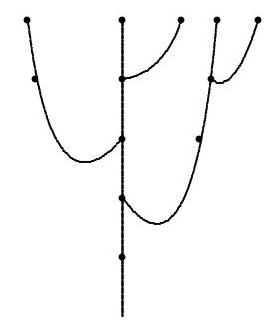 | 21 |
55,508 | 6. In how many ways can the number 1024 be factored into three natural factors such that the first factor is divisible by the second, and the second is divisible by the third? | 14 |
55,515 | If $n$ is a positive integer, what is the smallest value that the sum of the digits in the decimal representation of $3 n^{2}+n+1$ can take?
# | 3 |
55,527 | 1.17. One of the two parallel lines touches a circle of radius $R$ at point $A$, while the other intersects this circle at points $B$ and $C$. Express the area of triangle $A B C$ as a function of the distance $x$ between the lines. | x\sqrt{2Rx-x^{2}} |
55,553 | 4. Let $[x]$ denote the greatest integer not exceeding the real number $x$. Calculate: $\sum_{k=0}^{2019}\left[\frac{4^{k}}{5}\right]=$ $\qquad$ | \frac{4^{2020}-1}{15}-1010 |
55,566 | [ Coordinate method in space ] [ Rectangular parallelepipeds ]
The non-intersecting diagonals of two adjacent faces of a rectangular parallelepiped are inclined to the base plane at angles $\alpha$ and $\beta$. Find the angle between these diagonals. | \arccos(\sin\alpha\sin\beta) |
55,596 | A square-based (with base vertices $A, B, C, D$) equal-sided pyramid has its apex at $E$. Let $P$ be the point that divides the edge $AE$ in a 3:1 ratio, such that $EP:PA=3$, and let $Q$ be the midpoint of the edge $CE$! In what ratio does the plane passing through points $D, P$, and $Q$ divide the edge $BE$? | 4:3 |
55,619 | Let $S=\{1,2, \cdots, 2005\}$. If any set of $n$ pairwise coprime numbers in $S$ contains at least one prime number, find the minimum value of $n$. (Tang Lihua) | 16 |
55,623 | 8. (10 points) In the expression $(x+y+z)^{2034}+(x-y-z)^{2034}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained? | 1036324 |
55,650 | Example 6.20. 600 corn seeds are planted with a probability of 0.9 for each seed to germinate. Find the boundary of the absolute value of the deviation of the frequency of germinated seeds from the probability $p=0.9$, if this boundary is to be guaranteed with a probability $P=0.995$. | 0.034 |
55,661 | 2. Each vertex of the right-angled triangle $A B C$ with legs $\overline{A B}=4 \sqrt{3}$ and $\overline{A C}=4$ is the center of a circle such that the three circles touch each other and no circle lies inside another circle. Calculate the area of the part of triangle $A B C$ that lies outside the three circles. | 8\sqrt{3}-\frac{8\pi}{3}(5-2\sqrt{3}) |
55,678 | Task 3. Find all solutions to the equation $x^{2}-[x]=1$. Here $[x]$ is the integer part of $x$, that is, the greatest integer not exceeding the given number. For example, $[2.9]=2 ;[-2.9]=-3$. | \sqrt{2} |
55,679 | # 5. Solution:
Let $x$ units of distance/hour be the speed of the bus, $y$ units of distance/hour be the speed of the tractor, and $S$ be the length of the path AB. Then the speed of the truck is $-2y$ units of distance/hour. We can set up a system of equations and inequalities:
$$
\left\{\begin{array}{c}
\frac{s}{x}=5 \frac{5}{6} \\
\frac{S}{x+2 y} \geq 2.5 \\
\frac{S}{x+y}-\frac{S}{x+2 y} \geq 1
\end{array}\right.
$$
From the first equation, $S=5 \frac{5}{6} \cdot x=\frac{35}{6} \cdot x$. Substituting this result into the second inequality, we get: $\frac{35}{6} \cdot x \geq 2.5 \cdot x + 5 \cdot y$, from which $20 x \geq 30 y$ and $y \leq \frac{2}{3} x$.
Substituting $S$ into the second inequality, after transforming it: $S \cdot \frac{x+2 y-x-y}{(x+y) \cdot(x+2 y)} \geq 1 ; \quad \frac{35}{6} x y \geq x^{2} + 3 x y + 2 y^{2} ; \quad 6 x^{2} - 17 x y + 12 y^{2} \leq 0 ; \quad \frac{2}{3} \leq \frac{y}{x} \leq \frac{3}{4} ; \quad$ i.e., $y \geq \frac{2}{3} x$. From the two obtained estimates, it follows that $y \geq \frac{2}{3} x$. Let's find the time the tractor spends on the journey: $t=\frac{S}{y}=\frac{\frac{35}{6} x}{\frac{2}{3} x}=\frac{35}{4}=8$ hours 45 minutes. The required time is $9 + (8$ hours 45 minutes $)=17$ hours 45 minutes. | 17 |
55,721 | 3. Let point $O$ be a point inside triangle $A B C$, and satisfy the relation
$$
\overrightarrow{O A}+2 \overrightarrow{O B}+3 \overrightarrow{O C}=3 \overrightarrow{A B}+2 \overrightarrow{B C}+\overrightarrow{C A}
$$
Then $\frac{S_{\triangle A O B}+2 S_{\triangle B O C}+3 S_{\triangle C O A}}{S_{\triangle A B C}}=$ $\qquad$ | \frac{11}{6} |
55,722 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{2 \pi} \sin ^{2}\left(\frac{x}{4}\right) \cos ^{6}\left(\frac{x}{4}\right) d x
$$ | \frac{5}{64}\pi |
55,731 | Problem 8.7. In an acute-angled triangle $A B C$, the altitude $B H$ is drawn. It turns out that $C H=A B+A H$. How many degrees does the angle $B A C$ measure if $\angle A B C=84^{\circ}$ ?
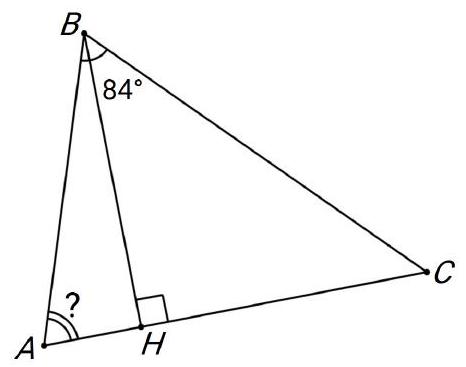 | 64 |
55,740 | A fly and $\mathrm{k}$ spiders move on a $2019 \times 2019$ grid. On their turn, the fly can move 1 square and the $k$ spiders can each move 1 square. What is the minimal $k$ for which the spiders are sure to catch the fly. | 2 |
55,810 | What's the largest number of elements that a set of positive integers between $1$ and $100$ inclusive can have if it has the property that none of them is divisible by another? | 50 |
55,824 | 132. Determinants of nine digits. Nine positive digits can be arranged in the form of a third-order determinant in 9! ways. Find the sum of all such determinants. | 0 |
55,828 | 7. In $\triangle A B C$, the three interior angles $A, B, C$ satisfy: $A=3 B=9 C$, then $\cos A \cos B+\cos B \cos C+\cos C \cos A=$ | -\frac{1}{4} |
55,844 | 3. The maximum value of the function
$y=\frac{\sin x \cos x}{1+\sin x+\cos x}$ is $\qquad$ . | \frac{\sqrt{2}-1}{2} |
55,850 | Exercise 3. Let $A B C D$ be a square and $E$ a point on the segment $[B D]$ such that $E B=A B$. We define the point $F$ as the intersection of the lines $(C E)$ and $(A D)$. Find the value of the angle $\widehat{F E A}$. | 45 |
55,858 | 4. (12 points) Choose several different numbers from $1, 2, 3, 4, 5, 6, 7$ (the order of the selected numbers does not matter), such that the sum of the even numbers equals the sum of the odd numbers. The number of ways to select the numbers that meet the condition is $\qquad$. | 7 |
55,862 | 【Question 10】
As shown in the figure, in square $A B C D$, extend $B A$ to $G$ such that $A G=B D$. Then the degree measure of $\angle B C G$ is $\qquad$ degrees. | 67.5 |
55,869 | U ohně seděli náčelníci tří indiánských kmenů se třemi stejnými dýmkami. Měli válečnou poradu a kouřili. První z nich vykouří celou dýmku za deset minut, druhý za půl hodiny a třetí za hodinu. Jak si mají náčelníci mezi sebou měnit dýmky, aby se mohli radit co nejdéle.
(Bednářová)
#
By the fire sat the chiefs of three Indian tribes with three identical pipes. They were having a war council and smoking. The first of them can smoke a whole pipe in ten minutes, the second in half an hour, and the third in an hour. How should the chiefs exchange pipes among themselves so that they can deliberate for as long as possible.
(Bednářová)
# | 20 |
55,902 | Let $f(x)=\sum_{i=1}^{2014}|x-i|$. Compute the length of the longest interval $[a,b]$ such that $f(x)$ is constant on that interval. | 1 |
55,912 | 13. Given the vectors $\boldsymbol{a}=(1, x), \boldsymbol{b}=\left(x^{2}+x,-x\right)$, and a constant $m$ such that $m \leqslant-2$, find the range of $x$ that satisfies $\boldsymbol{a} \cdot \boldsymbol{b}+2>$ $m\left(\frac{2}{\boldsymbol{a} \cdot \boldsymbol{b}}+1\right)$. | (,-2)\cup(0,+\infty) |
55,919 | 2. Let the height of the regular triangular prism $A B C-A_{1} B_{1} C_{1}$ be 2, and the side length of the base be 1. The centroid of the upper base $\triangle A_{1} B_{1} C_{1}$ is $P$. A plane $B C D \perp A P$ is made through the lower base edge $B C$, intersecting the edge $A A_{1}$ at point $D$. Then the area of the section $\triangle B C D$ is $\qquad$ | \frac{\sqrt{13}}{8} |
55,920 | Real numbers $x, y$ satisfy $x^{2}+x y+y^{2}=1, F(x, y)=x^{3} y+x y^{3}$.
(1) Prove: For any $x, y \in \mathbf{R}$ that meet the requirements, $F(x, y) \geqslant-2$.
(2) Find the maximum possible value of $F(x, y)$. | \frac{2}{9} |
55,942 | We draw $n$ convex quadrilaterals in the plane. They divide the plane into regions (one of the regions is infinite). Determine the maximal possible number of these regions.
Answer: The maximal number of regions is $4 n^{2}-4 n+2$. | 4n^{2}-4n+2 |
55,943 | 8. As shown in the figure, the diameter $A B$ of $\odot O$ intersects the chord $C D$ at point $P, C P=\frac{7}{5}$, $P D=5, A P=1$, then $\angle D C B=$ $\qquad$ | 45 |
55,950 | 4. In a certain company, there are 100 shareholders, and any 66 of them own no less than $50 \%$ of the company's shares. What is the largest percentage of all shares that one shareholder can own? | 25 |
55,954 | For a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of real numbers it is known that
$$
a_{n}=a_{n-1}+a_{n+2} \quad \text { for } n=2,3,4, \ldots
$$
What is the largest number of its consecutive elements that can all be positive?
Answer: 5. | 5 |
55,957 | 1. Which whole numbers from 1 to 60000 (inclusive) are there more of, and by how many: those containing only even digits or those containing only odd digits? | 780 |
55,994 | For any real number $a$, let $\lfloor a\rfloor$ denote the greatest integer not exceeding $a$. In positive real numbers solve the following equation
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=2014
$$ | 1958 |
56,012 | 7. Given the point sets $A=\left\{(x, y) \left\lvert\,(x-3)^{2}+(y-4)^{2} \leqslant\left(\frac{5}{2}\right)^{2}\right.\right\}, B=\left\{(x, y) \mid(x-4)^{2}+(y-\right.$ $\left.5)^{2}>\left(\frac{5}{2}\right)^{2}\right\}$, then the number of integer points in $A \cap B$ is $\qquad$. | 7 |
56,014 | 7. The number of non-negative integer solutions $(x, y, z)$ to the equation $x+2 y+3 z=2014$ is $\qquad$. | 339024 |
56,030 | Xiao Wang and Xiao Li are to process the same number of the same type of parts, and they start working at the same time. It is known that Xiao Wang processes 15 per hour, and must rest for 1 hour after every 2 hours of work; Xiao Li works without interruption, processing 12 per hour. As a result, they both finish at the same moment. Xiao Wang processes $\qquad$ parts. | 60 |
56,031 | 5. 1 way to solve.
$$
\begin{aligned}
& \left(\operatorname{tg} 9^{\circ}-\operatorname{tg} 63^{\circ}\right)+\left(\operatorname{tg} 81^{\circ}-\operatorname{tg} 27^{\circ}\right)=-\frac{\sin 54^{\circ}}{\cos 9^{\circ} \cos 63^{\circ}}+\frac{\sin 54^{\circ}}{\cos 81^{\circ} \cos 27^{\circ}}= \\
& =\frac{\sin 54^{\circ} \cdot\left(\cos 9^{\circ} \cos 63^{\circ}-\sin 9^{\circ} \sin 63^{\circ}\right)}{\cos 9^{\circ} \cos 63^{\circ} \cos 81^{\circ} \cos 27^{\circ}}= \\
& =\frac{2 \sin 27^{\circ} \cos 27^{\circ} \cdot \cos 72^{\circ}}{\cos 9^{\circ} \sin 27^{\circ} \sin 9^{\circ} \cos 27^{\circ}}=\frac{4 \cos 72^{\circ}}{2 \cos 9^{\circ} \sin 9^{\circ}}=\frac{4 \sin 18^{\circ}}{\sin 18^{\circ}}=4
\end{aligned}
$$
2 way to solve.
$$
\left(\operatorname{tg} 9^{\circ}+\operatorname{tg} 81^{\circ}\right)-\left(\operatorname{tg} 63^{\circ}+\operatorname{tg} 27^{\circ}\right)=2\left(\frac{1}{\sin 18^{\circ}}-\frac{1}{\cos 36^{\circ}}\right)
$$
Using the equalities $\sin 18^{\circ}=(\sqrt{5}-1) / 4, \cos 36^{\circ}=(\sqrt{5}+1) / 4$, we get
$$
2\left(\frac{4}{\sqrt{5}-1}-\frac{4}{\sqrt{5}+1}\right)=4
$$
Note that
$$
\frac{200}{157} \pi=4 \cdot \frac{100}{314} \pi>4
$$ | 4 |
56,035 | 23 *. There are $k$ colors. In how many ways can the sides of a given regular $n$-gon be painted so that adjacent sides are painted in different colors (the polygon cannot be rotated)?
## $10-11$ grades | x_{n}=(k-1)^{n}+(k-1)(-1)^{n} |
56,046 | Given that $a, b, c, d$ are positive numbers, and $a+2b=1, c+2d=1$, find the minimum value of $\frac{1}{a}+\frac{1}{bcd}$. | 25 |
56,057 | 27. If $S=\sum_{k=1}^{99} \frac{(-1)^{k+1}}{\sqrt{k(k+1)}(\sqrt{k+1}-\sqrt{k})}$, find the value of $1000 S$. | 1100 |
56,073 | 4. On the plane $(x ; y)$, plot the set of points whose coordinates satisfy the system $\left\{\begin{array}{l}(x-|x|)^{2}+(y-|y|)^{2} \leq 4, \\ y+2 x \leq 0\end{array}\right.$ and find the area of the resulting figure. | \frac{5+\pi}{4} |
56,083 | 12. Let $a_{n}$ denote the positive integer closest to $\sqrt{n}$, $n \in \mathbf{N}^{*}$, and set $S=\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{2000}}$, then $[S]=$ | 88 |
56,085 | I1.1 If $a$ is the maximum value of $\frac{1}{2} \sin ^{2} 3 \theta-\frac{1}{2} \cos 2 \theta$, find the value of $a$. | 1 |
56,087 | 34. Find an integer $x$ that satisfies the equation
$$
x^{5}-101 x^{3}-999 x^{2}+100900=0
$$ | 10 |
56,095 | 2. Define the length of the interval $\left[x_{1}, x_{2}\right]\left(x_{1}<x_{2}\right)$ as $x_{2}-x_{1}$. Given that the domain of the function $y=\left|\log _{\frac{1}{2}} x\right|$ is $[a, b]$, and the range is $[0,2]$. Then the difference between the maximum and minimum values of the length of the interval $[a, b]$ is | 3 |
56,098 | Aerith timed how long it took herself to solve a BMC monthly contest. She writes down the elapsed time as days:hours:minutes:seconds, and also simply as seconds. For example, if she spent 1,000,000 seconds, she would write down 11:13:46:40 and $1,000,000$.
Bob sees her numbers and subtracts them, ignoring punctuation; in this case he would get
$$
11134640-1000000=10134640 .
$$
What is the largest number that always must divide his result? | 40 |
56,173 | 49. As shown in the figure, in rectangle $A B C D$, with point $B$ as the center and the length of $B C$ as the radius, draw an arc intersecting side $A D$ at point $E$. Connect $B E$, and draw $C F \perp B E$, with the foot of the perpendicular at $F$. Then, the line segment in the figure that has the same length as $B F$ is . $\qquad$ | AE |
56,174 | 5. On the sides $B C$ and $C D$ of the square $A B C D$, points $E$ and $F$ are chosen such that the angle $E A F$ is $45^{\circ}$. The length of the side of the square is 1. Find the perimeter of triangle $C E F$. | 2 |
56,195 | 2. Given a quadrilateral $A B C D$. It is known that $B C=4, B D=9, A C=5, A D=3$. It is also known that at least one of the two unknown sides of the quadrilateral $A B C D$ is also an integer. Find what it can be equal to. In your answer, list all suitable values in ascending order separated by a semicolon. | 6;7;8 |
56,202 | 4. Xiaoling has two different shapes of cardboard, one is square and the other is rectangular. The ratio of the total number of square cardboard to the total number of rectangular cardboard is $1: 2$. She uses these cardboards to make some vertical and horizontal open-top boxes (as shown in Figure 2-16), using up all the cardboards. In the boxes Xiaoling made, what is the ratio of the total number of vertical boxes to the total number of horizontal boxes? | 1:2 |
56,225 | The product of $10$ integers is $1024$. What is the greatest possible sum of these $10$ integers? | 1033 |
56,226 | 6. What is the smallest area that a right triangle can have, with its hypotenuse containing the point \( M(1 ; 0) \), and its legs lying on the lines \( y = -2 \) and \( x = 0 \)?
(12 points) | 4 |
56,236 | Let $a$, $b$, $c$, $d$, $e$, $f$ and $g$ be seven distinct positive integers not bigger than $7$. Find all primes which can be expressed as $abcd+efg$ | 179 |
56,264 | 10. An integer $n$ allows the polynomial $f(x)=3 x^{3}-n x-n-2$ to be expressed as the product of two non-constant polynomials with integer coefficients, then the sum of all possible values of $n$ is $\qquad$ . | 192 |
56,267 | 21. $r$ and $s$ are integers such that
$$
3 r \geq 2 s-3 \text { and } 4 s \geq r+12 \text {. }
$$
What is the smallest possible value of $r / s$ ? | \frac{1}{2} |
56,276 | 4. In a pond, there are 25 hungry pikes. For one pike to be satiated, it needs to eat three other pikes. What is the maximum number of pikes that can remain in the pond, with all of them being full? | 6 |
56,310 | 6. On the faces $BCD, ACD, ABD$, and $ABC$ of the tetrahedron $ABCD$, points $A_{1}, B_{1}, C_{1}$, and $D_{1}$ are marked, respectively. It is known that the lines $AA_{1}, BB_{1}, CC_{1}$, and $DD_{1}$ intersect at point $P$, and $\frac{AP}{A_{1}P}=\frac{BP}{B_{1}P}=\frac{CP}{C_{1}P}=\frac{DP}{D_{1}P}=r$. Find all possible values of $r$. | 3 |
56,312 | [ Rebus $]$
In the numbers МИХАЙЛО and ЛОМОНОСОВ, each letter represents a digit (different letters correspond to different digits). It is known that the products of the digits of these numbers are equal. Can both numbers be odd? | No |
56,319 | 4. If in a three-digit number any two adjacent digits differ by no more than 1, then it is called a "smooth number". The number of smooth numbers is $\qquad$ . | 75 |
56,352 | ## Problem Statement
Calculate the definite integral:
$$
\int_{-\frac{\pi}{2}}^{0} \frac{\cos x \, dx}{(1+\cos x-\sin x)^{2}}
$$ | -\frac{1}{2}+\ln2 |
56,354 | 5. As shown in Figure $1, P$ is a point on the chord $AB$ of $\odot O$, $AP$ $=m, PB=n$, and $m>n$.
When $AB$ moves around $\odot O$ for one complete revolution, the trajectory of point $P$ is curve $C$. If the area between $\odot O$ and curve $C$ is $\left(m^{2}-n^{2}\right) \pi$, then the value of $\frac{m}{n}$ is | \frac{1+\sqrt{5}}{2} |
56,360 | Chkhhanov N.X.
In the natural number $A$, the digits were rearranged to obtain the number $B$. It is known that $A-B=\underbrace{1 \ldots 1}_{n}$. Find the smallest possible value of $n$.
# | 9 |
56,387 | 8. For a natural number $a, S(a)$ denotes the sum of the digits of $a$ (for example, $S(123)=1+2+3=6$). If a natural number $n$ has all distinct digits, and $S(3 n)=3 S(n)$, then the maximum value of $n$ is $\qquad$ | 3210 |
56,400 | We want to break down a cube in such a way that each piece becomes a triangular pyramid (tetrahedron). What is the minimum number of pieces that will result? | 5 |
56,402 | 8. As shown in Figure 1, in the right $\triangle ABC$, it is known that $\angle ACB$ $=90^{\circ}, AC=21, BC=$ 28, and a square $ABDE$ is constructed outward with $AB$ as the side. The angle bisector of $\angle ACB$ intersects $DE$ at point $F$. Then the length of segment $DF$ is $\qquad$ | 15 |
56,407 | 16. On the island of Friends and Foes, every citizen is either a Friend (who always tells the truth) or a Foe (who always lies). Seven citizens are sitting in a circle. Each declares "I am sitting between two Foes". How many Friends are there in the circle? | 3 |
56,428 | 1. Find the number of integer points $(x, y)$ satisfying the equation $\frac{1}{|x|}+\frac{1}{|y|}=\frac{1}{2017}$. | 12 |
56,429 | 4. Petya observes two ants crawling along a straight path at constant speeds. After 3 minutes of observation, the distance between the ants was 9 meters, after 5 minutes - 5 meters, after 9 minutes - 3 meters. What was the distance between the ants after 8 minutes of observation?
$[5$ points]
| 1a | 1b | 2a | 2b | 2c | 2d | 3a | 3b | 3c | 4 | $\Sigma$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | | | | | | | | | | |
| | | | | | | | | | | | | 1 |
56,449 | 7,8,9 |
| $[\underline{\text { Modular Arithmetic (other) }}]$ | | |
Find all prime numbers that are equal to the sum of two prime numbers and the difference of two prime numbers. | 5 |
56,473 | How many types of convex pentahedra exist? | 2 |
56,475 | Given the function $f(x)=k x^{2}+k x+k+3$, and for any $x \in[-2,3]$, $f(x) \geqslant 0$ always holds, find the range of real number $k$.
To find the range of $k$ for which $f(x) \geqslant 0$ for all $x \in[-2,3]$, we need to analyze the function $f(x)=k x^{2}+k x+k+3$.
1. **Determine the vertex of the parabola:**
The function $f(x)$ is a quadratic function, and its graph is a parabola. The vertex of the parabola can be found using the formula $x = -\frac{b}{2a}$, where $a = k$ and $b = k$. Thus, the vertex is at:
\[
x = -\frac{k}{2k} = -\frac{1}{2}
\]
2. **Evaluate $f(x)$ at the vertex:**
Substitute $x = -\frac{1}{2}$ into $f(x)$:
\[
f\left(-\frac{1}{2}\right) = k \left(-\frac{1}{2}\right)^2 + k \left(-\frac{1}{2}\right) + k + 3 = k \cdot \frac{1}{4} - k \cdot \frac{1}{2} + k + 3 = \frac{k}{4} - \frac{k}{2} + k + 3 = \frac{k}{4} + \frac{2k}{4} + 3 = \frac{3k}{4} + 3
\]
For $f(x) \geqslant 0$ at the vertex, we need:
\[
\frac{3k}{4} + 3 \geqslant 0 \implies \frac{3k}{4} \geqslant -3 \implies 3k \geqslant -12 \implies k \geqslant -4
\]
3. **Evaluate $f(x)$ at the endpoints of the interval $[-2, 3]$:**
- At $x = -2$:
\[
f(-2) = k(-2)^2 + k(-2) + k + 3 = 4k - 2k + k + 3 = 3k + 3
\]
For $f(-2) \geqslant 0$, we need:
\[
3k + 3 \geqslant 0 \implies 3k \geqslant -3 \implies k \geqslant -1
\]
- At $x = 3$:
\[
f(3) = k(3)^2 + k(3) + k + 3 = 9k + 3k + k + 3 = 13k + 3
\]
For $f(3) \geqslant 0$, we need:
\[
13k + 3 \geqslant 0 \implies 13k \geqslant -3 \implies k \geqslant -\frac{3}{13}
\]
4. **Combine the conditions:**
The conditions from the vertex and the endpoints are:
\[
k \geqslant -4, \quad k \geqslant -1, \quad k \geqslant -\frac{3}{13}
\]
The most restrictive condition is $k \geqslant -\frac{3}{13}$.
Therefore, the range of $k$ is:
\[
\boxed{k \geqslant -\frac{3}{13}}
\] | k\geqslant-\frac{3}{13} |
56,476 | ## Task A-1.3.
A billiard table has the shape of a rectangle $A B C D$ with dimensions $|A B|=2 \mathrm{~m}$ and $|B C|=1 \mathrm{~m}$. A billiard ball moves straight on the table until it reaches the edge of the rectangle, at which point it bounces off such that the path of the ball before and after the bounce forms equal angles with the edge. If the billiard ball starts moving from point $A$ and after bouncing off the sides $\overline{C D}, \overline{B C}$, and $\overline{A B}$ in sequence, it ends its movement at point $D$, determine the total distance the ball has traveled. The ball is considered as a material point.
 | 5 |
56,497 | How many ways can four vertices be chosen from the vertices of a convex $n$-gon so that the sides of the convex quadrilateral determined by them are diagonals of the $n$-gon? | \frac{n}{4}\binom{n-5}{3} |
56,501 | 4.8. The height of a trapezoid, whose diagonals are perpendicular to each other, is 4. Find the area of the trapezoid, given that the length of one of its diagonals is 5. | \frac{50}{3} |
56,521 | Find the greatest integer $A$ for which in any permutation of the numbers $1, 2, \ldots , 100$ there exist ten consecutive numbers whose sum is at least $A$. | 505 |
56,526 | 7.1. In the expression $5 * 4 * 3 * 2 * 1=0$, replace the asterisks with the four arithmetic operation signs (using each sign exactly once) to make the equation true. No other signs, including parentheses, can be used. | 5-4\cdot3:2+1=0 |
56,530 | Example 11 In the cube $A B C D-A_{1} B_{1} C_{1} D_{1}$, the degree of the dihedral angle $A-B D_{1}-A_{1}$ is $\qquad$ .
(2004 National High School League Question) | 60 |
56,533 | 10. The solution set of the inequality $\left|\frac{1}{\log \frac{1}{2} x}+2\right|>\frac{3}{2}$ is | (0,1)\cup(1,2^{\frac{2}{7}})\cup(4,+\infty) |
56,546 | 3. Let $z_{n}=\left(\frac{1-\mathrm{i}}{2}\right)^{n}, n \in \mathbf{N}_{+}$, and let $S_{n}=\sum_{k=1}^{n}\left|z_{k+1}-z_{k}\right|$, then $\lim _{n \rightarrow \infty} S_{n}=$ | 1+\frac{\sqrt{2}}{2} |
56,613 | Example 6 Color each vertex of a quadrilateral pyramid with one color, and make the endpoints of the same edge have different colors. If only 5 colors are available, the total number of different coloring methods is $\qquad$ . | 420 |
56,663 | Problem 4. (4 points) In how many different ways can the number 2004 be represented as the sum of natural numbers (one or several) that are approximately equal? Two numbers are called approximately equal if their difference is no more than 1. Sums that differ only in the order of the addends are considered the same. | 2004 |
56,666 | 400. Calculate the force of water pressure on a dam that has the shape of a trapezoid, where the upper base, coinciding with the water surface, is $10 \mathrm{~m}$ long, the lower base is $20 \mathrm{~m}$, and the height is $3 \mathrm{m}$. | 735750 |
56,668 | 79. Xiao Zhao, Xiao Qian, and Xiao Sun are practicing running along the lake. The three start from a point on the lake at the same time, with Xiao Qian and Xiao Sun running in the same direction, while Xiao Zhao runs in the opposite direction. Xiao Zhao meets Xiao Qian for the first time, and then $1 \frac{1}{4}$ minutes later meets Xiao Sun for the first time; after another $3 \frac{3}{4}$ minutes, he meets Xiao Qian for the second time. It is known that the ratio of Xiao Zhao's speed to Xiao Qian's speed is $3: 2$, and the circumference of the lake is 2000 meters. Therefore, the time it takes for Xiao Sun to run one lap around the lake is $\qquad$ minutes. | 25 |
56,683 | Let $N \in \mathbb{N}$.
Discriminant the cat proposes the following game to you:
- You choose a finite sequence (of your choice and kept secret) of integers $\left(a_{0}, \ldots, a_{n}\right) \in \mathbb{N}^{n+1}$
- At each turn of the game, Discriminant gives you a real number $\beta \in \mathbb{N}$ and you respond with the value of $\sum_{k=0}^{n} a_{k} \beta^{k}$.
- The game continues until Discriminant has guessed the sequence of integers or until fewer than $N$ turns have taken place.
- If at the end of the game Discriminant has guessed the sequence of integers, he wins; otherwise, he loses.
If Discriminant wins, you owe him a can of cat pate.
For which values of $N$ would you accept to play this game? | 1 |
56,704 | 1. In the set of real numbers, solve the equation
$$
x=\sqrt{x-\frac{1}{x}}+\sqrt{1-\frac{1}{x}}
$$ | \frac{1+\sqrt{5}}{2} |
56,734 | 1. (5 points) Find the degree measure of the angle
$$
\delta=\arccos \left(\left(\sin 2903^{\circ}+\sin 2904^{\circ}+\cdots+\sin 6503^{\circ}\right)^{\cos } 2880^{\circ}+\cos 2881^{\circ}+\cdots+\cos 6480^{\circ}\right)
$$ | 67 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.