id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
14,961 | There is a colony consisting of 100 cells. Every minute, a cell dies with probability $\frac{1}{3}$; otherwise it splits into two identical copies. What is the probability that the colony never goes extinct? | 1 - \left(\frac{1}{2}\right)^{100} |
14,962 | 15. Let $n$ be a positive integer not exceeding 2014 with the property that $x^{2}+x+1$ is a factor of $x^{2 n}+x^{n}+1$. Find the sum of all possible values of $n$.
(2 marks)
Let $n$ be a positive integer not exceeding 2014 with the property that $x^{2}+x+1$ is a factor of $x^{2 n}+x^{n}+1$. Find the sum of all possible values of $n$. | 1352737 |
14,965 | ii. (16 points) Find all natural numbers $n$ such that $2^{8}+2^{11}+2^{n}$ is a perfect square of a natural number. | 12 |
14,973 | ## Problem Statement
Calculate the indefinite integral:
$$
\int \frac{2 x^{4}+2 x^{3}-41 x^{2}+20}{x(x-4)(x+5)} d x
$$ | x^2 - \ln|x| + \frac{1}{9} \ln|x - 4| - \frac{1}{9} \ln|x + 5| + C |
14,988 | 设函数 \( f(x, y) = x^2y + 3xy^2 + e^{xy} \)。求 \( f \) 的二阶混合偏导数 \( \frac{\partial^2 f}{\partial x \partial y} \)。 | 2x + 6y + e^{xy}(1 + xy) |
15,058 | ## Task 2 - 320722
Let $A B C D$ be a square, with an area of $25 \mathrm{~cm}^{2}$. A point $E$ lies on the extension of the diagonal $A C$ beyond $C$, such that the segment $A E$ is twice as long as the segment $A C$.
Determine the area of the quadrilateral $A B E D$ under these conditions! | 50 |
15,059 | A school program will randomly start between 8:30AM and 9:30AM and will randomly end between 7:00PM and 9:00PM. What is the probability that the program lasts for at least 11 hours and starts before 9:00AM? | \dfrac{5}{16} |
15,061 | 10.4. Find all values of the parameter $a$ for which the equation $x^{4}-a x^{2}+1=0$ has 4 roots forming an arithmetic progression. | \dfrac{10}{3} |
15,103 | Solve the following equation:
$$
\sqrt[4]{16+x}+\sqrt[4]{16-x}=4
$$ | 0 |
15,143 | The diagram below shows an isosceles triangle with base $21$ and height $28$. Inscribed in the triangle is a square. Find the area of the shaded region inside the triangle and outside of the square.
[asy]
size(170);
defaultpen(linewidth(0.8));
draw((0,0)--(1,1));
pair A=(5,0),B=(-5,0),C=(0,14), invis[]={(1,2),(-1,2)};
pair intsquare[]={extension(origin,invis[0],A,C),extension(origin,invis[1],B,C)};
path triangle=A--B--C--cycle,square=(intsquare[0]--intsquare[1]--(intsquare[1].x,0)--(intsquare[0].x,0)--cycle);
fill(triangle,gray);
unfill(square);
draw(triangle^^square);
[/asy] | 150 |
15,150 | Condition of the problem
Find the derivative.
$y=2 \sqrt{x}-4 \ln (2+\sqrt{x})$ | \dfrac{1}{2 + \sqrt{x}} |
15,170 | 6.2. Lines parallel to the sides of a square form a smaller square, the center of which coincides with the center of the original square. It is known that the area of the cross formed by the smaller square (see the figure on the right) is 17 times the area of the smaller square. How many times is the area of the original square larger than the area of the smaller square? | 81 |
15,197 | The kindergarten received cards for reading lessons: some have "MA" written on them, and others have "NYA". Each child took three cards and started forming words from them. It turned out that 20 children can form the word "MAMA", 30 children can form the word "NYANYA", and 40 children can form the word "MANYA". How many children have all three cards the same?
# | 10 |
15,200 | Let \( z_1, z_2, z_3, z_4 \) be the solutions to the equation \( x^4 + 3x^3 + 3x^2 + 3x + 1 = 0 \). Then \( |z_1| + |z_2| + |z_3| + |z_4| \) can be written as \( \frac{a + b \sqrt{c}}{d} \), where \( c \) is a square-free positive integer, and \( a, b, d \) are positive integers with \( \operatorname{gcd}(a, b, d) = 1 \). Compute \( 1000a + 100b + 10c + d \). | 7152 |
15,205 | 7.6. Five girlfriends, Sonya, Tanya, Lena, Galia, and Vika, were born in five cities: Riga, Penza, Kazan, Belgorod, and Moscow. Each of them loves candies produced in one of these cities. It is known that no one loves candies produced in their hometown. Sonya loves candies from Riga. Tanya is from Riga, and her favorite candies are from Penza. Vika loves candies from Moscow. Galia's favorite candies are produced in Belgorod. Vika is from Kazan. The girl from Penza loves candies made in Lena's hometown. Who among the girlfriends was born in Moscow? | Sonya |
15,261 | 4. The function $y=f(x)$ is defined on the set $(0,+\infty)$ and takes positive values on this set. It is known that for any points $A$ and $B$ on the graph of the function, the areas of the triangle $A O B$ and the trapezoid $A B H_{B} H_{A}$ are equal to each other $\left(H_{A}, H_{B} - \text{the bases of the perpendiculars dropped from points } A \text{ and } B \text{ to the x-axis}\right)$;
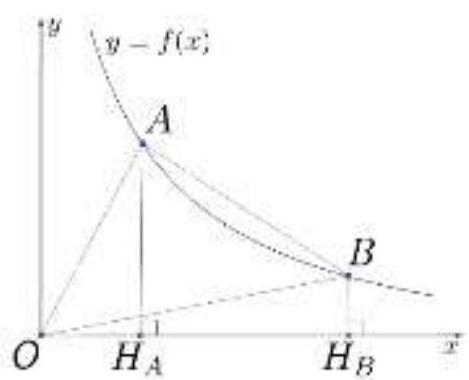
## Interregional Olympiad for Schoolchildren Based on Departmental Educational Organizations in Mathematics
$O$ - the origin). Find all such functions. Justify your solution. Given that $f(1)=4$, write the number $f(2)$ in the answer. | 2 |
15,268 | Problem 2. A group of adventurers is showing off their loot. It is known that exactly 9 adventurers have rubies; exactly 8 have emeralds; exactly 2 have sapphires; exactly 11 have diamonds. Moreover, it is known that
- if an adventurer has diamonds, then they have either rubies or sapphires (but not both at the same time);
- if an adventurer has rubies, then they have either emeralds or diamonds (but not both at the same time).
What is the smallest number of adventurers that can be in such a group? | 17 |
15,308 | Let's determine the greatest common divisor of the following numbers:
188094, $\quad 244122, \quad 395646$. | 138 |
15,322 | For a given positive integer \( k \), let \( f_{1}(k) \) represent the square of the sum of the digits of \( k \), and define \( f_{n+1}(k) = f_{1}\left(f_{n}(k)\right) \) for \( n \geq 1 \). Find the value of \( f_{2005}\left(2^{2006}\right) \). | 169 |
15,353 | Example 2 There is a sequence of numbers, the 1st number is 105, the 2nd number is 85, starting from the 3rd number, each number is the average of the two numbers before it. What is the integer part of the 19th number? | 91 |
15,394 | Is it true that in space, angles with respectively perpendicular sides are equal or sum up to $180^{\circ}$? | \text{No} |
15,405 | ## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 4} \frac{\sqrt[3]{16 x}-4}{\sqrt{4+x}-\sqrt{2 x}}$ | -\dfrac{4\sqrt{2}}{3} |
15,421 | Behind a thin lens with a focal length \( F \) and a diameter \( D \), a flat screen is placed perpendicularly to its optical axis at its focal point. A point light source is placed on the main optical axis at a distance \( d > F \) from the lens. Determine the diameter of the light spot on the screen. | \dfrac{D F}{d} |
15,425 | Under what condition on $(x, y) \in \mathbb{N}^{2}$ is the integer $(x+y)^{2}+3 x+y+1$ a perfect square? | x = y |
15,468 | Given an ellipse with its center at the origin \( O \), foci on the \( x \)-axis, and eccentricity \( \frac{\sqrt{3}}{2} \) which passes through the point \(\left(\sqrt{2}, \frac{\sqrt{2}}{2}\right)\). Suppose a line \( l \) that does not pass through the origin \( O \) intersects the ellipse at points \( P \) and \( Q \), and the slopes of lines \( OP \), \( PQ \), and \( OQ \) form a geometric sequence. Find the possible range of values for the area of triangle \( \triangle OPQ \). | (0, 1) |
15,469 | 13. Teacher Li and three students, Xiao Ma, Xiao Lu, and Xiao Zhou, set off from the school one after another and walk along the same road to the cinema. The three students have the same walking speed, and Teacher Li's walking speed is 1.5 times that of the students. Now, Teacher Li is 235 meters away from the school, Xiao Ma is 87 meters away from the school, Xiao Lu is 59 meters away from the school, and Xiao Zhou is 26 meters away from the school. When they walk another $\qquad$ meters, the distance Teacher Li is from the school will be exactly the sum of the distances the three students are from the school. | 42 |
15,492 | Consider the function \( f(x) = \frac{1}{3^{x} + \sqrt{3}} \). Find the value of
\[
\sqrt{3} \left[ f(-5) + f(-4) + f(-3) + f(-2) + f(-1) + f(0) + f(1) + f(2) + f(3) + f(4) + f(5) + f(6) \right] .
\] | 6 |
15,510 | In $\triangle ABC$, $BD = DE = EC$ and $CF:AC = 1:3$. If the area of $\triangle ADH$ is 24 square centimeters more than the area of $\triangle HEF$, find the area of $\triangle ABC$ in square centimeters. | 108 |
15,601 | ## 8. Diagonal Squares
Vlado covered the diagonal of a large square with a side length of $2020 \mathrm{~cm}$ using a row of squares with a side length of $4 \mathrm{~cm}$ cut from green collage paper. The diagonals of the green squares lie on the diagonal of the large square, and the intersection of any two consecutive green squares is a square with a side length of 1 cm. Calculate the perimeter of the shape formed by the green squares. Express the result in decimeters.
Result: $\quad 808$ | 808 |
15,634 | In triangle \(ABC\), the angle bisector \(AL\) is drawn. Points \(E\) and \(D\) are marked on segments \(AB\) and \(BL\) respectively such that \(DL = LC\) and \(ED \parallel AC\). Find the length of segment \(ED\) given that \(AE = 15\) and \(AC = 12\). | 3 |
15,648 | A customer bought several identical notebooks and identical books, with the number of books being 4 more than the number of notebooks. The total cost for all the notebooks was 72 kopecks, and the total cost for all the books was 6 rubles and 60 kopecks. If the notebook had cost the same as the book, and the book cost the same as the notebook, the customer would have spent less than 4 rubles and 44 kopecks on the purchase. How many notebooks were bought? | 2 |
15,699 | Two identical cylindrical sheets are cut open along the dotted lines and glued together to form one bigger cylindrical sheet. The smaller sheets each enclose a volume of 100. What volume is enclosed by the larger sheet? | 400 |
15,715 | The hares are cutting the log again, but now both ends of the log are fixed. Ten middle logs fell, and the two end ones remained fixed. How many cuts did the hares make? | 11 |
15,730 |
Let \( N \) be the total number of students in the school before the New Year, among which \( M \) are boys, making up \( k \) percent of the total. This means \( M = \frac{k}{100} N \), or \( 100M = kN \).
After the New Year, the number of boys became \( M+1 \), and the total number of students became \( N+3 \). If the boys now make up \( \ell \) percent (with \( \ell < 100 \) since there are definitely still some girls in the school), then:
\[ 100(M+1) = \ell(N+3) \]
Recalling the equality \( 100M = kN \), we find that:
\[ \ell N + 3\ell = 100M + 100 = kN + 100 \]
Thus, \( 100 - 3\ell = (\ell - k)N \). If \( 3\ell < 100 \) (that is, if girls make up less than one-third), then \( N \) is a natural divisor of the positive number \( 100 - 3\ell < 100 \), and therefore \( N \) is less than 100. If \( 3\ell \) is greater than 100 (it clearly cannot be equal to 100), then \( (k - \ell)N = 3\ell - 100 \leq 3 \cdot 99 - 100 = 197 \), and the number of students from the previous year is at most 197. | 197 |
15,766 | 9. Gari is seated in a jeep, and at the moment, has one 10 -peso coin, two 5 -peso coins, and six 1-peso coins in his pocket. If he picks four coins at random from his pocket, what is the probability that these will be enough to pay for his jeepney fare of 8 pesos? | \dfrac{37}{42} |
15,775 | 14. (6 points) A group of PLA soldiers formed a three-layer hollow square formation with 9 soldiers left over. If another layer was added inside the hollow part, 7 soldiers would be short. The total number of soldiers in this group is $\qquad$ people. | 105 |
15,845 | The kindergarten teacher evenly distributed 270 apples, 180 pears, and 235 oranges to the larger group of children. The remaining quantities of apples, pears, and oranges are in the ratio $3:2:1$. How many children are there in the larger group? | 29 |
15,864 | Given the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)\) with the right focus at \(F(c, 0)\), there exists a line \(l\) passing through point \(F\) that intersects the ellipse at points \(A\) and \(B\) such that \(OA \perp OB\). Find the range of the eccentricity of the ellipse. | \left[ \dfrac{\sqrt{5} - 1}{2}, 1 \right) |
15,865 | The edges of a rectangular parallelepiped are in the ratio $3: 4: 12$. A diagonal cross-section is made through the largest edge. Find the sine of the angle between the plane of this cross-section and the diagonal of the parallelepiped that does not lie in that plane. | \dfrac{24}{65} |
15,871 | . Find all sequences $\left(a_{n}\right)_{n \geqslant 1}$ of strictly positive real numbers such that for every integer $n$, we have:
$$
\sum_{i=1}^{n} a_{i}^{3}=\left(\sum_{i=1}^{n} a_{i}\right)^{2}
$$ | a_n = n |
15,880 | Let \( n \) be a positive integer. Define \( S_n = \left\{\left(a_1, a_2, \cdots, a_{2^n}\right) \mid a_i = 0 \text{ or } 1, 1 \leq i \leq 2^n\right\} \). For any two elements \( a = \left(a_1, a_2, \cdots, a_{2^n}\right) \) and \( b = \left(b_1, b_2, \cdots, b_{2^n}\right) \) in \( S_n \), define \( d(a, b) = \sum_{i=1}^{2^n} \left|a_i - b_i\right| \).
If \( A \subseteq S_n \) such that for any two distinct elements \( a, b \in A \), \( d(a, b) \geq 2^{n-1} \), then \( A \) is called a good subset. Find the maximum number of elements in a good subset of \( S_n \). | 2^{n+1} |
15,920 | 94. Even or odd number
$$
1-2+3-4+5-6+\ldots+993 ?
$$ | odd |
15,928 | The numbers \(1, 2, 3, \ldots, N\) are written in such an order that if the number \(i\) is somewhere (not in the first position), then to the left of it, there must be at least one of the numbers \(i+1\) or \(i-1\). In how many ways can this be done? | 2^{N-1} |
15,957 | How many solutions are there to the equation
\[ m^{4}+8n^{2}+425=n^{4}+42m^{2}, \]
where \( m \) and \( n \) are integers? | 16 |
15,971 | The target board shown in the figure consists of three concentric circles and two perpendicular lines that pass through the centers of the circles. The 12 resulting sections have equal area. Determine the ratio of the radii of the three circles. | 1 : \sqrt{2} : \sqrt{3} |
15,987 | A group of adventurers is showing their loot. It is known that exactly 5 adventurers have rubies; exactly 11 have emeralds; exactly 10 have sapphires; exactly 6 have diamonds. Additionally, it is known that:
- If an adventurer has diamonds, then they have either emeralds or sapphires (but not both simultaneously);
- If an adventurer has emeralds, then they have either rubies or diamonds (but not both simultaneously).
What is the minimum number of adventurers that can be in such a group? | 16 |
16,009 | Let $a, b, c,$ and $d$ be positive integers such that $\gcd(a, b)=24$ $\gcd(b, c)=36$ $\gcd(c, d)=54$ , and $70<\gcd(d, a)<100$ . Which of the following must be a divisor of $a$ | 13 |
16,051 | How many numbers should there be in a lottery for the probability of getting an ambo to be $\frac{5}{473}$, when drawing five numbers? | 44 |
16,063 | Can the sum of three fourth powers end with the four digits 2019? (A fourth power is an integer of the form \(n^{4}\), where \(n\) is an integer.) | No |
16,088 | 5. The diagonals of an arbitrary trapezoid divide the trapezoid into four triangles. The areas of the triangles that contain the bases of the trapezoid are $P_{1}$ and $P_{2}$. Express the area of the trapezoid $P$ in terms of $P_{1}$ and $P_{2}$. | (\sqrt{P_1} + \sqrt{P_2})^2 |
16,100 | Three [vertices](https://artofproblemsolving.com/wiki/index.php/Vertex) of a [cube](https://artofproblemsolving.com/wiki/index.php/Cube) are $P=(7,12,10)$, $Q=(8,8,1)$, and $R=(11,3,9)$. What is the [surface area](https://artofproblemsolving.com/wiki/index.php/Surface_area) of the cube? | 294 |
16,134 | 40. What is one and a half thirds of 100? | 50 |
16,140 | Task 2. A poultry farm delivered 720 eggs, which were packed in boxes of 6 eggs each. During transportation, 140 eggs were broken. The remaining eggs were packed in boxes of 12 eggs each. How many boxes of eggs were packed. Were there any unbroken eggs left that could not be packed? | 48 |
16,143 | Let $A$ and $B$ be two points on plane $\alpha$, and on the same side of the line $AB$ there are $n$ different points $P_1, P_2, \ldots, P_n$. Prove that the set of distances from $A$ and $B$ to $P_i$ $(i=1, 2, \ldots, n)$ contains at least $\sqrt{n}$ different elements. | \sqrt{n} |
16,166 |
Calculate the limit of the function:
\[
\lim_{{x \to 2}} \left(2 e^{x-2} - 1\right)^{\frac{3x+2}{x-2}}
\] | e^{16} |
16,183 | Consider an $n \times n$ chessboard where each cell contains a number. Denote the number in the $p$-th row and $q$-th column as $x_{pq}$. Prove that if for any $i, j, k$ (where $1 \leq i, j, k \leq n$) the identity $x_{ij} + x_{jk} + x_{ki} = 0$ holds, then there exist $n$ numbers $t_1, t_2, \ldots, t_n$ such that $x_{ij} = t_i - t_j$. | x_{ij} = t_i - t_j |
16,212 | Determine the largest possible value of the expression $ab+bc+ 2ac$ for non-negative real numbers $a, b, c$ whose sum is $1$. | \dfrac{1}{2} |
16,213 | Point $M$ is the midpoint of side $BC$ of triangle $ABC$. Circle $\omega$ passes through point $A$, touches line $BC$ at point $M$, and intersects sides $AB$ and $AC$ at points $D$ and $E$ respectively. Points $X$ and $Y$ are the midpoints of segments $BE$ and $CD$ respectively. Prove that the circumcircle of triangle $MXY$ is tangent to circle $\omega$. | \text{The circumcircle of triangle } MXY \text{ is tangent to circle } \omega |
16,248 | For which natural number $k$ does the expression $\frac{k^{2}}{1.001^{k}}$ attain its maximum value?
## List 9 | 2001 |
16,261 | In a class, there are 15 boys and 15 girls. On Women's Day, some boys called some girls to congratulate them (no boy called the same girl more than once). It turned out that the children can be uniquely divided into 15 pairs, such that each pair consists of a boy and a girl whom he called. What is the maximum number of calls that could have been made? | 120 |
16,278 | 6. Find the value of $r$ such that
$$
\begin{array}{l}
{\left[r+\frac{19}{100}\right]+\left[r+\frac{20}{100}\right]+\cdots} \\
+\left[r+\frac{91}{100}\right]=546 .
\end{array}
$$
Find $[100 r]$. (Where $[x]$ denotes the greatest integer not greater than $x$) | 743 |
16,281 | In $\triangle ABC$, $D$ is a point on $BC$ such that $\frac{BD}{DC}=\frac{1}{3}$. $E$ is the midpoint of $AC$. $AD$ and $BE$ intersect at $O$, and $CO$ intersects $AB$ at $F$. Find the ratio of the area of quadrilateral $BDOF$ to the area of $\triangle ABC$. | \dfrac{1}{10} |
16,339 | Given positive integers \( a, b, \) and \( c \) such that \( a < b < c \). If the product of any two numbers minus 1 is divisible by the third number, what is \( a^{2} + b^{2} + c^{2} \)? | 38 |
16,381 | ## Task B-4.4.
How many passwords consisting of 4 characters from the set $\{a, b, c, 1,2,3,4,5,+,!\}$ are there such that all characters in the password are different or the password contains exactly two, not necessarily different letters and two, not necessarily different digits? | 5670 |
16,398 | 17. Given $\cos ^{2}(\alpha-\beta)-\cos ^{2}(\alpha+\beta)=\frac{1}{2},(1+\cos 2 \alpha)(1+\cos 2 \beta)=\frac{1}{3}$, find the value of $\tan \alpha \tan \beta$. | \dfrac{3}{2} |
16,440 | 10. The Kingdom of Geometry awards badges to outstanding citizens of 2021. The badges are rectangular (including squares), and these rectangular badges are all different, but their area values are 2021 times their perimeter values, and both length and width are natural numbers. Therefore, the maximum number of different badges for the year 2021 is $\qquad$ kinds. | 14 |
16,449 | Given a convex quadrilateral \(ABCD\) with \(\angle C = 57^{\circ}\), \(\sin \angle A + \sin \angle B = \sqrt{2}\), and \(\cos \angle A + \cos \angle B = 2 - \sqrt{2}\), find the measure of angle \(D\) in degrees. | 168 |
16,491 | ## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0}\left(\frac{\ln (1+x)}{6 x}\right)^{\frac{x}{x+2}}
$$ | 1 |
16,498 | 7. For $x \in \mathbf{R}, n \in \mathbf{N}^{*}$, define $C_{x}^{n}=\frac{x(x-1) \cdots(x-n+1)}{n!}$. Let $P(x)$ be a 6th degree polynomial that satisfies $P(0)=1, P(k)=2^{k-1}, k=1,2, \cdots, 6$, express $P(x)=$ using $C_{x}^{k}(k=1,2, \cdots, 6)$. | 1 + C_{x}^{2} + C_{x}^{4} + C_{x}^{6} |
16,500 | ## PROBLEM 2
Solve the equation
$$
\log _{4}\left(5^{x}-1\right)=\log _{5}\left(4^{x}+1\right)
$$ | 1 |
16,523 | 11. (16 points) Let $A$ and $B$ be two different subsets of the set $\left\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right\}$, such that $A$ is not a subset of $B$, and $B$ is not a subset of $A$. Find the number of different ordered pairs $(A, B)$. | 570 |
16,544 | Given \(\alpha, \beta, \gamma \in \left(0, \frac{\pi}{4}\right)\) and \(\sin^2 \alpha + \sin^2 \beta + \sin^2 \gamma = 1\). Prove that \(\frac{\pi}{2} < \alpha + \beta + \gamma \leq 3 \arcsin \frac{\sqrt{3}}{3}\). | \frac{\pi}{2} < \alpha + \beta + \gamma \leq 3 \arcsin \frac{\sqrt{3}}{3} |
16,599 | Give an example of a number $x$ for which the equation $\sin 2017 x - \operatorname{tg} 2016 x = \cos 2015 x$ holds. Justify your answer. | \dfrac{\pi}{4} |
16,604 | 7. As shown in the figure, 10 identical regular pentagons are joined edge-to-edge, forming a regular decagon in the middle. 3 identical regular $n$-sided polygons are joined edge-to-edge, forming a regular triangle in the middle, then the value of $n$ is $\qquad$ . | 12 |
16,642 | Find the ratio \( m_{1} / m_{2} \) of the two hanging balls, given that the tension forces in the upper and lower threads differ by a factor of two. | 1 |
16,730 | In the $xOy$ coordinate plane, the curve
$$
y=(3 x-1)\left(\sqrt{9 x^{2}-6 x+5}+1\right)+(2 x-3)\left(\sqrt{4 x^{2}-12 x+13}+1\right)
$$
intersects the $x$-axis at the point $\qquad$ . | \left( \dfrac{4}{5}, 0 \right) |
16,732 | 13. At the lumber yard, there were logs 6 m and 8 m long of the same thickness. Which logs are more advantageous to take in order to get more pieces with fewer cuts when cutting them into 1-meter pieces? | 6 |
16,751 | In a square with unit side length, we randomly select a point on each of two opposite sides. What is the probability that the distance between the two points is less than a given segment $p$? $(1<p<\sqrt{2})$. | 2\sqrt{p^2 - 1} - p^2 + 1 |
16,753 | There are \( n \) girls \( G_{1}, \ldots, G_{n} \) and \( n \) boys \( B_{1}, \ldots, B_{n} \). A pair \( \left(G_{i}, B_{j}\right) \) is called suitable if and only if girl \( G_{i} \) is willing to marry boy \( B_{j} \). Given that there is exactly one way to pair each girl with a distinct boy that she is willing to marry, what is the maximal possible number of suitable pairs? | \frac{n(n + 1)}{2} |
16,754 | 70. As shown in Figure 27, Lele scored 98 in Math, 88 in Chinese, and after adding English, the average score is 95. Lele scored $\qquad$ in English, and draw the diagram for the English score in the figure.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
---
70. As shown in Figure 27, Lele scored 98 in Math, 88 in Chinese, and after adding English, the average score is 95. Lele scored $\qquad$ in English, and draw the diagram for the English score in the figure. | 99 |
16,804 | 91. A wild rabbit escapes 100 steps before the hunting dog starts to chase it. The rabbit runs 8 steps in the distance the hunting dog runs 3 steps, and in the time the hunting dog runs 4 steps, the rabbit can run 9 steps. The hunting dog has to run at least $\qquad$ steps to catch up with the rabbit. | 240 |
16,860 | 4. Three people $A, B$ and $C$ play a game of passing a basketball from one to another. Find the number of ways of passing the ball starting with $A$ and reaching $A$ again on the 11 th pass. For example, one possible sequence of passing is
$$
A \rightarrow B \rightarrow A \rightarrow B \rightarrow C \rightarrow A \rightarrow B \rightarrow C \rightarrow B \rightarrow C \rightarrow B \rightarrow A .
$$ | 682 |
16,875 | 【Question 10】
There is a "buy five get one free" soda, where every five empty bottles can be exchanged for a new bottle of soda. During a class gathering, a class drank 109 bottles of soda, some of which were obtained by exchanging empty bottles. How many bottles of soda did they initially buy at least? | 88 |
16,927 | 5-6. On a rectangular table of size $x$ cm $\times 80$ cm, identical sheets of paper of size 5 cm $\times 8$ cm are placed. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
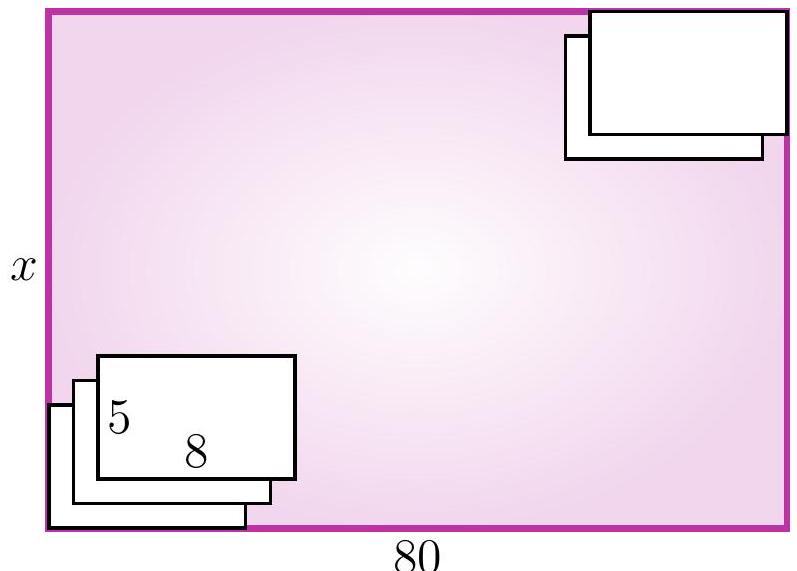 | 77 |
16,934 | The side chain of methane $\mathrm{CH}_{4}$ is given. If the 4 H bonds are substituted by one of $\mathrm{H}, \mathrm{Cl}, \mathrm{CH}_{3}, \mathrm{C}_{2}\mathrm{H}_{5}$, how many different chemical structures can be formed? | 36 |
16,936 | 8. Let $a, b \in \mathbf{R}$. If for $x \geqslant 0$, it always holds that
$$
0 \leqslant x^{4}-x^{3}+a x+b \leqslant\left(x^{2}-1\right)^{2} \text {, }
$$
then $b-a=$ . $\qquad$ | 2 |
16,941 | Problem 5 (Partition problem) In how many ways can 11 items be divided into two groups such that each group has no fewer than three items (selecting one group uniquely determines the other)? | 957 |
16,956 | 3. Find the numerical value of the expression
$$
\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{2}{x y+1}
$$
if it is known that $x$ is not equal to $y$ and the sum of the first two terms is equal to the third. | 2 |
16,958 | 1. In the drawer, there are 23 socks: 8 white and 15 black. Every minute, Marina approaches the drawer and pulls out a sock. If at any moment Marina pulls out more black socks than white ones, she exclaims: "Finally!" - and ends the process.
What is the maximum number of socks Marina can pull out before she exclaims: "Finally!"? The answer should include the last sock that Marina pulled out. | 17 |
16,976 | Let \( x \) and \( y \) be positive real numbers such that \( x^{2}+y^{2}=1 \) and \( \left(3 x-4 x^{3}\right)\left(3 y-4 y^{3}\right)=-\frac{1}{2} \). Compute \( x+y \). | \dfrac{\sqrt{6}}{2} |
16,998 | 10. Let $x \in \mathbf{R}$, the inequality $2 x^{2}-a \sqrt{x^{2}+1}+3 \geqslant 0$ always holds, then the maximum value of the real number $a$ is $\qquad$ | 3 |
17,017 | 1.4 Use the digits $2,4,6$ to construct a six-digit number, but do not allow two consecutive 2s to appear in the six-digit number (for example, 626442 is allowed, 226426 is not allowed), how many such six-digit numbers are there? | 448 |
17,053 | In a class, there are 15 boys and 15 girls. On March 8th, some boys called some girls to congratulate them (no boy called the same girl twice). It turned out that the students can be uniquely paired into 15 pairs such that each pair consists of a boy and a girl whom he called. What is the maximum number of calls that could have been made? | 120 |
17,055 | 3. For arbitrary real numbers $a$ and $b (a \neq 0)$, find the minimum value of the expression $\frac{1}{a^{2}}+2 a^{2}+3 b^{2}+4 a b$. | \dfrac{2\sqrt{6}}{3} |
17,061 | Calculate the value of the expression
$$
\frac{\left(3^{4}+4\right) \cdot\left(7^{4}+4\right) \cdot\left(11^{4}+4\right) \cdot \ldots \cdot\left(2015^{4}+4\right) \cdot\left(2019^{4}+4\right)}{\left(1^{4}+4\right) \cdot\left(5^{4}+4\right) \cdot\left(9^{4}+4\right) \cdot \ldots \cdot\left(2013^{4}+4\right) \cdot\left(2017^{4}+4\right)}
$$ | 4080401 |
17,064 | Let \( f: \mathbb{N} \rightarrow \mathbb{Q} \) be a function, where \( \mathbb{N} \) denotes the set of natural numbers, and \( \mathbb{Q} \) denotes the set of rational numbers. Suppose that \( f(1) = \frac{3}{2} \), and
\[ f(x+y) = \left(1 + \frac{y}{x+1}\right) f(x) + \left(1 + \frac{x}{y+1}\right) f(y) + x^2 y + xy + xy^2 \]
for all natural numbers \( x, y \). Find the value of \( f(20) \). | 4305 |
17,067 | Find the smallest positive value of $36^k - 5^m$, where $k$ and $m$ are positive integers. | 11 |
17,115 | 12. Let $\left.f(m)=2^{2^{2^{2}}}\right\} m$. Find the least $m$ so that $\log _{10} f(m)$ exceeds 6 . | 5 |
17,176 | 5. Let integer $n \geqslant 2$,
$$
A_{n}=\sum_{k=1}^{n} \frac{3 k}{1+k^{2}+k^{4}}, B_{n}=\prod_{k=2}^{n} \frac{k^{3}+1}{k^{3}-1} \text {. }
$$
Then the size relationship between $A_{n}$ and $B_{n}$ is | A_n = B_n |
17,180 | 6. Take a clay sphere of radius 13 , and drill a circular hole of radius 5 through its center. Take the remaining "bead" and mold it into a new sphere. What is this sphere's radius? | 12 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.