id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
17,182 | The measures of the angles at the vertices $A, B, C$ of triangle $ABC$ form an arithmetic progression with a common difference of $\pi / 7$. The angle bisectors of this triangle intersect at point $D$. Points $A_{1}, B_{1}, C_{1}$ are located on the extensions of segments $DA, DB, DC$ beyond points $A, B, C$ respectively, at the same distance from point $D$. Prove that the measures of angles $A_{1}, B_{1}, C_{1}$ also form an arithmetic progression. Find its common difference. | \dfrac{\pi}{28} |
17,186 | Example 12. In a box, there are 15 red, 9 blue, and 6 green balls. Six balls are drawn at random. What is the probability that 1 green, 2 blue, and 3 red balls are drawn (event $A$)? | \dfrac{24}{145} |
17,192 | Given that \( 169(157 - 77x)^2 + 100(201 - 100x)^2 = 26(77x - 157)(1000x - 2010) \), find the value of \( x \). | 31 |
17,221 | Let diamond \( A_{1} A_{2} A_{3} A_{4} \) have side length \( 1 \) and \(\angle A_{1} A_{2} A_{3} = \frac{\pi}{6} \). Point \( P \) lies in the plane of diamond \( A_{1} A_{2} A_{3} A_{4} \). Determine the minimum value of \( \sum_{1 \leqslant i < j \leqslant 4} \overrightarrow{P A_{i}} \cdot \overrightarrow{P A_{j}} \). | -1 |
17,227 | In the figure, the diagonals \(AC\) and \(BD\) of quadrilateral \(ABCD\) intersect at point \(O\), and \(E\) is the midpoint of \(BC\). The area of triangle \(ABO\) is 45, the area of triangle \(ADO\) is 18, and the area of triangle \(CDO\) is 69. Find the area of triangle \(AED\). | 75 |
17,247 | Four. (25 points) As shown in Figure 2, in the right trapezoid $ABCD$, $\angle ABC = \angle BAD = 90^{\circ}$, $AB = 16$. The diagonals $AC$ and $BD$ intersect at point $E$. A line $EF \perp AB$ is drawn through $E$ at point $F$, and $O$ is the midpoint of side $AB$, with $FE + EO = 8$. Find the value of $AD + BC$. | 16 |
17,265 | Find all non-zero polynomials \( f(x) = a_0 + a_1 x + \cdots + a_n x^n \) that satisfy the equation \( f(x^2) = (f(x))^2 \), where \( x \) is a real number. | x^n |
17,334 | In the plane rectangular coordinate system $xOy$, the equation of the hyperbola $C$ is $x^{2}-y^{2}=1$. Find all real numbers $a$ greater than 1 that satisfy the following requirement: Through the point $(a, 0)$, draw any two mutually perpendicular lines $l_{1}$ and $l_{2}$. If $l_{1}$ intersects the hyperbola $C$ at points $P$ and $Q$, and $l_{2}$ intersects $C$ at points $R$ and $S$, then $|PQ| = |RS|$ always holds. | \sqrt{2} |
17,339 | 7、The denominator is a two-digit number, the numerator is 1, and the fraction can be converted into a finite decimal. There are $\qquad$
The fraction has a two-digit denominator, a numerator of 1, and can be converted into a finite decimal. There are $\qquad$ | 9 |
17,359 | 8,9,10 | |
What is the minimum number of weights needed to be able to weigh any number of grams from 1 to 100 on balance scales, if the weights can be placed on both pans of the scales? | 5 |
17,375 | Let $ \prod_{n=1}^{1996}{(1+nx^{3^n})}= 1+ a_{1}x^{k_{1}}+ a_{2}x^{k_{2}}+...+ a_{m}x^{k_{m}}$ where $a_{1}, a_{1}, . . . , a_{m}$ are nonzero and $k_{1} < k_{2} <...< k_{m}$ . Find $a_{1996}$ . | 665280 |
17,382 | Let \(a, b, c, d, e\) be positive integers. Their sum is 2345. Let \(M = \max (a+b, b+c, c+d, d+e)\). Find the smallest possible value of \(M\). | 782 |
17,417 | A triangle has an area equal to 1. Prove that the length of its middle side is not less than \(\sqrt{2}\). | \sqrt{2} |
17,433 | Two circles of radius $r$ touch each other. In addition, each of them touches externally a third circle of radius $R$ at points $A$ and $B$ respectively.
Find the radius $r$, if $A B=12, R=8$. | 24 |
17,479 | 13. Real numbers $a, b, c$ satisfy $a^{2}+b^{2}+c^{2}=\lambda(\lambda>0)$, try to find
$$
f=\min \left\{(a-b)^{2},(b-c)^{2},(c-a)^{2}\right\}
$$
the maximum value. | \dfrac{\lambda}{2} |
17,486 | 1. Scientists have found a fragment of an ancient manuscript on mechanics. It was a piece of a book, the first page of which was numbered 435, and the last page was written with the same digits but in some other order. How many sheets were in this fragment? | 50 |
17,515 | 31. How many ordered pairs of integers $(x, y)$ satisfy the equation
$$
x^{2}+y^{2}=2(x+y)+x y ?
$$ | 6 |
17,527 | 4. (10 points) Xiao Ming bought 4 apples, 6 pears, and 8 peaches, while Xiao Hong bought 5 apples, 7 pears, and 6 peaches. In the following 18 days, each of them eats one fruit per day, with three days both eating apples; two days both eating pears, and three days one eating an apple and the other eating a pear. Therefore, there are $\qquad$ days both eating peaches. | 4 |
17,538 | B1. Find all real numbers $x$ that satisfy the equation
$$
\log _{2}(10 x)+\log _{4}(100 x)+\log _{8}(1000 x)-2 \log _{64} x=9
$$
Write the result in the form of a simplified fraction.
$$
\text { (6 points) }
$$ | \dfrac{16}{25} |
17,542 | A function \( f \) is defined on the set of integers, and satisfies the following conditions:
\[
f(n)=\left\{\begin{array}{l}
n - 3, \quad \text{if } n \geq 1000; \\
f(f(n+5)), \quad \text{if } n < 1000.
\end{array}\right.
\]
Find \( f(84) \). | 997 |
17,554 | In a park, there are paths laid out as shown in the diagram. Two workers started paving the paths simultaneously from point $A$. They pave the asphalt at constant speeds: the first one on the segment $A-B-C$, and the second one on the segment $A-D-E-F-C$. They finished their work at the same time, spending 9 hours on it. It is known that the second worker is 1.2 times faster than the first worker. How many minutes did the second worker spend paving the segment $D-E$? | 45 |
17,564 | Point \( E \) is the midpoint of the edge \( B B_{1} \) of the cube \( A B C D A_{1} B_{1} C_{1} D_{1} \). Find the tangent of the angle between lines \( A E \) and \( C A_{1} \). | \sqrt{14} |
17,603 | $\left[\begin{array}{l}{[\text { Integer and fractional parts. Archimedes' principle ] }} \\ {[\quad \underline{\text { equations in integers }} \underline{\text { ] }}}\end{array}\right]$
How many solutions in natural numbers does the equation $\left[{ }^{x} / 10\right]=\left[{ }^{x} / 11\right]+1$ have? | 110 |
17,608 | 7.2. One morning at 9:00, pedestrian Fedia left the village of Fedino for the village of Novoverandovo. At the same time, cyclist Vera set off towards him from Novoverandovo. It is known that by the time they met, Fedia had walked one-third of the distance between the villages. However, if Fedia had left an hour earlier, he would have walked half the distance by the time they met. At what time did Fedia and Vera meet? The speeds of Vera and Fedia are constant. | 10:20 |
17,637 | Find all real numbers \( x, y, z \) satisfying:
\[
\left\{\begin{array}{l}
(x+1) y z=12 \\
(y+1) z x=4 \\
(z+1) x y=4
\end{array}\right.
\] | \left(\frac{1}{3}, 3, 3\right) |
17,640 | The car engine operates with a power of \( P = 60 \text{ kW} \). Determine the car's speed \( v_0 \) if, after turning off the engine, it stops after traveling a distance of \( s = 450 \text{ m} \). The force resisting the car's motion is proportional to its speed. The mass of the car is \( m = 1000 \text{ kg} \). | 30 |
17,654 | 8. (10 points) The number of pages in the 5 books, The Book of Songs, The Book of Documents, The Book of Rites, The Book of Changes, and The Spring and Autumn Annals, are all different: The Book of Songs and The Book of Documents differ by 24 pages. The Book of Documents and The Book of Rites differ by 17 pages. The Book of Rites and The Book of Changes differ by 27 pages. The Book of Changes and The Spring and Autumn Annals differ by 19 pages. The Spring and Autumn Annals and The Book of Songs differ by 15 pages. Therefore, among these 5 books, the difference in the number of pages between the book with the most pages and the book with the fewest pages is $\qquad$ pages. | 34 |
17,658 | 10th CanMO 1978 Problem 4 ABCD is a convex quadrilateral with area 1. The lines AD, BC meet at X. The midpoints of the diagonals AC and BD are Y and Z. Find the area of the triangle XYZ. | \dfrac{1}{4} |
17,666 | The sides of triangle \( T \) are parallel to the medians of triangle \( T_1 \). Prove that the medians of triangle \( T \) are parallel to the sides of triangle \( T_1 \). | \text{The medians of triangle } T \text{ are parallel to the sides of triangle } T_1 |
17,727 | How many three-digit numbers can be formed using the digits 1, 2, 3, 4, 5, and 6? | 216 |
17,736 | Let \( x, y, z \) be strictly positive numbers. Show that:
\[
\frac{1}{x+y} + \frac{4}{y+z} + \frac{9}{x+z} \geq \frac{18}{x+y+z}
\] | \frac{1}{x+y} + \frac{4}{y+z} + \frac{9}{x+z} \geq \frac{18}{x+y+z} |
17,737 | For any set \( S \), let \( |S| \) represent the number of elements in set \( S \) and let \( n(S) \) represent the number of subsets of set \( S \). If \( A \), \( B \), and \( C \) are three finite sets such that:
(1) \( |A|=|B|=2016 \);
(2) \( n(A) + n(B) + n(C) = n(A \cup B \cup C) \),
then the maximum value of \( |A \cap B \cap C| \) is ________. | 2015 |
17,752 | 4. Lea drew a rectangle where one side is longer than the other by $3 \mathrm{~cm}$. After that, she drew two equilateral triangles on each of the shorter sides of the rectangle such that their sides are of equal length, as shown in the figure. If the perimeter of the resulting shape is $78 \mathrm{~cm}$, what is the perimeter of the rectangle?
 | 54 |
17,756 | Solve the following equation:
$$
\log _{3}(3-x)=\sqrt{\sqrt{x-1}-\frac{1}{\sqrt{x-1}}}
$$ | 2 |
17,797 | \section*{Problem 4 - 071024}
On a flat table, there are 4 wooden spheres, each with a radius of length \(r\), touching each other such that their contact points with the tabletop form the corners of a square.
A fifth wooden sphere of the same radius is placed in the resulting central gap.
Give the distance \(d\) from the highest point of this fifth sphere to the tabletop! | r(2 + \sqrt{2}) |
17,810 | 31. How many ordered pairs of positive integers $(x, y)$ satisfy the equation
$$
x \sqrt{y}+y \sqrt{x}+\sqrt{2006 x y}-\sqrt{2006 x}-\sqrt{2006 y}-2006=0 ?
$$ | 8 |
17,836 | Masha has 2 kg of "Lastochka" candies, 3 kg of "Truffle" candies, 4 kg of "Ptichye moloko" candies, and 5 kg of "Citron" candies. What is the maximum number of New Year gifts she can make if each gift must contain 3 different types of candies, 100 grams of each type? | 45 |
17,850 | Two points are drawn on each side of a square with an area of 81 square units, dividing the side into 3 congruent parts. Quarter-circle arcs connect the points on adjacent sides to create the figure shown. What is the length of the boundary of the bolded figure? Express your answer as a decimal to the nearest tenth. [asy]
size(80);
import graph;
draw((0,0)--(3,0)--(3,3)--(0,3)--cycle, linetype("2 4"));
draw(Arc((0,0),1,0,90),linewidth(.8));
draw(Arc((0,3),1,0,-90),linewidth(.8));
draw(Arc((3,0),1,90,180),linewidth(.8));
draw(Arc((3,3),1,180,270),linewidth(.8));
draw((1,0)--(2,0),linewidth(.8));draw((3,1)--(3,2),linewidth(.8));
draw((1,3)--(2,3),linewidth(.8));draw((0,1)--(0,2),linewidth(.8));
[/asy] | 30.8 |
17,851 | 4B. Three cards are given. The number 19 is written on one, the number 97 on another, and a two-digit number on the third. If we add all the six-digit numbers obtained by arranging the cards in a row, we get the number 3232320. What number is written on the third card? | 44 |
17,917 | 2000 people registered on a new website. Each person invited 1000 others to be friends. Two people are considered friends if and only if both have invited each other to be friends. What is the minimum number of friend pairs that could have been formed? | 1000 |
17,941 | ## Task 1 - 330521
On a street in a small town, there are a total of 47 street lamps on the left and right side of the road. On each side of the street, the distance between any two adjacent lamps is $35 \mathrm{~m}$. On the left side of the road, there is a lamp exactly at the beginning and at the end of the street. How long is this street? | 805 |
17,963 | Let $T$ be the set of all positive divisors of $2004^{100}$, and let $S$ be a subset of $T$ such that no element in $S$ is an integer multiple of any other element in $S$. Find the maximum value of $|S|$. | 10201 |
17,985 | How many integers are there from 0 to 999999 in which no two adjacent digits are the same? | 597871 |
17,988 | How many positive perfect cubes are divisors of the product \(1! \cdot 2! \cdot 3! \cdots 10!\)? | 468 |
18,019 | A car and a truck start traveling towards each other simultaneously from points $A$ and $B$, respectively. It is known that the car's speed is twice the speed of the truck. The car arrives at point $C$ at 8:30, and the truck arrives at point $C$ at 15:00 on the same day. Both vehicles continue moving without stopping at point $C$. Determine the time at which the car and the truck meet. | 10:40 |
18,025 | Each face of a hexahedron and each face of a regular octahedron are equilateral triangles with side length \(a\). The ratio of the radii of the inscribed spheres (inradii) of the two polyhedra is a reduced fraction \(\frac{m}{n}\). What is the product \(m \cdot n\)? | 6 |
18,043 | 10. (15 points) A turtle and a rabbit are in a 1000-meter race. The rabbit's speed is 5 times that of the turtle. When they start from the starting line at the same time, the turtle runs continuously, while the rabbit runs to a certain point and then starts sleeping. When the rabbit wakes up, the turtle has already taken the lead. The rabbit then tries to catch up, but when the turtle reaches the finish line, the rabbit is still 10 meters behind. How many meters did the turtle run while the rabbit was sleeping? | 802 |
18,055 | Which is the smallest positive integer $n$ for which $3^{2 n}-1$ is divisible by $2^{2010}$? | 2^{2007} |
18,091 | 3. Arrange $1,2,3,4,5,6$ randomly in a row, denoted as $a, b, c, d, e, f$. Then the probability that $a b c+d e f$ is an even number is $\qquad$ | \dfrac{9}{10} |
18,098 | Test $\mathbf{F}$ Calculation:
$$
\frac{\left(10^{4}+324\right)\left(22^{4}+324\right)\left(34^{4}+324\right)\left(46^{4}+324\right)\left(58^{4}+324\right)}{\left(4^{4}+324\right)\left(16^{4}+324\right)\left(28^{4}+324\right)\left(40^{4}+324\right)\left(52^{4}+324\right)} \text {. }
$$
(5th American Mathematical Talent Competition) | 373 |
18,106 | 2. $f(n)$ is defined on the set of positive integers, and: (1) for any positive integer $n, f[f(n)]=4 n+9$; (2) for any non-negative integer $k, f\left(2^{k}\right)=2^{k+1}+3$. Determine $f(1789)$.
(1989 Australian Olympiad Problem) | 3581 |
18,117 | ## Problem Statement
Calculate the volumes of the bodies bounded by the surfaces.
$$
\frac{x^{2}}{9}+\frac{y^{2}}{4}-z^{2}=1, z=0, z=4
$$ | 152\pi |
18,128 | 11. (This question is worth 20 points) The sequence $\left\{x_{n}\right\}$ satisfies $x_{0}=0$ and $x_{n+1}=3 x_{n}+\sqrt{8 x_{n}^{2}+1}$, find the general term formula. | \dfrac{(3 + 2\sqrt{2})^n - (3 - 2\sqrt{2})^n}{4\sqrt{2}} |
18,134 | For real number \( x \), let \( [x] \) denote the greatest integer less than or equal to \( x \). Find the positive integer \( n \) such that \(\left[\log _{2} 1\right] + \left[\log _{2} 2\right] + \left[\log _{2} 3\right] + \cdots + \left[\log _{2} n\right]=1994\). | 312 |
18,141 | 3. All seven-digit numbers consisting of different digits from 1 to 7 were listed in ascending order. What is the position of the number 3241765? | 1590 |
18,147 | Example 4. Find the general solution of the equation $y^{\prime \prime}+3 y^{\prime}=0$. | y = C_1 + C_2 e^{-3x} |
18,186 | (Following Benoît's course 2021)
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy:
$$
\forall x, y \in \mathbb{R}, \quad f(2 f(x)+f(y))=2 x+f(y)
$$ | f(x) = x |
18,193 | 8. The number of positive integer pairs $(x, y)$ that satisfy $y=\sqrt{x+51}+\sqrt{x+2019}$ is. $\qquad$ | 6 |
18,235 | 9.1. First-grader Masha, entering the school, each time climbs the school porch stairs, which have 10 steps. Being at the bottom of the stairs or on one of its steps, she can either go up to the next step or jump over one step up (Masha cannot yet jump over two or more steps). What is the minimum number of times Masha needs to enter the school to climb the porch in all possible ways? | 89 |
18,239 | Find all natural numbers $n$ for which $2^{8}+2^{11}+2^{n}$ is equal to the square of an integer. | 12 |
18,256 | There are 120 different five-digit numbers composed of the digits 1, 2, 3, 4, and 5. Arrange them in descending order. The 95th number is $\quad$ | 21354 |
18,262 | 3. (8 points) In another 12 days, it will be 2016, Hao Hao sighs: I have only experienced 2 leap years so far, and the year I was born is a multiple of 9, so in 2016, Hao Hao is $\qquad$ years old. | 9 |
18,269 | Example 1 Given $\left\{\begin{array}{l}\sin \alpha+\sin \beta=1 \\ \cos \alpha+\cos \beta=0\end{array}\right.$, find $\cos 2 \alpha+\cos 2 \beta$. | 1 |
18,275 | 7. A chord of length $10 \mathrm{~cm}$ is drawn in a circle. Through one of its ends, a tangent to the circle is drawn, and through the other end, a secant parallel to the tangent is drawn. The inner segment of the secant is 12 cm. Find the radius of the circle. | \dfrac{25}{4} |
18,290 | 7.1. Come up with at least one three-digit PAU number (all digits are different) such that $(П+\mathrm{A}+\mathrm{У}) \times \Pi \times \mathrm{A} \times \mathrm{Y}=300$ (it is sufficient to provide one example) | 235 |
18,300 | 24.4. (SFRY, 72). For each value of $n \in \mathbf{N}$, find the largest number $k \in \mathbf{N}$ with the following property: in a set consisting of $n$ elements, one can choose $k$ different subsets, any two of which have a non-empty intersection. | 2^{n-1} |
18,304 | At the conference "Economics of Modern Times," there was an intellectual tournament in which more than 198, but fewer than 230 scientists (with either PhD or higher degrees) participated. In a match, participants would ask each other questions within a specified time frame and record correct answers. Each participant played exactly once against every other participant. The winner of a match received one point, the loser received no points, and in the event of a draw, both participants received half a point each. At the end of the tournament, it turned out that each participant scored half of all their points in matches against PhDs. How many non-PhD scientists participated in the tournament? Provide the smallest possible number as the answer. | 105 |
18,321 | In the figure given, there is a point \( P \) within \(\angle M A N\), and it is known that \( \tan \angle M A N = 3 \). The distance from point \( P \) to the line \( A N \) is \( P D = 12 \) and \( A D = 30 \). A line passing through \( P \) intersects \( A N \) and \( A M \) at points \( B \) and \( C \) respectively. Find the minimum area of \(\triangle A B C\). | 624 |
18,336 | 4. Xiaoming formed a sequence using the four digits $2, 0, 1, 6$ (continuously adding these four digits in this order to the end of the number): $2,20,201,2016,20162,201620,2016201,20162016,201620162, \ldots$. In this sequence, the number of prime numbers is $\qquad$. | 1 |
18,417 | A7. The product of five different integers is 12 . What is the largest of the integers? | 3 |
18,461 | How many natural numbers are there whose square and cube together require 10 digits to describe? | 53 |
18,465 | An engraver makes plates with letters. He engraves the same letters in the same amount of time, but different letters may take different times. On two plates, "ДОМ МОДЫ" (DOM MODY) and "ВХОД" (VKHOD), together he spent 50 minutes, and one plate "В ДЫМОХОД" (V DYMOHOD) took him 35 minutes. How much time will it take him to make the plate "ВЫХОД" (VYKHOD)? | 20 |
18,468 | In the conditions of problem I.6. 98, show that \( \mathrm{E} \tau_{1} < \infty \) if \( \mathrm{E} X_{1} > 0 \). | \mathrm{E} \tau_{1} < \infty |
18,499 | Find the gradient of the scalar field given in spherical coordinates $(r, \theta, \varphi)$: \( u = r + \frac{\sin \theta}{r} - \sin \theta \cos \varphi \) | \left(1 - \frac{\sin \theta}{r^2}\right) \mathbf{e}_r + \left(\frac{\cos \theta}{r^2} - \frac{\cos \theta \cos \varphi}{r}\right) \mathbf{e}_\theta + \frac{\sin \varphi}{r} \mathbf{e}_\varphi |
18,519 | Given \( x, y, z \in [0, 1] \), find the maximum value of \( M = \sqrt{|x-y|} + \sqrt{|y-z|} + \sqrt{|z-x|} \). | 1 + \sqrt{2} |
18,547 | Find the last three digits in the product $1 \cdot 3\cdot 5\cdot 7 \cdot . . . \cdot 2009 \cdot 2011$.
| 875 |
18,554 |
Calibration of rollers. One of the components of a gasoline engine has the shape of a roller. A steel plate, which has 15 holes drilled in a row with precisely set dimensions, is used to measure the thickness of the roller. The first hole has a diameter of 10 mm, and each subsequent hole has a diameter that is 0.04 mm larger than the previous one. The calibration of the roller involves inserting it into a hole; if it does not fit, its diameter is considered to be larger than the hole's diameter, and if it fits, its diameter is considered to be smaller. Thus, eventually, the diameter of the roller is determined with an accuracy of less than 0.04 mm (rollers with a diameter less than 10 mm or greater than 10.56 mm are not considered; the others proceed to further processing).
Workers tasked with the calibration test each roller on the same number of holes, but, of course, on different holes. How many measurement attempts are necessary for each roller? What should be the sequence of attempts? | 4 |
18,563 | Arrange positive integers that are neither perfect squares nor perfect cubes (excluding 0) in ascending order as 2, 3, 5, 6, 7, 10, ..., and determine the 1000th number in this sequence. | 1039 |
18,571 | Given that the function \( f(x) \) satisfies the equation \( 2 f(x) + x^{2} f\left(\frac{1}{x}\right) = \frac{3 x^{3} - x^{2} + 4 x + 3}{x + 1} \) and \( g(x) = \frac{5}{x + 1} \), determine the minimum value of \( f(x) + g(x) \). | \dfrac{15}{4} |
18,605 | Find the midsegment (median) of an isosceles trapezoid, if its diagonal is 25 and its height is 15. | 20 |
18,633 | ## Task B-4.2.
Let $z=x+2i$ and $w=3+yi$ be complex numbers, where $x, y \in \mathbb{R}$. Determine the smallest positive real number $x$ for which the fraction $\frac{z+w}{z-w}$ is an imaginary number. | \sqrt{5} |
18,672 | 5. Xiao Ming and Xiao Lin are playing the water-carrying game. The two use the same water samples to carry water and pour it into the same empty basin. The game is scored as follows: if the basin overflows when Xiao Ming pours water, 10 points are recorded; if the basin overflows when Xiao Lin pours water, 9 points are recorded; if the basin is not full after all the water is poured in one round, 3 points are recorded.
In the first round, Xiao Ming pours 5 buckets of water first, and when Xiao Lin pours 5 buckets of water, the basin overflows:
In the second round, Xiao Ming pours 2 buckets of water first, and Xiao Lin pours 7 buckets of water to end the game, but the basin is still not full:
In the third round, Xiao Ming pours 13 buckets of water alone to end the game.
After the three rounds of the game, the total score for these three rounds is $\qquad$ points. | 22 |
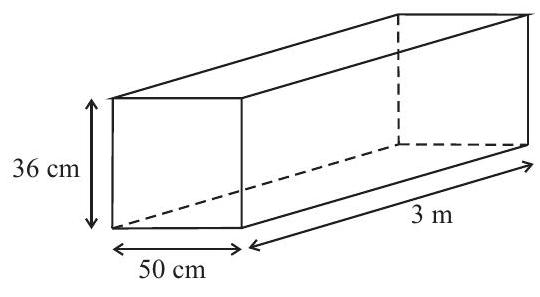
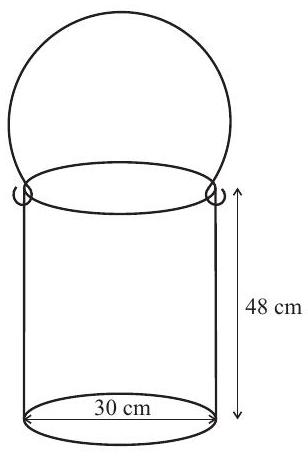
18,683 | To fill a rectangular tank with water, which has a length of $3 \mathrm{~m}$, a width of $50 \mathrm{~cm}$, and a height of $0.36 \mathrm{~m}$, a man uses a cylindrical bucket with a base diameter of $30 \mathrm{~cm}$ and a height of $48 \mathrm{~cm}$ to fetch water from a spring. Each time he goes to the spring, he fills the bucket to $4 / 5$ of its capacity and spills $10 \%$ of its content on the way. With the tank initially empty, how many trips to the spring will the man have to make so that the water in the tank reaches $3 / 4$ of its height?
 | 17 |
18,738 | ## Task 3 - 040813
On a double-track route to the suburb of a large city, a tram departs from the starting station and from the terminal station every 10 minutes and each requires 50 minutes of travel time. The dwell time at these two stations is 10 minutes each.
How many trams are in operation on this route in total? | 12 |
18,771 | 9. (12 points) Two people, A and B, stand facing each other 30 meters apart, playing "Rock, Paper, Scissors". The winner moves forward 3 meters, the loser moves back 2 meters, and in the case of a tie, both move forward 1 meter. After 15 rounds, A is 17 meters from the starting point, and B is 2 meters from the starting point. How many times did A win? $\qquad$ | 7 |
18,791 | Person A and Person B start from points $A$ and $B$ respectively and walk towards each other. The first time they meet, it is 100 meters away from point $B$. After meeting, Person A doubles their speed. Person A reaches point $B$, turns around immediately, and catches up with Person B when Person B is 50 meters away from point $A$. How long is the distance between points $A$ and $B$? | 250 |
18,866 | Example 3. Solve the equation $y^{\text {IV }}-16 y=0$. | y(x) = C_1 e^{2x} + C_2 e^{-2x} + C_3 \cos(2x) + C_4 \sin(2x) |
18,871 | 4 $[$ Parity and Imparity $]$ $[$ Residue Arithmetic (Miscellaneous) $]$
Solve the equation $x^{2}+y^{2}+z^{2}=2 x y z$ in integers.
# | (0, 0, 0) |
18,873 | 3. Find the number of solutions in natural numbers for the equation $(x-4)^{2}-35=(y-3)^{2}$. | 3 |
18,879 | Prove by computation that the volume of the solid obtained by rotating a circular segment with chord \( a \) about a diameter parallel to this chord does not depend on the radius of the circle. | \dfrac{\pi a^3}{6} |
18,880 | 3.129. $\sin \left(\frac{5}{2} \pi-2 \alpha\right)+2 \sin ^{2}\left(2 \alpha-\frac{3}{2} \pi\right)-1$. | 2 \cos 3\alpha \cos \alpha |
18,881 | The intersection of two squares with perimeter $8$ is a rectangle with diagonal length $1$. Given that the distance between the centers of the two squares is $2$, the perimeter of the rectangle can be expressed as $P$. Find $10P$. | 25 |
18,888 | Four. (25 points) There are several (more than enough) socks in red, yellow, blue, and white. If any two socks of the same color can make 1 pair, the question is: What is the minimum number of socks needed to ensure that 10 pairs of socks can be formed? | 23 |
18,890 | 9.4. Vasya, a truant, skipped one lesson every Monday in September, two lessons every Tuesday, three on Wednesday, four on Thursday, and five on Friday. The exception was September 1: on this day, Vasya did not skip any lessons in honor of the start of the school year. It turned out that Vasya missed exactly 64 lessons for the entire month of September. What day of the week was September 1? Justify your answer. (All Saturdays and Sundays in September were holidays, and the other days were school days.) | Wednesday |
18,937 | Prove that if in triangle $ABC$ angle $B$ is obtuse and $|AB| = |AC| / 2$, then $\angle C > \angle A / 2$. | \angle C > \frac{\angle A}{2} |
18,956 | Sasha wrote down numbers from one to one hundred, and Misha erased some of them. Among the remaining numbers, 20 contain the digit one, 19 contain the digit two, and 30 contain neither one nor two. How many numbers did Misha erase? | 33 |
18,967 | Compute the sum $S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{1-3 x_{i}+3 x_{i}^{2}}$ for $x_{i}=\frac{i}{101}$. | 51 |
18,979 | 8. Given $x, y>0$, and $x+2 y=2$. Then the minimum value of $\frac{x^{2}}{2 y}+\frac{4 y^{2}}{x}$ is $\qquad$ . | 2 |
18,985 | 16 The sum of $\frac{1}{2 \times 3 \times 4}+\frac{1}{3 \times 4 \times 5}+\frac{1}{4 \times 5 \times 6}+\ldots+\frac{1}{13 \times 14 \times 15}+\frac{1}{14 \times 15 \times 16}$ is $\frac{m}{n}$ in its lowest terms. Find the value of $m+n$. | 173 |
18,993 | Tokarev S.I.
Doughnut was snacking at a roadside cafe when a bus drove past him. Three doughnuts after the bus, a motorcycle passed Doughnut, and another three doughnuts later, a car passed. Past Syrup, who was snacking at another cafe on the same road, they drove by in a different order: first the bus, three doughnuts later the car, and another three doughnuts later the motorcycle. It is known that Doughnut and Syrup always eat doughnuts at the same constant speed. Find the speed of the bus if the speed of the car is 60 km/h and the speed of the motorcycle is 30 km/h. | 40 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.