id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
52,836 | 4.1. (14 points) How many six-digit numbers exist whose sum of digits equals 51? | 56 |
52,838 | Example 11 For real number $x$, find the maximum value of the function $f(x)=$ $\sqrt{8 x-x^{2}}-\sqrt{14 x-x^{2}-48}$. | 2\sqrt{3} |
52,839 | Example 6 Given a complex number $z$ satisfying $|z|=1$, try to find the maximum value of $u=\left|z^{3}-3 z+2\right|$.
(2000 Jilin Province High School Competition) | 3\sqrt{3} |
52,849 | 1. Let $n$ be a natural number, $a, b$ be positive real numbers, and satisfy $a+b=2$, then the minimum value of $\frac{1}{1+a^{n}}+$ $\frac{1}{1+b^{n}}$ is $\qquad$. | 1 |
52,853 | 8,9 Given a parallelogram $A B C D$. A line passing through vertex $C$ intersects lines $A B$ and $A D$ at points $K$ and $L$. The areas of triangles $K B C$ and $C D L$ are $p$ and $q$. Find the area of parallelogram $A B C D$. | 2\sqrt{pq} |
52,860 | [ Classical combinatorics (miscellaneous).] $[\quad$ Case enumeration $\quad]$
Find all odd natural numbers greater than 500 but less than 1000, for each of which the sum of the last digits of all divisors (including 1 and the number itself) is 33. | 729 |
52,880 | 3. Given the sequences $\left\{a_{n}\right\},\left\{b_{n}\right\}$ are both arithmetic sequences, the sequence $\left\{c_{n}\right\}$ satisfies $c_{n}=a_{n} b_{n}\left(n \in \mathbf{N}^{*}\right)$. If $c_{1}=1440, c_{2}=1716, c_{3}=1848$, then $c_{8}=$ $\qquad$ . | 348 |
52,891 | 39. In a chess tournament, each of the 8 participants plays one game with each other. All participants scored a different number of points (an integer), and the second-place finisher scored as many points as all the chess players who finished from fifth to eighth place combined. How did the players who finished in third and fifth place play against each other? | 1 |
52,892 | List 3. From $1,2,3, \cdots, 14$, select $a_{1}, a_{2}, a_{3}$ in ascending order, such that $a_{2}-a_{1} \geqslant 3, a_{3}-a_{2} \geqslant 3$. How many different ways are there to select the numbers that meet the above requirements? (1389, National High School League) | 120 |
52,896 | 1. Find the largest natural number $n$ with the following property: for any odd prime $p$ less than $n$, the difference $n-p$ is also a prime number.
(I. Akulich) | 10 |
52,901 | [Intersecting lines, angle between them]
Let $A B C$ be an equilateral triangle, and $B C K M$ be a parallelogram. Find the angle between the lines $A B$ and $K M$.
# | 60 |
52,907 | Problem 9.7. Two parallel lines are drawn through points $A(0 ; 14)$ and $B(0 ; 4)$. The first line, passing through point $A$, intersects the hyperbola $y=\frac{1}{x}$ at points $K$ and $L$. The second line, passing through point $B$, intersects the hyperbola $y=\frac{1}{x}$ at points $M$ and $N$.
What is $\frac{A L-A K}{B N-B M}$ ?
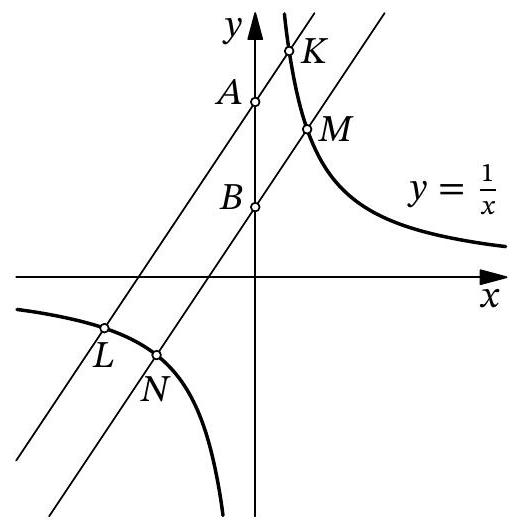 | 3.5 |
52,943 | 1 Let $w=-\frac{1}{2}+\frac{\sqrt{3}}{2} \cdot i\left(i^{2}=-1\right)$, then the number of different values that the algebraic expression $w^{m}+w^{n}+w^{l}(m, n, l$ are pairwise distinct integers) can take is $\qquad$ . | 10 |
52,962 | 2. The little squirrel has several bags of nuts. In two bags, there are 2 nuts each, in three bags, there are 3 nuts each, in four bags, there are 4 nuts each, and in five bags, there are 5 nuts each. Help the little squirrel arrange the bags on two shelves so that there are an equal number of bags and nuts on each shelf. | 27 |
52,970 | 1. Answer: $2019^{2021} \cdot 2021^{2019}<2020^{2020} \cdot 2020^{2020}$. | 2019^{2021}\cdot2021^{2019}<2020^{2020}\cdot2020^{2020} |
52,994 | ## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{n^{2}-\sqrt{n^{3}+1}}{\sqrt[3]{n^{6}+2}-n}$ | 1 |
53,013 | 10. Determine the value of
$$
2002+\frac{1}{2}\left(2001+\frac{1}{2}\left(2000+\cdots+\frac{1}{2}\left(3+\frac{1}{2} \cdot 2\right)\right) \cdots\right)
$$ | 4002 |
53,018 | 2. Let $a, b, c \geqslant 1$, and positive real numbers $x, y, z$ satisfy
$$
\left\{\begin{array}{l}
a^{x}+b^{y}+c^{z}=4, \\
x a^{x}+y b^{y}+z x^{z}=6, \\
x^{2} a^{x}+y^{2} b^{y}+z^{2} c^{z}=9 .
\end{array}\right.
$$
Then the maximum possible value of $c$ is $\qquad$ | \sqrt[3]{4} |
53,026 | 1. Let $n!=1 \times 2 \times \cdots \times n,[x]$ denote the greatest integer not exceeding the real number $x$. Then the positive integer solution to the equation
$$
\left[\frac{x}{1!}\right]+\left[\frac{x}{2!}\right]+\cdots+\left[\frac{x}{10!}\right]=3468
$$
is $\qquad$ | 2020 |
53,030 | 13. Given a right triangle, one of whose acute angles is equal to $\alpha$. Find the ratio of the radii of the circumscribed and inscribed circles and determine for which $\alpha$ this ratio will be the smallest? | \sqrt{2}+1 |
53,034 | Example 14. As shown in Figure 14; $P$ is a point inside an equilateral triangle $ABC$, and $PA=3, PB=4, PC=5$. Find the side length of this equilateral triangle. | \sqrt{25+12 \sqrt{3}} |
53,056 | 8. The solution set of the inequality
$$
\frac{4 x^{2}}{(1-\sqrt{1+2 x})^{2}}<2 x+9
$$
is $\qquad$ . | [-\frac{1}{2},0)\cup(0,\frac{45}{8}) |
53,058 | 4. A box contains two white socks, three blue socks and four grey socks. Rachel knows that three of the socks have holes in, but does not know what colour these socks are. She takes one sock at a time from the box without looking. How many socks must she take for her to be certain she has a pair of socks of the same colour without holes? | 7 |
53,081 | 4. A line segment of length 18 is randomly divided into three segments. The probability that these three segments can form a triangle is $\qquad$ . | 0.25 |
53,103 | From four identical squares, an ornament was created as shown in the picture. The sides of the squares are $4 \mathrm{~cm}$ long, and they are either parallel or perpendicular to each other, intersecting either at their quarters or halves. Libor wanted to color the ornament and found that the cost of the paint for $1 \mathrm{~cm}^{2}$ of each contiguous area would be as many crowns as the number of squares that area is shared by.
How many crowns will it cost to paint the ornament?
(K. Pazourek)
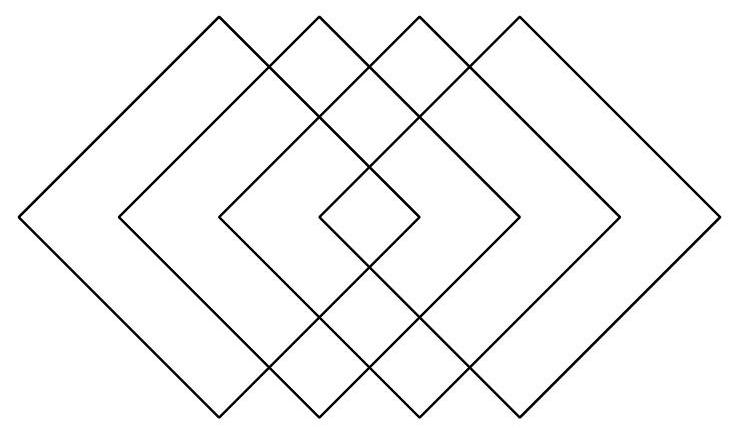 | 64 |
53,140 | ## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{\sqrt{n+1}-\sqrt[3]{n^{3}+1}}{\sqrt[4]{n+1}-\sqrt[5]{n^{5}+1}}$ | 1 |
53,172 | G1.2 In figure $1, A B$ is parallel to $D C, \angle A C B$ is a right angle, $A C=C B$ and $A B=B D$. If $\angle C B D=b^{\circ}$, find the value of $b$. | 15 |
53,190 | Problem 6. An excursion group of 6 tourists is visiting attractions. At each attraction, three people take photos, while the others photograph them. After what minimum number of attractions will each tourist have photos of all other participants in the excursion?
Answer: after 4 attractions. | 4 |
53,196 | 3. Let $x_{1}$ and $x_{2}$ be the largest roots of the polynomials $f(x)=1-x-4 x^{2}+x^{4}$ and $g(x)=16-8 x-$ $16 x^{2}+x^{4}$ respectively. Find $\frac{x_{2}}{x_{1}}$. | 2 |
53,207 | 1. Given 2117 cards, on which natural numbers from 1 to 2117 are written (each card has exactly one number, and the numbers do not repeat). It is required to choose two cards such that the sum of the numbers written on them is divisible by 100. In how many ways can this be done? | 22386 |
53,210 | How many distinct values can $x^{9}$ take modulo 999? | 15 |
53,215 | 10. Arrange all positive integers that are coprime with 70 in ascending order, the 2017th term of this sequence is $\qquad$ . | 5881 |
53,222 | 4A. Given a parallelogram $A B C D$. The bisector of $\angle D A B$ intersects side $D C$ at point $L$, and diagonal $B D$ at point $K$, such that $\overline{D K}: \overline{K B}=3: 4$. Calculate the length of segment $L C$, if the perimeter of the parallelogram is 28. | 2 |
53,236 | Problem 4. In a box, there are 50 cards on which the first 100 non-zero natural numbers are written, as follows: on the first card, the numbers 1 (on one side) and 2 (on the other side) are written, on the second card, the numbers 3 (on one side) and 4 (on the other side) are written, and so on, up to the 50th card, on which the numbers 99 (on one side) and 100 (on the other side) are written.
Eliza takes out four cards from the box and calculates the sum of the eight numbers written on them. How many distinct sums can Eliza obtain? | 185 |
53,243 | 3. A non-empty finite set whose sum of the squares of all elements is odd is called a trivial set. If the set $A=\{1,2,3, \cdots, 2016,2017\}$, then the number of trivial sets among all proper subsets of $A$ is $\qquad$ (powers of numbers are allowed in the answer). | 2^{2016}-1 |
53,248 | Example 1. A person earns a monthly salary of 200 yuan and receives a bonus of 20 yuan at the end of the month. After receiving the salary each month, they arrange the monthly expenses according to $\frac{4}{5}$ of the current savings. How much will be the remaining balance in the twelfth month? | 75 |
53,252 | \section*{Problem 1 - 331021}
Determine whether there exists a four-digit square number \(q\) with the following properties (1), (2)! If such numbers exist, find all such square numbers!
(1) All four digits of \(q\) are less than 7.
(2) If each digit of \(q\) is increased by 3, the resulting four-digit number is also a square number. | 1156 |
53,277 | 1. [5] 2021 people are sitting around a circular table. In one move, you may swap the positions of two people sitting next to each other. Determine the minimum number of moves necessary to make each person end up 1000 positions to the left of their original position. | 1021000 |
53,286 | 4. In $\triangle A B C$, $A B=1, B C=2, \angle B-\angle C$ $=90^{\circ}$. Then the radius of the circumcircle of $\triangle A B C$ is $\qquad$ | \frac{\sqrt{3}+1}{2} |
53,337 | Brad answers 10 math problems, one after another. He answers the first problem correctly and answers the second problem incorrectly. For each of the remaining 8 problems, the probability that he answers the problem correctly equals the ratio of the number of problems that he has already answered correctly to the total number of problems that he has already answered. What is the probability that he answers exactly 5 out of the 10 problems correctly? | \frac{1}{9} |
53,338 | 6. Let $\mathrm{A}, \mathrm{B}, \mathrm{C}$ be the three interior angles of $\triangle \mathrm{ABC}$, then the maximum value of the real number $\lambda$ such that $\frac{1}{\sin A}+\frac{1}{\sin B} \geq \frac{\lambda}{3+2 \cos C}$ always holds is $\qquad$ ; | 8 |
53,360 | [Integer and fractional parts. Archimedes' principle]
How many solutions in natural numbers does the equation $\left[{ }^{x} / 10\right]=\left[{ }^{x} / 11\right]+1$ have? | 110 |
53,363 | ## Task B-3.6.
A parallelogram with diagonals of length $20 \mathrm{~cm}$ and $30 \mathrm{~cm}$ that intersect at an angle of $60^{\circ}$ is the base of a right prism with a volume of $1500 \sqrt{3} \mathrm{~cm}^{3}$. What is the surface area of this prism? | 300\sqrt{3}+100\sqrt{19}+100\sqrt{7} |
53,380 | Example 1 Try to compare $\sqrt[3]{3-\sqrt[3]{3}}+\sqrt[3]{3+\sqrt[3]{3}}$ and $2 \sqrt[3]{3}$. | \sqrt[3]{3-\sqrt[3]{3}}+\sqrt[3]{3+\sqrt[3]{3}}<2\sqrt[3]{3} |
53,412 | 75. The three-digit numbers $\overline{a b c}$ and $\overline{c b a}$ form a pair of reverse-order numbers (such as 123 and 321, 778 and 877). If the difference between the two numbers in a reverse-order pair is 297, how many such reverse-order pairs are there? | 60 |
53,414 | 17. Positive integers $m, n$ make the inequality $|m x-840| \geq|x-n|$ always hold for $x$, then the minimum value of $m+n$ is $\qquad$ . | 58 |
53,415 | 5. For a given positive integer $n$, the number of integer points in the closed region (including the boundary) formed by the line $y=$ $n^{2}$ and the parabola $y=x^{2}$ is $\qquad$ | \frac{1}{3}(2 n+1)\left(2 n^{2}-n+3\right) |
53,416 | In triangle $K L M$, the ratio of the radii of the circumscribed and inscribed circles is 3. The inscribed circle touches the sides of triangle $K L M$ at points $A, B$, and $C$. Find the ratio of the area of triangle $K L M$ to the area of triangle $A B C$.
# | 6 |
53,419 | 3. A traveler visited a village where every person either always tells the truth or always lies. The villagers stood in a circle, and each one told the traveler whether the neighbor to their right was truthful or a liar. Based on these statements, the traveler was able to determine unequivocally what fraction of the village's population consists of truthful people. Determine what this fraction is. | \frac{1}{2} |
53,423 | 12. Given four integers $a, b, c, d$ are all even, and $0<a<b<c<d, d-a=90$, if $a, b, c$ form an arithmetic sequence, and $b, c, d$ form a geometric sequence, then $a+b+c+d=$ $\qquad$ . | 194 |
53,438 | 19.2.1 * Find the sum of all positive rational numbers less than 10 that, when written as reduced fractions, have a denominator of 30. | 400 |
53,446 | 1. Given vectors $\overrightarrow{A P}=(1, \sqrt{3}), \overrightarrow{P B}=(-\sqrt{3}, 1)$, then the angle between vector $\overrightarrow{A P}$ and $\overrightarrow{A B}$ is $\qquad$ | \frac{\pi}{4} |
53,459 | [Coordinate method in space]
Find the angle between the line passing through points $A(-3 ; 0 ; 1)$ and $B(2 ; 1 ;-1)$, and the line passing through points $C(-2 ; 2 ; 0)$ and $D(1 ; 3 ; 2)$. | \arccos\frac{2\sqrt{105}}{35} |
53,470 | [ Sum of angles in a triangle. Theorem about the exterior angle. ] [ Criteria and properties of an isosceles triangle. ]
In triangle $A B C$, angle $C$ is three times angle $A$. A point $D$ is taken on side $A B$ such that $B D=B C$.
Find $C D$, if $A D=4$. | 4 |
53,508 | 21. Determine the maximum number of different sets consisting of three terms which form an arithmetic progressions that can be chosen from a sequence of real numbers $a_{1}, a_{2}, \ldots, a_{101}$, where
$$
a_{1}<a_{2}<a_{3}<\cdots<a_{101} .
$$ | 2500 |
53,515 | Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
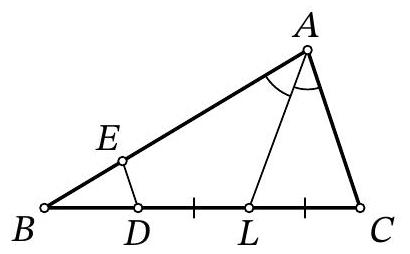 | 3 |
53,530 | 7.1 On the Island of Truth and Lies, there are knights who always tell the truth, and liars who always lie. One day, 20 residents of the island lined up by height (from tallest to shortest, the tallest being the first) for a game. Each had to say one of the following phrases: "There is a liar below me" or "There is a knight above me." In the end, those standing from the third to the seventh position said the first phrase, while the rest said the second. How many knights were among these 20 people, given that all residents have different heights? | 17 |
53,545 | 3. Let $x_{k}=\tan \frac{k \pi}{17}(k=1,2, \cdots, 16)$. Then $\sum_{k=1}^{16} \frac{1}{1+x_{k}^{2}}=$ $\qquad$ | \frac{15}{2} |
53,569 | Example 4 If real numbers $a, b$ satisfy the conditions
$$
a^{2}+b^{2}=1,|1-2 a+b|+2 a+1=b^{2}-a^{2} \text {, }
$$
then $a+b=$ $\qquad$
(2009, National Junior High School Mathematics Joint Competition) | -1 |
53,570 | Example 4 Choose $k$ numbers from $1,2, \cdots, 2004$, such that among the chosen $k$ numbers, there are definitely three numbers that can form the side lengths of a triangle (the three numbers must be distinct). What is the minimum value of $k$ that satisfies this condition? | 17 |
53,582 | # Problem 3. (3 points)
The sequence is defined by the formula $x_{n+3}=2 x_{n+2}+x_{n+1}-2 x_{n}$. Additionally, it is known that $x_{0}=0$, $x_{2}=1$. Find $x_{100}$ | \frac{4^{50}-1}{3} |
53,599 | 9.2. Solve the system of equations
$$
\left\{\begin{aligned}
10 x^{2}+5 y^{2}-2 x y-38 x-6 y+41 & =0 \\
3 x^{2}-2 y^{2}+5 x y-17 x-6 y+20 & =0
\end{aligned}\right.
$$ | 2,1 |
53,601 | 10. Define the "coordinate distance" between two points $P\left(x_{1}, y_{1}\right), Q\left(x_{2}, y_{2}\right)$ as: $d(P, Q)=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|$. If the "coordinate distance" from $C(x, y)$ to points $A(1,3), B(6,9)$ is equal, where the real numbers $x, y$ satisfy $0 \leqslant x \leqslant 10,0 \leqslant y \leqslant 10$, then the sum of the lengths of all possible trajectories of point $C$ is $\qquad$. | 5+5\sqrt{2} |
53,614 | \section*{Problem 6A - 141236A}
A measurement complex \(M\) integrated into an industrial process transmits to a transmission unit \(A_{1}\) exactly one of the two signals \(S_{1}\) or \(S_{2}\), which is then transmitted from \(A_{1}\) to a transmission unit \(A_{2}\), from \(A_{2}\) to a transmission unit \(A_{3}\), and from \(A_{3}\) to an electronic computer \(R\).
Each transmission unit \(A_{i} (i=1,2,3)\) can transmit exactly the signals \(S_{1}\) or \(S_{2}\). The probability that \(A_{i}\) transmits the other signal instead of the one it received is 0.01.
It is now known that at the end of such a process, transmitted through \(A_{3}\) to the computer \(R\), the signal \(S_{1}\) was transmitted.
What is the probability that \(M\) transmitted \(S_{1}\) to \(A_{1}\) at the beginning of this process?
Hint:
If under certain conditions \(V\), in a large number \(n\) of cases, a total of \(g\) cases occur in which an event \(E\) occurs or has occurred, then the number \(p=\frac{g}{n}\) is the probability of the occurrence (or having occurred) of \(E\) under the conditions \(V\).
For the solution, the following theorems can also be used.
a) Addition rule of probability for independent events: The probability that one of two mutually exclusive events \(E_{1}\) and \(E_{2}\) occurs is equal to the sum \(p_{1}+p_{2}\) of the probability \(p_{1}\) of the occurrence of \(E_{1}\) and the probability \(p_{2}\) of the occurrence of \(E_{2}\).
b) Multiplication rule of probability: The probability that an event \(E\) and an event \(F\) occur is equal to the product \(p \cdot q\) of the probability \(p\) of the occurrence of \(E\) and the probability \(q\) that \(F\) occurs given \(E\). | 0.970596 |
53,620 | $5 \cdot 77$ The team leader assigns 9 or 10 people from 33 team members to duty every night. How many days at least are needed so that each member has the same number of duty shifts? | 7 |
53,625 | SI. 1 Let $[x]$ be the largest integer not greater than $x$. If $a=\left[(\sqrt{3}-\sqrt{2})^{2009}\right]+16$, find the value of $a$. | 16 |
53,629 | 82 To make the inequality $0 \leqslant x^{2}+a x+5 \leqslant 4$ have exactly one solution, then $a=$ | \2 |
53,642 | ## Task 6 - 130936
Given a regular tetrahedron with vertices $A, B, C, D$ and edge length $a$. A point $D^{\prime}$ should have the following properties:
a) The tetrahedron with vertices $A, B, C, D^{\prime}$ is of equal volume to the given tetrahedron, b) $B D^{\prime}=C D^{\prime}=a$, c) $A D^{\prime} \neq a$.
Investigate whether such points $D^{\prime}$ exist, and determine for each such $D^{\prime}$ the length of the edge $A D^{\prime}$. | \sqrt{2} |
53,654 | ## Task $1 / 86$
We are looking for the smallest natural number $n$, which is the product of 3 prime factors $p_{1} ; p_{2} ; p_{3}$, and it holds that: $p_{3}=55 \cdot p_{1} \cdot p_{2}+1$ and $p_{3}>p_{2}>p_{1}$. | 1986 |
53,662 | Let's determine the range of the function
$$
f(x)=\frac{4-3 \sin ^{6} x-3 \cos ^{6} x}{\sin x \cos x}
$$
in the interval $\left(0, \frac{\pi}{2}\right)$. | [6,\infty) |
53,683 | 8. (1991 National High School Mathematics League Question) Let the set $M=\{1,2, \cdots, 1000\}$, and for any non-empty subset $X$ of $M$, let $a_{x}$ denote the sum of the largest and smallest numbers in $X$. Then, the arithmetic mean of all such $a_{x}$ is $\qquad$ . | 1001 |
53,690 | 9. Let $O A B C$ be a regular tetrahedron with edge length 1, and let $E$ and $F$ be the midpoints of $A B$ and $O C$, respectively. Then the distance between the skew lines $\mathrm{OE}$ and $\mathrm{BF}$ is $\qquad$ | \frac{\sqrt{10}}{10} |
53,716 | [ Midline of a trapezoid ] $[$ Area of a trapezoid $]$
Find the area of trapezoid $A B C D$ with side $B C=5$, if the distances from vertices $A$ and $D$ to line $B C$ are 3 and 7, respectively. | 25 |
53,736 | 382. In a rectangular coordinate system $x O y$, a ray is randomly drawn (at an arbitrary angle $t$) from the point $A(4 ; 0)$, intersecting the $O y$ axis. Find the density $g(y)$ of the probability distribution of the ordinate $y$ of the intersection point of the drawn ray with the $O y$ axis. | (y)=\frac{4}{\pi(16+y^{2})} |
53,767 | Task 1 - 110931 Günter tells:
"I remember our school's six-digit phone number like this:
I write down our two-digit house number. Behind it, I write the cross sum of the house number and then add the sum of the last two digits written each time, until six digits stand. By the way, there is no one in the phone number of our school, and our house number is a number divisible by 3."
What is Günter's house number and what is the phone number of his school? | 303369 |
53,773 | A line parallel to side $AB$ of triangle $ABC$ intersects side $BC$ at point $M$ and side $AC$ at point $N$. The area of triangle $MCN$ is twice the area of trapezoid $ABMN$. Find $CM: MB$. | 2+\sqrt{6} |
53,800 | Task 2. What is the smallest natural number that is divisible by 2022 and whose notation starts with 2023? | 20230110 |
53,801 | 4. Given $\frac{1}{\cos \theta}-\frac{1}{\sin \theta}=\frac{4}{3}, 0<\theta<\frac{\pi}{2}$. Then $\theta=$ | \frac{1}{2}\left(\pi-\arcsin \frac{3}{4}\right) |
53,815 | What is the minimum number of sportlotto cards (6 out of 49) you need to buy to ensure that at least one number is guessed correctly in at least one of them?
# | 8 |
53,816 | 1. (2 points) Boy Vasya wrote down the non-zero coefficients of the polynomial $P(x)$ of the ninth degree in his notebook. Then he calculated the derivative of the resulting polynomial and wrote down its non-zero coefficients, and so on, until he obtained a constant, which he also wrote down.
What is the smallest number of different numbers he could have obtained?
Coefficients are written with their sign, constant terms are also written if there is a monomial of the form $\pm x^{n}$, $\pm 1$ is written.
Answer: 9 | 9 |
53,834 | 10.343. Determine the area of a triangle if two of its sides are 35 and 14 cm, and the bisector of the angle between them is 12 cm. | 235.2 |
53,841 | Circles with radii 2 and 6 have centers at points $O_{1}$ and $O_{2}$, respectively, and touch each other externally at point $C$. A common external tangent and a common internal tangent are drawn to the circles. These tangents intersect at point $D$. Find the radius of the circle inscribed in triangle $O_{1} O_{2} D$.
# | 2(\sqrt{3}-1) |
53,873 | 3. Given $x, y > 0$. If
$$
f(x, y)=\left(x^{2}+y^{2}+2\right)\left(\frac{1}{x+y}+\frac{1}{x y+1}\right) \text {, }
$$
then the minimum value of $f(x, y)$ is . $\qquad$ | 4 |
53,906 | 1. Let the set $P_{n}=\{1,2, \cdots, n\}\left(n \in \mathbf{Z}_{+}\right)$. Denote $f(n)$ as the number of sets $A$ that satisfy the following conditions:
(1) $A \subseteq P_{n}, \bar{A}=P_{n} \backslash A$;
(2) If $x \in A$, then $2 x \notin A$;
(3) If $x \in \bar{A}$, then $2 x \notin \bar{A}$.
Then $f(2018)=$ $\qquad$ | 2^{1009} |
53,966 | 4. Flea Kuzya can make jumps from each vertex of a regular tetrahedron $A B C D$ to the three adjacent vertices, and the choice of these vertices is random and equally probable. Kuzya started jumping from vertex $A$ and, after 2024 jumps, ended up not in vertex $A$. What is the probability that this could happen? | \frac{3^{2024}-1}{4\cdot3^{2023}} |
53,983 | 2. Given is $\triangle A B C$. A line parallel to $A C$ intersects side $A B$ at point $P$, the median $A A_{1}$ at point $K$, and side $B C$ at point $L$. If $P K=7$ and $K L=5$, determine the length of side $A C$. | 19 |
53,998 | 11.069. The lateral edge of a regular triangular prism is equal to the height of the base, and the area of the section made through this lateral edge and the height of the base is $Q$. Determine the volume of the prism. | Q\sqrt{Q/3} |
54,015 | Let $A B C$ be a triangle such that $\frac{|B C|}{|A B|-|B C|}=\frac{|A B|+|B C|}{|A C|}$. Determine the ratio $\angle A: \angle C$. | 1:2 |
54,022 | 1. Two ordered pairs $(a, b)$ and $(c, d)$, where $a, b, c, d$ are real numbers, form a basis of the coordinate plane if $a d \neq b c$. Determine the number of ordered quadruples $(a, b, c, d)$ of integers between 1 and 3 inclusive for which $(a, b)$ and $(c, d)$ form a basis for the coordinate plane. | 66 |
54,027 | Let's find those square numbers which, when divided by 11 with a remainder, the quotient is a prime number and the remainder is 4. | 81 |
54,031 | 5. Two people toss a coin: one tossed it 10 times, and the other 11 times. Find the probability that the second person gets more heads than the first. | \frac{1}{2} |
54,043 | 3. Given numbers $x_{1}, \ldots, x_{n} \in(0,1)$. Find the maximum value of the expression
$$
A=\frac{\sqrt{1-x_{1}}+\ldots+\sqrt{1-x_{n}}}{\sqrt{\frac{1}{x_{1}}+\ldots+\frac{1}{x_{n}}}}
$$ | \frac{\sqrt{n}}{2} |
54,079 | 6. As shown in the figure, $D$ is a point on side $B C$, and $B D=2 D C, D P / / C A$. The area of triangle $A P D$ is $14 \mathrm{~cm}^{2}$, what is the area of triangle $A B C$ in $\mathrm{cm}^{2}$. | 63 |
54,103 | 17. In the diagram below, $A B C D$ is a square. The points $A, B$ and $G$ are collinear. The line segments $A C$ and $D G$ intersect at $E$, and the line segments $D G$ and $B C$ intersect at $F$. Suppose that $D E=15 \mathrm{~cm}, E F=9 \mathrm{~cm}$, and $F G=x \mathrm{~cm}$. Find the value of $x$. | 16 |
54,105 | 12. $f(x)=a x^{2}+b x+c, a, b, c \in \mathbf{R}$, and when $|x| \leqslant 1$, $|f(x)| \leqslant 1$, then when $|x| \leqslant 1$, the maximum value of $|a x+b|$ is $\qquad$ . | 2 |
54,114 | Find all polynomials with real coefficients such that $\forall a, b, c \in \mathbb{R}$,
$$
P(a+b-2 c)+P(b+c-2 a)+P(c+a-2 b)=3 P(a-b)+3 P(b-c)+3 P(c-a)
$$ | P(X)=aX^{2}+bX |
54,116 | Exercise 12. Martin is playing a game. His goal is to place tokens on an 8 by 8 chessboard such that there is at most one token per square, and each column and each row contains at most 4 tokens.
a) What is the maximum number of tokens Martin can place?
b) If, in addition to the previous constraints, each of the two main diagonals can contain at most 4 tokens, what is the maximum number of tokens Martin can place?
The main diagonals of a chessboard are the two diagonals running from one corner of the chessboard to the opposite corner. | 32 |
54,120 | ## SUBJECT 2
Let $\mathrm{x} \in \mathrm{R}$ with $|\mathrm{x}-1| \leq \frac{1}{5}$. Determine $x$ if $\sqrt[3]{(6-5 x)(4 x-3)}+\sqrt[3]{(5 x-4)(5-4 x)}=2$. Prof. Alexandru Cărnaru | 1 |
54,130 | 6 On the $x O y$ plane, the vertices with coordinates $(x, y)$ satisfy $1 \leqslant x \leqslant 4,1 \leqslant y \leqslant 4$, and $x, y$ are integers. The number of triangles is $\qquad$ . | 516 |
54,153 | 10. Given that an infinite arithmetic sequence contains 3 terms (arranged in order but not necessarily consecutive): $13, 25, 41$. Then 2013 $\qquad$ (fill in “is” “is not” or “cannot be determined”) a term in the sequence. | is |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.