id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
50,208 | Find
$$ \inf_{\substack{ n\ge 1 \\ a_1,\ldots ,a_n >0 \\ a_1+\cdots +a_n <\pi }} \left( \sum_{j=1}^n a_j\cos \left( a_1+a_2+\cdots +a_j \right)\right) . $$
| -\pi |
50,262 | 3. Given positive numbers $a, b, c$ satisfying $a+b+c=1$,
then $\sqrt{\frac{(a+b c)(b+c a)}{c+a b}}+\sqrt{\frac{(b+c a)(c+a b)}{a+b c}}+\sqrt{\frac{(c+a b)(a+b c)}{b+c a}}=$ $\qquad$ | 2 |
50,271 | Condition of the problem
Find the derivative.
$$
y=\frac{1}{24}\left(x^{2}+8\right) \sqrt{x^{2}-4}+\frac{x^{2}}{16} \arcsin \frac{2}{x}, x>0
$$ | \frac{x^{3}-x}{8\sqrt{x^{2}-4}}+\frac{x}{8}\cdot\arcsin\frac{2}{x} |
50,304 | Exercise 4. We want to color the three-element subsets of $\{1,2,3,4,5,6,7\}$ such that if two of these subsets have no element in common, then they must be of different colors. What is the minimum number of colors needed to achieve this goal? | 3 |
50,317 | Example 11 Find the minimum value of the bivariate function $f(x, y)=(x-y)^{2}+\left(x+\frac{1}{y}+1\right)^{2}$. | \frac{1}{2} |
50,333 | . In the decimal writing of $A$, the digits appear in (strictly) increasing order from left to right. What is the sum of the digits of $9 A$? | 9 |
50,347 | 4. The range of the function $y=x+\sqrt{x^{2}-3 x+2}$ is | [1,\frac{3}{2})\cup[2,+\infty) |
50,378 | 21st Putnam 1960 Problem A6 A player throws a fair die (prob 1/6 for each of 1, 2, 3, 4, 5, 6 and each throw independent) repeatedly until his total score ≥ n. Let p(n) be the probability that his final score is n. Find lim p(n). Solution | \frac{2}{7} |
50,380 | \section*{Problem 6B - 121236B}
If \(n\) is a natural number greater than 1, then on a line segment \(A B\), points \(P_{1}, P_{2}, P_{3}, \ldots, P_{2 n-1}\) are placed in this order such that they divide the line segment \(A B\) into \(2 n\) equal parts.
a) Give (as a function of \(n\)) the probability that two points \(P_{k}, P_{m}\) chosen from the points \(P_{1}, P_{2}, P_{3}, \ldots, P_{2 n-1}\) with \(0 < k < m < 2 n\) divide the line segment \(A B\) in such a way that a triangle can be constructed from the three segments \(A P_{k}, P_{k} P_{m}, P_{m} B\).
b) Investigate whether this probability converges to a limit as \(n \rightarrow \infty\), and determine this limit if it exists.
Note: The probability sought in a) is defined as follows: Each selection of two points \(P_{k}, P_{m}\) with \(0 < k < m < 2 n\) is referred to as a "case."
A "case" is called a "favorable case" if \(P_{k}\) and \(P_{m}\) are chosen such that a triangle can be formed from the segments \(A P_{k}, P_{k} P_{m}\), and \(P_{m} B\).
If \(z\) is the total number of possible "cases" and \(z_{1}\) is the number of "favorable cases," then the probability is defined as the quotient \(\frac{z_{1}}{z}\). | \frac{1}{4} |
50,419 | One of the sides of the parallelogram is equal to 10, and the diagonals are equal to 20 and 24. Find the cosine of the acute angle between the diagonals.
# | \frac{3}{5} |
50,424 | 8. (10 points) 12 Smurfs are sitting around a round table, each Smurf hates the 2 Smurfs sitting next to him, but does not hate the other 9 Smurfs. Papa Smurf needs to send out a team of 5 Smurfs to rescue Smurfette, who was captured by Gargamel, and the team cannot include Smurfs who hate each other. There are $\qquad$ ways to form the team. | 36 |
50,431 | 3. Find the minimum value of the function $f(x)=\sqrt{\frac{1}{4} x^{4}-2 x^{2}-4 x+13}+\frac{1}{2} x^{2}+\frac{1}{2}$. | \frac{7}{2} |
50,455 | Problem 3. Excellent students Alyosha and Vasya are listing four-digit numbers. Alyosha lists numbers where the first digit is equal to the product of the other three, while Vasya lists numbers where the last digit is equal to the product of the other three. Who will list more numbers and by how many? | 171 |
50,471 | 20. There is a pentagon $A B C D E$. If the vertices $A$, $B$, $C$, $D$, $E$ are colored with one of the three colors: red, yellow, green, such that adjacent vertices are colored differently, then there are a total of different coloring methods. | 30 |
50,489 | Example 1 Add a “+” or “-” in front of each number in $1,2, \cdots, 1989$. Find the minimum non-negative algebraic sum, and write down the equation. | 1 |
50,500 | 6. Two real numbers $a$ and $b$ are randomly chosen from $[-1,1]$. Then the probability that the equation $x^{2}+a x+b=0$ has real roots is $\qquad$ | \frac{13}{24} |
50,511 | 12.309. The base of the prism is a rectangle. The lateral edge forms equal angles with the sides of the base and is inclined to the plane of the base at an angle $\alpha$. Find the angle between the lateral edge and the side of the base. | \arccos\frac{\sqrt{2}\cos\alpha}{2} |
50,521 | ## 6. Light Bulbs
In the room, there are two light bulbs. When the switch of the first light bulb is turned on, it lights up after 6 seconds and stays on for 5 seconds, then it is off for 6 seconds and on for 5 seconds, and this cycle repeats continuously. When the switch of the second light bulb is turned on, it lights up after 4 seconds and stays on for 3 seconds, then it is off for 4 seconds and on for 3 seconds, and this cycle repeats continuously. Linda turned on both switches at the same time and turned them off after 2021 seconds. How many seconds did both light bulbs shine simultaneously during this time?
## Result: 392 | 392 |
50,545 | 4. An $8 \times 6$ grid is placed in the first quadrant with its edges along the axes, as shown. A total of 32 of the squares in the grid are shaded. A line is drawn through $(0,0)$ and $(8, c)$ cutting the shaded region into two equal areas. What is the value of $c$ ? | 4 |
50,595 | The bisector of an angle is a ray originating from the vertex of the angle that divides it into two other congruent angles. For example, in the drawing below, the ray $O C$ is the bisector of the angle $\angle A O B$.
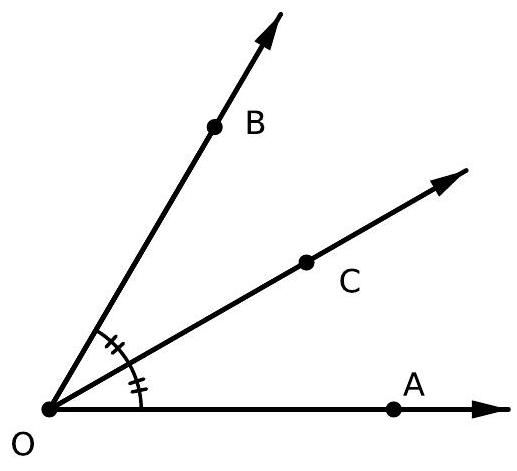
a) The difference between two consecutive but non-adjacent angles is $100^{\circ}$. Determine the angle formed by their bisectors.
Note: Remember that two angles are consecutive if they share the same vertex and at least one side, and that two angles are adjacent if they do not share any interior points.
b) In the drawing below, $D A$ is the bisector of the angle $\angle C A B$. Determine the value of the angle $\angle D A E$ given that $\angle C A B + \angle E A B = 120^{\circ}$ and $\angle C A B - \angle E A B = 80^{\circ}$.
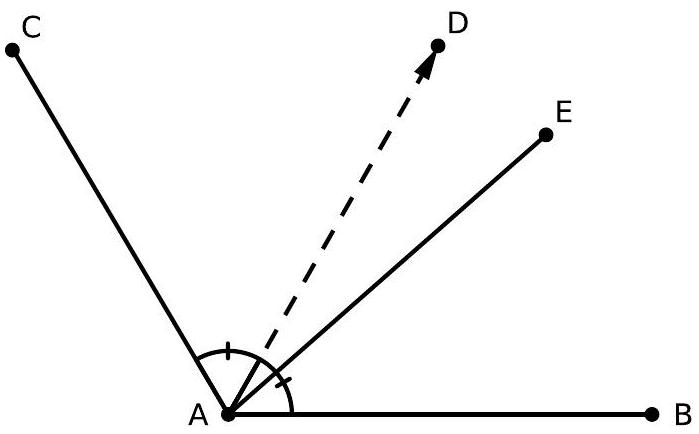 | 30 |
50,598 | 2. (2 points) In the quarry, there was a pile of 20160000 sand grains. A truck carried away from the quarry a quantity of sand grains per trip, which was some power of 8 (including possibly $8^{0}=1$). Could it have carried away the entire pile of sand in exactly 1000 trips? | No |
50,607 | ## 22. Age Difference
The sums of the digits that make up the birth years of Jean and Jacques are equal to each other, and the age of each of them starts with the same digit. Could you determine the difference in their ages? | 9 |
50,615 | 2.150. $\frac{2-\sqrt{2}-\sqrt{3}}{2+\sqrt{2}-\sqrt{3}}$. | \frac{(2\sqrt{6}+1)(3-4\sqrt{2})}{23} |
50,635 | 3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $1,2,3,4,5,6,7,8,9$ (digits can repeat) so that the resulting 12-digit number is divisible by 18. In how many ways can this be done? | 26244 |
50,641 | Senderov V.A.
1999 numbers stand in a row. The first number is 1. It is known that each number, except the first and the last, is equal to the sum of its two neighbors.
Find the last number.
# | 1 |
50,643 | 5. Planet Beta has seven countries, each of which has exactly four friendly countries and two enemy countries. There are no three countries that are all enemies with each other. For such a planetary situation, the number of possible alliances of three countries that are all friendly with each other is $\qquad$. | 7 |
50,651 | 6. Find the greatest real number $k$ such that the inequality
$$
\frac{2\left(a^{2}+k a b+b^{2}\right)}{(k+2)(a+b)} \geqq \sqrt{a b}
$$
holds for all pairs of positive real numbers $a, b$. | 6 |
50,667 | Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}, a_{7}$ be non-negative numbers whose sum is 1. Let $M$ denote the maximum of the quantities $a_{1}+a_{2}+a_{3}, a_{2}+a_{3}+a_{4}, a_{3}+a_{4}+a_{5}$, $a_{4}+a_{5}+a_{6}, a_{5}+a_{6}+a_{7}$.
How small can $M$ be? | \frac{1}{3} |
50,677 | 1. Let $A, B, C, D$ be four points on a circle in that order. Also, $A B=3, B C=5, C D=6$, and $D A=4$. Let diagonals $A C$ and $B D$ intersect at $P$. Compute $\frac{A P}{C P}$. | \frac{2}{5} |
50,703 | 12. Let the set $M=\{1,2, \cdots, 10\}$,
$$
\begin{aligned}
A= & \{(x, y, z) \mid x, y, z \in M, \text { and } \\
& \left.9 \mid\left(x^{3}+y^{3}+z^{3}\right)\right\} .
\end{aligned}
$$
Then the number of elements in set $A$ is $\qquad$ | 243 |
50,726 | 2. From the 1000 natural numbers from 1 to 1000, delete several consecutive natural numbers so that the sum of the remaining numbers is divisible by 2022. The minimum number of numbers to be deleted is $\qquad$. | 4 |
50,739 | 6. All natural numbers, the sum of the digits of each of which is equal to 5, were arranged in ascending order. What number is in the 125th place
# | 41000 |
50,760 | In triangle $ABC$, $\angle BAC = 45^{\circ}$. Let $P$ be the point on side $AC$ closer to $A$ that divides $AC$ into a ratio of $1:2$. We know that $\angle ABP = 15^{\circ}$. What is the measure of $\angle ACB$? | 75 |
50,764 | Folklore
Given a regular nonagon.
In how many ways can three of its vertices be chosen so that they form the vertices of an isosceles triangle? | 30 |
50,772 | 10. (12 points) The figure is composed of 5 identical squares. The number of triangles that can be formed using the 12 points in the figure as vertices is.
保留了原文的换行和格式,以下是翻译结果:
```
10. (12 points) The figure is composed of 5 identical squares. The number of triangles that can be formed using the 12 points in the figure as vertices is.
``` | 200 |
50,775 | 4. For the positive integer $n$, define $a_{n}$ as the unit digit of $n^{(n+1)^{n+2}}$. Then $\sum_{n=1}^{2010} a_{n}=$ $\qquad$ . | 5829 |
50,778 | Let $a_1=24$ and form the sequence $a_n$, $n\geq 2$ by $a_n=100a_{n-1}+134$. The first few terms are
$$24,2534,253534,25353534,\ldots$$
What is the least value of $n$ for which $a_n$ is divisible by $99$? | 88 |
50,793 | $4 \cdot 70$ The sequence of functions $\left\{f_{n}(x)\right\}$ is recursively defined by:
$$
\left\{\begin{array}{l}
f_{1}(x)=\sqrt{x^{2}+48} \\
f_{n+1}(x)=\sqrt{x^{2}+6 f_{n}(x)}
\end{array} \text { for each } n \geqslant 1 .\right.
$$
Find all real solutions to the equation $f_{n}(x)=2 x$. | 4 |
50,794 | Problem 2. In a football tournament, seven teams played: each team played once with each other. In the next round, teams that scored twelve or more points qualify. Three points are awarded for a win, one point for a draw, and zero points for a loss. What is the maximum number of teams that can advance to the next round? | 5 |
50,809 | 2. As shown in the figure, $\odot O$ is tangent to the sides $A B, A D$ of the square $A B C D$ at points $L, K$, respectively, and intersects side $B C$ at points $M, P$, with $B M=8$ cm, $M C=17$ cm. Then the area of $\odot O$ is $\qquad$ square cm. | 169\pi |
50,816 | 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller tells the other party all the news he knows, but is not told anything by the other party. What is the minimum number of calls needed for all five people to know all five items of news? What is the minimum for n people? | 2n-2 |
50,838 | There are $N$ students in a class. Each possible nonempty group of students selected a positive integer. All of these integers are distinct and add up to 2014. Compute the greatest possible value of $N$. | 5 |
50,839 | On the sides $A B$ and $B C$ of an equilateral triangle $A B C$, two points $D$ and $E$ are fixed, respectively, such that $\overline{A D}=\overline{B E}$.
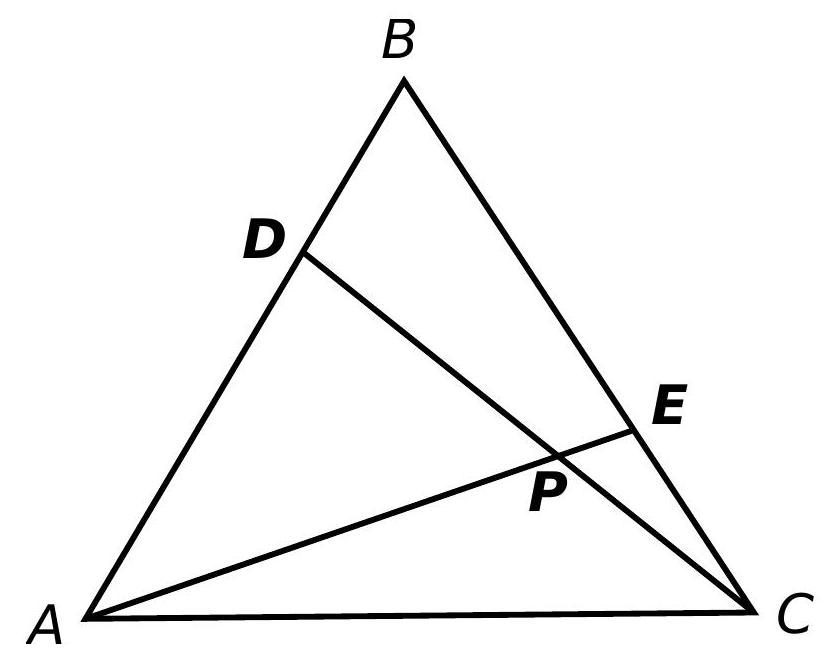
If the segments $A E$ and $C D$ intersect at point $P$, determine $\measuredangle A P C$.
# | 120 |
50,844 | 1.5.2 * Let real numbers $a, x, y$ satisfy the following conditions
$$
\left\{\begin{array}{l}
x+y=2 a-1, \\
x^{2}+y^{2}=a^{2}+2 a-3 .
\end{array}\right.
$$
Find the minimum value that the real number $xy$ can take. | \frac{11-6\sqrt{2}}{4} |
50,851 | Task 4. (20 points) A four-meter gas pipe has rusted in two places. Determine the probability that all three resulting sections can be used as offsets for gas stoves, if according to regulations, the stove should not be located closer than 1 m to the main gas pipe.
# | \frac{1}{16} |
50,866 | How many five-digit numbers are there that end in six and are divisible by three? | 3000 |
50,878 | ## Task Condition
Find the derivative.
$y=\frac{\sqrt{2 x+3}(x-2)}{x^{2}}$ | \frac{-x^{2}+3x+12}{x^{3}\sqrt{2x+3}} |
50,881 | In the quadrilateral $\mathrm{ABCD}$, the following angles are known:
$B A C \angle=50^{\circ}, A B D \angle=60^{\circ}, D B C \angle=20^{\circ}, B D C \angle=30^{\circ}$. Is it true that the angle $C A D$ is $30^{\circ}$? | 30 |
50,882 | 11. (5 points) As shown in the figure, the "L" shaped paper piece with a perimeter of 52 centimeters can be divided into two identical rectangles along the dotted line. If the longest side is 16 centimeters, then the area of the "L" shaped paper piece is $\qquad$ square centimeters. | 120 |
50,886 | 3. (1990 Vietnam Olympiad) Let $a, b, c \in \mathbf{R}^{+}$, and $a b c + a + c = b$, determine the maximum value of $p = \frac{2}{a^{2}+1} - \frac{2}{b^{2}+1} + \frac{3}{c^{2}+1}$. | \frac{10}{3} |
50,893 | Example 5 Find the constant $c$, such that $f(x)=\arctan \frac{2-2 x}{1+4 x}+c$ is an odd function in the interval $\left(-\frac{1}{4}, \frac{1}{4}\right)$. | -\arctan2 |
50,896 | Example 3 In the Cartesian coordinate system $x O y$, given two points $M(-1,2)$ and $N(1,4)$, point $P$ moves on the $x$-axis. When $\angle M P N$ takes the maximum value, find the x-coordinate of point $P$.
(2004 National High School Mathematics Competition Problem) | 1 |
50,901 | 6. Given complex numbers $z_{1}, z_{2}$ satisfy $\left|z_{1}+z_{2}\right|=20,\left|z_{1}^{2}+z_{2}^{2}\right|=16$, then the minimum value of $\left|z_{1}^{3}+z_{2}^{3}\right|$ is | 3520 |
50,908 | 14. On the $x y$-plane, let $S$ denote the region consisting of all points $(x, y)$ for which
$$
\left|x+\frac{1}{2} y\right| \leq 10, \quad|x| \leq 10 \text { and } \quad|y| \leq 10 .
$$
The largest circle centred at $(0,0)$ that can be fitted in the region $S$ has area $k \pi$. Find the value of $k$. | 80 |
50,918 | 3. How many solutions in natural numbers does the equation
$$
(2 x+y)(2 y+x)=2017^{2017} ?
$$ | 0 |
50,929 | 42. Find a six-digit number, the products of which when multiplied by 2, 3, 4, 5, and 6 are written with the same digits as the number itself, but in a different order. | 142857 |
50,932 | ## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
x=(y-2)^{3}, x=4 y-8
$$ | 8 |
50,936 | 18. Let the variable $x$ satisfy the inequality: $x^{2}+b x \leqslant-x(b<-1)$, and the minimum value of $f(x)=x^{2}+b x$ is $-\frac{1}{2}$, find the value of the real number $b$. | -\frac{3}{2} |
50,946 | # 5. Write the given table of numbers so that in each column and each row there is an arithmetic progression:
| $\mathbf{1}$ | | | |
| :--- | :--- | :--- | :--- |
| | | | $\mathbf{6}$ |
| | | $\mathbf{6}$ | |
| | $\mathbf{9}$ | | | | \begin{pmatrix}\hline1&3&5&7\\\hline4.5&5&5.5&6\\\hline8&7&6&5\\\hline11.5&9&6.5&4\\\hline\end{pmatrix} |
50,948 | 3. Write $\mathbf{2 0 1 2}$ as the sum of $N$ distinct positive integers, the maximum value of $N$ is $\qquad$ | 62 |
50,960 | 3. Given $x, y \geq 1, x+y=8$, then the maximum value of $\left|\sqrt{x-\frac{1}{y}}+\sqrt{y-\frac{1}{x}}\right|$ is | \sqrt{15} |
50,967 | ## Task 1 - 090731
Imagine all natural numbers from 1 to 2555, each written exactly once. Determine the total number of the digit 9 that would need to be written! | 705 |
50,990 | \left.\begin{array}{l}{[\quad \text { Pythagorean Theorem (direct and inverse). }} \\ \text { [ The ratio in which the bisector divides the side. }]\end{array}\right]
The height of a triangle, equal to 2, divides the angle of the triangle in the ratio 2:1, and the base of the triangle - into parts, the smaller of which is equal to 1. Find the area of the triangle. | \frac{11}{3} |
51,006 | Find all primes that can be written both as a sum and as a difference of two primes (note that $ 1$ is not a prime). | 5 |
51,027 | (solved by Alice Héliou). Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying:
$$
f\left(x^{2}-y^{2}\right)=(x-y)(f(x)+f(y))
$$
for all real numbers $x$ and $y$. | f(x)=kx |
51,028 | Example 3 Let $a, b, c$ be positive numbers, and $abc=1$, find the minimum value of $\frac{1}{2a+1}+\frac{1}{2b+1}+\frac{1}{2c+1}$. | 1 |
51,031 | 2.1. How many terms will there be if we expand the expression $\left(4 x^{3}+x^{-3}+2\right)^{2016}$ and combine like terms? | 4033 |
51,052 | 3. (7 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $12$, and $\sin \alpha = \frac{\sqrt{35}}{6}$? | 4 |
51,059 | 17. Find the largest natural number that cannot be represented as the sum of two composite numbers. (Recall that a natural number is called composite if it is divisible by some natural number other than itself and one.) | 11 |
51,066 | 6. The sequence $\left\{x_{n}\right\}: 1,3,3,3,5,5,5,5,5, \cdots$ is formed by arranging all positive odd numbers in ascending order, and each odd number $k$ appears consecutively $k$ times, $k=1,3,5, \cdots$. If the general term formula of this sequence is $x_{n}=a[\sqrt{b n+c}]+d$, then $a+b+c$ $+d=$ | 3 |
51,072 | ## 1. Six-digit number
Each digit of the six-digit number, starting from the thousands place, is equal to the sum of the two preceding digits (which are to its left). What is the three-digit ending of the largest number with this property?
Result: $\quad 369$ | 369 |
51,078 | Determine the minimum number of lines that can be drawn on the plane so that they intersect in exactly $200$ distinct points.
(Note that for $3$ distinct points, the minimum number of lines is $3$ and for $4$ distinct points, the minimum is $4$) | 21 |
51,107 | ## Task Condition
Find the derivative of the specified order.
$$
y=x \ln (1-3 x), y^{(I V)}=?
$$ | -\frac{54(4-3x)}{(1-3x)^{4}} |
51,131 | Task B-4.4. Determine all natural numbers $a$ for which the number $a^{3}+1$ is a power of 3. | 2 |
51,166 | 4. If $|\mathrm{a}| \geqslant 1$, then the range of $\operatorname{arctg} \frac{1}{a}$ is | \left[-\frac{\pi}{4}, 0\right) \cup\left(0, \frac{\pi}{4}\right] |
51,177 | 6. Given that the three sides of triangle $A B C$ are all positive integers, if $\angle A=2 \angle B$, and $C A=9$, then the minimum possible value of $B C$ is $\qquad$ . | 12 |
51,187 | (11) (25 points) The sum of $n$ positive integers $x_{1}, x_{2}, \cdots, x_{n}$ is 2009. If these $n$ numbers can be divided into 41 groups with equal sums and also into 49 groups with equal sums, find the minimum value of $n$.
| 89 |
51,223 | B3. In triangle ABC, the angle $\alpha=58^{\circ}$ and the angle $\beta=84^{\circ}$. What is the measure of angle $x$ between the angle bisector of $\gamma$ and the altitude to side $c$? | 13 |
51,233 | Problem 5. (20 points) Solve the inequality $202 \sqrt{x^{3}-3 x-\frac{3}{x}+\frac{1}{x^{3}}+5} \leq 0$.
# | \frac{-1-\sqrt{21}\\sqrt{2\sqrt{21}+6}}{4} |
51,255 | 3. Given the circle $C: x^{2}+y^{2}=24$, the line $l: \frac{x}{12}+\frac{y}{8}=1$, and point $P$ on $l$, the ray $O P$ intersects the circle at point $R$. Point $Q$ is on $O P$ and satisfies: $|O Q| \cdot|O P|=|O R|^{2}$. When point $P$ moves along $l$, find the equation of the trajectory of point $Q$ and describe what kind of curve the trajectory is. | (x-1)^{2}+(y-\frac{3}{2})^{2}=\frac{13}{4} |
51,266 | 2. The chords $AB$ and $CD$ of a circle intersect at a right angle. The lengths of the chords $AD=60$ and $BC=25$ are known. Calculate the radius of the circle. | \frac{65}{2} |
51,284 | 6. Given that for all $x \in[-1,1]$, we have $x^{3}-a x+1 \geqslant 0$.
Then the range of the real number $a$ is $\qquad$ . | [0,\frac{3\sqrt[3]{2}}{2}] |
51,292 | 10. (12 points) The preliminary plan view of the CCTV headquarters building is shown in the figure below. In the figure, $A B C D E F$ is a regular hexagon with an area of 60, and $G, H, I, J$ are the midpoints of $A B, C D, D E, F A$ respectively. The area of the shaded part is . $\qquad$ | 30 |
51,296 | Baranov d..V.
The hare bought seven drums of different sizes and seven pairs of sticks of different lengths for her seven baby hares. If a baby hare sees that both its drum is larger and its sticks are longer than those of one of its brothers, it starts to drum loudly. What is the maximum number of baby hares that can start drumming? | 6 |
51,302 | 9. (24th American Mathematics Competition) There are 1990 piles of stones, with the number of stones in each pile being $1, 2, \cdots, 1990$. Perform the following operation: each time, you can choose any number of piles and remove the same number of stones from each chosen pile. How many operations are required at minimum to remove all the stones? | 11 |
51,340 | 3.108. $\frac{4 \sin \left(\frac{5}{2} \pi+\alpha\right)}{\operatorname{tg}^{2}\left(\frac{3}{2} \pi-\frac{\alpha}{2}\right)-\operatorname{ctg}^{2}\left(\frac{3}{2} \pi+\frac{\alpha}{2}\right)}$.
3.108. $\frac{4 \sin \left(\frac{5}{2} \pi+\alpha\right)}{\tan^{2}\left(\frac{3}{2} \pi-\frac{\alpha}{2}\right)-\cot^{2}\left(\frac{3}{2} \pi+\frac{\alpha}{2}\right)}$. | \sin^{2}\alpha |
51,344 | 4. On the plane, there are points $A, B, C$ and $D$ such that $|A B|=|B C|=$ $|A C|=|C D|=10 \mathrm{~cm}$ and $|A D|=17 \mathrm{~cm}$. What is the measure of angle $\Varangle A D B$? | 30 |
51,356 | 7. If the parabola $y=x^{2}-a x+3(a \in \mathbf{R})$ is always above the line $y=\frac{9}{4}$ over the interval $[a, a+1]$, then the range of values for $a$ is $\qquad$. | (-\sqrt{3},+\infty) |
51,360 | 10.208. Perpendiculars are drawn from the vertex of the acute angle of a rhombus to the lines containing the sides of the rhombus to which this vertex does not belong. The length of each perpendicular is 3 cm, and the distance between their bases is $3 \sqrt{3}$ cm. Calculate the lengths of the diagonals of the rhombus. | 6 |
51,385 | 40. Solve the equation $x\left(y^{2}-1\right) d x+y\left(x^{2}+1\right) d y=0$. | (x^{2}+1)(y^{2}-1)=C |
51,397 | 3.16 A material particle entered the hole of a pipe, and 6.8 minutes later, a second particle entered the same hole. Upon entering the pipe, each particle immediately began linear motion along the pipe: the first particle moved uniformly at a speed of 5 m/min, while the second particle covered 3 m in the first minute and 0.5 m more in each subsequent minute than in the previous one. How many minutes did it take for the second particle to catch up with the first? | 17 |
51,402 | 4. Let $\left\{a_{n}\right\}(n \geqslant 1)$ be a sequence of non-negative numbers with the first term $a$, and the sum of the first $n$ terms be $S_{n}$, and $S_{n}=\left(\sqrt{S_{n-1}}+\sqrt{a}\right)^{2}(n \geqslant 2)$. If $b_{n}=\frac{a_{n+1}}{a_{n}}+\frac{a_{n}}{a_{n+1}}$, and the sum of the first $n$ terms of the sequence $\left\{b_{n}\right\}$ is $T_{n}$, then $T_{n}=$ . $\qquad$ | \frac{4n^{2}+6n}{2n+1} |
51,411 | Given a point $P(3,1)$ and two lines $l_{1}: x+2 y+3=0, l_{2}: x+2 y-7=0$, find the equation of the circle passing through $P$ and tangent to both $l_{1}$ and $l_{2}$. | (x-4)^{2}+(y+1)^{2}=5\text{or}(x-\frac{4}{5})^{2}+(y-\frac{3}{5})^{2}=5 |
51,419 | (11. Determine how many different ways there are to assign the elements of the set $M=\{1,2,3,4,5\}$ to three (ordered) sets $A, B, C$, such that each element is contained in at least one of the sets, the intersection of the three sets is empty, and the intersection of any two sets is not empty? (i.e., $A \cup B \cup C=M, A \cap B \cap C=\varnothing$, and $A \cap B \neq \varnothing, B \cap C \neq \varnothing, C \cap A \neq \varnothing$) | 1230 |
51,422 | 5.5. In triangle $A B C$ with an angle of $120^{\circ}$ at vertex $A$, the angle bisectors $A A_{1}, B B_{1}$ and $C C_{1}$ are drawn. Find the angle $C_{1} A_{1} B_{1}$. | 90 |
51,433 | 37. Overtime Work. A certain company offered 350 of its employees to work overtime, with each man being offered a reward of 10 dollars, and each woman - 8 dollars and 15 cents. All women agreed to this offer, while some men refused. Upon calculation, it was found that the total reward amount does not depend on the number of male employees. What is the total reward amount paid to all women? | 1222.50 |
51,453 | Example 4 If
$$
\cos ^{5} \theta-\sin ^{5} \theta<7\left(\sin ^{3} \theta-\cos ^{3} \theta\right)(\theta \in[0,2 \pi)),
$$
then the range of values for $\theta$ is $\qquad$ [3]
(2011, National High School Mathematics League Competition) | (\frac{\pi}{4},\frac{5\pi}{4}) |
51,454 | 3. The equation $x^{2}+a x+5=0$ has two distinct roots $x_{1}$ and $x_{2}$; in this case,
$$
x_{1}^{2}+\frac{250}{19 x_{2}^{3}}=x_{2}^{2}+\frac{250}{19 x_{1}^{3}}
$$
Find all possible values of $a$. | 10 |
51,455 | 98 For $i=1,2, \cdots, n$, we have $\left|x_{i}\right|<1$, and assume $\left|x_{1}\right|+\left|x_{2}\right|+\cdots+\left|x_{n}\right|=19+$ $\left|x_{1}+x_{2}+\cdots+x_{n}\right|$, then the minimum value of the integer $n$ is $\qquad$ | 20 |
51,459 | [ Parallelepipeds (miscellaneous). ] [ Parallelism of lines and planes ] Through the midpoints $M$ and $N$ of the edges $A D$ and $C C 1$ of the parallelepiped $A B C D A 1 B 1 C 1 D 1$, a plane is drawn parallel to the diagonal $D B 1$. Construct the section of the parallelepiped by this plane. In what ratio does it divide the edge $B B 1$? | 5:1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.