id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
8,350 | The diagram shows the first four levels of a school's emergency telephone tree. In the case of an emergency, the principal calls two students. The first level consists of just the principal, and in the second level, two students are contacted. In the next level, each of these two students contacts two students who have not been contacted, so after the third level, a total of 6 students have been contacted. This continues so that each student contacts two students who have not yet been contacted. After the $8^{\text {th }}$ level, how many students in total have been contacted?
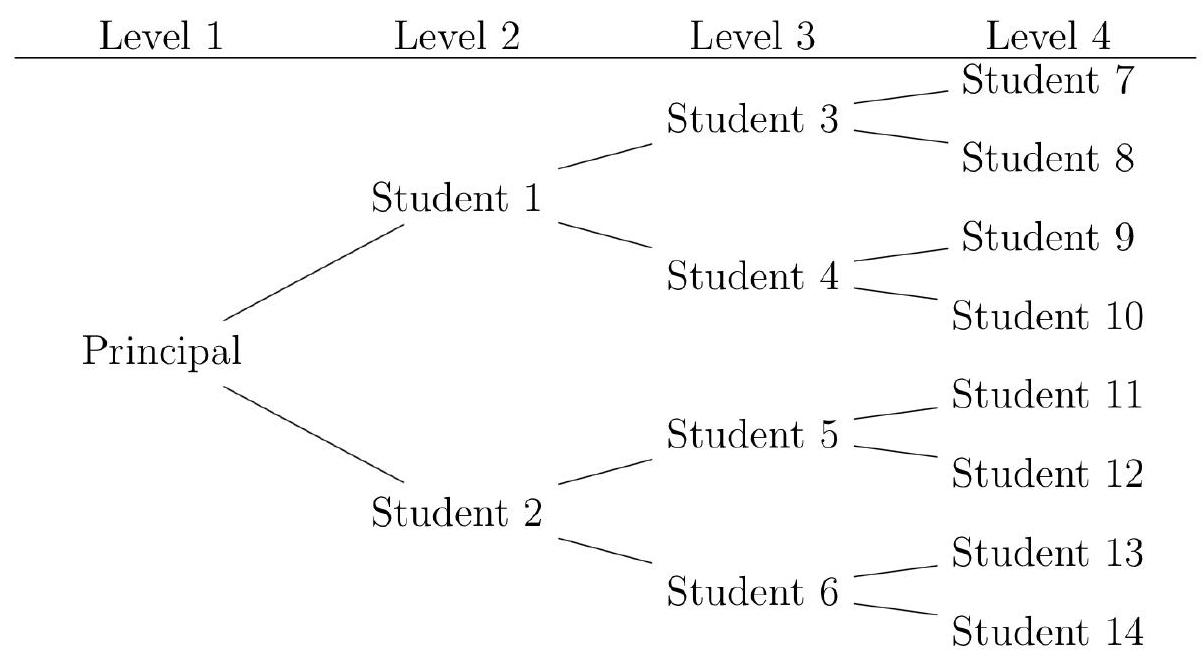 | 254 |
8,381 | ## 6. Cube from sticks
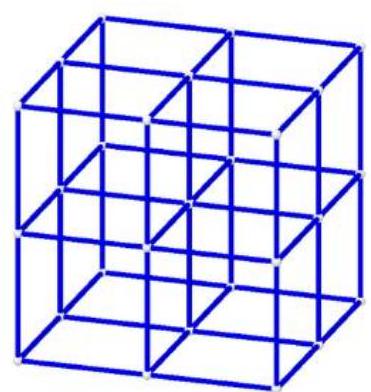
Result:
Cubes are made from sticks. For a cube $1 \times 1 \times 1$, 12 sticks are needed. To complete this cube to a cube $2 \times 2 \times 2$, 42 additional sticks are required (see the image). How many additional sticks are needed to complete a cube $8 \times 8 \times 8$ to a cube $9 \times 9 \times 9$? | 756 |
8,389 | $2 \cdot 35$ subset $X$ of the set $\{00,01, \cdots, 98,99\}$ satisfies: in any infinite sequence of digits, there are two adjacent digits that form an element of $X$. What is the minimum number of elements that $X$ should contain? | 55 |
8,395 | 7. The sum of 100 positive integers is 101101. What is the maximum possible value of their greatest common divisor? Prove your conclusion. | 1001 |
8,415 | 6. (3 points) Person A and Person B work together to process a batch of parts, which can be completed in 8 hours. If Person A works alone, it would take 12 hours to complete the task. Now, Person A and Person B work together for $2 \frac{2}{5}$ hours, after which Person A is reassigned to other work, and Person B continues to produce 420 parts to complete the task. How many parts did Person B process in total? | 480 |
8,501 | 3. Four balls with equal radii $r$ are given, and they touch each other pairwise. A fifth ball is described around them. Find the radius of the fifth ball. | r\left(1 + \dfrac{\sqrt{6}}{2}\right) |
8,540 | 9. The multiple-digit number $\underbrace{202120212021 \cdots 2021}_{n \text { 2021s }} 21$ can be divided by 21, the smallest $n$ is $\qquad$ . $(n>0)$ | 3 |
8,542 | Find the maximum value of the function \( f(x) = \sqrt{1+\sin x} + \sqrt{1-\sin x} + \sqrt{2+\sin x} + \sqrt{2-\sin x} + \sqrt{3+\sin x} + \sqrt{3-\sin x} \). | 2 + 2\sqrt{2} + 2\sqrt{3} |
8,547 | ## Task 1 - 120511
At a birthday party, Rainer presents his guests with the following puzzle, known since ancient times:
A snail begins at the beginning of a day to climb a $10 \mathrm{~m}$ high wall from the ground. In the following time, it crawls up $5 \mathrm{~m}$ higher during the first 12 hours of each day and slides down $4 \mathrm{~m}$ during the remaining 12 hours of the same day.
After how many hours has it first reached the entire height of the wall? | 132 |
8,577 | All the edges of the regular tetrahedron \(P-ABC\) have length \(1\). Let \( L, M, N \) be the midpoints of the edges \( PA, PB, PC \) respectively. Find the area of the cross-section of the circumsphere of the tetrahedron when cut by the plane \( LMN \). | \dfrac{\pi}{3} |
8,592 | Around a circle with a radius of 1, a rhombus and a triangle are described. Two sides of the triangle are parallel to the diagonals of the rhombus, and the third side is parallel to one of the sides of the rhombus and is equal to 5. Find the side of the rhombus. | \dfrac{25}{12} |
8,603 | Xiao Ming arranges chess pieces in a two-layer hollow square array (the diagram shows the top left part of the array). After arranging the inner layer, 60 chess pieces are left. After arranging the outer layer, 32 chess pieces are left. How many chess pieces does Xiao Ming have in total? | 80 |
8,606 | 3. Compare the numbers $x=2 \cdot 20212021 \cdot 1011 \cdot 202320232023$ and $y=43 \cdot 47 \cdot 20232023 \cdot 202220222022$. | x = y |
8,611 | 7. (10 points) It is known that a five-digit palindrome is equal to the product of 45 and a four-digit palindrome (i.e., $\overline{\mathrm{abcba}}=45 \times \overline{\mathrm{deed}}$). What is the largest possible value of this five-digit palindrome? $\qquad$ . | 59895 |
8,630 | 10. (6 points) In stores A and B, the marked price of a certain commodity is the same. Store A sells this commodity at the marked price, with sales amounting to 7200 yuan; Store B sells it at an 80% discount of the marked price, selling 15 more items than Store A, with the same sales amount as Store A. Then, Store A sold $\qquad$ items of this commodity. | 60 |
8,632 | 8. (4 points) For February 23, the boy Zhenya was given a chocolate bar of size $3 \times 3$, on each piece of which a unique picture is drawn, with each picture appearing only once. In each move, Zhenya can bite off one piece that has no more than three common sides with other pieces that have not yet been eaten. In how many ways can Zhenya eat his chocolate bar?
Answer: $\frac{4}{5} \cdot 9!=290304$. | 290304 |
8,689 | \(\frac{\sin 7 \alpha}{\sin \alpha} - 2(\cos 2 \alpha + \cos 4 \alpha + \cos 6 \alpha) - 1 = 0\). | 0 |
8,690 | Two vertices of a square with an area of \( 256 \, \text{cm}^2 \) lie on a circle, while the other two vertices lie on a tangent to this circle. Find the radius of the circle. | 10 |
8,721 | ## Problem 3
On the set of real numbers $\mathbb{R}$, the composition law "*" is defined with the following properties:
1) $\left(\frac{a+1}{3}\right) *\left(\frac{a}{2}\right)=1, \forall a \in \mathbb{R}$
2) $(a * b) \cdot c=(a \cdot c) *(b \cdot c), \forall a, b, c \in \mathbb{R}$.
Calculate $10 * 14$. | 2 |
8,784 | Problem 2. Masha's classes at school end at 13:00, and her mother picks her up by car, and they drive home. One day, the classes ended at 12:00, and Masha started walking home. On the way, she met her mother, who, as usual, drove to pick up her daughter at 13:00 at the school. Then Masha and her mother drove home in the car, and they arrived 12 minutes earlier than usual. At what time did Masha meet her mother on the road? (The speeds of Masha and her mother are constant, and no time is spent on getting into the car.) | 12:54 |
8,804 | 6.5. Ladybugs gathered on a clearing. If a ladybug has 6 spots on its back, it always tells the truth, and if it has 4 spots, it always lies, and there were no other ladybugs on the clearing. The first ladybug said: "Each of us has the same number of spots on our backs." The second said: "Together, we have 30 spots on our backs." "No, together we have 26 spots on our backs," - the third one objected. "Exactly one of these three told the truth," - each of the other ladybugs stated. How many ladybugs gathered on the clearing? | 5 |
8,805 | B. If $k$ numbers are chosen from 2, $, 8, \cdots, 101$ these 34 numbers, where the sum of at least two of them is 43, then the minimum value of $k$ is: $\qquad$ | 28 |
8,838 | A square area of size $100 \times 100$ is paved with $1 \times 1$ square tiles of four colors: white, red, black, and gray - such that no two tiles of the same color touch each other (that is, they do not share a side or a vertex). How many red tiles can there be? | 2500 |
8,839 | ## Task 2 - 240512
Roland solved a division problem. He obtained the quotient 36.
To check his result, Roland multiplied the divisor by this quotient. However, he mistakenly read a 1 instead of a 7 in the divisor and obtained the result of this multiplication as 756 instead of the given dividend.
What was the division problem that Roland was supposed to solve? | 972 \div 27 |
8,912 | (7) Let the set $S=\{1,2, \cdots, 15\}, A=\left\{a_{1}, a_{2}, a_{3}\right\}$ be a subset of $S$, and $(a_{1}, a_{2}, a_{3})$ satisfy:
$$
1 \leqslant a_{1}<a_{2}<a_{3} \leqslant 15, a_{3}-a_{2} \leqslant 6 .
$$
Then the number of subsets $A$ that satisfy the condition is $\qquad$ | 371 |
8,923 | 5.1. From one point on a circular track, a pedestrian and a cyclist started simultaneously in the same direction. The cyclist's speed is $55\%$ greater than the pedestrian's speed, and therefore the cyclist overtakes the pedestrian from time to time. At how many different points on the track will the overtakes occur? | 11 |
8,936 | 4. Factorize: $x^{4}+2 x^{3}-16 x^{2}-2 x+15$. | (x - 1)(x + 1)(x + 5)(x - 3) |
9,046 | Task 2.
Maximum 15 points
Solve the inequality:
$$
\sqrt{2 x+8}+\sqrt{10-2 x} \geq \log _{2}\left(4 x^{2}-4 x+65\right)
$$ | \dfrac{1}{2} |
9,047 | Example 4. Integrate the equation
$$
x(x+2 y) d x+\left(x^{2}-y^{2}\right) d y=0
$$ | x^3 + 3x^2 y - y^3 = C |
9,049 | Given a trapezoid $ABCD$ and a point $M$ on the lateral side $AB$ such that $DM \perp AB$. It turns out that $MC = CD$. Find the length of the upper base $BC$ if $AD = d$. | \dfrac{d}{2} |
9,081 | 8. Let the sequence $\left\{a_{n}\right\}$ satisfy:
$$
\begin{array}{l}
a_{1}=\frac{1}{4}, a_{n+1}=a_{n}+a_{n}^{2}\left(n \in \mathbf{Z}_{+}\right) . \\
\text {Let } T_{2020}=\frac{1}{a_{1}+1}+\frac{1}{a_{2}+1}+\cdots+\frac{1}{a_{2020}+1} .
\end{array}
$$
If the value of $T_{2020}$ lies in the interval $(k, k+1)$, then the integer $k$ is $\qquad$ . | 3 |
9,100 | Which integers from 1 to 60,000 (inclusive) are more numerous and by how much: those containing only even digits in their representation, or those containing only odd digits in their representation? | 780 |
9,107 | Let \( p(x) = x^{4} + a x^{3} + b x^{2} + c x + d \), where \( a, b, c, d \) are constants, and \( p(1) = 1993 \), \( p(2) = 3986 \), \( p(3) = 5979 \). Calculate \( \frac{1}{4}[p(11) + p(-7)] \). | 5233 |
9,119 | It is known that tangents to the graph of the target function \( y = a(x+1)^{2} + 1 \), drawn from point \( M(x_{0}, y_{0}) \), intersect at a right angle. Restore the form of the target function, knowing that the coordinates of the point \( M(x_{0}, y_{0}) \) satisfy the equation:
\[ \log_{3x-x^{2}+1}(y-4) = \log_{3x-x^{2}+1} \left( \frac{|2x+4| - |2x+1|}{3x+4.5} \sqrt{x^{2}+3x+2.25} \right). \] | y = -\dfrac{1}{16}(x + 1)^2 + 1 |
9,129 | 1. let $S$ be the set of all $n$-tuples $\left(X_{1}, \ldots, X_{n}\right)$, where $X_{1}, \ldots, X_{n}$ are subsets of $\{1,2, \ldots, 1000\}$, which do not all have to be different, and which can also be empty. For $a=\left(X_{1}, \ldots, X_{n}\right) \in S$ denote
$$
E(a)=\text { number of elements of } X_{1} \cup \ldots \cup X_{n}
$$
Find an explicit expression for the sum
$$
\sum_{a \in S} E(a)
$$ | 1000 \cdot (2^{1000n} - 2^{999n}) |
9,149 | 1. On the island of knights and liars (liars always lie, knights always tell the truth), each resident supports exactly one football team. In a survey, all residents of the island participated. To the question "Do you support 'Rostov'?", 40% of the residents answered "Yes". To a similar question about 'Zенit', 30% answered affirmatively, about 'Locomotive' - 50%, and about CSKA - 0%. What percentage of the island's residents actually support 'Rostov'? | 30 |
9,163 | Kája was supposed to multiply two two-digit numbers. Due to inattention, he switched the digits in one of the factors and got a product that was 4248 less than the correct result.
What should Kája have correctly obtained?
(L. Hozová) | 5369 |
9,175 | Walking along the fence from north to south, the spacing between its posts is initially the same. From a certain post, the spacing decreases to 2.9 meters and remains that way until the southern end of the fence. Between the 1st and 16th posts (counting from the north), the spacing does not change and the distance between these two posts is 48 meters. The distance between the 16th and 28th posts is 36 meters.
At which post is the spacing between its neighboring posts different? | 20 |
9,177 | A natural number $k > 1$ is called *good* if there exist natural numbers $$ a_1 < a_2 < \cdots < a_k $$ such that $$ \dfrac{1}{\sqrt{a_1}} + \dfrac{1}{\sqrt{a_2}} + \cdots + \dfrac{1}{\sqrt{a_k}} = 1 $$ .
Let $f(n)$ be the sum of the first $n$ *[good* numbers, $n \geq$ 1. Find the sum of all values of $n$ for which $f(n+5)/f(n)$ is an integer. | 18 |
9,189 | 8. Let $\left\{a_{n}\right\}$ be a sequence of positive numbers, and let the sum of the first $n$ terms be $S_{n}$, with $S_{n}=\frac{1}{2}\left(a_{n}+\frac{1}{a_{n}}\right)$. Find $a_{n}$. | \sqrt{n} - \sqrt{n-1} |
9,200 | A father drives Xiao Hong to a point 1000 meters away from the school and lets her walk the rest of the way. On this day, it took Xiao Hong 22.5 minutes to get from home to school. If Xiao Hong rides her bike from home to school, it takes her 40 minutes. She usually walks 80 meters per minute, and riding her bike is 800 meters per minute slower than her father's driving. Determine the distance from Xiao Hong's home to her school. | 12000 |
9,227 | Task 4. (20 points) At a refinery, a tank was filled with crude oil with a sulfur concentration of $1.5 \%$. Part of this oil was directed to production, and the same amount of oil with a sulfur concentration of $0.5 \%$ was added to the tank. Then, the same amount of oil as before was directed to production again, but this time oil with a sulfur concentration of $2 \%$ was added. As a result, the sulfur concentration in the oil in the tank returned to its original level. Determine what fraction of the oil from the tank was sent to production twice. | \dfrac{1}{2} |
9,329 | From 8 English letters $A, B, C, D, E, X, Y, Z$, any 5 letters (letters can be repeated) form a “word”. All possible “words” are arranged in “dictionary order” (i.e., the order in which English words are arranged in an English-Chinese dictionary), resulting in a “word list”:
Try to find the number of “words” located between the “word” $C Z Y E B$ and the “word” $X C E D A$ (excluding these two words).
---
The translation preserves the original text's line breaks and formatting. | 9590 |
9,336 |
4. Find the number of all 6-digit natural numbers having exactly three odd digits and three even digits.
| 281250 |
9,364 | Point \( M \) lies on the side \( BC \) of triangle \( ABC \). It is known that the radius of the circle inscribed in triangle \( ABM \) is twice the radius of the circle inscribed in triangle \( ACM \). Can the segment \( AM \) be the median of triangle \( ABC \)? | \text{No} |
9,370 | In triangle \(ABC\), a median \(AM\) is drawn and a point \(D\) is selected on it. Tangents drawn to the circumcircle of the triangle \(BDC\) at points \(B\) and \(C\) intersect at point \(K\). Prove that \(DD'\) is parallel to \(AK\), where \(D'\) is the reflection of \(D\) across line \(BC\). | DD' \parallel AK |
9,395 | Given a regular hexagon \( A_6 \) where each of its 6 vertices is colored with either red or blue, determine the number of type II colorings of the vertices of the hexagon. | 13 |
9,401 | 450. For what values of $x$ is the equality $|x+6|=$ $=-(x+6)$ true? | (-\infty, -6] |
9,421 | 1. Can the number 8 be represented as the sum of eight integers such that the product of these numbers is also equal to 8? | Yes |
9,430 | Let $A$ be a given finite set with some of its subsets called pretty. Let a subset be called small, if it's a subset of a pretty set. Let a subset be called big, if it has a pretty subset. (A set can be small and big simultaneously, and a set can be neither small nor big.) Let $a$ denote the number of elements of $A$ , and let $p$ , $s$ and $b$ denote the number of pretty, small and big sets, respectively. Prove that $2^a\cdot p\le s\cdot b$ .
*Proposed by András Imolay, Budapest* | 2^a \cdot p \le s \cdot b |
9,441 | Let \( l \) and \( m \) be two skew lines. On \( l \), there are three points \( A, B, \) and \( C \), such that \( AB = BC \). From points \( A, B, \) and \( C \), perpendiculars \( AD, BE, \) and \( CF \) are respectively drawn to \( m \), with feet of the perpendiculars at \( D, E, \) and \( F \). Given \( AD = \sqrt{15}, BE = \frac{7}{2}, CF = \sqrt{10} \), find the distance between lines \( l \) and \( m \). | \sqrt{6} |
9,485 | 11.1. Determine the extreme values of the function $f:\left(0, \frac{\pi}{2}\right) \rightarrow \mathbb{R}, f(x)=\sin x+\cos x+\tan x+\cot x$. | 2 + \sqrt{2} |
9,494 | 10.367 Express the side of a regular decagon in terms of the radius $R$ of the circumscribed circle. | \dfrac{R(\sqrt{5} - 1)}{2} |
9,534 | Quadrilateral \(ABCD\) is inscribed in a circle. The extensions of sides \(AB\) and \(DC\) intersect at point \(P\), and the extensions of sides \(AD\) and \(BC\) intersect at point \(Q\). From \(Q\), two tangents \(QE\) and \(QF\) are drawn to the circle, with points of tangency \(E\) and \(F\) respectively. Prove that points \(P\), \(E\), and \(F\) are collinear. | P, E, F \text{ are collinear.} |
9,563 | [ Decimal number system ] $[$ Arithmetic. Mental calculation, etc. ]
A part of a book fell out. The first of the missing pages has the number 387, and the number of the last page consists of the same digits but in a different order. How many sheets fell out of the book? | 176 |
9,566 | [Trigonometric Identities.]
Find $\frac{\sin 5 x}{\sin x}$, if $\frac{\sin 3 x}{\sin x}=\frac{6}{5}$.
# | -\dfrac{19}{25} |
9,575 | 33. How many people got lost in the mountains?
Alice and the Griffin had to wait several minutes before the Tortoise Quasi gathered his strength and could continue.
- You see,一began the Tortoise Quasi.
- I don't see anything!- the Griffin cut in.
The Tortoise Quasi did not respond, only grabbing his head with his front paws again. After remaining silent for some time, he spoke again:
- Let's say... Nine people got lost in the mountains. They only had enough food for five days. Can you imagine, just five days!
Having reached this point in his story, the Tortoise Quasi was so moved by the tragedy that he could not continue from the overflow of emotions.
- Well, that's enough, there, there! - the Griffin tried to comfort him, patting his back.
- Can you imagine what will happen to them if they are not found! - the Tortoise Quasi sobbed. - But it happened (and this is the most beautiful part of the story!)... Yes, the most beautiful part of the story is that the next day the poor souls met another group of lost people in the mountains...
- What's so beautiful about that? - the Griffin asked.
- The most beautiful part is that the first group generously shared their supplies with the second - they divided the provisions equally among everyone, after which the food lasted for another three days.
How many people were in the second group? | 3 |
9,580 | 8. If $x \geq 0, y \geq 0$ are integers, randomly chosen with the constraint $x+y \leq 10$, what is the probability that $x+y$ is even? | \dfrac{6}{11} |
9,581 | Standa and Jana received two three-digit numbers. Standa added a decimal point after the first digit in the first number, and after the second digit in the second number, then added the resulting decimal numbers and got the result 50.13. Jana added a decimal point after the second digit in the first number, and after the first digit in the second number, then added the resulting decimal numbers and got the result 34.02.
Determine the sum of the original three-digit numbers.
(K. Pazourek) | 765 |
9,585 | 12. All 45 students in Class 3(1) have signed up for the school sports meet. Apart from the tug-of-war competition where the entire class participates, each student must participate in at least one of the other three events. It is known that 39 students in the class have signed up for the kick shuttlecock competition, and 28 students have signed up for the basketball shooting. How many students have signed up for all three events? | 22 |
9,622 | The altitudes of an acute isosceles triangle, where \(AB = BC\), intersect at point \(H\). Find the area of triangle \(ABC\), given \(AH = 5\) and the altitude \(AD\) is 8. | 40 |
9,635 | Determine the number of pairs of integers $(a, b)$ such that $1 \leqslant a \leqslant 30, 3 \leqslant b \leqslant 30$ and such that $a$ is divisible by $b$ and by $b-2$. | 22 |
9,647 | A line parallel to the bases of a trapezoid divides it into two similar trapezoids. Find the segment of this line that is contained within the trapezoid if the bases are equal to $a$ and $b$. | \sqrt{ab} |
9,668 | There are 100 students who want to sign up for the class "Introduction to Acting." There are three class sections for "Introduction to Acting," each of which will fit exactly 20 students. The 100 students, including Alex and Zhu, are put in a lottery, and 60 of them are randomly selected to fill up the classes. What is the probability that Alex and Zhu end up getting into the same section for the class? | \dfrac{19}{165} |
9,674 | In a tournament with 5 teams, there are no ties. In how many ways can the $\frac{5 \cdot 4}{2}=10$ games of the tournament occur such that no team wins all their games and no team loses all their games? | 544 |
9,676 | Example 8. Calculate the integral
$$
I=\int_{0}^{\infty} \frac{x^{2} d x}{\left(x^{2}+a^{2}\right)^{2}} \quad(a>0)
$$ | \dfrac{\pi}{4a} |
9,690 | Find the smallest natural number $n$ such that $\sin n^{\circ} = \sin (2016n^{\circ})$. | 72 |
9,695 | Let $a, b, c, p, q, r$ be positive integers with $p, q, r \ge 2$ . Denote
\[Q=\{(x, y, z)\in \mathbb{Z}^3 : 0 \le x \le a, 0 \le y \le b , 0 \le z \le c \}. \]
Initially, some pieces are put on the each point in $Q$ , with a total of $M$ pieces. Then, one can perform the following three types of operations repeatedly:
(1) Remove $p$ pieces on $(x, y, z)$ and place a piece on $(x-1, y, z)$ ;
(2) Remove $q$ pieces on $(x, y, z)$ and place a piece on $(x, y-1, z)$ ;
(3) Remove $r$ pieces on $(x, y, z)$ and place a piece on $(x, y, z-1)$ .
Find the smallest positive integer $M$ such that one can always perform a sequence of operations, making a piece placed on $(0,0,0)$ , no matter how the pieces are distributed initially. | p^a q^b r^c |
9,711 | XXXIV OM - I - Problem 1
$ A $ tosses a coin $ n $ times, $ B $ tosses it $ n+1 $ times. What is the probability that $ B $ will get more heads than $ A $? | \dfrac{1}{2} |
9,747 | 2. In triangle $\triangle A B C$, the sides $A B=5$ and $A C=6$ are known. What should the side $B C$ be so that the angle $\angle A C B$ is as large as possible? Provide the length of side $B C$, rounded to the nearest integer. | 3 |
9,758 | 9. Non-zero vectors $\vec{a}$ and $\vec{b}$ satisfy $|\vec{a}|=|\vec{b}|=|\vec{a}-\vec{b}|$, the angle between $\vec{a}$ and $\vec{a}+\vec{b}$ is
$\qquad$ | 30^\circ |
9,764 | On an island live 34 chameleons, which can take on 3 colors: yellow, red, and green. At the beginning, 7 are yellow, 10 are red, and 17 are green. When two chameleons of different colors meet, they simultaneously take on the third color. It turns out that after a certain amount of time, all the chameleons on the island have taken on the same color. What is this color? (It is necessary to show that it is the only possible one.) | green |
9,802 | Prove that the following equality holds:
$$
\cos \frac{2 \pi}{5} \cdot \cos \frac{6 \pi}{5} = -\frac{1}{4}
$$ | -\dfrac{1}{4} |
9,807 | Task B-3.4. A sphere is circumscribed around a right circular cone. A plane containing the center of this sphere and parallel to the base of the cone divides the cone into two parts of equal volumes. Determine the cosine of the angle at the vertex of the axial section of the cone. | \sqrt[3]{2} - 1 |
9,832 | 1. A printing house determines the cost of printing a book as follows: it adds the cost of the cover to the cost of each page, and then rounds the result up to the nearest whole number of rubles (for example, if the result is 202 rubles and 1 kopeck, it is rounded up to 203 rubles). It is known that the cost of a book with 104 pages is 134 rubles, and a book with 192 pages costs 181 rubles. How much does the printing of the cover cost, if it is a whole number of rubles, and the cost of one page is a whole number of kopecks? (20 points) | 77 |
9,839 | ## Task 4 - 070734
Given the equation
$$
\frac{x}{2}+\frac{x}{3}+7=x-\frac{3}{4}
$$
In this equation, the addend 7 is to be replaced by another number so that $x=11$ satisfies the equation.
What is this number? | \dfrac{13}{12} |
9,877 | Example 3 As shown in Figure 3, in $\triangle A B C$, $\angle B=46^{\circ}$, point $D$ is on side $B C$, and satisfies $\angle B A D=21^{\circ}$. If $A B$ $=C D$, find the degree measure of $\angle C A D$. ${ }^{[3]}$ | 67 |
9,878 | Example 5 On the Cartesian plane, the number of integer points on the circumference of a circle centered at $(199,0)$ with a radius of 199 is | 4 |
9,892 | 4. 42 Find the positive root of the equation $x=\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+x}}}}$, and prove that there is only one positive root. | 2 |
9,915 | ## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0}\left(2-e^{\arcsin ^{2} \sqrt{x}}\right)^{\frac{3}{x}}
$$ | e^{-3} |
9,952 | Here is a fairly simple puzzle: EH is four times greater than OY. AY is four times greater than OH. Find the sum of all four. | 150 |
9,961 | Folkpor
In an isosceles trapezoid $ABCD$, the bases $AD$ and $BC$ are 12 and 6 respectively, and the height is 4. Compare the angles $BAC$ and $CAD$. | \angle BAC > \angle CAD |
9,962 | 6. [6] Let $A B C D$ be a convex quadrilateral with $A C=7$ and $B D=17$. Let $M, P, N, Q$ be the midpoints of sides $A B, B C, C D, D A$ respectively. Compute $M N^{2}+P Q^{2}$ | 169 |
9,970 | Example 6 (1972 US Mathematical Olympiad) Suppose a random number selector can only choose from the nine digits $1,2, \cdots, 9$, and makes these choices with equal probability. Determine the probability that the product of the $n$ numbers selected after $n$ choices $(n>1)$ is divisible by 10. | 1 - \left( \frac{5}{9} \right)^n - \left( \frac{8}{9} \right)^n + \left( \frac{4}{9} \right)^n |
9,990 | 2. Variant 1. At the intersection of perpendicular roads, a highway from Moscow to Kazan and a road from Vladimir to Ryazan intersect. Dima and Tolya set out with constant speeds from Moscow to Kazan and from Vladimir to Ryazan, respectively. When Dima passed the intersection, Tolya had 3500 meters left to reach it. When Tolya passed the intersection, Dima was 4200 meters away from it. How many meters will be between the boys when Dima has traveled 4200 meters from the moment Tolya crossed the intersection? | 9100 |
9,993 | Alice and Bob play a game with years. Two game numbers 19 and 20 and a starting number from the set {9, 10} are used. Independently, Alice chooses her game number and Bob chooses the starting number. The other game number is assigned to Bob.
Then Alice adds her game number to the starting number, Bob adds his game number to the result, Alice adds her game number to the result, and so on. The game continues until the number 2019 is reached or exceeded.
- Who reaches the number 2019 wins. If 2019 is exceeded, the game ends in a draw.
- Show that Bob cannot win.
- Which starting number must Bob choose to prevent Alice from winning? | 9 |
9,997 | 6. The minimum value of the function defined on the real numbers
$f(x)=\frac{\sin \pi x}{\sqrt{1+x+x^{2}}}$ is $\qquad$ - | -\dfrac{2\sqrt{3}}{3} |
9,998 | ## Task 3 - 040613
A 6th grade class made various paper triangles. The students wanted to store these triangles in a cabinet in their school's mathematics room, which had nine compartments. The students had designated three compartments for the equilateral triangles, three for the isosceles triangles (i.e., those that are not equilateral), and three for the scalene triangles. Within these groups, the figures were to be further divided into acute, right, and obtuse triangles.
Check whether the number of compartments was correctly chosen! | 7 |
10,013 | 6. 72 students line up in a rectangular formation for the break exercise. Xiao Gao's position is the 5th from the left, the 4th from the right, the 3rd from the front, and the $\qquad$th from the back. | 7 |
10,022 | 8. A hotel has 90 vacant rooms, each with a unique key. 100 guests arrive, and keys need to be distributed so that any 90 of them can stay in the 90 rooms, with each person getting one room (assuming there is no limit to the number of keys that can be issued for each room or the number of keys each person can receive). What is the minimum number of keys that need to be issued? $\qquad$ | 990 |
10,038 | 28. From the six digits $0,1,2, 3, 4,5$, select 2 odd numbers and 2 even numbers to form a 4-digit number without repeated digits. What is the probability of forming a 4-digit even number? | \dfrac{8}{15} |
10,048 | The points $P$ and $Q$ are the midpoints of the edges $AE$ and $CG$ on the cube $ABCD.EFGH$ respectively. If the length of the cube edges is $1$ unit, determine the area of the quadrilateral $DPFQ$ . | \dfrac{\sqrt{6}}{2} |
10,050 | 1.7. Calculate the determinant
$$
\Delta=\left|\begin{array}{cccc}
3 & 1 & -1 & 2 \\
-3 & 1 & 4 & -5 \\
2 & 0 & 1 & -1 \\
3 & -5 & 4 & -4
\end{array}\right|
$$ | 40 |
10,065 | 8、On a birthday card printed with April 29, a child erased two positive integers $x, y$ between 4 and 29, resulting in a five-digit number $\overline{4 x y 29}$, and found that it is exactly the square of the positive integer $T$ corresponding to their birthday: $\overline{4 x y 29}=T^{2}$; then the number $T$ corresponding to the child's birthday is | 223 |
10,110 | Two circles are drawn, as shown. Each is centered at the origin and the radii are 1 and 2. Determine the value of $k$ so that the shaded region above the $x$-axis, below the line $y=k x$ and between the two circles has an area of 2.
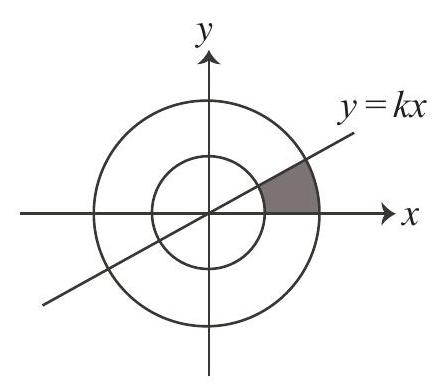 | \tan\left(\dfrac{4}{3}\right) |
10,116 | Sasha chose five numbers from 1, 2, 3, 4, 5, 6, and 7 and informed Anya of their product. Based on this information, Anya realized that she could not uniquely determine the parity of the sum of the numbers chosen by Sasha. What number did Sasha inform Anya of? | 420 |
10,119 | 5. Given that $n$ is a positive integer, the maximum value of $2022 \times\left(\frac{1}{n}+\frac{1}{n+1}+\cdots+\frac{1}{2 n}\right)$ is | 3033 |
10,163 | Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy:
$$
\forall x, y \in \mathbb{R}, \quad f(x+y)=2 f(x)+f(y)
$$ | 0 |
10,219 | 1. Several boys and girls gathered around a round table. It is known that exactly for 7 girls, the person sitting to their left is a girl, and for 12 - a boy. It is also known that for $75\%$ of the boys, the person sitting to their right is a girl. How many people are sitting at the table? | 35 |
10,236 | On three faces of a cube, diagonals are drawn such that a triangle is formed. Find the angles of this triangle. | 60^\circ |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.