id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
60,295 | 2. The distance between points A and B is 90 km. At 9:00, a bus left point A for point B at a speed of 60 km/h. Starting from 9:00, every 15 minutes, buses leave point B towards point A at a speed of 80 km/h. The bus that left point A, after traveling 45 km, reduces its speed to 20 km/h due to a breakdown and continues at this speed. A passenger in this bus is considering whether to continue the slow journey to point B or return to point A in the first passing bus. How much time does the passenger have to make a decision? | 3 |
53,232 | 2. There is a bag with 16 letters: А, А, А, А, В, В, Д, И, И, М, М, Н, Н, Н, Я, Я. Anna, Vanya, Danya, and Dima each took 4 letters from it, after which the bag was empty. How many of them could have successfully spelled out their names? Explain your answer. | 3 |
16,239 | 74. Qiqi was doing an addition problem when she mistook the unit digit 1 for 7 and the tens digit 6 for 9, resulting in 75. The correct answer to this problem should be $\qquad$. | 39 |
22,644 | 5. Two trains departed simultaneously from points $A$ and $B$ towards each other. It is known that they met at 14:00 and, without changing their speeds, continued their journey. One train arrived at point $B$ at 18:00, and the other train arrived at point $A$ at 23:00. At what time did the trains depart on their journey | 8:00 |
22,068 | Exercise 8. In a tournament organized between 6 teams, each team plays against each other team exactly once. When a team wins, it gets 3 points, and the losing team receives 0 points. If the game is a draw, both teams receive 1 point. Determine the values of \( a \) for which it is possible that the final scores of the teams can be the six consecutive numbers \( a, a+1, \ldots, a+5 \)? | 4 |
51,331 | A natural number is a [i]factorion[/i] if it is the sum of the factorials of each of its decimal digits. For example, $145$ is a factorion because $145 = 1! + 4! + 5!$.
Find every 3-digit number which is a factorion. | 145 |
9,960 | 1. Evan's analog clock displays the time $12: 13$; the number of seconds is not shown. After 10 seconds elapse, it is still $12: 13$. What is the expected number of seconds until $12: 14$ ? | 25 |
55,800 | 1. (15 points) A small rubber ball moves between two massive vertical walls, colliding with them. One of the walls is stationary, while the other is moving away from it at a constant speed \( u = 100 \, \text{cm} / \text{s} \). Assuming the ball's motion is always horizontal and the collisions are perfectly elastic, find its final speed if the initial speed of the ball was \( v_{0} = 2017 \, \text{cm} / \text{s} \). | 17\, |
836 | 1. Let
$$
S=\frac{1}{2}, E=\frac{\frac{3}{7}+1}{\frac{3}{7}-1}, D=-2: \frac{5}{3}+1.1, A=3-0.2 \cdot 2, M=100 \cdot 0.03-5.25: \frac{1}{2}
$$
Calculate the value of the expression $S+E: D-A \cdot M$. | 45 |
29,175 | The real-valued function $f$ is defined for all positive integers. For any integers $a>1, b>1$ with $d=\operatorname{gcd}(a, b)$, we have
$$
f(a b)=f(d) \cdot\left(f\left(\frac{a}{d}\right)+f\left(\frac{b}{d}\right)\right),
$$
Determine all possible values of $f(2001)$. | \frac{1}{2} |
16,241 | Given real numbers \(a_{1}, a_{2}, \cdots, a_{n}\), define \(a_{n+1}=0\) and \(M=\max _{1 \leqslant k \leqslant n}\left|a_{k}-a_{k+1}\right|\). Prove that \(\left|\sum_{k=1}^{n} k a_{k}\right| \leqslant \frac{1}{6} M \cdot n(n+1)(n+2)\). | \left|\sum_{k=1}^{n} k a_{k}\right| \leqslant \frac{1}{6} M \cdot n(n+1)(n+2) |
29,247 | 41. a) Each vertex at the base of the triangle is connected by straight lines to \( n \) points located on the opposite side. Into how many parts do these lines divide the triangle?
b) Each of the three vertices of the triangle is connected by straight lines to \( n \) points located on the opposite side of the triangle. Into how many parts do these lines divide the triangle if no three of them intersect at the same point? | 3n^2+3n+1 |
20,114 | For some positive real \(\alpha\), the set \(S\) of positive real numbers \(x\) with \(\{x\} > \alpha x\) consists of the union of several intervals, with total length 20.2. The value of \(\alpha\) can be expressed as \(\frac{a}{b}\), where \(a, b\) are relatively prime positive integers. Compute \(100a + b\). (Here, \(\{x\} = x - \lfloor x \rfloor\) is the fractional part of \(x\).) | 4633 |
13,364 | In trapezoid \(ABCD \) with \(AB \parallel CD\) and \(AB + CD = b\), the diagonals \(AC\) and \(BD\) are related by \(5AC = 3BD\). Find the area of the trapezoid if \(\angle BAC = 2 \angle DBA\). | \dfrac{5\sqrt{11}}{64} b^2 |
33,919 | Determine all integers $n>1$ such that $\frac{2^{n}+1}{n^{2}}$ is an integer. | 3 |
51,109 | Example 4.29 Place $n(n \geqslant 1)$ distinct balls into 4 distinct boxes $A_{1}$, $A_{2}$, $A_{3}$, $A_{4}$, find the number of different ways to place the balls, $g_{n}$, such that $A_{1}$ contains an odd number of balls, and $A_{2}$ contains an even number of balls. | g_{n}=4^{n-1} |
58,982 | While investigating a case, Detective Bashkovsky discovered that the key witness was the one from the Petrovs family who came home before the others on that fateful day. The investigation revealed the following facts.
1. Neighbor Marya Kuzminichna wanted to borrow some salt from the Petrovs, rang their doorbell, but no one answered. When? Who knows? It was already dark...
2. Galina Efimovna Petrova, coming home in the evening, found both children in the kitchen, and her husband on the sofa - he had a headache.
3. Husband Anatoly Ivanovich claimed that as soon as he came home, he immediately lay down on the sofa and dozed off, saw no one, heard nothing, the neighbor definitely didn't come - the doorbell would have woken him up.
4. Daughter Svetlana said that upon returning home, she immediately went to her room, knew nothing about her father, but as usual, stumbled over Dima's shoe in the hallway.
5. Dmitry didn't remember when he came home, didn't see his father, but heard Svetka swearing about the shoe.
"Hmm," thought Bashkovsky. "What is the probability that Dmitry returned home before his father?" | \frac{2}{3} |
51,213 | 28. In a square $A B C D$ with a side length of 1 cm, draw quarter circles with a radius of 1 cm, centered at $A, B, C, D$, intersecting at points $E, F, G, H$, as shown in the figure. The perimeter of the shaded area in the middle is $\qquad$ cm. | \frac{2}{3}\pi |
56,568 | I2.3 Let $f(1)=3, f(2)=5$ and $f(n+2)=f(n+1)+f(n)$ for positive integers $n$. If $c$ is the remainder of $f(b)$ divided by 3 , find the value of $c$. | 2 |
58,215 | 2. As shown in Figure 2, in quadrilateral $ABCD$, $AB=10$, $BC=17$, $CD=13$, $DA$ $=20$, $AC=21$. Then $BD=$ | 10 \sqrt{5} |
61,117 | Example 6 As shown in Figure 7, the side length of square $A B C D$ is $1, P$ is any point on side $B C$ (it can coincide with points $B$ or $C$), and perpendiculars are drawn from points $B, C, D$ to the ray $A P$. The feet of the perpendiculars are $B^{\prime}, C^{\prime}, D^{\prime}$, respectively. Find the maximum and minimum values of $B B^{\prime}+C C^{\prime}+D D^{\prime}$. | 2 |
58,782 | \section*{Problem 6}
Find three non-zero reals such that all quadratics with those numbers as coefficients have two distinct rational roots.
Answer \(1,2,-3\)
| 1,2,-3 |
50,780 | 12.94 The equation $x^{n}+(2+x)^{n}+(2-x)^{n}=0$ has a rational solution, the necessary and sufficient condition regarding the positive integer $n$ is what?
(15th Putnam Mathematical Competition, 1955) | 1 |
58,684 | Task 2. Determine all polynomials $P(x)$ with real coefficients for which the polynomial
$$
Q(x)=(x+1) P(x-1)-(x-1) P(x)
$$
is constant. | P(x)=^{2}++ |
64,955 | Problem 11.2. Solve the system
$$
\left\lvert\, \begin{aligned}
& \left(4^{\sqrt{x^{2}+x}}+7.2^{\sqrt{x^{2}+x}}-1\right) \sin (\pi y)=7|\sin (\pi y)| \\
& x^{2}+4 x+y^{2}=0
\end{aligned}\right.
$$
Aleksandar Ivanov | -1,-\sqrt{3} |
56,538 | 1. Each cell of a $68 \times 68$ table is to be colored with one of three colors (red, blue, white). In how many ways can this be done so that every triplet of adjacent cells in each row and each column contains cells of all three colors?
(Josef Tkadlec) | 12 |
68,721 | XXXV OM - III - Task 4
We toss a coin $ n $ times and record the result as a sequence $ (a_1, a_2, \ldots, a_n) $, where $ a_i = 1 $ or $ a_i = 2 $ depending on whether an eagle or a tail appeared in the $ i $-th toss. We assume $ b_j = a_1 + a_2 + \ldots + a_j $ for $ j = 1, 2, \ldots, n $, $ p(n) $ is the probability that the number $ n $ appears in the sequence $ (b_1, b_2, \ldots, b_n) $. Determine $ p(n) $ in terms of $ p(n-1) $ and $ p(n-2) $. | p(n)=\frac{1}{2}p(n-1)+\frac{1}{2}p(n-2) |
67,744 | 2. $I=\sum_{k=1}^{10}\left(\cos \frac{k \pi}{11}\right)^{8}=$ | \frac{257}{128} |
68,156 | 7.1. (GDR, 74). What is greater: $\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}-\sqrt{2}$ or 0? | 0 |
57,593 | 24. Brother Bear and Little Bear went on an adventure to find treasure and obtained a treasure chest. This treasure chest requires a ten-digit password consisting only of the digits 0 and 1 to open. Brother Bear first entered “1000000000”, and the treasure chest indicated that 1 digit was incorrect; Little Bear then entered “0110000000”, and the treasure chest indicated that 2 digits were incorrect. If the treasure chest no longer gives hints for subsequent password attempts, how many more times do the clever Brother Bear and Little Bear need to try to definitely open the treasure chest? | 3 |
24,673 |
In the parallelogram \(KLMN\), side \(KL\) is equal to 8. A circle tangent to sides \(NK\) and \(NM\) passes through point \(L\) and intersects sides \(KL\) and \(ML\) at points \(C\) and \(D\) respectively. It is known that \(KC : LC = 4 : 5\) and \(LD : MD = 8 : 1\). Find the side \(KN\). | 10 |
24,798 | During breaks, schoolchildren played table tennis. Any two schoolchildren played no more than one game against each other. At the end of the week, it turned out that Petya played half, Kolya - a third, and Vasya - one fifth of the total number of games played during the week. What could be the total number of games played during the week if it is known that at least two games did not involve Vasya, Petya, or Kolya? | 30 |
22,115 | Condition of the problem
Find the derivative.
$y=(\ln x)^{3^{x}}$ | (\ln x)^{3^{x}} \cdot 3^{x} \left( \ln 3 \cdot \ln(\ln x) + \frac{1}{x \ln x} \right) |
66,756 | Let $a$ and $b$ be given positive real numbers, with $a<b.$ If two points are selected at random from a straight line segment of length $b,$ what is the probability that the distance between them is at least $a?$ | \frac{(b - a)^2}{b^2} |
25,836 | 9. In the tetrahedron $O A B C$, $\angle A O B=45^{\circ}, \angle A O C=\angle B O C=30^{\circ}$, then the cosine value of the dihedral angle $A-O C-B$'s plane angle $\alpha$ is $\qquad$. | 2\sqrt{2}-3 |
58,849 | 30.2. Find the largest natural number that is divisible by 37 and in which each subsequent digit is less than the previous one.
$$
\text { (7-10 grades) }
$$ | 987654320 |
64,033 | 8. If for any $x \in(-\infty,-1)$, we have
$$
\left(m-m^{2}\right) 4^{x}+2^{x}+1>0,
$$
then the range of real number $m$ is $\qquad$ | [-2,3] |
65,279 | Example 2. Using the parabola formula with an accuracy of 0.0001, calculate $\int_{0}^{1} \frac{d x}{1+x^{2}}$ | 0.785395 |
5,431 | 5. The figure $\mathrm{a}$ below is a cross-sectional view of a sealed water bottle, with the upper part being conical and the lower part cylindrical, both with a base diameter of 10 centimeters. The total height of the water bottle is 26 centimeters, and the height of the liquid surface inside is 12 centimeters. When the water bottle is inverted, as shown in figure $\mathrm{b}$, the height of the liquid surface is 16 centimeters. The volume of the water bottle is $\qquad$ cubic centimeters. $(\pi=3.14$, the thickness of the water bottle walls is negligible). | 1727 |
34,230 | Problem 10. Points $M, N$, and $K$ are located on the lateral edges $A A_{1}, B B_{1}$, and $C C_{1}$ of the triangular prism $A B C A_{1} B_{1} C_{1}$ such that $A M: A A_{1}=2: 3, B N: B B_{1}=3: 5, C K: C C_{1}=4: 7$. Point $P$ belongs to the prism. Find the maximum possible value of the volume of the pyramid $M N K P$, if the volume of the prism is 27. | 6 |
23,213 | Legs \( L_{1}, L_{2}, L_{3}, L_{4} \) of a square table each have length \( n \), where \( n \) is a positive integer. For how many ordered 4-tuples \( \left(k_{1}, k_{2}, k_{3}, k_{4}\right) \) of nonnegative integers can we cut a piece of length \( k_{i} \) from the end of leg \( L_{i} \) and still have a stable table?
(The table is stable if it can be placed so that all four of the leg ends touch the floor. Note that a cut leg of length 0 is permitted.) | \dfrac{(n + 1)(2n^2 + 4n + 3)}{3} |
34,339 | 5. (8 points) Solve the equation $x^{4}-(a+b) \cdot x^{3}+(a b-2 c) \cdot x^{2}+c(a+b) \cdot x+c^{2}=0$. In your answer, write the sum of the squares of the real roots of the equation. | ^{2}+b^{2}+4c |
18,179 | Given $\triangle ABC$ , let $R$ be its circumradius and $q$ be the perimeter of its excentral triangle. Prove that $q\le 6\sqrt{3} R$ .
Typesetter's Note: the excentral triangle has vertices which are the excenters of the original triangle. | q \le 6\sqrt{3} R |
27,991 | Example 4 Let real numbers $a \geqslant b \geqslant c \geqslant d>0$. Find the minimum value of the function
$$
\begin{array}{l}
f(a, b, c, d) \\
=\left(1+\frac{c}{a+b}\right)\left(1+\frac{d}{b+c}\right)\left(1+\frac{a}{c+d}\right)\left(1+\frac{b}{d+a}\right)
\end{array}
$$ | (\frac{3}{2})^{4} |
54,981 | (5) If the odd function $y=f(x)$ defined on $\mathbf{R}$ is symmetric about the line $x=1$, and when $0<x \leqslant 1$, $f(x)=\log _{3} x$, then the sum of all real roots of the equation $f(x)=-\frac{1}{3}+f(0)$ in the interval $(0,10)$ is $\qquad$ | 30 |
34,762 | 8. Let $A B C D E F$ be a regular hexagon of area 1 . Let $M$ be the midpoint of $D E$. Let $X$ be the intersection of $A C$ and $B M$, let $Y$ be the intersection of $B F$ and $A M$, and let $Z$ be the intersection of $A C$ and $B F$. If $[P]$ denotes the area of polygon $P$ for any polygon $P$ in the plane, evaluate $[B X C]+[A Y F]+[A B Z]-[M X Z Y]$. | 0 |
64,023 | 1. Vasya can get the number 100 using ten sevens, parentheses, and arithmetic operation signs: $100=(77: 7-7: 7) \cdot(77: 7-7: 7)$. Improve his result: use fewer sevens and get the number 100. (It is sufficient to provide one example). | 100=7\cdot7+7\cdot7+7:7+7:7 |
28,062 | 7$\cdot$70 Alice and Bob came to a hardware store, where colored tassels are sold to be tied on keys to distinguish different keys. Below is a segment of their conversation:
Alice: Are you going to buy some colored tassels to tie on your keys?
Bob: I would like to do that, but the tassels come in only 7 different colors, and I have 8 keys.
Alice: That’s no problem, because even if two keys are tied with red tassels, you can still distinguish them by noticing whether they are adjacent to a key with a green tassel or a key with a blue tassel.
Bob: Of course, you know that all my keys are on the same keyring, and the keyring can be flipped and rotated, so when talking about “adjacent” or “three keys in front,” one must be careful.
Alice: Even so, you don’t need 8 different colors of tassels.
Try to determine: To distinguish $n$ keys on the same keyring, what is the minimum number of different colors of tassels needed? | 3 |
53,463 | [ The sum of the angles of a triangle. The theorem about the exterior angle.] [ Criteria and properties of an isosceles triangle. ]
On the side $B C$ of the isosceles triangle $A B C(A B=B C)$, points $N$ and $M$ ( $N$ is closer to $B$ than $M$) are taken such that $N M=A M$ and $\angle M A C=\angle B A N$.
Find $\angle C A N$. | 60 |
24,520 | Find the smallest positive real number $x$ such that
\[\lfloor x^2 \rfloor - x \lfloor x \rfloor = 6.\] | \dfrac{55}{7} |
23,558 | 13. A and B are partners in a business, and together they made a profit of $a^{2}$ yuan (where $a$ is a two-digit natural number). When dividing the money, A takes 100 yuan first, then B takes 100 yuan, followed by A taking another 100 yuan, B taking another 100 yuan, and so on, until the last amount taken is less than 100 yuan. To ensure that both end up with the same total amount, the one who took more gave 35.5 yuan to the one who took less. The total profit they made has $\qquad$ possible values. | 4 |
69,089 | $\left[\begin{array}{l}\text { Tangent Circles } \\ \text { [Pythagorean Theorem (direct and inverse).] }\end{array}\right]$
Two circles with radii $\sqrt{19}$ and $\sqrt{76}$, touching each other externally, are inscribed in a semicircle (i.e., each circle touches this semicircle and its diameter). Find the radius of the semicircle. | 4\sqrt{19} |
6,547 | Find the number of integer pairs \((x, y)\) that satisfy the system of inequalities:
\[
\left\{\begin{array}{l}
2x \geq 3y \\
3x \geq 4y \\
5x - 7y \leq 20
\end{array}\right.
\] | 231 |
24,460 | The sum of the first four terms of an arithmetic progression, as well as the sum of the first seven terms, are natural numbers. Furthermore, its first term \(a_1\) satisfies the inequality \(a_1 \leq \frac{2}{3}\). What is the greatest value that \(a_1\) can take? | \dfrac{9}{14} |
68,792 | 10. Given that functions $f(x), g(x)$ are periodic functions defined on $\mathbf{R}$, and they are monotonically increasing on the interval $[-1,1]$, which of the following statements is true:
A. $f(x)+g(x)$ is a periodic function
B. $f(x)+g(x)-|f(x)-g(x)|$ is monotonically increasing on $[-1,1]$
C. $f(g(x))$ is monotonically increasing on $[-1,1]$
D. $f(x)+g(x)+f(-x)+g(-x)$ is an even function
Among the correct propositions is $\qquad$ | BD |
11,924 | Given a triangle ABC, let I be the incenter. The internal bisectors of angles A, B, C meet the opposite sides in \(A'\), \(B'\), \(C'\) respectively. Prove that:
\[ \frac{1}{4} < \frac{AI \cdot BI \cdot CI}{AA' \cdot BB' \cdot CC'} \leq \frac{8}{27}. \] | \frac{1}{4} < \frac{AI \cdot BI \cdot CI}{AA' \cdot BB' \cdot CC'} \leq \frac{8}{27} |
30,247 | 24. Let $A=\{1,2,3, \cdots, 4 n+2\}, M=\{2 n+1,4 n+3,6 n+5\}$. For any non-empty subset $B$ of $A$, if the sum of any two numbers in $B$ does not belong to $M$, then $B$ is called an $M$-free set. If $A=A_{1} \cup A_{2}, A_{1} \cap A_{2}=$ $\varnothing$, and $A_{1}, A_{2}$ are both $M$-free sets, then the ordered pair $\left(A_{1}, A_{2}\right)$ is called an $M$-partition of $A$. Try to find the number of all $M-$ partitions of $A$. | 2^{n+1} |
61,494 | What is the maximum number of integers we can choose from the set $\{1,2,3, \ldots, 2017\}$ such that the difference between any two of them is not a prime number? | 505 |
12,495 | Let $a, b, c$ be the sides of triangle $\triangle ABC$, and let $S$ be its area. Prove that
\[a^{2} + b^{2} + c^{2} \geq 4 \sqrt{3} S + (a - b)^{2} + (b - c)^{2} + (c - a)^{2},\]
with equality if and only if $a = b = c$. | a^{2} + b^{2} + c^{2} \geq 4 \sqrt{3} S + (a - b)^{2} + (b - c)^{2} + (c - a)^{2} |
65,221 | 4. Piercarlo chooses $n$ integers from 1 to 1000 inclusive. None of his integers is prime, and no two of them share a factor greater than 1 .
What is the greatest possible value of $n$ ? | 12 |
68,525 | 23.16. (USA, 75). The polynomial $P(x)$ of degree $n$ satisfies the equalities $P(k)=k /(k+1)$ for $k=0,1, \ldots, n$. Find $P(n+1)$. | \frac{n+1+(-1)^{n+1}}{n+2} |
62,010 | 3. (3 points) Let $x_{1}, x_{2}, \ldots, x_{200}$ be natural numbers greater than 2 (not necessarily distinct). In a $200 \times 200$ table, the numbers are arranged as follows: at the intersection of the $i$-th row and the $k$-th column, the number $\log _{x_{k}} \frac{x_{i}}{9}$ is written. Find the smallest possible value of the sum of all numbers in the table. | -40000 |
33,912 | 11. If the inequality $\frac{1}{\sqrt{20 a+23 b}}+\frac{1}{\sqrt{23 a+20 b}} \geqslant \frac{\lambda}{\sqrt{a+b}}$ holds for all positive real numbers $a, b$, find the maximum value of $\lambda$. | \frac{2\sqrt{86}}{43} |
21,891 | Two circles touch each other externally at point \( C \). A line is tangent to the first circle at point \( A \) and to the second circle at point \( B \). The line \( AC \) intersects the second circle at point \( D \), distinct from \( C \). Find \( BC \), given that \( AC = 9 \) and \( CD = 4 \). | 6 |
54,219 | 1. The solution to the equation $x=|x-| x-6||$ is $x=$ | 2,6 |
66,374 | 5. In a certain social event, it was originally planned that every two people would shake hands exactly once, but after 4 people each shook hands twice they left. As a result, a total of 60 handshakes took place throughout the event. How many people initially attended the event? $\qquad$ . | 15 |
30,047 | Problem 8. In a right triangle $ABC$ with a right angle at $C$, points $P$ and $Q$ are the midpoints of the angle bisectors drawn from vertices $A$ and $B$. The inscribed circle of the triangle touches the hypotenuse at point $H$. Find the angle $PHQ$. | 90 |
27,652 | 16th USAMO 1987 Problem 2 The feet of the angle bisectors of the triangle ABC form a right-angled triangle. If the right-angle is at X, where AX is the bisector of angle A, find all possible values for angle A. Solution | 120 |
60,768 | ## Task A-4.2.
Let $S$ be the set of all natural numbers less than 1000 whose all digits in decimal notation are even. Let $\omega$ be a complex number such that $\omega^{2}+\omega+1=0$.
Calculate the sum $\sum_{k \in S} \omega^{k}$, i.e., the sum of the values $\omega^{k}$ for all $k$ in the set $S$. | -2 |
52,143 | 8.1. Large sandglasses measure an hour, and small ones measure 11 minutes. How can you use these sandglasses to measure a minute? | 1 |
53,151 | G3.3 Let $k$ be positive integer and $f(k)$ a function that if $\frac{k-1}{k}=0 . k_{1} k_{2} k_{3} \ldots \ldots$, then $f(k)=\overline{k_{1} k_{2} k_{3}}$, for example, $f(3)=666$ because $\frac{3-1}{3}=0.666 \ldots \ldots$, find the value of $D=f(f(f(f(f(112)))))$. | 998 |
24,362 | How many unordered pairs of coprime numbers are there among the integers 2, 3, ..., 30? Recall that two integers are called coprime if they do not have any common natural divisors other than one. | 248 |
14,866 | Draw the altitudes in an acute-angled triangle \(ABC\) and denote the feet of the altitudes as \(A_1, B_1, C_1\), and the orthocenter as \(M\). Show that
\[ M A \times M A_{1} = 2 R r \]
where \(R\) is the circumradius of the given triangle and \(r\) is the inradius of the pedal triangle. | MA \times MA_{1} = 2 R r |
64,823 | The door of the rabbit hutch is made of a wooden frame and wire mesh with square holes. The frame strips are $5 \mathrm{~cm}$ wide. Some nodes of the mesh align with the inner edges of the frame as shown in the picture. The inner (mesh) part of the door has an area of $432 \mathrm{~cm}^{2}$.
Determine the external dimensions (i.e., width and height) of the entire door.
( $S$. Bednářová)
 | 28\, |
2,764 | Two unit-radius spheres intersect in such a way that the resulting 3 parts have equal volume. How far apart are the centers of the spheres? | 4 \cos \left( \dfrac{4\pi}{9} \right) |
14,886 | Fill the numbers $1, 2, \cdots, 36$ into a $6 \times 6$ grid with each cell containing one number, such that each row is in ascending order from left to right. What is the minimum possible sum of the six numbers in the third column? | 63 |
5,914 | Given the equation $x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}=0$, where all coefficients are real and satisfy the conditions $0 < a_{0} \leqslant a_{1} \leqslant \cdots \leqslant a_{n-1} \leqslant 1$, and it is known that $\lambda$ is a complex root of this equation such that $|\lambda| \geq 1$. Prove that $\lambda^{n+1}=1$. (1992 CMO - Problem 7) | \lambda^{n+1} = 1 |
68,481 | 2. For $x, y, z \in (0,2]$, find the maximum value of the expression
$$
A=\frac{\left(x^{3}-6\right) \sqrt[3]{x+6}+\left(y^{3}-6\right) \sqrt[3]{y+6}+\left(z^{3}-6\right) \sqrt[3]{z+6}}{x^{2}+y^{2}+z^{2}}
$$ | 1 |
13,304 | 520. A circle of radius $r$ is inscribed in a triangle with perimeter $p$ and area $S$. How are these three quantities related? | S = \frac{r \cdot p}{2} |
61,036 | 1. Calculate: $1+\frac{2}{3}+\frac{3}{3^{2}}+\frac{4}{3^{3}}+\cdots+\frac{10}{3^{9}}+$ $\frac{23}{3^{9}+3^{10}}=$ $\qquad$ | \frac{9}{4} |
53,152 | Initially on the computer screen - some prime number. Every second, the number on the screen is replaced by the number obtained from the previous one by adding its last digit, increased by 1. What is the maximum time it will take for a composite number to appear on the screen?
# | 5 |
66,057 | 5. At least how many circles with a radius of 1 are needed to cover a circle with a radius of 2. | 7 |
33,693 | 14. Let \( f(x) = A(x^2 - 2x)e^x - e^x + 1 \). For any \( x \leq 0 \), \( f(x) \geq 0 \) holds. Determine the range of the real number \( A \). | [-\frac{1}{2},+\infty) |
62,846 | B3. A figure consists of a square $A B C D$ and a semicircle with diameter $A D$ outside the square. The side of the square has length 1. What is the radius of the circumscribed circle of the figure?
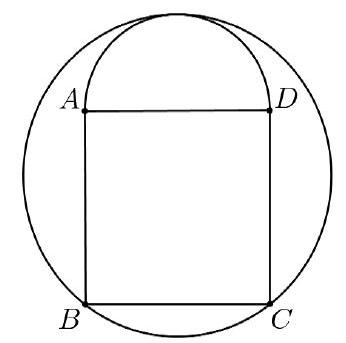 | \frac{5}{6} |
60,590 | 9. Team A and Team B each send out 7 players to participate in a Go chess tournament in a predetermined order. Both sides start with their No. 1 players competing; the loser is eliminated, and the winner then competes with the No. 2 player of the losing side, $\cdots$, until all players of one side are eliminated, and the other side wins, forming a match process. How many different possible match processes are there? | 3432 |
11,454 | 355. Find $y^{\prime}$, if $y=\operatorname{arcctg} 3 x$. | -\dfrac{3}{9x^2 + 1} |
7,737 | 2.1. Trapezoid $A B C D$ with base $A D=6$ is inscribed in a circle. The tangent to the circle at point $A$ intersects lines $B D$ and $C D$ at points $M$ and $N$ respectively. Find $A N$, if $A B \perp M D$ and $A M=3$. | 12 |
56,754 | # Problem 7. (4 points)
Natural numbers $a, b, c$ are such that $\operatorname{GCD}(\operatorname{LCM}(a, b), c) \cdot \operatorname{LCM}(\operatorname{GCD}(a, b), c)=200$.
What is the greatest value that $\operatorname{GCD}(\operatorname{LCM}(a, b), c)$ can take? | 10 |
32,985 | 19. As shown in the figure, in the dihedral angle $\alpha-E F-\beta$, $A E \subset \alpha, B F \subset \beta$, and $A E \perp E F, B F \perp E F, E F=1, A E=2, A B=$ $\sqrt{2}$, find the maximum volume of the tetrahedron $A B E F$. | \frac{1}{3} |
54,229 | At a certain school, there are 6 subjects offered, and a student can take any combination of them. It is noticed that for any two subjects, there are fewer than 5 students taking both of them and fewer than 5 students taking neither. Determine the maximum possible number of students at the school. | 20 |
55,396 | We form a decimal code of $21$ digits. the code may start with $0$. Determine the probability that the fragment $0123456789$ appears in the code. | \frac{12 \cdot 10^{11} - 30}{10^{21}} |
53,525 | 7. In a bus without a conductor, there were 20 people. Although they only had coins worth 10, 15, and 20 kopecks, each of them paid for the fare and received the change they were due. How could this have happened? Prove that they had no fewer than 25 coins. (One ticket costs 5 kopecks.) | 25 |
9,347 | Given \( x = -2272 \), \( y = 10^3 + 10^2 c + 10 b + a \), and \( z = 1 \), which satisfy the equation \( a x + b y + c z = 1 \), where \( a \), \( b \), \( c \) are positive integers and \( a < b < c \). Find \( y \). | 1987 |
52,123 | 10.22 Find the largest 5-digit number $A$ with the following properties: its 4th digit is greater than the 5th digit, its 3rd digit is greater than the sum of the 4th and 5th digits, its 2nd digit is greater than the sum of the 3rd, 4th, and 5th digits, and its first digit is greater than the sum of the other digits.
(43rd Moscow Mathematical Olympiad, 1980) | 95210 |
6,366 | If there are two points on the parabola \( y = ax^2 - 1 \) that are symmetric with respect to the line \( x + y = 0 \), find the range of values for \( a \). | \left( \dfrac{3}{4}, \infty \right) |
59,947 | (1) (20 points) In $\triangle A B C$, it is known that $A B=2, A C=1$, and $\cos 2 A+$ $2 \sin ^{2} \frac{B+C}{2}=1$.
(1) Find the size of angle $A$ and the length of side $B C$;
(2) If point $P$ moves within $\triangle A B C$ (including the boundary), and the sum of the distances from point $P$ to the three sides is $d$. Let the distances from point $P$ to sides $B C$ and $C A$ be $x$ and $y$, respectively. Express $d$ in terms of $x$ and $y$, and find the range of $d$. | [\frac{\sqrt{3}}{2},\sqrt{3}] |
65,681 | ## Task B-2.3.
One year, January 1 and April 1 were both on a Thursday. How many months in that year have five Fridays? Justify your answer. | 5 |
14,727 | Regular octagon \(C H I L D R E N\) has area 1. Find the area of pentagon \(C H I L D\). | \dfrac{1}{2} |
23,976 | Real numbers \(a, b, c\) and a positive number \(\lambda\) such that \(f(x)=x^3 + ax^2 + bx + c\) has three real roots \(x_1, x_2, x_3\), satisfying
1. \(x_2 - x_1 = \lambda\);
2. \(x_3 > \frac{1}{2}(x_1 + x_2)\).
Find the maximum value of \(\frac{2a^3 + 27c - 9ab}{\lambda^3}\). | \dfrac{3\sqrt{3}}{2} |
52,594 | 5th APMO 1993 Problem 4 Find all positive integers n for which x n + (x+2) n + (2-x) n = 0 has an integral solution. Solution | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.