id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
4,365 | In parallelogram \(ABCD\), side \(AD\) is equal to 6. The angle bisector of \(\angle ADC\) intersects line \(AB\) at point \(E\). In triangle \(ADE\), an inscribed circle touches side \(AE\) at point \(K\) and side \(AD\) at point \(T\). Given that \(KT = 3\), find the angle \(\angle BAD\). | 60^\circ |
65,103 | 10.16 There is a five-digit positive odd number $x$. In $x$, all 2s are replaced with 5s, and all 5s are replaced with 2s, while other digits remain unchanged, resulting in a new five-digit number, denoted as $y$. If $x$ and $y$ satisfy the equation $y=2(x+1)$, what is the value of $x$?
(China Junior High School Mathematics League, 1987) | 29995 |
32,533 | LV OM - III - Task 5
Determine the maximum number of lines in space passing through a fixed point and such that any two intersect at the same angle. | 6 |
58,239 | Solve the equation
$$
x^{2}-4 x+3=\sqrt{1+\sqrt{x-1}}
$$ | \frac{5+\sqrt{5}}{2} |
58,301 | 3. Find the smallest natural number $n$ such that the number $n^{2}$ begins with 2019 (i.e., $n^{2}=2019 \ldots$). | 1421 |
52,037 | B4. Bob and Jane hold identical decks of twelve cards, three of each colour: red, green, yellow, and blue. Bob and Jane shuffle their decks and then take turns dealing one card at a time onto a pile, with Jane going first. Find the probability that Jane deals all her red cards before Bob deals any of his red cards.
Give your answer in the form of a fraction in lowest terms. | \frac{39}{1100} |
33,971 | (5) Find the largest real number $\lambda$ such that for a real-coefficient polynomial $f(x)=x^{3}+$ $a x^{2}+b x+c$ with all roots being non-negative real numbers, if $x \geqslant 0$, then
$$
f(x) \geqslant \lambda(x-a)^{3}
$$
When does the equality hold in the above inequality? | -\frac{1}{27} |
31,091 | The centers of three pairwise externally tangent circles are located at points $A, B, C$,
$\angle A B C=90^{\circ}$. The points of tangency are $K, P$, and $M$; point $P$ lies on side $A C$. Find the angle $K P M$. | 45 |
26,804 | 8.4. In how many ways can all natural numbers from 1 to $2 n$ be arranged in a circle so that each number is a divisor of the sum of its two neighboring numbers? (Ways that differ only by rotation or symmetry are considered the same) | 1 |
67,387 | 3. On the side $B C$, resp. $C D$ of the parallelogram $A B C D$, determine points $E$, resp. $F$ such that segments $E F, B D$ are parallel and triangles $A B E, A E F$ and $A F D$ have the same areas. | (\sqrt{5}-1):2 |
21,410 | On the lateral side \( CD \) of the trapezoid \( ABCD (AD \parallel BC) \), point \( M \) is marked. From vertex \( A \), a perpendicular \( AH \) is dropped onto segment \( BM \). It turns out that \( AD = HD \). Find the length of segment \( AD \) if it is known that \( BC = 16 \), \( CM = 8 \), and \( MD = 9 \). | 18 |
64,617 | # Problem 3. (3 points)
The sequence $\left\{a_{n}\right\}$ is defined by the conditions $a_{1}=2$ and $a_{n}=a_{1}+a_{2}+\ldots+a_{n-1}+n$ for $n \geqslant 2$. Find the explicit formula for this sequence. | a_{n}=5\cdot2^{n-2}-1 |
3,570 | Compute \(\sqrt[4]{5508^{3}+5625^{3}+5742^{3}}\), given that it is an integer. | 855 |
1,946 | Given a cyclic quadrilateral \(ABCD\) where \(\angle ABC + \angle ABD = 90^\circ\). A point \(E\) is marked on the diagonal \(BD\) such that \(BE = AD\). From \(E\), a perpendicular \(EF\) is dropped to side \(AB\). Prove that \(CD + EF < AC\). | CD + EF < AC |
65,031 | Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
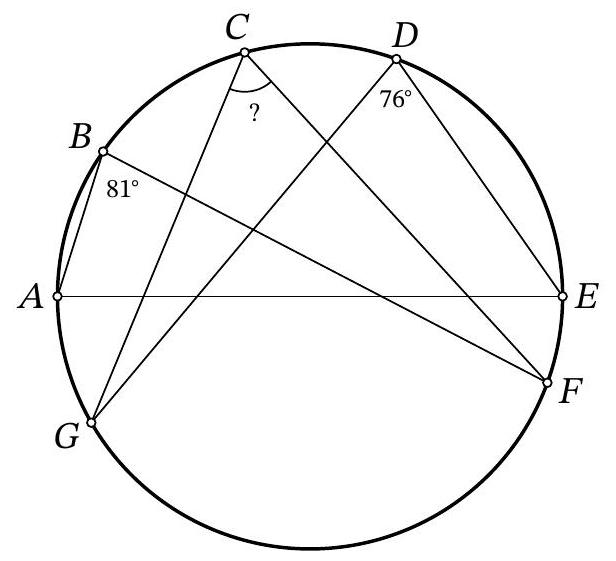 | 67 |
55,385 | Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
 | 3 |
56,370 | 5. A $5 \times 5$ square is to be cut into two types of rectangles: $1 \times 4$ and $1 \times 3$. How many rectangles can result from the cutting? Justify your answer. | 7 |
62,494 | 9.1. If Petya performs a certain task in such a way that each subsequent day he does twice as much as in all the previous days combined, then the entire task will take him 12 days. How many days will it take for Petya and Kolya to complete this task if Kolya works in the same way as Petya?
$$
\text { (4-8 grades) }
$$ | 11 |
52,223 | 6. (2006 National High School Mathematics Competition Henan Grade 1 Test) Let the function $f(x)(x \in \mathbf{R}, x \neq 0)$ for any non-zero real numbers $x_{1}, x_{2}$, have $f\left(x_{1} x_{2}\right)=f\left(x_{1}\right)+f\left(x_{2}\right)$, and $f(x)$ is an increasing function on $(0,+\infty)$, then the solution to the inequality $f(x)+$ $f\left(x-\frac{1}{2}\right) \leqslant 0$ is $\qquad$. | [\frac{1-\sqrt{17}}{4},0)\cup(0,\frac{1}{2})\cup(\frac{1}{2},\frac{1+\sqrt{17}}{4}] |
51,830 | 16. [10] Given an angle $\theta$, consider the polynomial
$$
P(x)=\sin (\theta) x^{2}+(\cos (\theta)+\tan (\theta)) x+1 \text {. }
$$
Given that $P$ only has one real root, find all possible values of $\sin (\theta)$. | 0,\frac{\sqrt{5}-1}{2} |
61,747 | 4. Find the function $f: \mathbf{Z}_{+} \rightarrow \mathbf{Z}_{+}$, such that for all $m, n \in \mathbf{Z}_{+}$, we have
$$
(n!+f(m)!) \mid(f(n)!+f(m!)) \text {. }
$$ | f(n)=n |
65,579 | 2. Two supplementary angles have a common side, and their bisectors determine an angle of $60^{\circ}$. Determine the measures of the two angles.
Mathematical Gazette - 10/2013 | 30 |
63,100 | 10. At each of the vertices of a cube sits a Bunchkin. Two Bunchkins are said to be adjacent if and only if they sit at either end of one of the cube's edges. Each Bunchkin is either a 'truther', who always tells the truth, or a 'liar', who always lies. All eight Bunchkins say 'I am adjacent to exactly two liars'. What is the maximum number of Bunchkins who are telling the truth? | 4 |
56,591 | Exercise 2. Let $x, y$ and $z$ be three real numbers such that $0 \leqslant x \leqslant y \leqslant z$ and $x+y+z=1$. Find the maximum value that the expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2}
$$
can take. | 1 |
50,504 | The diagram shows a circle graph which shows the amount of homework done each day by Mr. Auckland's Grade 9 class. Based on the circle graph, what percentage of students do at least one hour of homework per day?
(A) $25 \%$
(B) $33 \%$
(C) $50 \%$
(D) $67 \%$
(E) $75 \%$
Hours of homework per day
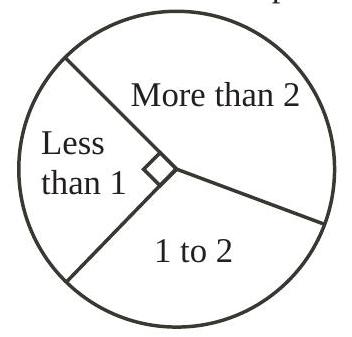
Part B: Each correct answer is worth 6. | 75 |
65,231 | ## 13. The Scout and the Drummer
On the occasion of the village festival, a procession was organized that stretched for 250 m; the scouts led the procession, and the musicians brought up the rear. Soon after the march began, the youngest scout remembered that he had not tied his neckerchief, which was left with his friend, the drummer, who was in the last row of the musicians. So the scout ran to get the neckerchief and returned to his place in 3 minutes and 18 seconds.
What was the speed of the procession, assuming the scout ran at a speed of 10 km/h? | 3 |
53,536 | 3.2. Znayka cut out a semicircle from paper. Neznaika marked a point $C$ on the diameter $A B$ of this semicircle and cut off two semicircles from Znayka's semicircle with diameters $A C$ and $C B$. Find the area of the remaining figure if the length of the part of the chord lying inside it, passing through point $C$ perpendicular to $A B$, is 8. If necessary, round your answer to two decimal places. | 50.27 |
31,247 | [ $\left[\begin{array}{ll}\text { Cylinder } & \\ \text { Cone } & \end{array}\right]$ [ Tangent spheres $]$
A cylinder with a base radius of 1 and height $\frac{12}{3+2 \sqrt{3}}$ has three identical spheres inscribed in it such that the spheres touch the upper base of the cylinder, its lateral surface, and each other. Find the volume of the cone whose base coincides with the lower base of the cylinder and which touches all three spheres. | \frac{4}{9}\pi |
68,246 | 2. In triangle $ABC$, we have $\overline{AB}=2 \text{~cm}, \overline{BC}=4 \text{~cm}$, and $\overline{CA}=2 \sqrt{2} \text{~cm}$. Let $P$ be a point on the angle bisector of angle at vertex $B$ such that $AP$ is perpendicular to that bisector, and let $Q$ be a point on the angle bisector of angle at vertex $C$ such that $AQ$ is perpendicular to that bisector. Calculate the length of the segment $PQ$. | \sqrt{2}-1 |
51,108 | Let $ABCD$ be an inscribed trapezoid such that the sides $[AB]$ and $[CD]$ are parallel. If $m(\widehat{AOD})=60^\circ$ and the altitude of the trapezoid is $10$, what is the area of the trapezoid? | 100\sqrt{3} |
27,052 | Problem 10. In a triangular pyramid $ABCD$ with base $ABC$, the lateral edges are pairwise perpendicular, $DA=DB=2, DC=5$. A light ray is emitted from a point on the base. After reflecting exactly once from each lateral face (the ray does not reflect from the edges), the ray hits a point on the base of the pyramid. What is the shortest distance the ray could have traveled? | \frac{10\sqrt{6}}{9} |
63,823 | 6. (10 points) A deck of playing cards, excluding the joker, has 4 suits totaling 52 cards, with each suit having 13 cards, numbered from 1 to 13. Feifei draws 2 hearts, 3 spades, 4 diamonds, and 5 clubs. If the sum of the face values of these 14 cards Feifei drew is exactly 35, then how many of them are 1?
$\qquad$ cards are 1. | 4 |
18,714 | Arrange $\frac{n(n+1)}{2}$ different numbers randomly into a triangular array. Let $M_k$ be the maximum number in the $k$-th row (from top to bottom). Find the probability that $M_1 < M_2 < \cdots < M_n$. | \dfrac{2^n}{(n + 1)!} |
8,704 | In quadrilateral $\mathrm{ABFD}$, $\mathrm{C}$ and $\mathrm{E}$ are points on $\mathrm{BF}$ and $\mathrm{DF}$, respectively, such that $\angle \mathrm{BAC} = \angle \mathrm{DAE}$. Lines $\mathrm{BE}$ and $\mathrm{CD}$ intersect at point $\mathrm{G}$. Connect $\mathrm{AG}$. Prove that $\angle \mathrm{FAC} = \angle \mathrm{GAE}$. | \angle \mathrm{FAC} = \angle \mathrm{GAE} |
32,545 | 5. [5 points] Given the numbers $\log _{\sqrt{2 x-3}}(x+1), \log _{2 x^{2}-3 x+5}(2 x-3)^{2}, \log _{x+1}\left(2 x^{2}-3 x+5\right)$. For which $x$ are two of these numbers equal, and the third one less than them by 1? | 4 |
63,412 | 9-8-1. In Midcity, houses stand along one side of a street, each house can have $1,2,3, \ldots, 9$ floors. According to an ancient law of Midcity, if two houses on one side of the street have the same number of floors, then no matter how far apart they are from each other, there must be a house with more floors between them. What is the maximum possible number of houses on one side of the street in Midcity? | 511 |
61,378 | Every phone number in an area consists of eight digits and starts with digit $ 8$. Mr Edy, who has just moved to the area, apply for a new phone number. What is the chance that Mr Edy gets a phone number which consists of at most five different digits? | 0.41032 |
51,046 | 3. Find the smallest natural number that has exactly 70 natural divisors (including 1 and the number itself).
(16 points) | 25920 |
22,745 | For $\pi \le \theta < 2\pi$ , let
\begin{align*} P &= \frac12\cos\theta - \frac14\sin 2\theta - \frac18\cos 3\theta + \frac{1}{16}\sin 4\theta + \frac{1}{32} \cos 5\theta - \frac{1}{64} \sin 6\theta - \frac{1}{128} \cos 7\theta + \cdots \end{align*}
and
\begin{align*} Q &= 1 - \frac12\sin\theta -\frac14\cos 2\theta + \frac18 \sin 3\theta + \frac{1}{16}\cos 4\theta - \frac{1}{32}\sin 5\theta - \frac{1}{64}\cos 6\theta +\frac{1}{128}\sin 7\theta + \cdots \end{align*}
so that $\frac{P}{Q} = \frac{2\sqrt2}{7}$ . Then $\sin\theta = -\frac{m}{n}$ where $m$ and $n$ are relatively prime positive integers. Find $m+n$ | 36 |
53,484 | # Problem 1. (2 points)
Do there exist two natural numbers $x$ and $y$, having the same number of natural divisors, such that $x<y$, and the sum of all divisors of $x$ (including 1 and the number itself) is greater than the sum of natural divisors of $y$ (including 1 and the number itself)? | Yes |
27,633 | Asahanov $H . X$.
The number $x$ is such that among the four numbers $a=x-\sqrt{2}, b=x-\frac{1}{x}, c=x+\frac{1}{x}, d=x^{2}+2 \sqrt{2}$ exactly one is not an integer.
Find all such $x$. | \sqrt{2}-1 |
4,049 | Let \( m \) and \( n \) be integers such that \( 0 \leq m \leq n \). Prove that:
\[
\sum_{k=0}^{m}\binom{m}{k}\binom{n}{k}=\binom{m+n}{m}
\] | \binom{m+n}{m} |
19,457 | There are \( n \) boys and \( n \) girls in a class (\( n \geq 3 \)). They are seated around a circular table in such a way that no two boys and no two girls sit next to each other. The teacher has \( 2n \) cards, numbered \( 1, 2, 3, \ldots, 2n \), each number appearing exactly once. The teacher distributes one card to each student such that the number on any girl's card is greater than the number on any boy's card. Then, each girl writes down the sum of the numbers on three cards: her own and those of the boys sitting adjacent to her. For which values of \( n \) could all the sums written down by the \( n \) girls be equal? | n \text{ is odd} |
67,951 | 4. (8 points) There is a sequence, the first term is 12, the second term is 19, starting from the third term, if the sum of its previous two terms is odd, then this term equals the sum of the previous two terms, if the sum of the previous two terms is even, this term equals the difference of the previous two terms (the larger number minus the smaller number). Then, in this sequence, the $\qquad$ term first exceeds 2016. | 252 |
17,117 | Given the set \( A = \{1, 2, 3, \ldots, 104\} \), and \( S \) is a subset of \( A \). If for any \( x \in S \), neither \( x-1 \in S \) nor \( x+1 \in S \), then \( x \) is called an isolated point of \( S \). How many 5-element subsets of \( A \) have no isolated points? | 10000 |
27,295 | B2. An integer $n$ is called a combi-number if every pair of different digits from all possible digits $0 \mathrm{t} / \mathrm{m} 9$ appear next to each other at least once in the number. Thus, in a combi-number, the digits 3 and 5 appear next to each other somewhere. It does not matter whether they appear in the order 35 or 53. We agree that a combi-number does not start with the digit 0.
What is the smallest number of digits a combi-number can consist of? | 50 |
27,504 | 8,9 [
In triangle $ABC$, angle $B$ is equal to $\arccos \frac{15}{17}$. On side $AC$, a point $K$ is taken such that $AK=12$, $KC=4$. Find the radius of the circle passing through vertex $B$, touching side $AC$ at point $K$, and touching the circumcircle of triangle $ABC$.
# | 12 |
13,901 | Prove that \[ \lim_{n \to \infty} n \left( \frac{\pi}{4} - n \int_0^1 \frac{x^n}{1+x^{2n}} \, dx \right) = \int_0^1 f(x) \, dx , \] where $f(x) = \frac{\arctan x}{x}$ if $x \in \left( 0,1 \right]$ and $f(0)=1$ .
*Dorin Andrica, Mihai Piticari* | \int_0^1 \frac{\arctan x}{x} \, dx |
64,140 | Problem 10.1. In each cell of a $5 \times 5$ table, a natural number is written in invisible ink. It is known that the sum of all the numbers is 200, and the sum of three numbers inside any $1 \times 3$ rectangle is 23. What is the central number in the table?
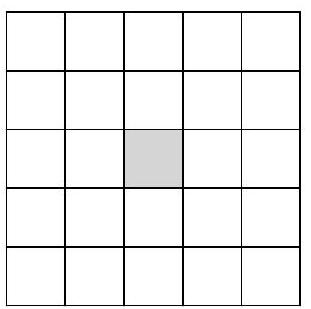 | 16 |
60,020 | 7. Given the sequence $\left\{a_{n}\right\}$:
$$
a_{n}=2^{n}+3^{n}+6^{n}+1\left(n \in \mathbf{Z}_{+}\right) \text {. }
$$
Does there exist an integer $k \geqslant 2$, such that $k$ is coprime with all numbers in the sequence $\left\{a_{n}\right\}$? If it exists, find the smallest integer $k$; if not, explain the reason. (Zhang Lei provided the problem) | 23 |
57,904 | 31. How many planes of symmetry do the following have: a) a cube; b) a regular tetrahedron? | 6 |
22,329 |
In a park, paths are laid out as shown in the diagram. Two workers started paving the paths simultaneously from point $A$. They pave at constant speeds: the first worker on the path $A-B-C$, and the second worker on the path $A-D-E-F-C$. They finished the work at the same time, spending a total of 9 hours. It is known that the second worker works 1.2 times faster than the first worker. How many minutes did the second worker spend paving the section $D-E$? | 45 |
9,574 | 10. One day, Xiao Ming went shopping with 100 yuan. At the first store, he bought several items of $\mathrm{A}$, at the second store, he bought several items of $\mathrm{B}$, at the third store, he bought several items of $\mathrm{C}$, at the fourth store, he bought several items of $\mathrm{D}$, at the fifth store, he bought several items of $\mathbf{E}$, and at the sixth store, he bought several items of $\mathbf{F}$. The prices of the six items are all different and are whole numbers of yuan, and Xiao Ming spent the same amount of money in each of the six stores. Then, Xiao Ming has $\qquad$ yuan left. | 28 |
10,976 | How many of the first $1000$ positive integers can be expressed in the form $\lfloor 2x \rfloor + \lfloor 4x \rfloor + \lfloor 6x \rfloor + \lfloor 8x \rfloor$ , where $x$ is a real number, and $\lfloor z \rfloor$ denotes the greatest integer less than or equal to $z$ ?
Please give the answer directly without any intermediate steps. | 600 |
29,771 | A convex body has six square and eight regular hexagonal faces. We know that no two of the square faces share a vertex. Determine the volume of the body, given that it has an edge of unit length. | 8\sqrt{2} |
18,543 | What is the smallest number of points that can be chosen on a circle of length 1956 such that for each of these points there is exactly one chosen point at a distance of 1 and exactly one chosen point at a distance of 2 (distances are measured along the circle)? | 1304 |
62,554 | ## Task 6A - 291246A
In two urns $A$ and $B$, there are exactly $m$ red and exactly $n$ blue balls in total. The total number of balls is greater than 2; at least one of the balls is red.
At the beginning, $A$ contains all the red and $B$ all the blue balls.
By alternately taking one randomly selected ball from $A$ and $B$ and placing it in the other urn, the balls are to be mixed.
The process begins with the removal from urn $A$.
Determine all pairs $(m ; n)$ of the numbers $m$ and $n$ for which the fourth ball moved has a probability of $\frac{1}{2} 2$ of being red.
Hint:
If an urn contains exactly $Z$ balls, then by random selection of a ball, it is understood that the probability of selecting any of the $Z$ balls is $\frac{1}{Z}$.
More generally, if from $M$ possible events $G$ are considered favorable and $M-G$ are considered unfavorable, and all $M$ events are equally likely, then the probability of a favorable event occurring is $\frac{G}{M}$. | (4,2) |
64,174 | 123 A cube with edge length $n$ is divided into $n^{3}$ unit cubes by planes parallel to its faces. The number of pairs of unit cubes that share no more than 2 vertices is $\qquad$. | \frac{1}{2}n^{2}(n^{4}-7n+6) |
9,681 | Find the smallest real number \( A \) such that for every quadratic polynomial \( f(x) \) satisfying \( |f(x)| \leq 1 \) for \( 0 \leq x \leq 1 \), the inequality \( f^{\prime}(0) \leq A \) holds. | 8 |
66,066 | 5. Let's solve the inequality $\quad \frac{\sqrt{x^{2}+x}-\sqrt{4-2 x}}{2 x+5-2 \sqrt{x^{2}+5 x+6}} \leq 0$.
Domain of definition for the numerator and denominator: $x(x+1) \geq 0, \quad 4-2 x \geq 0, x^{2}+5 x+6 \geq 0, \Rightarrow$ $x \in(-\infty ;-3] \cup[-2 ;-1] \cup[0 ; 2]$.
On the domain of definition, the original inequality is equivalent to the following
$\frac{x^{2}+x-(4-2 x)}{(x+3)-2 \sqrt{(x+3)(x+2)}+x+2} \leq 0 \Rightarrow \frac{(x+4)(x-1)}{(x+3)-2 \sqrt{(x+3)(x+2)}+x+2} \leq 0$.
If $x \geq-2$, then we arrive at the inequality $\frac{(x+4)(x-1)}{(\sqrt{x+3}-\sqrt{x+2})^{2}} \leq 0$, and $x \in[-2 ; 1]$.
Considering the domain of definition, $x \in[-2 ;-1] \cup[0 ; 1]$.
If $x \leq-3$, then we arrive at the inequality $\frac{(x+4)(x-1)}{-(\sqrt{-x-3}+\sqrt{-x-2})^{2}} \leq 0$, and
$x \in(-\infty ;-4]$, which is within the domain of definition. Finally, we have $x \in(-\infty ;-4] \cup[-2 ;-1] \cup[0 ; 1]$. | x\in(-\infty;-4]\cup[-2;-1]\cup[0;1] |
14,360 | Given the quadratic function
$$
\begin{aligned}
f(x)= & a(3 a+2 c) x^{2}-2 b(2 a+c) x+ \\
& b^{2}+(c+a)^{2}(a, b, c \in \mathbf{R}),
\end{aligned}
$$
assume that for any $x \in \mathbf{R}$, there is $f(x) \leqslant 1$. Find the maximum value of $|ab|$. | \dfrac{3\sqrt{3}}{8} |
64,009 | Example 3 Real numbers $x_{1}, x_{2}, x_{3}, x_{4} \in [0,1]$. Find $K_{\max }$, where,
$$
\begin{aligned}
K= & \left|x_{1}-x_{2}\right|\left|x_{1}-x_{3}\right|\left|x_{1}-x_{4}\right|\left|x_{2}-x_{3}\right| \cdot \\
& \left|x_{2}-x_{4}\right|\left|x_{3}-x_{4}\right| .
\end{aligned}
$$ | \frac{\sqrt{5}}{125} |
56,682 | We select two points independently at random on the interval $(0,1)$ of the number line. (By saying that a point $P$ is chosen at random on the segment $(a, b)$, we mean that the probability that $P$ falls within any subinterval $(c, d)$ is $\frac{d-c}{b-a}$.)
We know about a number $h$ that the probability that the distance between the two chosen points is less than $h$ lies between $\frac{1}{4}$ and $\frac{3}{4}$.
What are the bounds within which $h$ lies? | \frac{1}{2}<1-\frac{\sqrt{3}}{2} |
7,908 | In the Cartesian coordinate system \(xOy\), \(F_{1}\) and \(F_{2}\) are the left and right foci of the ellipse \(\frac{x^{2}}{2} + y^{2} = 1\). Suppose a line \(l\) that does not pass through the focus \(F_{1}\) intersects the ellipse at two distinct points \(A\) and \(B\), and the distance from the focus \(F_{2}\) to the line \(l\) is \(d\). If the slopes of the lines \(AF_{1}\), \(l\), and \(BF_{1}\) form an arithmetic sequence, determine the range of \(d\). | (\sqrt{3}, 2) |
2,504 | Fyodor starts writing pairs of natural numbers $(a, b)$ on a board, where $a < b$ and each number does not exceed 2018. Furthermore, if a pair $(a, b)$ is already on the board, he cannot write any pair of the form $(c, a)$ or $(b, d)$. What is the greatest number of pairs he can write on the board? | 1018081 |
33,749 | Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
 | 4 |
28,839 | 9. Let real numbers $x_{1}, x_{2}, \cdots, x_{2008}$ satisfy the condition $\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\cdots+\left|x_{2007}-x_{2008}\right|=$ 2008, $y_{k}=\frac{1}{k}\left(x_{1}+x_{2}+\cdots+x_{k}\right), k=1,2, \cdots, 2008$, find $T=\left|y_{1}-y_{2}\right|+$ $\left|y_{2}-y_{3}\right|+\cdots+\left|y_{2007}-y_{2008}\right|$ the maximum value. | 2007 |
50,867 | 8. Let the arithmetic sequence $\left\{a_{n}\right\}$ have all terms as integers, with the first term $a_{1}=2019$, and for any positive integer $n$, there always exists a positive integer $m$ such that $a_{1}+a_{2}+\cdots+a_{n}=a_{m}$. The number of such sequences $\left\{a_{n}\right\}$ is $\qquad$ | 5 |
15,605 | Let $\xi_{1}, \ldots, \xi_{n}$ be independent random variables uniformly distributed on $[0,1]$. Using the inclusion-exclusion formula from Problem II.8.60, prove the Laplace formula
$$
\mathrm{P}\left(\xi_{1}+\ldots+\xi_{n} \leqslant x\right)=\frac{1}{n!} \sum_{k=0}^{[x]}(-1)^{k} C_{n}^{k}(x-k)^{n}, \quad 0 \leqslant x \leqslant n
$$
where $[x]$ is the integer part of $x$. | \mathrm{P}\left(\xi_{1}+\ldots+\xi_{n} \leqslant x\right)=\frac{1}{n!} \sum_{k=0}^{[x]}(-1)^{k} C_{n}^{k}(x-k)^{n} |
1,840 | Given an isosceles triangle \( ABC \) (\( AB = BC \)). Point \( E \) is marked on ray \( BA \) beyond point \( A \), and point \( D \) is marked on side \( BC \). It is known that
$$ \angle ADC = \angle AEC = 60^\circ, \quad AD = CE = 13. $$
Find the length of segment \( AE \) if \( DC = 9 \). | 4 |
64,142 | 96*. A piece is broken off from each of three identical rods; the break points of all three rods are chosen at random. What is the probability that a triangle can be formed from the three resulting pieces? | \frac{1}{2} |
23,525 | Triangle $ABC$ has $BC = 7, CA = 8, AB = 9$ . Let $D, E, F$ be the midpoints of $BC, CA, AB$ respectively, and let $G$ be the intersection of $AD$ and $BE$ . $G'$ is the reflection of $G$ across $D$ . Let $G'E$ meet $CG$ at $P$ , and let $G'F$ meet $BG$ at $Q$ . Determine the area of $APG'Q$ . | \dfrac{16\sqrt{5}}{3} |
66,092 | # Problem 9.2 (7 points)
In a bag, there are 70 balls that differ only in color: 20 red, 20 blue, 20 yellow, and the rest are black and white.
What is the minimum number of balls that need to be drawn from the bag, without seeing them, to ensure that among them there are at least 10 balls of the same color? | 38 |
59,596 | 13.1.1 $\star$ In the first quadrant of the Cartesian coordinate system, number the points (lattice points) with integer coordinates in the following manner: (1) $(0,0)$, (2) $(1,0)$, (3) $(1,1)$, (4) $(0,1)$, (5) $(0,2)$, (6) $(1,2)$, (7) $(2,2)$, (8) $(2,1)$, (9) $(2,0), \cdots \cdots$ (as shown in the order of the arrows in the figure). Find the coordinates of the 2000th point. | (44,25) |
64,007 | 52. In the left table below, adding 1 or subtracting 1 simultaneously to the numbers in two cells that share a common edge is called one operation. After a finite number of operations, the left table becomes the right table. What is the number at $A$ in the right table? $\qquad$ _. | 5 |
20,741 | Let \( p \) be a prime number. Let \( \mathbb{F}_{p} \) denote the integers modulo \( p \), and let \( \mathbb{F}_{p}[x] \) be the set of polynomials with coefficients in \( \mathbb{F}_{p} \). Define \( \Psi: \mathbb{F}_{p}[x] \rightarrow \mathbb{F}_{p}[x] \) by
$$
\Psi\left(\sum_{i=0}^{n} a_{i} x^{i}\right)=\sum_{i=0}^{n} a_{i} x^{p^{i}} .
$$
Prove that for nonzero polynomials \( F, G \in \mathbb{F}_{p}[x] \),
$$
\Psi(\operatorname{gcd}(F, G))=\operatorname{gcd}(\Psi(F), \Psi(G))
$$ | \Psi(\operatorname{gcd}(F, G)) = \operatorname{gcd}(\Psi(F), \Psi(G)) |
51,214 | ## Subject I
a) If $m, n \in N^{*}$, find the smallest number of the form $\left|5^{2 m}-3^{n}\right|$.
b) Compare the numbers: $\frac{\sqrt{2014}^{2014}+\sqrt{2015}^{2015}}{\sqrt{2014}^{2015}+\sqrt{2015}^{2014}}$ and $\frac{\sqrt{2014}}{\sqrt{2015}}$. | 2 |
58,776 | 3. A circle $\omega$ is circumscribed around triangle $A B C$. Circle $\omega_{1}$ touches the line $A B$ at point $A$ and passes through point $C$, while circle $\omega_{2}$ touches the line $A C$ at point $A$ and passes through point $B$. A tangent is drawn from point $A$ to circle $\omega$, which intersects circle $\omega_{1}$ again at point $X$ and intersects circle $\omega_{2}$ again at point $Y$. Find the ratio $\frac{A X}{X Y}$. | \frac{1}{2} |
61,209 | 365. The lengths of two parallel sides of a rectangle are 1 cm. In addition, it is known that it can be divided into four rectangles by two perpendicular lines, three of which have an area of no less than $1 \mathrm{~cm}^{2}$, and the fourth no less than $2 \mathrm{~cm}^{2}$. What is the minimum length of the other two sides of the rectangle for this to be possible? | 3+2\sqrt{2} |
28,706 | Question 68: Given $a, b \in R$, such that the equation $x^{4}+a x^{3}+2 x^{2}+b x+1=0$ has real roots, find the minimum possible value of $a^{2}+b^{2}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 8 |
24,294 | At 1:00 PM, two identical recreational boats set off in opposite directions from a pier on a river. At the same time, a raft also departed from the pier. An hour later, one of the boats turned around and started moving back. The other boat did the same at 3:00 PM. What is the speed of the current if, at the moment the boats met, the raft had drifted 7.5 km from the pier? | 2.5 |
27,360 | 8,9 [ Inscribed Circle in an Angle
In an isosceles trapezoid, there are two circles. One of them, with a radius of 1, is inscribed in the trapezoid, and the second circle touches two sides of the trapezoid and the first circle. The distance from the vertex of the angle formed by the two sides of the trapezoid that touch the second circle to the point of tangency of the circles is twice the diameter of the second circle. Find the area of the trapezoid.
# | \frac{9\sqrt{2}}{2} |
62,371 | 7. If a small ball with a radius of 1 can move freely in all directions inside a regular tetrahedron container with an edge length of $6 \sqrt{6}$, then the area of the container's inner wall that the ball can never touch is $\qquad$ . | 120\sqrt{3} |
59,958 | 13. In a $2009 \times 2009$ grid, each small square is filled with a real number, the absolute value of which does not exceed 1, and the sum of the 4 real numbers in each $2 \times 2$ square is 0. Find the maximum possible sum of all the numbers in the grid. | 2009 |
18,544 | Minimize \(\boldsymbol{F}=\boldsymbol{x}_{2}-\boldsymbol{x}_{1}\) for non-negative \(x_{1}\) and \(x_{2}\), subject to the system of constraints:
$$
\left\{\begin{aligned}
-2 x_{1}+x_{2}+x_{3} &=2 \\
x_{1}-2 x_{2}+x_{4} &=2 \\
x_{1}+x_{2}+x_{5} &=5
\end{aligned}\right.
$$ | -3 |
8,604 | The formula for converting a Fahrenheit temperature $F$ to the corresponding Celsius temperature $C$ is $C = \frac{5}{9}(F-32).$ An integer Fahrenheit temperature is converted to Celsius, rounded to the nearest integer, converted back to Fahrenheit, and again rounded to the nearest integer. For how many integer Fahrenheit temperatures between $32$ and $1000$ inclusive does the original temperature equal the final temperature?
Please give the answer directly without any intermediate steps. | 539 |
58,797 | Problem 5.1. At a physical education class, 27 seventh-graders arrived, some of them brought one ball each. Sometimes during the class, one of the seventh-graders would give their ball to another seventh-grader who didn't have one.
At the end of the class, $N$ seventh-graders said: "I received balls less frequently than I gave them away!". Find the maximum possible value of $N$, given that none of the students lied. | 13 |
58,746 | The decimal digits of a natural number $A$ form an increasing sequence (from left to right). Find the sum of the digits of $9A$. | 9 |
57,467 | 8.2. Solve the inequality $\sqrt{x^{2}-x-56}-\sqrt{x^{2}-25 x+136}<8 \sqrt{\frac{x+7}{x-8}}$, and find the sum of its integer solutions that belong to the interval $[-25 ; 25]$. | -285 |
7,232 | Shapovalov A.V.
In a small town, there is only one tram line. It is a circular line, and trams run in both directions. There are stops called Circus, Park, and Zoo on the loop. The journey from Park to Zoo via Circus is three times longer than the journey not via Circus. The journey from Circus to Zoo via Park is half as short as the journey not via Park. Which route from Park to Circus is shorter - via Zoo or not via Zoo - and by how many times? | 11 |
66,401 | Example $\mathbf{3}$ If the function $f: \mathbf{R} \rightarrow \mathbf{R}$ satisfies for all real numbers $x$,
$$
\sqrt{2 f(x)}-\sqrt{2 f(x)-f(2 x)} \geqslant 2
$$
then the function $f$ is said to have property $P$. Find the largest real number $\lambda$, such that if the function $f$ has property $P$, then for all real numbers $x$, $f(x) \geqslant \lambda$ always holds. | 12+8\sqrt{2} |
30,664 | 2. Let $a$ be a real number, and the two parabolas
$$
y=x^{2}+x+a \text { and } x=4 y^{2}+3 y+a
$$
have four intersection points.
(1) Find the range of values for $a$;
(2) Prove that these four intersection points are concyclic, and find the coordinates of the center of the circle. | (-\frac{3}{8},\frac{1}{8}) |
53,761 | 1. Fill two $a$s and two $b$s into the 16 cells shown in Figure 3, with at most one letter per cell. If the same letters must not be in the same row or column, find the number of different ways to fill the cells. | 3960 |
19,006 | The extension of the altitude \( BH \) of triangle \( ABC \) intersects the circle circumscribed around it at point \( D \) (points \( B \) and \( D \) lie on opposite sides of line \( AC \) ). The degree measures of arcs \( AD \) and \( CD \), not containing point \( B \), are \( 60^\circ \) and \( 90^\circ \) respectively. Determine the ratio in which segment \( BD \) is divided by side \( AC \). | \sqrt{3} : 1 |
64,697 | Let's share a thought: divide every natural number by the sum of the squares of its digits (for single-digit numbers, divide by the square of the number).
Is there a smallest quotient among the quotients obtained this way, and if so, which one is it? | \frac{1}{9} |
69,096 | 6. How many solutions does the equation
$$
\frac{1}{(x-1)^{2}}+\frac{1}{(x-2)^{2}}=\frac{2}{x^{2}} ?
$$ | 1 |
12,406 | A circle with radius 1 is situated between two parallel lines, touching both lines. An isosceles triangle is positioned such that its base lies on one of the lines, and its vertex is on the other line. It is known that the triangle and the circle have exactly one common point, and this point lies on the inscribed circle of the triangle. Find the radius of the inscribed circle of the triangle. | \dfrac{1}{2} |
53,044 | 8. Given that $x$ is a four-digit number, the sum of its digits is $y$. If the value of $\frac{x}{y}$ is minimized, then $x=$ $\qquad$ . | 1099 |
55,597 | 11.5. A rectangular parallelepiped with edge lengths $\sqrt{70}, \sqrt{99}, \sqrt{126}$ is orthogonally projected onto all possible planes. Find the maximum value of the projection area. Justify your answer. | 168 |
65,152 | Let's divide every natural number with at least two digits by the sum of its digits! When will the quotient be the largest, and when will it be the smallest? | 1.9 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.