id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
1,582 | \section*{Exercise 6 - 021116}
Determine all real numbers \(x\) that satisfy the inequality
\[
\sqrt{3-x}-\sqrt{x+1}>\frac{1}{2}
\]
Verify the result! | [-1, \frac{8 - \sqrt{31}}{8}) |
1,592 | Count the number of ways to choose a leader, a deputy leader, and a team from $n$ people in two different ways. | n(n-1)2^{n-2} |
1,604 | 35 Let $n$ be a positive integer such that $n^{2}+19 n+48$ is a perfect square. Find the value of $n$. | 33 |
1,613 | On the faces \(BCD, ACD, ABD,\) and \(ABC\) of a tetrahedron \(ABCD\), points \(A_1, B_1, C_1,\) and \(D_1\) are marked, respectively. It is known that the lines \(AA_1, BB_1, CC_1,\) and \(DD_1\) intersect at point \(P\) with \(\frac{AP}{A_1P} = \frac{BP}{B_1P} = \frac{CP}{C_1P} = \frac{DP}{D_1P} = r\). Find all possible values of \(r\). | 3 |
1,616 | 1737. Let the dairy farm of a collective farm have data on the milk yield of cows for the lactation period:
| Milk yield, kg | Number of cows | Milk yield, kg | Number of cows |
| :---: | :---: | :---: | :---: |
| $400-600$ | 1 | $1600-1800$ | 14 |
| $600-800$ | 3 | $1800-2000$ | 12 |
| $800-1000$ | 6 | $2000-2200$ | 10 |
| $1000-1200$ | 11 | $2200-2400$ | 6 |
| $1200-1400$ | 15 | 2400 and above | 2 |
| $1400-1600$ | 20 | | |
Find the arithmetic mean of the milk yield of cows on this farm. | 1560 |
1,620 | 12. Six weights look the same, with masses of 101 grams, 102 grams, 103 grams, 104 grams, 105 grams, and 106 grams. Place these six weights on a balance, three on each side, and the result is that the right side of the balance is heavier. The probability that the 106-gram weight is on the right side of the balance is $\qquad$ $\%$. | 80 |
1,628 | \(\frac{\sqrt[3]{\sqrt{5}-\sqrt{3}} \cdot \sqrt[6]{8+2 \sqrt{15}}-\sqrt[3]{a}}{\sqrt[3]{\sqrt{20}+\sqrt{12}} \cdot \sqrt[6]{8-2 \sqrt{15}}-2 \sqrt[3]{2 a}+\sqrt[3]{a^{2}}}\). | \dfrac{1}{\sqrt[3]{2} - \sqrt[3]{a}} |
1,675 | Problem 2. Solve in the set of positive rational numbers the equation:
$$
\begin{array}{r}
\frac{x+1}{2}+\frac{x+5}{3}+\frac{x+11}{4}+\frac{x+19}{5}+\frac{x+29}{6}+\frac{x+41}{7}+\frac{x+55}{8}+\frac{x+71}{9}+\frac{x+89}{10}=45 . \\
\text { Mathematical Gazette nr. 10/2013 }
\end{array}
$$ | 1 |
1,693 | # Problem 3. (3 points)
The sequence $\left\{a_{n}\right\}$ is defined by the conditions $a_{1}=0 \quad$ and $a_{n+1}=\sum_{k=1}^{n}\left(a_{k}+1\right)$ for $n \geqslant 1$. Find the explicit formula for this sequence.
Answer: $a_{n}=2^{n-1}-1$ | a_n = 2^{n-1} - 1 |
1,708 | [ Irrational equations ]
Solve the equation $\frac{x^{3}}{\sqrt{4-x^{2}}}+x^{2}-4=0$.
# | \sqrt{2} |
1,755 | Condition of the problem
Calculate the limit of the function:
$\lim _{x \rightarrow-1} \frac{\left(x^{3}-2 x-1\right)^{2}}{x^{4}+2 x+1}$ | 0 |
1,764 | 6. Given a rectangle $A B C D$ with point $S$ being the intersection of the diagonals. On side $\overline{A D}$, points $E$ and $F$ are chosen such that $|A E|=|E F|=|F D|$. Determine the ratio of the area of pentagon $E B S C F$ to the area of rectangle $A B C D$. | \dfrac{5}{12} |
1,768 | Someone wrote down two numbers $5^{2020}$ and $2^{2020}$ consecutively. How many digits will the resulting number contain? | 2021 |
1,774 | 3. Now, subtract the same positive integer $a$ from the numerator and denominator of the fractions $\frac{2018}{2011}$ and $\frac{2054}{2019}$, respectively, to get two new fractions that are equal. What is the positive integer $a$? | 2009 |
1,797 | 1. Question: How many real roots does the equation $x^{2}|x|-5 x|x|+2 x=0$ have (where $|x|$ represents the absolute value of $x$)? | 4 |
1,799 | In the USA, dates are written as: month number, then day number, and year. In Europe, the format is day number, then month number, and year. How many days in a year are there whose dates cannot be interpreted unambiguously without knowing which format is being used? | 132 |
1,807 | The function \( f(x) \) is differentiable on the interval \([a, b]\), and \( f^{\prime}(x) = 0 \) for all points \( x \) in the interval \([a, b]\). Prove that the function \( f(x) \) is constant on the interval \([a, b]\). | f(x) \text{ is constant on } [a, b] |
1,865 | 21. The formula for the volume of a sphere is $V=\frac{4}{3} \pi r^{3}$, where $r$ is the radius of the sphere. In a cylindrical container, several solid iron spheres with the same radius as the cylinder's base can be placed. When water is poured into the container, the volume of water is six times the volume of one iron sphere when the water level just reaches the top of the container. The number of iron spheres in the container is $\qquad$. | 12 |
1,878 | 9. Given the set $U=\{1,2,3,4,5\}, I=\{X \mid X \subseteq U\}$, if two different elements $A, B$ are randomly selected from set $I$, then the probability that $A \cap B$ contains exactly 3 elements is $\qquad$ . | \dfrac{5}{62} |
1,883 | Given two positive integers \(x\) and \(y\), \(xy - (x + y) = \operatorname{HCF}(x, y) + \operatorname{LCM}(x, y)\), where \(\operatorname{HCF}(x, y)\) and \(\operatorname{LCM}(x, y)\) are respectively the greatest common divisor and the least common multiple of \(x\) and \(y\). If \(c\) is the maximum possible value of \(x + y\), find \(c\). | 10 |
1,916 | Indiana Jones reached an abandoned temple in the jungle and entered the treasury. There were 5 chests, with the knowledge that only one contains the treasure, and the others trigger a stone slab to fall on the head of anyone who tries to open them. The chests are numbered from left to right.
- The first, fourth, and fifth chests are made of cedar.
- The second and third chests are made of sandalwood.
- The inscriptions on the chests are as follows:
- On the first chest: "The treasure is in me or in the 4th chest."
- On the second chest: "The treasure is in the chest to the left of me."
- On the third chest: "The treasure is in me or in the chest at the far right."
- On the fourth chest: "There is no treasure in the chests to the left of me."
- On the fifth chest: "All the inscriptions on other chests are false."
The last guardian of the temple, before dying, revealed to Indiana a secret: an equal number of false statements are written on both cedar and sandalwood chests.
In which chest is the treasure? | 2 |
1,930 | 4. Let the natural number $n$ have the following property: from $1,2, \cdots \cdots, n$ any 50 different numbers are taken, among these 50 numbers there must be two numbers whose difference is 7. The largest such $n$ is $\qquad$ | 98 |
1,936 | The minimum value of the function \( y = \sin^4{x} + \cos^4{x} + \sec^4{x} + \csc^4{x} \). | \dfrac{17}{2} |
1,945 | ## Task 2 - 120712
Determine all three-digit natural numbers $z$ that each satisfy the following conditions simultaneously:
(1) The number $z$ is divisible by both 9 and 11.
(2) If the digit in the hundreds place of the number $z$ is swapped with the digit in the units place, a new three-digit number $z^{\prime}$ is obtained, which is $\frac{2}{9}$ of the number $z$. | 891 |
1,961 | [ The Law of Cosines [Isosceles, Inscribed, and Circumscribed Trapezoids]
The bases of the trapezoid are 3 cm and 5 cm. One of the diagonals of the trapezoid is 8 cm, and the angle between the diagonals is $60^{\circ}$. Find the perimeter of the trapezoid.
# | 22 |
1,962 | ## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(\frac{\arcsin ^{2} x}{\arcsin ^{2} 4 x}\right)^{2 x+1}$ | \dfrac{1}{16} |
1,969 | In a circle with center $O$ and radius $r$, let $A B$ be a chord smaller than the diameter. The radius of the circle inscribed in the smaller sector determined by the radii $A O$ and $B O$ is $\varrho$. Express $A B$ in terms of $r$ and $\varrho$. | \dfrac{2 r \varrho}{r - \varrho} |
1,976 | 2. Is it possible to form a nine-digit number from the digits $1,2, \ldots, 9$ such that there is an odd number of digits between 1 and 2, an odd number of digits between 2 and 3, ..., and an odd number of digits between 8 and 9? | \text{No} |
1,977 | 6. As shown in the figure, in right $\triangle A C B$, $C D$ is the altitude on the hypotenuse $A B$, and $D E$ is the altitude on the hypotenuse $B C$ of $\mathrm{Rt} \triangle C D B$. If $B E=$ $6, C E=4$, then the length of $A D$ is $\qquad$ | \dfrac{4\sqrt{15}}{3} |
1,995 | ## Problem Statement
Write the equation of the plane passing through point $A$ and perpendicular to vector $\overrightarrow{B C}$.
$A(-7 ; 0 ; 3)$
$B(1 ;-5 ;-4)$
$C(2 ;-3 ; 0)$ | x + 2y + 4z = 5 |
2,030 | We place a mouse in one corner cube of a $3 \times 3 \times 3$ grid and a piece of cheese in the central cube. The mouse wanders randomly in search of the cheese: in each move, it randomly steps into one of the neighboring cubes. On average, how many steps will it take for the mouse to find the cheese? | 21 |
2,057 | Let the sum $\sum_{n=1}^{9} \frac{1}{n(n+1)(n+2)}$ written in its lowest terms be $\frac{p}{q}$ . Find the value of $q - p$. | 83 |
2,093 | 10. Observe the pattern in the following expressions:
$$
\begin{array}{l}
1 \times 2+2 \times 3=2 \times 2 \times 2 \\
2 \times 3+3 \times 4=2 \times 3 \times 3 \\
3 \times 4+4 \times 5=2 \times 4 \times 4 \\
4 \times 5+5 \times 6=2 \times 5 \times 5
\end{array}
$$
Use the pattern to calculate: $75 \times 222+76 \times 225-25 \times 14 \times 15-25 \times 15 \times 16=$ $\qquad$ | 22500 |
2,113 | ## Problem Statement
Calculate the definite integral:
$$
\int_{-1}^{0}(x+2)^{3} \cdot \ln ^{2}(x+2) d x
$$ | 4 (\ln 2)^2 - 2 \ln 2 + \dfrac{15}{32} |
2,127 | Task 12. (16 points)
The Vasilievs' family budget consists of the following income items:
- parents' salary after income tax deduction - 71000 rubles;
- income from renting out property - 11000 rubles;
- daughter's scholarship - 2600 rubles
The average monthly expenses of the family include:
- utility payments - 8400 rubles;
- food - 18000 rubles;
- transportation expenses - 3200 rubles;
- tutor services - 2200 rubles;
- other expenses - 18000 rubles.
10 percent of the remaining amount is transferred to a deposit for the formation of a financial safety cushion. The father wants to buy a car on credit. Determine the maximum amount the Vasilievs family can pay monthly for the car loan.
In your answer, provide only the number without units of measurement! | 31320 |
2,134 | Problem 5. Given trapezoid $ABCD$ with bases $\overline{AB}=16 \text{~cm}, \overline{CD}=8 \text{~cm}$. The sum of angles $ABC$ and $BAD$ is $90^{\circ}$. If $M$ and $N$ are the midpoints of sides $AB$ and $CD$ respectively, calculate the length of segment $MN$. | 4 |
2,173 | 3. Let real numbers $a b$ satisfy
$$
\begin{array}{l}
a^{2}\left(b^{2}+1\right)+b(b+2 a)=40, \\
a(b+1)+b=8 .
\end{array}
$$
Find the value of $\frac{1}{a^{2}}+\frac{1}{b^{2}}$. | 8 |
2,190 | Each cell of a \(50 \times 50\) square contains a number equal to the count of \(1 \times 16\) rectangles (both vertical and horizontal) for which this cell is an endpoint. How many cells contain numbers that are greater than or equal to 3? | 1600 |
2,201 | A prime number $ q $ is called***'Kowai'***number if $ q = p^2 + 10$ where $q$ , $p$ , $p^2-2$ , $p^2-8$ , $p^3+6$ are prime numbers. WE know that, at least one ***'Kowai'*** number can be found. Find the summation of all ***'Kowai'*** numbers.
| 59 |
2,210 | 1. A palindrome is a number where the digits read the same forwards or backwards, such as 4774 or 505 . What is the smallest palindrome that is larger than 2015 ? | 2112 |
2,220 |
Let the function \( f(x) = x^2 - x + 1 \). Define \( f^{(n)}(x) \) as follows:
$$
f^{(1)}(x) = f(x), \quad f^{(n)}(x) = f\left(f^{(n-1)}(x)\right).
$$
Let \( r_{n} \) be the arithmetic mean of all the roots of \( f^{(n)}(x) = 0 \). Find \( r_{2015} \). | \dfrac{1}{2} |
2,225 | 5.2. Write the numbers $1,2,3,4,5,6,8,9$ (that is, all numbers from 1 to 9 except 7) in a row so that in any pair of adjacent numbers, one divides the other. | 5,1,9,3,6,2,4,8 |
2,230 | 9. $n$ people are sitting around a round table. Out of $n!$ seating arrangements, how many different seating arrangements are there, i.e., how many arrangements have different neighboring relationships? | \dfrac{(n-1)!}{2} |
2,241 | Given \( f(x) \) is a function defined on \(\mathbf{R}\), for any \( x, y \in \mathbf{R} \), it always holds that
\[ f(x-f(y)) = f(f(y)) + x f(y) + f(x) - 1 .\]
Find \( f(x) \) and calculate the value of \( f(\sqrt{2014}) \). | -1006 |
2,252 | ## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 1}\left(\frac{e^{2 x}-e^{2}}{x-1}\right)^{x+1}$ | 4e^4 |
2,260 | 3.303. $1-\sin ^{2} \alpha-\sin ^{2} \beta+2 \sin \alpha \sin \beta \cos (\alpha-\beta)$. | \cos^2(\alpha - \beta) |
2,261 | 2. Nanda and Mike both have a note with the same five-digit number on it. Nanda puts the digit 4 in front of her number and the digit 8 at the end, resulting in a seven-digit number. Mike puts a digit in front of his number. When they compare their new numbers, it turns out that Nanda's number is exactly 6 times larger than Mike's.
What number did they start with? | 49998 |
2,269 | In triangle \(ABC\), the altitudes \(BM\) and \(CN\) are drawn, and \(O\) is the incenter. It is known that \(BC = 24\) and \(MN = 12\).
Find the radius of the circumcircle of triangle \(BOC\). | 8\sqrt{3} |
2,292 | A circle is tangent to two adjacent sides \(AB\) and \(AD\) of square \(ABCD\) and cuts off a segment of length 8 cm from vertices \(B\) and \(D\) at the points of tangency. On the other two sides, the circle cuts off segments of 4 cm and 2 cm respectively from the vertices at the points of intersection. Find the radius of the circle. | 10 |
2,300 | Given that point \( P(x, y) \) satisfies \( |x| + |y| \leq 2 \), find the probability for point \( P \) to have a distance \( d \leq 1 \) from the \( x \)-axis. | \dfrac{3}{4} |
2,304 | All three vertices of an equilateral triangle are on the parabola $y = x^2$ , and one of its sides has a slope of $2$ . The $x$ -coordinates of the three vertices have a sum of $m/n$ , where $m$ and $n$ are relatively prime positive integers. What is the value of $m + n$ | 14 |
2,316 |
4. Na grafu funkcije $f(x)=\sin x$ sta točki $A\left(\frac{\pi}{3}, f\left(\frac{\pi}{3}\right)\right)$ in $B\left(\frac{\pi}{6}, f\left(\frac{\pi}{6}\right)\right)$. Zapiši enačbo premice, ki poteka skozi točki $A$ in $B$. Koeficienti naj bodo določeni natančno (brez uporabe žepnega računala). | y = \dfrac{3(\sqrt{3} - 1)}{\pi} x + \dfrac{2 - \sqrt{3}}{2} |
2,317 | To be factored into the product of three factors:
$$
\left(x^{2}+x y+y^{2}\right)^{2}-\left(x^{2} y^{2}+y^{2} z^{2}+z^{2} x^{2}\right)
$$ | (x^2 + y^2)(x + y - z)(x + y + z) |
2,334 | What is the minimum length of the edge of a cube that can fit 2 unit-radius spheres, which do not have any common interior points? | 2 + \dfrac{2\sqrt{3}}{3} |
2,399 | Using the seven digits $1, 2, 3, 4, 5, 6, 7$ to appropriately arrange them into a 7-digit number so that it is a multiple of 11, how many such numbers can be formed? | 576 |
2,424 | A triangle $\triangle ABC$ satisfies $AB = 13$ , $BC = 14$ , and $AC = 15$ . Inside $\triangle ABC$ are three points $X$ , $Y$ , and $Z$ such that:
- $Y$ is the centroid of $\triangle ABX$
- $Z$ is the centroid of $\triangle BCY$
- $X$ is the centroid of $\triangle CAZ$
What is the area of $\triangle XYZ$ ?
*Proposed by Adam Bertelli* | \dfrac{84}{13} |
2,460 | What is the probability of randomly drawing three different numbers from the set {1, 2, ..., 10} such that their sample variance \( s^2 \leqslant 1 \)? | \dfrac{1}{15} |
2,471 | Find the total differential of the function
$$
u = x^{2} \arctan \left(\frac{y}{x}\right) - y^{2} \arctan \left(\frac{x}{y}\right)
$$ | du = \left(2x \arctan\left(\frac{y}{x}\right) - y\right) dx + \left(x - 2y \arctan\left(\frac{x}{y}\right)\right) dy |
2,498 | # 11.1. Solve the equation
$$
x^{4}+2 x \sqrt{x-1}+3 x^{2}-8 x+4=0
$$ | 1 |
2,519 | 5. There are 200 different cards with numbers $2,3,2^{2}, 3^{2}, \ldots, 2^{100}, 3^{100}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a cube of an integer? | 4389 |
2,523 | For points \( A_{1}, \ldots, A_{5} \) on the sphere of radius 1, what is the maximum value that \( \min _{1 \leq i, j \leq 5} A_{i} A_{j} \) can take? Determine all configurations for which this maximum is attained. | \sqrt{2} |
2,525 | From the set {1, 2, 3, ..., 14}, select \(a_{1}, a_{2}, a_{3}\) in increasing order such that \(a_{2} - a_{1} \geq 3\) and \(a_{3} - a_{2} \geq 3\). Find the total number of different ways to select these numbers. | 120 |
2,537 | ## 32. Xenon, Zephyr, and Enofa
Two friends at the races were speculating about the outcome of the next race. One of them bet on Xenon and Enofa, while the other bet on Zephyr.
- I bet,- said the second,- that if my horse finishes in the top three, then Xenon will also be in the top three.
- And I,- replied the first,- bet that if at least one of my horses finishes in the top three, then you will lose your bet.
Suppose the last bet was not lost. Which of the three horses, Xenon, Zephyr, or Enofa, in this case, has the highest chance of finishing in the top three? | Zephyr |
2,566 | Given a triangle with sides of lengths 3, 4, and 5. Three circles are constructed with radii of 1, centered at each vertex of the triangle. Find the total area of the portions of the circles that lie within the triangle. | \dfrac{\pi}{2} |
2,568 | 2. Find all digits $n$ and 2018-digit natural numbers $x, x=\overline{a_{2017} \ldots a_{2} a_{1} a_{0}}$, such that
$$
n \cdot x=\overline{\left(a_{2017}+n\right) \ldots\left(a_{2}+n\right)\left(a_{1}+n\right)\left(a_{0}+n\right)}
$$ | 2 |
2,574 | 4. How many natural numbers are there that are less than or equal to the number 2019, and which are not divisible by any of the numbers 6, 9, and 15? | 1526 |
2,583 | 24. Let $f(x)=x^{3}+3 x+1$, where $x$ is a real number. Given that the inverse function of $f$ exists and is given by
$$
f^{-1}(x)=\left(\frac{x-a+\sqrt{x^{2}-b x+c}}{2}\right)^{1 / 3}+\left(\frac{x-a-\sqrt{x^{2}-b x+c}}{2}\right)^{1 / 3}
$$
where $a, b$ and $c$ are positive constants, find the value of $a+10 b+100 c$. | 521 |
2,592 | A group of tourists was supposed to arrive at the train station at 5 o'clock. By this time, a bus was supposed to come from the tourist base to pick them up. However, arriving at the train station at 3:10, the tourists started walking to the tourist base. Meeting the bus on the road, they got on and arrived at the tourist base 20 minutes earlier than the scheduled time. At what speed did the tourists walk before meeting the bus, if the bus's speed was 60 km/h? | 6 |
2,610 | ## Task B-2.4.
Let $A B C D$ be a parallelogram, and $M$ the midpoint of side $\overline{D C}$. If point $M$ lies on the angle bisector of $\angle D A B$, determine the measure of $\angle A M B$. | 90 |
2,633 | 5. Given three positive real numbers $a, b, c$ satisfying $a \leqslant b+c \leqslant 2 a, b \leqslant a+c \leqslant 2 b$, then the range of $\frac{b}{a}$ is | \left[ \dfrac{2}{3}, \dfrac{3}{2} \right] |
2,649 | Given that \( g \) is a twice differentiable function over the positive real numbers such that
\[ g(x) + 2x^3 g'(x) + x^4 g''(x) = 0 \quad \text{for all positive reals } x \]
and
\[ \lim_{x \to \infty} x g(x) = 1, \]
find the real number \(\alpha > 1\) such that \( g(\alpha) = \frac{1}{2} \). | \dfrac{6}{\pi} |
2,669 | Point \( D \) lies on the base \( AC \) of an isosceles triangle \( ABC \). Prove that the circumradii of triangles \( ABD \) and \( CBD \) are equal. | R_{ABD} = R_{CBD} |
2,685 | Given that \( a_{1}, a_{2}, \cdots, a_{n} \) are all greater than 1, prove that:
\[ 2^{n-1}\left(a_{1} a_{2} \cdots a_{n}+1\right)>\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots \left(1+a_{n}\right). \] | 2^{n-1}\left(a_{1} a_{2} \cdots a_{n}+1\right)>\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots \left(1+a_{n}\right) |
2,698 | Problem 2. (4 points) In a box, there are red, blue, yellow, and white balls, a total of 111. If 100 balls are drawn from the box with closed eyes, among them there will definitely be four balls, each two of which are of different colors. How many balls at least need to be drawn from the box (with closed eyes) to be able to assert with certainty that among them there are three balls, each two of which are of different colors? | 88 |
2,723 | Let $x_1$, $x_2$, …, $x_{10}$ be 10 numbers. Suppose that $x_i + 2 x_{i + 1} = 1$ for each $i$ from 1 through 9. What is the value of $x_1 + 512 x_{10}$? | 171 |
2,743 | The circles \(O_{1}\) and \(O_{2}\) touch the circle \(O_{3}\) with radius 13 at points \(A\) and \(B\) respectively and pass through its center \(O\). These circles intersect again at point \(C\). It is known that \(OC = 12\). Find \(AB\). | 10 |
2,783 | 4. (10 points) Arrange $\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \frac{1}{7}$ and the average of these 6 fractions in ascending order, then this average value is in the $\qquad$th position. | 5 |
2,807 | 1. Factorize the expression $4 x^{4}-4 x^{3}-14 x^{2}+12 x$ $+6=$ $\qquad$ | 2(2x^2 - 2x - 1)(x^2 - 3) |
2,813 | Let \( n \) be the smallest positive integer that satisfies the following conditions: (1) \( n \) is a multiple of 75; (2) \( n \) has exactly 75 positive integer factors (including 1 and itself). Find \(\frac{n}{75}\). | 432 |
2,817 | In $\triangle ABC$, $\overrightarrow{AB} \cdot \overrightarrow{AC} + 2 \overrightarrow{BA} \cdot \overrightarrow{BC} = 3 \overrightarrow{CA} \cdot \overrightarrow{CB}$. Find the maximum value of $\sin C$. | \dfrac{\sqrt{7}}{3} |
2,829 | 15. (3 points) There are 300 chess pieces in black and white. The black crow divides the black and white pieces into 100 piles, with 3 pieces in each pile. Among them, there are 27 piles with only $l$ white piece, 42 piles with 2 or 3 black pieces, and the number of piles with 3 white pieces is equal to the number of piles with 3 black pieces. Therefore, the number of white pieces among these chess pieces is $\qquad$. | 158 |
2,830 | Elsa uses ice blocks to make ice sculptures. One ice block can make a small sculpture, and three ice blocks can make a large sculpture. The leftover fragments from making 2 small sculptures or 1 large sculpture can perfectly form 1 new ice block. Given 30 ice blocks, and ensuring that the number of small sculptures made is greater than the number of large sculptures made, what is the maximum number of large sculptures that can be made? | 11 |
2,834 | One day while Tony plays in the back yard of the Kubik's home, he wonders about the width of the back yard, which is in the shape of a rectangle. A row of trees spans the width of the back of the yard by the fence, and Tony realizes that all the trees have almost exactly the same diameter, and the trees look equally spaced. Tony fetches a tape measure from the garage and measures a distance of almost exactly $12$ feet between a consecutive pair of trees. Tony realizes the need to include the width of the trees in his measurements. Unsure as to how to do this, he measures the distance between the centers of the trees, which comes out to be around $15$ feet. He then measures $2$ feet to either side of the first and last trees in the row before the ends of the yard. Tony uses these measurements to estimate the width of the yard. If there are six trees in the row of trees, what is Tony's estimate in feet?
[asy]
size(400);
defaultpen(linewidth(0.8));
draw((0,-3)--(0,3));
int d=8;
for(int i=0;i<=5;i=i+1)
{
draw(circle(7/2+d*i,3/2));
}
draw((5*d+7,-3)--(5*d+7,3));
draw((0,0)--(2,0),Arrows(size=7));
draw((5,0)--(2+d,0),Arrows(size=7));
draw((7/2+d,0)--(7/2+2*d,0),Arrows(size=7));
label("$2$",(1,0),S);
label("$12$",((7+d)/2,0),S);
label("$15$",((7+3*d)/2,0),S);
[/asy] | 82 |
2,846 | The absolute value of a number \( x \) is equal to the distance from 0 to \( x \) along a number line and is written as \( |x| \). For example, \( |8|=8, |-3|=3 \), and \( |0|=0 \). For how many pairs \( (a, b) \) of integers is \( |a|+|b| \leq 10 \)? | 221 |
2,855 | 13.236. The master is giving a simultaneous chess exhibition on several boards. By the end of the first two hours, he won $10 \%$ of the total number of games played, while 8 opponents drew their games with the master. Over the next two hours, the master won $10 \%$ of the games with the remaining opponents, lost two games, and drew the remaining 7 games. On how many boards was the game being played? | 20 |
2,867 | Let \( f(x) \) be a quotient of two quadratic polynomials. Given that \( f(n) = n^{3} \) for all \( n \in \{1, 2, 3, 4, 5\}\), compute \( f(0) \). | \dfrac{24}{17} |
2,888 | ## Problem Statement
Calculate the definite integral:
$$
\int_{0}^{5} x^{2} \cdot \sqrt{25-x^{2}} d x
$$ | \dfrac{625\pi}{16} |
2,889 | A settlement is built in the shape of a square consisting of 3 blocks by 3 blocks (each block is a square with a side length $b$, for a total of 9 blocks). What is the shortest path that a paver must take to pave all the streets if they start and end their path at a corner point $A$? (The sides of the square are also streets). | 28b |
2,890 | 1 An integer is a perfect number if and only if it is equal to the sum of all of its divisors except itself. For example, 28 is a perfect number since $28=1+2+4+7+14$.
Let $n$ ! denote the product $1 \cdot 2 \cdot 3 \cdots n$, where $n$ is a positive integer. An integer is a factorial if and only if it is equal to $n!$ for some positive integer $n$. For example, 24 is a factorial number since $24=4!=1 \cdot 2 \cdot 3 \cdot 4$. Find all perfect numbers greater than 1 that are also factorials. | 6 |
2,916 | Two spheres touch the plane of triangle $A B C$ at points $A$ and $B$ and are located on opposite sides of this plane. The sum of the radii of the given spheres is 7, and the distance between their centers is 13. The center of a third sphere with a radius of 5 is at point $C$, and it externally touches each of the first two spheres. Find the radius of the circumcircle of triangle $A B C$. | \sqrt{30} |
2,939 | A rectangular chessboard of size \( m \times n \) is composed of unit squares (where \( m \) and \( n \) are positive integers not exceeding 10). A piece is placed on the unit square in the lower-left corner. Players A and B take turns moving the piece. The rules are as follows: either move the piece any number of squares upward, or any number of squares to the right, but you cannot move off the board or stay in the same position. The player who cannot make a move loses (i.e., the player who first moves the piece to the upper-right corner wins). How many pairs of integers \( (m, n) \) are there such that the first player A has a winning strategy? | 90 |
2,967 | Let us call a ticket with a number from 000000 to 999999 excellent if the difference between some two neighboring digits of its number is 5. Find the number of excellent tickets. | 409510 |
2,974 | A10. Amy, Bruce, Chris, Donna and Eve had a race. When asked in which order they finished, they all answered with a true and a false statement as follows:
Amy: Bruce came second and I finished in third place.
Bruce: I finished second and Eve was fourth.
Chris: I won and Donna came second.
Donna: I was third and Chris came last.
Eve: I came fourth and Amy won.
In which order did the participants finish? | Bruce, Donna, Amy, Eve, Chris |
2,981 | Three, (Full marks 12 points) A store sells a product that costs 10 yuan each at 18 yuan each, and can sell 60 units per day. After conducting a market survey, the store manager found that if the selling price of this product (based on 18 yuan each) is increased by 1 yuan, the daily sales volume will decrease by 5 units; if the selling price (based on 18 yuan each) is decreased by 1 yuan, the daily sales volume will increase by 10 units. To maximize daily profit, what should the selling price of this product be set to in yuan per unit?
| 20 |
2,986 | ## SUBJECT II
Calculate the sum of natural numbers, between 400 and 600, which when divided by 12 give a remainder of 10. | 8534 |
2,988 | $ABCD$ is a cyclic quadrilateral inscribed in a circle of radius $5$ , with $AB=6$ , $BC=7$ , $CD=8$ . Find $AD$ . | \sqrt{51} |
3,041 | A regular octahedron has a side length of 1. What is the distance between two opposite faces? | \dfrac{\sqrt{6}}{3} |
3,056 | Dima is driving on a straight highway from point A to point B. From point B, a traffic jam is extending towards Dima at a speed of \( v \) km/h. The speed of the car in the traffic jam is 10 km/h, and outside the traffic jam it is 60 km/h. The navigator in the car continuously shows the remaining time for Dima to reach point B based on the current length of the traffic jam. At a certain moment (before reaching the traffic jam), Dima noticed that the navigator showed the same time as it did a few minutes ago. Find \( v \). | 12 |
3,068 | Example 3. Find $\int \cos ^{3} x \cdot \sin x d x$. | -\dfrac{1}{4} \cos^4 x + C |
3,069 | 4.1. To the fraction $\frac{1}{6}$, some fraction was added, and the result turned out to be a proper fraction with a denominator less than 6. What is the largest fraction that could have been added?
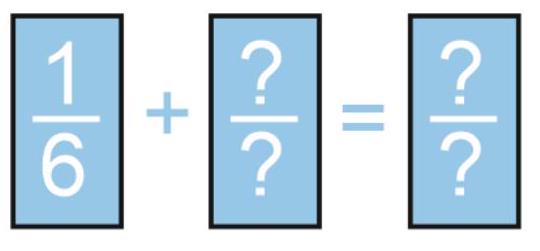 | \dfrac{19}{30} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.