diff --git a/.gitattributes b/.gitattributes new file mode 100644 index 0000000000000000000000000000000000000000..b4142b465b0247a43021d923f87e69b7d262c4c6 --- /dev/null +++ b/.gitattributes @@ -0,0 +1,36 @@ +*.7z filter=lfs diff=lfs merge=lfs -text +*.arrow filter=lfs diff=lfs merge=lfs -text +*.bin filter=lfs diff=lfs merge=lfs -text +*.bz2 filter=lfs diff=lfs merge=lfs -text +*.ckpt filter=lfs diff=lfs merge=lfs -text +*.ftz filter=lfs diff=lfs merge=lfs -text +*.gz filter=lfs diff=lfs merge=lfs -text +*.h5 filter=lfs diff=lfs merge=lfs -text +*.joblib filter=lfs diff=lfs merge=lfs -text +*.lfs.* filter=lfs diff=lfs merge=lfs -text +*.mlmodel filter=lfs diff=lfs merge=lfs -text +*.model filter=lfs diff=lfs merge=lfs -text +*.msgpack filter=lfs diff=lfs merge=lfs -text +*.npy filter=lfs diff=lfs merge=lfs -text +*.npz filter=lfs diff=lfs merge=lfs -text +*.onnx filter=lfs diff=lfs merge=lfs -text +*.ot filter=lfs diff=lfs merge=lfs -text +*.parquet filter=lfs diff=lfs merge=lfs -text +*.pb filter=lfs diff=lfs merge=lfs -text +*.pickle filter=lfs diff=lfs merge=lfs -text +*.pkl filter=lfs diff=lfs merge=lfs -text +*.pt filter=lfs diff=lfs merge=lfs -text +*.pth filter=lfs diff=lfs merge=lfs -text +*.rar filter=lfs diff=lfs merge=lfs -text +*.safetensors filter=lfs diff=lfs merge=lfs -text +saved_model/**/* filter=lfs diff=lfs merge=lfs -text +*.tar.* filter=lfs diff=lfs merge=lfs -text +*.tflite filter=lfs diff=lfs merge=lfs -text +*.tgz filter=lfs diff=lfs merge=lfs -text +*.wasm filter=lfs diff=lfs merge=lfs -text +*.xz filter=lfs diff=lfs merge=lfs -text +*.zip filter=lfs diff=lfs merge=lfs -text +*.zst filter=lfs diff=lfs merge=lfs -text +*.gif filter=lfs diff=lfs merge=lfs -text +*.json filter=lfs diff=lfs merge=lfs -text +*tfevents* filter=lfs diff=lfs merge=lfs -text diff --git a/.gitignore b/.gitignore new file mode 100644 index 0000000000000000000000000000000000000000..15c628e670d8824ca2c557bda6edc885c77a34b1 --- /dev/null +++ b/.gitignore @@ -0,0 +1,26 @@ +*.pyc +*__pycache__* +*core.* +_ext +tmp +*.o* +*~ +*.idea +*.mp4 +*.avi +*.h5 +*.pt +*.egg-info + +# Build +/build +/dist + +# Virtual enviroment +**/venv + +# Dataset images +/spiga/data/databases +venv/ +flagged +assets/ \ No newline at end of file diff --git a/README.md b/README.md new file mode 100644 index 0000000000000000000000000000000000000000..9a3b249e02e555ca4470135003163d1212eb2939 --- /dev/null +++ b/README.md @@ -0,0 +1,12 @@ +--- +title: SPIGA Face Alignment Headpose Estimator +emoji: πŸ‘€ +colorFrom: pink +colorTo: green +sdk: gradio +sdk_version: 3.22.1 +app_file: app.py +pinned: false +--- + +Check out the configuration reference at https://huggingface.co/docs/hub/spaces-config-reference diff --git a/SPIGA/.gitignore b/SPIGA/.gitignore new file mode 100644 index 0000000000000000000000000000000000000000..8746724fe1de020bf5068d4f2f0d18cab2b9660e --- /dev/null +++ b/SPIGA/.gitignore @@ -0,0 +1,23 @@ +*.pyc +*__pycache__* +*core.* +_ext +tmp +*.o* +*~ +*.idea +*.mp4 +*.avi +*.h5 +*.pt +*.egg-info + +# Build +/build +/dist + +# Virtual enviroment +**/venv + +# Dataset images +/spiga/data/databases diff --git a/SPIGA/LICENSE b/SPIGA/LICENSE new file mode 100644 index 0000000000000000000000000000000000000000..d06b4d08ab920bff3c8e3bb8693cc4ba3ab03075 --- /dev/null +++ b/SPIGA/LICENSE @@ -0,0 +1,29 @@ +BSD 3-Clause License + +Copyright (c) 2022, aprados +All rights reserved. + +Redistribution and use in source and binary forms, with or without +modification, are permitted provided that the following conditions are met: + +1. Redistributions of source code must retain the above copyright notice, this + list of conditions and the following disclaimer. + +2. Redistributions in binary form must reproduce the above copyright notice, + this list of conditions and the following disclaimer in the documentation + and/or other materials provided with the distribution. + +3. Neither the name of the copyright holder nor the names of its + contributors may be used to endorse or promote products derived from + this software without specific prior written permission. + +THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" +AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE +IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE +DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE +FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL +DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR +SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER +CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, +OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE +OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE. diff --git a/SPIGA/MANIFEST.in b/SPIGA/MANIFEST.in new file mode 100644 index 0000000000000000000000000000000000000000..fb5d16ae38bbce073e0bf8fc6a722fff99198128 --- /dev/null +++ b/SPIGA/MANIFEST.in @@ -0,0 +1,5 @@ +include spiga/data/annotations/**/db_info.json +include spiga/data/models3D/*.txt +include spiga/data/readme.md +include spiga/eval/benchmark/readme.md + diff --git a/SPIGA/README.md b/SPIGA/README.md new file mode 100644 index 0000000000000000000000000000000000000000..1d3c7b7b94ff8293ef4de605af25c437303ee65a --- /dev/null +++ b/SPIGA/README.md @@ -0,0 +1,217 @@ +# SPIGA: Shape Preserving Facial Landmarks with Graph Attention Networks. + +[![Project Page](https://badgen.net/badge/color/Project%20Page/purple?icon=atom&label)](https://bmvc2022.mpi-inf.mpg.de/155/) +[![arXiv](https://img.shields.io/badge/arXiv-2210.07233-b31b1b.svg)](https://arxiv.org/abs/2210.07233) +[![PyPI version](https://badge.fury.io/py/spiga.svg)](https://badge.fury.io/py/spiga) +[![License](https://img.shields.io/badge/License-BSD%203--Clause-blue.svg)](LICENSE) +[![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/video_demo.ipynb) + +This repository contains the source code of **SPIGA, a face alignment and headpose estimator** that takes advantage of the complementary benefits from CNN and GNN architectures producing plausible face shapes in presence of strong appearance changes. + +

+ +

+ +**It achieves top-performing results in:** + +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/pose-estimation-on-300w-full)](https://paperswithcode.com/sota/pose-estimation-on-300w-full?p=shape-preserving-facial-landmarks-with-graph) +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/head-pose-estimation-on-wflw)](https://paperswithcode.com/sota/head-pose-estimation-on-wflw?p=shape-preserving-facial-landmarks-with-graph) +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/pose-estimation-on-merl-rav)](https://paperswithcode.com/sota/pose-estimation-on-merl-rav?p=shape-preserving-facial-landmarks-with-graph) +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-merl-rav)](https://paperswithcode.com/sota/face-alignment-on-merl-rav?p=shape-preserving-facial-landmarks-with-graph) +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-wflw)](https://paperswithcode.com/sota/face-alignment-on-wflw?p=shape-preserving-facial-landmarks-with-graph) +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-300w-split-2)](https://paperswithcode.com/sota/face-alignment-on-300w-split-2?p=shape-preserving-facial-landmarks-with-graph) +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-cofw-68)](https://paperswithcode.com/sota/face-alignment-on-cofw-68?p=shape-preserving-facial-landmarks-with-graph) +[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-300w)](https://paperswithcode.com/sota/face-alignment-on-300w?p=shape-preserving-facial-landmarks-with-graph) + + +## Setup +The repository has been tested on Ubuntu 20.04 with CUDA 11.4, the latest version of cuDNN, Python 3.8 and Pytorch 1.12.1. +To run the video analyzer demo or evaluate the algorithm, install the repository from the source code: + +``` +# Best practices: +# 1. Create a virtual environment. +# 2. Install Pytorch according to your CUDA version. +# 3. Install SPIGA from source code: + +git clone https://github.com/andresprados/SPIGA.git +cd spiga +pip install -e . + +# To run the video analyzer demo install the extra requirements. +pip install -e .[demo] +``` +**Models:** By default, model weights are automatically downloaded on demand and stored at ```./spiga/models/weights/```. +You can also download them from [Google Drive](https://drive.google.com/drive/folders/1olrkoiDNK_NUCscaG9BbO3qsussbDi7I?usp=sharing). + +***Note:*** All the callable files provide a detailed parser that describes the behaviour of the program and their inputs. Please, check the operational modes by using the extension ```--help```. + +## Inference and Demo +We provide an inference framework for SPIGA available at ```./spiga/inference```. The models can be easily deployed +in third-party projects by adding a few lines of code. Check out our inference and application tutorials +for more information: + +
+ +Tutorials | Notebook | +:---: | :---: | +Image Inference Example | [![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/image_demo.ipynb) | +Face Video Analyzer Demo | [![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/video_demo.ipynb) | + +
+ +### Face Video Analyzer Demo: +The demo application provides a general framework for tracking, detecting and extracting features of human faces in images or videos. +You can use the following commands to run the demo: + +``` +python ./spiga/demo/app.py \ + [--input] \ # Webcam ID or Video Path. Dft: Webcam '0'. + [--dataset] \ # SPIGA pretrained weights per dataset. Dft: 'wflw'. + [--tracker] \ # Tracker name. Dft: 'RetinaSort'. + [--show] \ # Select the attributes of the face to be displayed. Dft: ['fps', 'face_id', 'landmarks', 'headpose'] + [--save] \ # Save record. + [--noview] \ # Do not visualize window. + [--outpath] \ # Recorded output directory. Dft: './spiga/demo/outputs' + [--fps] \ # Frames per second. + [--shape] \ # Visualizer shape (W,H). +``` + + +

+ + +    + +    + + +

+ +***Note:*** For more information check the [Demo Readme](spiga/demo/readme.md) or call the app parser ```--help```. + + +## Dataloaders and Benchmarks +This repository provides general-use tools for the task of face alignment and headpose estimation: + +* **Dataloaders:** Training and inference dataloaders are available at ```./spiga/data```. +Including the data augmentation tools used for training SPIGA and data-visualizer to analyze the dataset images and features. +For more information check the [Data Readme](spiga/data/readme.md) . + +* **Benchmark:** A common benchmark framework to test any algorithm in the task of face alignment and headpose estimation +is available at ```./spiga/eval/benchmark```. For more information check the following Evaluation Section and the [Benchmark Readme](spiga/eval/benchmark/readme.md). + +**Datasets:** To run the data visualizers or the evaluation benchmark please download the dataset images from the official websites +([300W](https://ibug.doc.ic.ac.uk/resources/facial-point-annotations/), +[AFLW](https://www.tugraz.at/institute/icg/research/team-bischof/lrs/downloads/aflw/), +[WFLW](https://wywu.github.io/projects/LAB/WFLW.html), [COFW](http://www.vision.caltech.edu/xpburgos/ICCV13/)). +By default they should be saved following the next folder structure: +``` +./spiga/data/databases/ # Default path can be updated by modifying 'db_img_path' in ./spiga/data/loaders/dl_config.py +| +└───/300w +β”‚ └─── /images +β”‚ | /private +β”‚ | /test +| β”” /train +| +└───/cofw +β”‚ └─── /images +| +└───/aflw +β”‚ └─── /data +| β”” /flickr +| +└───/wflw + └─── /images +``` +**Annotations:** We have stored for simplicity the datasets annotations directly in ```./spiga/data/annotations```. We strongly recommend to move them out of the repository if you plan to use it as a git directory. + +**Results:** Similar to the annotations problem, we have stored the SPIGA results in ```./spiga/eval/results/```. Remove them if need it. + +## Evaluation +The models evaluation is divided in two scripts: + +**Results generation**: The script extracts the data alignments and headpose estimation from the desired ``` ``` trained network. Generating a ```./spiga/eval/results/results__test.json``` file which follows the same data structure defined by the dataset annotations. + +``` +python ./spiga/eval/results_gen.py +``` + +**Benchmark metrics**: The script generates the desired landmark or headpose estimation metrics. We have implemented an useful benchmark which allows you to test any model using a results file as input. + +``` +python ./spiga/eval/benchmark/evaluator.py /path/to/ --eval lnd pose -s +``` + +***Note:*** You will have to interactively select the NME_norm and other parameters in the terminal window. + +### Results Sum-up +
+ WFLW Dataset + +|[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-wflw)](https://paperswithcode.com/sota/face-alignment-on-wflw?p=shape-preserving-facial-landmarks-with-graph)|NME_ioc|AUC_10|FR_10|NME_P90|NME_P95|NME_P99| +|:--:|:--:|:--:|:--:|:--:|:--:|:--:| +|full|4.060|60.558|2.080|6.766|8.199|13.071| +|pose|7.141|35.312|11.656|10.684|13.334|26.890| +|expression|4.457|57.968|2.229|7.023|8.148|22.388| +|illumination|4.004|61.311|1.576|6.528|7.919|11.090| +|makeup|3.809|62.237|1.456|6.320|8.289|11.564| +|occlusion|4.952|53.310|4.484|8.091|9.929|16.439| +|blur|4.650|55.310|2.199|7.311|8.693|14.421| +
+ +
+ MERLRAV Dataset + +|[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-merl-rav)](https://paperswithcode.com/sota/face-alignment-on-merl-rav?p=shape-preserving-facial-landmarks-with-graph)|NME_bbox|AUC_7|FR_7|NME_P90|NME_P95|NME_P99| +|:--:|:--:|:--:|:--:|:--:|:--:|:--:| +|full|1.509|78.474|0.052|2.163|2.468|3.456| +|frontal|1.616|76.964|0.091|2.246|2.572|3.621| +|half_profile|1.683|75.966|0.000|2.274|2.547|3.397| +|profile|1.191|82.990|0.000|1.735|2.042|2.878| +
+ +
+ 300W Private Dataset + +|[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-300w-split-2)](https://paperswithcode.com/sota/face-alignment-on-300w-split-2?p=shape-preserving-facial-landmarks-with-graph)|NME_bbox|AUC_7|FR_7|NME_P90|NME_P95|NME_P99| +|:--:|:--:|:--:|:--:|:--:|:--:|:--:| +|full|2.031|71.011|0.167|2.788|3.078|3.838| +|indoor|2.035|70.959|0.333|2.726|3.007|3.712| +|outdoor|2.027|37.174|0.000|2.824|3.217|3.838| +
+ +
+ COFW68 Dataset + +|[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-cofw-68)](https://paperswithcode.com/sota/face-alignment-on-cofw-68?p=shape-preserving-facial-landmarks-with-graph)|NME_bbox|AUC_7|FR_7|NME_P90|NME_P95|NME_P99| +|:--:|:--:|:--:|:--:|:--:|:--:|:--:| +|full|2.517|64.050|0.000|3.439|4.066|5.558| +
+ +
+ 300W Public Dataset + +|[![PWC](https://img.shields.io/endpoint.svg?url=https://paperswithcode.com/badge/shape-preserving-facial-landmarks-with-graph/face-alignment-on-300w)](https://paperswithcode.com/sota/face-alignment-on-300w?p=shape-preserving-facial-landmarks-with-graph)|NME_ioc|AUC_8|FR_8|NME_P90|NME_P95|NME_P99| +|:--:|:--:|:--:|:--:|:--:|:--:|:--:| +|full|2.994|62.726|0.726|4.667|5.436|7.320| +|common|2.587|44.201|0.000|3.710|4.083|5.215| +|challenge|4.662|42.449|3.704|6.626|7.390|10.095| + +
+ + +## BibTeX Citation +``` +@inproceedings{Prados-Torreblanca_2022_BMVC, + author = {AndrΓ©s Prados-Torreblanca and JosΓ© M Buenaposada and Luis Baumela}, + title = {Shape Preserving Facial Landmarks with Graph Attention Networks}, + booktitle = {33rd British Machine Vision Conference 2022, {BMVC} 2022, London, UK, November 21-24, 2022}, + publisher = {{BMVA} Press}, + year = {2022}, + url = {https://bmvc2022.mpi-inf.mpg.de/0155.pdf} +} +``` + + diff --git a/SPIGA/colab_tutorials/image_demo.ipynb b/SPIGA/colab_tutorials/image_demo.ipynb new file mode 100644 index 0000000000000000000000000000000000000000..847f4fe6d0dcbdc79f09a691302c127254b7305b --- /dev/null +++ b/SPIGA/colab_tutorials/image_demo.ipynb @@ -0,0 +1,197 @@ +{ + "nbformat": 4, + "nbformat_minor": 0, + "metadata": { + "colab": { + "provenance": [], + "authorship_tag": "ABX9TyO+yWmNPw3eBl9Z5zvQYH17" + }, + "kernelspec": { + "name": "python3", + "display_name": "Python 3" + }, + "language_info": { + "name": "python" + }, + "accelerator": "GPU", + "gpuClass": "standard" + }, + "cells": [ + { + "cell_type": "markdown", + "source": [ + "# SPIGA: Shape Preserving Facial Landmarks with Graph Attention Networks.\n", + "\n", + "[![Code](https://badgen.net/badge/github/spiga/black?a&icon=github&label)](https://github.com/andresprados/SPIGA)\n", + "[![Project Page](https://badgen.net/badge/color/Project%20Page/purple?icon=atom&label)](https://bmvc2022.mpi-inf.mpg.de/155/)\n", + "[![arXiv](https://img.shields.io/badge/arXiv-2210.07233-b31b1b.svg)](https://arxiv.org/abs/2210.07233)\n", + "[![PyPI version](https://badge.fury.io/py/spiga.svg)](https://badge.fury.io/py/spiga)\n", + "[![License](https://img.shields.io/badge/License-BSD%203--Clause-blue.svg)](LICENSE)\n", + "[![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/image_demo.ipynb)\n", + "\n", + "**SPIGA is a face alignment and headpose estimator** that takes advantage of the complementary benefits from CNN and GNN architectures producing plausible face shapes in presence of strong appearance changes. " + ], + "metadata": { + "id": "zYVrcsnLp7D0" + } + }, + { + "cell_type": "markdown", + "source": [ + "## Image Inference Example:\n", + "SPIGA provides an inference framework that can be easily deployed \n", + "in third-party projects by adding a few lines of code.\n" + ], + "metadata": { + "id": "6VGcBElYwZQM" + } + }, + { + "cell_type": "markdown", + "source": [ + "###Setup the repository and load image:" + ], + "metadata": { + "id": "Pxj4tBskykGV" + } + }, + { + "cell_type": "code", + "source": [ + "# Clone and setup the repository\n", + "!git clone https://github.com/andresprados/SPIGA.git\n", + "%cd SPIGA/\n", + "!pip install -e ." + ], + "metadata": { + "id": "N6Mvu13ZBg92" + }, + "execution_count": null, + "outputs": [] + }, + { + "cell_type": "code", + "source": [ + "import cv2\n", + "import json\n", + "import numpy as np\n", + "from google.colab.patches import cv2_imshow\n", + "\n", + "# Load image and bbox\n", + "image = cv2.imread(\"/content/SPIGA/assets/colab/image_sportsfan.jpg\")\n", + "with open('/content/SPIGA/assets/colab/bbox_sportsfan.json') as jsonfile:\n", + " bbox = json.load(jsonfile)['bbox']" + ], + "metadata": { + "id": "Lf0RwuFW9cSC" + }, + "execution_count": null, + "outputs": [] + }, + { + "cell_type": "markdown", + "source": [ + "### Inference and visualization:" + ], + "metadata": { + "id": "E4u69_ssyxkY" + } + }, + { + "cell_type": "code", + "source": [ + "from spiga.inference.config import ModelConfig\n", + "from spiga.inference.framework import SPIGAFramework\n", + "\n", + "# Process image\n", + "dataset = 'wflw'\n", + "processor = SPIGAFramework(ModelConfig(dataset))\n", + "features = processor.inference(image, [bbox])\n" + ], + "metadata": { + "id": "Mck9eHXKYUxd" + }, + "execution_count": null, + "outputs": [] + }, + { + "cell_type": "code", + "source": [ + "import copy\n", + "from spiga.demo.visualize.plotter import Plotter\n", + "\n", + "# Prepare variables\n", + "x0,y0,w,h = bbox\n", + "canvas = copy.deepcopy(image)\n", + "landmarks = np.array(features['landmarks'][0])\n", + "headpose = np.array(features['headpose'][0])\n", + "\n", + "# Plot features\n", + "plotter = Plotter()\n", + "canvas = plotter.landmarks.draw_landmarks(canvas, landmarks)\n", + "canvas = plotter.hpose.draw_headpose(canvas, [x0,y0,x0+w,y0+h], headpose[:3], headpose[3:], euler=True)\n", + "\n", + "# Show image results\n", + "(h, w) = canvas.shape[:2]\n", + "canvas = cv2.resize(canvas, (512, int(h*512/w)))\n", + "cv2_imshow(canvas)" + ], + "metadata": { + "colab": { + "base_uri": "https://localhost:8080/", + "height": 401 + }, + "id": "I6o6piO-Dju_", + "outputId": "123db829-e9f6-4257-e6e3-ff9f4be8e18c" + }, + "execution_count": null, + "outputs": [ + { + "output_type": "display_data", + "data": { + "text/plain": [ + "" + ], + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAgAAAAGACAIAAABUQk3oAAEAAElEQVR4nJz9Z7BtWXIeBn5p1tr7nHPN8698V1d3Vzs2fKMBwoMESIEUQVIjGlEiGdTMSDEzjKBiIoYxEfNjJvRPo9EfBo0EiREkJVKaCZKyFAkaOIJw3Wg20A5tql3ZZ687Zu+1MnN+rH3OPe+9KqChXS9unXvuMdutLzO//DKT/q8/+SPMzKzMjGBmVk0552BSFREliKqKJBFhYTCziKROOBFn1iSScu6pT5qSqjKpqubcM7OIQoiZVVVEiIiZiQiACLUHEYG9jcLaAweIiFWY2QksHYBqXoqth2G53mw2m5OTh5vVqQ8bvzhfnzxYnT7cLM88Cic5ml1dHB7xYja/euX4qZs3nrpxcOVosThYHBzPZnPVzKokwqQkzMz8yF5cbh5v/wfae7x/CA67fA3tv+odNn/71zx2WtqvEUFE7TF5UCAiOBARRubu7g4zj1qGcb1ers7PV/fvfPUrr3zlK1+5e/fuer0ehsHM3A21AhER7V0RYWbu7oRSSvuWWuv2e1Ertz2KiIhg5vYW1kQMZiYKERFpF1cSMQBJ6gZSIVZmZmYSElEiElEATMrMAQrqI+DuhqhmEVHd3L141ZzMysVmVaxYhIV7RLZ5EBWrolpKYY/M+fBgMdj52flp38+t1HGsWROCVqtlqUsDwok8UMtRl64fzd/17DO3n7l186lnr9+4fXTl5vzwuJvPUpc1p0V3LETCILiGE5zgAAZRf/S6uDsiyDw82plsp9TaFl5KqWPZbNZlWA/DsFkvLy4ulqvNarVaDZvNUIrbWGqxWh2O6fpakCMQHASA3M3da63Vg0RLKdUBhFBETF/KzG0HiIimi0UREUEAEAygvWy6dsyXB0IuzKqcRVOWJJJSUpW+k9wlEUkppZS6rmuPiaLT1HddYk7Kfe66JF3K7cPHsa43m9F8PlvMFvOu76XrupQzZ3UfLy7q5sLHdR03VqPUwczKMJYylOn+rEOJcRxrHcdxY2Ucx41ZqaW4j1armUWEJsk5d5oODhZHh/2V6zePrj11fP2Z2eGVfHBMWVkT0wwgdw+vdRhrHcdhGIe1rc426/Ww3qzXy/XyfHWxHMZ1KcWG9bhZex1rHUFSgizYWISZiVlFVANgYWYmFs2HSVJWpkBOkkUQocTBBKDhSkpJchIRzUlYNSVWFu20y6xJuyyaQxI1ICYWESYSTJ+ww8ndIh3H8WJ9sVqtzi7OT09PHpw+uP/wwXJ5vlyuNmPUUuE1EbEbeU3CWeSo768cX7l29ebVo+tz6Y76eUd8vJipahbVlJJyAohFkmZNCiERVU1EpJoJRCTERCosopJIEnNmURbVnKMt7+22D177Tz7519/VRkREkVKaIVSVmS46RilYHNj8YDw6Wp4+WG+WVkuvzFHVjb36sNks15pSSkmHQUSJhETIw8m5GZs9SN8H33ewC4/v1eVj/G8/ungHY7ND//2f9M7PwyMi4BMSNeAYhqHW2jDdPSiAgJnXWt29vTcA93CbQAxARLvzYBGx/RZiMgQIEDYzId6dhPaTmRFoiI+AqDYDIKJBoaoARAQAkxBJgMAS0d4eLGJmYSCi1B0MZbTqygumqFaDXDR1kknYAoYI83DYUAarB8fXK3gzjKlfpBQXq1XOOR1ftSFZqV6M3FWTSyB3MptxnqkmEVXiTNQxMoUgmEAiICCkwGm6EcLhu5uircl2lrB9vHv+sV8bEnu1Bl6IZsvCzUst7gGAGQBvL1oAiPYfoSE7MwuhuotIEMzqN3lf7dZg+5zf1T25u7X2t3YSfvuPEhERaR6jqjIxIqzahGS1WhmHUsdx9GrjuBnHsZQSDekNwzjUWsZhcK9DKVaL1VrHwd0AJyLbWHhYspTU5skjiEBMJErMwkKsTNy8tQBzUoWbmXrilJohSTWV3EsaYuRaS7VSvLgXq3WwTQ2uTkYimpkYTACGUkAkKqop6UY1ZU1JqEupE2UKEVFiZmJVYjIbc2RLiQhIxCHhRAifTh4DIGFuFoC4OcrYunpPbkSUHt2ypjGllFI1g5k7EZCTMqQT6ZIu+tnh/GDRz7KykCNGCowb0zxbtCtErM06Jc0sk60TFiJRVSImZgKJComwKJGyJJZEJKxCOl1sugR8Irr8DY9ixDcHrY/cikRMFMzMsITEzCxH3EmMhTaDdzObzxezxbBcDpulrU+jjlIllSHXKqVGMStWx1K1tIDGAtQMNRB73tA+oDcc/B32bP868Ts8/45v/qZev1uHzTdvv002oL2LpmjAJ1fBo7mGHkKsLMoymIdt0SUsIsytuk1RBSECQQhCAL5d8u3lFrKLAJqXt7us232j3dlrEdX0gLjdAw0OSEhEiFhEEMysADzggWhnPqJ5skQkmgKEYKZunoWZpcs5JWZaDhercfAIsIA1S47O4MH9/Nbh9QenJ6v1QCLd7Oj84kI0SZrbalVoFAJFrexyeFUPrpDOOC1U5zn3TJxAOVxhHJWDQBwkDgpQgEAhMVxeswAC4YEt2r8NXG7PeXtsZl5te3XcrZiNzYNHgAhhFh7mBidDxPRd5LEDbooIVQ1ChCMuI8532vZD7d3jb9IPCzxyOLs4g/lxO/fkpnubsAgpeURYuJnVWoaxDGUcy1BKKeM4NgfFzMZSatBQbCx1GEst4zCOZrWWIgS3cDNEJGUqBGCopVh1D0CYRFhEhDWxCFgAUmezUMDDzcxdIYmlEDNrSjlpl2UYQFLDzWuppdpYmrtBGmAnLh5lLGMZq5u5E3NSVVl2kvq+n6U0iHRJk4gKd8KqmigJKXMCDBa1glNyhBAHUxARC5hJhFiIiYnRTBeRtFXmj1ypHa4KiIgYxMwC4mYxiJIwiYKQCEk4MfrczXM67heLrs8sAk/MFJuwuilVSbNoyjmrJmbNKWtKTMxJJt4GEoCwijCLBtqyFmJhUWYBieYUNC14BO3vaDyx69/Mbff2tyIcABFEBOwAWMT1IHJJszkfHPjFUZ0djBcXm4vz0tFqeU5WabPWceg8kkeMTnMCAA8zE1DAY4oALrf9nYx3MADvdNfT78a9ArD/8n1j87Ynan+xxQ4c2nqO4IBFwCf0hztFIEJVZ7PZYrHYbDbNB2yBJAB3ABwB34ULiFqdiCLau+EO97A9XGs2pmF6c1giwswbpbAz89sIoC3JhgMJTM33V8kAiCSCEEFgimbOCAwOZFESGUafL7qUctK0GYZhGC5WS/MY2MZwStk8zGLw6mMNx8NxdXScZX5tvqCjq1cOjq8E03o9ZlFlKWPZrM5tWGFYHvXiiwUvriBfqTwbPGUkDwkgAuIjwRESYJA6EcCPXfVL+NsFSvtP7uEm+dYybwk3+MRmubtbqQ4zC6A6BRqtQ9uADrE1ABFhARaNiMnO2u9sAESkfe0+TfQ7vmt7kI9bte3b6cl78snvlW0UQEEgNIcw3MKL22hlU4ahDGUcx00ZN5tNtXD3zTBayDAMQxk3w2ZsBqDWWkuWoHCECyHCiBhoZiM8pqiUVEiUmUmUiAEKCg52dwhHc2WTclWxLLWCRDRr12sZuIoTWXiptZh7A2iVCoJKO+qyXo/FLIqqZS5FiwNEyBEsDQdpHIcIJyZiImf3iQENErCGMLGSKJhZlFXBLWRgJg4maW4TpjO2O6U7CJ3IImahiThqoOxMrMHgLJSZs/Ki62Z9f6U/6FJWColIbBxj+FjHlfaLIxFpuN+MlmpWVcnCrMIM4i22NxJfiQlgMLEmIgITIIC1nWOWtsJ3O7rbJgsx3Te+O55HgO+d7sMwIgW5u7dVIUog7kQ4d2QmtUrqak4l9Sl1NZuKlvUKw8jrDTbrFMeZRYiEJhsQFBTuDbX37mPaBl/N2wXextl5Z0vm+67x7nFzafc/fLu9feTx2Lra7c/lnyKwlwMIBLZZgYY4EUEEIe40Hc4Xy342zObjelObxwp4ODH5lrlu2FurOeCNpgAaX2Eegdjxy2a221tiapcRmPIT+wag3Q/YkgCq6ggATEokAJi1lEIsLOKltpix+RgeQYhuFiweMZxdPBiKmYFVlWWMpEzrYk7ULRZXr1x/5vYzzz3/wuHVG8fHV46vXsvzWQWCycHuHhVmERGMoCgdDL6JYcPFvBgZmKkwVuTO3DNQS5cYHkyCqEICakBsl07xDkkvYRG7u4WZzQzmNN2woO265UDLEkRUDqcp7kK7KkzkRBSwxtczNbJgAl9QuBNRu7dEtZQxIiZKbYvvW35h4v3dHZgYWhF5p/v5EuKZI8LDQfLY/TzZdURbuUHU3gLILsHg7i3n1y56Y/84wMQRIYxwMy/DsNys1rX6ehiasz+O1RC1RAlfDcN6GDbDsFytLKKYWa1zjcRgJg8PEFdjBoENxKKaOpUskpiVJXHScG4EnRNExKMys4kEC0kSrZKz1KK15r5WX5iPVmspRTvAglKWNCPJVXoiqW6pFE6dn5/XMhInTbmf9V3f5b7PIirSdR0DAmHVYHJmEQkmZyJRKEvuNKeUZ6lLkjInDabGixJzu/mDiDFZy/0L1JaYiNQSwpxEG1kjIkKURMgDRBTWp5QZR/P5fNYd9P1CZl3KKafEAIxhZptxWGnq513X5ZRBrJqVNaXEqjJROu3yMxEzCRETCxFhe/8BCAKIZIf1dIn127jkd+H17178du9xwEHeOJu2X50IETiUXCkpM2vK2nWlI03deHaCMiRHqp4cPQs3MraaERG1Ew0Q2d5ieAT0qz0CuztE5kfM8uVjt30rPZ0hIvKYHtAjbr/T2ztQv70BaLjfDEAjixtkh7m5NZPQWH4mSinN5/PDw8P1et11XQu0iSS8kQ7s5lMQEGFBATgoAHc3bwnJANwnighbEKcdTfTk/u+svrAET0KAlJL5JdY0VyNpBpOkREzjOFpE7jsi0py6rhvqysMDHHx7NK+GGiCSSnPp5leu33jpAx987vkXF/NDpjRshhpBzAaUamO1YrWaRcAre7A3khipy6nTXlJ0lHysNpbRfO1F2TOhQ1zPEUIcrozwkaygEbfEEZc2mHZ5l+1lehtsbT8DAHii60DuEQ4LwGop7ZYOdwr1aNGtsnsL84nI9gzMhLOYKJ2GuY9dhe09SQBqNQCxtd9P3l2/zdaMR/sKbI2Qu6tO0R5dcpKx+2t78UT+iIhowwLxMFCYhdew0W20Og7DMKyH9VhL9dHcgkq10Xk11vUwXqw367EGUYBJc41KQAI71eZsNpARbcnrJCmxKqsQCxGTKjwM4GALAxrDScECIdJEWrp+FhHBLYHgzKKaay0gJs2cZqTZkAC28Gp1M46LxdFQCgt3krqcZzn3XVZmZe5SYgSjTExOUk5JctKUOPeae805d7Pcd5ISJdXUMTO4+UqTE02B7aUi2t5vj5Eo7RFfAjQTgYlEWIhnXT6c9Yezft538z53kXJLgjJpGHv4wAFoni1SzilngqSURDRpFlUSiAizEohZmytHxEwa21t+IgkICDQeqnFvEznQDAA/stO/47ZvAB65TSfc3z4OYiZmIkRLnAAcIsHQJJJUc0qpLxBbniYRDaBWdgditxTNjABnJ6J9QN9fUeSXmPuoh/72RyS4dIEf8/p3jx/5nHcgk/aPfR/9d6srHlUBIYICHkHNo5+4BQ93BmVN8352uDjYrNZezaqNgFk0FhnCzbf0CN9KSvCoYfPtk7szMy348GZTH7vC+5Gf5JYrIndvF0Y1t9xSLdb8iWs3b/SzHoADm3FYLBaStNa6XGUHJPfnq0FAhej4+s33vvz+p26/++q1W5X4fCyl0vmqlFLd3FGHcajFiMQROfccMo6l1ijuG/NNNQ8HhZBTBIsSRFgEIqyMqjWU/e6yLLLOMx33MtdeZZAoZBXu+2j7GPLGNhR4zGl4BP0DzRUQTG5eUh7NfbTqTiQIgElAzoyWyw9c6otArElEwAoEhTXfv6l6Lm+z7VIB0JxxBDfq73flkF1mKrdB/JMmhPa22Ea9vEXn9quyUpCwBREziINamqmWYbMq1UopFhwgNA+DiVVIE2iEZo8IEAszqQipQCkJPHVp1qW+7/tu1s9mXderpqRJJJEICTOJk5M7mMhpu3Mtp5kkRfIeRNkdTCBS1T4vxtlRtWLmwSJpJnnmIRFwhEcUq8M41lojMKmlmLukDDCQVSkcVJQZRJoSJ81dp0lTyqmf9bO55py6jkQkZVFt6N/OlYC4ncYAIph4P9++O8+MyTMA0PgfBgkxYEk0Ky9ms8PFbNF3fU59zpk1pU5VlUjcUBySSTvt+pmIasqqKaXcjkckNaPKzES7n0IgIWl+nzfnAN7QZ0pHsO4u+eSbPMph/c433DuxQAFwcz0d0UwdEUhBwkKJnACh4BzMBFLOCaylWJjb6GMpF8uh7yVnFaXmDHo4g9ES7pduXJPKNAHGjmlB7B0IPRIBTBQWAYEsvAP6y+UBom12PCKwD6zvcG7eKQLYPWgyUGCLSG6IcHO411qtWpTqtTKLqGhq996sn83GMo61jGPZaQTdwyzMJh8xAuGTW+cGAG6IrZ/32NX0CI/gR13OdrmmFMLORE0ugqbU5ZwB7meznLuc8mYcU9KLi/Occ+q72awXkVrrerVeXpTiWI2ro+s3X/7AB9713pcPr19PqS8jnyyHGtjUWK3HcajhVEvNyZlIiat5Sp2ENFZyaQVEHlGNNgbzcDMPK1GZBCQcpCoRRuRMdsDaUZlROcq4dZCvzvg45QQGjbT1yqxZxHa4NB1sXObkp9zMpbM0oT8hmvZYmKX9D6MBnpN4TP5ygBRqgVItzFTEfFr5oiqq1HS0cHfd6btiKxT2ui9HhoiET+kc4G2W5N7vsR+iNpjZBnOsLM3vyk30Pcl7aJ/mRTM5EbsMMDOLMAJkRIyUkmoSVRFOWdNGQWJBwepQJ5ahDmDSjrULUqkWAU4p59R7yUqdkHJkxrzjzDSfdYdHx4cHx7P5InUdiYpITCmoyclq8e7WG52WJEditYTO3ZsYp7IkSSllq3UsxYklddrNKZK3ZUhkbtWs1moRop2KECIxUzghknC4k3SNRGlA3/e9qKqmru/7vmdVbkSLKGkiooBPVrPdOtuLwozwRxL408WiCVsYRIACLd2gKaek89wt5v3BYjHvcpe0zzmnrKoqSYjZCoTZnYmm1ciiOXesiYhDEqXEkreqJBZpqQ0CIYias8ktYnVv6E9hxAzRRhOSCJgN3kKAfY9pi4+C7Y22U6kBUcMaDYyWAWlEPAhgOMGdIe7WwjgSMgIoFMIBEglWE2NNsdxYzXx0JZj8/NQ2tXu4Tn7GVfRKyIFHOFKmCMbkc4FADndjgoeHmbsXJg8QAlvVzXS7ezRsb+AX7kFgYnMiEIQJ0oJNEBhI0XhdBE+kT0uW2x7O71NPTVuJfZd/u7wZTXziAVCYT9SwNf8TZt6o52AJqRyVEMrSd5Q1zbtUeykDSmkcz/bSeIQ1sfl0nZo1QLg7AcViwnT3ra+HCDizsBR3AUsgpaQpdanps5OK5q7LuRfRZrNZtes6SZmYN3VcW+FBzi/Ok+rR0RFr6vv5OJaTh+dmvinl3mDdYvFd3/cjL3/ow4uD49VoQ43zTb3wrow8btYxjFStN5/lND/sbhxISD4d4rUHy4eng5EFIYIHt0q08dh4rD3M2VzD1RBjrZqketRxBFENF0lCffZxwbQY5Mtn9aqWF4/oxStpIcxRma36KEzOFBEWRGGO2tK7jS+zas6kZByFYQQHEVjBKShV6oOrsAlGMs/KLDkgzB2zALDwlghRQmUM1TkiSFkZQiTEMul0iRgQoksG391tmw1qzzUWiBhovN8TSjxFApwDAXdi56goxImYBdH+JaZEUOWmxFKAA0JILELNBQQRzAxw1bTF/yyirEYRFCYKF6Sca+q7fmbDOJvPuBqlPjgZtBg4gyxmoocRV0rZDENEMIsKd+SMYArlUMGsS31OfZcPDw9zd6h5Qamn3AWLaGroTxE8JbQc1TggEURgkYKgSCOQ0DtaflZHXyMTcXEWDxMN5cqcCALAAxESGp4amiWevDtnrkwhDGIxnaXUsarmnFJOXVbJmlRSIhHNeZJW0kSms+glVTIljSIQ5GgA6+FuTmAKRjgLE4HgQs5hYqULIwYo9Wm26GeHs0Wvuc9d165EN28Ijwh4dd0EEVS167qcs3DS3BERSZKkIiqTcFsurebOBBHF5KkHE09s1dZB3vd89x/8NnHAY85y86ceeZIeZ8r3SPfLz2/ZrenpfsYeHsZWqRSsVzZsxofWMRsCVsjn6GeUUkgiJjgRT0xro07MPHyrydh5dh5BcGLQVrZIoPaZzSAHmKUZABIOkukSezAomGCTT+hTKvpx5c8E91t1zWPES6taiAi4AaAweLgbJHaBWWxz2gQYWHIn1YLXnDKnTnKveUi5FKvesnHuFtO/Rkl5+E524uHbQOgyENlmAhEI8+i6dDCf932XkxCRsmjKKaXmOLac4mw26/tG8ngZN2MtHu4RmtLxwYw1qep6GO6dns0PjlfmD+6fHF699qHv+p5v/fbvOL56rQY9XJX1YGP1Uor7Oqp14Um579Oi7ztNbvXOxdmyrk83dvdifLguFmwRHiTEBozho4cRN6E/AjSltkAcwhxEKF7MTmgdZY2yySl3XX8Y9Mpbpy/b7PfeXhzmzmPgpOZjEIjAEVSFAhxwhNVKTcRDYcTG4gRnDfZgC1aIEkEIieAiPJsV9xpwCEUiMAgeYVN+jYQ54JXYwh1Iok6YpLRbL6FVezSJV6NcbLthMuntFp2cjCciOUfzUQIwR3JiTcrdFsdzSk0ikljzVNkpKpJUhRtdfJmQECFNKedG96lKYjaGwInUXFNK2fqu1gVFcMq52lDhkKBsYA8eIojYt/V0kwAB0HB4JQRzqFDf6azL81l/fOX6/OBIu55kSlJOB9YWjkdT63I0C0jMTBEWrKokzCKN/7FYRSQUACFC7gw4hxFqqwVhEAsjqBnkCf0FNGlkIErEgtxrzqpJc1LJ2vUiIlMwtBVYboUSRBTktHdJ6LfhQqYL1hADQkQRRKSNxybuk8y6NOvybDab9V2fck6JcqdJSVJEKOVQcUJJqlm6xImEtdVNqIhkZhadqPx99Kdtwoe2yeidgKcVQO2/8skHj9EajwEfbZUkT37Ob7PRE1t72lUjW1RDP/KQY1xjHK2OcULwSla1xfB9H10EC5jI2BEeXt0swszgns2nfN2krfDpcJna6gRRUEwFw0TKiVlIhSkoGIyWpKpmExvGREQN/RszvH8sl5aGLr3+/QiAJ/SPyV/zOrl9pTbSEOYwb3rqGt6EJ5MugrU9FkmaVEZpvMEOOMwuM94NOCaPMsJ9b1FtRU1ElFPqc5eSENFyuRyEUkqHiwNVzTm3BGBL9uaczWwsm3HcRISqCiEnSVk6BTSfX6xGj/mVa9+49+D67Wd+6Pt+9PYzzy2uPrup/vACo5XNMI7FmpT8wEdlzl2XUiJmc9w9OTs5P787xnL0TdCqxgA2ogogQi08wigCVGsVIg5QMMDkxs4SUUqRlJRAFEnGzbAM5RF0siwnXXesV5ZvnV4P/z0vPc+RYBswMwfQDPVARA6YO5MClREWPoCdNJjBDjJmVqUknAWhLDkxWTUXj+JkYDJuRliYYNUJxAx4UiEmDi+xxzNNmbnJbxCpzQyYGYO2RX++L/vZLcPHFqN73XG3zJSEs0rayjinTC5NosMdI8QMJRYhnsBxyjeIUMpduwFa/p8EDCZQAJFK9POI4uFMRNpJcRmrgYhzgCNoqC3iDHfflaYjgmqJECCEkJRzlnnfHx4cdP08933OneSeSCcACQ8j2gpwd2eAQCQaLInFGo1BAnCRwm6N0wAZB4VzUz+Yj0AjLYjRov4gkNCUjWRmqJJKyolFuetTSpI0aUcqKXXErJqnSqZ2ArfoyswWFXhEHvLNbC1pLMyJpaZEBGHJmXKirJxVsmQhJQjD0WjYFmoEkEN4G6QRSSvJEdLJlAd4IpiIttmG6fphC15ELfCkLYeFR0Ef3xyI7784nogYJuPxO71x/54mAqUE69E76sD9jDarWLkP67pZpc1aypBqjcODuhijn0XWYAniiDA0MUyYu4ezeau/tm121BsPsz0xjary7fkwdmZhVyYHE9gmrndbckYBC8dEAeGxc7NbnDUm/H3cAIS1nAQ1ej4szANO4QRQS0iYW62lVcyjNSlolz5pyppyyh2tNMDmqBbmMItqYTYZYPfwifWf1D8ekzeKLfp3XXdwcECiXm29Xnuts1l/eDDv+75LmZgB1FrHsQDDwcGB8Hh6dkrkKWnXZRHp+t68pi4Vs/W4Cu3W6zEqvv/HfuKF975M3YyQ1oO7+cVq0+qDHJQ0sbIUZ5ah0tkwrkY7X6+X63GMeDjKpqIGiocJNRaOwGWrEychYkYEHECBSXgJBzxQayu/IfcXU7zrAy+++WD55bcuZjK/WNXKMJ7/6qdf+dKXXnv/u59/5ubRwexA4O3WaynEgHkkwAND2MasGODgoCAGkwu5IpQ9iyCpwoVitEoGMhi4CXMBkBBXOKLWCkLlECa4RJADKqm5k9swa5ItWOOmzbzaTog5jmNss9Pul37G/sJsy5SYRKjLmkQTc2LKqjlpStq1zjAqSSUnFSFVUWJNnFVEpEsqIpjSANyo/0u/jJWJCAwn6mdMwS1Y1ixjyaXqZijVA9xqoZOiLTlAqhAAq7XWCgZBmGlqXJG172ez+SLPD3I3k9Sx6CQ8mejlcPdWGdP0uJNshsV3+RDhYHICKoEDDBZWpjpuhITY3CfeCZO+2ibmIYKpMCspEUOyUs4p95KUc27MiuTEPEl9WLdk+tYhfgwt8YRhxlR5HpMGcnrGObboT7x1spIypaRdli5RUkrCQoEIL+ZR2FyCNPdgIckULiBVUoGAVVlAwkQMZppa49BWuf+2OL5TFETELimxD1u0JTH2yZl9N+QJEA+RSaa/jVh3nz99VK0WBG7CVCJsRTu7cHhrMBxJrEqkjlICiCNiLDLWstyk1ZDXo642fDgv8z66hK5v5djE7NWEG6XiQx3d3cJsqqt1i2geJbfqaCYHWhmTqAa5amKCCjNPnpe5TwbSWwIR0XQOzFHr/nnYLdQw352EHQvk5uS1QXyrm9rKhIPC4C7E7pOy1MzMw8wjqBV8EYlImn4yby+vAOY+5RSmkgAArRypyS+IGz/Q9q3rusPDw4Ys43pDgePjw4P5PMKbpx8em/V6s9m4e9f1XTfLOZ+fn7tb48PmB4dBZMSUupP1WnJ39Znnv/Dlr734vvf/2E/8m5RmG+cSPI4Vy4vNag1WzTnP+s1Yyjh40NqkGl0Mw/lQzjfjuvroEaIeuQmazCsTO8E9zH3qG2FmpXD4PGW4URArkqiZRVBKyc0AYoqPfduLLz03e3Bx/e4//myxYsw2bi6G89/6tc+cvP61jDoTf+mFp1968fkXnn/2pfe8tDjqUt8PXjdIymCZQddOY7Wx+ojgitFa1yRlTSlqhjsTJxY24xooNlZjlkAwc3XLquZOAiYzjmIVCBDp1I+It/GcTDqfltUxq7WGVTNLKY3jSETtp7unJC22K6W0TPt043Hrb4Ok2jJ8uYWKiVU5KydlVUnKXZcaWCgjpcmJFZpKpbfwJs0AYCcfYkerBRPl6CWchMDK2vGwqWMlHdxsHFoQEw5YuABmJuRmRmiSXIhIzjkl0ZS6Ps/ms8XiaDY/lDwLllZGAqAVXsO5oT8HzNoajCTqCGFwhCPGUpQELMQVte38GLm3oa/jEKUqbxWPQYidApCYmCVALClzyqnrOc9YVHNizSLS9G/MSsLCiZmEAVzi/iUk7olKLivL9xBgpy5rz/DWn1TmLJpUq4gq91m6nGZ9Ti0sMwOFubOZ1UQR3rSTaLLaZtYlETVOkghMgXBiAQOtHnSyAc3DdW+50EvRzNY8fTPbk+j/TW77XjC28WBEvFPvHWl5n6xRk2mS3FHKwqrjGOOmLsf1ycXs2jmO53w4o4O5d7NghaqoJuJK1OIAh3vLwyOqmYW3JmVdbCVx1JLePLFgwmYGYacmP6btITfJKgHRxGQAmOOxSv6YolWPvevdVqy7hxmHhVlbDxRoSWggxC08doaWiBpzWqqbw4NYEkiIlVhBEkQOVPf9f8AjMYftomaAiBpTdHx8vFgshmG4uLgws9T1t27cdK8XFxeLxbwBfR0LSxKRruv6vgeodSJikX6en3nu+TsPHhpEZn2aLd7/oe9613ve9/lXvvojH/yOb//O71qu66bEMHixMo4F62XOOXX9WLFcD+tSLzZlLHZR8mpTl8MwGJDz6KigCEY1Ckvbe1wDHFSDSy1OCCIWsRKrocw1E8ItQOwRo1UWGqs5KCX6jTsPf+6znzs8vnGRbOlD4bB68uDOV2Hrl19+6alrhz4sX/3Kl75UNnfv3PnH//yfHz791Ld+58eeffG95xsjosw5kyiM1cCVzEgWI87Hel6JC5MlcWTNVepIw0BsxJ7UailBYGEBFauIAAUYrbbIwwUkKk6i2jUcbATNzqmceH83MxvHMaWUc25NAEsppVwW9O3KtYjgXrdRbKhwFu5SmuWc5JIIyppUNbEoC3FryhJEoHAKBjmREymah71tASmtiSQFT4oViDAJ3CRYWBNrV3PRNJRxFFrXUqTla0GTaNsdFEQOIdEsIqnL2uQGfd8vFt18IbmTnDlllhw0lb+1rNi2qL1pNiiYI0BEvhWxa6IgUK3MQprcqmkJs9qNNo5WSoQT7yCICBQ74qflblMSTZqaukE0daTSlgCxEjORQJiJhGJnAPZhcL+J5CXiRbRWHwHz6UGAHFsr1E50n7s6m1E4cyhFElViDo86GlsE3F1iBCuFtUQXa26KI2VSBqFZJprQnyggk+u9k4TvYsYdQPxvA3H8tgnh3/69l2YAj9TuPvFqCMwZxByakDpOPeuMdc2+4gIuG1mNZbXGaYfjmRwt/OCINXPXRe6gSiwURIjRbauECUEEXMLJY2zK9xa7CLfgF9EFWEAwRtSWA9ha+4n7b5kAc/e2ch5t53UZAbjvzL7vunXWqhRWipXa2H9pGoKWHGtZmWhRFG2dQR/HWltaI4ha87UmQwdHkFn4JBB8knGiSWq09UKef/75iDg/P1+v10Q0m83mB4cnJyeAJxFmulvHlBJjKgRpBEWtrRIVN2/cPLp+fP/0bF29P7x647kXF9du3nzXe8p83l8b+ODozZNlp3m9LHU0AucgPTyuwMXoDy82FyUGo3WRofKy+GBeIEhaPYrHaNU9TBxWZ8KZAxYEDbAFig1BcGrEHGp1QiRiwDysulUPQQyjFXeq/DOf+vLJgztXDu7P51fBjPXm4vXX3vyt37S3vvzwtXr3YH7Yp0Xf3bq9+Nj3fNetZ57/F5/52qdfvfcw31hWSv0sC/eqiVjTvFfJKfrO06LkMtD6Yjx5YKd3gldWBw5oRyqm6u6+Dqq1MnEwiMiIKzOHj14CCGqtViaVfUp5SsZqq9ThiHBxd0OYWRWR5um3B0TU2rW2ZM8ukdNuTxYSYWVpnb0yc+uXK9Jgoj0AC4hDWaTV9zGJCAuURVhIJADaVoNOKz0wNROLphNyEmcmBUQUnFIqVVLSTaEoQoUxlALsqCpRJXcmIhFlVs1Zc8p9N+sXeT6Trteul9SRKIleuk7u2FZuNIcARAIKIuOJCCNCi6IdIGZxCglXczdtS67WcAubqFcAqqk1TmaR0BBtBbONiknUEqiStjV8wpKCqYm7KOoOAB+BwSfAbNr/raf7GOo2qjyxVNEi0qWM3phCQSokxARyL+a1ukUt7KMHuzlBEOA+Wlymk2DEvPn5TeqEFq1FhAcIHrbdY57y02/DVf3O274JeQcbQG9zJh59wXQaCLvr8Q6vqgQKuBMgitSxZuKMIDKnYQw3bBCj+ibFalEPBu4y9zN0M1M11WiFbxbuFlarmxGMt7R9p42ccwqq5ElFxFVh7uRkTnAQwivzpSxhWg7UKnoCAO0Z/t1dGxHbrm07LzzMqtVa6lDG5shNBqDJcdQ9EJoSIkSVRSKi1Ormtdg41lKsmjegN/OWxHZEE/9sZT/wbd3DJJ5G7OzGc8895+537txp3kDf9wcHB+fLJbzpJbzW2jpcdSmbmTA3kmEYx9yl20/dPjo6Oj8/W242N59+8foz777+zIuRF6+88XA5vnV8dEg1hhLnJ2dZkoAWfa9Zz8zOzs8fLoezjS8rhtB18c1YPdzca5g3hUgzU2ED4CgAeUBZmmDNG7eFQHBjb8G8HsbI/SznOg4WIJax+mixGWtde0G6ee292X14uNHwizdfv/PZT8WDVxcH4yyTdsVRQ+JseedXP/7zz7/08rPv+4H16w9fPx95doghhCqjkrt0OkskEb1goXmW8sHxtf7w6aObt9Yn9zand8fThxhXQlWoRoTMeRiHQLTWCpWZjWs41+BwjpDWplRSzl3OnSq3EKAJtolaWycLr+42ZWpbik+EiUpFkwkRoZQySYZUZFIIcFLputwlVWUVdDnnlNNW0pOagoWbHzm1idCGeEIi20qr5hzLVAncVgBTa3LMQUamreExeYA0rLTOM0LISceck1mp1d1LLcBW9AxiScKcct9SE91slnLHXSZJRNoaWzUgoRZFT3V0MYkVtxpzZooIJ3CEMhHAIuExJeHDI9yiiWktWl1FRAtImJqAR0TVyJoBACAgTQwgSYKkRtNhKuxtRHo7CZe5tL3Ff4mAe2gwsQ/u1lzCLWwGYvpoFhHRlBLgDOcgncwv4LZtfzeUcVVqcK0eTkQqIqnzbUsWJqKwABxUKBq3bi3XCSI03CcCyPeJfoK7O00sPPY0OdizELsYYlcn8hj6P/KuJgLFVCK7TbOCiEutZgB4m6CG0qTS3Kc+JgeWyWskFlOMKlBJnJSyaQCDYhSvEfDlqGPSC7ODkfqM3HE/p5Qp5RC1dtnc3KttjxSiEIq+l8yVQ5SQ1MOJcoRkJAoJ50phEUwQgInR+iO162wOGE11dFOlH6GJ1eok467F3MzMzVsfHjODh5fWNLE0jce02og68ggfbWQSK4NqJuKIqGZOqOElrCIKfKQojIARBcHDKlml6uIwCyGp7lOMDG8tavr5/PbNm8vl8v79+wCEmZjmB4fL9aYMlVt/G+Vt2s0sTEPhAaDU0s27a09dz7P84OKeL8fZ0Y0f/aN/+v4pXvvyW9/42hfurB/QUfrox773cNGfPDw5SJqFFwdzZpxenL96Vk43ZVltab40Kj6ONSyilKguQVLDQR6lohZCMLLQLBwjhRGUSBjCSNJbMatTHG2EknzpK7EFsYSV4BisbsKXbiR5HC9OljHXDhHj2Vu/+fF/whevd9h8zw/84Xe9+D5Ay1C//qUvvPL1Lw5ffeXr94d6b378zHsKaO6rW4fp9tXFydnF6cUAz5uxSPg6/JQgSfueZ11/NLvRLa5fefcH6vnD1ZuvXbz5Gq9XPG6IN7NMETXcQ3RTHay1GvvAMQqZMCGp5ixJOSlTa7KUJrENNYfX4W6lJO5G2ozQSsV4FMeGzPtcCm02NSWOqM3D6CSyUqeRJDJ7VihbkiQMplAh4mABKTm5qIASMZNyo3eIWk8zhjBYCSqSW5YCcKJQTttaoggiJ3V31g7RElfJmUmTdB2V2pmlsmlZX3cj2qWmyCFNYNqyTcycpiLWGYmSKmSnoiWq4WYt+OWp0bJugxKn5u3ShFTCACO0+dwt8padg2m2X1i3wyvKnLZtGGhf2WmT2oC3qcqtpIU5diQK084SMBAesUUEcxdQ04P5Fkh522cpABOt5s5CopqTW2G4ENxdiIWRQGYO89Zot8IsRi5VBseKkXLIwnimjXWgiTUzImIEMYc3TGri3lZvQlvt09YGbXvOxFaks0Pht32MvRzA75YFikur+Du/t90rAMjBEaqiSSm13uBhblYGlJGErSLGCq0xDpE7pGT9iJRDk0sKgpBEmJp5OIsYk4sQk83H6BNn5lkOEp130i04ZUCCJUgqCOAgbp3ZWtsXhtPUf8Emv96b8ik4wt0QblbdPWqZQoCtHHPq2GmVwhlQ5lprO1QHRliEAwyxcCrqTefQ2s2PtYy1FrPiZk3otsvyt1twij3M4EQCagGBW9SbN28eHR09fHhyenIqwu5htV6/fsPNV8sVkwBuYI4oYRLsYAh5ikgYfVSWZ59+KkumEucPLtau3/m9374s9vf+3n/3az//ibPTs+Pnbv6BP/GTzJJzP4y1Xxx0s9l6rBfnywdnq5MiZ5u6LHZRyxDk0FJ9HI2DjWgcqzFZrcJMrGTOTbMKMHuEQ0VZE/NoLZEIVa1m0VArsBwHuBcrbqhAdZeUSnUmKAWVlV08+MKnfgnlLGdJMvvEr/36L//KJ69evXV0cPz+97z00ovv+sYrn3v9jddPX31rfuPF1Pcp6Pd+1/ufu46vff3Gpz77tbWLNQkKqJgVK5vRz3m1zDTLdNHp8ez6tfdcu/X8S5t7d9/66ivj+T2OKjaiFkYkGBxu0QkhIERQDuVWUpRTl3lCwydSwcU5mVcGCUuVoRSBk9FYfUoplTKoqrsLc4S1QCElldYKLKXtpz6yTe59BFMrs+ak0lLEoi2VKkBrH8A7QNzl6nbo2eCMonUjFwQkpahmubgZLPs0rMIAipickkaptwzz7mdqqjNmagqLSfjvuz4WT25PYkjr2zXps+MR1AJgW40JtkNa2idsNUW8+9gm+9ZtX59LHmybLt0pKC+5Vp9a7NK22ma/A80+/3P5i++KfVojUKFQ5qbeFBESAgqDaqAKS6BKy0DGlB4PG8FJYQ6aipq85XsFDRGoVYUQuTehJ0DU2kF78+t56iNP5q01wjtB/2Nm4HeL/u29vv3Hk5DmcbZo7xw19AUACghICBxhVsNHsrGWMcqYQoEAjM17DzJgdJRAskgWXJy4yShTeI4wISNyIhOOYaQ+Y5YkOJCkV+EuKAcxmKPVOYPCyQlMaKoeJ6eYbD1aU/g2AcrDW8rZWjnu5La0bPDu8HZEUrsFt4xR45PMPQIOkyDArHXniRpjrcNoY7FSfSzNCWaQgpUlScqlmFONVvNF4MmDCnN79umnrlw5/vIXv2zmSTTCBZFyVoqL5QWHBYWDg9hBDjYKojBEUCVw5nj2hRcCHE4PH56Yybf+/j/67m/99r/21/7a1cWV//tf/ot/82/9Hbl6/O3f+VECbUZfXL3uIm+dbU7OlusxCtKDwU9WdeNurJNCpJjVKZelmZl4U9yCuVXjRHEr3Cr9wyiMwylSeOScw7yUQnuzH4YGzyLVrZoXMxCR+yzlPsblvW/85r/8F/XsrqL6LHfzo5vXjh88PI1x9ZUvvvHFz336hWee+rZv+eDpevNgLDZ49UpZf+5nPp99c+X4yqK7MtM81DqMtdSCEEerJeWTta8qnw51udBD5Z4Pj56++uJzL59+/Qv3X//6+YO3Oi45apaSaqXqI0aPUilIO1JlTZq6nPtOdFdvtZ8KrrXaOJpVIVZNhYVo8Bo9CQWPtOEAhytN+YCWSGhUT86N8FHtpjrS9jM1pokayUCqokkSS991IpRERTlEWXL4lPtivrQBu4W/j4mtIZWAPTkjQaqZuldE5+aprQSzVhbFJLLtQL7b2nwnEZl87W9OY7IPQbHtckpEEW/ftVfe7hNa8L17Zqd6IiISfbJb2CQemlpDNV6qGapWcLp9Zlf+ac2dmTbsJWVbX6Ktkk9UkxMJkZMIa1IRJslWxxG1kDvnzoYNaiGmABuMozBVNS9E5LE1YsG8xdDYu1rTNYsI4t2uUNuTQGxDhH2If/Jx/M45gHe6XG+f8X1SA3QZarQ8SUDday1SK2qxYU1lRB3Ii1gJLwEQJeZJ8uRsaIrNai3QVRZ3kjAFKsFATmREMKHiMGfJ0N42Qckd5FkAbq1huHkVrQUVN54azchzTLop3to1uLUqTERFONwQU0//dgJbVp41uZkFPDxrcneDOQjuwR5OgSCwRYSDiKtHdTInCy4WxVCDjIREWTPpSFJImIQ9LDxU2MOYQ5hvX7mxWPSvf+OrWRGSCVsZqIjXasMgIgZHi2kgxNG8tWp+BM0sT99+KojPB+cUdwf/oR/7w0e/52Of+uKX/+1/+0++/4VnPvXrv/Hjf+j3ffh7vn+QdHq+ql6g+e5mff/kfDAaQ9e1nqxKcTKSsdQylghPLPN5D8RmHPs+r8eS1atbbY3yrbZZZJQEwUFRAlYnGo2AlFKpxR0B90AFnVyckfBsNgsWEXipi5zmZPe//rVP/+JP0/ndKxlXrl47unFbUsd2fvPo4JlnXzy9flHNvvBbn7+4ePiBj/yee688vLlZ1oJlSedn63pxcnRw9vSzz/Wzkrqu62di3TCMXix8dDdob6SGuHNhJxIHXTo1XiR+6sUPXXnupYdvfO2NL31uHM572zANWoYk1LrOqwh3WfqZdPN+Nu9I83ZSo2ybr0VEMfNUzUqSNIwbIQY4aqCUsKCIMPcyTo0F3HLWqVtkY+6VU+vhIJS2/3QiMkMokrAKZZWkLeU0lbmCRUScOPAITONtM5+Aam7+JBEBAVfyAk8WwR7mzu4aEVOvG4bVSVdK1PrfNR58N3eoZUcbLvo3BzKPQhx2O8l7jsJjBTv7EcBjz7cI4JHmSvuS923Dvt3PidVoPzH1c8RuHlxr+bV9ZirJiYB7kxBureA0YlekE1Fp3kBEyNimuSZbmK6ibCgqWJp3yuxKgVYcMkVYBK/msNZkGu6ias0t2p50IpqQrXn3wkRTn7b9Y74MfLa8zb79373gMfPg7rQXT9EU0oYhDK0RjxBzm/wDIlHZ/7Tdua7hZMGV1FwsYrPRcUQtYoWscBmiFA+HMAlA2NRKqJISDFHASEQAMTm05bbM2MOIHRHBqZLVDTwADhJwV1nhqJapS0TEKs4OMMEpyDEJEwHwtpMGAFhFeLgjXCZtPwgQ4fDwbYOXdunbH6J1GN8OCG0nyhBk5uQA2USCYCw1nEv1Ur1YFIvRogacxElYkmhmGUlV3IM8qyA8UTDz9avHN65dv3PnzaODA2FO2nv1atXNWKSWOusSWiUVk1uF8KSTAlJKWvDUzduL/sqr989uvPDSw6G8+D3fNnvPB/7e//C//sBHv/1DH3j5y5//fBV89Id+8KLSZqg1tFasT1ebUs8G3yCN4E3FhlP1WupYx4EJmePKvLt2fBSEaiVgdx9crMcLkT4oe4TBQWAVAwhi7muzrCRuyoRAa3/kAXOrDhBr0hbvJgKcmOlA+eTVr372l39h5htVe/rGtdE9IoZSFhG1jD6u77/1etf1Lzz79HK9fPW1184HWke1xKfDeJS0O7hyntJwcj47cxE5PLxKxEIU45BQZ0nIrQ4GZVY28Ol6HCqK917KIuWrL374+NbTb37xs3e/9lspqrNyzpkxunFKLGlq1gJp6L/rudY2tMaJUsciU8F6a2EVRFh7qUG1E3VV9zAKBKeETqhT6pU7QSey6FJOlBN3napS0jYi05mZ4cIsFErQ7ayfhsWSErEq1JwxgR3Htk5oFwrsNg8iAZxYCW4O49CQYFxKvduqbg+UhS+RRIDWhUKmPkTb9R87rf72xZeu4VS4isfwZ08T9QhS0ZYjfQy79g3AbpFOb2yc6p5VuITBLXMz+f7ROmmCiZonSL6tAWolyRHuU+/3hr0cKKUSYFbDbarh92hsGKRnEW6JemLSzmqFB5tzyjGuUddtji+rEpE2XEWbMsFcS22J5d200X0cB1pRIyY/s2mnoumr8Ni2OyP7tu5tn9//+U79LwiTxhnbcbJP7tslBQQE2iSeQKm+Hmi50YtNLNcyDBiLVBOvNcyJnchabxGAgiIoavg0o4NJtJW7q1BLyzTATuYWjs3GYUFwEIeRW/IDRBRhC3cV50CrAW0ePCBE5q2FNjimyhKQ0xRHxRQ7QKeLv73129FNziwhEKrs7kps7iMDTDB3oE0Th8MjillxH92KWQ00VXmAghWspCopZcxYOLmCQoOI6Pq1K9evXD07fXjz2s0+J6s1pxQeNg1eilLKer02s+Lm8GoebbgCkTvCeXHlZnSHX7979rEf/QMvfPjb1txfGP72/+8fXjk4/ui3vv/Vr75J3D37vg8tiUePLHmpGEsdS11vSiUdjdbu6+rFPQhBIRIzwe0rh9cWC0Wsx3p2/mC9Pr+S5Onnrj31zPNfeOW1u/dOQ8gJQmEGFgHzODhzhBkcrauge2snzkoQ4Gjet9tOQYySyb/wiV+pD15Pw7nEmHKyAIi7lNajOdHh4fGwWmZB2VwUKzdu33xwsYLrcnUu/fEqwqrPlTpmcWzGUUUv/Lxuhod33pyh3pinKJtufmBBaytQns0W165dp34+VnuAWGddlbh+eO35b/ve2+9+6VO//HNno82UixNn4txr7lLqVTVpUsnKSUiUEwAhac4nUwSrcKBND2u9jwxWrGoJNwpD120GI1BKuVPvM/eZDzLP+rSYpYN57nKWpCllmvQm2x4GzJ2qqOYkmkVlmvcwFTduxwLuY9+UONxDyR2+tECNgOAQouBWpoCY4G+n6mzFADS9C5g44DYYkTjerl/APjI88vwTL9viz+W+7faTprZtjxiMt/0Vu/jj0c/ZvYZ8V8DUkrxTbbFHS9j6bqB37Izf7vi3+l0iCq+x7da1q9VlTZoST+KrxMzqZFN3SKPCJIwq8CDtmIQ56Y7PYZ64nUlsRARnANHK59qwhAm2sG8Dntz2z8ju1O/bAHo0bXJ5ed45ZButWPhWcU/tX+zdVftmJoAaruGoHquRloOsR10PtB5sucZ6hWEML+CAtKGvQh5UgSByBAUFyIOIQyyksqbE4kQB0sZ0MzftjlfzzbomcnZGmFEUQ2Lq1LKGMlgBbv3GtmWTHIimR96S+ruJMRGMaWoNpmqMPTE+mNJ+TeCkJGPqtOdai5k7LDymQnpywIMi2MEOIlESIxaWrLmk5kHAuanXmISkT/npp54Z16uD+VGftNfEDOFLN6d972q1qrWa21hKqVbcjLhUJ5LrN27E1Zt865kf+94fvvX8ey9K2tT06qt3vvC5V//6//tP28nZ5/71b77rwx+slM9LlVAusdrYcrNhkW5xMK7HWutYfSjFAQ4nL4czffra0aFSj0K1bNabKx2/96ln5rO0WCzWm6Ff3n/XcW8YctcH6elyvR43zkrcalumG0lEvGXLGRRgs6zkQDhyUGL+tV/42TtffeXDz1+5oHJ87RpzlPCjo+Pj4yOcnNdSPMgj+iQlKgMn994aA50frh7cu3rlWZUUYZtxLFFylqDEzlI9aT68du3ulz/7xhdfu3HQffA97/7gBz+4qvX1O/c++7nf+Op6uHXrqatXrh3ces6vXoV2w9l40NPRwc1v/4N/9Euf/uQbn/71zWiHs0XXdyyaUhZNWVj2vP69rXXAEBGHp1C0ccTCNWtXtcCNwihqmEag6zTLuOhkMc9HB/3R4WLe54NZ3+UU0kkbVvVoU4DExEKqnBr5I6qaA2BVIglnDoo9/+xtoB9orXKDnNq8MheQC5ourhXBoHHOO7+Zp7ZD2AHfLs3gdJli3cei3bfvo8ReheYeP/MEn7P7uX/seNSu0BM2g3bxOoDHGvr65SJ6ZAmbb6dvOzx8W5vTXtH+YZszACKswCtFMHxwRJCwRFMpMgmTNK0rC7NWqs4jKBMZM8iDU8fcE5K2ndidiJZLidhvd49Hz1QTrVzagCe3x87s7pQ107KP14+fxNg/b3tXkiCigbr/mdvwbJv3370nWotK4+peKoaBN2usV7RaYrWO1QqbwccSUWmWMNm21l6fKAzOzEQwhjWDAvMwJ5mm4jCzi9SWN29qg1pos7FGjLnC3at6aERil1CHCycBEyGIiIUp4K3OGiUCahwt+sAUslNMA0ibsG+3iEK2UrDt3cPM1W3qLwTYNKmrRq1EJELmDGH2qXRFVUsR1VRTl8MDLkIeVSlERCG3rt9MquzQOS+6rhNlJiHbuTgRDmCz2FipY92sh8Ecm1pKtdVYbj71zAZ0+33vf/lD33Yu/ZtffvXW7Rfd6eGds+/9lo8div7CP/9ZNz2+euuNMg6RMJR6tj4vGMOVuIz1bLValVqcCOiYw0wkbh4fHPcp29h5VYnZ1cPDRa9UBKWe38+h3/Kep+fzA7fzbtbn2dEI+eLX3/zaG3cvvDiJc0KQsqoqgQwgOEd0KkOpEZxTGs7Of/6f/5OvfuqT73/Pi4uOvvNbv+XBxdnpaqlMqZ+PwwZ1JNA4lrMH93xYbTar6qU/mIl2eRiG+/fpubHPXbOC4bEZBhPpcpJgD+tE3vvyy+P1xdd/6zc+82v/ilcnv/f7v+/FW+95/wu3Pv7xT33ly1964wv1jOcvvPTea7duPv38s9duHK2djnp9z7d+z4u3bn/q47+y2Zy7pNaTn3f6wjYllwDAEdyqzaeWwswsCri4qpuWsmtdxtJ1HYsjSkp0lPlgMTs+PLh6dHh4sOhz6vucNBlnSQnNhWnaefMIV5AIt+7fbeTnNuErRDxNMn87/+wRxAwQY3K4goOMdusbYJpEkMLN+6GIIPBO27MDaJ4mD2Jb23WpunkEl9wblUDUpmy2/hWPqVfe3gbs49W+uX2EvdiDJjffYeOlEYpWrXLZ7GHn4zeNX6v+2faBbATRZX3+toCDrNQw230sb3vhNOZHmZWFhDG5nHCnYGUKotT6hjPn1hRAvQ7CKizRaqMdRC2QNPIgUabWF4xADJAL7czsFOwAEc5o44Mn1g/TfGZ2d2qte4gmhb85iNxqu3JtXuDUIYcojNydprEqRCDHxNjugpU9u0AordDc0QYUupNDAC2ka0vLjayWdv6AV/frxVsy3Juvl+bF2QysJEpJKIUTkICmBG5NBMdAJVFGQmvHGxYgEDsLwOq5dRB0MDljXbON4qtlJY15tlwse+2qZm9zSbsBSZ1hypTEGhmDIFb2EAqCIAxTZIgg2TncorRzYnwywAGglNJ4FzYmdxZhiEeU2mIZuBCCzJGVag1hUfEKEU6mBVVCJHdzYyEgCzPx1aOjg/l8WA+HB32fOyVWEWYS1NYVstkwCrN52WzW63HZH9JqKLmsYcP1fEyLg6Pjp37423/szsn4//pP/sp/8B/9pfsXFyrLl993O2P98z//r3/x1z/zZ//Cv/9geUGSbV1XmxhMi20K42wzbjwKCDmX9XqW9HqWzdny2pX51SxdHTJZn6lXkeQi605YQJFECbPrc6UQz4eHh5xmI+jijXynxJVbz9w/XwZqKSYMCutzdhgRu9nGDIRe5N6br/3Sz/6Mrc6+9/u/42CWNmV5997d+w/uC/NiMZvP+s1ms66jLU++8ebrq7OHZXUeXiJiLCX3R+/6PT/0+p1Xb2G5cmHKqBqokS1C61Ay144Bp3Pp+tsvvXjl6Qef+cQrX/j6dcQf/MkfvXFjce2p7/jkv9Kv/saXX7/7Vn1lKfbSZ179It+6/uJLL33oqRfWK5nd/MBHf+KFr372469/5dOZIWJEcGpN5gTMYGGisOAgDyeuU3W3E0yFI7EXUkJlChZN3Idzpy6IeaajuV69cnDl+Orh4mA+W3Qp55RFNFImlin05zY7yMLdYLLtIiOqLCRCzGLSYSrnbE6kwxnUxpqgVShFvRybSlwb3RpAAzsHCKAQAm8/pNXIBMIZERRTbACBaDsXNhEv4GDyMPdi4UBs2/tywKdhHa0SUIknZSMLR0Q0rYYHEVoZdmuA2CQF/Khh4O3oDkXLom7F+hHhNnmhl5Zn6twQ0QTzW7Fni2taCX6dei625lURLYcZHK1he40IQbhZuFObhwwqrSd8a1pArsrB4iLODIQmCrhHsAaNhoBTrikxURCJMgva6r6sL2j7NNUABCTCg7aNw6gVnuLSfm9h+NHQaWfn9yOvJ6zlLg6aIiOaKDx67PWOy0Gjj38RmlWKIDhtz7p7OKgYhjGWSz87i7NTPzvx85NYntFqiXBiFZVWpwcQuBVsERG3/E4z0h4uEY1DCKc2D7eVbDEJKBBKEsyCcIw1Yp1ZmTmqU45qgeSuKaS6B1lUIXJ2r8KkTMRiAJrkPJxDADh7ALadybU7D7sIbOcRpJSa/ScimNeoCDFcZrQsotZtbeaWx2xkrkA0t5EWRVngNu9z33VXDo+t1r6fzVLuc9cav4hwVhIOZp5mcIa5e7dZH/r8YhgllVpSkpDZ4t7A3/GxHxCR/+Jv/NT6Yvn8c8+/cf+1o8P5OG6Oj48//iu/dHjjdk15PYyrYbjY2KpgrG6GOlruZ8TgcV2H1UHYc1evdWEjza4czjMjM2emxPAwFBdSMDHLbDHrRJLIvM+ZK0jXm/Ebrz949StfLst1ns+SlWDvu0SkXuFeiIjbLW4lE33ja6989QtffOapm9cPX/C6Xp4/PDs/2WzWOfcpycHBwdnFcrNaPrh3b/3gzYuT+3WzjHFdxrW71+q8Gr/3xpVX37jr42ooLHzIzcs0WLhEWANrhjvAKfWHt7/tOzdf+9JvvPLKtZ//5Z/4yR9/4fqt5/+N67968+onfvXTd16799ZrX7324nsK4fOf+c3P/8qv/eh3f9/1fPtgLh/82PcdXT362uc+XYpf6ZWKi0CauiCmIm6jbe/yCDhFIDzIwUyqnDRbNjYOMHtkjixy2MuV4/746Ojw6HDWL1JKKXUpJ+Y2y5P3V643bTK1odpKRCzCNKWgMbHH4Ni2S48gGDDNSGtKjnYfE1G40zYp+gSbsEf0byWU7VNocg+3LcqJ9gWBO+d6f3PfFbi3lHJTHjVV9jS5dtvfa2oXsQWZ8LhU+zyJdfsu6e7bd/i2vydbWxD7z08E0bbpy+X4kWgNYHyn9Zg4IvddvrrZoUvSHm3iMfa58Zaklal8diqbBcAioqyPnO9Hct8yXUsitN4SvJ0N8BiP9wRx/+Rh77M9+7+6T9elZY+wCxL3zECrZW7zSZ74unAuaH3YIxBMTl49xiJDkeWaz87p7IROT3B6ShdnslkTUUACmBrzk0zB4xRKcuyn9ZsPERZNkcMU3qw4CRjEYIe14gsO9hgLWchYadbnWQyjcaqeEzRHBVUvidylVoQwBCCGyDRPgiZL1kySsux2g/Z2ifYMwH77/r2+8A5AVQGIOzXlwLZ0pWX4RRrfk6AeoLDSz2YCHCyO2hmezWcH/UyIE0vWJCpZIMqtmW1O0zDCcdjYuOpGu8LiNpLQyaa+56WXXnz/t//dv/N3f/bn/tlf+sv/T4n6P//9v//DP/ID737hfcvYFE5H125elFjWWFZfWozBFWkcNqopUfJxpZtNrpv3v/jcravHb927c3w0t7oRlQh4oEYgQnzsRMCUUsrSCdNqtT45OYVvVLQa379///iwQ6LRLq7fvGqs5+crRwweNbDarKp7G99y987di4f3X3jmtm/WVler89OTk4cpSc4ZQKfS9fMybt54605Zr48PDtiGcxvGcTs6NGBWfvEXfvpEDl4eln03H2p1SeFs1WBFQInJmYl4tOogFT7nfPDcu/tZ/vmPf3p8ePIn/53/3buePowf+Igzf/rjn7331sN7r339Rvfu9z791Hq1/kc/84+On775+3//7/OY337Ptx4f3f7qb/zruloe9DpBo085qylH3/oNtnJDb/GiM0FaJ1gWZXCEBM9yOujzlUV/cDQ/PDjs57PczyWpaJaUmLdtBfacuUsdeuM6mgaRlZlBKsIBcq6ARzBaXeGjbQ/ardhubA970oP87Tea9HkT/UtET5qOS/DZguxOXdN89aAtmPC2fYVMFmxqdhATk98QIXDpSD25S7t1emlwCJfgjn3Qv3x8mczzaA0o4N4a0iOa1AN1OwwHj5FTbb4eEXE4jJm3YdQje7XdYULLze9DKFMQ1MywHd+MNl+CmYmJg1lIFaygRpMTmCD02BfE9ImP59kfec0T0L+zkNus/m4a4iNJ89jju+OJCAAI9yGYa7C3/rIOqe7DyKfnfHIuZydyelJPHvjZiaxWqZTGH7b5UwYmoOmFdWv4dkao3TihLaUTgXZrbJX8qAQmjhAKD5ZpRp+Y01hjufLZWuczyjlyhiZIT33HmUsnlNW7xJJYdGQmkDBxKwNH68gHIt3tBu3t0q4D0u5sTPt92UHucrFNNu3RKc1TBBACauUII6sy4fjwoLVDmfWLLuecemXJqlmTCGuiLnFKqZWbtwnHLFopjKyCl8UsIs+Obz77vl/65Od++ZO//n/+S3/xR374B77w+c+89rUvndx9udx65uqVK4X1Z37pl2+9+90HV65uqo8eBnaCEYOoDEv3QjG+/O5nXn7u+tn9B8cdE0UBGJZECCFMSbRjmXV9W6G12noYSimr5RJcZzMlpms3rj7zwsGDs4vc99du3roYx0988reW65UtS238GmIzrO/feZM9rszy6f0HKhhWy9XqfDHLQxn7rqPwg8Vi2Kxe/fo3knB/sDi9++q4uri4OB+WZy0dqaogOrnzdZ9fLw/vzp66URiVucKtuhuUiTgp8xjEpMxag3yE9To+9dwBxS/+xsfP//pP/fm/+OeevX303R/9yMXDk2F10RdavfV6r8gHs+/86Ec++cnf/Cv/6X/2p/7kn/rw+z9w5fipD330937+E798uj4/SB1blQaFKhFuQCCkdY30YAc3uZ47oWZhTkrkGtxrOui740W6cnyQu9n8YJG6TrseIpQSqxKzQmVLeV+uC4SHMRNEmLlaELU6rMmHYzQ9mBEU2xEErRnuVOM6ATdtW/RcgsM3s01v2ZtCuI8+sQeEscs+ThXiuzxBm8lBU+1vm+EaVAEJoQBJNCL6Mex6Et8eW4/TM1tAx/YFkym6fLgF/+k1O4Ph+3/f/+rWAnr/SHeH3wxAC6v2923/Bbs/7JLnzKz7u7L3TcLaqm1br482I0AD00hYTCa9sUMwt53x230lHhsYsIf+bxNG+XQ9pl3yKcrbnSPa9s147KQHvNkQClCNWG9ks6HlMp+f6OlpengPJ/f54oSWF71bstiARBOLOFhzCiKLaFR8uzd8ryzQCXvDH9DqFAAIMbkTRVjlSCRkZiSSRWGOarVIHTbYrJCUuw6aJfWY9UU5Fn0czvKil66nnIU53KPUMFdiEBnDgTa/4BGL3S7e1gd57NxG2KTfbTMVat03G3u+QLsbREiCAHFBx+F9l1PqECESOeeu67rcCXGaRsqrJhIVVmUKnYaAOhE4vHKRoNzli2GDdHDt9rNf/K1vvPyhD3//D/7gvM+/+os/+xf+zJ946unbs1kqNa5evfLFz3/h45/4xB/6I3/EVpvNMBQbAXWuYx36WceAgOfz9Mabr9fVeT+bJ0lsQYg+aU5JmLLqLJOwuPny4vxkvQEwjmPXdfODa6pq7l0SjziY5b7vNqcPH5wsuQ6+XsdY1suNA6Pb/Qd3uNaL5apsqgrXTTl5ePfWjeOUZL26WF5czPru4b237rz15o0b172W+3fvlHEzjsOwWjYuAgERvn7zxoPT0/WwvHjj9Vu3X15pbFDBIqGtpA7MRhjcEwscEpHWtFS5r+n2089dhf3KJ/5V/NR//R/+X/7C89eOfvxHvverX/itzercVthkOkq3Xn3r1Q/evqXny7/9V//GH/yJn/jBH/q+Z25d+dAPfP9nP/Xx9emSnKlp9M0JUaMCEAcM4S27GIjqNjAiCzSBHQe9zjo9PsiHi34+77vZoaSUcsc5t5ixNbOJCMfORZbLpU0+rZEgSQJMItuYRhUGUTAjwhCtKn7qNXiJD1N3mak3zpPO9T6O+3ZC9f4LmrvGzDGl6XCJtnsI2JYzYmqs2JzK3aQLYmJmckaoqrZgKpijWrN7LIKYWtDvQd9uzy6PaOeq41GI31+G+yqgy9fH1OSgAXwbOzixevsBRExHxMxuwLQ/kZLSjg3b7knjedrbmbcDbIkAVLNdsKL7dqZVc7TgpTqxcAjH1M+odbVm9womd4/tQGOgpWri0cv3yIWkt1H9v83LYgdnAACr1d1r48Kqt97CsWO9AQQYYiA4UQ0eq67WenGOizM5fcAP78fDuzi5S8tTDCsbRjGEckw9jgAQsGvVeblDIrIb3wi6rDdutyoRbUt2W18fbk1TKTxaTqbphISqjaRCGyVRiHqXfT7j7tpsfh3zRcwWkZUxvcvDoxQiUgGYTGV3aXbqKWqtOFq5XLsP3NvPNsITgBOISFsDLBHU+ra3I5EAxixtJsnBwbwOY1Ked7M20iul3HqZt+pQURJtxZ6UVbj1p6uVWLOMFhZW1Uo6OCThp5997vjoh4+v3rhz586DN994/ta1o8Pu7smdxeFTz92+gVq+/JnP3Px3/9SwvOC6ziGbYcW+vnn1apr1Jw/vw8udO28dd3rYz4XZ69glTQwVzDSycpclJRbmcXCad0JYLi+6Ls0XB+7p7KIMtfSz7GbDei1na69+vlovT09f+9qrD07OWVOe5QcP73uYbYaTB2eHh8fh/ODe3StXFgeLWa1jWZ1THe+9fvetO2/Mu+7swVteyrC6WMxn64sTUm5jY4lhZu9933uee/GF//F/+bmzN17/yA8eLqssAxTGESEMQlNwBEiZnMjNM5MbBu7uiuqtdx1/e/zLj//LZ/7BT/+7//s/2T19/Y//W3/ov/7b/93Z/Qfj6iwnv3IwP73zxtNXDk/n/NN//+9+/bc+9e/8uX/v6Ree//DHfvBLv/zzm+UydbMwlyC0aROAjU4OAk+lOtHaX7tmpJyy8sFMj49ni0U3m3ddP2Pumpi/EQDTGnHQtgF1m3qxjZIhEkwCpggy99hWb05IEwL3MrYq8RIAc5pi1+0nAAiaEpgNmXgP3u1RDn330yOwBzWTD7QXF7s77d3n+9ukdG+42VxHeBgMYJEmzPOpFQ5ImKZcdQTT/j68E8rtY/02Atg2e9hFCbFnpbY1AWhS78fJovBd4mLvK7a70SggYGK/L/F9f5faKfII3TMPjR9uKKru02ypR945ja5q2SUQBEwx9bOUHfTIdiawiFAUPOqr7u8EHs0J7z/e/W/fwZ9y6kRmO4HjdDC7bbqoUHLUyijG61HPl3p2GqcPcHHXTx/Q2T1ansT6ArV6dSdVSSzCSYO4FTdAuIn2dvvT3P12jnbZ/OZsbx+SxeRiM7MZmBkODwdTW4MUwqWEMQoTESvVopyu9Pmm9Ll03Zi7Kiw0igvqViDbFFciVXx7TS/Dpmg5gu35x7ZBYLuh92/62PUI2ouidlPCa205FSJAWGezftgUIYhkUdl1FmuTJdrjacDf1IALzCzhLFJFu9RHFBtXXR2qRKljyrOL9djPDz/xqz99tJhdP5prh6vH3fyoe9fTN5+/eXU4ucfj2lenLz11+/RsdQGbzQ6u3Tj6xptvzd2uXL9+3PcHyqhlajvMpBKLzPPMfZKuE86yXK4R1vUpd0ocBCbG2UVZbjZv3H1rNp+v1yuOeP72M5/9zKe/+uo33nzrLoLalOThwsfVWc7y5utvPXX7Wff69a+92nXZax6G9cMH92x1Nm7WJ/fuHM0zuS9PToHomIZhPQwbEDRpLQOzlDq89dZbf+LP/pm8uP0P/pdfQy1Zk1hQoCMaYCBJwkKCSXMYIbFKQZCF9QycMvP1F6585KP/4J/9qxefOf7Bn/yJD334vT/6B37of/pv/4fN6dkrn/rXH/nYR+cv3BqXFx9479N2+uZXfv2X//pbb/7pv/Affvjbv+Xd73//K5/9dHXvguAuRM4EM56CNBDB3QiWhTVltbrousO5Hh32s3nOs066LnW9UEsHSgAydbJiRIS07l+tv83eHHPZKmHAZK0ykQDQ5ShpqVzDWi0jLEoDeZrawE08e9BlefAjKPRIDfwetrpPzYL3lkYEgqe/xh7g0qPU0E66ExECGFpjdHg0f9YjnFMP9mCmZhpabnIr23kS4vb3cF+m6Luk7qOIt5+3248ApFHLEUTbTnCNEt6mc9sXPH6Wth/e/vfY87sT2+Kt9prYez4ADQ9MJU1Ua1VtmYBtoqYNps4xNYvAlKycHuyRdzSVbzy+xdvp/WObA8D2fwTyfWvfaKGIWmt1I+Lcd83zVVXeo4Osejj5WHkouFjF+UWcnMTJA6xO/OwhL89ps55uShLWZETBuxS/gKgN9Wk3PbaBwORixyPqr4iYZhpNAmVEwKJGgJAaDV+8qX1bq0S05m8gSBBc2BZdlyypp2SiRqzkouCO3a2UglLJgp2Capv8EU2mhsuqR5roKLScQeNfHbZvHXlrvVt0ExGIsFprGxlbS5sczyAoxlLCjJRbVw9mbh13KSapxl582ahbFmGRnCJq8cRcymq9Ojm6ckRHV4cyqPQvvOul5Wr9K7/yy/+HP/cnDhazf/bz//SpZ9913WUuBz6sVsP6/huv3T4+vHq0kGpXZvmgwziuZXl2+8r1RdezxdnpqddycDxbzDNHJCEhEgRFJef1+XozjgeLQw9U99l8dnGxPDk5PTnByfnFycXZ62/eubi4OLl3/xMsZw8eLjfL1tls2Gz6Rb8ZVseLfPfuWwd9Fq8XF8uo4xiVY35xdrpZnsd6uTw/7bOw14uL88R8eHiI8JPzC1Ud3asZEcwqEX3lK1/5xV/8xT/w43/81z71jde+8oq878OCUOYZwKxbqs4CNJTCIay8kTIr6dASm2B2eCrlxlPvSmdnf+tv/u0X3vfS7d/zge/+nu/46me/8Llf/dSdt+5+7Qufe/q7vqPSePv2FfnQS5/6+KfvvvKVv/af/Kd//j/4P/3AD374pfd/8Otf+GK1msOFxD0sHGD3NlWiCgWzd4m6nI7z4ayTea8H89zNeum7SJlTFuJJTANGRJNIACh0yaLQNofEzE6VqOk7g3RqLjNR7kArOmm9ZJxaEdMWobZZw8mnAe97LZdrbW/RNcl0k+z7Vly0w50tQHpblPBLmuXRT5oMgLmDiEXbeyicieAwqxHRAgAloOlQpyadFBMEvj3E7R48GQHsbw1Zdutx9zgi2rRhALv63ul5urQx7aXTE5NalqZ+dG9nA7bdYYnQ6nl3p4x2x6GJiKw6nDxI2Y1ENVApNGDS6DCvoBBKLK0TjmGbtphUumEO4qmoI1oIMUEPeHtXTLXEiCCmKfffnmDatoAgqyYiEbA2EcUcEaAIIxBJluAwWBPeIMiYZVNmFyPOz3h5xqf35eweTu/T+b3x5AGWGxmrONXqpISOAgkkTXXU+ui1gNfNd5oqAJqmHCxNOz/RU7EtCGyD04hAbgS42TTTjRXEcA8Y8w6KQZESA+vqVseM0rEY5lWIM9idiLuOrZgX34w0RldFVIMYYGM25soczBRtpGdEEAeFB7XGZq3xKIWAwlmhTpHhg22oVK4u5gwnC7fiUc2KVwtCIa1eI8I4c61JOLtlt+pFwCocUSk4CmlOEs4hSsykBA6iWZfNBg9bHB3IYlHnh91MluuL44Obm+VZ6mx2PPtf/8XP/uN/+jN/5t/7sx966pnlabl+47YvH5yvVzev3+BxmIsViqtXr33lK1+5ejg7OtCL1X2rpXi9uDhbncm73/Wu2WLGHl7B/YKYTs83mw1pPrx3b3zr7l0w3713780337x7/77XqLVqSiJy//79QNx98GDcDLeuXU2K1eZ8XJ4z5qpiQx1WQ7/o1uXswb231hfL5555FuuL9erChosyLpsbVIrPFodZ88HRUQRYVAnLvh83q2F1brUwgiP+6f/0jz76oW/5oe948ac/9Usf/fC3kuVx3PRcGL0ROyNIipkFLCCIHEGKtUYwQKbEQ55fffnDb73xyt/4z/7L//j/8x+/cP3oB37f937t059/7qlbX7nz2tXXnnr22Rc2m/Hpl7/ltQer9Ve/vH7w+f/mr/w//OH/7Ud+8vfd+mD6xuc+dWUzpEJGcJoYOrgJe8fRZ8yzHCy6g1nfdyl1fdd3LEk4q+QW1geBaMolNpgJgm5R9jLybsXykienZNsOYMIxTW4GVTIX5iBLQDXnLXHLRFYthPcd//0+PNP6wiSOREzd0DjayKJWTeVhEKLWCDECUltKPiimhiXkFuZkQR4Nx8ysVScFYMEeJFTDRoRNvXnb+Jogdm4urbfWZxJtoOMO7qdgYipRfoQdan79fmU2bQl3d6e4jABalA6AiX3/eaIAHBxEzXZGrTFRNe5uFJBo6qSGB61L36WnJiLCiSDYTkJrZVoNkfZzGGq1EonwtlX0ZDF3vTy2hrYB/TZc2Bqb/ZCNMbkA+8bxMWN5SWU84lkDLc2CCGxbTu7iI245S0S0PAMJcevSDBi8Ft6MtFrRxbmfPozTe/zwPp0+9JMHvlz5UBoVIiQhqBEp52k46H448mRu5+22J6M/Itr1j20vaXrjdit70CQ2bl/kROPIw6hjcfMKBJOJbHNnklOPHhZUN2sMKxuQODGrsphIEnbm0qp+CNEGGxCMogrcAkBrmWeoHlMh+Y6CnEKqqNMTHu62o4narbEGOkRrKwx4x8rBQmwkALmx7+mypkhDuJZKTIeHx9EvNmk+VhwtDt39V3/t165eu/IL//JffvKTH7+4WN66ebuMw8npxmjUnrVnUs8d1HwzDK985Svn5+c3b968OD3NWTl3A3DtmWeS0fnpySwpJa41Xnv9jTdfe/XevfurTfXAcrUczTx8PWxsMtjRdV3X6fJimZQfPHhwdnZyfHg469NyeXH/7p2r166p8sHh4s7du2b16vHN19948/Thgxs3bs9ns3GzLMN62GyqDcIK4PDwMOfsjiAqteauu3nr1tWrV85PHo7rxXp5sVpeVCub9fCf//W/+pf+o7/8T37pXy/f+tq1Zz9wIR1COpdKKERGkVWFHQ5mYoRO/dlj2Gw2Jw++9sXP2Ftfu3V25+Lr5//jP/yHf+zP/6mPfOgjH/yu7/rFn/n5524/e/+1t25fezqlvp8tvvf7vu/s4Zs9rR/cffXv/K3/ovDmD/yR3y/ves/rv/U5i4oIVCMQhykjCWZJDnpZzPPhvO86TX2fUkrdjJhVs4pCGoNGW4n+dnLWXuZzd5NP9/N2Tvj+WvAIIramq2cWFicDw2jLd3t4+L5X2xJsT3rWgaCY8sbTz93ybA3VCFHrtHIDcNkKfGKrlY+YYiCYTXmvZloIDgcYTSM7zcKKAJnV1m20he9TZ+R20z/iX1+C+CMs0G7bzXXFHh+78+IfCwuCYp//QDQd6JbY93Aibg2FLbzWiACnIBAJwhstc0lPb7eIHchhRwrg0S6n2t40FQ4gPIIv57s8Anz7x/kkGn4z295lfrt2qVsBqO9taNZMGFs+AsQsHTzCDNWxGWm1pvNzOj3N56f28AHu342TE9osUzGurcUmkQqEnSe4bz+ZeWryh935+u2O67HzsP/k7lCaendaQNsMDosYWTD7elnfuptv3abFxrs0EjtIAHXmymTMmngGFvjpsq43QRrgnHOIgDmEL1Sg4sRBEhROZEpmFLabX28WURFtkmkbNt3G2rVRM2bFPWqtZlN3iFJKazdEoA1Tmnj+ADu0NdNRResHxLLVzjkBFI4ivaTaO4R1ntLBXI/ONnHl2vFrr7/++ptvPrx/58GDh3/sj/2xZ595ziNe+fqX8kzf89RLN27f1CzEsCjVx5TzM888M2w2Auo4D+ulWJyd3b84O3vttW+szi8iPNxKGbKoA7PD4wBKrSJSam0l0mUY+5QO5v3F+XkdN5vVcrM675TnfRb4+cnDxbw/OJjN5rNS6snDe4cHc4Q/vH/v6rXjWzeveynDsIkwZjqYHYQjpeSOUkpK3RSYluJWCTyfL5KyKuecwn05ljfeevNv/tRfvbq49Rs/949++M+8y1NfIiWghGvEiAiC0rYHEZK6EjgMBH76qaduxea1i4eH9fT5F579//70P3725fd++Ds/9r1/8Mf/+S/9ysWbD67fujWs1leuH7rb7du3vu/7fu8v/cw/Pj5enC6/8d//Nz/V++rH/80/tHlxePWVLx3U2tVqgBC6xL3yokuH824x7xfzjhNrziLCIiyJVajJB4R3uL/3k3zbfuDSCLSXPdp9aMJkgjMEgtZQRcRFIi4XzqQhnGpetitxb2VdOoiYWuFTIMwjArYvskEArYan/W5bdN19jlvriRVRp6Y6bc+bd+0wD6NpNIpFWDMfLpf5A3cnatEJQJPgon3/HrJfosEl7x9TNmLfl41tDmMHcTvMcZ+M4i7TiV25QOsCZE7uHIHqZBEexhbS8hOP4NVjgdS2+vPSeD8GWSqqDY63GqvGpYU8CoO79zxpq7/5bedNNNv25POxjQBa189a6+XBTOw7B1IYcQ0MjmEjFxdytpSTh/zwHs7u8sP7enYq61WMhQB3AwmrBDOEVbWZmdZRjugyZNkltMGPhEjvdCD7+7x/QnkbhdE2qmhHYDAhlPVyeOMtPb6atLPrVObYGDE4qoeFUIoIE48u5ax1WRpRI0NiYeYUyl2XQsUlFeESAOtkZXxbZQ4EzNo/ilprqUOttdo4cWrbny0h3B64e62VgIE8adM/O6VgCLjNm730XXaVQRFhZJqUczJOhk5kfn6+PrkYhhK/8ZufLusN9fr+97//u7/7u4Xlr/6Vv/bV1+/HfPYd3/U98/nR+nxdY9ysRxWZHy7CcXJxfuf1N+7feev1116LWrOqxdCK1VV1s9lExFNP3SLmh+dLUe1neRgG4rBxNDO4K8vq/OHpw4fDMJRxLJuLK1evHh3069W523jt2g3yuph1dy7Oxs3q1s3rVsd51928eYPDNmVTbWwVfgRUs2FowzVpHJfurpo4aqklrHotcAin+ZxZmNZDjPLlL/+W4ZVVvv6FX33/S9/94+fIOWkNH9zEPZriwMMdJeJSQgcsh/XB0bHM59fyU8OMViX/V//V3/3DJ3gr4cWPfORf/bf/YHl2Uat/5KPHZ6cXZVy++93vvvfqe7/4uU+7DOu73/if/87fnnX9d/+hHztdXYzf+PpBILyIIJPMWI5n6WDWz+bzrusihaY8TQ1JiUVFNQjgSYsTRO4Ontq/TzUkDSIiJtdtPymE7YIGUUSbtYsAM8eULfCdp9VGS00jBjERq0TbThD7QkHEjtDf5hEa/bxVzkQYsUwRQNSY5KRosch2Iy9ezd0iLgnzaMGwV7fitTIM5mh8UzVTM7NgYqHdd7G3vr27cTETEGBPqfkI7/+oAbgEjemP3szJDk6b2xiY6iR2YwCiWrSQzqOUkYohDIAroSlfH7cA2/9PaZuJatvHtEcMANGWRWJyhLZyMNkrQ52uaGzB5VKx+8iH8uUshZ25Y+LH7MX0PEvsZF470X1zEdrMJqJaa5OyTvfEdCUgTmQmw6ibwdfLbnlOJw/1wX05ubu59yYtH9LqItc61kogFSWmJsgOERAzZOpu2ICetiFtXM4unkqlmX3vfO0Oav9AYnu3XUZV4duVFNHmTRMhXInMqkDq2enmla/MJHURdHUIycyZOYmqezhlR1AgHR32QLlYc/WWDgnbeAUsU0oslUWzKHGgMUiM4lUCE8BbMTNrXL/X1kskYBGx1z2viSIIYDNjpmEYOTiJKLEyhJnhJFCVNjs+MVm4I4rVxIlFSMOIWbtudrguenK2/qn/8m/9uX///3i2WZ8vV1GGD73/vX/i3/rjzz/7ws/9/C/8+sc/eXDjucHHZ59+6f6dlRbL8GG0s+XJxdkrm9X64vTkzddfl4iDrJRks171Pc/nc6ummoZh3ToSP3j4gFLHFOGWVcZhEIQIF69KJgiycZYYNWZZbl49cqtRh+PDWRlXs/6Io56f3Hv2qRvzXi8uNkcH8+PD/z9lfxYs25Zdh2GzWWvtvbM73W1fW69QVa8KVWChMQmCIEgUSYkiqUDQpkSHbImUGBYd4Q//OPzrH4cYDtsRDn9YIYcs2gQIQpRAGyaDpCG0hNAUuur79+pVve62p83M3a215pz+WDvznHurCoAyom6dlydP5s69155rzjHHHGO+3bSqkRnGmLLEYrRNRDFmVQ2hns/n3oUsY5VryaPkJHFs0wimKWawTEyhrruuDXL1mV/8+aPbL9z9yI9khKgGYOxZygIjNMIMls0sRyPEiodIwVW3PvThN3/jFw/cfO4Xt1587XNfffMRpno2Ozw5unry8I2vt7deul8frC6265OD5tXXPrQ5Px3ee7Nehry5/IWf/ce8an74z/7IZ7/1tgGCCZs1jlezsJyFuvbsCJkpMDI7F8gxsDNCRdoROiYhQvLOdsDBPl8rweW7l/AAsGsGmmUiMrX9BlAmjhRERNDtyOk7HcM92+dmeV0irO2C6Z4VoyKWspnttPKhjPaqWmayXfoLACWpyTG64q832VzDFBAJRTOoQs6guSRAyEC7QTbdC1Q8i+Dvb/Pr47yB8MDu5+c2gOv0f/dSu6G+PIURoqnbYZOKhohqzgAGWUQEskhKrECT+P5uZ8LJuLh8L3w+sZ4O9ZkkdffRzOymNi6CITAVF4Fd1fDHgTw333RXZuDu7Xbr4bsVDBPPcx8zCzwIpqpxTDeBoBACMyOAQwQgUkAT7Efu+9C1sN3w+oIvzvn8VM6ewOYMxlaGGHNmZiQGIiMyJqWitkBqhroTlrpRxt40ff6TPIoly821+0c9DFAQkIDMSYKnTzfjWHWb6pUXq9UhzJajr8wtc+WMmJAdCNa+nh2EIWJKKKI5xXG0nHJM+467SUajIvme0SxlE9EkJgKqptl2rg6l65tzTinmLFnEDPaVVmELqCoAilg3DkQUgss5Z2BCEhHnr89VjNF7r6rk2JDZ1eRnQ3JnV91/8V/9v95+8DDFPlSz/+jv/J2Zp5fu3b51fPLz/83P/8Iv/MLJ8Z2E8MM/+Mk6VKePT8eLy+7i7Gpzuh02rHE2m6VxXFRsklPs8zg6x4umUc05x7bdrK/WH/349xeDwDo47xwTgUFq24omC2yUJGaMSkRk+c6toybw1dUWTY4OlueXF1Vw52dPVdPx8UFd1/326vbJkUMYx0EljbFXzbNFk4Zx6Fsz8746PDzE4r3OnjKaF8ssOVrwhJBzHLstSkxMgLUTwTzE83d++5//7F/7nx2uXvmIZqXgoooxleTZAKUwuJgTwmCCVbWNw+reS3j3hfPu7IOfeP03Pv+lF1/qT156Ibbti6+++OCdr5iE3/3M73ziR/50FaqH5xfLanbrzouby9PudD2fNcPlk//3f/6fv373f/f6ax965403muDqYKtlPa+5ChwCoXcUHLDDMt+DRI6KxS6SM9CigLZrGP5xGO8fCQRMkfjGBkB0k/V4DZnjvh34fEWxi7kGucjPiVjOkEYVkZyhaP2WbcAgTx6804eLZFVLMUqOInlqC0/uYUzEwlSaJZLFVBUByRXkiW7G5X2PcGJkPm9YYnu+/w3Hru8E+q+rhJs/3zxjNwuI4hMgSlmzJBVVTarqHJtaVlUVArYSRk3xWcNKvPHY/+fNj9v38ADAMfM0W1ZmQJwDRHRMNpks/9GX+ZlPLf8/XcxpuODm17zeixANYRKAK0mpmex64gCQUip1wLSQmJwSgZpkzcJdx+2Gt1ewvsTLM7s407MzvTqD2JqKoSlRscADAiAjx4BUIEPHRAXtoWe+mu2GBv+ECNf3OjOln7L73f5nREFzpCis2WcJa+y+9rV08dTduV2//Gp978XWa6oIiGoIDDpiRQ3gPFPKaIaSSLKT7GLMklVUEZwamEqKOQlmJRFScGBRFEWKv4TZJCWoujfeU0AzRRWQXFogMMk6EhGrFfZtzkKsRiXNSCqkwipghGomKGDzKjhXZ2U1J+Z+9uf+2y9+6cs/8EOfjLHzs+Xrr7/eOJ4F+v3f+93/+ud+bhzSrTv3ZwfhUz/5o1/48h88ffB0+/DpsL64fXfFAVBsuOzVNHgX0zgMLSJUrh66Tdv3bdsdHh+/8spLdV0/fPDo5PatyjsRScM4DiPkzEiQxUBTP45xtJzQueW8do6ePHr/4OBgO+SUhjh0aNJt14yQxqFpqhyTD3S1bedNFdNAhLNZve3bNIxgVLyuttvtfL40s67rsmbJ2SQRaIoDmIUQGBcUrFcegMgHbS88ytW3v/Tr/+wf/di//7+8+4HX+pSBEMokbZGYNESHitgDmKEQuCqMw/DiJ3/k0//852d/5vgn/t2f+pVf+dXPfOaz1F94N0Rr49ivH9u99fcFX+cxfuDWMfv5rdWdh9sY03BYBbs4/Zl/8H/83/xn/9lnxvHDh83BjKuKQ0XeI3syz+Acei4m4sgE5JAIyAETGFJxW0HcM7yfCxzP3C/P+q1P+Tso6EQQJyIg228AzJBznnAPvQ6jkwnejW7z7n6ccH/ZN06zSM4WO0kpjtFi1pw1ZRMFQCXa4a8IgCWpTyli7CWllLKqlODvfWBmqCpCR4CAoGDgPDhSJkd4M82fYvezcwDPHOcNfP8m4PPcz3CjwQvfEf0BgMv2ogYKpCApy5hUREGI2fsAjIYmqlkRVMlIJ12w5+PSc6H/O6/dTeTGkXcAiMzFPol2qAuUlvF+CnbfY/6ej2tYH3Ev8Dc1SZ47RDOTaWLQAHEnh1cS0gLqqfN+qgNEHJPEbAQgajHydqvbta7P4eocL8/k6SldXeKwRYuAAERi4DwBMjAZUhH6gGIis9PFseePfeI42/de9M+dxP25fvb1NiFh++9bfll6pohqgobUtVWmIfeby7N27A6OllQd4SwgMBqgqgWX1EiE1VSzlYzeDHN0ZiYiORsoq3BOPqW87slG0JhESPIU/UVL47dQqc3MQK5hSpvGBLJkNc0pAVp0VteBkWJKlkWDL6Mrs3mTRYsieVVVWSSLNoAqwFX12S98+Z/80//P2+8//PDrH06x//Tv/OZLr/9gHcLDt7/9za9/5dF7b9+9dw+Njg5WvKD/37/++QePz2vXQDceLQJDN2y7BioxPT4+HuMYx67vt1VdbdqRALebNlT1crk8uXUrpnhyfKg5J0kmmuMocWwCS0x9v805ucri0BIRGqrIO++9c3BwEIdu6NrHDx8c3Tp5/OjBtm0BLFf+8uy0bTd+jLPF0oDMdLGYt/2WiarFIicl4rpumJmdzykN40BM/TCY5jr42WyhOXrHJomGLEJRmcwqi8BjqPzF21/9xV/4r//G//R/fnL/RbYqalHxNQRzZlSs6BSNfUIENQqIx7e+76Of/K3f+sO/+Xf/vZ/86//Or/7MP7k4f7DRMxt7c6HdXL734L3jk7uBvZL3YbaoDnx40sZLMrszWz5969s/+1/+w4/8xJ87u3r48v3XFsEap75yHAIEB8GVLBgIEdnMBIDRwGzSRIPpLsGilTPNHv4PeuyCAE3yagUI2kH0u/fTIrFmMCmaTKoG1/fXDRqo5GyiOaecRkh9HmMahjwmyzn1g8QEADqpeVFpVxTUNMUBYpdijDGKCBfbmhCc8xhm3lc+BHTOVQG9pxDQOxcq4jLhvJv9tKlpMB0hgt0MuoWoCgA22T3eEISbUJod4lFes98798HZwMCygKqJgGhOolnKWJ8PDTGjY/CUNQEoqANTGIUACnT/zMl/tt8L360C2LVeiBCcuOL3xjpN6BkiqiiSQyRDIkMTRQMiwCJQvdvA8Iaxl2refx0iAqPCYC14lk4X1XDC+kWpHC2XijiLqrJkq9C61Cc0rgIaMyAL8mAKgDa4OIZ+W3Vrv7mkdp2vzsPjp9y2Lo2gAEJGipVLnMB7VWR2BIzmEbgMfAGrAABPM4FghsAmRh4NQNEmny4EVWHcSQHuQcn9OdynSAAG+8FpU5Dd/kkwSegBAmSfxVTU1GMPENRY8kGyKxmtvqtLTY0iqTMGhkQYTZHRyKkhWkWFQCwKppqzoGjISGAgIBklzmHL2zWklGKsRJLklEsnOKtlBVHSMqrgDFEwaSpk6CFFJgquItM0juIbdKGXDF1XOZ9EsioQOViCYlComBRgyOLq+UgN8Pz3/uDz/+inf/rBk8cfef31RYNI9vUv/MFbb75lgBfn58F7X1V3799vmmbWNJftxdWDxy8sV3lMrmG2FDcjI/S2WSzmXXuZs3bbzfrycj5fiOTZajlbLU+OT46PDyuHw7YDAEdEBjHF2PdV5dfrS0Qc8sZUq+ycCiM4tLfe/vYY4+Fy/vTRQzO4OD9fLhabzUZVZ7OZU3vw3nvRbHZrfrBavPv++57BETrgar6KQzTWplkAUkwiccg5IkHdNIUSzgjD0DvnE5EpUHOLxnToWEPoTKN0MowUn/bf+PVf/5mn//bf+l8cv/aDgD5aEuuCE1VRImHniGqAAJZSEpJIs1sffv3zb3394bfefvkjr738Ix97/OTrx3l+FqTh6qBq5Gq9fP0jW9Nvnp4uMg45Vc1ic3XaM11h3yz4rV/7N99/dPf8OGR/mENyc0IGYzImMPPGxfMD0QAVSy0OhhhwR7QoFXxRDxO8HtjZ9ydt6iTt48mUAiMYIYKZIAiCgpkjMLIEjtRzccC2MmBVhNeFp5zvuaaCQHEZF1RViSCKEjFHyxEkse2U8SVq7sahAwJDR1ghOlETEZEoliCtU0qSFAzVEMRjDlDVxI68QwIfvIWaq4Z8cFWwyhsREBfPUAJEUZxEeq9FWW4e6jWkU4aJy4yoZjBDRVMtmJoiEAGN2SOpOTU0UIAMJghK0dDE0pjjIKpKbK6qmjlwAz4IOUHIlhAzaQRJgFFEkRmMiowaGyGw3TiqsgMDkBnQtQqpmAgCuOArBkc8dURLRN9vHaUNMrHcEVVtGuiaBkaeAX8m/GS3dm4+nvtPnQR0oAwOG5qBikJKxWuexhyTWDZVS46IkElV8+iyesk8dK67Ct2Grs6p3dj6IncbGyNl4XIZgNW0KExd5yJEsOOA4Q1VvH3Xd/+v7Uqe71o9PfPMdy+vkNHv+mlkZmnHCVJDj1Qrgqo5GzjnBt1BNfvI97nXX0/Ht4yDAx+AnZmCkitK7gqKYKDT7qJEYAyARoAGigCMQMA+zDVk8WOm3sZYJ1HJkiUJZIWUVMdEAAIoYIJGRmwGoGKIBtKPMx+qwEq03qwDe2wqrlGKBwjomIb5/IC964bRBzTierYQw6985cv/9Of/6eOnjz/xiY8ZWN9vHz9+HGazCtxm29V11cxC0Z/2wfVj550/XCxljKhZDQ5WK+/c+fmZWTo/PR3Hsaqap0+fjkNySPdfeME1VcqJGCWnIeehb+tQ5aQ5p4uLi9Vqudlcdd1GJG22G8/cXfRFu6LB+dnpk6qpN9ur07NTIkZSs5TS4JxLaTg/i5vN5fzg8PBg9fjxw1nTsOOUhYmePDk1k8XqiCn0YxzHwVXeh1CC32w2895rjqEKninn7AjiMBqOCKamy+Vhrppx6GF9Fbv28Vtf+Rc/9w//8v/479z78J8SU/I85FxzRYgOQUydgSI5ZiWPiIu7L9x+6dXf/cMvHb786qsf+4FP//Iv90Oqm5n0iZ0bU972fTI8PTv90PG9fuiqukLmJGnIesgzG9vf+Vf/4uVP/fjTt95+7Uc/jjwaKxAjByzKvjBR/m4s3+9Z8l7fCH8ibHQPAxfpoAJqMzMDTY5yZlpeMdFA1L6rr+wuyE5DKxPDGUEmYWtG75AIQyBLJC6OXdZoGgGciqpp1qSaNY+qggXcIG++EnbsKq5n3Mx801SzBfnK1TN0jn3QSRZ4N6e2g1luZv3fcwO4gRpN/pTFWJzAzKhoFBXHcRBEMsmm0XQ0yZDQclaJgIDOhXpuocYwU67NBSM2UFTHkFBQEUzTpGOK0/+mSkMQUVUAqJT5uGunTzMRZoIIwfsqeCZyBfQr3Kky7GAlpmvGyc+raElTLr3nvRTEjceNi/98xJfdybppkCZgTnjn4GVJLKsQOi37qGNniGYuZmfCSXmM9TiElKjb+nYT2iu7Ovd9B20rkFSSKJiKZ0cMAuAYmb2qMbsy5bi7os8s45uhf7+x2w2xueeQome2vZ2uyHfcAUUxCQ3MHBbrVTNzEDgDqQJTYkiHFb1yq/6+V/Dlj+TDO31YES1JmLQQ58xIJ716napmQRVUmUYZlIoCvIIJqEBWAvPOXMhoo9KYKScXMwiyMiglATUUsJJ1TOwfcIwmKaNByuno4HCrQxRNeexMGLCuPDqOkitLKQ2RAZGRnSpvN8Mb3/r6L//Grw7D9tUPvjzGnr2Lwzhbzg4ODzddOjpa1nU9ny9ExEzW63Pvg3MeEeeLJg4jmm42VzGOmlI7XBHxOI4AgGhHxwfz+YwZHz96UNf1wXJhOQ0p5TS2acwxdd0WEdPYtut137cxjuv1lWNnMaWUqqoKfbfZbMjx+fn52dnpYjFfLBb9sFWLbdeO47hcLkPFTV2try4uL87u3L0/Dr0BPnzw/mw2Pz650w2p67qUbblc+iqoZRHxPhQCbQF/u65DxCGN3lez2UyzDDkhc6gr55iYseou1/323a/80j/9v//Ff/ff+8if/okLQXaNKjhChwIqWSWZQ2Xg4D04xx/+2Pf/+q/90raX27defPGDH3vns787R1weHNx58cUL1bOzy3p5yLNZC7KNcRHAz+fQbuLQYeCDmmT99M3//jfCePn933fv6KWTHAiQCSuGkgOUCExqxMUF77vcuNODvsc6/66PgqQCIiEBmRkCEygCMzgGJsuT2qaBKSkSghHIVD3vP8Vgl4jtrU+tjOKheU/E6AlcyDESKbECCEq0MaU0msUdyUjUFLgGNEM259V5qBuumtAsqGpcM3PNzM3m5CoOlTGDY+esuF/RJIM25awFxf+j0v8bdCBVNSQtuOsEoZtqBlXRpNksm0PUnECT5B5EUyZVIyasAoUGZ0uoanO1ugocl4kMNkJFICjUA6NkxKrKgKbFdYcQGQQAFYEti9HksmU5FREcA3DM3jvvGREcme7nlQp0YaVWUVLdwYVAigRGBGTqgJ4JnX/MmiinpuAohLrr78M0QKEKpjkjs4LEGHNWT+AAXNaQkh8TxxSiVMPaxxHblrcb3K5xfYV5oDiqBzZlxx4CUiHFCHvP5BCVySFy2QYRp2HFm4vbdo6aBYW0/aa5z32+x9K/BvCeeQEKEJoRKII5JLYSdpF8jiRQNbhc4N1bqw+8QC/dteOjYXFL3Ix4gepVMBcPGoQ8FtiMYAc6lqpbVM0KUgUEDKqaSKJwUspQC7GAH1MeY51jnxIJ1UIeGMBhHk0Lq0AympEaFI8HMgNAf7nZZJZ53YgIEXjvU0qbdltVbrmsFRWcYw4J6OJq+4Uv/O5X33ijx97Vbhw7F7wDz8HfPjxxobl97wCZAUBEhkFSSrP5LISqa0fQ3Ldj1242l5d15ceuJcKUh6qqQYXRCFTiqMFbjker5WK5WM6brt2MXS8iQ9+rShWcmfbdZru+uLg8N7Ou23rnUz/GnG5Vt548eaSaUxr7vt1uN8EjLprTpw+dc1dX66qqNuuLqq4J7MF77y6Xy+36sh+G07OL4+Pjo8ODGMeLy/MqLI6Pj5wL5JxoEsk5S/lSaRxFpIzLVFWlCklUJbMPRUTcOawbO3R0OJuv19uLx1/7tZ//f1xenX/yU39jnWAEYHaBgEE9I6mpAjJU2s3ndPziyfHB4p23vnX78Ac//JHvf+tzv0dE6N3s+GR1cLRRi2bbzfqdzdbnsev7g6rWdoMIlkcCc2D54YPHX3bf+PwXf+zVvwreW4GBYLKNMADbzfrgjWL5j1jn3+tG+I4/ACA0QjBzHCxJUUyNkpWL0R5Mw/PlOG4o3T4zfzMlrnYdW82AkKvG1AgZg2KKGL1VRcRYFbpkPSpoygY2SUNww565qrmqXN24qg514+s5uxDqJlS1qxtynnwooluECcGK6K6J6g6q0B1j5Y/eA2BHz4TSRIEiP2ioAjmDiMspj6PFjGqsGVRQs5gi195XvmmwmVlorG7MVegr2Tels5IRAqmSIQPx9Allq0Q1MDTNMTEzqgIpOg+kRdMbLPFEgiJfe2ZUVGJyeoP+iDt+KCISBigDyorkgAAMC1VJCW6IApa+EZGa0bOK2KWkKBCOlS4TTLZeNikSgNhUkmhKYkqqFaKO0anWOVcx+ravU3IpUX9pfY9dr5uNdK2X0TQxmRZpJyRiVgD2joAVkdCxw+JGxLxPc57p3+xjfeEpw7MNE9wRk8sO8fxVf7YJvDsVmJklxYCAJhaFfA1i5F1X9Xq4wBfu08uvunsv6+Edq1bAlTiH4FkcAkWwyAqQMCvn4u1tpoJIpkpgFpNHM1VQIiPLCgoagSK6lGgYqRt424V+HNptBVoDBODe0AsEDo3CuZiDfCWpAzATQwIuvtsOHHftSCLn3fbO7dur1cKyDOPIOc+Xx4AQ6mpMqZ4d9qP84ec+99ZbbzMziLbtpp4188Uc2d26fXc2m7PzvmoMIMaIiCGE4jGQYsrjuNmuK8/bzabdXuaBmXAxX6y3XUo9APX9dhj6g4Pq+ORQVdBMc9peXXZtO3R9U9dj3/V9/8K9u9vtOqW0vjzvt9sYhxijczx0UUwPDg7Ozs4QsW3bnDOAOef6vkspbbfblBIRMjNFevj+u+zc9krErO36um4qzyn13djfun1chbkqm+nl5aVoco5FVCSHEOq6NjMrPXYzK5KfIaQ4RsmI4BkrrGG7qRduVXNFF0+2j3//l3/h9PLyz//1/4mfLSW3yo49EhNnbcg8x4+frCrOV5f6A69/4Etf/PyPfuLjr7xwP1QVJnn51Q99871H9/xieXg4J+Ssm6szqtzTx+fNrSPvAgXo2qECCgxzsu2TJ5/79O9/+Mf+zOqlF9GHnMQ7D0VRZbpDqZi1UOE079kf0xTLDhn+rnH+xnDMNQyABedG2t1pBAxkCGggfRxKpESblEbNbo4WXNsuAkAWMbPJCxcRiy+1QVGiImAwwxjAO/HkAXMWyuYBJWWxrFmI2bsa6gNXNy5U3DQUKq4bDI5CU4UZs8MQ1DFXNRRnXECiKcECNWQqQhR7xgfs0vzvdU7K2SCgrIYEk1xPFpTkVG0cXDe4MeZxtJQZMZuy81XT5HqGVU3NzKoZ1TNxAYnUwJFDBFIBU8tRczIRMDMgdl5EoDgSF/l3BDAVIswJ2JEGQ2JmBBIZXAjsMATPhMSADETmClW8RDe9pjoVOgwCohGqETvHXEiwz6+JcmpoN3Q8qTjhFF4n1Y4993f3EblQP1U0CzNqSqYZAWtDSNLkVI+j225814UUOQ4Yt9AP2A3YbjFntWwmAMqlX8XF5pgBGcwcuwLF3Nix9/scPXfBVHUnm/f83mA720X64xix13+nmRiIVBEUKbPZbFYfHdevzPjl+/Di/e7wVj87AlyxVAG890pilFFAgTRLdDl5MZcASptLlQxAMgJYzpi2KGYGhp64MqCUNcfk+g2s13h5iZdXurnCPAhBYAYFrxoUZoY1YkO8Yr/y9ljHNsGoqXgZEJpIDLWTLh8fHTVNs16vc87zeTObNUcnx55xHGVxcJDJ/eanf+sPPvfZV156WSQ/edonyfcOjg+OT0JVHx/fzlKSDmT2s6bq+14Zrq6u+i7WdZ1ylJTJO0bznueLejFr7t298+23Y9d1Mcahbw8Oju7euaU5xxSzSLvdLOcL5xyCOUJJkcCePn6SUvLBjX0kQAI20ZglxqGZzx49epDyiIhjH4koBM+I3aYdx7HrWu99RsoAEiVmCVUtasMw+FDfvnXSbdZu9NVq7hxut+ssVFdzZhZN221bukht2wZH3vvKe0SUFCXDkJIjBIN6PndgALaYN4vVant1rpYPVjPwcpW2b/zOL/Vnj37yp/79Wy+9NKSIfkbMXoeDWl88OfjEndVs7k83q4PDozT+y37dHh/fuXX/pe0331wd3/+Rj3zit3739z/erE6OVsuKnvCYu4t+GM4urqo4VE1d1bURj21PFsGqL3/xq6//wZd/eHU7rNysDlkTTuYgUITOaQfMA8B0z5af/kRrfUeL3HcQCzyMYAhqwFSYHobCGDwxGyHtAQcr+P91zf38u99IuUrGCQjIbuKnGAQXMDlzpIAY1SlmIsEOrWJyTD6ERqqZn819MwuzGfrAVU0++FB79szOeYdu8rOnMmFlWFJmQpxMLeWZIbU/Ag3bNwCwYMc2yR+BZEsRhoTd4Lpeus7GQUXBV1jVXC9otuDlHHwFoQZfJ2QAYiNEszGhKcgAEiElkCxiikWEu0RjVRUVUUlkhhIJMBMbOyEidM45712ofB2cC54dTf13LOSOG7Nq+zy3BG4kAi40XlRVNAUTBHfzC8N3IOlwI4PeSZfCbnlNDYCy5KRspWaYBUUgZxThLDxGlyK3bT32oe9cjDC00m5wTD6LS4IiAJoRDJEnNzcG3Dm5Y8GteHfB9AZl075zA4PS8b7x9M0i5k9wIzzzqMEUJUHOnvqa+M7t+oWX+KUP6J1btlhKXUGo2c0AK2NWJnWGpgZJ1RAt5NS00fUR+o3mBDlTEYaKCVKyocfNaey7DORmCz44wmpesQti2PZ2dWUXZ3B5zkPvyBKBIgCRV/UqIUsF2BgdoDtgqxyuYdwKtiK9aKHPEvmDl+80s+ry8jINoxG2beu9JyQRM+D58vBzX/zKl7/29ZdeeZHIuqFbLOb3XnhxeXi0Wh4i+zFKFRpEUsRhSClFABiGjOjMMGfz7GazZoyD9+7endurZcNkTROIQbQk5g5ALy5OzXAYBufcarUah+68bS3L00cpjqP34ersSlWbpm7XbQF8Hbq6qYno4PDw0aNHRJRzHsexaRrHvFm3KWUAIAoArEoiWSSJpDQOYxJmbppmu143s9nx4UFkPT19IsIhLCJGcsHMFouFmRFhzplAY4w5jt774Hg3rg6ElHMGtPmsTmKKCL6uQgAO5rrx7FJTu/767//aT5/9xF/9my/9wI/kyIxu4f2H7q0+eGdF2/Zy1MsYe4Gf+Mm/+t47Dw7q1a1XPnT5xtvvPjj9G5/6t9e9vPH5L/jXXmoO3OGy3nhHZuvNloYhKKALd06OPvD6R7/5B58dNHft8Ev/8r+DevFjf+UnAAHcDckXLAZHk3iVUcEt/qQL/pl7BHfsQ5y8YydeZHk/AmSl4LkK7JyMI5WWJGqBRggnf97n7smJWwnTMi69SKRA6AqYXcyYGIQkcyMuA5vmwjLKQuQp1FpXWAeuK19VFGoONbL3ziMzcOkPAhTWD2IxKLDinq6mOG2SsCM9/RHp/3O/ZUAzFkuoxmaYhWK0YRg3l6nvRJSrCmc1LA/h4CQ3jdWVkAPyht4AnYBBIjVMYjlq6lEHUzFTAgLmzDvOztTEFcuSJPo0qJlOgtzOOSfsqvl8drDw3gGCqZBzk+Mvg7Op1NrNhu0InlZSZiaE4mlXGjeG/MwX3sMge2x9yp13HeHCo1Xc8SWt9FUgW8k/lJgtii/DiDH6mPwYwzi6duvi4IaO46jdtolJx+izchZEMEJDUjRCnXi7gIbI3pPh1Im9qcI6pSkIZPt+tKg4dgCWcyp2d/s1vd/zHXOZ0tZn8pQ95fXm5HVJfYRIrWI4WS1ffcl/6Pvw7gt5cbyt7niunFplSMIaKKFml7JlQ2NURYWYfR/p8QU8OY/DkxQHy9mbaT9aipCiDEO9PVORjBRdGGaLsDoKi4WR0y7ZegvrNWy3mCN6NlQAJVIvxqoBsAL0yDOiGWAgf2W0IVm7vEk5M1ezRRJxjp8+faqqs6Zph261PHjx5Reb+Wzmm2q2/NrX3nz48HEzm7d9v748E0mHd+/V8zmRMyQCYuacjQjHFEVkvd5WVSVZmXxKqU89SO62LYA4gsVizgw5jc4xIc3ncxVdX21SSov5kp0jxLoOOY5Pzs8dUc75/OxiPptdXVy0mzFncY6Z8erqcowjgC2Xi6RjPavqusqmAAHQnHcpJ2fOs0spMRIjoYFmNTT2jgiJctXMGWk+b5q6ubq6Ou/XAmTKAG7okyFXddX3PSIyUwgBC99CkoiMpkTBOXCMoALImuPl5ZodCUJKeVBBRR/CycHiYBgvzy/i22/+xj/7px99vP7hv/zXgnMHwb16sDqAPLJLzH2bNn3uM95+8QPvPHrHqlXM2PXx6dnln/uxn9g+fPLFz36W/DA/rg4SmogYpqTnm87P8SppOD45fPmlb73zsJrPHz14fLBYfevNt+6/evvo9iHqRFGYuBxTe86sPG32zOIu67uQ2eHmszv4dIr7O/4olXBUhBCnBHpi0jD5KjjvorRgZFS0Pgl3jpPPZ9b67AACAhETMyAhEgFJ2XeYyRyzs9D4RgSSghI7TZmM0AcKnp1nx5OxUfE8nyYhygcoAJapjOneL9+TAA1LBXAz4v0RFcA+ipZdT8xQgdUgi6UsY8rjAHnMIG5W1wfHuDq01YnMD5Lz7JwZKpAZsgFoxhwxJeyjjp2mFiwriBGD9+ArIyo6quVzRSSlaDnC2KGWdgmK6Hy+CLP5PHimMpxl7NyO6W6I5NAEzHDyod9NfRlmNibjYtKrgoishggESDtWKREV1pCY0p4YzGxW0KSi50RoxgBmxqZmxmaGGEk9oBMHOUsS7Nt5HKtx8KnFYXR93wxjNY7YtTAONvRoRqLGlAuxHhkJHQI4kYl0T6amqTjGkIoV85Rd90ZKT9ss7xySUSRnyYW5kJMQ78k/xR8YysKEXNrroFb88sgm5j8YmaECAhuQAQcnoY3zeXrhA83HPgkvvppXx1DP0AXmquzbAoZoxOYQnVIeWBGiJZLkN5f16Rm8/U769rfp6qIuzqWqIFJuS29AWdDMoRGPsh7wyfmkz2/TQgAT8mQglYGNyZsAkQJlwArQGTZiC3OzlI4wXHk71VQ56hHEYt2E988eZdHiVP/aKy82s/roYDGbN4vDFxDd57/wy3FIH3z51T/87Gd8NTs5OlgcHYtqM5s754cxGvoQQtJcRm9K+6QMdYuIdwzmSvQkgk07EOgwdlUzd4RX262qzutKDU20rmsj69uu7/thiMvlsu27bIgctsPGCLKlceydY/SAqoiglAxZgMckoaqWy+Vifugcx5i2V5sUU9v2IlJV1f62YcasUte1r3S5rM3k6ekjMYgGSFTVlaQ+Z0MKCcQHX9UNO1dVgYhyjjnnIsNh/UBmIDiOQ7EytaKOmfuUkmdSFZXEhMZSzV3qLobL8bf/1c9sLx789b/5t5bVIWb1q4ZYNNmxW3z2G994+8FT8l4sWYrK0vctZlNwP/Tjf+79d756/u7b2/f6U/MiSswJ1aE9HYbDDKeDwe0P2Cbbon50fvHGg4fLvj8/Pfu3/upPJhj3MV4REHCHjZYojgAIsqsFxMDyhNrbddYPBR1BtEkxjncOS1Ay+4KDI2KR7odQkairMjoy1pwSgTMEAAaYZJz32dUuyCoC2mSDjsiMTIaIFPQaUS7HwozecPAM6iutdFAyyIZkPgRHjswRwGQkKQUbKITSiRBlBUdHwklxHiboCgGsNLQ1pe8V+vfQ0P4riJoaogEpopImUKUEaFVdwbFznhYHsjiE2VKqykKFzD57VjUUSz2nkWNPXWdjz/2FjH0eB2Yn7GC2TNqooZIHBgMVyFmGnAfVKHFIY4acLEfIMQRHta/8AjAhRXSA7JiLWhkxMhm5XFycd+TO/YMmK2AAxKIV/t258eUUPIOWoAEiFTf18g7l7AAQm6rm4vJIjOwsyxhpHHno3Tj4vqN+QzG6IVLK1nc0RlRFKAYshri3WjDEEqhxl2SUdvkE3JdS9+aOXX6WmIkIi6jYvua1ySdoujFU9ojW7ge9gR0hgAExoSEa7LSRsyEGHI4PZ69+YPWxT9rdV+PiSOqFATGRI0JHwNMknRqqqokagGWhMVK7ra626b335N239eK0Hsb9SKGjm30L1uKMoVL8jTCLmSHy1Nwr9NDpHJXpFxMwAwF0M0eOIGWruA6akRUCe6q2aOb46eWlR3Uek8jR8fHt27fr5fzw+GixOvTV/Opi887b7y9mdVNXR0cHSVKoK8+urhwRdX1f142v5qrarbeb7TrGGEJgRwZqBqLZoiybGkAljTEOY+oJtO+7d999d3t1Hrzz7EMIKcl2226utiLSDi0RrVarcRxF1Dl3cXkFSOSM1YEaMRK6iuvN5ipvM3J4+uTpdrs1s6ZpiGg2mwFATjlU1XEIKaWu63LOhS0a4zCmCADkXIxRTBHR++DmSxPrNpsxZlHwoZ7PF46XYz8cHBxYFoHU1JU4kkwqosxD36eU9lJfpfhkJjBGxMpzzmSSEZk9W+X6viekz/7WLz55762/9/f/05duL49X88axAjQ1DOP2a1///Ac/8OrM2QmnOau064PKHzXV8sUX7t46GR5XM6LNdjSEMUWzPCaoGNu+J+8Oby3vp/7tB++44LPpRz/+0Z//xz99+7D5xJ/5IbteSzdozTd+njoBBoBFoOa7OBHehHwBriVydu+zDxWTjKgRk/NV3cQqxNxpofYTgdpz6vPfGWeJaSdWSjvYY3ecBXMqpBhm8o4lODMSBQRm57xn76koIIGJGZiCimZlJgMr6kBTjwHQkL5jK7o+qu88tpvP3/wXSVGnbUqIsKo8ewKrzYyDVjNrluIDulCGUhOZyehi4r7F9grbrbQbHbtBOtOsKt4FapyAiqmWyVqbmgxF/lGLRlIaLUdLg+VEVBlmduAcGpXaCQCJmZA9MSORI/LPIRnloTxxQCdZKJwqu+/1eGYDsOtnJpIllrMByKxoORkaoRiOifrOp96NbT10dd/7Pto4Qj9gHDElyIlwL7N0/Sk40ZAKi63Ad8DMe1Kz2bW+m+1YnmDmiMxAUhYz2OnfEXHSXHRrdwtrKkuRbNJaQoDiIoEGYIpAYKyKqJEsOpdmFR4fuE98OHzwQ3p4e5gfjm6GITCQY3YGxkUGEqUsrayaBbNwjHXX8+lleufb47e/jadPQhrRnjur+7vBECatwd3RKkAZj5l6enudFgQoVY1DY8BsWYGZzDNEUWTnGE1GMFvOZxfjsCSOgdRxszh85YOvVYvl0a3b1XzGrq6rw3/yj//bs7NzxsMYu5OTw6vNFYB4XxzQzDtXVRUTb4YhxkgGDIhqmrIn3mw2hQvUD4MVdauUurZ1BABwdXWFKov5Ud/3p6fnIqIKwzD0fS8ghE5VxzGFEBaLVdd1m80mSyaCECryPsVRTev5MufUbXsAHIahruu+71V1GIaqqhh4GIYC0c5mM2Yu7yM5AgIz931vZmJKRHXdOMPV8qBezBEdslO1LDZ2LaJ/0rar1aqq/GW7HYYhxh4MHEIaY2E9FVoBEQEYlZa9ZhFiAhGpZzND5FCPts3bK4rbJ9/q/2//53/wH/69//TP/4W/eOdoVh0cZqYPfOzDX/zm19759pfv1pwvTyvptNMlyYsH87bVuXMOmMmSdi5UIfh2sxaSlMa+2+ZxXN699dY3t0eHh/Oq/kc//dO/+Xu/96c++tpnvvCF7/8zP7SHVvCGisA08PQskLsLDJO1yDP3O00tte8aB75j3SICEfvQzHzdjG1nqmZCjtBArTBBv8eCv7nNlHkAgB0MJWq7AoaJg/MExY9714wldA6YCh1eTcAQBNSKxJUB7Oa1cJqHzqY7sZjnt4Hvhf880zq9fs1kZaiEEGoEJCQmTqBGzlwtXJGrANFUTLNZxDjAtnfrS726hH4LsTfL4ok4sEcIQatKQyXBmZusavfovZqJiEpOEk2i5NHyyFnFMrK5QOA9eU9E5B1SaX17ZHJc+aKNfRNzs7I4aAKK9gUjfbfL890vGOzUg4rCVDklZVUxoRpnxDFS17m+9XHru23db6tu8G2EmDAmytGbmQpRUTFWKBXnzZ0fC2F3WnMppTL9XNbTbhHc2JwRUfZubYiAoKaSBTKQok3KJDt4sLzcAAUnvzOa9gAAMSEzMDHSTBAXlXv5xeVHPiQf/cQ4X0q9SL4CrgiZDJjJgQpYUhOFrEIKmJRycjnSZuMuNvjue+7dB3R2ScNINxoV1+Lpu+VWtMIJSeXGJHOxoYBJiv3GxZDypdgQCYuTbWB2SiSChoJUO7/NOqZsPlDl3WJ+/wMfqA4OuZnXByt2dV0vLh63b7757bbt3L1bYxwOVwchsgLklOq6YeeIPaht2s3V1VXOaiZV5VVVNRPRfN4Mw0AUYs4iSVJMKZUQWVXVMLRgmFLamS+piIxjPwydr6tmViHa4eGKyN29e/v27dunZ6fr7VXXd227vdpGZg4hAFhVzyRZESzKOQOA997M+r5HZBEp4rKXmzUALJfLA3/Ub9b9OKSUxpSIaLaYI2JVhaaZzZpKJI9prKomhMYxDIO1bbder99+65s+uLqqmqYKVQCDrFJVVTnzIlL6z6rCpHVdofOeqapCODiIw8jOKXHTNN3l+dAO7XC5PZX/4v/6f3ny5Pzf+sufmt/DM6Se/cd+6Id/41+89buf+cNZbKuxj9L+4W/8yp3Dw27o27NzVANj8iGBLWazFHsWlZg0j0O7efDeOxfnp0B4GvODs3Un+eMffe3Hf/InJ4vWaS3dXCfPFMp4rc5mtqsAnqkY/tiB+X1Dsdz7igDIoULnBclU0LB4siPQzTf/zje03c0MUGaBAcAATVVMxDSbKhIjewJihYDXSr3samZGcoWqjqJmCpZVJzd7IzLBKaEEZJyKgKIMBrsV+Vwp8J2Pm8+bGUiexpLQEzk1UiRhVkZwniggOBVAFYwJ0ojjFbYtXm30ag1DqxrNCdWeuSbnkQlDldlZU4Hz4L1p6c5MFwthN7WKpqiKqqCKSh597X3tzXvnHLIn54HQ2BWPLIfEhQDDuyYGQJGKQsPSLWFiJudKUxmZp6u+u/ZFWXO/FERUZBpiQkTbkYLJDFSZWXJmQKdQZXFj74eeunU1bJu+922n684BQMoOzCNkU83CjuyG5OneJwDxGpks0yWFtem9y5JhF/rxxoMYi72cmTk3MZq0lOrPruZdBbN/UgEBgFSzAThyDAYEES01zewDr1Uf/Qi9+upwcNd8bS4wMqFzAB6RDAxFim11Vq+AY3Q54jBSv6bLK3vvYf7223R26voWVIox97SD3uCkmhnc0KqdcLByJ05HvDfu2H0LNXAFGctshMVEwtSQ2DGm5LzriTXHA+eWi2Z1NGtOTpa3b8Fs7ucHHGYuNFU1f+vijSePn4TgEc17pyp11XQxlahHgHEc47g1cGaWc3aEJuqYVdURI0Ob8sP3H5gqos1qP600IudcXdfdZp2S5MmQj8ZxBNCmqdAxgOZsGrJmPT09XSwWTVMd33plsVzGGLuuOzs7u7y8HIZhHNNqtdrH36ZpSjLOzCHUZWNwzlVVFWM8Ozur63q5XIa6atvWOcfMVVUdHh6mlBBtu22RKYQmpWRAoarNpAk+V8HyGMeYQIduG4JfrVbe+1Jq1HUtIoW/hIhmyRCCd3VdO8JQVXVdr9frBLiaN43Todo2fboaZDNu/tl/80/efe/BT/2H/3FaHipUJ3dfOrp1/2y2IIgBsxN+6xtf/aV/8f8l5qvTU0mijqqm6ceBmVeLZX921jhnMW4vzm+9elgzXqyvQjVfzWY5xs987nOvv/7qKx96DRByziGEvGfH3RA3hF0mC9OTsMv9UeTGa55RIIabf7i/IW/eeiAE6IC4ns84+HEbgyMTMZxGpiYId+/Vate1uN3oQheDEbWsmgEAREyEDIyYyFTN+0C0ZwACYoCiDKPF71JJZVJ6MzLNiojOAYCxEbEhZMt7JGCPsBDgPt2++cV3Y6QAz/mjIKqaIiAxuIDsEZ0RmSdiBiXIRpJoHCEO0m395tQ2rW1bjZEc4HIWg2rlmOaGDpiFnHkvjoxJb2A2tjvjxfGYvBONBsU4MbD3vgrOh+ycsXM+2E4fs4Dnjl3Yb1+TVCQAEpCbXGKInJXtkelmzVggCNvl+PuTtScHQ7GWpokJRICMrFnZwBvS2ON2M8vRpYHG3o+D7wfcdmyRDcEyAagamODOoenGyZ1yk7IR7ReomZW9IaUEsNvVsRQEk7NdESACAjDLUxtsQjv3AzKmiqUFQig2FYiACKBFPwsMWQVIM0OsQnj5xeYjH7WXXxsWx8pzIu+QkZABaWqvmIKWiE2Sacx+2/q+ha6Fs6fp0eP06CGenTUxQo5gAnBDbmlXmZU5OtrRMKbNoQzcIAG6/Zp4NoPCqZ1WrNDK36KpA1VrCBOYZll652czOj4Y7tz2h4fWNG61onrOoTElh+6zn/usgTZNWK7mY+xdDIZ0cnzHsc85x7GLMSM74nK5YIwDIjhzqtr1W+cckiGZY6+at9vWTAgtpWSWY0wqMI4ppVREg0NwZtVmu3ZUFbmFIvCrclHXddf1WYeqapj55OT2Jz728X4YN5vN+dnF+dmT0jPIOZvZOI7TbD6MzFyFUFVV0zSIeHRyfPr0tB/6EpSTSHGAqarqlVdeeXR6NsYxhDrlXNXN1WYdJM2bed/G2XKGDvu+jTEaQR/H7eMHi2Yxm82ISFWrqloul6rqnBvzqDmq6lj2NNX5fH54eNKPQ4qDkJsdHXMT01XHCft4+Wu/+M/ffvDgP/pf/2+b1cnR8vje7XtfFWHH2y7fOj7+wAdebTdXjx8/brdrYowxKbNjzuN42DTovE9Se3v/m2/cP77VX17eOlzh4jgov3t5+ed+/Mf7vh/GWNc1s4d91lZuJSpmMLuU7hrRvnnf0T7a76M8TLn+dxmRvRFY0IAN1YiAHQVvACpKNlm0P7Nz7P4S9gvdprlLMzMtFqcqkgEK+J3VlGwipyBgybjK/jPN0oup5NKwRlJALA3KsqGZZigOH7zDD4AUrm28zEzhuqrYh3jYJc17COjG4aNO3nJsU1uUiNkMKCuKYMo8DNi10G1su6X1mZS238xZU+e5S57UO8AKkQ0dEAuCIgIaEuwsk/eFEZTWpoFXrUwyMvpQz5ar0MzIB+c9luhPDIRIDEwwAWQ21VjoeH9FEYsdOxmic47cM4k/7r3idmkyGOwsBo3IwYRHY3FyJwUyQBWLOShgztJtbXsF/ZbbNfcdtK11I47RXFZEAMEiczZN0z1fYZWPNjPk6w0AdtIlu+ng4nV+PWVuVkCk0uuHkhICFuk4vRk5bXIF2penDiYRvBKazYsI4ciQlk39wn07ud3WR7k6ZnaMNBmskhpgJjAEySJqKmpD4q732w2cPdHHD/HhE7k4x27tclTNBAo4DbEX29UCeu7Lved2Qtjfhzfb+DdvQ9xpuSAXCHSym/PBQBwjGLBq7QPPa17M68O77uhoYIzgvK8J/dHh4Te+/uaXvvTFu3dvnRzNqspttl3dNGoOodps1swUQu3nVT+M5Qik+KwCZC3C1dlEPbvVYpmzqjJoInIqY+liEVEIdYoiKrPZbL2+JKKTW8eiuR9HRByGMQSdzRbttk8pee+GdczD6HxYX6zfeuPN+/de/NCHPuJOuApus1lfXV2N4+i9Xy6XAND3fVbbbDYXFxfOOVVdLBaz2ezWrZPj1bLturOzs0UIKaWmaUTk9Oz0tQ9/8P33H27brlku1PDW3TunZxczhtv3bpvq1dVFPVSnZ0+HITlHoZ7FMfVnZ3Vd37t3T1X7vp/P5845DqxaSxpjjKByfnnVtu18Xgbsmr5u1ts1zPyKfLe+otxnkG9/7jf/4f+h/w/+k//VnY9++CP37/62Rx/80AeoZz/yoz/2ja9+4/HjRwBKhDHlMaWq8nmMVNUHsxlebYOadv3pgwczdg0SsvvkR78/vfHGT/y5H3/vvW92fV/PGiZGRBWxnWVF4RTqjfpyXwTcWG67m66kUjg5TBCWqbLr0uG5PWAXQBGQ0ftQNwOvQQxB1fa2e5NeOSKaISHZtYoy7lWWC99INYtmAFMt8LDmZLobyiZiMxVVUDAQQjI1FYHJF52Qij/TFMIEEiIWuwDY8UVxJ3U87WH6fPyBG/vWd2wAKMY4KWvTdJ+agUhAADWICYbBthtor6jb8tBJ6tQhhACzWa5rq2sgQmZhM2ADh+gMS381I6qWCmO3/WDxMVQvlpEc+4BCdbNoZgvnKmSP7IvzDzICMjACOSByfi+7/8xWBuQmPTwrqt6ExTiUS069J9JOKTiCmYhIzqUlgQWhJyJ0pkaABCYxO1FWyEN0OXpN1m5oHDiOuWtzn2YGyQqFRQyRnEdEBVHVGyKe19EPCwtn9yjoASI6RzrJD4GhsWNUKAWZ4c332e0HQJbHvfsBT5uiihrQhA1NAAsoAJcdCQ0EUWuvy0WeLUdugBuyVMivAKpoUjTfwUCyJMOEPI7UtfHB++ndb8njh7PLlscBMYHlnUsZATLoTibXpkWHu/r3udMAZrCbVJleu2/OGe4G4gppqhQTZAAZVTU75GKo6rCiqnKL2VjNjPxsMa+8Q18TuqvLq1/8V/8aIc9mlYH0wzhfLCXrMPYVuP2ATBxHyVmNUhyHvoupZ8IQAgA6PzFsx3E0IzN1zhVtQmYu1SoQGGoBTxBxGAfRvFzM2bmu7x0XQ2D0wROSD25zZaaWhkjEVVW/9+7bl+eXr7zysjEw88HBwXw+H4ahHFtx1FsulznnGCMzxxiHYdhuttvLyzt379y9ezfUdc5ZzEKoksi33n73tddea/s+ZxNFM7z/QnN6ehp8vVwsFrZk71xwp2dPRAQBVycHjNS27ZOnT09OTpqmmTJqwnnTqDZ9ux2HHpG6vm+37byqF4eHYbmcH4a2XTu1k8PlZR48atsNp9/43P/z//S//w/+7t89vrs6qP2Yh/uvffB4cfKFL39VY0w5ZRFGG2McUw7eq0Lb9UehqhqhmJ3Re2+9dbhaktj6/MJfXMow/sav/5vjW8u261YHB8FTsdmCndpzMTIvAYAms1kwgxt+HtdRD7AMZl17+U7N1GezeNylbmYTnwgRiLmu65YdSiYi2aEZ+0BW/i0cmqJTVmwUbBJ4Eyg7leZinVV0i3Wc7K4NQMxMTYooqDITE0KpCBEnUDcz3fA9JgDkYmEP5r23PdC963YAe3wus9o1QeC77nxFT6ho9VoBHCIYmgpmsWGwvsN2g92G8oCaUu2prqxukvdQzdDVDhwSpxANAIzNHACASlE1sx159brXioTMDKFsC8i5qhrikAW8gqiSARdXouKOVWzSmbFc47I5TlpARCX9RiKmifteWnaAZmTEgIXGWVrdBqrRVEESqQCAGLELzldVp0WhO8VIOS6ck26D68s6bkPuvA5N7KFdp37rGZXNZyNEZEfXVSESsIrgxNCy/TUrDDVizjkTITFDibZoQNP3ImIlBHKmKqpmHNgTmkh2CIwAVpyzEJFMDZiKgSjAJOmvgCVpRiRmBiMzM8cE1mREC4KcmJgdJjCvxaeOXbHAyKoABiSMYwq9+svePTlNb30L3/76YtySul0MZ7yGuhS4tE5s5zQAu/tDEAGJrtP/kpKAQmkFM6NKIVArgGFxdivD+pOkN6i6lByayhjEGtGY6ghmTOSSukSk3vmaKuerT3/xq2++/U0XoqlUzWI2WxBRPw4G6lwA4pgSe1eIaGN/lWIyGfPYCVLl2TnXdS0AeO890zD0AOAcqYKbLcvdSAiW2suLi4qbdnPFRMF5NNAoi9mMAddpHdg5hBjjfFHfun1nfbUehxEAgGHbbziw4PCNb3317t0Xgi8eBJWZFTrQbDYroT/G2Jo651JKY05xHDZq+vAJgh4cHt6+e//o1p1RISY7PX/69rceHx4fh1Al1SwWHN29+2K7vexjH5oqaVa0O/deyDkPw2CgvqkPlnXftn3u85Brq2tsJFlMMmtm9XwpBnN2pnl9td7GcTh7Ohu6pqmOm2ZQ3Qz90e37l2enfdw6XW8vvvoz/+U/+Auf+itVppfvv+4Wh6vFwdj3aYyKqihF0oEVRejk5Q8Ss6aU5ZRpuDObX52eL+pFH8GCe/jeOyD5c5///Md/8Ac23XiffR+Fi0X2zu8kY5lqMQDIsgsqAHtRtaLdiwxMDGhaWCKAimRICJMaBE1OgNcElfIzoQAKICiSqyoKIQ0RAIB26RROvJbyz1CavVaMZACKyr5atjKsm0EymJoIguaYYjTJgohmqqKFXGQiiJrLPMNUXpBNeT8jMrMDZCmi+ezVqXLOOXvvHTECEjk0I2YwMdzByYTIaKBIUwY6QSh2jRopAQKbiWXnSFTB1ECUhoFSsrG3cdChM5TkwLzXcIhVxSE4z+LIiJTA0MoMFZiZJSg+OZNPspgpmrKBAiCyOFUC4khGpgTChi6PWWLSGNXVwCAi5ByVySEgyOCY/U7r7Jotg4TJrMT+wpMtuwIW8IimPWESaDUsoVUka4qoAmpAXPIfb06lF1Wn1jiPY6vbtfUt9Nu8WVdxzO2GxyEgOkZVI+Zdy/XZHXWaS8ByGW1nX0OMgMje7eV6pp3MEHaMoGmzJgLTyjlEBAUCBCKRBCoAxSqMykSbqOIuOyglTlkxMIFLBogZyZmQAvQJ2567XqsBsTJTcIVeBMhkapAziJkIj5nbFs+ejO+/PT56xw2dxhGue0hTb2NSVplK4x0cd51Z2C7rh/0v9rkY7Iat9zWp7eQvENGkNDAAAFAkSzRVMGIFSskL+BA6IilFHgACaM6f/u3fFE1147ttMoAsqinXTTUMXRwH4GCioDb0fc653fYiUv7WVDbr9XK5rEKIMeaUACB4l3MxONOYkqoSUfCuUDG894vFYuwHQ6ycV5XYd1VVHxwcbNuOmeuqPjs7vX3r+P79Fx48eICIMQ2hqoigqqsKQhnqLos2hNA0TUqpbVtErKpqsVgcHh72fV8GBcZxFJWYYhz6mBKQqxerw1v3yIVm0bz97XfOzy8OD49ni4WOUVVXq1VTh4uL86aZHRwcdl03DEMI1Ww2Q8ZxHBaLxaxpri4u1CznfHp6Wjdz7/04jM2sbprGrB779uDwsNtuTPLF+XkXXFVVTRXquunadrFcuKp69ORpHmO3vfzX//IX7r3w0l/883/rX/3abxzM54EhW45jRwCS0xhHcs3dl18eAV//6Pe7vj/tRxCtFgvddhuVETGqrLebtcps0z14+HSz2eZ0Lf91nUJ8B+xjpXW3+0UREp0IPoSohlhSod1Li5nGjQ3gZkiZVG4nDJmdC4n5+u+uSUfTIp66ipOCfTE2FVWRcmwqJlK8ss0kp5STScoAAGq75WeqInksyKualdiFyAXDQGIih8UtHJmcd47NCTsP3qtzXPjbBswOilk6l1HQfQf8uhn73AMNcfKGyWYEYiAKojaOkqKN0SQBI7BDH5AZqzn6gN4RYRETLg1XletzuA/T+4u14+cWlikhmMPKHGgSzRaHsd2sHYJHBPKIaOAFASok9OUWd+yvtX2ue9wF4pviP+0iETI7YDcVR3umlIKIlLFfkUwpoSoTsyimBECaFG3yGZX1mvq2SWMYBpeizxlzhpwdIho8R8S58eOEP+7mayZ1NgJIWCQCWc1ox01GIKe7tNf2HOddeiGqKrCDlQwJTbMqlbQFrGhLIGFB4XHXTN6Bn0zMAyopExp3Y73uYb2lsM5CWgUGjwWlE4SMlBFEWYG6zp8/kYff1Iff4u2510xIojI1s29chmsnhuuwv0PnSgpf2r97vt3uVi5rAoq1Q9nVbnx/RAAVzTmnxAigaSoMwVGMMMYw5HE0CwZVoWfL177ypS9/5QtU+3EYm6ap61pFj46OYurHcSSGwC6l0t3M49iLpphi1/XzeQ0AbdvGOJQTGEIwM2bOOe/AU0UEkbQdO4dZVTebDYEeHx613UZTJqKUkve+SG8SO+fctqouLy9fuP9Szvn8/NyZQ8TZrJ7NZjGO3vmc82w2m81mZrbZbJqmOTg4aNt2s9kAwOHh4Xw+DyGM42hmm01bB5fjEOMwjP16fVXNlwrjye2Tpp49fvqkEIpCqERkGEYmKH87m81Kg6F8nZij91VKUtczWEHbtkRuNnP9MMYYKx+gtziAqjJaSimEoBlLj3ocxzj0IYSmqXPqfKD792+fXqyv1p1z/ODdtx49ePu1F+/1mwvSBNJL7od+4zybWXV8/PoP/vDv/N7vd0M8CfXy6Hhcbx5dbfNydUkIoabZLPVDHWa379/fdv377733gVdfKUwnItqx6I3BdqL3O8rZTmZgB+xMkbcoKuCuP7frt+4Unm+wrm+uW9gvWSRk9lU1EFlWwEmg9yaKYgCkoKImoqIl+kuMIpI1ApjmbDlLTpoziKQxQsopJgRT0dLGLYDRGAcD0CLqQw6JSv6rheHCDomJuKhmkmNmct5pqNh79p59QGawAMAEjtk9Q4X93oNRaIBqxZlVskDOkLJlQVHNYqZAABzAE1YBHWsIxM544kEBTJwUeeYc3jilz/KRdjEKp+kgjFnGru1672rQEYCN2YChNkAgMWAjQEZHLuzfheA6cxS0XfwnRCzxyHuP7KerBSSl6YqQcy4Gp6TKkljVS+acUFFFCJiRHaKOg11d8jjyOLjtppZMXYtpdEAEYtmISFRp15y5yWc3swn3gN1gCKIhMJOaOeemLbE0pREZHRqYWRa5ri7VJI57UWqAyQPZVIsjspohEfFUd9pUS6ARAzDS1BlH7wDEVNHQRUnvPQyr4wCMBynKCrRR1YSkBiTGWVnEx96ePpX330pvfw2ePq5T0mQJyCED2I0xawMDECnbwBTc1fbb1/5slMPeb8Z7IBVt6h7vt4aJ3IRoOYGo5KxZyASKbW4WYnApatvhxSVVh8QBqoTku+7yD/7g08FRlNh17exkRkTBh+12SzwJLLfbDpHHvstZRKRdb81sOavLxjOrAwCEELqukzR673McRMR775iNaDIeqLwkKfyZdnN1dnZ26/ZxGsZtuzlYLrMqmhS2qBqcHB4450D1pRdeWM7nT548YuYQXFM3wbELTdd1PvB6c9m2bV3XVe1V9ag6aGZV13UGst6svfeiaTabzedzR4Sm/TCE4M3Ue0eufvr06eHB0cnJyWbTjjEm0aZpmJnAqtCYGZMnouATQgIwICjbVUppuVyuVquubdfr9WKx8N532zalpAgiAppXq1UcegKbz+cpDqoqOY/jCPPZclGt1xtid3S0MtCui4jpZ3/mv/rgBz9mIrHfprFv240j2G632eDwhZeXd+75+eLR49OjF+8f3rrz/sNHj7o2A73y6v1b9+62cVy4cOfFl5+cXpyenf/KL/3Kl7/whb/9t//2ax/6vjIqMVWOxb9lwklAC/qvRiC7iXrhYkJnRRdFFXYmslLq4knyfZ+uXmf0U52wp+6Rd4UdLbCbxr8ZzqDMW6pB1uK9oDGnGHOK/bhWM01iOec4Ss6WJY9jUM0xFfwHCuHaVETHlBCLcgwZEpMj54hZvSMiYCJiM5ApxYTgnffeVTX7wFXwdeNCsCaDBTIxUoDA/D1Vsp/dANQkUxYdR8xRYwLJpaYCdlhV4IN5hiqY4ykA7Zqpe9LHza30+t/dJdlH/0kMAcDAG0oySqLn2/W4XXfzxu6lRUYHwAiIhN6DYygqz3SjArgZYsqX3IelIrDzbFDG3VGCY5cleUCP5IG8ZIuxaHN7AO8rA7Kcaeip3UC7CTk344jDYN0WY5rwayQAZkbmIhd03WC5jo57OvAE+JgAMDEhiupuMAoAlc0ACFSxuNper6z9ePAEUwIiEHp2auaYtazjEjMBijIgkkPEqTJWAymvYQV1puPTs/iNNyhGvLOhg2O3PNT5IqETBU3iFHwWd3WW3n+3/9ab/vRJNW4xG5gzdBPCBAiAJoo75g/RDq8HACJUmRKlm4tsv7HtcCG6uUfuv4HmsvkhgJmgCZmCqFjOxXDSMsWYLi9Xt46Hi8uqCjnWo+oQ44P331VL23ZzcLAqLMnC9Yopqup6vXbOEXFOomoxpn5ou65rhvr4+NixQ+RhGLsuFn6kSBn+IpGsKgCQc2ZmVSUk51yMcTabpTF2XRfYzWezYvnQ9b0jzCndvXfv9Oy8ruvD1YqI61CByjAMgLpcLABtiNKcnJSZLzMrekSLxWIcRxE5ODgoCXvJGNq2XS0PYhzu37/73vvvbTbrey+9stmsb99bdgM+ffr04OgQAKqq6oZxyvTjWNd127almbxcLs/Pz0OoSAkAVsuDzXo9m8232+1ivvQunF9ebDabw9WBgaZxICLnwjiOs6ZJ46CqXNcpJQEbx3G9Xne9HBys+n7MWQ9WS7ANgXVD+82vf6Wpw3JW9f02xajkslmYr174vo+0AvdefOXxt749ZJ2tVq13B/fuf+ov/5Wu315uL8cMxPCNt958enq1Wh7Efnjj69/4tV/7tQ9+8IOwz3JKeo/TzVO0+K0smus0AqSIWhSfD0UEU1UGMwIEUwBUKFLD34kCGbKZFsFGRSoKDJJkzyi9SagvB1QYeDlHzTnFIccY4zAOrYpIypqzxASiJmAqOWU0K/R1MyzMXwIIXCGRGiIzIjkfiFnNnKuL256IAmoWATNy7NhyNiCwQgTNBGwWzdcEUNSPdkwLfH4buPmtafJPMTMBEzMlBHZOS9IcggVvVQXOm/foGFAmO/ICv4iqGdwYANpXZlDoi+WZqXICRPTFHkDREIE5gnbDcNVunua8vbx69dUUHDkiH7yNCZ03MXDgSkb/TEApP9N1/IUbJcZ+AzAgna4cglkAR+wBHYqEONIwYkqaBUCpqs0gdgOn2MQYLHvJbhzGdq1xqBi50HWRAUktAxPY3sN3l73u8giYFBquWVqghmVvNpgCTU5MgsWaQNVumN7AbkUjETHY1B1lIzYw2DljEDEgFC9DAFJVIlcSmFJiURIhyCis5kbNDx6MQ4+nj/XwoL7/Ep7cyejFqAKuValt7eE77Vtfo/MnLvYoCooAxeil2P3uzvPEANVnzCtNbapiAeEZOVZ45ovtKoDrrErRqKRzk+63qGYBURQ1lYwZVJBNUo55vHz3Xc7oG8YK82z2xpe/cn76WCTP5rP5fC4izApGMcaURyIgIklxzDln9d6r5MqzXy67rj07fTyfz5ummTXFQ1GjJJVJgg0A3M7OotDMEKCqKuecpNFEr66uVvMFkqHB4eGKiLq+N7C2bZu6qqpQpgHqul4sFgCQ8mhmq9WKur5q6hijmTjXlHumqrxqBqiqqrq8vCyc8qOjAxFxLqQBAGG+WKy33dOnT1794OHV1eXx8cmD9x92Xee9X2+3SDxtIcuVmS0WK0Rs2xaAFovV1dUVMoiIajefLbfbtmnmQ9eb4dHRUc55fXk1mzdN0+ScQbOZrdfrOvi6rnMazcwRppTi0A9jl1JerVaqIDkfHyw3RDlFTbFNg2XvPDbz2ZCNhFbHdxYnd0elu3dffO8b37xYb7/4xtf/1Me//8/+6T/9ja9+zTRth83Z+dMxpWHIoVqtVss0XPTb9td+5Vd/6qd+6vDkeIr+zxrfWcF1CtGtUA8LgWeSdjMzMFFDIjUFJSCjHfJ+owO8D1glUChYkYVSAyRGcgYj7Fhkz1UAtm82EImKWEoaUx7NpJDviMiFYFKk14q6MzvHReoVdjNJAgiIIlLCCzITOQMTpgyF+1j0JIwI2ZHzxI6dD+gYnSsKdGaWJQEBF/3pvTKYFWmA7/ZAMzBEMEZjJkAgnfqCTFZ58wGCN3JFk4d0Gu0FQLsuxp45M/udYDKpKQO/z+NQqqDZNJr1qnGMw8Xlxflld7XRnF78AHAIxAFEQMSSOFddbwA3rwHjdU91J6dMWNimU7zZ7dgKBEDEhAxmlNWNiYbB+j6YqSdGEMnQddoPIJlSxJik3bIkJjUDYmc4kZMYgJmem0u8iQ/un5mOU01EyrLMMZbxSzaTNJjpFApvVACGSMjIxUOMFQiIcUcpvZ6q5qmXMD1lpEVahFABQSRkiL5o7mtIUongaRrWZ1y54eFDf//l+tY97ysHzP2Qz8/o4TfD+amLEZIBVYClp04IOyzvuldW2L437gcEEN01fp8xLri54MqpmaqBGwuiqF+ZaM4ZzFTERC1rBskoCApoBEZZ0uVlTmlVQ+LUDcuvf/ELs9pfrlusqouLi+XiIKXkOAzDENMwnzfeu4v1JaAROueqGBVQQxVEA6K17bbr2hCC99Ma8z6UPlOBSsqlFBHnXJlHL+XFfD4nhmEYQnDEJU+fz+fzfozz+cxXzeXlpUPyxLUPL7/w4qNHj1Ie5/P5rG4Aib0rk66lbVs0nI+Ojsrgd1VVm83GzIZhKIt5uVzmFIlgtVqenZ1+30c+xt6llO7cufPg0cOmmRNRP45TsZLl8PCw3Ibe+xjjfD4/ODgY0zAMw2azMdHKewDYbDZ1XcdxLGMH/dBV3jGzmvR9XyK+c67gMOV9GMG6lJJcXW6rqiLEOKRZ3cAKNtvUddv1pnOeDk5ucwjSD6988HVfL+MwzlztXPit3/6dv/43/p0Pfvi1b54+vby6Gvt2SNuziyez+fzq6upTf+lHl/OD3/s3X3j06MELL7/0+MmTw5NjgCnX0OfiLxTqDcK1C/i0JFUVARUAsmBhziGCKFAhaEyveSb9L5wOBSkV6RTEVNSYJljoJmQEAGWSByZrDwBGcogePXlQZx5QjIFBUcVMgKAmdM6xw8kGt8RmpbIBKCABYJmJVISE5kzVRMEmViQjMZnLzjE5D4iOAjExe0QEBqJn1JN2pPHv9SjKlWTgIJCJlfBiDo0JAkMISEjAZIaFoa47HkcBePBaEvs68qsCgJrS7r9vxMLySjGQBDmCtZL6lNpuPOu6cX2ppsT+5bppqhrrGoOhqWPy3+Xgy2YwjaMiOzcN0SEiKOyIJEXinwnA0BNpVojiRTkmTlHj6BwboKWoMXFKnDONg8ZRU+ScUQQJnKPJpA5pkh3dfdbUCN0zOxFgL38nxdxUK2LNubAT0CzHWJYTWiwzJsQ04SoAMI0/ApMjdoaEyEVUCIjNjIh3y7EM2BJNwnsEADkLEQOIibpkhiCoquIkOc0ssYoYNjJcbsd15y63brFCQ+17uTyH80c+jpYEgLWkD4rE10226dMnBpDdzCyeNaC/vlFvDulMrn5lwyv9EgBTtZys4P6iJS0CUVPNqkJmBIQkZohUOWdm2G/WD96xmr765jfee/dbZ+0wPzzYSDo8OEQgVd10a+d4dXDy7rtvX63PmayqKiAdxzEEd3nZ9X3vXMg5AZiq9H3abHKR6Ch6cLthvamdqCoIpDaR6Lx3aDCbzQYzkUTeFeW4upnXdY3kmNAxj+NQ8ui7d2+/+OKLV+uLxWLhglPC2XwGpkXDvKkrBCsOjlD0f1bLrjsoLKCU0vn5uUhW1Vsnt9bbNgp8+ctf/DN/9seHcZw189VqdbXe1nWdRE213W7iMIrIYrEoydA4jpvNpvQSynjBdruF+RwA7ty9+81vvnnn7u0QQt92RX7Oe195Xi6X68uLdbut68oxEaGZjeM4n89TGnLOANT342I2N5M8xqaqRRyidn3KKt0wNKvFwe2D43sv9MPokd9//50nDx69/tGP/cd/7z/5yje++uk//MM7huvL84vLR+Shay3ldHx8+OYbb733/rtglsbx93/v917/2Eev19iNxMLK6rcJnJwK79LzLMCQlrqSTNRIUdAIJ55/kUm3KXjt9gAAVDGjKfhbSjkm0Z1QPDwLP0BRWy8bDwE65ywgATA4nhX7WzRCQxAwURNEmJceAxo45pJfAYKWaVYwJCcldBgYoBRj87IpMBUqEKCJS4VSaGJc1IYREckwMztiRr4OJqVmf46uOD1f5IvJEMgcFxkKIDIWIATvyBW776LkWGw0dx2UQo7S8vMN9H8Cews0BKUjCbBPBBHKqFDRhjMRhKQQAXLWrk/vvP3ObL6qFwf3m4WvGwwBmB3tuvbP7cCFklgg5bLJTPAykYApkZgRIEXzYhYzxWgxhqiuyzBkiYPSqEwUl+O2xxwby24caxOUnMeetDDUHSMXI05AJXYZSGBnx1aUuw0RQSBPGb0Bl61PARFSGszAtKQDSkCSM2CZC8dSUaiV8Q+yMpdHDOQMuczCFYIbEajppPyjqjmXW2Lf1EIkk1zoxUSonChrnaFsk4nLtJcJII8RHr0PZ0+gqgAxpWSqpa0DhAAmlhkJDCRlVXXMCJhVJ7m8YpRzQ3fFiuDzhKWWeZZSke2uGpGBZFOHbhK1MDERUcNU6hhQyWSqklSzGgg7Y2JyRMShBoOgIFkwdf0VnL8H752eoqfZ4UFHvpmtNJUlqQerpUj+0he/0PftbFajQRojVZVoTjGuFsuLi4uYe2bn2AOo9z7lcRi6nLOqjGMuc3ZM4KvKNM+qUMY+gQCRwEBVGYCaoMqmCcBEMpgMfV/X8/l8lsemClzXs2EYzMzXlR+bbBA4LBsylcZVbl7QajmYzwpMhIia4tFyeTCf4Z3bFxcXMcbVrBGRy6urlCT48WjJZxcXZw++feuFD6w3V4Yshpu2I7BZ5Yet2GQ0j6vVCgBcUZo3AQjOhRBqMxxS3nb9vXv3Vscn6/X65OSEmReLRWvatq2jplBNqip0XYtgVRW8Y1UdhrbMKCCqShr7tq7rbGqSqtqZkWYesnZ9H+vxQ3/qk6mpJSezdHV56Yj+/t//++Nm+43PffbV27e++IXPdo/fqXNnvmnZvfz6D82Pb222n77cXqzq5V/5S3+5vVivzy6XRwdASp5AybIQkahQGeAvYUDZAEvMVTMyBgC1MrCfwQAdqZlRMQRCUDZEJVBkNCUgUoWs4gQkq5lJkhzHsReJZlKs6qdtptT6iIBAaKJqDASBAYm9N6sBDI2QqGxFaoX2o2IkHhVBARTYBUNCduQZlaZ5SgQoWqEmalYENcsxs+PS/zAE4Ovi22503Rh2FG2E4h9W9F2m+Uuc8GecaPoA5hDA0JTBintX+VrsJor5Xrsdi3/Ybm9UnZBtA4eUpczVGpkgIIFmEa+qOmDOZOCY1cwI1Yr/jjNFUrYEkCmNEocUh9xSPXP89NtnLx08ujU7CouVhoghOJ4yx+d3MaJr5iXs90EsMkJGagyAYpTER9F+pH6EYeDYc+rMRhFpZgtyfrhMxe5R04imaRwgjgRGjgGgMLaL+WW5+gRl6M/IjGDyZYNytstxqpmqpGxmjkl0VFEzFSgNKlZTNipdC5yMntmIy0QzFoItMRDv7eQnWwEBBC4EMjCiwrKlYrisOoFzWUSmwUadxE116iyUiggRAETMNOdYnnTOyY7raWo4caYBzGiX7JNO3sml6CnlS/mTm4DY9cW6MbWPZojEu56wSckC1LKSkshYEvA8tV6NiCh4RSQiBUwpI6IqSk7ekxo8XV92qho8W7UITVRVzVVVMfOTpw/ffPMNM12tlilFmMY2YLU63Gw2ccxN05yfn+esztFisRBN3nuzSlXjOIpGAGvqir2XOJpKVA0hGEDwPufsmaqmTmOcWjCIIgkR1+ur2WzunXPOnZwchdCknEPwVe0Xi0VRCmLiJL1zjonmBwf90CO6ug6r5Twl6fv+8OCgqqq+7/u+v3vnzsOHDyn4erZaLZfvvPv+fDZzPrTb7fvvvX1wci84d3619cH36/5wtdxcXTSzZr3p2LkYo6qenJwUYYlS3BTxnzLZMI7je++/f3h4oGl88uTJrG7qpip1w+nTx/P5bLmYM6iqDH3b971VHgBQpVCkACCnVEbMPDtAABPnualrHHGbdLzcYMoz59fj6EMdmD75wz/04r07Q3vVrtff+PrXHj1878CpEGawq779a5/85Je+9IXtev1jf/4vfPq3P/3f/eqv/vAP//B2u1kcrRBRxfZD5rjLa6c8dye3W36tCKhmYDlnLlrxBKrTmA4UvSdEczC10MoQpapGlZgMVHOO23bYbmPXOwWrJ4Ux26sR76hDjKhEAOiZTQqtGc15QkIE1EmBRkVUFCOgAiqhgiEpApIDx1RmE6j8a1NYIEwIk4/5lOTusF6Q/QZwUxOJys+7DLn0F6f0/xkI12CCY0ujEUs70/biXvTcXM+N+uFZQKnsD+VbwbTLmJmhqFouTp5lq7hZhIioiqlkkSKhoKCKBjmrZIvd+PTh09XJbX/rhOvGsnzPDWBS+dg1fsu/BITKBEqqoJkFMAkN0brBd4N1Lca15Y3mrqqCd8t+FNDBl7Ns5tBMFazYkpWaiIG5+PjarnGEZW5P1BBBVSb6Si6THaBmosyMAHmMyLJbuypZHAdP5ByrERIjoiAWUSNkJmLkvcz11GqeGg0GaAhl3lG0OOeZKMhoKqY2NQgQUQSBCrOoHEZJXkq8zikXLRFgElMzK6Mr5ANOsqCwb5dNU+y7dSZybUSzXw2IaFrIGIg7jrDtzACmF+/wuunFE4NDQUQTqEgZ0y3NIwBAsiwZprybixiSohnTaDogdeSeDOuLmIAor6NzYb5aDEP/jTfefP/99w4OVvPF3MwaX6VxTCn3fZ+zzufzOGZVfeGFF/q+34vjpzQCQAjeOQeGKjl4ZgJGYM9MWDmczebEJFnqKrTtJng6OTqpQzWMbde1k7KsoklKYw+Ai9k8JzWwHGPf9ctZHaP4EBi07/rK+6aqg+ec43w+l5TnTXN0sLq6ugqOD1fL2yfHDx8+PDpYXV5eMtJqMb9/9/bl1baqqxTju++/f/rk8e17L0qOQ9czs3MuhDAM/Ww2O7+4uHXr1mazQcTDw8Ou67bbbeFEVlUlIuWeurq6ms2ag4ODy0slorZtF7OmDCVcXl6A6eFyrqqmue/7Ing3qwIzF0W8cnFTSiZKzMjsnHNV7dgFgatevvK7v8fiDj/woVu3TuD2CefUrS8/8we/+/C9dx69/26wHCVKwFby4d17L7x0v7K4ffjuj/7Fnzy+98LTRw8/+gMfFzQgMzXiSXJ8WkI3CcdF/wR3fP0yKKOaNYkBWSZjZgadBicLrcgEDFBU1SCJWFbTnHMahmFztR6uNmnbURLvgzhB//yH7sInOmIgIABjYyRiZz4QMiBM2VZBdbKSMxSFrEXQsmTLRqYqRdgRmMo4EjoiJl8m5IvPDNGOiA2m+UYFcP3ASTR/Mn0s2TaYTcB9EVOYmt3PdysVpubBVEN8B971xz52/YGSdmYR2dldXQef6xNXLNmwnJmkWdAU1cgQBYbtuD5bz8+389UhheT27KvntoGiAYE3HmUYCohMAVVZgWKEsce+t7at1p12FzJe5XHtCZnqsdNxNEyRTTyqgZJIqa8MQXFyImNElUxEJQROp6Y05xFV1IqUuErB/q0I38skDcimCIZMhCXwFs0pRHbomArLnhyyY+eIKU+LCwhRyjdRMDNGnkKnToxJtNKUHM0EAQgp5UREpmbMxWDy+lqWITVCcq60FkWVirDULilgIkDQLBNDU4tdl9pOiqNwUhHRrNhJ7NvdVk6JmTH7/RK8vm1wal0DAIiWYhJUQVQLD1pF0lj06MpdbQF4apgDEKacMiAwQwg6mz/t1+cpu8Vq2MZAbubD+++9e3r+9Orq8oX7d4+Pj1KKT58+Pb84SzGbQQhhvd4uFouD1VGhMy7n88WsNjMzMSY1EREgQARHXiUzIYI0oSIiR8homtNyNjtYLVazigm9d9vt1hEcHSxjzCoKQDmLSe66ru/a2Wxe1U3lWdJYzZdHh0fr9XYUXSzmMY6AOp/PmuY4xkFVg/OVD3du3d5sNu1mW9f14epARDRHM5MsVahWC2X2L7/wwsX5+fnpk4PDo6bywxgdudPT04PlfBxG5533fr1ez+fz09NTIprP59vt9urqyjlXZuUQsa7rnPNms8FZ472vQlXVQXNS1eVy6RxvN+vtdts0TYqDiOQ0juMocWRm73257kwFFxpCFQzEREjBMxf8+KqNb33+Mx9brdrA3/zyF9ZnT+eU/tKnfuK3/vtfNYmYE9buKuaB+a/+pU99/gufuXzvgcT85Tff+guf+ks//3M/+/W33vyR/9EPAQARqVzHkO+Mxde5v4EhmJqYMVkhd4GgY0YERoTJd8VEVQxSSiKaUkox5b4/Pz+/urzoNltSaNAf1HM/A6omaffnkPTJ6IMmpHOnSeDENURcpOtQYef1KswCKUsZgS2DqSXPm5qKDMDsnDGBQ0BiV4Y9CXDXu0YwRCbeR9NyKopO2jT5IFKoQ0UdutxlE0SsO/YFAk3yDDsNAtgxD3d1/P+g0I+ll1mEIYqdjQgyPBuwp4doFlGRrKKm2bKAZjSrvWdAVJJRt5fd9nzrb4/1TK4VFPab2+5Ab2g/7XTWDEAJRZVNNLbU99z3MHTQbcNmnYd1jhvQ6Ju5Go59b5nJxFkOaCICKaIIOXKODac4JSLFlaWcSjFRVZyYBUXxVAkwSyrs+CLps9uUAAGRmJBKimTIWEilzgMiEDEw+wCIgGwGOM2qiBWSG5qZFDYVGZiIqZGBFudKE0QpddVumyzKQEYYvjNd2i+a/Za5/23hm0EpYwEsT1vd/gX7XGP/RmBGzJLzNG5TegM62ZaVTHP6Q9UJxspiogQgIpqzZjGJRDS0LQCKqSFw8CEEcaEKoYhDiCoQuRAi6FBXT3J6uO0yVRfrIQA3s/r9d9997/RxzPHll19erRZPnjx599131ut1jKOqEbH3ntkPwzAO6ejoqK7rFAfNqao9MxccjxFyTqYiiN674Ch4dkSAtlrM6qZRVQRbX5zGYWSeXDsdU3BuXjfBB+eCAWw37a2jQ1ERNSR0qD4Ek2yiJrJaLpxzFxcjmnrmugqzpgIAhxTHuFwul/MGEYdhALO+H3LVTDqtKUEVRGE5X7x0//5FO24uz+aHtwpOMJvNum5oZk0/pvl8vtlshmEgotPTUwCoqmrb9WWOoVw9IvLe55z6vq/rSlVn8+bs6Tql5AiK4sXm8rzolRbvTBFJQ59SKq7FOHEBwDk3DqNvgmPMksAYJLPi3AFZWj9+38Xu4dvfzH37O7/x6wFj7UklpjTS7LBL8Gd/4idffvnV/uLy8v1Hl236xP1X79x78fjkVj/0681VjNFxgCIXDpOJHt4UuZxwxYmXggYlypugwpSooWQzEbAySikiWXQYx24Yx5i6ftxst5uzq9Ozs8vLc4c489Xt1VGFOK+rMY6lrUpM021SGNq70MmIVsTpiIAmX6YJFaayOyExgKkymANQUFTVrNmAS0uBEBwgmypyKFzMCQsuQilEu54HXKNdN0gWiKigN8VpbDdYI5Zhd0BFMQxgT1mZvHdwh6f/seG+3P57DlX5T0YsQzNFa6FYTJau4j50lzOjNrFaVVVyNBHUTKpgymQB2QEF85Sou2jnV72fJ7cP8UUBFa63Kb25AeAOX4aUMY40DtR1vNm47RbarW422F7FdpNlxBAk0xjHFFPla6daEfqoBKo5w6RLAzjxgg3MIOcJslBTjaXSKi1nFVFVMSh88ZQSMRMTICETI5btvCidKgAgF/9odA5x6goYFl+CclENrFzKEpELN8YUk016J6ZmoFb0jZAmicQCF9mkOI24E0qa5CF2FQDutNtuOMkAADhyWvRbVRlQShIBhrrTSLkh9ml7LpiWifCpMYVl3e9WSQk05cKZGWQFNSwqpilLTJITQh5zAtMkRSGOVVXEXOOJOaWMZoqEnoacUuUuAj0e+sshXw4pm1/Mm3cfvPfu+98WpQ99+MNNXX37W99699131uvLAlMoGrNTVWYtqbGZLebzeR0ATVVD8CH4GAcAqgKzauV9CIEJEBQBHBPIeHW+nTWz4N1y1khwIfimroIPY4pFCmI+XzrniWjoo4GlPK43W+e88yGEGaBjxNVixkwpxeV8TgTBUWCez2eq6sl12FnO8/nczJSzitTea131w6CKTRWCc2PM5Pj+vbubb327azfLw+P/P2l/0mvblqUJQqOac6219z7n3HtfZYWbm5t7uIdHKhEEoQiIyFQKCUEolQIkGtBBtOmABOJf0KFBg39AA2ggsoNohiCjyCjJcHN3c/Pi2SvsvfvuPdUu1ppzjjFojLnW2fe5RYoUWyZ751bn7L3WXKP4xje+T5hrq3kYlxrzc9zv94j49PQ0TVPQfqZpGoYhCK8BfOE6PFPV0+mUJZW6TNN0uVxKK+4mTDnnb7/99uOPXk/T9PjwPudMbiFaZ2Y5JTRnZsksIuoFXRCx1ZZkzMzLPAPir//iz95+TqxLLZfl/PQv//N/xomT8HxaWvW7Nz/5u3/nP3r/1bd//if/9stvvv3v/cf/w3/4D/+T/+f/4z8Fhx//6Ed/+Id/+N133755/ek07Zq17TH3VWoldt8AwAMu9a6Z7gCKCEDujGBlKaANrCFC09pqLUUv5+XxeLp/On738Hj/9PT0eHl6fJrn825MH93d7cdpV9LzfNylm4h39L31sXgWOJZ+CHEVV46nLeKyh9g/GIIzQCiIopo1s9pMwYERyNghATAioBCaOJhbI+SYxAb1oEe4KwAHruoz7VGjr8f5irDjqsKLfce3X5//anX+hwDM1dehgh1mIhrDSAKLSTNekXe8M4i2lNDCIVJrBbVELIhClFCSJyzYjm1+vIx3pa8Bbx5bL7H+qmGhFaB3tVQazjOfL+npxM/P+Hjvx6Odn5fn79w8DzuZXjVHgAV8BqtgxdTKecZSOA4RoJkSuDeNpW2vDfqqk7rV8Pm0OHBmYJFNI5gDyorpCzMyKiIJMAExCQMzcqcV+XonELpGoW+DJguilSEYuKKZI67LI9EexEaVt4jBAdIEL7SbzLzcPGbudcRqmYMrS+361QdHagrgGmfHvDVEWHU8rg7f6m629aEAgETuCr8JRuxL8ObkABrOkwpN1Ze6LMDk5lWdBRkYCedldsvWGiEDoQIoekN4h/rF8/PD8zmnQ+Lhy7/64pv3X7nA7//0D5jk5z//xddffznPF429y76x2NzdDMwsJ7xcLgiuCx/2O0D0pmpNayUCZM4cxC8lACEep+Gw26Wc97v94XBgJnC1OLutmdnhcJdzHobhcLgN9QW9saUsyP7Zpx8/Hy+tgaTRFJtBYhmmPAz59u4gQsw8TWN3gnS4vTmUUpZlGYYhJSmlXC4XrdXVgDDn/P7+fhjSkKe6lN/6wQ+/uX+4nM5DFlt0WRZmXmqNEH84HM7n8+VySSnW2UBVa62B/sczPAwDEXotrdWnpycW+vjN65ubm1bm8/lUloXRb29v7+/vY2PudDpFjxur0cfjcZBEFB2ruS/OiVN2RiAH9MPt9Ph8PD/U169e/97v/uyXv/iTcnqGj+5+9MMfHc8P59NjUfof/4/+pzt51ezx6bvHv/13//6nv/N7/+f/0//F6ikB/60/+APTxkgPDw+cQt9lPbrrPCA4AoChzh7cBbCOvRO4gxsYEzRT16qudWmlzPN8Kcfny7v7h28fnt49PT+ez8czns9tKa2YD9Nyfz5ywjwlKlly4mCGrSc/yI4euAr6VixapJ6+3LM617sFbcPc1BVMHdS8Na3BeEYi1OScKKRNUwYEJAcLwniXv/bvo1BXnRCAQR+ouhmvjA+EIGsEraOnAe8E2g8t0/5/e71kvi24r7i/q5k1sLaNDDu07N6DTqfIN/MWsyVtDd2FaSDKwmMexjRlHsUTNLg8XYbns6BZICiIxKv+JSIEjXr9GsDVVaE2OZ/xdJHTszw9pecneHyC58d2Oc16SuMNDjvH3EpNkqZR2BZUtVLa5TwYMBKgNXdtzd28NVMjd1cjMw8Z7xUa6u3mWms7owHkNFiMvZlJQsxPiHrQBxGLni+aNoQo/Le9anAwdXejoI6aAkbWsdaLf+vlTwf03LvO7ZoO+3UiFiEMlzQCiPxEsGmvrYtlAH1rQlt1Xw+qu5lyTzk1MCtaB7zrWUA3dXAkNNUu2e1kTiQhY9sHSjE5iLQK5ghYltmbWlNTbWVRrdoQWFISFHGE2tQAlLoeg7kvc9UxH7X+6unyy1//WvONFv3iq7+Yy9kJf+unPx3y9Mtf/OK7t99dTpeqtQcmWH3WVki0tXqZTYTGNKlqqTaMkiQTemiI3WROwuM4jkMeh7zb7YbE+8OBiLUpEZhhzklkykmYGYVzHkUk5TGl5OpIdLlcjufnlNJnn96Uaq1CqQaOc20pUcqDu4twSun29mYYBtVm1RIzAJRSaq2+Ut2T8HAZVHUuZb/fPz4+p5Qk0eFmXwHuny807kPsWN1zzgAQ3NPXr19/8803YWCQcw7rmw2UC6ROm52PxzdvXj89PC5F34PfHA6IeNgfnrRpXZh5t9udTqebw05VL8d6FQb7pljAzUzc1JDNALRVxGZqKfHE0pZzYnjz6u6rX3/59Hj/+Hjz+tWbpdZ/+D/4n/3+7/3Nf/1P/vlXf/5HX/7qi/dLlVef6Dy//+brf+9v/fTj168fHx4++eTTX3/7fjrP05RhZURs0CUzb77TUSF59/cLy8aYCSABu6M11Wq1LMulnp8vp+fT+bScj5fzZa7FLwUUk/NQTJ9Ol/2YLyU/XU6Sci65W06tUo8hBYR9YAimGqK2bAZQDZWDvxBrZ2ZufTVWtbm21kotc6nFzRI4EYGqizIiR1AIBItiuQu8y8hHtXi9D/FCy19VsR3cW1PsaE9ntXgIqV1NMjYtme+9/l2dga0RvReqG6fIwV27/0Gg9MEh9N6edCB69WQMOhygIoJZYyKWJIaD5DENYx5Tykkyc7Kq5XiRcZlBpoqIEkNxMwIn4L6JwQ5EZlxaLu6XhZ+f8HzE50d4eOfHZ3x+tPO5nE7ldpdv36il4/PRmibyBM6GdC71PEuM6wVRHVXJzKGYqTUttRBgkGnMNNhG2u17EGP7lhAlbwkJCdMwNG0mWaabTrsCBwDuCjoWK4pu6u7aNBqkmKL46h2EuNqtkLMWR2/WEIiA27aeAhCpJi4xEjJjNByO5MEhIwJGI3J3cYkM3fVR3BFiJ76FVLlq4xiVmSIiuhES9VXAq+UvkBTLXGqAGPsyVqukhIYO1UORQrKCAwGaOhoxtFIMVa2aN63VldCSgeUh8zSelpkQ3WCqDOzKNjChAQ3jdwO/JfvTb84XnCzJL//yl/fHZ+b0+3/jd0fJf/bnf/Ld/Xf3T++aNiQ0UCAAIEJB6oS4ZjWl2OBbHBmFkyRGF7Kb3X4QSUle7YfDficiRJhEdrtdmPEyAI3ZHUhkyEMaht1ul4eJQ7scQ3o9IEEfpsP+8Pp0Oo/jyCz39/c5OTMdzJxh2u1rbcM4UhIHwpTHaU+UY/d0fCXebLlcOF9yLd6OIsdl7pYG33333XwGRkKmw35X1S51mSQd5+qqpoCIjH4+Pn300Uf7aXh+fk68r2WeDjdEdDwef/KTnxyfz+Ng87zsdofz8/vT6Xh7t7+czk/376HVw35iosN+d3yq5/N5yOLuj4+P4VV5Ol1U3dUSJWAAcwhWGyq4VwNiNg1yuGMiNl3K5Y9/+XMiPlv10zG/u9/vb37ns987f/XVv/j6//p0PH53//nD47t/8N/5j2718tXbP6uPb9/+VbHL31lOl3Kr4/5wWpY8SEyYtrXtCEYUYCRAh1JjxAkOTOaNGM2LuymKS9aqZtCaquNiqJxhOHjxZTljNlJGZzTXhvOpLrwUycvQUiqSMicRdHBDcyTQFn66AijoyCzoANVIwi87dKJ7xDRVLAaleFlMq7aCruyqqo5k6Gjq6lrMfREf3LLzXkmQCZkM1NeQTV3uCGClBXWmjRlB+IxZDA67fJD3XS7HrlAZ/1IxatGIYhbrrIiI+oGC0AvqRbYuffUasRMmVSHimDmFqBCYu6cITwQQLo8YXleOSO6q1swKaGFTNrjh6YZf7fJtHvYyjTQNxCIufkZBde98+ODkM1LgCIQkAAwGphVqhfkClzNfTn58gqcHeHzU44PPl3KZIcnu1UeYxvl5iRZO68LQlsszPh+hqYRgUEWzBmrg2rREpYTubmpEBEgrWz9AnnhFyDfKRExMQKjgnDKlTJxitAvobsDYXV3M3aypqTWN3deeTsHdm195aV69Vl0qtBo8neBBOYGDOTJzd0SIYUkIWsV4hwk4Al9Efl+LAlRvEN2HW1D6OM54X/sCpnWQ+z3qxVVF4KsUB3N4dq4zA2ZHbK1580zoHthJq60G/atpdUd1G3eTDMNSqhAzSTTT1ioTLcuClGaWd6R/9vz+u+eiKf/xL/70/nSkJJ9+8hEZ/Mm//fnD89PlcpnLLCzb6Gnt1Bz6aNAqFRECF7I2JT7sp/1uGofhMO2mcZjG/Or2MI5DD/rM4ziKSBJh5JySSJKc8zgxcx6mcRztumxyaEFvcG+ljdMeAJg5xMtqrYg47neSk5lJyjJkU2jmRDLtdojkakTkaklEUmq1LmdDIOKLnU4ppU8++uj5dCKm5AiJxpyXOjMTo4vg8XgOZQhVPZ/POeeXkl/1cDiUUt6/f7/f71tLy1KWZQl3YkK6vb11refzOQu52e6wTyktyxJ+9OfLAgCZKaVkcXbBBbsaf2uNEsWwNOTttrPBiAD+/PwAJAh+Op/fv7s3g8Pd9Ktf/WUa0+df/urpeOQEP/3Jjz/55JNf/Of/SNv81Vef/9s/+v/81//2335//+6jH/zw/vGplDSNY6cb/DvGldhxf4OQbwT0zv1nIHQkQ3Jgtei+SQ0VCClxGgSqQ00pYYNaWpmXZZBaxlqWWlItS05CwBiFlq2R1xQsxmzdtRhUvfPiYzmn+wJDq7XV1opqUzAgIAkrMEbCUPNXjDvVGqL5QqQEgkBg6NRj9Sofg4hbkQ3uDiF7bR0keCnG7eXJxZUAYrBu+qxg2obl8tW1DQLidn76t9LORTQzClDaLKRu+lfxT0I7CKhXqfgCOPccYUaOQjwkmmTajze78Wac9sNut7s5wDg6iRuI1wI6uAIKEUpY8Bq5IQFJXFlujcqC88mOT/B0jw/39PCAj496elaryi6HndNwmXVeGhkkBHJjq22ZWau7kRGYNg1RmhYfo4d2SgZGq7uAIRBzuPDgypxFJOccNABkEkDkwKvIDRBjN11dN2KwNjNV99bMjBDdg5/r7uWl27s63AaxrY3rUJdDLAgMey4Q6Va/wR0OIc8VNKMQiCJ4OTWmBg7apwqtFiJSgForBcPKzczw3yEt61dLKIEnbGfIqRsnmBmhh0yH1+qmYADugqTM6OAp1aaSB2Key7KURVKKB7mYUaPEQk6V6ZnoL48P//abr0/57he//Kv783Map3HajZK//KvP7799a4mXZRnyEJD3RlQwb4hI6OaehRgtsxym/IOPX/3sd37nzetXSZKrjeM4jeNutxuHDABEFDrJKSVmTinvx12SjESckqQBiUWERerqGQvgIhKarwjQ5uXmBsxsWRYzTymdz+fT+bTb7x08SeYknAYAaqYiyQFFJMhzgMSIRFRKGZI9EzbT0Mff7XYPDw/Pp9NymgVwNw1m+Hi6ZGFbdDeOy7LknBPL8el5t9vtxunp6UlYSlpOp+fdbvf09EREACTC7kqUmHmZz4z06tWr58enUoqb++lEROM4zhe9XC7hMTC3Oo47ZvYUfgyhv+ZmNl9mSSkG/pHqtmQwDgkAlmVxACJ+fLofhvQoWVsrbXn/9MAplXL+N//mn//dv/P3LsvZtbam/9n/+x/9zb/1B8P8/PgwTLvDPM9yxUD9jWfyKg10UhADAYubGYqhGokBNnA1sKCjAyEnZmP15sokBqpmc22XZTnP83i5pCTDkFsriIklhNF8hQQMVAGj7yIAR1tNYL3vzpqqqro1A4UwsuWEkBA9hDEx+KmIHGPkVSiCKH67u2uYASCt5pYA1+V5rx37z0LzmE1+b9h7VcN1lipFTLF1hIgfdPlXz7h38qgFTG1hsqhm3loXsHBvrQVQDqvFE2CvQbv6hPd1WWiKTVEtU5qy7NJ+v7uZdodht0/TDpNAEkyCiYXnMwxJUwKxEJqM4SeSICA0tXnmy0znZ3x6wMdHf/ctPjzA8zMdT1BLYx9uDr6bnIbLfDaDejmb1QlanZ/8coKq5EbMbg0BAFrs2hk4EQtKr6bNAZGZDQyYEYCYqUd/RCRMk18dzbgIrWqiaJvUzFwbgG8jcPe+E9s8tg4C0Csbz+tK2A5QyClADSFODgDdPwhYGJmj8I5CN1S1cV2Ri9y9qbEBIlj84LruEMSxNlBjItXKSB6WFaDb97HrwwFXmODVPCpGZLjd/r7KApRyK6VZrbW2pYTIhDZVcm/1uJzGlNEUFd2NmdM4kJOWStNhkfxX8+nfvnv7HvGXX33xfDkP44gih2l6en//9utfo0MtFVZ+iK7qqnE/Qr4o2vspDW9e3/7kxz/42Y8//dEPPr493IikIQ8iKaU0TZOkzMxEnHOOViC+TjymlIlYUgIkSRmJmloQvqh78XW7G0KchnGZLymlXAYDJ6K7IUtOwzCa2W6345Q9AgdJrdUAcs7oQZANOVIxs6KUx2mPhIillPPxeNhPpcxTTpelZKQsdDMNp7lmwVZbSty0TrsRLl7qst/vlzI/Pz9Ortra69eSJZ2Pz+O4YyIjAkMz3+123337dhpSSul8fJrGSU2tVSJ69erV8Xh8fHgfF/bx+JxSYsRqjQCBefUHwdaamcWIOKbNtpbAu2mIDbLLUsHx3bt38+lEBOoKBPNlTpJ+9au/+vTjjxw1TYmcz5fjv/43/+K/+9//j4VwPp8YqaQEAGES/l8e+uNXDuBE4GTESqwk/X/AzdVQgBKQAihCTSwNKwqrqRmb2VLbspT5fB5ESpaaWIiQUre34zX+hgmfu3cBHF6F72NIbBjzPCJKgkkIhyQJVsSeUWIqFwoTgNgLCuKNRklhbmjmpkASGjDbh137Xe3vYYv+7gwvEWkr89fw1Dnm38+a1q4TxlWO0bihGFYM5tC3RPvPNTNVjaQXERGJkImYLN5hrN9F9DbHBiPmJLyX8Sbf7KababoZpn3a7XiafBw8ZRQWfff1kMGyuCQgISZgBjQHrEuBeeHzhY+P/PCeH+798T09vKvv39O8uCoxSU6821+QLk/P4mRaEoOAwnz2+QRlIaCEBK4WeCKRE4BZokASyAyQyYmYmEW8P/C4Ib9I5B5O7JtASRdlIHBt1Uy9NTPtaJJ12r6Zujkjhg6ad/CkQyhbTY24tWqMwiI9cISROTpS8CwxKnygTvp8sY1moxcCgal1tpabGyGaqZYGAK5qTR2UAMwN3WLhIMquiK0fngn3dQVme6tbFnRzcK3NWdjda6uu6k3JQYgVmrura219Y9ndGcnVtCokbwS3440TnAC+qPMvzg+/Nvvzd+/fPh5THt09E5+ent99+24+X9x9Qbe1Eolk1ruTdQiYhW52493N7pNXNz/54We/99PfenV3t9vtJA/TuM95HIZBJKc89uSFuNvtEcHMhBNzysMkLOqAxCGTmwQJIaB3FolgZ2Yx40kygENO4zS2eFcIfF7Ot7e3wzA5EAq7rzXEVcRExKUUMxuGAVGBaJqmLPL+/TsH243jOUnLHuypTOCJaoHzeQZtyOjaqrYsfLlcrNXEZOrWGpqRgxDMpYE1QeYsrbVSlrApvlwut4ebulzm+QKMQhjj32EYbm5unp+fWWSZF3cP5mspJYiYLCzurbXW2rZp3A9Ja4TYWhNG5tHdL0s1rXOBw82ekY7nIwAR+MO777764lcG3lT301iW+V/9y3/1wx/99r//3/g7nEYZc3jhfrCO/iEp6DpyhYa3mwGyghmJklcoRskpVatNUQ3NiJBTGr3pINnMkJNxq+1Sar2UZV9zqfM8pwADw3MbkdzqOgd1vrJoN0cKJz90IkILlxeJfmNDj1cEH30dDzr0dVzv2Wv9UA4c59nMDBTIV4QpHrp+5GAVUnQP70KH65L/JVVslyuccwL9D0ALIAYYfv39I7ozRvQ3X39KwDiwcgquq8P+ExEAHKNEIEBDB1BXMAfV5IgoiWSH02HYj2mX8m7Y38i052nSnGEUZxJ5+DXvWbKoJKSEoVQMrsuM8wLnC5+f0/ExPb6H776p79/q/T3XCujGLtOYd/tz8/OyoKqZclsEDMsZyplbTUjsXTgb471SDGMNAZA4fFWIEyAhiRMTr4oLcTVDkS2+BAMEDBc5M2+6bug1a6rW0B3dYlu4tsZE4K5hDd95ZQCJO8GNOoEnAroxIqE7AzOzrEm2G8dtm9xdfo9Wr91rwLTDNe6g6N41/cPWLpYJY5NA3cDWE41+RX++fsZsdUazK29IDFUT6HQMcAhWk5u3ZTa1UBGI6JxSyjmXVmKXwmMnHkJOC+Zaj37mafeU8fNy+fNy+fP7hy+/e0RmQmQidLi/fzifzqVVAHCh60ci3r6ZJRZAE/RxSNMgn7y5/e0f/+D3fvqT29v9bpqmacrjfhz3u/1hmnbMAiDb7sKW/BBRJDGn+EDBs7U+UVPuyF9c+HAi4ZzkYud4J5QkbikwPR6ficTMJKVYEG9qzGLQVw7XHyfMbKbAwikLYR7qkNKYB9f68Uev/e39fCZrZcppfjoOOQ3C6LAQlerzPE/TlHOOL07ns+T28PCQUhrHSYQC2Q8jyXEcVWtKaT4fn56ehpyPz89V22E/AcDT09M4jjnnw+FwOR9TzqqqZs2NmQ3R1WqtgY24+yYWFHkdVQHRVY1IhHa7XWtPSGIO81IQQdXcnE3LXP6Df/Af/uN/8o/ef/ctEwmm+VL+6T/5Z7vD6x/++LfHcYyGeJ7nWHTwlcv0vbjTA/HaRzuiIiqykikn4+ScnYuhOipSQ8qEkFNCIPOGEFTFpbR2mZdZaBDKwmWcEotyRjGiyHAfZKD+NXdhnzgM7oDg3O0Cw+k3VIk4xNc2y0lYy7zIARqkTe82BmRmwe1pBqut8Qef2pwcNLZHvX+/33hl+vN71b5/ELXX0g5Wja9e+Pe1WIvI5u5w1eFtiOsmSOMEzNyNdqM23lAgNzQXxyzjkOlGDvvxZpoO03jIw56HEXLGLJgTJhZ49ys8MO92PuydRiVxxOaVl4KXC1xOfHzipwf/7hv79a/s/p1UJ2EVspRtTJRym5WU9fQEpgjNrPh8prJI0wSEnMzD60asswYB3DgREQOxOhInRAFicMLe0PQPA4gr2NyiDwRzrQ29J/eqfe3NzAjC9sTc3bSFd3PIzIHHCi62fqkISfruCRKLsAAiGzjHCjFSz9wrpxMAkKmDL7hywBDIfe3uHM3RO+6PYGbqTVsr4K7Ne+XSMZN+Ml+wnSvRN1VFJFvFxbbyPypnoJd8gACobqqgXcTC7GWZSFVTEiYKtD3qx9aausOQmqkyfqPLn12efvF0/9XjY61+Mw6CRA7n5+Pp6Xlp1RAA4boG2XIV9s1kH8b86vbwo88++t3f/vHf+N3fvjlMh93hcHd7e/tqt7slyXncSRrAAfTFalQEc87Y+eYQRAQGMgBkQkRwlJ6gsSthrQZErZlqXD8yg9vbG3d/fn4OxToiSWmoptA3fZBjcBpGp4CMqKpmLpKIEF1Tzoebg7ZyfLoXpHEcDrtpWQq5jUM+X5b9mOf5mRCz0OI6n48ppVrKkPiwGw1pN6XT8UiI07gjKI+Pz69eUUp5ni9MWEoZxxHMa112u9233711a+M4xvRiGrOI5JSBvZZSa71cLtM0CYliVzdARGYmot4WMOecvAY3pd+hcRzbbueAc7PzZQHXnAWFW/W6tP/7/+0//env/vjz41/eHQ6JU6v+1Zff/vqrb3/045+GU3zcl1KKXPVba71E2wFARCQAAwUwR0NyZCcHEkcCEkdRW9yRMDERkjElZzADZ6OUHIa2PC+lzIsPC6dLGoYzc2JO4AgJAQygF/vbAwKITuxBx4i/ESrOgEyh6B9pgLvGPwJAvaZXx5NjABta0oFhUEN00JCk2RrcD2K3O64y1wjw/T/+8LV6VX24V9bdaF/q+pcE4B4jBuy7Sg5m5N6834X+lrBffwoR0zAVAQy/QAPwsKo1F6eEOEma8jTmaRz2KY+UMiRxjmvIQCTt/ut0d7DDGx9eAe8Vk6ov7TIsBc5nPD3508P86y/96y/4/Xe5LAzJjLoCgMhymevsqEBaCEzIl+UCdUkAWYQdSUSt6zGbdwQPATghshAxAzkwcool1evrah70TXAz9wqhBBcLw9pH4tb5v+rarCvodIJwPDNCFFPakH9VFCAiYWIhQjNHZknJovPwYN1JMDkdgSD2I8gRmlvHH301hIu4H6XKmqkA3F3jd0KYI5pCVSXEcBzuM2B3Yrk+amugc2ZaStnWs7cH4OqXTg7eTAG0tSj8a63BAorPTsxtWZzQtbm2NA6ArkDEouaa8FnLr+bjXzy+//Lh/dOl7KaDt6YGCnA+nUsp2o0+Ok95q3GCmMREJDQKv359+6MffPzv/cHPfu93frKb0mG3G/f7m5tX+8PdMEwkGTkTSxhy47pWQdSFHUWSkfe+mUiAkAmBHZzWrtnMrmoujE+nqqXWmK9F4Xx39xqRo8CnJKXUIQ2IhAQS40ozrS2k/CUlcEVDKwYAQx6maWrL5XI+78ZMeHs6net5SUQ5Jwe92Y9fv38c9/vbm8P9w0O8i8en57u7u6U2M0P0yLK73c4MLpf55m4fdVtKiVEY8fRcgXkax1qXVmstKiKn04mZTasBEhMbV9X5chlSjvIlrGN8hQTjdgP4KGJmAOFs2HcRLvPizlHathYCKo6In3/+q/3N8Pr1R8/H8/DqTSkXFvuLP/+LTz79gXq7ub3d8nFcXlSNCBV1wwsUg4gAhm6ABuYAhuTETixpTLlJWlCSY4PIt8AiCQDcGcHVq7uUQg6+lDLPM1NKaUhpSJwodmrSNoqNsN2xT++D3M2fJE5Rp2YjkSMjMyB7OMBckfOD4wEAiMArv87NGMmgmTdAglb9r0XtPvOO6G8fiq9dva5Rmi4m/2EWQYBQ+fI+Uu4uYGZRL1oMftFD1WEVlrb+PmGFraL9IaJVyRFhFTONDwXmhJiIRhymPI5pzGlMaeAkJAmyQBZKjCJCT9/R21e8+4z3tXIt5QLQki5UL/z8sLv/Dr74nN69Xd6986aOWbE2xzy8sbQzzbZcbD6jNQPLhK4mRgwpoYeZDyAIMyA6IRN6PPNEaoDhwkCE5q6O0NDdrQSmAeZkbm4Q+BvM5hqL2qaKRE2bqSYzNCczMyOmNQQDuBMyIgZPl0iAGBCTpIBQiRAl+pAoKDq+j4hRiBORuVPKMThy96Bsrneb1gygQORW1ztk7org3lRrczMyAnd1ZBJmQEJ3VGtRyBtorBW7OwEGYUAQwGBIWZuSsLsTc0ioErJDP4Fm/QHsl89U3aqu6/u9CQVCSTy42nxeMAvmYdGWCMrN8HUafvH+3RffHOenlpiLF1bgnGqtgZJLR5qgkbuTqgoRx0DGIVECqeMkH92Nv/uTT3/yw4/3WcaUb2/u7u4+GoZdloEpJx5JRHggJmSBldkCzMQU5T8AMAUu5AAgLJFwALlP7RhAw0gzYA0lRAPQ1qZxFOb5ckGA/X5/Pp/HcVzK4oQibGAYwjHmkXA0isdI/C02REgkCeCSl3HYPz0+JUYc0+EwnC4nBk9kxcoocGBrl2dkvr09vH887g+3y/HclIZxen5+NjOmQsjuOI37Za5tUUFuS7ndH47Pj1XrNI3v3n23G6eLGwFe5oVGDBsAES5LNVUiGiS1kAJFEiTVLgkVChzBGqq1+draKribeq1JRBOhQk7D+XRyBfcYJGhry/PT/ccff/xwf7mUOY9D1fLu7ddffP5nP/3ZT+pSYsywv72ppuCWRBhpEwjCTd4KX1K4u5sH0E0s2Vq1lDUNTRaVpBWATNIIAe+2mZxUwcDyMFpbipaZ05hqmc/zURK4oGWBqibE2loGRCDw5s6KjiiI3aUEOL1IuyM59dTlAJGSAKLUXxtvx9UzBgTNQ2gfELRXM+quhA6b8IUBuIOCGzv2CW3U7CvCswFkG1QbZSBTpxrCFbkDAdx0S0jbEpl38YEuh+NqXVLUPXaQwY3cHByB0FqSbERGTGlQIm1uoAiO2qCql4pq2WlAGoBEYUQexZjVoVWosbZqDglQFIZafWiwPBxVp8YngEZW9fwEj/fz26/911/j+3fcGiM2sIqVxmEax5P6UmYwFUIzSwTeSisqED4znaLCJMGrNQRO4mEOB8jrvkXIC4J5p8sHzym43rVBb8fMoYTuP0DoxENw/dcFPXd3bX3ER0Rqa71M3H3duDvLMbOBM0cDFR4xyCzbKfdVC+V7jd41xrepongodHdjL3Nrqkoeb3IdyiMySWyPR1wWSQDetK7ITi81Ysdv5Tm8/Nz1r6zYS0w1KHwDOuwT/BBZ1erjmkhKRqQhKY3YWiNKNzc3CH4k/tXjw5+9e/vucikRjhGIqNY6z/OyLP2nO3hnSuB66I1IyIEJOfGb13e//Vs/+vij17tx2O93r+7e7G8OQx67/xenJAmZhZmYfVWZvb6kZhaOSC8tUCgdIXVV1PUvM1FUo0QU4Mk4jsGfcfcg0W+ohYKLSNwYcgoq2EZjNbNlWdKQwiFBAQFARIZxHIZB6wwAN4f9/cNz0+KqQ5ZyXG72u6fT+bLMmMecUyllmqbz6XSbDjHIDWW3ZVlEJGUuS8lZ5npCsFIKWEtpiiE2E+Wca13mec6DmJmqJ5Ea4DvAkIfWGoKnlBAheosNM8SVFxRUWkaMG3c4HIZhaOdiV2QtIgLw1ur79+9fvXrFIksp4zAS0Xw5H5+eHp+ePvroo8vpnMch0KoogLSvPkVh1NFIQjK/rnY3VVoAZGJmSZIzSSM2ZkoI2lqQw4E5DUMLwz7EstQLXURERIaUc055ERGORcuo9piD6rjOc9e5nYT4CgsSOa4GL71Bhw043d5mFMrxVX+4ViHel9OISEEZelm2dQfrWpwfUnfWn/UypXj54gpE2r5AALArf/IXZB96KNk2lrrUj3XZa9+WExCAPTQIeLWpDClsiECgoEoGDJCQEnIOEgs4enNrboqm7hwTfEm3P8yHTy9nNTlbfV+toc1siz8/wvOTffdrfPc2zWdCMgcj8ru9DePF22nW1jQhshu5JdDWCpsLUSJGRGICIiIJJwPEmPp68PERYlvBHVxbx3bczKH21iwuR9+JUESD0IIGQHetjZjQva23ELFvx8RSG6ITMTMjCSAgJ2ICYE6JmAmcmGGD1LFzRWCNQF3Az7s3PfzG16qPFBElLM5D5Nmtz3PiSXYAZAqj08h6JAQAQmgesQ8gfA/MHIB79fLXEoCvJhXxdYzBHdBhGIaAgHLOL0cfscZCNBEQjMMITM1MzRrxd/PyZ+/ffnE6PoJqZnTwqjzkZVnmWurVSXUA8O3yhkYvMIAITYN89Or29mYfWmivX7++e/XazCL6Mwe3S5CZiZFIfxOlxK/sDTYqlFkX+v7eVY8SePuMItLX3wFCjm2/34eIgjAFJSCl5C/suyvyn5muuEpOqZmKyDAM+5vDd29PYVJ/c7M/z5cszCnN87k2YEYsRuDjkJ6eTjKJazsdj69fvz7s9t98882QMg1oTXfj9P79+5xlt9uFO9BSSkpyc3NT57osENtwy7IsiwZ3RYSjG4jrIiJoXmt19hgAhOBoZLuY6wRkHwcgfhmSFf2fr5V7ay0sMG9vb8dx1FrnNO/3ezN7enr61V/+1ccff9xaG2BYZc5iYf2F1vISy+iDJwJfXgRMxCkNwzjWeW61mLuiCjk7iHV5XQ58wBCcsLV2Pp+HFGY/IiKUJEkWpHCKXoODQ+gEbzkgCNaAoVMNgF3eZ60lAWBVCYiRwctZMldYaZe2TVzVaEU7eyAGwC5TBtvMADupxwHATeFqYP6SHjre774C99ChrBeU22zd/nWA2HwL/k//zg4AnZwE4F22CJEIRVAEmYEpmhoAV22tFa0LVGPT7JgcMlJCouDBeuieNW8J1MIEV8aPf1pxaI3r4xnP1ZYTlmdqMx6f6XL2x+/w9IStVYAGLIeDT3uXfJoXB3Jr5k7e2I2sZndiSCRMhCTIFIaLsF6vGiVJfC4tL0E/lDzUzBRQtwQA6x+BO0H/G3EUrVTOCdVtHYtvESQCH3MiZmZGTg5AkQCQiBIxOQBJKED1qcp1aHiJTOvpvv6NHqeAAPphIQANXVxwa2raAEDXOGWIiOCgV9QjdwAkFJZS5+jhnRAdNA4p4ZUlMFyXzKHeQ/0ompuqWW2VWBAxiINR3ooIEoIwuCMLAwCTmZ0vZ2hp2d18XcrnT8/vrN63mjmzGTZzsVJK9BAvVwNB+z4OMiO6IxoRMvur291Hr1/tx+HN69s3b968evUq5Qwk4zhKziklJKErOVzi3gFcF2jb78BarsZcB8HlwwSwTrZ74AsDlkh7oaTv3nFwWoVaTa2UwtB9FK5Vb1trBG7uzcwCbQOgJNN+79/CMpdIY7txej6dlnNJCJnxME1Lq9XUVbNQqFtp86i+zex0Puacl+Wy2+2GYTgej7eHfWtlt9uhv7Qv22SPmWtbYj3iavKvke8DDkbuSEJ8xvgmtDp2RO6PP5rn2QHGcbzMc3z/aZriusWuQCnlk08+eX58jFTKzI9Pj2/fvv36q69++tOfttpSzt60uYsIrVi2rSsI8QzCh6+t4HAilMSpSU55GJa5tNaIAIQcCEM9k9GZKDF7qoq1FVs0z0LUtRyRIONEiMiCq4JC8J06NLh6X4P1BZzYXuqxc0sA26yuh9+eAxzITIMtcx39+zQxAPdgPHsvtq4LsuvS3lUJsIsLrMLBfdO0ixR1g+74F3DVOXVTP18L/Kvh81W3oSFEAAjNjIlYmIZsgs4hboQQa6+ttrp4VdQmCtlBmiV2dkBVBkNXVENV1eYmBk4AosNHzbBWL5czaMXlWZYnvTzL+aTzGZZnalXdMQ9KlMYRZHy+zOCIbkKe3EjdTa22LCyOWRIioiRDUNOwTYyLE+nMzRDA2wJua6Dvm9AAbgFle1+87hclhgHrRaytIYA17SsC3YiOtkzALE6CRMgcFi1AiChR7BsBUicbIREJIdE1VSAsauN76bU371Ur130iY3wP3b8C1EA10jgDNreIOICohEAYBqhEHJWJAUgeoop3rSGt0NzVTZDsSgpUmAO7oPV3okNayxaf55mZh2EAgKj1zIyT1JisqrHDsixmJjk1olMevnx698XT8/2yLOpZqJR5EDnN57kswZO6PvQGCG7CYqZDFgBnopRoSJQEX9/dvHn1+uawi5JzGEdcAeI+VnEHgJh/b1EerpubD6NJVOUrrPCSiGspIuKre1qE0fP5HJVjjEkjDpoZsXQgrqs2vvCXIr2llLxWIsaU1K22hYiW0khkt9u9e//+5uZmSHxzs1etp/NlTFLVmimDL3WWNBDl5bJkxmpal4uNeT8Oy/lyScfD4QbMmDneQwT61poIPz09DjLEGw6+f2Qjd01p/ezkdSkigt1b0ftkm6jWul2luOAbohV/Yb5chkkiTQZnNDqA4K1+8803d3d38zzHQlx6/eZ0PP3JH//xp5988od/+Idv376NNIbuai7DsGUpW7coohqOO0JEhhb1LxEBCwjIMA47m4qVZWmtadUkqbkisAEiMOWk0GoDZKpFVfV8uTDzsAzzsPAiJ0HooAABAABJREFUzphDkYM9foxj7d6QYUfVQJIEGxABrC3b3NU7bd99a68j7vcQQhAK0muUjYeoUzBfnixFt2bm2twMjIJl59sOvBm4i3vMGSjweu8WMXoNFl3FfLwqIq/jiZluTYa9vDU3r8hh+o3E4kwoOYov7DrwaKFyZc1ahVahNmyVq4+QB6CMkBBMFzYhE9OEatbUsyOxtHxTljLXi84LzSeZH/z82J7f+/lEVhmqkVViQx/ubuFwMxdzRdNGplk4DLkAIKVBiNmBiMC8lVkRkNBCdkbVVEPeORadzZaIZC8z7sjFXXm6L0l1cyt3vabJY4fIMajQK6/8JQEIO2XYKm5KQAgxY1ypAxAgFXZVCdf2G4GeLfR/rw8IbDD8UV0NeuGgZKtCCK4wfTwzBEBgCEToxNA9xxxMAQLKBNcYGQMAmLZobsA7WGHrElZvXWP80EsYI8SI79fXgRAHllYquHNK2hQI53luw/DlMv/rz7/47ul0KnU8vHJ1QHKm+TIvrcZMYwvEzDxiNjOiGEopETj4ze3rj1+/+vFnn3726ceH3RSkfuZEJLKyU4jdzEJwWFWRO7EPPuy3rr/2dQYDYbK9tsO0AqFbSIIV0/er6ilAoZSSITDz/+R//jv/m//Vd//g7y529RIRItLWOlrsAMxqNEyjo82z728O7+/vAeBwOLTW8O4GXe/vHzPxrNW1mqpIIkAhLLUOOZ+en6ZhPOyn+XJ5fnwa88A3N0zs7qfTKWcxraoaMkgh5+DusQ6N5LXWWotZB7JEJOx6mGmaprnNtrLCETFomrH2QavxQFzDiPLzPO8Ph7AnQ8RlWeI+MvPlcrm/v7+7uVkuc2vteDzudjuS+vXXXx8fnyKuEWKSdJ4vkVG26L/eoA/u2nWniCzISMlFsiROKeUkixk5ECEYEpK7UTjAiLjxsmCt9XQ+piynOXEWZgKmTEIGmAGpi6tja8IWUEnM/5EIDSCe3ytG9RajnQH8JQcAIIA6gEWBBf0h8r6rY1uIxwB3+96vWadZx0jWI9B3Dsj6Q2E9iNEGfHCl1j/+oLW/pv+tlcrWbHgw/Qg8RlaElBglYUouiZMgiQOt2U5Vq7m6NlLNCtl8cEgObE4GaBre7NRUtYHnGKnJsdlS2lIr14placdTfbpvj/d3aEwKBNXN05DubuX1m5OiFk+YAYERM7iBgRswIqQQ23IHazXYAdo0Mps1dVUiCo1iMAdo65VybW2bxii0LpcRmID1TGvYt/soEK3gLDM7vSwW0eZdzAyc130QxNAvCw0hNMfu0WNxZKPDvip4435u04G/1pS5u9PKvA4+Zz965rTJjq56UBiWZQx9SwVlZSh3U+KAfwDR8AUBX8WpEJlU1baVYGu9QnFH33iwDsAbFBAetu4+X+bBx4EYEbwauONqpfCL9+/+6t37pVmGfCe74+no6MZYal2VHjAi7Ppzt/lFfGEpyX4/ffT61X43DlmGIU9DV2yNpykPo0gilrA2NLU8DPbXQv9vfEVQcwDvxkTBRNSVptV18zf0f3ufW/5rraEwAPxn/3T///rHp//g75Utl29wrZkxQGtqbkQkIsxkaI726tXrd9+9K8HEddjvpseHewC9XGZ3G3O61FqX2YDB0F7akUZEt7e3p9PpcrmUsiBwznm5nIchRVhXVRGZlznefyklpSQQb94ROW6iQR9v9M5vLQIiFsc5jxp/i8LbF8xsCk9PT2/evDGz8C1YliX+KBTrbvb7gNFaygBQS/nu27f39/cppdPpdHt3Z2YEGBMFWoer/QGJ6enVj+0nA4KcY7FIn4ZhGOa6pFYrGjKCEzp2czsAMiGvSMLYWmltnmchjmaOWWYgchCiRsRMTohNgVpwIMiog4jkcUDW6t+2EsE9cs0a/X3NAQg1OOPeH9jVRys8YgMOUu9yMs3N3RDMt4ZyLTgMrW0JwK9eeLUr82EKeAn625Q+3l8Yj8Sgevsu4PHwMwAG+CM5kyRkAmB3VzdVrbWUurRSvCmpsVt2zI4ZgN3JDd1dKzTG1ryJm2Ng0NVgqVqWRZa5HB/h+YHPJ7YKbpgJmD0RHw64253UTotJkyERkQgTWiEDAyMkNzSHwEBQW11mcyWGWmsX91BTd2sa4T4+ZKD8MYiLWOkcFxsciYkMrPsRIIakjiNGdAvX4lBti0o/AhYzIzGlZMiI0E0iI3EQmSNhDFMw1urC/n2DGv76a6sscMvMwQvwEG5V7pwg75OcDxHDNSJB96DrByKoBqHuC101zizkyHvRgRD1PiEFX8jMQmK6dwMA2McQoH1A0gnjYZ2Wc4baKCViia2GRZsnObn/0VdfPtRWAQfO9bKgGiZ6Oh23PoMIo1IGgLJUdwMwEUJXYmTC16/vPnp99+ru5u725rDfT+PQVEmVM7CwiIC7qoaJJ6ccAn3dqfU3jYK/d8U8KCjgGBvdGooDEn8U9zrCX6AcgWgPKVXVnLO6zeeZYhkw1GLXM5ZTsnUCYe5Nm5tiYiJuDkScUsZhvLu7e/fuXRJJWebLZT9MZ3leslnxlGQc8ulSVY05ZebT6TQMQ601pTyOeVmWy3ya55vD3Wvkw+n56XK5fPTm1TRNT0+PzEBE5/OJmXMWM4sNtZxza+YegaZXLyFiEaLi2Pe/cmQRRKy1alPzfqfcvZRCzInYStlGxPM8h3KcqgJCmBjvxqmUUod2medxl7786ss//dM//eEPfzgd9inn/eFATGUVnqOrRbA+cYUt9HdTKkQkYjZ0AU6SUsopJaEatnaI8T9kNgvZSUzCTbiSa2vzfCbClCXnRI7hsMhE4i5uZGqICRO4gwMyS+QbckIMM3c31yvxHP+Auo0YTDNHR6idR+ENoLfRPQG4m7kaBMdazT1AC/QO+vbtLbfg360yMx8khm1h9EOXJwC8woOum6o+UAAI9tuWLDpDRYTzQCwsmVNGZgd0hGbWfb9KrcvSaiNVNGPD5JS2bYjYwDQFbbg6GyMgkYgWA22+HHV+hOW9Le/BLszGqo68pAy3d+nNp5gmv7RUi5M1rdkdahVwUABDQjQrjoH8GIFXnd3MlspITbV7R7UWO1zbdep8G1WI7QtCdO6afIgNEDk5GhEzQOf5EgMAiwSSHsAOiUiOYW9MnqEAIAEzE6K5IxoQIhkTd9IVuAQM7R6q69toKwhYiGTqBORmhKStddBJ0cwIirmaqm/MPDMwb27Y5UH7IxJANkXx7Yiu19YvoULqTWmdhrg7IKgbA5EDO9ZaKRyY3MyVEKJFMIW+mk7eWlVVIV7mWVsDRGBsYCPW4qQggrwTAhq+Bvzjufx8scdpPy/LOCY3Y0FQg3Nzcwbuar+AbQmxT3QO9+AW0tc3Uz5kfD3Sxzf7N/t9loQknIY0jCmLELqZYD6fL5Zsd7gBb8PAiLi4QWx/rfXiur5yNWBHisc4HraovMyMmBR8WRYmYhQ3G9NY6+JI1qq7p8SgFREs3HfKEhuSYAq1gTsHd7DTBI0YCbMDNFVHIExQS+wjVzof7m4ul3NOMoo483BzaMtyWt4hGLaawQsYIJq1Zj4kBmvoCayZQ0p8PJ+ejg9pGqzqNO3Ox+dMiO5ZfJnPSDkNudYqOfkyd4gPwpoXo2AnYSKa55nWWjJyQ3wdU58g/AXSXbRpGNGoMsmQUplndU8plVbNLI/DgKNVc/fT8TLkqakeL7OMY2KTLH/5q79A9I8+/cjAx9uDiRB40Ra1yDarN+0tSHBYDN3QFIAycwVHNwYWyolL4oFJiVopbG4GJLlqgXB6Z8qaQEZlhcTqfimV54XSLMBR2XGSIfZ9wdWBgVuq5MYitVVkAhIAoO6ztP6/uYMj4GK6uohAXwzq50rcIKaLXZ5hHTRGQMB1LwcN2EHbEhTtjaNGhK4GppGQtj4gDKTMDBA25YYtyhNED+HugF3b2d1BsZe53sVDycIYzZCESQbMAw9TygOhCCcnrx6uL1Vt8TpLaUN1rI4Fp5r2yrnRMCI5ojfXKpDIvZXFhwTgwGgJpJiVWrRVmy9wPsMyW2uOpoyYxFMebl65jKe5krNQIvGExLVaa61VQUCzZgXc0c1baWAI2moBsBiiWAzKzaypu4fSRVhII2JoIvq2si+hDwoQ/0/ktC54YHhgBZgDwCIioffNIiyibhD2YR1WX7Wa8cO78OHr31n595c6GDp6rCVD0Ls0bHp8PXawUsriuzn24cKW3Nd3038D1pq3b7pF16nqfYvM0dzJAyKIzTVH7GYRsFXQFBpW4TCMzFoqAgjz0qpqkE3dAcP7mHMiojxNf/XzP7mYneYFwvUJrTarteJqZ9aTU7fDdHdPzN4l+kCEpmm42U+H/fTm9avXr17tdjsixuCAUxIRdgqJRgCotZAnEWBmIY6tIe81COJKt3u5I+tsLOJaq83NGFCISylB4tl41u7uroho3sxxkNRMAdxMmRC5m56athYioCugAQCAaKaxYaeqRJzTYGzFXUR2ux0Rnc+X/WGvrSHARx+9eXc6zrUwEyshgLVqxEJMKalqK3VZFiAWkZzz5XK+HI+73eH2cDgfj6XUccxlYRYpl7bF8RfcgDBUp1pr0ebCqlkbOSB2IKKo7x2heuRMZk6EXmt0CYzUYjmZ+XjsjR0ijrvpeD45+sPxKY1DrdUQ9nqzlGUax+enx2matLVxHJ+fniglQUwpBcUo3tWGpG3XPz4I9uSNuP4KCYU5AB0n9BDxccw5aWthXqrQVHUYBiestdbW5mVJwzKQBAgbi5Ae2lYOBWeu7K2RZOKETAjVsQfT+JidyeN9d2CDxmBlW7o5YloDv294YC/k1+kaE4HGGNLM6/XnNTN0dDPUlxnAdRHj7uuRxquzvZJb1vHzVenj4etrYS1M6OBNbRRBFpaEkiQlFmESIjY0dHM3b2q1WWveDJqxInsomqIgE0j/+A6u7hywd+fdIYAUh7k2KBUuF5ovuDRCIJY5ed6PcrjDcVfUS/UEnpDIK7Sqy+zLTOaKjqZmCqqhwubWzKq2ggDdessCI7pSuQNwom7pjLhJs1KsZW1iT8zIZO6xRhUxwRGQJA65pNSxX+GouoPdjwCAL2PhD6CG/7JY/xteMRcycDDXIPX3E9YbQlhVCrbTE/vETsixS0yE/LJn4JsEoPeovlFdN/qagzP27XDTxhHGe61wNZCw7R+4iLQghziYKrjHswduxCwpJaR5WfSwuxD94uuvL+CqGpTwh4eHQI0AUfhlBWGQzilqrblbouxEgjCNaczpsNu9efNmmqZxHIdhGoYBSZhSjA3JKSaxRHJVmmloza4nPtCyoHG/bFnHPHNrn80s4ItgucQnXQ2T+5stde4/l4hWtVdEDP/k77EWfb2MvT5YC9stlgHiOO5NbX9zi/B8fn6OKzzuhtu7m+PlzIuDKVNIeDUg8FYhXCEM6jKrJgJnSefLkYmGPL159ep4fEwyDtM0l0utNbwnNnC/f5CVxR9fIGKM04XXuRdRKWXbCBu5M19VVYZuUNP7iTUexZJgHLzQSopL+vT0FPeo1pqq1FK+/eabX33++TAMh9tXl7J8/OlntSypOwZjvKvtLVnXqoQg0wWg2xsFQyJyopABF2ELARRCMnZgBHE0twQxZM5J3Byh54B5PhMDghFCzMDWT5TdTZKrEhtxiS2f/sx4H8Cu7dQ2pOiby9tzau5IAuuztA2c+kzYXw6Iu3uQ+si3QG8rEGRm0Yb/9QSAVyYwHxw9+N4UYf2H3B0wDVzdIAaDRMiJc5ZhwJRIGEMqP4hYplpqXUpbqpZqpXpprC7ACYCAqTOwiQDNHNRU+3JztN5uKMfW5mXhpeDplC4zLU0FG3EdBPbTzes3F+OqNI47qI1dfbnUZfG5UGtkrVoDN0SEWrQ2RI/Qr9owoLWIj0RugQgHdE9I5ABIJCsvuw911zcH4QxDBG5B7VxvEjkQp8QpB44QG3Hx72D7bvCy2PX/TwIIpwFCNG9xM6Pv23S6PWCK9TYbOEFYwEEUIcgU1l1bAngJQ+6tLqjmTb1F2eKxK6HozV4O1va6jmWq6iscC2ClLqhWa1FTRzBti+thyIqsau7K5CfVL4/HR6TaFmYchlTrUspMYXgjvOjLj6g1aIVABG5GBDEmTcJ3d3dv3rw+7KfdtBfJRMSUhmk3jKNIFklWqqqOQyaSkPWKxxNAw6ODkMC7qG5gbleXvHsk9GsVf8Esp4SItRQA6GQMQnAl9Mvp/Pr1q8RcSnGEVe2D/nf/h88A4H/7v/wWG4eCN6w4eLxoZaNuQwUAEEnWhGW4vX11fHrmnOzipS1Dzm/u7h7uH+Z5IXAhEHZr3nTJkgickA1jSt8MELGRgmpdLjYMExEZ4G5/8/bddzmny/nMzJyTa3T/iKvmT0qJiMIoJiSaa+libWGjtjE+UR0AhIWI2ireWWt1dYgZUlxJgBj/llaBMNbCS6uIeP/4MO13425AgGkYHx4e3r97R4htqQ/3969fv4pzuyw9E8SMeuuitgYAAWDF+YkghGtFUISYsSOvFtoNQi0DI4CBJ0oyMKmbt175VW3nZTYAxU4G2fgdYE7cjJm4IjISggd62mVxzV+GwFsU/uDRi0KL0lXfAv0zOGBAxg7gTiuf2MGC9r19E3PDcCMwvX5At++2VhUvLJL+Wr9JfOfta4gL52AI6qZuLJKGwZiTDJQySo5xpgFw5KBmWltbitXmpUFVbCoNkyF3URuCXncSGrmCmRsgiUDKlBIlkZl5BmBtYlqXS7ImPLkkH4bdzaunCrWZN0NycW11Tq3MpyMshVUJuwwBuJM2bQ2xL0CBNiSKfd2AqYBQcgoYBwkJJWJ6VBNbydYlPBG7z3vo8xAGXZKZKbSaWagzf8QhbLv6cq8Ho6bv8OKaUNYT4OteFeL1rvx2a7e0EUVFJNvWGgMavFDvA6SGXu73c0aEoVbTUzQAx8b2VRLa4hoRLWUBMPcGbkxQSwWmYB8HUSIaf9eKiFobMVt3RCLv1OwuHL3UBU1rK64NCd0MgQlZDWQcPFRzM+swfv3w8EjQ3G5uDsOQVfXVq7tSilkydyNb8UzftJpTEtNq2lyIwEU4Cb+6u311eycsCJxkyHlkZpHcddYAEVFVUxoIsZmbGZPH/iMRtRa69nFlEIBpVXSAteqHleV5DUAjYjjkNS3khAjLsrjbppJvZqWUPA744WWPOhIC9XrZ7+mTBlw1W2qtROjADrQ73OwPN/MZvO0fH94z85B4P+bnZxyEzK0Kt7ZYbQucp92u1oU45cStObiam+S0XM4hdkbEy1zefPo65WEuc61VVXMWIgoaklnbhLJpFQOPdxXx11dQKHIAwCpmELHM481vejgvoQ0QzCzEJNar0VfSVPV0Ol1O57MkLXU/7d++ffv555//1m//5OH+4XDYX9uQ5ZyjCfBr5KQ/MoR9YdAdjBidAAlYKA/JG7dSkQmVhIQCznRFz+621DK4schcS3zPCuZ1ASYWoXVrxN1zEmZuyASzcHbAF76PWTAX7OUIf/Dsm720hs3meMschrrrWenDKURALNYAQN3AoyNfY7jHEmYcHv3gOl+9rtsCfFnfuVIA3ZCAyCjIHiulwYBhZhbOE6Yc/6OQ/+ymRs1q1aVYbboULI2aYXNplo3EaeBEHrpbCN5J1c4MSSwLJnFhQ5JFWHMyglJnaIuAN2h3N69uf/TjgsN8AWyIVdFLrUebj3w5Wi0DoIRLjmmzatZcG5hjqNOsLH43g8RA3HFBYSAEJKBgi5O7A6FI6ukdUa1T+x2chNdhAAomAHAIvW8GohB3a50bTkhIzN7JNS9K/d/LwC+Etg+n89d/9JLP3U2baQO1FsV2rAiumjzQGSb9Hof4XTx+hMhJQq/V3a/PxssPCO1vVW/KuhFeY4MRNuTipVIIksD6rWJUEjGizoupojkF7hSPKADnYWmqhLucK1lN/NXx1A43n765G8ZRRO7v77v2QMde4sg6gIfGTJfOr2UuBczTwGPOP/zss9evX+120353GMcx4j5Taq315W7wYODUWh0RqHP2N6wvtDx9fWyYCMHRnDrZqd8gQXKPSIKgBjEdiUVZc/emZmWZp3FMQqVUQglCZwedPrzL7m6qzLzGB98aUACIPbKcc62FJOU0FbNXr9/8+bu3t6/uSplNK4Ld7KfjaVqWxTE9H88ExgiXZZaURAQJhLP7Msp0PJ9qmZnSMA2qlZmLVgDM42SzZpbL5WJjTsytabAk0jDFOdy0mOJtE1EsPANAjIUCCxpIYJ2IdFbKms+2bdhhGJbaUaPa2jhNz09PgXgEhni5XJZ5ruPkpZ2Op2Wev/7yq48+/hgRY0sgpRTL4UEy3uJXdCQ15hAIRITcQ+H6ChlD0UTo7IDIQG4IccyNcHDsZBcvJSMYeGutmDZ3KEtUsExEoc/muk6SqJQCsYSmkeDCfynE2HsQ9w812rBnAGrAAEiERvyCFADIWh1G52S4RXDd4IPteQSAa17/dQL4a9FlY6b277B1DPEfDSFkQgMMjTJiJiGM2p8FCTFa2Igcqq01a+pVoSmoshoYDErZnYEQiVkQ2T0eKHQAZXIRzxmzgDAyieXsQ/bEylBAd2PKd3v86NXZpZybV5koWa2tXXx+bJeHtFRWM6RFG7t2B3qwUMzUaugoxJSEHEDEYhMqvAsTA8ZSHyGnWHxf2fE9CwszC0OH8VcPXoAXujwJxmQ4/j5w145fJweBJlznYr/6wv/andlu6oafbgWFmyY3BuxTRbPQfEb/4Ad416knRorfJ+zKokDo2OcC1z8uYE1VRW+q1VvzdYAMDkyIwe+J729d6cnBIVCybc/E47s1llDm0E6nInRTQHbAUI4ttZ5L0bu7m89+8LMf/Ojt49vL5dxaa1rMTC08tbWYh1pDrEph181XAd+N2QCGIX/00Zv9YTfkNObMwtGOQFf+JQzZ+mDgxQMJELKfUTAAwDrXf7ldpSy8KmPT1bxkuzsflJxmTIQS+L7nnEXI3VMSBFE3XPGNuHSqKutwQt1LKcgdjLSqcetxVYlw7xY+KCnBuHP99LPP/uovfvnm7vaLLz4fsuynaTcNz8e0tHka8/F8RiA3r2VGnAS5WiOi8+U4jUMrdXdzaK0NIwGTKzTVm8Pt5f55GIYYvaiqu4aURSezDsPWjsQHj9I7yvaggcZvrsopBgAtVI9WplAPLmbLsjTrqFop5ebm5unxMUC5SLTzspxOp0/efLSbdmVehPn56enXX3/98WefPT8/73a7/X4/DENsEmxhbrtZtBVMAEFlZEYQ4kGwsRduQjCkCjEsdEFyhlgNK0sx1w5JE7KJqkIQ3cwUvGq7zHOnBjoYJBYyzhSMSgVTdbUoC7Y2DtYkFBEG1hwZCQARDRN0pgZvBRwCRloLxWJgwtVCEnCzwHk5lpFlf2M8+V5sueoArruBtY5EdAwjFwQWFuY05HHglGkYKWcSDgqhubspmNZaW6laA/1vVBXU2SADJQcBpvBso7DCCocldGYcM07Zh2QpoYjwfiwPuFhd6pKnbNOAdzdHRLi0enGu3rRxOWt7tvmhnh4mw7DvslJSR3Ad0Jo3YgIAToyALOwOzEIr1k/CFJIMREAIGpwRYuaw3uplPJJ5//tRVMMVLBNrvuuV6/gmRF1sjtSXcFduVVQB/jKId1B78eC9Tga2VgoxKYpa0c1a0ArNVFsXNAjmGK0tXnQAkb+YVv04QMTmRhYycB1c7ucGuuGzWxDLuv4UE5tbb2Xale8uEfSna6syECD2Y/th6gN4dTMlZqTojQhZWqlBZuab/cXBMr+/f5zn+XK5uHvIBy3L0lRV1bo/M7sa+Ys5atXGRCnJfjfe3R7GYbi9vdvv9yEStz1CYewF7tg9lwiR+uyHyNZ9y7gFQXTpZeoqrItdFKEXWRtihoiq0V6Ym6FEYcgAliURgbbKzAZmZiKSo/Hqot1QWwu5aVw/kYULOGJk4qhtI0SmlGqFpkuSLHv6+JNPL6fju3fffvrZDy5PD7iDKadpHC7LMg7Dfjc9Hc9Zcqt1ZZxxEp5nV1UCqLUisWrbjTsHu5wvSMRE1WzIWYTOpQB4sP6j/o3dq1iJ8pD3YdwatVpriCAxUsppmWdzSymV0jCqCtyGnRCLDhEO3b20ikxBrYnzBERq9vT09PDwsB+nUpZfff75z35//PLLL29fvx7308PDQ4yjeyPSGhMFw83cCSEkLiLyUjR3wM4CnIxkl4bDOLYlL5dTq0VrLZcLGKA7YALIjk7MTqjoqETM6m6grqETb1Vba61yY2ZdVEyMgYnQMOpPV2dzV0OKBNA5GduAAq46gI40YGfTGvM2B0LEGoQ9YSAiI0d0QkIw+GD8tiVCs5fEsM1FrpPE+qNhxY22ndEX7BGgewwE0z20VFMeKA2YErEgMRD0EYc2rVH7N2tqrVlrqMbmbC7ADM59ltE3ZpEIREzEU6IhW86QBJicUHRv9/p8afMJkfPw+va1DgeYwbwNyFCfUznfeFue38J8pLI4cQMwh4TUus2sM4nkAQAwY6+kiIS4S+70pEtJBHoGJmB5mR5FsiV0iBuCsA2vui0XIDCgI7EhhmwHISChNmTi7vxmQND9X3wd+Gw3rN8t7qbLm7WLu4OjoKCTuzOAm5oqe8hNg1aNilwjSUQzQusqmxsJOoBCdTfkvqQTAAQAhDmDxrsAI3CtDUohczLDWkwVzBxQ3UhyYnIKrAzAwazF9m801+xBp0ZE1LXgNyBt7JZYyKojsjmO066alzpXN5v2lSd888kT0dPzUVAf3j+UUljEFOalNnUnHvJoAAHiE3FsGcfCaijyjgPf7oeb3fDZJx/nPB3Pmm80JWbh5p6ZiRI5I5J59IVs7ikNYK7WwB3NhMmtIQ9mofBByMzM5l2Endi8S3/79oB0zpCZNhWRePYZoak6oeS8lEJmLAYIzbpxbjyziUgdmreYAEmioM14c8eVT7kSM4IkwwN5k6aNkFLef/KD33p4PCEnkhn18ur2cDo9X86wLGUa5HQG1eLNHaGByzBdLq1/W8P5Mo/jOJ+PQ+JXu935fMopjUOaZxdmdyOh1spS2jBkZnRH1eorx4kIU2JVjf21APraUpjIXRczyoIAapZzbq0FYm5gtVQzB2ZEoFU2Aw3QfMxDCCjFnRXmy1yenp/evLrZ73e//uZXn/3Wp7vb3fn0fPfm1bZXaITnZUlDXrTlXjtbR9KZQ/+EOUf/jmxODYgasw3SCuxvRqu1LOflzPVyaWUGtIaCrkjAiBkJagPVBGQ6dzUGM2aaW3VCZBJgQCJv6pBCekC1VVWnsAnZgi8RmSmCmCkRmTdEDO2CNXURElnrRSStLwMgJyCE+KOwJAXa8scWshERbSsqPlR5uFryIuzWle7UvCuXODgQKrgjEKNakTSACOUR08jj3ocJ82AExE5g6J2QAq24Ni1Va/Wl+FK42NAgN0/OqMZACViMzL0RKLlnQCHc73W/92lP0wHSlGRgJGmuc2vnUiozprGIHNVsaQLuSMkWtmWez3C+cK3ioNailndzX4mbIgLcAcHtGoUImm3T3UB+O9oT+jy0Jb1oyQEAbRVBYHLvcdoBCLgjDTEj9xZVN+OLvJKtYlWIpFc3g5nXwn9dqAwqunugfWsdGpvfCgDQ1AE8uK1qFmBCtHARyNfwRNgXuKHX5B6gP6wM7t6S48vsQZuyg7u3VnCtdhERgtfMGWNt0t3BidjcgPpyOSLiWkQQ8TrYxI7DhFwMgiOf5zlNO2fJU7oQjq9u225CwNL0L/7yL1Rhmqbn43FZlvhuGpcMqdYacHNU7jE8RBFiHIfh1d3tm9evWm3LvNwdbqdxirOeh2xmqgaAwsGkWI0Yr169Ld0+C4A7xAo0rmCah3h4eIdx1P7aiiJSSsIsiGigxBRKQd0qZ9UZpdU7d4sFUXltUZ6uTO1jEBoiOXEdWmtq6uihM1OWwkQi6fWrN2/ffptTsstlGHcfffRmqe1c1JnHIS/PFzdTJXMAEkd2NQMQTqWU7ImBzufj69evay2InoecUprnOaW+vl5rjVWk2OldlmUYhoD+49EIdtCyzsYJkJNUa+D9yYrPsiJC3jVTVVfOd2BrFN9nk5SIC6K1LWV5PD4PQ0KEb7/59e/9jb/5/v27T3/0o2EYzufz/nCIoxcb7VHFInJfdERkIEAKpha5oxmJgLBKMqveUNsCqm0ZypSX83k+n+hCXJmJlloQizAyUVNlAlKotapXUKutYadKw34cQw8gNi0JwBwQMTpq/NC11Nxpzet9xRJWCrKvq9UrAQzxg0wQkDIRgcUv0wtic9UB4KoZf/2nW8UZrw8EJKLb7wanAY9jzE9C341ZwrcLiYHCohsRkEL/palq0xbPaGm1Wm1ZjRVYMRkIsDhShJtgxJBQSk04DZmnUXY7SxlZQg5HANkBqhumpKT386UYDyhWZ3BFVVxmfT6muQg4xwVpbgJDGggwsRCiiDTQeLZplWQIDg+TwLVKT08GpEBdJtOtE+d7JI2eAAEAhfkKwTd74fm6uZk6oKOvRsNXNB5Ev9L+dtP1ltCmRYMrpSTuV789pqCOYK4eWgRgSghmSohI3eOTiAKyiPyxJZ7Y5AvgOy4CbE1GFLEaZlYV1MCDS2oIgMTIDCIkiUUAAb1XqYR07SHRlSBZiKg2WzlUZLU0N3VTcKuVMinRNEyN+WlZ5O725vWbt8Uuy/Inf/ZLFhnHwbvkgId0qIZJJXQKSrziPeScCUGSiCRmctOUaAj+CgWYk8xM0moXhT2tXj8GL1dj3dYhgj5qW5cb4lKZG/YJW//t1po2X8kCMR/HeHt/nTaznhZblmUT5b6+F35Fwc55wCtMNoAXJDwvJYgYxtzmGQA+++yz9+/f1TKP03Q+Pec8jOM4JKnWdtM4L81L/1mlzJKG1hqZpDFHCIg5alTTOSdEPJ/PV+AD9ViPHAOAYG2GabCtxz6lpK2F9WOM0CWnqs3MYqLgKws+liKY+1qHr3OUYK0ExPRCLnA38LmU0+l0Goebm5tv374tpezH6fnx6ZNPP3PzUipy97YgYleFdSuWHTCCCSADUGjuoDNRbEOiobKZMLq2JOM0lHHM0yjH4Xy8h3V+1lojQDVkdDRkpOLgGNJh2EyXVlKTwBMY0MFD6MNXtuj1vY7Pq6ZrBxA4q66p6wXe3G79NgQCALyq2MwsGoctj24x5HrkcF3rtCtas15RP4OTGYMvQow1IneXMUvKnAYeBs6DJEEOOwTELhBgFihtbbVU1dZa06ZkAM1ZMSll9QwsCME6ZyQlRCaShEOmcYBponGAnDALCiGilMu5lbIsi9dSdaFhoGxIlDNAXUtN1SxywJzBHVsWSSkJsRAlFnBgYaY+VAGAlPPLRWHZWgDY0iySAKMIEUGI5SJRJHVcteO5s9kQwBG6XJ+qthg8RyiF3jogAriq4hp+SGS7AfE49WnBi4HMBy8iCuF1rZUIrQUrphIoc3AWyR16mQxR5UTtaytOjWAE4IgUtdUm0BhJqFforgTQtKI5gvchrTCmHG5KyEKIXQs+GKVBcetFA28hDFaZ32VZBMU8REwAmIyQ8tAAFyJN+ZMf/ODhMl+MmsPd69dNQJt98cUX5/P5cpk9BFrW5ix+bmDiAe8CgBBNQ96NWZh205gkJaZxyCnlrYKOdBAwC3tgAkHOe0nGUVtt1ye0fQgxZuDxnDDzKgNuCBD5iUigE3UQEUtbIjLSOqmOSx2RMcq6lBL2m24kL7OKbc7f38M6xcRtHtBqTtnAzPrTnlKqaj/72e/86i9/WcrsSNrscDjsj+en83smTEnmZbFmkqnWypyipVqWCyLO85kZ7+7uYusiZ9ntpmma5nmO3drWNKV0vpwQuqrPOI6xBx4srK1eGYbhcjzFRQMAd4sisdaSktRaEYE5DqTjuscbWQEAgnlhZuM4zvMM6+Vl5qZNVcNkbZymn//Rz/9bf/8f3N8/vHr95nA4XJZ53O/iQgXE5DEsQ6eucwVMSEE5RHADIQBAQkYHluwmCM41uQ6ShzROaZimKR+PT+fTkU7n2goxehMmbAs4m4k4oDWNNUxUvSzFAM2AkYaUHNb6mTDUYrcVcQBUBwzxLO+TJ4/VPXD6kKMJa6Ow/SatSQWxP2UflozfLyKvoz98qPNz/dfU1c3DFqmZEhEnYWHKA+ch5ZHzwCmqQCJE7TQPi2LR4nw3ra20pWitXBsbsKIoJcUEzAAMjuBAGMYdJAPvb/jmBvZ7GkfPCYSByMklg5MqhZ+4t1rxUisYjZJFBvcl5WnYaT6fEuIoROSSJCQSgyhCSAAebu/B8HfiCPaAYQJMwNx1PNdrQpwgkLh12h5tUQwegQk3iygmVVWrpbRWa/iE12ZuwMzOpL4OZjeTFnCr83XcwabrnQCIITPh9QCfQnvOm9ZKAKYmjNpaNBjuzvxCL9KmFNrEvXUIoREiYl+l6rddTVjjGqi5NVdzrQBmrtbUCVmyMxEnJEJJTtjM2Pq5jPiLiCEsbOoiYhjFr6zlHteyEKMDgmMxFSJHVKGF+PUPflQkPT49lHHnQjIkIvju7a9jmYiZIvTGg1tqiyGquy9LGfpyqQvTMORxzDklIhKClFmYCTEPQygfxNRdWDauG14ZsGxPmq3KprjegWjaMPoBBLXq6zKwattKLexKeb51J/ThEm8koS3YbT9RRPyKS66rQD8imret+ot/GL/vYIGPO1FKqbqmlMzGjz/97E//+OduOgyDgd8eDo/H42V53o2Dqs1LnS+z5OFyPg7THgCqtoA049s+PT3FPTWh3W4XCt7RdgQyY+qllGh6IvT3LV+R+A60ngoCZOFSWh4zEQYYGChCKQWA4jsIS1CJ4kcg4m63++qrr/b7/ZaS1Szl3FRLq/OyLJd5HKe333zzJz//49/5gz98fHz+9NMfIEttKpxNO/+4mknX8gACJzdQRwgbmdiFNCCP3U4zwtC0EHE3bYMMIw+7OqY0TmnckTws85kvc+UChIZ8QWTAAgWISykOaAhLq2qmWYeU3X3MGYN1QQRETTXuZtClAGIFNiq1+K+6d/xoOza6uoTG+fEPc0O8AvO/rhXgpbmH69+JMwQfqgtvf7mZUgiUhaReB8AFOZMMQXHcuhMHi1FjP5mmtVZvqqViNWxG1bABVmPFbMwOXaASABAbujJiHmmaasqaM49jE8EhBQeUCATPRz8+wfls86X6wjQBODJXGKYh57zLeDygkFnSNiSRLPGkReXS8TJwQ8VNYgIBiboFYPBXr6LAlgIAEAEMgZDMQxSALGiU6+ML0A0HEBBc4wYbmCFRFpAMWaLqvF6xQ3fSBvayT9RvQtAizDGYqVtg8rCl7RcZADD2NZoyQhBFWFxbw3XsgdRpZyICsbdlzuawmsBsZ6U3mG7d3c1aK4XAITgAHLJXIXoReCA5oWvbkgd3U5GoYtjMQotaWwHq6sHNmpYCaDwkceGcCxANoxz2fHNzfzpW5PFwo6cTshxPj6XWYRiWUqZpCsAtEsCNpKjBiaiUcj6fSynjMAQ1bjeOtzeH3TTknBOxBGi5gTCr8A5iKN/RFnO32x4kP0T01lLKtkZ/Yt6ULaL2FxEEiH4CVm/CSBzMjFd4zvceSF4Hnmb2v/8//vh//b/4UlW7lZQ7IsZ4o1fE2APrBgQjIhJWK8Mw1OVyHQ5E0uuPPvrpz372X/ybf8nkzDiO+e7mcFnKd/fnJFxrRTDTZua1zOYIJGZ1miaztiwXAIstWRG5vb09Ho+llForEYzjOC8XBAjTx2jCNgXpTR6DiPb7/TzPriYizWpo/QcBND7+MAxm0OVrosZaA6K7n04ndz+fzy8XzaxqA4ZaG+7wfD7f3NzWejk+PUeboqqHw+F0uSBisGxFhjiG2ixRBGdiJHYns/AgDOg1pJ1QUvy4TtChhpKYBAlRRsq7lHeX89Pz4wOcjw4kapkFk0PQqJhC+JIhATi2AD4AUYPx0p09eAvQq3ce9mZ9C9bYKVIvZ/Ia0tlC9hat4pwIyksUWRmD349p25n8sB/Y8EZ3jwFYyLz0qjNJyhkkA4szI0lcq8g6uorNWFO1ZrXVWq1WqpVqBTUO3B+cABkAkYEagDk5ZYacLWfLmW72tN/TNMGQjcOP0wBA/PmpPLzX43O7PLs45ETWpnGc8ie7PE6ghzTejGfwNiyXvA4laFWcJ6KgOfKV9k5cmuACBZ+ndwNXV6VXcwjbhezw/1YTIgKhbtIcaqZqZg0QmDElzCPmjDJsYl6w9XFmouZqrTVYgdHgy5hVg/Cf0RXPiUPZwMGDqYLOSH3D2TuczYZRQPVWBkMdgaTzbFemq3X84XrDmYisNjezVtdRhqEDMwEzSUKiaImAOPoZvNJy+d4r8Hp3x1BaJUJCq4oCrdl8Pg2Hu2bOY54Ot2Uajku1nA+Hm5YSzJSH7CdMKSFAUwWAqhEaAADmuXdO3dKd6HQ6OfiQUk4yjgMz1Vpy4pxfQiqtbN2XI0DI0Ovx7z1sJIyI3le8MUAhty44jAg5Z611LaZs7SQkav9NN/C6sLr+HdzovBHg1hi3tQUxR+ldCPQSe5vUAQAiaNPORWCWnN1aVWutFbXXbz76/d//g3/xz//pp5+8Oez3p8t8d1Oenuen8zykfJ6Lu1FH0ijIOdM0hcBnwDtmNs/zSjzNrbVluUSRvswlfmjU75u7Q7xnWIvNnLPWpqqGigSA1rQQdWN0QkJFxGZmai8qZpGnHx4efOU7bRHN3QRoXhY1a61dLhei4csvvvzZ2/cO/N137z/+5JOcRwBAUwAQEXQDs9gABXTAQOfE3KA7aivi+lwTbiWXB/ETIFFSYUwDDRPngXIGZJSEpxMhMlIJob21le+DDzPUFvNCEXNABmquwrwZWHpr9KIRBIHpuEMIDbhpVJdbTt1C1nqeXzaTAF/O9vVjeJ0trk+4u0MATetf30YUvvF/HLpwYlB9c3LJLJmZgWU9wM193XNWU9UQgAgwPBWV5mbAzgRI6EgG5ARMCAgK7MaIg9A0wDjiNMKQPScXBmFgNAQHk8v7d/PjA7VlBAdVbI1cd9N4e/fDCXnUeWQamWk5J3aqldbVUEQ08LUDAKeXC2dmgGhRvmPf6oLflDDj+WSiZn1DPVbbAV9EsQHAwbVV07CTx5RHyIOME6eB8i6lTIih9ehuquZmXCuYozZszdVUm2ozNVSG1qzvz7Tt+3uYawEhuqkKe1NlQALp3SKw4vqOmxs0ZiIAbTUGFUQkzskV16CSkvhq4x4qum7mWoXZWz+WwIIc7N/AwaiZqzq6byzm1qJvRSJazUcNAJCoaVNTIkxJYoKu6uomwsN+N9fSxgFFVBs4XNRcOA35sN/reV7muZSylBLyKU4IgJKSu5daw2c8kBp3YKFpGHbTlIVzEqZO2qmtddikr1/GgwUvT9GHeGh8TFxlUrZnbBvOB6hjRIzo5gR0Pp1ULedYMuDAb2KNAnpruPVzTsTuMelB3Pxg/UUcBgC2wAersFcc423RCRGn3aTaOKXmlQCmaZc4mYOWS2n+49/6LSb/Z//0H9/c3t7c7M+X+eawL6VW9f00Pp7m6G9FiABKWfb7z96/fw8An376KSCcjic+HNz95uZmWS6hw9Fay5x2u12Id0ZBE2VWrP6uzREMKcWfppRaKQZdVxUcmAWBtCmiuHtrrXWNNt6GV75RsFb0bIttSy1NGwM+H4+ffHx4fLz/+c//i797+/cfHh7uXr8ZUw5zLopiGwDdvGFmRmvohm7aKmJ0aoFxhHhXmGUAAnrgG2E1FHp4mBDFzMbI9JKYZaGeNgCgW+MRatPloo6oAeQ2FQyYDmIhNGBSQABG9eYIROCO4FFMW+8GEKizAT/g8xARwMpm5HUY2WGuvnMTQea62vkNOQDAVlcQv2pVYWWhElPU/syCHGGGUBJc7SepmfVFH/DYoKnNatPWtLbBkR0ZWNAFgPryqQMSmDsaMEFKPI182PPNoYwjDgOmvgAc4Iu7S3l/n1tLCO4uZgTOZjevXu0PP8S51vpACcksTTftcmThxEzC1i2rVqiGEIghZBgQOV211b7WZYDb4dvqOAYw7LYe0RZtasHNjYjAyB1M0RGqqhrJuE/TK8w7GnbDdMDdjphidhmNgrbmZlBdWwMtpM10gTqTG2hLZSpwqboUXRo2M0dHAjQDokQoCMQJ3JWpghth3lRAEH2dJJsgm1V1h9D4NzXAWlUdEWxgZTSrmlJ2A0cCQ6gamD2GcA0RpdymQYMqQYQOVmsCEsC2khRxpbTHNoBai+dILXRYW9O6LMW1KJoLcZJBkhO50EO9JNpfzqf0+u6U0gnx/tKG3W58enxb5vP5WGutrSoAYveypFaReRim01JRhmEYrZa6zIl5yAmaTim/mg77cRqHMY/D4eZOJJNzZnF1RG0OgglBVm5crNr3rtuQHJCRkNggBkiEjkzd6NwJHRwY1czBECENE6l2wpg2IkIHMvG13oKu1woA2MwRHUmIcBWYIyeBdacsqDKbnDIDUrcUIoLNqB2CoGQGzEmhEYsZQMpYi5o/nI7D7vbv/bf/w3/1L/95mee98KtBfBoej8Ucdnl3qaVpA3IE200TgS7lgiTqlsfd6TxfyrKbpjrXcRxKmd0quGltaZf2h93lchFgd29aHSxJgurCDICmDZizyKUtiLAbh1oroQCCNhcSVIKqKL4bxuemyUHJg6ezOqD0bo8ImCmOLJladRM5LQV2SZfLjV6GnXzxxS9+9ns/+/STH13OLimlUcAXQE8yEACYmhu4izAYABpj01a9OaYklIwIgB2JHMggNCH7lNg1ZDMUENzGcQJwQDcKin41cmcAQq68zDOCL77ISLVptVZbbcTEMGASzIwcfJc+tGd3MTerpA4ObujeWokxAPYqhMJokhjQgXv9MvS2tHcH3X4eXCHM6bZlTAd3DOE1wM6z2jLAy1IAAiFW0+ACmVcOyJcYSCiNkidKCWXAdWD20jS7O1JrDdSsFqgKpXHVpNgUEIYMlNxHbAM0xsqsYOaqgEwp+zDpMPqYfZdtN9mQQEIEL7IxOrCU59mrkhFxQidzAcP9tOcky/E8ingDkSSckHMCAtgolRviH2vTL70SXI/I4TdU/dtfAwBEkGBMEiJC87bqvwVNrfOaa21qjsScM+WBp13a3Q77gw2ZhAnQV58ZaWpqVo20UsuuzXSUOlhrrRZkd3ZVUDWtata0matmEpEEmE0hSSJAREXsHzfeqqw576UQcEP0Vi+qFZoFXsdo5CBIJOAxcUAPV2TybnGJEOr5WWLnEBHCMkHVbDXLXC9Ul7iK6SWtAmEGgIyqaM7mjHJqc2lNUkZfUHJrreXESSgnS3Isy5P7siyX0+nh7bunx8eQBqPApIGge1uaOzRRNLjMF2Mch0yuiCBMr+9uP3rzZhzyNE7jOI7jGOgzJQEAFmaWGFawvLR9USZEEUQs3eXow57aPlRHgeCVMBHoMHxA4DGz2BhfEwyoXkOLuP4XgzgEV3KSsOqg2crc3ebJQcgJ4K69DHtemlokHsYRvVrNywVbrcL8N373d//k53+0aN3vxstcno4zE+UECqKtlGUexwMzv3v3XSklZzidTiGtY1oQPUSWAuQBAK3LfJn3h72ZLcsSw4B4Msi4e+Ct6FCsDjDH1B3neWZKtbaYUdVaRdJuN13OC4DXq0u0vfyK9xK3xMzmeZmmnZk/H49v3ryu2p4eHt6+/eaHP/qd8/k8woisnAVWth5DBmsGIInRxZazAbkr1AaA4JHIuiYZ4EbT6/s0UVUxM4GMeUBQiB0CuwUgDBN1d8s57lRZCpB7sxAEtFrBIUlOkplEqOuXAEPYkSOZddkoy3k0U9uWluOU9D7SejtKsuqUrNDib4xfcQFXRGeLCd87h7HVUlWtC4iFOAISMwmzCIkgdTdDxCtC+VYwmZsZmoGCm6E5G7lFqY+ClNA4FtVQMaRnBJDQWShlHwYfM+VESVwIOD702pyZSzsXUiaQJBMjaBp4OIx5rOWs9cJi0Jqbgpo3BweXtWe8CvQxU/X1lxv2/b2L8tcvUByCNd0BAHAkU3dER+v0eatNq7o5JKYkPGTejTgNNggdJhIGQFSDpqjqTUENk5JyTAK8NW+jN12WpWClhuyJXBKMbtVq06WmylaJMI28Y5KA0oAArkj4QfKJBxK0C5C7q4F4O7U2e2QLDMtp1OYbFyDaOQfovpAsmDKnDCThRxyScJHGdHV9QkQmbq34KjfUXM0sbJi1KSqwuhl4VSE2RC1t//quspxatf2EN/vF2vly8mFczqfL5fzum28upyNhj2vqK9uUkIkFulk2Ec2X89zKq8OUhO4Oux989umb13djktevXw/D4EiqpmrNYcCY9DMQ4WpsufXI2yjYwWN83cuvK/5c/7ArWSAwEDPjjv92UiOgmYe8dN8mc/ec89Zl6yb0vw73NpRye7pwhT7MDNRiKwo/xEbmuQQUQMTu6K7MiRATVG9LLePi+vxwD2Z/8/d//1df/OqP/vTPkGB/2LVTWUoh9CzsyEk4Cb97f89EqrosS855GNLx+ayqiVBFEFxVhQBFDOhyOg/DAF2EWN1cmzJyjBDGMUeoyjkIWqH9QOM4Wq//dCM1IdN+vz/Pl6WVDVu4TgAf1hnUCQWtsfCyLKpt2h3+xT//Z/+1f/+/2cplmFItF2BLmc29a5NBRmTTBsTuIbGzQJnNmrZGjEgSNF8AAHNEuF6GCkJAIjQU15Y4eTY3JVf06Hh6v9I6Ug9UEQm8GTQfAEbgHedMiUgYODa4AAGlb3maRzOp7ioswBk6IcQJDABcG1J38kKSFZh8kVT6ftzfqH0Ajr85AQCABXITVcvqUcGyTlAlESdmIRZaB6iwjmpeiiE1VwM1VyNFUAQjsRAjx4SUyIWUCYiAQBEbMgGTCXtmHzLk7CKcEyXBrrsTGj4O7qKXgtWxETKiIIHs06TnpczvuCmaUV3IGjSFgK2pi5RRn3QYEnVhnKvneZvb/Fd9MXMf/PXtLVgB33BkA0cyJsmJdyNPO8vszNhXstapP5lCHz8QshthysiOIAaXljSJALFBRTCvtS6FL0iWxMfkQ+YdeM9EAHV7b1uKJiJXZcDQZWpKsKiBGoDV4ggMnsKNysDdAmT1IKwBppQxZeCEIrEVDR5rDeaghCgIRbtCGWKfjkbzEMUEIzKlpgXU8f9L2p/H2Lal92HYN6219z5DTXd8r9/Q3SSbzSbFsUmqNViD4cQKlERWIEceJFuOAVlSHEdAgsgJYOgvK0EERZEVQEpkxEmUSJETRzDiIIqsxJJtiRRJk+wm2SS72d1vvvO9VXWGvdf6hvyx9jlV77HJGMjBw31V956qs88+a61v+g1O6NjgX5Ao5awAigi5O3v4YLfotODQD8+2u2cvXrx4/mKR87rrrsucYLp7ELXmsrvnnMIaQd37Pu+v9rVM53fP1svhdLUANwIQJgAQkcXqJKWemc2DIhyI4EDqPmrzzZCpA8WXEA6KxLd31LECOJbAczxgbNRcRISI1jxtQ6ZDlQxB2CjaAXCs0BFx1l86VBUtotzO+lXVY2ZptW77XBwgtoTGvG3huTGsYczc972v1p1wIrxEuHz5/MGDByD5F37pq+olpRAL9QDClLuxmrvXMi2WKw9nAreactclAVMHCLflcjHtt61F3EAPbfY7DEPDCEFEnY3zYhxHER6GIad+HGfT49Z7YGai2TWMgJilquYkxyHnJ+yqP3HDj0XSfr/noTezzWZ7Z1gSwk/8o/90GJafSm/mxYCIdSqMHVHMrD+W9ooRwZgAzSNAK2gJcQKkCCSGlgMHgM1g/HYVLTgQgDCHZAoAD44A5whwA0CYiGgaIxxQZ9BpAAUMlJfSLTh5CDkzEAY6ROuqB1Lusrk1Sj8huhu4zb/HPYIIHCg15hrCTCWOw2r6to+bsx4Bwg8zzo89v9XB2lYyE8LsC0JMSNQcbUmY5hEge8TB5P7j2HFXNEdzVEcNVkBHdyIXDBBIjEGgTeoN50E3BJMKY99R38PQQ5cpMTEGBVAEBULjr7q4NrghhqGbSWaa9OqjR1nOJQDBJRx1qtstNepmQKNfHo/Cdq3u0bS24kC1n4sAn+dOfuDsHOLbgbF5Y9s2Q+zbjUVoqBuotYa7Oag3Y3MKQA8yDwogYoyDpeJUbSrg7mru6tUhgJHRnZEdApiESFBcnFMXADqNEMTRQSAYo3IYM2WUFIAsAqS3G1sxjzrRTAmZnMo4VSMuiqqm2jqh2WcBQgwDIi0FDw41lDtvk668AJFjUpuIJ59w7vVDg1cCQGj9RJoWgabW5QRUDcAxDMIclLA4JKIy6tn98+7uBS0W2HXqOpbp/Y8+urx8FVYXXU4B4c7M4zSah7tBM+wD0FIROcyBwWvtsvRDWi760/UiC3eJuywppWEYZs9CJGJxdyABIIcgkOarcXu3HAu+uN05nIsDOubmt0vgNvkwswhsvV0zY044q8V9+/35ibgChync8QbigaLRGi9WasNZ3j4E1S3lfkbHHvokiEQQ4ZKHBQAyU621Wy4Xpi9fPF8shs985jP0/nsfPn6WGCxQx1oMFsvF5uoVEZVpZElgOuPTAQBAawEAIRi6zkwrBGhw49R4QIQgkaSjBL+7E0GTBT2/OBWRWqdjPCMi1bm7VWttxWiT+pifgHT7nDr2f+YzaxaZiGmaMlPXda33mij/2te/9vDh6xH69mc+i8IlHIEhOgTIOQdEsFQNiFA1rEZmNu7MasoDhYX3njoECZ9NOxjRWmocitCGo4FAglSRk3RgkXJjazXSDu0hLIzQKJwCgZAZ1mm5lIGCsSk5WyACIxqDu1NKHpQkg7ipRpt/zJPlAKYAx2BqmJ1oaQchNrCAMzPgJzqTcHsxA4CF4S3vqWMq09q4rYQHAJKm5NW+FuZEkpkTMQOwBfCt/XIEsLk7WKBpFGcDVOdgbujNQCFhw9QkhQA5JbSAAGB0QVwuYlhY10HqpO+MAAhZ+BPC9DLWvYcnYQHiYDDXq+s9YL/UXnKmgFrGcU/TNnkFZJhxVU2zviE+AH/DYPlf6hHHXK4thYMEABySFPeWUhGzMItboDk7skEUDfeoGtV8KnU/Ralam72WRwTTYXEgOJhyoQ4jcYFa3HdW2bAjYQIw9EAOjIhZn6UVTYeWdbvahrKrXjEkFMAw9SrTnm2SqGGG0VAn6gjmjkEYFoEG0UbcnDKyBIuTzAYW3jBCAY3kcOvlYJa1auhRZ2CzQilXNyeeINQdslT1AsHLHlJO3TBG7Pdjp77djeM4jWqb62v0uHNx8ezFizaFhgOYzwDM54OyReKGRVAtfabT9Wox5JPVctnLcjGsVitoujTdwCk1FJsDMCdkApjNiPzWMjtA6T6ZUx2GXREH8D4cTvAGyjRrHnYADRQRTZYJD/3jwxEGDQTTups3xURrrOOBSHGEYLZXaTTGPuXWUm96lu7OzDnn6nisaMO17WQmBoZaJsrYEedSB0CSjJyfPP1otV7cv3/XIJ6+eGmbUhFSzuHa2jv7aVq0yzD18JwEEUdVIRBJw9DvtteETQjoptCEg6IUOLWw1zoIqrrdbttlM3POiZnLdOAMMoNDmxghNH2ZOMjkfvuH2cdUcvf7faMib683p2cXYfbON7/24OG9115/KJ7cyFW9dMzC4cTktao7E+mkVCced7G/9mlvvEmLlSzWDEgQreJBJjxOvWzWZoNG40TipiqUFwBCLWFu1Ch0t8oEE1ASzNwtZDFQl4xCIWpEVVflgyuUI0YoU4dC0E4uB8SDmzTnCCWnpjxC6DF3pxAOXcTf5HYdDq7j2p6PqflxPNLwoAzPs7rl7OsrrRvDAdTw0HGLY3xsmTZ+EniQA3lIMBtADbCgQEZMyMJhHgjgbtTuX0o8CK6WuhhiMcDQQ+4hIQoAAzBgE0hCB3DZTteowZwEAd1wMoAAxigFUhdCWiuV0mllCuJjr/X/vyP/43204/0DiAN4DACCicIRA6DJAra5U4BXi+owKZBimKnqfrJxKpudjzXMvGoF1FDAIEYSQg4kDPKanXOuA0yBmxE3EGDeByxqSCFQFGAgBSMDi2oEN/J2LdWa9xMShICRO7tbnrqqOSJ5LWgG6IENeAGEABJ2mGlSEk4ZUm6qTdjkoaqZ1aY3h7OvHsEtYPvxUacinPfTRLkbXVVo9OoeISTDoAnTYoGpe3F9vTg/jdboKLbbbcs4Mid0u768yomTCBx8str9bwkLU2pgOLMqwstF13WJGftEQtillIW7nFJKXT/03YCckLkTAWJCaRh9B7jdAbwdz359GxrgY+nV7S8iAuBmVNDKhcOA9wbYfvu34SFewsergeMNBJjV1qBNGtRUtes6uJ3sM82GdADunjibtUkLBuTgwATMsj7j3O/KtJc8SCb/yHfTbr0fplpMsUuDGr3cXYNbqdolMTNCaNoMRKSqjDFNJQtD2GKxuLq6jtla2909pdTnTkTGcSxljoiq2kTUWzxoDAb3toOwjUNaQ8bMicgtaqmHthY1P4Zvux8PBcF8t1v3qeIUXs9Ozp48/vDdd745DMPbn/4sMYepgBsieu36PiLKNDGxTorjFreXfv3M9huSNGhBJKPc9g8gulqzu5s//YiAoMBG00REIg5gSU0jKIgBqbm+hm420ne56xfDyZCXORJU8KnaZjNtd9NYTSsmQWJgpoQo2FRggsIdffZ2CgL2QEclxzb2ajEADtDQ/zItoLZ2jwf/cSl6NLFibKd/OzXanzlnJCFOyMLMM0EZZgLb7V8+t8G1ggV6kKMEgTkqkBMjSgSBEUCgkyBoAKCkHjN7ZsuJF4P1PeSESSghiVCrAGZ5awAA2Y17CRALRE7hCIFWAixkb5JUOEU060Qkar0ibFauHkTYvv52+P7/H49P3EQAiFkb59inDPcIxyZ81+6PeWh1pAg1mwoBxwRaprLd1d2o4zTtRytVS62NREZBjNSRZEiLJIn3qBa617iOaR927cWKSoHTrXWFFtEDgUbJqUdh7nKUGRdMiJISMQWkQIHMiMQkkUJZmIUZlAAOnqhE4K7WxEwRWRrMXliEUgJOgbOEUcyC/hbuGG1J0EyXjQiYm2Axa+NghEuS4sZdurg4rwCqWva1gDFjjXCt0i9S3xXVal62eyu1l1QA6lSmsuckwtQ2vZlrhDoEgghW1ZySMBNRznyyXqfEi8UA4EwowhGeRFLKuQmAz40cabRaBGg90U9AIm6WSDPrDgD82El9OzDMUB8iImqyHXCQ759hJEAkGO4trtLRksQdbmk9/ec/OQDAl35s29Lb29gEPCKCyFm41RCZuVUPbnGkoSA0HwJHAGapASwIQODqER1C6juSBFDO9htVHctkFq7Y9+tnz15dj4g5p5Q2u715jThl5v24NzOrJaW0ubrcE/ZdivCcUkA4uloA0DiOpZa+H0TEHUS4Vi1lbPeqifSZ3Vhdtt5De/s5Z/fgnMZ9MQjGdu9vaeR+u4e7m80/vt/vh75bpL6Ok3bj0OVHH33wxhtvlmnPJDUsIRKzQjCCJAmtGjrtJ99e+eXz8urJ/vLFMCzcHQghGDFS7kA4mnRKmwrpjKaINkVyAAeEmZgNQkjedjELMXGkgVhyHlIeOlkmTKjgRSujQOg02n4KCkjInHJOzoCChOTo7IBAYOTuEPNOjVAinKXeYG5Hw29aAXx8rWogHrP/+QcBWhOhfTvrPRCJJOREh9wOD2o0x80RB6hbxIwbZHN0oGafYAEGGCgoAg4QYGHVmJGJ3ZGIgYVSor6P1RKGBQ69d5lyCnFkRMY47kUEgJDN1S5zBiYjzW4rgRzQ7Sz1mVURgJjJI+WEAI351ZwEHGdST2PzztPaA2H92MNChxtnK/PmmugQcUsrY76euQMUjefv7gRgHmEW1bAYEYGCanDCMhVAdlU2rruNl3HaXV/trl+O+0moAExTFZAUskw5B3DUJMaZtipW0x5jB3UML1yLaN2Mm130ymurI9TBZZmmLvW4n0hIOAMSSYoU0aVqED0LeZLmlqVmBdETUK1ubqYFBMCBECmQggHArVDKDqiU1VEwEAq4o01kClZBtUEbgglFIrHkDFXHsidhr46EEQgZqlYm6Uk203RZLvdhQcyEm81Wcg8pX9aC/bAa+qvdZuMQYDbuFoyqY3G41nEM7BlXOb+sI0q2asjRhESDKTjUyjov7pyeroacxJNI11HO0CVe9MtOFou86qRnSkCCyAGzi1Jb7IelfMS12gF3H0TpwL6ZSTef2Fqtp3EcJoGBIAOARnN3iQbc8BIA0TyBj1BtIAyvx47kP/qpJQB86cc3ZsHR7AFai3gGC8woDmaNCEBsqWa7eDNstuXujBThhAjNc4PQmKurSAIAK1PqF/36fD0Wh1RrkLO4T+NO/HItYJhHhy2agU1qOae40ggi7twqkJgpS39xfvHs+TO42o9hFGFhwFGs+AREBNp6UwkxN6AOEYUjYXIw02BmnP2wERBKREDUaQLhMjkgNJFgvqVM8LE2IyA2iXtgCApkB7ja7M+WCwCbxv35neW42W4uX9VSUGC33WZO6/WaA3WcGDAhTdPYwViijq6VEXtW3+v2OUgQE0hRX2LqKPVuhgEUTm4R4Qch4HZEQyAKilAEkiw4JSyDU4dpVYctI2bpc14IJiIBQywqoQBQtFzWERi6YYBhwd2SOhFm8IAKgI6NRRaRUBzUCQAZIxwUAhDIqa3DufWI0PwAKeJGzuEYHiI83DysLZ8Dqql1Cw6JP1LOAyCyJJGMzAHNAEMCmngaMAECh0FwO0IDzcEqq6dipNC50ORUHWoTeQNTQnWcKqkiBghB10PmGqy5h2Gg5TpWS1ouaNFDR9RxCLvQ7DIRRkkgQqD6NO2CCqTMMz8YgtCmYikCmZGk9T3oNu5/3rftlgBCeNwOLLeSio8ngzEL/B+jwifjasxu0TMSyMCqmqqqO3tUp2rILhxRvPqoVffb7VR2r3aXV7U8nnZ7opHoutYO0xK7E4Qc1rMNAMlhMg3TyXBCmzxG06nWsZTYTLnQ3tOIZQV5l6xL1gSBOykJqBMW4U57zim0wrJHZ3c0Uzc1M3MDaKrlcQxqiEjIQAAUxIySOWcHJmQMi9BaS9TqVUMNmA8EDXR3LwU8mFnLZKoYbu4KXrUyWGsbFYMaSikDwsliGSQjwLBaLu/fG7VY6KS63+0IQTCiVGSexqkArJer9ODe7p339/sSgJKSIDNBFsZAQbpzcXF6sgSfylTcLCdpxPVhGLquY0ntOgkZD/4NiOiAh5mYHTvztz/fY/J044JwPINayv/rzqZ22LUQEgdhrHn8hICEt4xbkZh9lvydcSaIKCLsB/YvIh6UBw3iNpz0FhuZmj/lXKAcpFLbBm/JXiMZEBmzAMCwWJ6d3yHiWgohLvr87jvvLIbOELajaylJ2BGyJHOLiFpKRDBCEtnvt4vlYGYn6xM3JKapKJTSmmkeobVKYJtSpJTaPWll8VHY+Tg5PN7MJvOJSACmGhEByEcFxNtPvr0HY54YN0FA2O22Z+fnbt7lvHl5/d67761Ozn7kh784dPnZs2cnJ2szZWatLeIEE6e+G9ZrYY0kaIWI1QPLiPvMIRQE0PgZh3wXAlrvBxggEBkIiW4AwcSCJAEk3C26DA7MKXFOlIkSGFhSsBoAgQg5V3NZrnCx5KF3AgQIrQARFZxbCUgAFoeDqB1acfO/w8nVcux5Gdy0vm+pzliAtZUcc8vxJsVunQORTETISUSYqalkHA/P9kQAPLpXI2KohjmoorpEkAObozpUh9pyFiAnrIpqUBUYgzGQUIRTR4tFLAcceusSdAmyUGJKDELI1Pi2TXsfAKQjrAZh5mTVoQT2Qc4BGMjNd/0oPBsN9vWJIxsbIM/D8WMI1vZg+GSKd1hoN395/Km2htq456CmOd94Q3QgCHANsoDiodVMTff7cXs9bp9sNk+m/VPTTZJrgEv1geGE4AJ9BT5UPak0hERUrfXa7NLrZtLtdal7r5sJ9hWn2JqMVDfc9xEZnJyS4mCpR14o94RmtS+Zhr6Qh2EAm6qaalW16u7gftQBwZaSMSEhYCAyEiMSw2w+3EjL8+6dDctuhFHRA2yWioSGKXPf1zFJYk6laMSsQMcEauXFq8tudTISUp+pk23Zje7VtNayHhZWiwTqblr3C4noEFYni6uLU3+12VZNw6KYTtOIVpfLxdn69OzsrE7bOm0ZNSXpu+7i4uLi4qLrOkrSLB/nVJpmV+dAxjmVbECPdhNuXLk/UerGAff26ykjdFNG3Ixtj/Vl64DfHi0cvkIApyZHA9EcyhH42PABAL1l1QAfnw3cpl/4QXk3DrTh2/MGBCYC9/Y2FYkk5WG5MvfzUrLwR1pPz84Asb7YadTebDuOTATh036MABautZhFQCDS9dV1mC2Xi+bi4gYubq6J2QLd5nvYhgeI2FQ6jhrFx5t5s+8QvZWMpimlCFNTCItbt/32Pb+9bY8C0UQ0Fb28vLy4c2+z2ZycrPa77fbq8sWzp59+6+3dZmtVh2FQVfNIKeWUvLr0C6TISXC1xlrJFZCwMVANwMCmAtBwoQDNrwC4ocoRGWa1sbmUbD59gZAhWJhDwAyRhRKzMLAzACIs10Lc5YyrdVE1EewXmBKRu6lNhIQOgOAgDhhoTR0ag6A1/w9Hvx8OZwgwCGgL4faiPS5L90BEmMGJFHPqz0gEnFhERDhJzA7m7HGUGGpJEuOBAXAz+HIHDzQnDdJgDaoB6j4ZFwJtfOSIGmiOamHWWjGUBLscfQ+rnlYLWHS86GnosBfKQombYHeDAgd6G4fLgETUTlmjlEVIhJOkLlEmTsSEJCw8J6fQgMp+8BLCAzKygd0B5j+PC+s2GuT2roZb7Uicx9IObTQdgRHQ1F4MmvxF9aaf7KxOxYpOCAXd9/Xyeto+3+8+3F4+VnuZ01bkVfVrwGVQ8QCzyUpfdjXoBHpG16A922h2va/bbSkbG6/HVDDGOrlaouvAjjE5ADKUupC0BFoTXeRea4mUM7oJECbAZKpuZlabTlVD7+EhUh4rJkkdSxcsSByOGGFqXppCnIU5He5kI7K0ChICqrqphjkjokiFbGYVtKnqM3EKQnMtJRNrLYVg2aWpTAVsX/aTe7ieLhdY9eWrS1C1qXTDYtlL6tJbD+8ZwONXm9007kpFIkm0XixP1+vN9SV4Na3SYZ9zl3Pf913XNR/nBmrGJIjc2vBN3gUO7ZU2C8CD3NvN+fLx/ABvSQbFAcBzpIPFLU5Jaw0ds/JbqJUbi7Hjq3yiTj2ej3HE2NFhF95UBXh7bzcoTnx8ztywWMRMhKqBJAhAkcApwElMUl6uT5qAea0WwcWk2ss1dLvdbjtNOu3GduAx1hqIICJ1glrrNBVV7VMXDcrpwUQsTCgqalWbznOjkjUs6WKxQJwrg4810wIIMeeMtU6lYjgzRDSbu5s7/4mge7xF7RPZ7/cIAf1SLWrVy831/WFJhPvd7tnTx3fvnJ+dn1xvLs/OT1ixlALoAYZJhFPOyXIHOnIYuh1mC+weZBGmgAiNLxgch+IKAINAms880By/Z6VwAiBjJashjsCJW9LL5BihNgwAKDnBsgrgZAGpc8REWqfJPQgiTMGJGSGwbdO2SBvwJ24Vq3NpcDCDOS6M9kVbEi1FwEMuYRDNBBeFiZglERGyNJ1MlswiTaQfZjfJWSQNgRGYKMzdW78UoPXg2CBVg2JUIkaDKaIiNPS7OgVwzMxqYMYs1GVbLmi1hNUAiz76hB1jx5gYuPnszmtjJmQAyAJJCBWAZFZ4Zk7MCcNkVqw4ApDnO3RcN0fUNuLs4HhcRsfleBRtv72HW0rSJCT94HY0T/mi3Vy92XLutdYKQV1CAXWNOiUGNCjTuNXN5bR9tt8+nfaPI14QbKpcVkfuhZIRTarJKnrdWZC5IOCqqxybaSpTlL1No3ptiihSEa/cGU3Cw6t6JYvsukY68diN+3up437oslAW54pM4I0tpC1FhwhGYiJzpWbxKExMQYQszClaRmNGEBYeaqYK5nSArwHiLKBhblXBw1ShCQKqZmEQaawzbEYixGWqViswlWLd+RknGssEQtN+X1xX/SBuPWIKaIo/7p6ZE3OfZJk4Yeg4MrGwrJZdymxerdShk3Had5LNVEQ6Sa3h0Fr91shezYDegoWaz2qb7jTAPiLO/dR5eDtrSR5X0bHMP2b3cKtJ3bZbHJglcKsa4IPdptZKIHAY3x2VzXCGKEMT0KZjDX8bbnQrEcaDGOQhDsHx8m4/J7DpCDbLioR2mDiQSOpyv5iLiTO7W3U/TWu16vXqanNxupie7L2WAlwjum5qPP9mXDOOo1aLiL3umTkxlFIIkFkgyIniAAlt4s9H2lrT7BvH8YDhmU3NVKeWwidhtVnZDKAG0HHHfSwSH7b2MbJGhLlX930pedyvJe/3+9PV+ptf/9rrD+5fvXy1Xq/Rw6t2KaEHEwMFCiFEplyBQXIigDDTIm2GGQzWGhhzmUws2HyQkA2CkJs2IiDdzGOJWCRgHvirVvCwAIoAUESWzAogi95cwM0BzcJQMkvUHbpzhJmSiGklwSYORETG5GrIFDBLrMxml9BA162XaMduTVuiH/OT8GhgHiYBpFYUMwuJIBKhkHDbC0cHynZchiMSMSdzR4DMEgjm2mSTST0ZcHGeFItRCR8NipNSs/1DAK0KnPLQByFkgT7HkGzIsuhp6KPP3GXKDIwk1BpcAdAQeq1PTwHSBWAz1BGBwOabIciZsNnRH7MkgBnWenx8bAHdbvubHSq7WaYRDzV4Y5CpKlGgAwA0WpdXbVUnOMKh7+PuWtSqmZonj1Dwal6j7BMbAWrottZXpbws0yvVK8KNx9bBcmZgR2yyyQTEIFB9uqojBhbYZzCD7fWujoCVyCNx11QfDLFE03SHAqAGGWBFtAMophgmjDKlIafEHQpq1ZnnjuCuYI6EhJhEGm0ViZAYORNloARB7gqqYeaq4X7U0Jj9PpiQCe3mxhJgo9hoVR0nYHRkb9QyQhYp11tiopyy0HB2UjBqHUsFG6dax2FY2n7XIdbd3t03u13qOiDJuctqJ4vu06/d0w8e7QyAohMhQC2V0WudVNVdkkjXdTnnJkEzS6zNa5qBBAGQSJAdARwcoin+tMkZHdOk2TPzY7A5OqhP11rt4EJ8rAyO0Orbx/ftcxwRG0+qIe3aYPaQPcRhDTK42i0G8jHbtUPr3G7Ztx2fdjxV49Bgwfm9GAI7GCITeYRwCiQcEFJK7cqr2m4/mqpqIQgm2mw226mw9LVURKhVE7MeHgUpQw5XTEDEy2HY7ier2gBJOedjKnoUCh3HcRgGPrjdHRX/I5ypJdXRopqaoxsh3PbK/o0eN9EuYBxL1w2Xr66Hfvns8ZM3Xnu979LV5csui2pRLdvt9dnZWYvaXRYgQEJBQWKCgcA9FGwCr2CARhTk5oHueHAPRQSgIBQUICQSnPG+cOjtzXceEZCCiJsAw0FM3hFIJDkTBAMYAnYGGgRAQH3j0AcTOs2kXEc0aq/qMsu9OByUO8EiPG5bSII3C9hP1EyASMQNsUTMkjNi6/YLEAcyCiMJIMacPs/YYkTEtmMORbKrBcy0GFcT86RB6lItxur76juTCuQSNbyqMwI0WIRTTtEJdMn7jvoe+x77jrpk0vrPgeDAMudE7tg8YyLAXAaSJt7SyilqyFVowNk2kg1k/MT6iI83HD9xa+jWoa+3bKHMrNYqIimlqvv5ByHMXBK7g1YF5yOg6Namd0cFqOElbGyscgAy9Mq899i4jxCjB3Yd5gRBhmFo1tLosB44gD0AR60Rk3gNpcJYDEuQIhk0h1FzKujFrDpVwpI7dq+tJDTNBl0de+1SKZaVUZpNc4A1AHG4E2N4IBIyk8yEb2jNH5g1tC0izDHAVfEQJhsEth2NAnyckzd5DADAgB5ZPSoGUASiQZC75GRURy2eOgNXrYgJzKbrjSTMAFhqGA45d+6Sc3HfFyMuQ9eje6J4+/UH33j/cSBEGIADoIhM202Shl91mW0f25pGYEImSgx0KNhJNJyAUZAAZk9tvNX8aWsD6HAu36T/cQv91gJDO0abys3xPPrEM/HQ9j9GC0Q80p3i4wwDO5KHb6c0t5pCt6fBx2UMhxr01p5v1y2IYbWh64UQ3GcyZ1vnnepqXc4vLsq4USuCIEjT3Yt3PnwWNkOZiYG5qWhTBNZqSaD5urQ0YtH1k9ZaLWBWzG1ydbvdrtkDdF1Xa8VD8+poalaK5U4QAogZIpjnKlzV/ONH2Ld73G55qUMxFaRa68Xp2bvvfPNTn/rUV3/xFx7cf+0LX/jC9noz7valH6jJtEWkDinY3JrtQ4QhABNEkFtgRQhkbttJHb1t5Jb5I9OxMdJ46Yd5Uvu2zSIdmcFsVoZpJnjgB3oIEooBIAEomAMIk4gbkwi6AjOCoROImBmgo+FceRg6zpTI24UfUvOq+tisZT7fEICYmAOBmI+nPxIip5bgU9P9JTq4fbWHtMK0aQm5B7k3TAMSNUiVhEM1KqbTBKPiaKEYZmGBGk2OgfoOGSBhCFtmSgQpAQswNcYgEzRWPhIdsRJzRDMzM1n3mdQRUZlZmjAqegQzMwvNoaud1NAao/gxYs5NBLjZI7dKhNvgDZzxFayqxxF4O/NUZwlMdECeudqu5qrWuEyklDMOSYZFcBfB4ejmk9sOcA9QCJ1YEdSckiiEEWhEISsYe/cw6IB5omruDEGIFXyvaJQhkyMRARIC7mqNQEcKkQJiodUU0QVhcF0UXE77heSuqwFca6mlQiORM0lKOZPgfGISUcvoAymA3MHNEdpbK6H1KMUGiCIczI4Yh6O/jVNMm24JQIBXDQgQQaGw6BfDNE7VbayTCS0Ww37c5+F8MvNSQpWYvUyL5em4m87Wq3efPnWE0SoSN+Gw5XLAsTjaW6/fe3G1IYLEbeZsxBTe+jmyWi67rm+OsokYmUmEJREwkiDgP1z8499evjTjlxxUyxwwDqnAYWnMgkhwaPq3WeuRZAcAhDju9wgoSdzMI1qafXtW7AdlEbiV1LtZqzZu5yhzXAHgBkVtAek4lz4kzl3Xu3szC2wA1uO6Pb5oNNQRtJE+pJTcW0dF0Ks7tzK762bK1nqadpvLab+NUtzs7sX50+dXezeIqKUCoqkycZeT1mpqESjMpurhCDQMAxYCqEfVpnYH+75vSFC4JXXXNtHx23EcUxJEq+bMwpI8YCrl2Of+TR437zfC3cd9OV0vx3HUpZr6tB9rrb/wC1+5uLi4d++eqV5dXV1cXIi0VMEaBaYJ8UczqKEEwKaOGORICOHQ5t9NMHNOO+eIjTADZWZSVlv5c+RFJsJjGeQAfNgpzXuQOJo5CoZDRJ2rTCSmYCImAEIn9CBoyjiAyI0C3DzaAcC9aYk36C+ERxDd1Kx8xPiDIqEwApBwkxdhFiDEtvKJiMmhzXvn5s+tHgogzehbgJn9gIFJqFPlMK/m42TjCJNDdZuiFocgFjGrkAgZMDFlgS5BTpQzCpMQEcE8lJ5HKDNQyZstefsCwENWBMTIyCa5QduC2YRL4kRIbuYubdYV5IFMTRqBmjbtreQuWthoAgwNTeoI6QZ2NveazNTdCLwNu/yAmAl3MCcPA6qBEEhB5KEx1jSl5HLvYrz7ab33JuahT4yO0+V2evx4i7p9NV3vy5S45jxBnjCJuiJOaHsCaLPzZpVcvYyuBOZYRjdDEoyOlRk9MKoDsIBycO6ME6Fsio6IRhymHfjax9Gl+lrdQkc3xZiV6mslZHIASUmIhDiITCRykkoRQcQQYNPEEBTFowZ6IPo8lBQMomBAADcMCDeIIOBiFkGBrKGO6A5eHAhUfaxemSEydskle3jd7KrXnU7bcbNOFwQUoeTTAHaaaHv9ajsMC37Q1NQMifpkm+nu+ZKgTgpWJ06dE3CX61SREgIDEJJoQJK+Bi/SQqCXyNIvPODhZ74DAP4Hr/6NP/3sTxHRNE0eSOSIepRaAwBmAuIANAxkRNBwB3DEAxyz4dPcBQgAyNqoDrRMhAwUwrNuDwk0naWDDsvsPGW1Hlxm5qSk5djOFIR6MGo+SlU0RpKFm0UgR4N9ArfUFZA5SQN+OgALI80whxY8MKhB1tgDgVikOKNI7tk8rY3dfNxNHDOg7f7d01997wlg8kiZCKOeDv211ejS8/3Y9cbCiz5fvnqFQcWKOQon6Hqt04z58UDEJIRA4QrIEZFzLqWoaimliZsS8TQpS0LksSg7MstiudqPparetj+bdy/OtdTRfcXNCcCtWoVpEiG+vr6+e/euelzcuff8yZNf+sqXf9tv+9Jisby8vEwEq9XaqzHSIX0rDVpDzMIpzFggOMJd3SGyOJupYAAoBBJSAEFbAQgcx5wyiDDaseLRYGbejFphNsBFhkitjdESMQh0DKOoSZWgqKuBAQH2XRjZrE3tc/1g4eBC4A7apBLQIxQwQWOmNcvaCGjcrTkwzYOjQ4LPTAwoAUwgeDAya7Q2JDz0gg6EBwBsSFhEDwu3lIdMAxlmt1SueTJQhTrZfrR9jdFBAZzC0clSYsJwQc8cmYGZkRkYmtsjeTAikiMRSxBS08l1REcvForTpHVSWXU9VouAigQ5YYAIcxZ1NaZgYoIjqiduEO4fyxTwgCoFgJkHNAeem04R3qqhWqEfEC0gNhDkIeeN48iFAiFcoxoHnJ91b7yRXv/OuPNGXi57Zi3Vn76KqrzfgY5m1YhDBKkLRZDUzEkdcoWpAlVrUOqpujtSCZurygBrarHmbupIlcWlT4v15FCrU8oAZlqNSMHVvbpWCAVvbSgHd1UMTdys+ICIkBmb3Q9T839rgnVWi2lBLd4gXIeClwg9Iok0xf9PyCu1G9ZyJg83a01KMldJsi+T5Gwi6p5SqmoAYaq73fb07J5IwibIHvG57/jOX3j56leeP9vu98vl0gDzMJyfnlyYiqR7dx587Z1391OttQ6LXnWKgL7vU8qI7RdANDVTbOZA3TiWn1z9F+0i/178J//843+WiT2i1LJcLhHx3/3M/+4fDT/5p5//61/a/zhi8jAiQkAPb/XwsY4UpIioU4lmN9R87b221XVgsR4xeQgA5BHUlktL3IMPciW37x4iYmDruckt8/eIwBkYDg2MDkABHoBIeGzHEZFWjQhijtmZDRtDGIkQgykAK5kHeEZ0EWC0iFzLsFhd3L330mrVUiwuLs7zoxemsdlszk/XdSre58Uw1KrLRa+1MPenpydJaLPZbneTGgaDA4swIrh7KaV5Greej5q3ENuGybXOMYAY+74rdYaxsszsAZHmYfrJIfAnFlsbL5tZIm5VWq21lEJEL168uLi4YKLHjx69/9773/Vd39V33XazbQLjzH3To5+pvofPTGjOmoOCDmh6ZgEdw8HdwKzhzbnxvW913ea2XgAA+EGNsU3kAcARWi+oHc2EGAAUBypWG6oJu7C6QQCycM6ETfoHwhCYsTaFY3Vvpxa1ux0BGI3d8jGMGRyuAZhxNqnmw3LmAxfswDk/JCR49IKHFhsCo4GCKC+GJB1HZgeKiYPR0IrFfoqxxKRQI2q0biERYScoxNx4OAfBGiQgBIK5wsYD6M4h2ro2QHWtGtW0qpvLgiUMPHxkcASfnQXIo3XVGJq+PTaZVfpEALjV7QFoMiwHdjPiMVDOf95SXQeKG833Rgpt5Z+3DwLahgzHcAzse3jrs/zZz6XXP6enD7zr9qb7q+3LTdkvT+zsgqwwIlarIQCSU/KIAloQlHKWBXMkCzYnDgoNwuRJTIvzrGdNUAwMSUm0G6xfVko78xoETIIVXV0jEC0l77oqUDOHsFKol6hOFgkNCNqa4xlRm4Glcf8wnMLNzbXC7PAZQRjNPYtQRDQcHZnZb/kQHO+2N0mXNsZHDAg1pZSJiERG1ShTJynMkFu3BZApAnSqobFcrp6P0+feeOPZ9eajx08evvmmaUjfXV/vf+RHfvg7P/PZD97/8MVm9+Gjx103VC0RkHOW1g1MHZIAMhEDUkodS97tdvsJ33j/jT+6+Rd+/u5X/rlf/Ge/9c67L1++Wq9X9x7eEeafXP7UX7j4SwBgZ/bvPf6rOedh6JqZbW4CDACIKEhmqs35p5TE4oihUSNAiJkDPNyJcqvQuelYwGz0O5NH5qJajknGn//Ld//0n3h8nP3GDdjsFgjSrYUaDw3DFnjbhR0ylaCjIDkRogBKzCitGXwZrcXd8lMWgCDJqYs86NLOXFXLpKrj5Cvli9OTD5++cC377bZL9Orq8u233gQkkfzy5YvLy6vzk/VyuXQ1CNqMpTQ3U5pR1w3/cwyciNg0Idrb7/suIkop5DOuiYj8Vius1JpyblXab6R330JFSunYBGuQpGPgfPHiRcdyeXm53W5rrV3XbTabBk8iPmC0ImZh8BaDmY654DzCgUAIkmSmFhhmBEQAIXiIEYfm881Qp/0uJCKH+Y7MTgONwBp40F8jAQCBRisFgOTZzdxj7rS4tKQeEcENnKNZTgvDUazaPQLdnQLNG7J7ztnx0KPCo1DYHP+YGi3mOAdFhFtnIAEEtDVDEOCEIilJTqlnTFgB3HJwCglDLa6b0XYlJgcNsMB5ut7c44UTxwwbYRQiRids1MhjD7nFTIdm4AyoFj4jyzFAlsQgDoGJeaSoAMAURIASyIbmcBC89miF2a8vAuaz5tCQ/UQCdowBtyoAMHM4mCTceno7/emwDQMQQJBXC/jU23H/TT27X1d3AMnrtO9QTw0mZYLE2AHp85eAwqlTDwUElxFgQlwN64TQBXSqbMnDG+q2mGlABQxk5dhWdQdLPS+Wtlhfq+5BKke4EQaSBBPkzH0v5+dych7Lk9Fj3O0xsngmH22qrZuBzCEETe+bkgNqMbcaaq4Thh70Dw9ZUsO3hYtkOBjkftsAYE1EHmf5Ggi0cOlyBQWmviECI8wBHUQkdR0GRjGiFCmtur578eIHPvMdP/mNX3vvww9WpyfJ9LPf8dm333p7uVhmkfDIObOIaiXmvpvBJyyJRYgTSeryYrvbXz15+fjJs/0YzPJd/p1/+Mt/aLPZpCEPw/D1X/v6r37tly4uzu/fvw8/BADwvR9999PHjyJiGIaTk5M+51Frg9yB6fzWVCPC1Yp5Im79ejAjgohmdVLb6AxRcBa3P/SGD0uyDUVvvj8+mrKIWVG9PbvSGZTsXgMIwckRAGiyepxlqSk2bipxVQC8oQXNggAeHl6r/ezJT3/x+ocRGSUSQO8uFG52Mo673TgU70o8vH/v2fNXqhUjd7nX4mp+/+697WK73V6VWsy97/q+6xDJHLAoYlSbnV7aS8/YHlUiOdKUZozWfE7rNJXc9ccD3d2RqeX1n4A8fdvFVmtNKcGsU2UNqvTs2bOHDx48efLk9XsPVPX9999/7bXX7t271+zJWgDoum5mbBxGOwAw8yHbi4YFBBBBIDM5IJoBkKnGbA7It69uTv7bjx5PU0RvomYIAUExW3oRNL89CAgG8GDwQIAQwaGvVMC11RizHAgbOjdt6oDSjG0jAm5pZUccktLDbGnOehuM9VABHK4L6WCX1o6/+NgZSE30FACDmFhStxiGBYZwEKqSG1fjojZqbKvvNfYFaoABAxM5ICWEIGRBYg5GJAACpGPh1V6t2accKpdwiAhzV42qNlUvFcwlI7RFiuQeKCkbYDg6JYUA5JgTLGhDuuMHc2T3HG/KjMRoML5mxoQ3vsGH9z/rFzbWUAMjtdEic7JQwJiZCo1oiuEUNCQ6u0jnd8viFPNKTVEwL6gL0jCGgGnSy43nUdVJJEptBJFJcYe0gPCuQ4QUvrIMWoQwXNV8CjSSncXYEREDUEj2bjlFlJDitYIxYQAZAvZDPj1Z3b2zevBwfXFnfXpWDfjqenr2NJ49AqhQ99lREpEIipAk5ATAbgfQoRbXKbRonai1Hah1CwmZW9qBM0zSYTbGuUFCNuFHiwiCNuivzSOXKQCBcaqVglydmQOChPuhBzUJdsZd1Vd67bW+fffe4zr98je/eXHvzsMHD37v7/7dq2GRiN97993tZtPEk3POSG5WIbWSlt0RkADo+YtXHzx6stmVlPuhW/37P/y3//r3/k0A+I/+xv9FtZ6uV3fPL548/SBMXzx9+u/+xb/wtbe+8Z3vfOZX/au5y6vVerFYnJycZJFh0f3c+Vd+6/4HAYAIVAt4qCp6UNe1HdPAcURELIBu5ogcEYRgZk2gMMAbaAQR8TAEPi46OIxP57HhLQRRRIDbbhoDCZkBmuaDWNQ2nM45+2H091fe+Gv/ePUz/9pHf/K3PPv+1mbpuu7oTBAIP/rjPwwAf+yb//K/+s6/0nUpSwcd7lU5L7vFyWJ1XmpMxR7c9ScXTz58/qpM+9olD3z58uX5Z04x/HS1fP5y3Gy3F2engnR9dW29mZsX1wP8yQ9cubbdbpPjjv8UACmllJI5TNNUzAKIiDAIkOkWp/o3CQDtF2L40SbTzEopL1++XK1Wu92OiD788MPLy0tmXq1WTUE6QlqTiog4yTHtMwgPn9PknFSVmAIBwwLIwxvWxK1CNE2UhLd85Y4XJiyH3QAiYhbYNCNbHdBO5wBH4KbFKehEVmp0uR3LWkEaGRZJERu0hnOHWhExDMJVVRGa1iWA42wW0ArWw1E25/fMrSJpCHlmQURiOiJcA28ylDj0rxDJgFi6rl8Oy2UgsacUiODskdWlaH21qa+uYTSq4DXQA2Zpb5LERsAixAiJoUn4tIsjbAC8Rudr815EbOa0HOjqdV9gUmom4gBO4Am8midEj9RGWx7ogQ5uAUfYRmuLtqjufsNsAIDWW7z9USEe3NIOjyN9n5lprr/mhmOTOEdkpKCbYAEaZhiYSNZLXgyck2cREA7yTkBQ0WC7U+kqJ+oXut1QVO64TBUBKsaEWJlHgiqIqUvRi2uiaMjbCrwtkSTlYbhyaAK0O7NtqVM4JCbB5kyf8mK1XCzv3c33H+Dd+/TwIZycMVC33fPZee0kwKLupYyJmxNgCuJoP+3WNH7DFE291lBt6tbtZsaB8NLSmdv7MA42Ve1BzGYWhxYkMU+ldIuh6xdWJ2QSTFnyNrThL1S1jIFpCEBNNFohAazja+fnL1+9uFgt75yt95vLIQsFv3jxNMBbSGYmJLdS2yfOnCXlqp5BPnr0/jjpYrUiSonxl177arvaDz///vc9/sLV1dWbb7y2HGSzuQ6zl69ebc6udSq73W633QbzarVaL1c5pz/6r//3AOCPf+Nf/BPf+iN9Tg0QJUjAYE33hgVS6y5ShDXTJAAzc63ect45I2y369a8qj3cbfYFa3y6W4sQACK81gkAG1wJiKb9yEncvVRz9931ph2XP3v+83/54V8BgOniL/7Zn/mzWhURu65rw+1hufi5i59rr/gz65/5w6/+UEkpwnMWTj13Q788XZ+VarHf7+s0vvXa/ScvXhB4Q3Nud3tV1To+vH9ns7l++fLlG689XAxdLWMpkyA4U2lY6MOVH3ffEa0UBxhoSuns9HQ/bqdpqnoDnDWzqAAks6Xab/yIA9lVRPBGssfHcez7vmGNttvtMAz7/f5Xf/VXf+iHfkhE2iB6WHSzVh20WDMrIcdMP6LDVL7tcvaDiNjcqADAsKY6GTErPuEhiYwWy6nJ2nG0sAcwI0EdEMLBSZibSGXTj3EMdwkhCAKEMGvaglAxmmMEBhpBQ496tGO/WYwHEJGHx68jUOAB1oK3AsBNP+P2nOC2KACAOwCG5G6xPhuWKycBB6wAVVktq+Za7NUrv7rifTENcGxkoEZ7R0JidD5IF87G9g0ERS1xPq7vVmOjB4SjudeIseKkMClOih4CFAJk6GImgO4BdFB0oYZEbxj8dquPIXB+3Eah3WDlDnMPPMD14DfQIGyPhhec15nZDOmAmSoMjNwLDGQZPAEmyCIMHoZKubMldT2kjrtFGnSgGLVMdU8NBRsSEJooeunWw+nJ+oS7haCEJrSpaA3m0cbgUsnGqSLug0YrBTUYhZkwGJTd+m5x9vDh+afePLn/ej6/GE/WsToJoFjWQKIyxrSH/bVcmggQMxAiCyA363gzO5B+q3sNd2ICZJQ2NMAmDNiaP47H+c0NUDIOo7Omvebu7gbN+xpR3aZaEmZC9OouIUwRUaayhITBxFLJ96rUSYSS6cVqsXv1Yjxbvfutb4z7DSO9uHzeGhoALonnwBMREbnrAPinzn/pO771ma7r79y/E5REUpfwj3/rj/6v8X//o5c/+N3vf2Z51iO5qg7dw5cvs6r+8f/RnwGAf+L/8cXf+3d+aymlaLx49tzdn33/i/bp/2f9T/63Hv1XFouuH/pOkoi4GjOje/VCkiHC3Yg4QokEgSLCVSHAaRZXmZVIrFXYv+44a7Njs0Pb5Cg+4aZKhI4IVkPRzHa73Xa79cD9bufum82m1rqIDF8EAHjrV994+tGjg760EfE0Tcy8HBb/9P6f/tZnv/UHv/LPvHz2cpqmnBgglCLchEH6xd/7r/7Ul+/90o/+zc/c2Z6erpebsUBTzIj48IMPXr9/RzgNq8WLp882m83J/XuLrp/SmAiNXJjVZs+y9l5ajx4PfuLtrQHANE3eDHnVzKLNS44HUHWDgy3zbxQAWorWEo5GrEgpIeB+vz89PQWAcRw7kjYTfvny5ePHj99+++3DXGHRbGq6lGa8FkRKCeiA+URo0C7E1mwhInF2cA8PAp9L3xkHQMcaogWANvBtg9+2azAQoLFFmrEpgs6xJxBn3kPbX7MjkAA07TIUgEByrGDkDfvkOgMmZj96CndAJOBPAGjnE464HYO3AwDCzeD35pmHAxOBpOv7xaofFpKH6hAQmYGhpggax/ry+f7pY315Bbsx2iC6vdfmKDk7CzRFltbzCUREQpQZbTkPQuZu+6HRWjWK2370fYFRY6rgIMxEGG6YgtRAAY5tGWx9peCmIXVoVmN4OHhKKQ7BZu4CtR4RoR8pmB/HFB+/aJM7OJxxjRnQ0tXmnd5cUjJLC3fci2eORJCRegT05pbm5OYRgSJ5WCwxMW5BrypUE2ZJzBGCMayX5xcnr92/+8ads/OT81WXJErCKFMdFa5LPL/a+7Pd5YtXPk37UioBCDGJMFJCAmSnYTV0JyfDnbv9nXt0cmbLofSDByFbvvBUtrB9ac8fp3HHFJKEJc/tiEb5dwPTcAOzdszTUUJnXh8IiG1odZQSmmvdmx4iuHnuB5JULCqhEC1SlpwwI2tBhDLuw0G6IWfSarvd7u7y3FQNUgEfQ6lLYMBuZ4vhakLX+vzJI62jmo11jDlUmxmbOSMlESKywC/9wT8GAP/i6X/zT77/r5ycnaeuV3OM8jvLj//ol38AIeiMx2lT60RAwrgYhp+98wvtQ//g84+v/9aVu3PutNb9dnv+08vf9re//53PffTj//EXvnn59dXp6vT0dL1YLvoh56xTiQjJSac9NmAzMSAyB6K5OwPFAa3fKuyWEsMnctv5VAhu9asHeKjWI1YxItziJ09/6q985q//yMvv/yO/+Ic+evR4GidTa6f/y5evcs4A8Of+h3/m65995/4vPPhG/HIrPrqub7yt/Tgh9196/0tfii+dnCyf4JNayzSOAZGWudRK4N/69Df+o9/59wEA/9vx3/jKD3zq9de+/s33IGKcppPV8smTpw/vXZj5Ylhe8ctXr149uHvR93m5GMap6G7kIASMGVZ3423g0JxgAwCQsJaqpklSo22XarP+CoQ2q2f82Lr6to/WX6q1uln4rAxBgABwfX3d+DqL8zuI2NjIT58+/fznP7/f71sMWK/XHiFN+iaOJ8Gtz+R2J50oWj6nao4ezZyWHGzWgjtaBEIb/2IARIPeMmODhAI6GAF6ADqqG4M0MM887/FgTFrK/JJIMEuJCIASSOtRIQBKkLcCaEYBEZHHUfHj5vRvf8b8G+kokhAzi+fQ+UG6hYrBAJCcF8tVv1xLN9QA5hQYoBO6Uy3l8lV99mx6+ZKmMWo1xPCY++mHaw+Gdvq3lB+wRRxAornb1MIAtNO85fAe6jGpTxVqjaIwVXAXRnWL7OSGDhRBJuHsYEbI5mgkBqGqWYjaGLgNamfKRAA11CMGAjCqe8z+5y2l1WPL9fCJk5liU4Cd924wUFgQUvCUDZVl7FKZ6gK6V666Ok18F3GVUq8EhO7mCLlNcwm4Xyzu3LuzLzvFsh+35hlEGEO8nPTdnTurB2+9ffHgjeXF3bRaQWYUNAxQlQrdflq+2q6754vM+PwpbvZQFdwboj+jLvqh64Z+WMj6Tn96nldDt85pGBIBuBbwadXZyXp5djosBrhCc4cgdBTiCAdTsCJ1p2VErRgcEIAeSMQUzoAUJI4sksQj1MIUwc1NkACTgpqNDuZoCqr7LYYEpuIxgvGir0Wn0Sk0piKuTAl5cYUcmMcyTQtddP1OCyTK3CMhAem+9usTWC4zd7ap/fnwyx++82I77vfaPIOq6vbHxo/+1Ku7P7v4oZ/Ov/Dmt9rS/+U3v3F6uRaKTJXCJydzRxI3ZYAhJ3QN96KaGH7o6ef/yJf/wJcf/Mo/8/P/1NnD1ePHj8w1Uex03F5uvuevPfwCPhSafnX5i8v1+vVPfer8/HzRDxcXF5nlZ+9/9UuXP+ilMDNIcqJgblm+uzNS3/VwEE+CRtBCcDO4fbq5gVZ3L+ZmNi9ICC3VPYggnADgr37mr//0+c//9PnPv/UrD88frTygap2mabPZmvlutwGAcSzwa/okfTQsFjlnBBzruC/7nPoAINB3v+uj7330hanWcdwX08WwIEJyW+Zktb72lbvtiu78/Oq6lof3H15djc9eviJA96DcfePdD77n89895JGQN5vrzfbq7HSdEvaJC8LeFUMRaB7LAdRxUivGGVjMTIStejBF0FhLFyySu06IaFINNyE0CyHgNnqbsQbcwiQ22cYIDxdiIdao4REIIjzW0klKnDS81MrTtNltF4tFv1y4+5Pnz7757jtvv/32ZrOpDpeb7dnZ2XY/rtdrM2tIemB3DyKJuJFTJsJAgQDghEiMXOvUtDMpINTCA5PMGVIb87i23IgZw40acdUjqKVVzYUPwhyaET1HRDCGR1Mmpix5MgA2aKUEICE5eIs6kpNpBAAyoFoTznIA4k8GzvlratNYauq9zfECcEb9OwAe4ZQOlESTpNUaV2feLY0zaohTaDEwKjt5+tQ+/LA8fsRFLdggKxgLo7k0UWwWSoklOTfJMQlOQUwpU8pEkomwyRpAwEx5CVSnSbGqjyOM+9hPXCqb1XEUCG9ICkJkIAJAdAQjFCJCCKCwAGkNZ8Jjh+d4oLfwFgcA//HutOaBHBtEB+ZwHIUbD+NxRIyDbcCMqIJWjgV4UBZaLLp+gdIZMSECeJLkxogaXlbrjuRit++ePH8ql5xSPuv7GmR1TMAnZ6f3Hr7+8I03zy4eLNZnacjc9A0w2B1LdLksIJ86nJkuyj6VKSMGhprXUgFzvzg7OTlZDEsZljIMeb3Ii076IYO7ThUAgmXopeuVERGa27iwuBt6eLWoNUzDLGwGLbZYfegPYjgEharSoV6QwwKbaxwkdwcEj+Z0j0xMGB0zd931tDXHbpE2++sOscviQE1nQk1D2ATVQqt2Iu7AQEPXXWnVsCWnadqdLlfTuJ/KFICmEAQO/sGffHn1I/tXP7J7Uq7/yRe/94/98h/4ubu/8iff/6OMJEw6TQ6BIRJgEBhuU01MHYuFempObPQvffUP6lds3E/jp0bkePb0EVgd+rzbTET8/ucfv/aVs3G3eXl5uR/Hk5OT1x++plP5v/72v/fXf+j/DgD/+D/4PxEhcnEgShkAiCWlhAHm1hRyPqYtEXKclwCAR9gRK+phYM2hpjkNhYOXMPMfePw9P3X+8wDwxi/d/+DlBxFRrOx242azachbraaqjdW6u74uSVYLTzkP/UIY18v13/0n//7f+V1/FwD+l3/uL9x/cA+YiGjc7cftlarmPPSD/Vv/xn//5+7+bP1/vnxv/8H9Ow/v3bv74eMnwGLmfT88e/Zks93evXtvv9s8fvTebre/d/eiH4a02TMRkwmTA9sR2hfuFpOVohoRfd8jIosgkZmCh4diSPMPADP34MylGJInxmLtiDhYsMahjIAbvCkRBcxwIFVV4nbD2+i7lDKO43q9jojHjx+/+eabKaX9uO+HfrvbEVFKqc0MGqav/SAcAEuH3s6cFiJBELCIqwHE0dmNiD6We8/4wI8l44jY6Mc3f+sR4E4YB0bNXDA1cIowqADMFKyGWAUnhoRNJa5hC6gFj/l0a+VX3BKE8IgjyqYFErxBheKBWDerzrZ0t1+sh9VJt1wBd2FIFBwOAWma6PJq/9Gj8uyF76dazJXMIwiQSISSJCZgYWCGpsXLCZmDKYiBKJqs6VGbHaBdXNO1M1UvtU4jlBplgupRFYoKEUEABhtHw9ZiGAYEJA83CgVPRI0B0N51a0I1ovTcbMKPfyYf/3iO9wtujQTwcPYdi4P2wRInquBAAMAiSgzM3BR+GuwBiTEyYQ0QgeWaNSSIq2KAichisSAWzsvtZoM+DcuLYX0+nJxT7pxZhSkRChMEGBtpkEDqUjf0y8WwWKfNKE5qalrDgGnZL85Ozu+t1stln3gYuM/U5TQkdkdyBjPTpoQfYYTC1EJdhJmbei1aR9Lqqm5O80piYoKG4iBEwkA0M4CZUtFYSO6zHG27dfOS8nAMIhz3Y14vp2lCADdl7NQ858wpq4cw95IDoLhtrUDqE8Or3abvhlomAFAtSEQYjVo2bXfoAQ5mHmFIafkT+eqLewB445fO47fHf+erf2Do1+v1mWkx9FonN1XF5oiCqm51NJtFY9EQgahpQyhxaNTVyULkwW6z3WyygP/Fv/UfAsAX/8Znfvj/+PbVdrN/f3dxdn59+er1hw9/6vd/pa2fnzz72R959n3I5IESLjkRM0a0NshtRmv7gpCPycftTM3MVRXCaq1WJsTglo54lFr++Z/6fd/5a2985tc+9a0PvvXixXNzQ6LNdhsRIvnq6jLn/it/5GuPvvf59/+Nz336a69nyUKwXizPz+80E/l3v+vd9nL593VvvfeWu09ay7pQ3L26vJ7G8Suv/crf+V3/r/tfPnv7P7u43uyePH3qQSmlalFKWSz61Wr16NGjz7792dXJ+vFjfnV5/aZR3y26bpvyyBoIbh4O3DxdHduslEutLeAd1Hw5pczuHgZhACiM2KVpKlatYyCAIFRrCNpokvy3ERvtt7WxXBs5uDse9LGbhXLRykm2+x0yLRaLq831k2dPP/WpT11dXc16HkT7/b7NEnjGX80akW3RHTb8oYXSqhEUbww7vPns4DdFrB477/Ax8T5oN6Adu7M4FRMCk5OEGwYohAuZQ/vpWaY9KAgEsK1gR3fnQwD4xKJCgCbJDI3k1Ojr7ZiCAGjdeQhwIBHJ3WLRrc/zYkV50IM4DJrHNHbPXmy+8Y59+FjGadrXqhFOERzubWqOiJyYcsIuUZe9T5QFEqMI5RRJUDiYZy/rw+wkItA8tOEmJp0mmkaqRkVRHao22QhEoMBQBydwRmsWJtTs4QiQoknqeTQBu5iBpq0LBvTrAD/HSBhzAovHMe8cDBCO9POGWG0dcKCE5I0mYWEeAZLSsEQRTCKSKGf0kQEL1JRIsklySZE6FKGU0mKxWixX5gmBKXx9dq9fnkm/BGJmRsZgAiLAMA8HsqbL1SXuBkx9IKmBe3RJhpy6oR+GxXK1Oj07W6+6PHSYmbLELAnDFEGVAQLBiRCI2uRDVdEVTN2Ka238izbS8VbO0k0AaMIdR2wGIoLPVdQRthgRACHMNdzCIVz6XFUVw8MowM0QiXNPnL1G7visX3y0vSx31J2gIucFqhnWbhjIJyK0sN12yxFRdZG7xFRLW3rCzJ/+q3fu/ezwxi+e5C9Jw5gvVwstU62KUyBZGUcwRuIGEOQm2owxTWMwtuBlAeRAZouc636fUkqZRfjFj27bm33/C89/GN7q+zRN5er6JYY+fuS/+z/8vviv+xeff+EL7366ykjCQAyQIczNIqIpkUzT1C7suDOtMcwPk08Pr6aqCuam1cysTO5GCFqLVwWHWutUy6efPXjy7KPLVy8onJi24y4nFpFpKudnJ+9//tnP/KFfAgD6F/DH/vIPMHPO3Xq97pMsl8vV+uRf/fq//Ne7v/nFqx/5wWe/paaau0VrzVvg+Z2622z/F1/6S+++/v673/n+nS//ztP/5N7u5fPdbp9EihZE3Gw2b7/5xjvf+sb+tbHL3Xp98upyM5Y6dJ2klDtZAozTNKk1xcZoVLhD8nRw3PSGcUopZcQ2xWsIoMzYL7uhH1hoHKexVLOi3iQw0TEwZu8+QjK3lqhFBM/i0ppyZ2bTNBnWvu/bRm4iRYh4eXn57rvvNu53KaVVD6q62+0OvOU5jzliCOmQqB4DAAIihXpEEM9E3DAzFvnNA8DNVwde2HzUuM+e0u2fCBEIKNCb8DegGTJ5MBBgMAE6mhMSEDSwAQY16pO3gulmIo3t0CP2GSbH4cdzD1oa1MjuQcJd3y+X67NzHi5CkgMjBGOkMJ6m2F7j++/bux+ky810uQGD8KbfTSKzpz0gOiEKYZdwyJBS5AySTBhz+zZBkmCKxgZoFxmA5mCOYaBGVVlDzMUAzcJdmNncwo2JyZ1cUTUNQ2s0SJeYw1VtVtgDbFgtdxJudHmDiCbnNPf1bno+AMC3UBktDMzKX42+HXgsDgAaToyDDNwBDQlQ2BloWGDOTkhEEJaYwApiBBmApUTDoru6us45rVarvvfcLdRSrSFCq/XZan0GFsgApqzAGOiWUm5KOyIJsAQlSIlTRkosssq0XnZa9iA1y3iyopMVn54Oi0UnTC0mRlOqCUdwDA9VMHd3bBkQAEKUMoZVCnfTMG+ymYBAzBbBzRid5hKKmUOtbdlocH8id0U4bgalxI3rohgBmLpcpn1EZJJaCpA48KQBQAvJF8Py0eULh3ChSbU3W/aDBhZtboKyubpMQIIJ3d54+HAC+/p7H7DTcrWQlAjj9KeynPByMbQmA7hZrVaL1YpoCBEFDNBMwXxS01qnqgBgViICiWvV692IRA64324r+nYsxe31r97/7X/7e9/97sdf/A8+Kyk7FcZERFqncaSHP3fyJ771+x48eLBdXOW+74cByN1rnZi5WfUiHGTgbi+8htaLiH/nr70BAH/yj73jDkSkVYnAiqoWN6OIWUM/wt2mUn7m4stnX+9LmQKh7/olD/0wjPtpuVwA4Or9VXuh7/voc/fv302p67qu74e+77s89MPw49df/PGf/FEiooQn6/VchiNU9Zy7oet/6+5LX4VfBoAffvGD7559c/vimZnGERMBsN/vFovFN77xjbfffguQqvqLF5efefstkZQ6wankhPvJzY04RVDV6gDa2K0z7BtFRNXcrXqkICDAcIxIJIuhf+uNTz18cP96s/3me+/v3/nIGtceUUjcnInnczlm+d7byD0za8rHdSrTNKlZVR0Wi3GaVut1qfV6s3n85MndO3c2m03XdS13aQpFq9UqDCKCAlKfXG0+qXnOVefxaGtHzy2hb9Nzv33+3j79EW+OkZY10eFX0q1mtUVAy1GEMZxRIjoDhDho7TXjAfMAb11odJxN+vRGGPzmtY4JP7axBB9vFxE6BBCh5K4f0mq1Oj3tFuvA3pCa55dozdOer6+uP/jA3nk/XW1prKQz6iciiICBhLgXFhHqRAm8cYByhtwcHxN0KbqEKUESzCkYkemIFiAHLRWrwjRRNZwKF5OAUmpuwnFB3vpVHUMF7Bk4M3cr6XNiRFdJTBBoBu5t5NsUowKAk+Ahnh9v9G2UcRvWH7/Aw2NGg0VrxAXLbMHqgAJEDMLS2K0ydGm5qk1OGZEAwx3dISzARHLXgfnUdd1isdyPNaUu58V2dIu4OD+/e+dCiKMaRiGILjgPGZlBlRTIQBVdtVgUR6DULQYpm76n0zNBk5T04o7dO/PTM1qveDmkRZJMFARNlZwRGYA9sBqqIxLMphLmtZjWqGNUbXomB1zYDWvDfIYE+S22SER4s4UCAoCq2rquEbG93kjXg6TJdHFyauGAyECMcH29z6crlFzUkDmK3l2dDvjhuB/XZydj3Q+EYT65Y8oWqrVAkycF+PC9917/9FvXOr776HHKvFquWGi7uRTC1XJx587Fer1CgFCrZZz2o+lEaASRQszBVMdSt9tdVd3vx/04bjY7JK6qgfji1VUxTbnblykthsurK9UqRJ//9978Ar4JECAyJAR3AkwphfvXvuO9n/hD/5/ve/8z/9w//qfa6ZOHAXZbEQlXR2wA7ZlFccuizppC2KFvpgcKRpi6mWoxVTDbTdM07iIi3KZp+vd/2//7//Y7/z78S/Bn/7U/CgAkvMy9R6TVgogAKKX0l/6tP/POdz/6ng8/x+uUUl4sVjnnLnUppdwlQCBCEhJGs8rAyA3n64hMXf7vfvAnfuTlD3zXt95+/LkPGXz38slU6q6NkCIA8Nmz58tF//Ly5ePHTxCFuXv3vUff/bnPdYtBps3Q56kq74u6ucGkDgYsrHUegghH69QjgrC4l1qrEDDBkNPQp9ce3BkS3b84e3D3Qsv46uXl4xfb1rq2j+9fOLRqzQwQmwHZTUvhADltNIimEdRKkPfffx8i7t692yCoLdMfhqHWmnKOo6rEATsO5uZ6EFeaoZPUPHsPM4A4mEKT3Bh5fvs64LbwzuFwuWk+zwczNqopRRJzkAAPTGEQzboGyJuVCAZSBNA8TgD+hGHcIWFFnqEsyHPNgISIDqCAIj2v1sPJaVqv07AyFrLmEOuM1lkZ9jt9+sjef89evvLdDvda1YyoHXQCM0u0ybBTl6RjGDrqk2eJJJAFu4xdhzlDzpC7YJx5YRDoAO5gDmqwLzhWmioWSx5ghuCcsiAGIwE6YOQkXRgJ56HDvkcRpECPRJk9uCpVRZqJGE29oKpiM629tXqOGf3N53ErSs+fMdiMXZqf2P4SHYXIvDUlIRxBup67vkpT2EBEJ3eEIAwi6vJQJnefFsN6P/lUNOceSYJRuv7unTuJSUsZtaiQlxQ7gC4ZszE6Z8Csk5f9flSvHtF8lRP2Xdy9050shz5drtd0/x6cnLAw9Bk7poxoSAwRABbBAeLhZUI7yAy0NrR7uLb/3ALMY0bOzsu9dV4j4MC2nkHrEZFyiqmazQ5NLcNtln7uHhCcUjWtZoiYiPfXG0lJJFf3RHnolyUiarl/cvZyP2p4cbu8uloOy2J2VcbGvg5vOD++evXyTfksWqwWi26xOjs//+DRRznJejl0OQ1932bvVYup1mnUuieo4D4ZaLVidn21vdpsduN4vd2/ePnq8eX1WPRqc11NJ7WxFAuYSum7AQJykibNu1otupSY6e46D10iwiSEyP/5H/yVdz73/Bufe/L5b77xg08+J6lzCIBF63IIEnHTKJrdlec8usmyz/f4pjho0desupm7Wa1l2je+ktZpmqZfevMb7cnvf8/TT3/9NZhnip4kI2LfL0Ryzvl7P/pO6rth6JkzEDiCYSA4hTEIIkqzMm/TZncPZwK1CYPD4IsvfnDPV+vl4v7F3ecPH+7241h0u5/2+33XJUYBgNdff/2D9z86OznzgMvLq6dPn56fraeyC/OpqghPpTVnrJqGWjMqaeddE2OIgP1+zISq0S/T/TvnfWY09Toth/Onjz74ru/63N2Li/t3Xl5vx83UgC4BHz9dm2ycu4PB0XytNcHbsQ5Mu2mk66vFYvHy6vLi4qKYDmm4vLzMOd+9e7ftdGbe7/c55/mXuJsqpdRQJx5hbtQ8RGc0SdM4YqYjZxvsN6WtfSwGHE+hw3ZyuyUeN3tUzK/tgYfBLSNygLWMfjaVC3CApsweAUe3OLhVdwLOM4D2Xg/zdGrT5iS5W6/7s/O0OsFhEanzQAHyUAxjK7jb1sePxm99yz/6yPajq4O5IRoCYDBGRoDWkUiJsiAR5IRdppyg76nLmDN0HXQ5uhxZIPGhv40B0SbAbhZqOE48VSpOahjobiwCCSXlFBhg0TxdJQASdVmgT9UBCCX14E4s1BYJ1VbbIqIjCAvedvq99Um0L1pqD9B420fT7YMJMBI0nXcICGARIAFHaD1uYXPkrufcAzM0DcaZAELEIRBTAQCBEAAS5vPzU+aOpZPJU8596utmU6dpO20kPBgUXJiMEXLGfuFpcTXqy+14Sbmos+TU5X7IFxdy995ySOW0p773ZV+GVJNElzAzC6cKSNikP5EbibEqWetsQoBhE/6sBWp1VTB0D0Kay9KZr4GHSADUKJeHkrdN3iJmYrCZetjsowAIgebNPRmYOcyYOES6vtexpNwTEYV51fWwfHL9rKp2Q797uYmADXgRdDM3Y5GUkwSG0zTuT07WF2dn0g+IcPfiHMLrtFsul4vFIjxSlt31tkyT1qmM+7DJrU7bqZRaqr54dXW93T9+9vzxsxcfPnnyymA7jtV0rKoQkruqisTL7bj/rdP23yz5P6Xlvy05SZ/TajHg6xcX52c5CQLklD/9y3ff+Z7nAPDmL15suuvlGmhPy9UKwlRVUpeSNNMYb+4xzEQcEbVpf93qCzdYGzFChQingMk0wonCXd2qef2v/cc/Zr/HPvv11z77tQfUFOPN+tw1HTwhZgQBSizS56YX1kSD1bXs6ziOq7zCnMEdGR1mIhICaK1alJARhdwIoE95tVq8dv/B5eV1qbrZ7WudEOD6x8b1V5d379x5+viluw+LZZmmDx49PjlZnp6ejPtdSpISs0ExQ4AIUA0EY24jj6hVmQkAUhJ0XQx8drI+Pz357NtvnK7X19evnj95nJlfvHi+Wi6GrlsvF9vpuuUkdotR3E7ednubLknOuezHJsRPiO6mWpmplOni/ByRLl+9WgyLk/W67/vHjx/fu3fv7p07qtYQROFhOmf6ETjrlTZFipRnrgYEz14LiEjE1FS4CRHdWikwJ93fDnByrADi4PJ8iFgwB4MmGNuGb94QjRWlCU5CKxqbNgUAxzwscIBmEoAEeJhg3rx8ADrSoctER1VCIELO3WK5PD3vTs5xWDgnE2EgDgNFt4pl9Our6dGj6aNHeT/tLCKiejhiMCIiEyREa2hPZhJprr/Ud9B1mDKKgCTIGYSBOVjwoAPR7pOHkzuqoZqPE4wFikLV40g5kMRY3J3ngQ93wIA2dN3Yr6x6zuKmQEZD6G7CZuTL2GqceZPNRVY71lvc9kMkR8eIQ/kFfDjOwD0YUZAQAMxbDIBwJzNFQsyD+b5utxRlsTBcRnSMyKCO6EQBDOiJfM81mBwSBOasnSBTj3TWLQncwI0Iw2sd93srDOGXl9N+lzoxEl6dyMnFqxIb9d1yXUFyXpysLhLX+xdxsYYu16Hj3HFEIXZuiBnCIBC0MEcQBEesVDa033AxNkQOq7VO11j2ZCWqspsBBoETBrk6cjhhxkAHmyNABCFNWpOIozfBqLAgwlpbz9QJkWkFwBbMgegwdAs13ZVd7vu0Wk6Bhqn5C9U6cQJeDNsn0x3gai6djK6jF+mW0zYwCAj3PlWLJHnSMSW+WK85JwB87e75o0ePOlqen91bLM87SFic3UL3VrfuY0Q11/1uu9nun7569fxq9+jF1TuPnr24HveKyKJMqU/1x/f9P+yKGYK629am7b9Z9HdY+R3G/7DzfwA61t1+2u72d8439++cnAxpNfQ/9rfefvOXL77zG6/v+5I6MR0JUi17s4FS78Ctum8u246MIs3iAsnhkGccjwZEVADM4mNEOIYCWNUy1l2tU9X6xi+f/6lf/f3u7tkBAJmrowPHrMESAA6oDjCaEgsECHMSMdUuZSQZ8dpSR8Kp7zBlYCKRqUwdIkSkoTctpdq03yJin4cEcH+98t3++ulzBfjm8w0AxL+zee1v1e/73u/6yi/+yurshPbpW++9+/pr904WOeVOeMrMZBMooKNXh2hEhmBp0HlgJkIOxGXqTvp87/z09Tvnb967l3PKzLXYtLt+/PjJ4uRsebJaXF/fZR7Vq4Wq39bRo4PtcCmlFuvy4L5DFrWSu34qYx233A+hFcPu37v76NGTabfbXF5dnKzrNL7/zrfunZ8NSbyMWEN3W172uQXsUACsOougcDi2cxSxMdsRmZk9AhAbNnVuT7Xjl2aQaADgXLcgImlzk4ommoDW8nugpvljQK0/EzMXOYADQ4ICWs8WiVPT4g0gDMAwQk5z/QgznxhupRbte5RGVwMAsHAgUfBAXKyW/dmFrM+gX2LqhDAHYCh4kCuUES9fTh98WB89l63xDrpi26I+Yzo55YwYCpy54048EWaMTih3QD2lReQucg9Dj4vBu85TYpEgdkEKYGtNZAMttN/D5RVstrHb+76iRXBCZnAWSZJTsqgM5OZBkQmBJGXx3Dl70x7KboIKk4AZ4I3UxMdqrltFwPFvDnfpaO95+97dwECZD/+GCBqBGNGOeAoOSCicEmVxRkMMgtYlDEP3hDGFgxXzabkacpeJVlryXkfOgIHJyb1z7azAXm0qVc2puKKmbLgbr6pdVYXVoluue+mplxOlk+UmSRm6ocvU9esurYQ75iycmTkQAcIQvGmPaI1xH9NE5uCtoWPhBq37HB7uQHx4xzCrvyHireEVBEQ4N9tkU4iGkopjNQABgDi6gWMwQ5+nsFGnru/219r1nQPsdrv16R2qobVgQNd1ebE4vXPxzvvv33ntIQujQxQbt1sMaklTLSWJIMLzFy+6k5PlcrlerxerZa31I/9w+ifofHPBJAgYPos7BoJ71KLTuJ/Urnf7x89ffvDk5Tc+eHw1Wrc+HxYy1Qqq33r3XQDo/+cr+XM9iSBx35/Ez1xf/Y7nAID/aLX3EUwTcdnVzfjs8ZPHq9+//P4P3ur64eFXTkuuhGNiZME1reFAU48GDknSWmPMAojRLisADlI5re6cO7aMWtwPuHOPUFczU3OP2cK+tX3a/ICRrE5uEAnG2tiNAEBOUM1cLYl0KSPAYrEYun6ZpO97YqatpL4DxNRlYhpLBWJwDyAzhQiEIMJh6JZDv1oM68Xio+9/2TbF9Y/ur/43129/+u31erXd7c5OTz9874MnT58u33qjqYyxcEqiTRcJycIlYURUdQBIiQK50ds65rOTk4f37z24d3cY+pTSWOp+t99tdshlr77Zbsdpurq6LgacBTEdG7kAcGziI+Kxy3+cCbubu7mr1vroo4+Gfuhybk/uu365XL54/vz58+f3795LyCJSS0EGCOdD4pyzHBspeEwlP3FMzEn9AdITx0MYbtS6DxWBOzToJ0BTkvD5pZppBDermGNHOiBs7jszhRM2Ki/NbrhtpflhhhBxQNV8/ArnPToHJ2KIYCIUznl5etqfnMhioL7TBpYMR3NyiKnYq8vy6Mnuw0ey2YJDqVqnau7IiTgHcSIRRhFKJKlLnJj6FH2iPmOXKWfLmfscXQc5cZcxJRIJJiNAg6YC4bVCKTHtfT/GONpUoFYycos0LAjI1YWZgZXcEd0biJEiovZ9AkMAZwAyZEghCaw2xP8njv728IPS+i2k/8fnAbc/Zrh5zhHGi0iIFgiGiEHOHGytmkFvqx4AmIwhFDWheUZIWBLXLsdi0RNLGAZMJysQIa9ViZw6Xt6t1+Pm+Uvoh359Bil70D4J5KxiLpEXhNkdrBt6ivXZSd/nawrIMvTdWeITxkG4TzIwZQ1UNMUIDArFWnG3g/1+1v0BjzAMb/skzMKd6KbJerOAIg7TKoiIxXq9vbo6SPUe/ptd2Ni9qrkRDKuFrIZKVHVyJEiyujjzWndWz+/dBacoEzMRJQ1QhvXF2Ze/8l9cvPaQkBJixxIs27EEODdqk0MW2W+2J3fujtW7rnvzU2987de+/n/4Oz8BAPGP+9/x5LcHzvL3JI3olswMqO7K9smr6w+evPjo2eWmWL86ndzrftLQ3Y/Pts/wu+Lu//a1xWr1+qfelG6dfjq9+rc//Oj//OQpfXR69+Lxo0fVkcOS2dWfsW/8madfhqd/+Hf/4IP794liiokIWHCcpsUqkJBmr4U2AsgIQcyIbBDoiIY0IyQbKFsa+6dqUbOYQe7QGBoaTkkMgohqrXMDJLy5kKraWHQ31pevrnb7abOb9mXaT1M7erqUc86rYXF6enpxdnpn1Z+erJfL1aLrZ3sW5tx10iUi3u80gESE0KtqqBKACPVdGoZu/RP57H8au99hyz8vpeqHHz3+Lb/lt/yDf/AP7lycr1eL589ffMdnPp2ka46DRBShzNx1VH7rXv/+fDAyY7Vg0L7v+9z1QncvLt54/fUH9+4QxqvLq6/8wi9++MFHQIDE0i9qQJ875m1oBafttD1wPCFJap9xE3lu8SAx1amworvXWls7d7FYjOP4/Pnz8/M719fXb7zxBkSsl8sw+7WvfX05LATJW8OokiRJAcDUhBHpoBn8sWPh8Lg9cMZb9Cs4pvCtuTNvHwc7iK5ERBNymztCEIhh7gDN+KF1/sMwWkuKmdyJ3dGJCZG8QT8RySki2u+83Xe6yXQBiAkBMKhtkEDmPi9WJ93JWhYDJnHCmQwQgWCoFTZX8exFPHo2bEvd7msZjUABSTLnDiUDsgglwi4LEqaOMBF2jF3yTqIjzxRDhuWAix66FFlQmrVMG0EHhs3uj7XGWGw32Xbr40QlDJCkA3cE9wDBnAic1WYQBmHBcLfEmJDUgohNNZCBJYgBPikjdfsD+/VRobX74TAE/sQPHv++BY9m9wkMAWhBwAnAQQ1L9VpCK5CQkPoscwru2bXDsuo1ZZbMqoHki3VOvRHFbj+VKNLnaWuvrsfH+2m5WMrJOVG/2U+T1sycT/IS2DsbVqKeanWKrutSFu0YupyH7kJoJbwS6pkzUUI3RzQExOBQ2u/weuPbrdUCVsADtFgt4E1L2MOaT8nNApqXKSDjzQTFap3RF2pyDACN0dd2PwhCCrNpty+Ie5365erq1atwGLqu67uqNVMiRnJ0JEPsT1bDQGnoP3z06K2Hr4UFB7Ck0gFOBSIYMDMnwO04WlUEPz1Z9X1+7/NP29V+7e330gtqtkzQbI+73iOwVNUYNZ5fbZ5f7UfgYX3uIuJoZaLg/BPDxf/qPv4e/Pzf/aG3fud39stl7hZ5+WDI+dlH75189zcx4Pf83t/7/MXVV37xF7/x1S8HRvltTXYQfvL8qz/wvr35xhuY0czGUjbb7dmdAEROKXe5ywPn1DCLRBKE5ACI3pxwfDax0HBHACYgppSS+1SqujdTRITZFyUlCgefhXMRAq3qk6fPnzx/8ezV1fWujupjdfVQV0KMiEQcEU0qYMj5dEH379x5/cHDB3fv3L+4s+z7PmVfDLFHSYmYkVqLW8zMdAo3BkwpDX2/Xi71z+P+f2ZB+KrbEKdw/9Trr1++eM4Er15trzf7k+Uqp6ucJ5GJ2aep7v8nXv7HDgCLjgEhNRMht7CaKK/67q3XHzx8eJ/QmOXq6mpzdV2rerNLtC2lztSYSJghIokg0nEAUEpx9+VymVLyWQ8QjkhTRGz2AI3n1YgCu93u/ffeB60PHz48Pz3bbDbvv/Pu22+9JcwzE7W5mAWQiJsraBNZ+rYx4Nf/fUQcdsRtNtZxN0UrAebY0GIAIiC3hgJ6eBgA0CxECoiHGDDL1pPxLLPu5OAO3KQWZ0uZ2z2N+QIAgprbFjQeM6bULZbL8zs0DNR1ztzwLBTBzT96c6XPn8fT5/LiGq/3UawCKSHmjoGkG5Bz04ghCBLmLNwlyASDxCLDkG3R4ZB9NfB6iYseFh2kBJKACREcW8cSMBxrtVJhP9l2F7sCUwVzQGFqumQJhUVOz8dXL8N2XWLwKoSpMVhcRXoHI6TGoFPA5poaR4mlA1wsDlSvX/+xHYtx9+NgAACgkSaOp+HhyTYnykSECZU7kLIbYbOz3SWnzhFdmCRHeEQNK6xTR1PhfRoSc3JL4DR0TDi6l4CdiAXAdSkvrq53BrhIJ2fnpfCra93ttwucHpwt1wPSwMuTrDGMexv3Fd0Td0kgy1poJbRg6ogyIs9hy8DdKSqMY97t6stXtrlGV3QVRHWtZQItXgo5enjzvWw07SMFZi5hD7GwTFNKab/fJ5ZwJWImRGSR5O7uqsWZPLyAieS0kk7HClNNkq6vt5mWLDSWimPN0nG/KOFp6AX17OLi6vp6P5733K2Wq+tpmkvXAIoQxCF1o/nly5dptVitFv9fxv401tosOw/D1rT3O5zh3vtN9X3V1V1DT+xuks0m2WSzRYtSqCGOEseIZQeGFEO2f8gyTEWxJNtIECRAfgSQ4jiOFEGJYChAIDiBYMNJECCMZEmURDanJtldzWYP1TVXffOdzjnvsPdea+XHPud+t6pblF4ULg7uPXW/e95377XXetaznuf+++8ev8V/4L/+5KMv7P7t1/9EjKLJiNk0c4xRrZSCHOZsKefbd++dJz9/52FxKMXM1UqS2Dz33L0X//Erd1//2OLoZPXDJ4vl2ikkX37jt3/z13/pH+h4gWZ//xf/vy9+4tN/7j/4hb/75t/83f/j79j/ZpT/Fbb/BOzv6++1b4R2cedkKQE54TiOwzAsT3QPGjIRCSAGCcUNHB0dmcgPalz1ORFXG2YiAcBcNJWSc3FAry1BQlNXN2QyUy2lCoK++da7j5+cokQMrfQNznm17tTRQedp1lKGv7zZfXF792/ca36lLSWfzZsnb775nTffurk+eun551/52EdvHB2tF4vlusuJWaKaOWDTdkSEWjTnohlN+77tumbQXJJNRXfjJJvd06dPf+onfvz/94u/WErJubz1zrs/9rnPLRbLYc5EQ4iBi5U/uD8s+ee5+WVBN0ejIEKw7OLzt2++cO8ugW53m3rWrddHl5dDMkMW8zrvDW1sVEHdplKI94PEFWGjvTij1T3OLPW0q/p39fu73a6igqvVahiG09PTVdfcOD5ZLpfrxfL06dO+6154/iNNjKnMZpbnhE0U4mIWmCvx4Qprgg+miR/6zp59hHgI+nVUq/YcjdxNzSpYCuCHkYJS6T8FPOw7beCOVYCdAAyRiSG4uxUnJcJgqFBZFWpOLsTu/gM9mirbDxHdAUWIQne0btfruFhh7JwZWBiIzFmdVMvlVjY7Oz2jzYhjhqQEgkTUCLAxR5IGa+UFHshZUJqAjUDD0Dfat9o3sFjI8cqPj72N1LUeBSUAIwJaFSKFgm6eExS1caI54ZxhmnzOmjS0LcXGteQ0CzVCxyd5HCKap4lJHJGsDnfZlZU8EZEzSZjdxZ0OtOvvr9euh/jDLTq4SNYD3K9++ozade1/cYBq0choFECiaZiKPn7Cx4+F2NWAyE3BM+mMlizPXHaBRqeOqCdgAgiURFMpQy4bVB3nnU4QEExtUnMJw6C72UpxLTObr9sQ+i5GVfeIoeG+jzkEY3TwAN6Ah0o0AnCzAq6cgdWgFJ4mvLj0s3OcE4ExgZVZcyJ0NT3cF1JVFL5iQOOB/HN1J68WPREVLVDUFbRYzpqzlVJKMTdw1dBHIx5zAaecS2QGh4YjFLCU672eNZNqc7yazQGgaZpS7Onp6d1bzzWxtTTFtrFxE1h0N8RV57lozg3i83fvdrH52ve+dnl5+eX/6hPPf+X5n/rS5/gGOVuV73N1FO67ZZpLv1geF98+fOJI45fTu3/ucfOrzXN/7eTk1smN2y+88olP3Hzu3o07z3Wro2axDm0HJNsBH7z9Fs67Vqc8D4X4m1/7rX/4//4voYLp/2uKf9y9FOrbZP7d19+SV55vIofAWctmtz3OGZncKy8DEdkJA0aDmuTVgVN3r8ghhNCYzSnNDlDUcyk5FwMsalnVDBDZvdQWqJkNw3B+fv7o8ZOLXQrdes56tt0YBQVMKcW2I6I0DMMXt0/+3H0AuP/vw0d++WPIzM3xspE8Tafb7dNvfvO7b7758kdfeOmFF176yO2+7wCoaZuUTXMC4nEcwBTMEUGYmhDWi8Xp5tKJQrPIuVycnQ+73Wc+/alXX/2GKjx+fPbkydMQmrbtFv1SYZhzWf/VZkNJ/jF0v0zgBd1i4LYJR6vlvTu3Xrp7j7ycn2+BMYZ448aN7eVw+vRi3O6wHpZApqWuPIL9qqsi6ldbkojqbEEN03WNppS6rgOAnPM8zycnJ5vNZrlcu7uZPnz46PbJzZP1EQf4yEc+8vjho4/cex4AYowE6LXr4qn20pivOJS4j+//vMtt7w+xJ+RUz1iDqrNSbSTgmdwAAoETGQBXXR1zr63lGtBpL7NARNXxCs2vHCmZqHozAYB/n0UrACCAMCGhGbI00vXd+iQuFhhbDsFJHBkdUROmAuPsu6E8PtOLne5GLqYKxcmQDZC6fQGBHGqtKAyByaNAwx4F+tb6XlcLWq396MhXPTbRmwCBUXhPjzQ3c1RCyOhuKduUYZxsGHU7+FxNGgRKARW3oioS79yB7WW5KFwSGzAQudUxSySo83pIpGYogsSu1+GdD+D7H0L/r73rBxR0H4p6z35g7qDuAg5C0moex3n3zv24uNEo4TGYAna9YXYboMxmmmwOIRVksEJuiIqqwRTyzPPgWkIRKcjFsJgQu6mrs1NgubXA41CactF4aCgbasDQhTYEDqjkDi7gXGVKzAwsA3gpRZKwqabsw2AXl+XsXEouJQtaSnNOc3U+c9u7IF1JZ1+/XXCw7vRrFzMDVjEqBDdmU1VEEhZvYs5uhMZoTgUBAnPbpLloNkjJ900c6NfrjVnXtfM8l5JXq9WccpR4dnH+3GpR0IXZ3aMwhtiHqOp5mmGY7jx3a5x2w/bSrIBp37d91zhoTQwDIqGI2DzPbdsfH+P55cV3vv2thxfD+//bx8NPjcOXxk+89cIn33zxE5/+wq07d6Xpjm7eDosVtz1INKd52DSQ18GWkRLjZUq7n9jsH/3P6Y2j5bi5NAIFdKAx6/nm8taNowpJ51KmeVYzJGJiIkFhJkEmNNCaBgKAOwH8+m8uf+ond3VRskiac1Etqns4Awgc88FhzVSnec45n52d3b9/vxTjZv3Nf+v1pz92cfv/dKv5VVKgYR6GaQSmeZ71H+3/5PLf2tPTU2Juj9aZfLcd+9g1bftkc/nk937v/unT4fzeSx99oV0stHTmmDIhcMpzyimlyVQRPMbQEvVts005FwXzzeXl+dnpT/74j3/rW9+TCBeb4eHDJ89/5F7fLxZTTu7ZnH4993+yJTNo1bX0bb/q42qxuHXz5Nbxccs87baAuuhX0rY6+3K5rCUfVPFBRECcpmm56MY5Q9Ya/SsXCA4tvat8v8IsbppSEqke5HsiQykl5xxj3O12Ps2PHz/+2Mc+tl6vl/1Cc/nO733r05/5odDI1a9lJGmErw8BXdsX/oNz7Q9cz0DU2rM3YzOwAlb8Sh4KEYkNEA9uoORURysNwKvnCVFNaB33Pt6osOetmCO4U3VTdxb+AX8W1mYysXBo+251HBZLbFqQgCy1UQ0GbEBFdRjzZsMXOxxTLsUIVcSMCCQiW+MoghKZGauaAyMLW2BsgjfiXS/HR7Re4/qYV6vSkQexKM57Fn2tbhAr/9NNC6hCST5nneYyjJZyF1pU05ypYVcqmkRu3Ylnp/NuwyH6NFUSrmBA10rKrQohahaIQow0TdcC/R6e/tDD+2AP4Fmgv3q0/vscAFxNdojAiCgg8azz46fevtlk4FF9l2HZY3SRTJRnSFa2hrkYAM4CEa2AZdNdGS91d2GqVgLNwcfSolNJw/lTHRoqcx9gEaDBOdokedvDDQ9ABAokTExMRocdA+hgWhxqwlhsKGrJpq1dXG7vP8jn50stZlq8eCmWk5VcdZAqbonExAyIqh6qnlJdaAe3nFpc7+2roG62WmhrKTnnYqbmXsjnMiuxxWBCoemBqZSiU2Gvi9S7xdIQsAlG6KV4sVvHJ+dnF4C4HYfFNDrhNI1pnhnCUdvKnpJHSEgO28vLcRw5BCJaLlchRIKDa407E5ScmQJL3A2n77/3LhJ0bXvjt9fbnxoB4CfPfuTOKzefv3uv7ZfKXMdjY2iMw5xyw7hs49zFzlPVBtPfaOa/2vHPy9F/FthL3zfDaG3XAYUa8XMpgBRijE2Tcso5ISGx7FvBEsxs3/pyQ9wrtvzqb/R//t9/XAMFEe3pWE7EYoAUhLLYjNVcxcxL0cvLzYMHD+c5paIPPvf+23/2AQAUe/TCr7wojayaVVFTkpObtzUlfl66PxbHX0xGNsx5c3bBhG0M2y9N5VcCxgjCb9x/HzZn0zh+9KMfOblxk4XcCZhKUXd1NwBn5iAMJd+8eXP3/oOi3gROOT9++OjJk0c/8qOf/fXf+C13v9xub84ldE0IYdH3SLgdR1UNSH23cs2RYdU1x+vF0aIlUw7kZqvjVWxbadqLadv1XWwiD5MDqalBmec5zykEiUFCCHPKVxsWD+yM64U+CeVcKuQrLPOUYijzPMfYMPN6vX7v3ffmlC4uLoZhMLM7t+/cRnzjte/dv3//7kfu9kFIBBBDDEiYNZNRTTg/BBv8wGbh9dB/9eKKDaSqdZ9cAUr7iGRWB8mwYtG1nWt+8CfeT+QQkQMjG/re6raKUdSgRuZ60Lv8IAu0NhFYYtsu1s16jU1nHChGUDNEMICinrKOc97u8sVWpuzZSjEG8tggumADxNojCbEEJgHPjBACBeHSRGwiNUEXHa2Wtl75YgFdh62DMAgBIaCjg5teeY+YqmfVVHROMI9lHNJu9JzjgixHilrPclMQvfWcbC7Tk6c4zWLoiMJxNA3pkkUcWkUCnJkVQVFdKFYGlbtWaQN3Y2b1A5Sxn8R4NiynpnUxAR5EvQGKWR1aKUWD7AOfiJgSOUZQRLAQzLWZZ7vclPfeguxwNsPizI+XdCK6nH2RkDc4pQDHjg3A0ArQnFjn2d7N46XvtpyRxuDnxOfeTJTPx+3Ds74/WRs0VNqkMSe2XQCTfmnUBHQmIZ+lTKQD4sBTknBMCkC9IaihGY1QunlaP77w19/ZvfMOpYE9IyrkAsVEOefMIMVywSIxAsWCVUxFYG/kA+6A8qx4qmtXVUsuQq45uyt6YjQAdcIqpisMwFhAKTROuN3tAIBWkksOBhIbbhcXaaa+My9uhmM6Wi/vrE8ePn0ii/bB6ZN+tUypEHpkWvUdKQxpcIawanMeLzcXaZ46kabrb91+TtqF5iLmLIhECqDqKIYhAMudF15pT57bDNO9/8/j7am+/NbLRfTNdx5stv5Dn/3c6sYtYTLLWhIyhcCyWt574YX7b32ji10ItvBCPq//xkL+r0tHnNfzxeVGQlgfr1V9nMa2WzXLo0KiVfnWwTXF6irIDEhmAEC/En/1rxz9pz8zfekvXP5Pwfd9MECo9zOl2dOgaXIzAwZpNYFRUIeU99yy3ZAePHy62c6b7S7lLL+0X8B3vnnvY698ZnXz1smt20o0U+iDfPu3vjpu5s+dfvbyh6fju8//7re/ffnkvd3F2fiXN8NfvACAj7zwAkuAfvHOZhi/91ZCfQXm49WSRFTDmMqcErAbZsQcI/k2L5qOnBLBDEqaHj5+/Nobr//w5z7/6qvf1GE6H8bLaVoIN00wK2QSPJZcnK0LcHSyjgSRkNACscSokTnEtl/1yyXHkM2zGfUIpyXnVNHIrDmDZ8hNDNHbbFY1sgkpiKhqMQ0UKkfeTFWNOJQ6oc8hzznnklIOHNAUTW+dHD24/+hiNzx6enr37t1CtLxx49ZH54f33z86WZ+cHJtbAVNQZgOG2ZNARKcDrLMP0O4O8kwF+grVqbTLvQ3JfsbbCLHYoU97DZSuzGklQHA0I7M9M8wBnQj29ubu5BScqUAGApQ6Y7I3rqxS+SBgdNUHrrp1jJXag8CxiauVrFYWGpSGSNCJkdXdoZQ84zza+QWdbprtbFP2ZLFEciUhEzBiE+JlDwRAoK5CLRIaUxYsXeNN48sOj9e6WuF6iW3jASUy7DV/gIi91PwGyQwdwJyKc8p5GGG34WkH40COpOqWyRtUZaPgLCW0YXUjrI9tc4F7MaMC5pYncEek/X2ojjdMXgW9DQBBhH1P0tqn9fCDrh8IAV299wptPHy/Dn04ItZCiJCCg293Sqc+SeomHBY4C504zQUXCZKiJQ45pW2GRHPJedTp0qatDbs8louz9ORUt7vmfFem6TQlv337+eVyKUsOjIG17VQppd0OacetgBLCBLoF3bkWNBcPjFLlUNGUtOg4+MVmevvt/Obr85PHcZ6AAVxzSmWePBfPCoKICEheO+TVMu3QKsergXV4ditqrU1MrmV/n93dDIlKyeruhI5ogO4gTLthIANi4j6wxjLnENucy16sW83cav67Wizee/hgcbz2lErRUkoQAfdGwslqke0MSso5uftut22aKCJHR0er1fpA0K15GeHemZqliesbJ81iudltxznfuXNv+3Te0nx042i5XJ2dXv71e39j/PL8p1/7d34q/6FsrikRS8n66R/69Ou/99Xh7J0FN9IUzi5MoW2JqORkquv1+s6tWxeb3bDbvvMLm29/+as///d+4vbjO6FpkLFaIrNINa4CIHf/K8f/+19uvvLL7Ve+lH76Z6YvHfiFCHXsv5TtsFNTRyzuFIJrRpGm6xFgHIaU5sePH7/33ns5qxvG2LSL9l/5I38I/tjipXc+033pdn9yY3l8w4R2xS8fP3QwzenV3/mty2H8mZ9b/9yXf+ZoKf/g7/3iq1/89foox58a2t/oEIC6xUWa3334+GjZIkLTdk6e1cyrlScQgQiv18vHZ9s2xoK1r0hzTm+//faP/siPPf/889/+7mu7YXz89MlitQwhaBVyIfTGQaBv4831sgt8vF5N04wkzNIu1zdv3gIEkgaJiRuUKTStIwBWapoVze5AEgyRmWKM4zhex3/cHZGappnnea9G615UCb3SQ5m5bVszu7y4qA2u9Xq92+3uP3jQ9b2q3rx5s9aWT54+PTo57hZ91zbFTa0AIZK4HU7ryijx/SBw+eDWuMYTcawt2QMHCODZbHCN/le9hMr7v/oNfmAbwmEaHw8jOABV+41I2NGREK+cIQEAgGmf8QMAevV8rxQNiv1CFgsIAUOoE+BQNTJVrWSf57zZ+W6AYfKxoBkCYhCmyERKhEIUBELAKuQMJozCFJhQCNvGu8aXPSwXtuiwjR6FgwCj7/0gD1WRe7U3QDNQ1ZzTNFtOPs/zblOmKYiQOgO4KRaDYiAqk1PTr3ixyhKJpjokSW5lmtplYaYqnYRIyIwcAKd65/75QN21uAY/qKy7zh16dkjQnhbjAAaOTMjk2WNxGocmThLavAOM0rSB0JJp4zjn7DRFc89zGua83drp+by9mIbNbrs7v5yfXtquNMNsJZ8Lxc040XK1uLmYtjaee3u7R1n5VCgMiIxCCBPpBZQhZgiKNCDYKN6igpaipfB2W548md94I99/ty2JStZsRK5pLvMMVsB8zy9jrlOaeO2zPytRr92W6x0Ud0dks+JICkYieZ4KAMaY3QCpa1vGAHkAtYKYI/Vdh8zSxCFlksDM7iDC63Y1lswsIcg4TquTo904hRCYQMwZEc2FGAEuLi9zKeM4EnHbtqvVar1eI2IIgeth4i4S1TN5iA7HxzeK6Wp9nLTcSfr07OJiu3v06Mn5+fmjz55//d/4BgD8ze1ff/LXzl/6xKc++vIrXb+0XNbL9cuvfPK3f/3dMmfB0K1vgjt4SSmVlPu2e/7uvbZtpynF/27/6p9+GwDCfy/83P/zJ9u2bdsWgMCr4Uot4xER/6X05V9ufgUAfjZ92WmfIe7rU7N5ng2wqBughMbdum6BDLlkFnGAzXZ3cXFRihFK0zc3bty4dfvW3Y987GT4SPvxO9ivm+MjWSxQeKV68ei9edr2ndg0Pn/z6B/+1H9z4187efnvfGIadsu/utz5pvlKhH/oI267vkuAjPTwcrN+/LTtFyjV/FCrPlGt/ISpjaGJcuN4PZ6frxerPsrF08dtt/je99740pe+9Pobb8xaKrRy42idcy7V7ZCx6eJ6tTw5XjWMfdeenNwApzEV4HCxHdu+O2p7Fmmy8W6KTS8hOKAC5FIckIUAuOsWl9tzPIj1wjV2Xwghl7mU0jXR3YVqtbrPZfyg8pJSSinduXNnnrKqnp2dbTabx48f37lz59atW6Xkt7eX77z73g999rOEHEMsqkxCIgzi5nXUMbA82w0HgtxV7N7DywfhJ9iLyTg5KDgBOrIjAF1FxL3XwNVvqBX2/ncehKn9eunAZEZOXAO9HxJbByDyA6pRdX6Bqh5VbEO/4KYtzBgYkap6EIC7FUgZ56S7EYcZ54LFSjZ3pCDYBOAAQthEjMJExHUGzQgMBUEImK1ruO9t0UHXQhNUCAiQQaQSmdDArSiYVau8/YFQVHPRnEpKNo1pHCEV4UCuDIjm4IouaC4ZOEiL3dLbxbzbRAciC0QlJzQg9hqKjNCJgZnqsByhw96Eep+H/bMPhN+nt1NP+yuqqF97Px48iSq4ZymVeZS0c2GH4EOk3cLNIWkTompOujGbpl2aNrvd6TmcbnaX56WM4zQM2TyhZY0UGgqmJiWVfLGddu1xs9k5TBloufK+w1YAURxggLKBPPbQUDEdRxt42GYs7jlZTn6+SWdP86OHYbfBPAesWpMFNKtmcqhs8eqmUKWL6ga7YrxdLe7rr+txWEoxAyBUB0NQBwhUHDJCAQ9N2zQti2wvN5BKSbmAlRa79SpIM+VSAKs3QuG9peo8z6FtVqv14+2lmwPCnDNYbjmQOVchCqYq7mhm7/3wxav/7us/dVH+CPzxKRcDFGHTjMjIJBBIAkkIZohoCtk0ZX1y+vTy9OnNkzWBla/uWRMff/2l8fz0937rq99+9VWRUP6w/+P/zi9+6pOf/KL9zHe/9epuswlth+CnP/L4m3/mvcVX5Mf/H5+OsUHzQPz5R595Fd4GgJ/afH59dAIATdtxEDvICNasjpn/k81f/gPTl788f0lBHcAPP1VVV0tzGqfELG3bupOqTtMARTjEQJhynqYpZ10ul1Ga9er45ZdeunXrxp17L8TlDejX0C/l6MhjoEZ8u0NQAotiEPzyC0+m//jyfbh8/EfvH/31dfse+9+LTQyx5axQSkGJQDTkvJl1UliSMBBSmKdse0ABF30zn2/Xi17NIsBwuXnx05+8PD1Nc3l6dvqyl0988pVvfvu7OefHjx/fPD5qmsatAAAjIVLbxCY2WFLftESMHJbr4xv3XsrFLi7On55vASDnZEZdu4yxQeKkStWSlXhO+SS2XddtNtur3Xd1ANSHWA3oiYivCnVEdx/Hcbfb3b55C8xyzqvV6vjoxje+8Y3aFgaAR48evfzyy8vl8vbdu9vN5tGTx/c+8jwjmhkDMFTP+Wu8z0Oi7viMEXQYRHCHfbPT/aDOANUYBxDBCSqlB2r7tkb/D1YAzyLP900m1Wodhc0AqprytYGvaglfjaqA2N2QAocQFwuMAaIIiyMCWNWktVJ8nm0YfTPSdoYxYzIoSkQehJAxNiAMErAN1ARGQgA0dStAAAwaGIW17WjRY99620IjHsiYqltt7X+Ym5uTVecv11JgzjalPI2Ycxl2ttvZNAaAWC3I3QCcEA0d0aUUn3MO3SI3LcVWp1LtkAEBrTABVw0NACPGECr2Vn1NqrN2LayunKn3pJdDH/4g6fdsFGBfo9FV/eVEdAXhOTwrzWqXh4Rj04ymWTOmAYOYtFgojQkUuRFg5Gw+pcvN2bAZdC7TZsChzFsr6qpcsgFgK6xIBJ2js6I4UsF5a+wMSCoXngMVDCVzg0yJPKFqSBNMqVyaXpb5bIAxYUkwT7wd9eIszEMDhSy5mRUtKZVxh6pAhMyOzBIwhCrZBj+oGHJ/xg7yg7OEqhIHzcURi5ohqAGEAACLo2NAamJM04zqlosgHp/ceBQ0lxLbZs7FWbrlol2tT3cbIEwpMbMhNk30DZRSmDgEKHNeL1dtaFwtiozjRP26/iVf+7cfv//Dm3fhn/4bv/uNL5x+jrCyPhyZWAIHLLUlgKjgZta4z6l87IUXCNDcNhdn60X7C//mn3rtlbefe/XOdn544/adBvl4tfrbX/o7bz73+reee/UvvvkLf+yjf/zJo8fzMBDC3/nz/835p8bzn4Q/sFv/0DuvOAAg37t393/wf/6X3/j4Oz+9/XxqRgCMsRGOiLWpu8+gmbmY/Wz68oEFUY2nwFStaM45pQzITbsAJyZxyMSh7ZaxaXfnj//+H/21r/2bv/fS37j9I/c//Zkf+tzl2bmZLdtWABdtg21D/QJihBgLwqpbrrpFYKYmuqWjX90Dev2vxj4QCUXs0jzfPDo5315WMerhZ+b+n8Iwl91c1uZdEKqauxiTFUIw82XfSbGc0yKGi8sNuN++fefhw4fM4c033/jkx1/59vden+d5mqbT09PFYkFE51+cbn11QYhBwmqx2J7POWcmY6C7z93dFW267rMf/eGHDx++++678zhN09R3fWhkSgmJSp1QdOco05RDiFcVec2Um6apucjVHgeAJlRVZ1VVEUnTPE1T0zS3btzY7XZvv/32R194se/7YRju37//wgsv3Lx5M6U0DGO/Wq2Pj4dx3O3G9fERs+Rc3IEp7DvMRFXnFRHdzTQTogOoqh9ifQW3HZ41gR2hSpM6kCsCgdu+CLAP8ov84BgBhwHiK2ULvJpj3VNC90ObBgeVM9jDVIRggI5A1IQYQ2ypaSgISfQaDNUJXK1ASjBNsN35xQY2g8wFirkTcnB2kr2QAzJ6DC5MLG4GqmTMjIZqgTCKd12JEWNQBmR2QpI9d1C98kIczLwomnsubKa5YFGaShknGKe8ucRpEohYh5hqh4wcGZxJ8jDQlMQpNP2MJEDizG6g6jlj4+DVEZOcDIkR66ENgFBVwvkAj8E/77rKfOtZe/3F9Tddf/c+IDJLaHJKOSexZAV9JEcMbYszchOlmOwybRJsi8+FZyhTgezoaAVAQRyYwBHqOFoUDIgMpMXnGUMbaAujXvJsYc5NL7EhZoWsMM26U70otrW4y5wLl6zDUM42Mo7oGTEDqO0tJDMe+AJY8V2s6lR0/Q5crcsPXVeVEBEp1Ay6zrJzNo99F4QLBULcbYaSkyAjQEppu9s1t1amPo6zAXWrJfftTD65BRbXHELY5hJCYKZxHJu+NzcmjiKLrrPdPO1Gd9+Ow3a7FZGP/u7x+z+6AYCfvvgREzJ1IOQgRFKnNASxkAFAOFgGCuuNkyNhfP/9+8/fvXPZbFNKx4/bfFMB6Pz8dNhia+OLr568+TIAwL3fXmXcsOWT1UoIP/X6R9/+1AMA+PQbH7tx82R9fNR1i+V6lS196r1PwAmFtjWz0HQUYjG/speqbslXiOJ+vm4PDXsppcxJS2m7hYTGnYI0DnNLtU2g37j19b//818BAP/3/A/+Z1/+wo9+fnOxefXVr2uep2ETh2XfLNr9KrWkmBzv3r5769atp9M5taFh+MLL93Zf1u43e+29DXGz2WLb3r55ki1dbHfzXxou/8PNGcDNj/f3Hz0isBfuPkcAzFyyu0MQISjVvTUS3VyvLeuTh09e+dQnHz15+uT0KX5Xf/4P/6Hn7jz37rvvDsOw2Wzatv32v/Pgm//WewDwJ3/+J9Oc0jS3sckpcdOBe0mpW604hDTNz9+9x0gP378/bLY6z4joaMSRmJEIHYiCOVa0ZxzH2mO4KlURsXaMOAge2Pr1O4vFYhrGChnFGIlos9k8fPhwsVicnZ2dnZ299dZbJycnd+/elSDZDCWsjpphHMvp+Wq1QidXIKnGnPU4sqqQC+Cgtp+UrNodh6vqv+ke864pcD0IeO/suI/y/oFgchX3r75W8sD1I+Fqvz1T+EEirvYeB4wDCcFZSALFSCFwiFRN4RHh8ClgTj4Nvht8s4XNDocJ5qKlmHuIAZAxCDQNRMYgKOQkzkzmiERGyABMFpFjxKaFJkKMENjoqvBV9f3YdmX+gBoWhayWzHbZd7OPM4yT7wYaJs4ldJ1E5iAUGIRdwAiRXXwa8zjxnMHQnd3ZzADMtZQ0s1u9h0bozk6KRK5g7oTPhMJVlT9I5PqB19XtJiK71p+5HvQr+g9XiFBdEcQNBHWdx8lIhAKymykU0EbYQgBrTI9kLTFs52F2Y0cKwZ3ZLBC716FwSlwYnd3BTFgkNiikWdvUkYNzsjhCCtYIM3oxm8p0OU7nyXcWMnhOmuY0bHyaQY3ECzipakmaZ88KVXRkn5yyASHWgPmMLPsDmyJXZ8DhJfrejJoUnGMwxLHk4mnRdsNu6mLYbS+dgGJQMC++WPWXl1uKDQhj02xSskameZ6mKS76qrKxXC4vdztIs6p1ITBxHQZGBFV9+ODpnD4dQvjy3335J57+0J//7J/NnKVpidDUmZmEARmro67VJVjRVGDmLjbW9bdvHvdNILOLs+SR+sjjOAZI7q67s5/+L+7c+42f/vR7H98195ElzclocLMv/pev3PrN7pNvfqxpo6nmaRaJWsr6+IgDu5fqKBJjIxI+RE9UVXDKOTPzvjl41QY0r/xaDpFCNAVgkiZCQfOsWT/78NP1nZ986+WU0q/8ylfu3nmubxsiRSigyfK8Oz+VMmOMyTxjd7w8eenFV568+71+uYCcAXzxKiUpHINmbZmPTm42MSwXCxHZ/IH36u8fvpS2X98+PcPjo37ZdRyEMzuLCM5uAuaB2yYssk394sHDhye3br/88iu/97tfn8bp/fffe+mllx4+fDDPc7Vif/Sjl/XXbn86L79WhmFY962Al5xz1nGcFkvr2pjnKY27AHDr5FjA+xjee/z+6eWFlTynjEQMEtuOUFLaNk0zTVNN7asUaO3xwmzjOKaUVqtVFXU3papYVc+D3W738OHDpmlCCDHGF198sRYrpZTHjx/fv3//k5/61MVus9luzSzGeHF5OY5j9Qy4CspeT2vdi7gxVL05++BOQUepPuxaD4D67qtfcf07UBmSzzbXs0bCoYXphzTi2etDU9kBaO+9Tu77usMRDAiEOAQKAizMASu/sbo4qlsqPmffjbbdwXbAIXFSUEOiKl4CTBijB4EgIYiz7KeWCQlACI0cmVAIYnAmR0Yk2wPvAOaAYHDwwDCHolCKZdWUKbmNsw+TjZNuR90OlFKPBNXIkN0YOZALU0PSt5KHrQ6DpJkB3Nmc2Akc3VRzljpRiQjOiA5MWClbH2xd1o33z478h6dHaLU7Rwd8bT8Q+4GT4FmaLAyAoRLUE6EgpMlT4SmLQM7mJbtbQUPmhlqXHPqGiwxGjADeIvpuiCllN6gOqjPugmBttxiAERaCGERcWo4dxphQGGDOyQxUy7Cdd5PuPBbC7Hk36rTL40BaJUfcvTAUtawlQ9G9KDgx1o9ZeShXeNc/YzDi6k76YZT18HN0AGIBkSHNlas/DEPbNFYSIpRSCmMMDRJtLrdEdHJyc3DbbTe27ACkDGPbdkCcxpmIQog5n1EMwrTo+lYEsmre93Katj0+PgagnPXHLn6ka7tiVXMJvHIDJTqgmQMhgKtZyRkRmREAQuQeWrMjMNf1rGn0Mk/DyF6OF03OJZBLhM++dpuajM5uvogyT5ObEeAnXvtIt2ibpo0hhBAWbde3XbdYSmREL3l2d2Kmanpei1Hfp4DgXjngIfIVXmGH7mKUYEgiYliZyA4AppBzCaH52//5f/q1W79792s3wovchWYatqvVqmvtux9//7/62f/75x587l//2v84RGFEMUhQ3O3lj7389nfvXTx917VI0yJCa2FzuVsvl7dv3elX61z0aH0kw+7j/8Xzb9KDo9/sXnn9hZsvrG/dXB+dHKMZGoUQyRUdI4DPGRlWq0VRDLEdU3pw//4P/+iPHB0dnV+cvf7Gmz/8hS+uVquzs7Ozs/Ou6z/9t+/Sv4s3vtq/+J07Ccd5nkvgpmsfPXz0+PHp2fnl3Zd3x8fHfdflOW03G2EB0/Wyf+nFF88vt2eb3ThNczbgvY60O5hpraIq+KOqIdRHHmOMrqV2fQ/31uqJS0RVOKiUEmMU4a7rbty48fTp05zz5eXlbrd79PhRu1revHP74uJCkI6OjjaXl2dnZzdv3swpYbXRtr0tgaqCm6NXD2cEeObtAwiMAGiVH0f7oIwAqlZ92ysb8XCufKAIuKoUa4i3w/zBB7chPjtBDk07dUMAdKxGkSRRYuSmYeK6w73Caeaas01THgbbbHWzw2HmlLwoqAEiCbIIxYAhGJMSEfHe/aRKXh4+Z7ULdEJgAdobKYI/a7bu2yL1ANB9BeC56KQ6zjaMPk7pclu2O5kzI2IUjkIiJAxMIExtExad7Mb3wpxxSk2emAUMtRR0ZQg2D6CXQD3SAoCKD02l6YsQKaGjF0R0LcBUWzD72TjV+he7A+L+rzeEaj/qAMX3DJnajKlQ/95WGKDSsSrTiwSBCEB8IUjYEU5ppmk23nG/MjbzoiWpirO0zcK4yNIWgqqBwYN7jm2Zk4MCgWqBAiLBJRSQyTxTUA7IoV0s2ya2kXl0TI5uDKbzDLPyUEQ1qJdh0O1Wp5HdyFUCepldk5XJptlyRkND5CDAUggELUZBcgYFkGpmCwfuWm1DqWu9D34YT60Iq6AjefFsaNTE7TixBATUNCmYuXkp5GCuuOjgZJFjIJRWWmNEYABnIi8FpCluhKIOath3fQhNFxsv+RhpmYqkZO4KMGgxomkcEKBtu+fufsSBwR0KMiMikAM4MgVHM68yBuiGqlpNWFNRR+bYSIxVIBhN2yBDmgMhB2bihLHrO3f0kt1zMSd3dGeOy9Vxv+i7xbLp2tD265PjbrlQJELqgqBaFIkUiQKzMLOrSQilGBOZQxOjmbljUf+VX+sB4Ce+cGFoxCCRoeuQmdARyckjNQCUpkwgYPjKtz8ylUu3MdsEZNLQNMN//bP/6JsvfO+bL7z2mXc+8cobH1dAafqRWgA/Wax/4sd/5lvf/PrTJ49UZ2IqyHfutG/86ddOf/TBp/5vL69+rb91fPN4tcqv717+T+62sTn52Hq9XHZBGgpBRC2bmgOWPCsLtVHUoqLg9s7d25vL04dPnj58583nnnvu4nLz+GJoRO7dee787HKYyzTno19b/Eu/86mSR38uu5ecAYhzts35hc3To7fePHv06M6d2+v1SgKp45BSuzgyohYZDHLxBLTLpREsJQchIk4pA5Cqp1Tcve97RJ5LVtWmbTeX5+qmgFNO7Gbu85iIiJGKZtWyXi+H3WaxXF5uzoumkuez0ydHq8V7b71559bNkYkQj1frYRiqY3DOeZpnVAsh9F3vaAUMRYjITTVP7h6IrFieJ8Dq2Y5alLl2TGvA3JNT2at1jVcVIDgQTNQOfpMfPAaA3NzACRHV9NCEgwKV4lQlu9jq7AESIjsgibAEZKYQUAIiuSdHT+Dq7qrsxXMu26E9HXQ74JQ9Z/LqvUwCplgIyRzcmTAAKAIxA2EGK2hGSOYaJJqQMRkTB3Fi5CpFc03tyhzMUB2KwpwxFc6aNjvdbWG49MtT2V6GVJTDgBw4BpEYmCNaYG+iLo706IZMeatZOWfMCfPMWiIAMXsuVhTchGmyPcavYMhkuDevql6eVVfb/Vlu+wGs/wcUAs+O2A990+tpz3Tgne8LNiBEQY4ESMG55NEnZonEBNro7MUJQmz7JcYQGa0N6L2AY1ENjZfioEhYLFeGoAIXlAVSMi6ARsyhYQRPmq24FShZwEAzl4SqmHOa5rTd2DxjyQRGjK5a8uxl1pxMlRCJubgxIjKR8H5VgTtcpy1e4yZ/X8+88pvNvWhWNWIWxDkVAAjCwzTrPAPTnGfZ/75gTNy3w1wWXegWizkliwGIHUDdcylAaGam7uBRQhsbBCA3VGUMFY82gJTy5bx9+vTs+XvPF4XlYoF7T20kItiDs+gOlUdUwZbK1NrjMAC14bxcrRoEIgwxXl5cFNNxGNQcwJpFn1WrnWxNr0REQuj7Ew4hxEgSYtss1kdttwAmdW9j2zUhIAoTEiMxs1wVTBWB3Csu0X566Nd+vQeAL37hMufqbcIowizuXjMSIAen0uQMTWhbr7PuzNM0qGUmiNx//LvP/+4L3wOAj3z9+HS+f7nZDWMq0neLxT/9l3/p7T/65k//v7742d/7bMrzar0esr710hvf+VOvAQD8af/ir/+wWfacV8v1nVs32tis+i5KiEyRGMBTHkk45zzuiDS7exXL7Lv28uLi4y+/+PjJk2kcPvXZz373tdeH3e7rr766Wh+pu5ay2e6aKE0QcFfV1XJd5smBdsMwjKOwgLuVcv748fb8NEbh2ECIyFENSi5RgqqllPfT1EQIUI1/4Rpxo5QSYlTVCg3Vh2VmzBxJylQiQO3cqqq7pzQ7eC6lbdvKJastmbOzs5Tm2MSUEgB0XafXFkDJxdVKzleRoK5/LcVyMXMvaqrA5O6V9l4Ne/c6zzXeO4A96+te2TfWx+1XlhsHzoV79fkBr5qUiAe5MvcqpAuMB+PuuuwB6xCnYIiASCxU1aggOBiZQi4+F9pNttnRdtRp9lR8b0/v1VkeyA+0mQKErtnRwdjRFQqZeVVeYAKqHtOM1eKxHngHU5x97DB3NSiGWffp/zjrOOo4wjDaOOowWsrC0vVLijHEyDFiaKCNtFjgckn9QmYdXS2YsuXI6AQlu5rWIm9fJTkCkFc9gCA+oRk4gZnXnVRMtdjBQ+6ZMcAPiP7/3OsKEao1BLi7E6PV/q0jRfJ51rzzEQM5AiMFdHJzalsOgWODGFFLZPKUNUZwAzMkKKrF1ZAcyFHUaS4lZSvmuRRwM1c2LWVGzQiOVtiTpzmP07zdQprICkMtXsxK1pxMk5YMVjFDJBQiqTR8QIQ9o6CKUPlhqOSZFcZVtlLvW5VKBwB3rDcfzb1atqlpSovY7PIUQyiqishtK6ulEbsmRprn2UmyWlgulULOgwMws5qpqQgzsQibagdE6hKIhOaU1CHElvL8zvv3X/n4J29QWDQNqqJV4wa6Pl5fxUeu1IMP2dOewsTMIUhCl6aRtutX6xu374zDQEhMlEsxqwPPFmNExBhDjC1xwyJIHNumW644NLkUd1ucrPu+FzDfe1RhVauvB6o96xBWjV+svM+DHwhwJRM7IwvJ/gCoJwGxKWj2qV2vV/Nc0lymEQEJaNwNEPxf+W9/5rNvv/TSdz4yzGfTnMfNdrvbOXXvvnzxS3/kHwDA/EfH/+FX/8TZxfnD9x8Opey+uoO/CABw++snXRsICgZY9v3Nm7eXfdfGGIi8KIAJc7RmHAfkmZDGYXBXI1LNXdftnj69dfvWYtGdnZ32bffSix/97vfeePPNN28/d3e5XJ5dbJ6eni769ni1JAkVpnAO4zgOl5dFXSJqMVFzNs9Q3Eoxo+TG3LTuXke3ALwqLB2AR6s2BlfcmNoWDiGoFjPruo6Zh90GAPrlAgoAADGHJiLi5W47jrs7d+40TXN5eXl8fJznZGbb7fbk5OS111777I/9WMkZAdrVSksJIkEkpdR3PcKeTlIPknoJcfFiuaR5dndkAmFgMgKr2h4fPAAQ8KAD6Fcn2RU//UNYK17RfurSIXoWuBAIeE/dQERkh/00D4fAEoEJqo6EIwBkIzO3ZDAX2s1wuaPLnewmy2U/1wbViHhv1lj5867EpOqVYqMKBmiIBIQGUOmhwAIsVfjWqTrIHrB3cwQANVD1YpAL5OJTLsNkwwTDCMPow4RzEkdBFgkUhIJ4CCWK9x2ulrDoSytimJ3c2Iz3fgD1rrGpmrsVByCqLQkBEGfROgPttUtelXJIZL8hK4XgKtX9F1B2+uB1Nd0HH8DvSIRdHU2wmLPlYvPOCAkoho5JihKmGRgQERmlidg0WAplhWqPgESqUq2U1HMuZoiAnmcw15y8FC8ZTMmygAmC5nmaz8s0a5p1Gtns0ADxkovqnOYRvYBVXUlUQA5CUoctvKo5O4IjMNFhRX7gqrervjNnrXO2gYJmLGqgWooReGQepgm0gGMgTuht3xfV0b1p2sJ84+TWOIxEIJ0Ak4EXLUQCAiySS1KzKBHBwdxKaSWyG4uAg5kpkyLNSR8+PUeW2zdXbIY5I5CBmFXTwf3jYGaA2ooDRD58EAeAGFtETGnu1yc5JZTYdIt5mudxEmFTQ6iIrYoIAKoWRJQQS/HYtnOam8USmOaczPH4xo3QhMDsWRHRihJzEDlkZniVahwmQ6uZy544iOaIKMQ1baQDv0BEHADIxHKAxWR6dOMWqqbNZZl2muZSsmo6O9s9/7UVxLlvI3jBZbPu4m43L762rB959ZXm8YP3Lzc7A0i5EOHPf/ln089On3z7xXgLY5C+72Jc3Dg+OT4+DoSmKsK1XWElh6ad53G32aipa3ErblG7ZtH32+3m9q1bZ99747uvfefzn//8O++8P6f89OnZzTt3L7cDEQ3jNM3zatExhWlKkWmz3ZWcm64TIocMBmbmAIziDmhgKQOwu+MetYdqqFhLqHEcm6a5onXUcz2GEJuYJu26TkuqyT4ijuMYpQlt03c9oavZPM+7km49dwcR79+//4UvfOHi7Dyl9PDhw0984hOPHz8+Ozv7+Cc+8eDBAyKqrQV3H4aBmn0b/6qfn3MuJUdTLQXcETHnTF6VG9x8nwzvNSEADBzci8GHmJ1XUeh69L/6Dl5jFiEg1IzBK+WiRh7e94qRHTGGRkSAyfcEFaqTfLO5FYUxyzjZxc7PNjQMMCVBKADsdffvR2kdnKD2kZWMDUpNHBEM2CkQEhkBMiuLcwAOzkSMvu+V1g/sbsZVm7IYZfWklM3n4tMMQ506HmE32jiLQQiBWUIj1ERro3YtrdZ8tPZVX5ogSpMJK2lBFXZkyMkIrCGc50lLqaV+NmVCQ8QQMIjmGcwrIwgYiinjB9Rcr6NA++SRsDZeOIiZ0ZV5gPuVUmZta1T6p9d8Gfcte3cPIfoBL1EvuZQ87QQBTZGbEMBGInIjRxSVFgWABduwB2LUoLgoaD44NZbiubCr5pmmSXNid9QkoAxeylymqaRtHgcvKRAGREZDLVZyybOWrJrACzPV9hMiIjChIDLHgIgAJCzE5IhOaPva5lkOcp3QYmbMoqrzPMPBwoiJhDirEVgjXKZkDaOI9O20HYwodL10LU0lT7lfd0lN+rif2mMCEKssO1UtOg0DAaKBl6QQMco0pcFtV3RWdw7bKZ+f7+59/M5v3fzmHx5+AmOLLFVGrYIsIjGXUkEhdzfd19RBYp3ac/e27dXUgZahabrFNE1elIhKLgJYPViuEk8zkxAkuiGAhFysb7vQRomh6dsQBcGJCIhrY33fGX/W06t7fr/8Kq50lX8w0KxqqkTRiwITIxFRMYtNdAJlBzXDoVssOxHPS9O022ym3SViGcfddnvJEkMTBR0Dtcf9djf+wr/6r773+bOT3z7OouFo6Y4KRoQhiP5ukhVEkRtHR7fv3G7aVYxN07RNE+vBRQgp5ZxSyXlflJjutpdm1oSIvZayfP/Bw0XfdU18/713Pvbix+7du/PWu+9OaX7y9AkgF7NxnHbD1LWNcJWQEiKObScspRRGgKzVGbFODBuQ72UFyzRN0zwfuqcAAE3TTClXr/baNq/YTs45NB7jHr1JKflhbCWEAABTTm0UDkKAADYMQ0qp7/uU0sc+9rF33nnnYjdst9u+67/zrW9//JWPH6+PNheXInJycoKIR6u15lKrkOo9cJWJj/MkiKYKAFUIFvdW5MZM7q6HcFM/RmUDXI8/dUPVr9frVz904K6KAD8MlCDWhiyCObCZGSIzEocARAqO6rUgtmKq6giTKaSEuzGdXeL5pV9uJGfMpUWK4IjABLYHgsABtDa9icwTEZsrEotwAUdEc3cOzgLERoLCldfkAHXQal+CA1biv6hjMc9KqeicYUg4TpySjzNlA6DipW370DXcBepj7ho6OaGTY1ittG0KsxSYC0kBM8jmSoTOiEZuGdBLmsMebGUgBmdjKrWyZmFwqOqLxHU+73ro/9BJcHWj9x/jX6Qy2D8yQMc9E9cJSJAtNASoWS1NG9eM0u+NehkNDSFCJJK9/a7DfgTAUcERTaGo56xpLmkscyrz5PMEKbmrazK3cR7yNGqaERK5MTiZE4JrKTlbziXN7hmrm7UDMQvHEJrarkEkBK5P2okdCdDgisYLAHtPMz+ksVqNlq6ylTrXXkOk5qylkBu4G6gachOmorsp3Xv5JWyXF9Pom7H2adrlYnAT5pSVWFRnRBymCRBDCJvdFs2jBHGNMbqQxrCbxoeby9EsdItS5vcfPvzz/7v/CwD8z779P/pLb/8pBzf6wDMVEUMwV/c6BfJsy+0vwmLWNG1KKXAAR2kJAOZ5NlWoA+QhAICqgiqKuIGZ9su265dNt+iXC6zO4K7u9fFXfcbaCMPaBnyWN7jnnJ/pE1QYzSwQCdLltBOKbdtFCchhztmJgKhpWmSMyLNjDlstpe/7nAYnQgKahjklSymVPOdUPzizLBYN8snRO+vdYnbAbFaKAoOIFC1R2vXRerVenJyc3Lhxs+3WRCyhggyG6ESEEkLstOSYIiOSmZaURjUsUcJ6tXj0mBxxuVycb3evv/76nTu3n5xdnG92SQdESrmME+yG4c7tm0GaeXfhIbZtXxHTlKY0zxSKlayqSZUdQxOdOOVSSjHVuq3U9tIIfd9fbnc1ytcjWVXbtjV3CZKm8eq4BQAiijGSsLqRGcfg7jdu3jw9e1JzO2Y+Pz9//u69J0+enPtpKeUnfvInf/trX//mq9/4zGc+E9ZH4ziO213XdSGEyfM0TSJyRUKtFQkxF1MDI0YgdqwmqyVIqJFf3UgEazKTi9RxrQMz9UNRyL8PiLAr1WgAJHrWbqxK5M61+CAWDoEk+B7MMFByU3c3g1yS50G3A5xty5NTPb3gXKIjIyiicBBAVCBHtL1+EZqhcyUQVsAfydCdENAViCEINMFidGZHBiJAsFqkIJDv/c6wqKtZyjgXmLMOcxkmHSYdBhsGmCefZyuZmTEKxACNWGRaLejk2Fdr73uPEZmkQC6mxT1BEbRAWHNzL+bk8zxHAGYxZyZjiF4SiRAxAJqqKRijMvAHY8SHDoArwI2I7FpP5l/8QhcwraijBRB0g2y5FB1zcSzuRmRuCOiFQQWZjEAcpOLrDgqUraqzWp4sTWWeShrzPKZppJQ8zWYFSt6NA+TJtRAYujGh1IrTrKS5Sj2DFXCtMqwoQUQkRGYB4r1rPCEz+xUB9Fr794rd7O50iF911Wq5ckeiQ368L06ZwM1R2MgNYUypXS6apnvw5FQD9xwAaZzSyc0YECiIqSLzfggZ4SqnExFXtWKGzm0DnM8eDzNCJrzcjceL/h91v1Xv+VdufIPeMgJw/AByVR/mszYb0tWLq/OAEM2sJC2lBAqBRVWjwOyJJToUQFZVczRHBoqNxLbp+yWFpuk7llCPSc0zmgMgEzGi7V3+GA4KAfv9bDbPs4gwoB9soYjITGOMR8uVcqym52rKIk7oZiDcxjYAclJbT7RcuJbF0ZK3l33fpnGsEjc5z8NuN01TLmUuuWptuQNzpXagC7t42zbr9Z2u6xf9oun6ruv7bilNW7udDmpWYC+pFUp2KoEY3RS9lDR5TvOUibyN8c7t2/cfPQ6BtaRxtyXiV1555au/8w1wR8bYNIA2DGM1wxKRGJrYhDynpgmtduO4szzneSrTpOgxBkdApiaGUgz2EK5X9K+uigqdX8n71KM0hCAss7uZ9X0PAEHIzKZpMoOu6zhIXcRZS0X/14vjZd/X8u7mzZvTbnjttdd+9POff/nll7/3ve+tVqt79+4tl8t5nud5dncRGcdxmqa+72sHokoNVvxKEQxcpHo/VDLDPp0XkdoDOFTe+wPgWS5/bbnCh84ABzS92o8HF25ABPCCiCSODohcvTyr1Yp7nT4obqjqmsuwuaDzx+PjJ/ODMzu97JQ6FguRY1AwDZmJwYAJoYr0gAOQ7xFpdQNzRxJUq6IvQMxIzuJEToIkTggIVssAB/cqcK3BAdShmKVCRW1KZZh0nEqaICcqBa0gQGga3tvHo3fC6yUuF9Z1JsGQAEDMswGpo7obIBA5cd1b4F7yjGjmagaGNRoyh4BEJaeGGSqmSM8A2Q/B3I7XHsO1bmF9DP+cyw5tU68TsYRASMjkToX3BjXFimua1VjVQQuVBt08g83FhZ0FawVQKqOgaJ5VS5rHnKc07aZ5zMMA01TSBKqQZy+ZoTZ7QZC8lGKKYF6ypllLcjc0q0J+FKQyzmoFR0R+DdXZFzEH26MPLUr4oDzG9Qqgvt0dXKthSWYgzbkYGpObcQw3btwep8nVYytBJA3jar0a55lWCzUzcM2KSNthp7nEGLPZMAyLxSLGuO5ihYLONpdjSZPm3TSTsDqsvhI+/7duNv/9k//ga3+8HutOBzTuMGeDSEyMhKZwxQHbb5IDVbzkXJvYTFy/y0RVVaYmetVsBABijNy0TduScDUz4BCrUL8QAxgAMyEBWNlneXuAwwwAf7n91b9y9H/48fMf+w+f/PmC5dnB4A4AIqKmJAEc3By5MnDBwAMRA3EAXCwaoTwP87id5jH2vcSY295UVbOqjrtNSmme580055zTnOZ5InNEYxZhllZu3Lrdtf1qdRzbjigIhyZ2TdtQPXgUkMhBRQISipBp0UToLuSaZs1zTpMpuHkTY9u0bt7E5vHjJwb4iec/dvvWjdPzi2ma2hgv/+fl7A/m5/7u7tZ318vFquv6EEVEur61ouoGTWDmTMgIQCQhcOwwxHk7lpyLGjjWsVVpRE0riUtYCikAxhiZpW1aJOz7xWZzWRfnXnAfILT7VCallNJMDrGRNM0XFxfH6/WVofzNmzcfPHjwzjvvvPTKx0spb7zxhpt1fX9yfFxULy8vu75fLJeXl5fDODYx5rKfLcjmxOxUtKi6I1Uoda+1c7WPVBUQQhCyPQR0dUI8C/aAHzoD8Oo/h7oaoSb4iA5GrjXaEnEtDrQUQzR1UwX1NM/zbtxeXDx579382rfnJ2cylF4FmwV3nccIbQMCCliIBYlZUAiIrOr4HiJjLsXdiZiE1QTBkQXUTc0rQZDYiAAQ0OEAn5gZmruaF9WUPT2zfCnDaHOCnLAUVBORtm2pCR4Y20DLPqyWpYnYNCACCAQonjc5B7E2GTYUQFUcVA1C61ZIjcrcLHQsBqABWL0VisWSo86IFBtBACtI4bon8D5tRcADP/RKv6I+thoUavJIxG6ODkhsbuh7R6gDBwvAHTDtH6cjGxIFZs2WxdsCJaPlvNO049RwaX3eDM0qxFaEaxMbAdVUs7pBnicCL9MWcuY0yDik7aWlXb27rhkBSYgRTbMDqhYvGd1cs5XspoiI1USbyYCFBSQCRRCuaWHN/X1/FhgiEYUq2lE/9f58YAMtlaRERGYeqhyju0I2KMQOVgStMBSdkxXwruFOKYZFp204P79sumae54uGsuDN9er903MMUhAwRDYjZE0lgQDydhwyUVFfBXF1Ih/HEd1KmsbLc5HYhW5MCa185q8t/8KTf/3u6kien2y53qH31LAhkJvOjgQIwAiORFhZwWYISqkUdyw5M9g0DHvQrzbTaraAzISCcb97odI0JXRLbmJVSRQkBDD1sN8p4kjmZu7FtUEGMxRyKMRccvkrR//ZL7e/+st3v/Ll8af/4PQz8zy5LwFA3QnJAQ1ZEJDAwEIITlTc3A2puDMQNKsOWklTncunkhJSaWOXc24czG21vqlqWsouz/M81/G3g7kYIGLo+rbv+q4XCZVSycxN017lAsxsXhAjVXoJmRJnjA2tgDGm1MxTKmm+3OQ8genRcrFeLIdJp0IXl+P9d17/2PM3x/HCEaY/MF/+xwUAvt689cr/4rm+X77wsRdPz55mdwgxNBTNNBWmaLNGAiYCDhBCAdLsqqAORCSAwYAErQmx7eekBgTIDiAhEgsgF3VzT6rBAoc4z3PKKsJ48IgvpTQiMcauiQQohNMwbC4uPvfpT4+7bZrm0yDvvPXmrXvPxci7i3Oxj4oqu0kbgSFpzq7toru4vFR0Zt7NEyJyiFoKNG1oMM+zmYshIQEDIF6RTQIzIBI8ayNfZVGHcJmvcq8KtgEAEl9ZDyC4o2M1JEcAdkAyhbbtGQMoGhQlmD1AVhynMuzOHrz75PXvXrz22sUbb5XNpAokzWp1NPbTOrdHsYlbZJFWghk2EAoyBlFGCBEoIqJpVk05J0ANhCiUmy6s1uTRqBAjNaEY4j5jIXbAYg5uXgggeyHFMidLCaeJplm3l7y9bOehbEbfJdtNluYYI7UMLeGi1fVaTm7bculdZ0GckAHRQcbt0EATVEBxVnC3OvVbp9Jy0VwyEJpwccxqjogUqOpEV/YF+rPM9vvZn1en7QcvJHBwpFqL6sHF28GtzgTWrs6hKeRX+tNXxzghhjqwjtFtTrnknNM8zeNWQguLMvMeVa+UAzMzNVMrczYredxqTmnaWU5aMniuak5gVlMNcCdwVfWcVNWtuOaqJcSElUBNJMRMIRJRJUJJjFf5+7XLr+YkELGOUCIieO3vkxkULQCkxfY1FRhWL0qklJNpNRWnUUsjJH1rUeacYtvstjtiNgSOcRhHEcEQZjNkBwAtxYsJMYjsu0+qXlSFAGCY01TK5XaHIv2i3xYHgFJKQht3W42djiOkJKFzdNtzQh3J6mAjM1f+pZnBQcp0T8l3jV07z3OFEg73BPd0KdW6gavqABJRbGLXQlX/dq8EM3JXPawqJPMDDI1Uhboqb+9Luy/+cvurAPBz5WeLpqsKYF9oXnH+agqihUgQ96q+CIBMgREZwQ1MCdy7Lk9jKVlqoKzzCkiAuLSSUqrhxt0rVw4AUGLTNFUSBxElhD1WDlfQnxNXTrABuBAXcyRCQsYeyrpMw7zbJhmQvGnEEI6OVo/PLpklqe42Fy9+7KNvv/OuI/Kv2gUUAOh+WRBxsVjcvfecWslaYuwkUEypOJnZYrEiK0xswiCCwI44pawGzhCksjxBQmiaJjXpSuBB1do2sEgpeZ6nEGIlec/j4O7M4s+8rPe3d7fbVZBNRGKMm83m4x//+IP379+/f//y4mK9Wn/qE5/81jd/7/T09OTkBJmWR2silCjTNA3TSOC7zWXf9wRuqnZQRjdzFnG1NM0hRqwz9oiIWLvWdKievz/+7KvvZ93HK8qyXZm8475W3PuauIEbkgQgrixodTR0UMXd4GenT9/4zne/8bXvfe1r+uBJmEqIPbetNLQdpjSXFJscY88sYDNSY9xBQEAO0aNQjEgRALR2EfMIYMRATNovQ0rRkDlCEBQGiNREBzCoMDa7FTdUUDPzAqbFi3op87Arw6DjAMNk0+zTDFaEObSBGvEYqA24XsajNSyX2kQX2nvwmEueZ3QIFgB4KuqmBMCEoICAqpoRuW3NgnrJGQkUQ0AWN8U6DmR7IPsZ7vGByPcD438dY9vPs10DhawWlnUi7OpXEe7poX4gidY1x4hAOGty08hUh/tzRT93WzzQnGvE2Y+3zOqqOc+WZrec55HAkdBMiVmESLjklMGh9h61kvMLIoqIVSboPoVnYiYOzIxUz4Na0JCIsJBq/v7PXXdIpbs5WGC6qlKZyfe+K1By9qJWlBER2S0DkBPs0Lr1YrTSNb3E9vF77zcSj46PpiZII+Mw7ObcrnsDbETIXE0LAxOM48AIMZA4NU1ksGypX3TDtJNFv1ostmp53M1T6qNA7VW6lnGIOXXWKhUHghr3YR/Qmcj86oljnaskEjMDK8xCJBXYfZaF1YE40qbleruYuWkbRZIYbQ931oPYXJ8NlCDt93klIypVqUhz9//o4i98efrST2+/WKz4lcTINTSgwtlOmEvJKTciwkSOhKTuhCAkSEhtywRElNJEiDDPInsJTDwYlbBga1ZH4eofaXX0FPGK3VjXZz3e6iRL3QrwTOLYEZ0RjNjJSELXtqlfTIsFWC55VnfIuW1j0wbOSgZpTmenTz732U//5u984+Ro5Uc2fdna34CLHzp31xqdj4+PHdHNY2jZCBCzA+RMxBIDhjBnU/M5ZxZyDshCyOg1wUI6iDrU/DqEkHNGpnqqmRYR6bquzvrhAfINIZC7qpqWruu22+2N45O6BYZhEJEXX3zx9775zYfv3//UJz/55OajeZ4r9Lfb7oDA3PtFP2zHIBKFL06frlarEMJUufy+F+4HwOpQxoaHIL6/rsf9H/j16olcD03PcCR/9hUB3VwdACQbmoM7KoC74TTYk8dn33r1W7/yj978zjd3T7edN+wNRAlhIdK4QSp5M5eE2wjWlimYR4WeGkGS2FCQEFtzMoRSctI066ygAGYI2K+6oxv9NPXukYmiYOCSDVgBoAAjgQFaVbFT06yWC+QCOZdx0mm2OWGayTSXGbQwI8UArUAXcdXhegXL3rpGo5iI78FnE082lwkNrTTohOARxRDr1H8hKiGG9RF7YDNIg24Gz+LMllzqzaW66vz7O7u/T6vXrFhVnbuu9PTMhwjrOX31sGGPM9RJP7FqqYFomhGcybXkhoncvFhOcynq4BmRkNy9aDE1QLBsAKa5uJXAxJYJEdRjiADuJRdTPLR7wEH12VAJgh0GnYIpMLNIpCDMEQmR93KJdc3pPnc9fLZDHlqx76Zp1Gwah6xZqj+2o7kDoamVUhjJAImoEIkEyqWYOgAfddYFN/fAQ5pIZHG0muYZWjHTospNdEJkEuRS5mG7FYe+aUt2TLnh0HNYL5Zp2lJsk/nllEZHEBl2l+7VD6vdXj45u3j60eXSph1PQ2zCCFGZCASBAYmFGcm11jDIzMy1H4B1zCrNRd1i25iZCF9tOeZgbiWrxBBiRMKKtAqxg6ta9VSyoqUUTyXKPhW8Wks555yTogDh3pGC8Ke3X7xyMlHVv/637v17f+btq3xWRBRciOsEgObCIDWV2Evc477u7NoFU0AiD4mEwSGnpGYAwEDCKDHSoXl1FYAQUVMVW913pwFgb1h2ZV7oe9m8OmeDpshg7iCuVoS577qyXoPO49gSo1pZLvvjo8VmGFNSVzp/evri0dFxH5AwEOKvhNHT/fvv7z75SkpT5dcjBwAAw1SMiPM4A8cQY9P3IKK73TjPKRcUcaAqqxebFivmfPDmqzetaZpSCgEzk6pG5koNmqapZjl7F5fQ1N5sRZzZyMzOz8/nea4d5qZpbt26dXH2dNH9yL17d994443tsF3Sct5tQxBzs5J0nudBg8g87OZxuHXzFrGomQOEekvBYtuklLyU+hfWyTW4Rk+6HvE/9PrqSV3RTK90Z7D+hqtRYHCrjskpFzNHcgdQxd355RuvvfkbX7n/6lf18iIUUQ/UdE2zFG4Q2AoC+HYaL8ad57GxLauKes9tyzGGiCwSI5MYeNI8lTSVKVnOWtQ1xsXi+ObJNK5K6bQsmWIIFBtiBCAHBUNkcEM0N3UsBUvxXCAXnWedZ5iTp4yleCmEwG3ELnrf+FFPJ0d+tNa+LU3wELzafJmDuVjKVqhAms3RWUjmUggo1Omp2IajFS6XWsRz6SSgUZ4vCIVYCMiwNjoPgmdXcxZXpcAViP8hdMhdRMC9qO6bB9dEcup0ytVecnf3Sr1ydzdNV2HVNdepDAFTtwiuYEzQCKaUU0pF1Q98mqtYHAEcDEqJtO9sopYa683KoRSsRcbeDh3BrA7EsuxfiFAQ4gAIXv0ckOskFyKyEGJVKfAralpdf5XyjDVnBKqTlvUPM7O2badp1DQ7WiVozUkV0SSsj4/jnSMNDFmHeTo/37Rtr25AOI+jgMzzvLx7slUt4OM4QNGSU9d2aZ4D0rzbAbg5kpvlbBjM4HRzuUtpyhmRUD3POZXcCM85IZRQkp6dxSaUSO7iVsBBPSGwOTLvJzau/vgrdj9T4CaUUipFCBFZGAkVCdwXTScVvUUCAHUXRDVjZkcopRBgCEHVAZwOQyFEVbbMVbWUalRXpUAVACuDRQ9Hb63Y9pUic1IrpRCzm7lalUqOMYZWiNnV8DA6JDFE7zQjsdT/JU2zmQERsmiVdWSu/zTLvo5BiVfxxa8VqdfIUntblTrJQ4juwAhIBEjAwn0PZU7Dpo1Bp6mNYZqmdde1jB7Q5jLvhtOHD1984YWzy8uzc5xzCRKQvF90VbZznKembXPWpnFLKY1jaHpCWi2XjlCsAMDlbreZRhQhCCFEkUDEWozpWUGWUqqvU0pdWOwhNX425F8/fmUKlVIE0czmUszsI3efZ6Sjo6PHjx/fu3fvS1/60i/90i/du3tve3lx+vTx0dFqsegePXpwdPTJPI/LxY3t5nIuaU7JzDwEctttdxvmZnVUsX6q6ujuNfOqbbS6ra7MBOtB+4Pgh2u888PK2f/oKhPVKnawxxfq8ysluYIZeXFLuczT8OTt7/32r733u789nj0pKUE4kibyskeSUooQu1qxPM1jmodpvJjHJ5ZnUm9IGmmb0IQQ3IE5IFPWPOQpl5KhjPNsZo3JYvVkfXZ2Z7d9Tg26binCJI7grVbVaDJkACtA2T1nKuqqmjObUyV05WS5OADFKF1vXUvrFd44glsncLRMTbTAKmwO5IDmrkXKXLR4HRMJ1BUyIzIHRcgIzdEqHB1NxFkagWhWQm+w64DFbO+7tAfxQeAHXc+snQGuRHoBwF0rnRbMqiIHPMv9D8/mMNsNUAVEDcwqUL/fY+BWkrtbMVALyMW0E8pWp6u91k2qZuiG+215EOfcjw5V6goykBseUC1wQ3AHIyD0PegoLEREHOp8Vn3NzMWckWsPAP0ZHHlV3Lj7lULh1edCRAcDdInBDed5LqZINKWZRHKeC7hWEak2CsQ5pcJ087k77z96eH5xGZumrmYFaPuWmclpN42xawPakGZQIFVBKGkqaVZwRje3rgk5Ta2EyXGY5qSIHAWx5MlyZmJzyFqePHlkH33BZ8inTyRK6KKqFQcKrRM4m9fmNj97alfhz93VjZklhsoGcXdAJBGJje1BmmdZGxzkTcysjq3VNEBECPYbnqob4F6mRqkRfyadZCLR3WtzpSaG9ZFV8isL11AeDseVq/VNq6auuYq2VuUvIkakAByDlJIxJc2FFDxnYJbQeM5e3N2l6uMDYaXTwLM8lA4iRQBAV0ZJhA57ji8CQQE1Y0I0JwkpUTUZOVqtLM2Uy2aTFhKO+/bWenmx2Y1eXG3cbD5689hMAz8l1KxKjCHw5ebCrDAF5sAUJ/O+bdOYDLxpOml6IrBp3G62D588MQdHNPdykP8k4oPywf457mWfzdxNtdRPJCLDbqyPuAL9dVRqD40CVJGJYdgtFotxt7t37944ju7+0Y+88NYbr12cnfer5d3n7337299++PDherE4ffgIUV1k72E77ERk0cTtxXlxim2LiJNqfeG4H6E8sKOf3XDmfdvu+6+rw/gH/vT73w5uOk9u4CigAKmU7W57+vS973ztrd/5rd2DRzQ7UIuho6bFwAWM9uVCSWkex804boZpczlsc5pzyuAYOASJIYTqXcHMBp61AIG6TWk287W0T04fLKZhAN9pSQh3ShXovxmtpwaw4WpbzMWwOCa1nG1OOs2eEuQCRUkrYzpQCNB2sFzB0bGf3NCjtTWthuAsSkTIlDKoQVFBcytFGRVJSZVYEQwhoU1W1osO2jYBOkdCZFNhx65TCX7t5lZ7gN/nAfzA11fSH1d44vef4Hh4s2vxQwlwFWXcDVBBzd0QUHO2YghAZl6dDokdqXiFz+o8QDnIdz9DZBEATNGNEAkcqI6eQeXlAjIRQfV82EuJCRPvDaCJhQCrOA3y9SlfODgKuT87K69Cg7ubK6AXzUyhaRpVR6RpmsyMAnlyRcAg85wyYFj02zmdvv7Gdhxi0+aU7ty6NabMQcY0m0MbWhZRs7FMsWmgAOSSUwoxRpYpTYFFS07THJrFQsJut5tNpykpszMwYAASkpzzPM+/8/L9P1ayWsZS0tmpLnvulojIHJ0RYT+efoUIX/uA9STY1+lmQCQ1HyfmjIAHI7l662tYBwA1RWRAqEqf9XEz42G3P/PucH9WzBGR6TXWxzNO934pmRnYVdOeoNKR3QlRzRCIwMCJfG/BQygo5qqBkEXcrG3blFIdZl4uFiVnVQM1RqwOVkbohzzBr4mRAYCVfTlyOI8IsdJR9/DnvrXAjCYusmg6a/scmxlI3XvmdQyJKPQL1ZLGoUzj88/dfuvdB6ebOUSZ5+kAxYS2a2PXu8HmcuOqMcbYLBb9UkQcVMv2ydOnT05PKQhCbeSQKVox4yLEV+hlxX/q15QSgNcQX5sBVx/nkJ/tRf1KnodhWMR+s9m89NJL0zCM4/jw4cPnn39+ueiZaNhtQitAdPPmyXe++61PvfQKursVd6/tE0Qct9ujo6Mh78bdwMQcg7mXUkgY6gTDlT3kIXR8f+L//SHoBxwDH+oHHFrB7FZU68AcJS2bzfT09PFbb77/6m/k999rk5u1FhqJfWAhUyNUK6qaS5qmYTdthulyN26mbFkxIzvgYGZp8nn2SutgAsSqYUQs7szEp6aCkOddef/tqahTQOdGJFbJy1xIRZgZkdQ5m7uCqpeiKfmcIGUsBcxUASlQbLHtZHVMN27a8Q1dLLGJJEFZEBkd0ADVvdiedlqwMImRO4KhKxHGWLJy0xiRAhozUgAtSAlDxBiQpBK/8fcl9F+/6R9owgC4W5VxqvA+gCOyl2fQOe6fTRVBsjpHV3/j3kIIrDJK3JwAa8tUkwphyVqzeABnwgrkALgbA4Ca1Wmh2pGsahfoXtX6mLkqxtfNjDXuEzkyktBe8+4Z3hVCA4S1qJKq/vesNwVXNOSrtfgBoMBMTQ3BVKtMHDOXnLNp7DsqdnG55RiLQ0Zsuq6YLbt+SjnEIBJYPas6QpSQU0akKpXet+1wsQ2IjJRSNtNUStu0KeeuaRggl4wOjx4/ned84yN3tuN4OUw5JQcGpNf/kv2Tv/jtvwXffvd/+WfbENNut3vwaHnbMTQuDVCoQIqjEaKb55QAiSm4e238OjjthXX3bVh3z6Uo0RVscn15lFIMnJkJqZRSSz1mrjP/7o6M5GRude2oGglTJe75fqoT93IaDAfFvcNwE/BBnLWi1QiQp9nB+ZmtqSIz+D4xIGF3JCMEUOYYY5WZw1wCCYFaRY2IhMUBTLy2H+rzfRZ0sEp6IBEhVbdDM1VWN9urarsrEzJzMWBVUg1uEWE0FfT1skfHyUQtX17m87On3XJx69bJxVjmbKGJR0crK0UiE7oII4Q5ZVJbLJYijQFLCLvh8un52ZvvvLMdRw/B1IWrEbOkadUAAQAASURBVDRKEAwRzGAvbwm10VVKcYBUcoxBiEuemblpmt1uVx/o/khglhAQQAsRYtu21X5yvV6/9957i67v+75pG9fy5PHjbrXsl8vnnrt7fnq+2WwEYLns3IEJVYubBeHt5pIQ5jQ3uandrD3K5EbMrgofnKEh/Gclnx+IP1dPpAaWAzT9gQMA3N1NEFPJabfT7XZ4+Gi4//Dx916b3ns3jjMWMWkKtUItAVieixc1c4d5nqZpN4673bDZDVtEcSc1L26KZPt/Awkc1AiQHJvQMDE4kHBiVXBnKWibzdn9d99SQ0NYG55o4b5tdWmMQCTmkDIXs1zynMo8Y85YCqqCupCQSOh7WizDyTEfn+TVWruegjixE4Gjq6Jb1aYUKdIAaAFsyAkyQwEuHpL1SjJlWNeELjYKYVLsPKhE7NZFLkIeA7oyFqi76wDiX3vt1/oBiHWEcj88Wis6QLc9ecNKKQH4emi4+lq7FtUDuR4B5OCOxZyq4mutJNSc3EwJUtWJQoT6WW2vLIpmWuX+K+BTexjmVI12kMJVG8LdAckBGAMTm2OUhpHN3YWRqDb1zAoj14hTnWjq15qoehWtsvJs8e1zX0A3cROvCt+Wc1YgICw5G5mqq3loozuUlCjGbNlHla5T8MKU84xMDNRxaBAvLHkTsWskWZpHRAX2dtUXg1TytMlisMJw7BhSSm24gPLw8rzr+lXo83YCg4Ie3M6GdPoH9lvlN1556+feewm0rC4cvISbt+dAxsDC5E4OirBHh10lBuLqXuRG6ASqBmZN0xTfUyzB90f1Hp9RrXov7iAsXjTn2b0wISGCg7oCGDMaFEDjAKEJiGBopSgRMYcYBRxKUawz9bzvK6AwVHFdd7UsIoCADAZ68GjDIE31s3N3MK16w+7V/4i8DuAQAwEROZsRzdMU29Zhb2BBEhxcoah5aJqUEiJa0b19CgVVFeIobJrdSnA3BS1EQCAllUHz1AE2TjqqPX3MTx6t5xHEUw8XaQqtLg1omkMTm2alhAWKMM7bHTI37XK1Phq35y2vENRzxK7ztr+zvgWpjNudz1Ox+OT89HffeuO1J49K22mxYBrIzVLB4IyAQKGR1mC3M1VmzDlVTmdAaJhKmuqpWUeyuq4nEndHlqyWzTsRdhYXd41tUMvZ8tnp0wePlp/8+CdiG27eOX785LQUHca8WCz7fnXx9Mmya0KJXddxiGVOSIEIXN21AOhuuFzQKlJbpix0ZTcCVTuanpmiAyA52xXf/DoUSXX3IZjvA0ANULXr8+wQQIDqL69k6prV57lcbsr52fj4fj57WkZVIw9EUULbOGABLOiog2rJOQ/DMM/zNGzLlKGgIZoT1qRln+s6IMwIgsTIAZkBAxIysggjI6EzQ7fQph01n54+jm81Eyrn3dHN52g05D0xlKryaQGbFWelbDAXNhcgIdOGdd373Rv+3M1w47j0LYVmZgSkapeM6qqFyExM2rjwPFspAFwcjQS4BYigEgKmUlLORChNQAhUYJ4dREK3oKYt01SteKxmyVen7jWsv3I58fB9ql1ev0YQcvB9GeF4zYT6Q6X03u3hWv1X30aAFTu+qg3R3A8WO3X6Wou61+ldQ9k/bgdg2sO1qsoUfC8WiYjoUFOzZwwlAKwGQIjISHZIb+na3K+7X6M+uQg/O7K+vw2+X7CIiOo11DjRgUZjbuApZ2aGolHC5TTNqhCjmip42zTIwdRaibzXqMgYY40+Bk7gEphArBQruZobqTuzdE1bAm12u1TyjdureRxMdZxmQKp/0PKvUviP+M/QT//E927NmBwCk5btNjEzMSIjNx6oEJohEYoI125vZXwemnKVBb9vsSIhgh2meOAAmFRGbGByN3R3L1c6D2bFgA5ZhWMdPkZEQtvfzIpI0JUdfIVr4Mqo7sAcQ6YrgHs/ss4sIqWU66kGMuA+WSevUleHRiIAGEBoRWJgES0FAHPJWo3EkQMRmJdSXLVr2v3jRqzDR7SHTWr1qqpmDECCHIU1FqVhA+dPytlTv7hAy23AXrjvYmDW0IY4zSXHQIuTGybx4ifn/vWYsq3X6xijrJZashoumubk9u2nF1vX6cnTx2XKwjwNm3fefe93v/XtYU7GYnvbrYJERbVoOTo62mwnFmmaZhgGOLCVVKss/L5DXh9LjNEPuhEVe2eWcZxCHTFxXy6XFxcXw2arqtvLTQgBiW7dvvX+g0fMPGy3jHTr5q2nDx8Mo3OU1XpNJMxmBk2MpZhOtctvJWcSRuTa3anBAfYEXzYzPggmXs0i/f5w0Ae33ocvh6reDId/xcHUwQAckFAIOWIQQ3C3krMBCKaU5pTSOA7TNKU5VVwDkIDcK296PyvphAioAakhbpAYMPB+9YgwSeQmxr6X0FHsCtDp+Xl+n8FcZ4UbyhJL27CQMAkUn2dMmYqxAQCBASC4CPctH63oxhEfr7FvOUZnJnZAAifU6vDnCI5usuyPcB59mtDZPQAHo1AgGAZEnDXvpsHy3FIdUPYoDcaOukXiSBxMDR0E+XqwpGtqENchoCs++PVyDA6C3bUMOyT4H64AquNPRQa8fnVHgErWQa9qFQ5aC2u7DkztqSm1lME9G+w6dEjXZg7w2gUAjvuIhkyVsLj/r7rWfPAM+H0W3IfIas8WIqLWAw4cEUuVOMqZA6GRq21346RuMZgZi5QmqqAXIaIYIgvm3QDqOqcQBQBJnRG1smAtM4Cp55zqjkXCpmkoCBDsxnFKs7kxOYCnkou7o45pDv/E/mT60V/4E38w+XuoGGNI00hSAClIK20/p3FEcMHIzR4OBqeDYGEFNKjyIK9prbh77RpbKYhIzFoKuvdtqznXMX+uYx/gXuE+3zeHCMX3/h2Ee/sXuWo2wH7iGK9ClR8kHveHTZWDRUTEwIJee8267+UjaaUkoEPNHa71FD+AHjBVe3THam29/0c119sLXddpzrUR7bX5bzV5PuQB7u5qoA4MEAhig06bJ9N7b5f778huu3BLWrJnQe2DJGcnYMHLnSfNTPA7/5MHv/avvQt/Ez7z/Mnd524jQNO056dPnfwGcSmpbeLp/QfDOC27fp7n9x49/urXX/3/k/bnwbZs6V0Y+A1ryNzDGe70pno1SUaleQA1QhKyAINNA+2mDXgIgnAIIQbjwD2Yju4mcPiPDrvDuLtx2LTBCNxhHG23Ddi0jO3AdGAEQtY8VGkqqUr1xnvvu8M5Zw+ZudY39B8r9z773vcK3OGMilvnnZN779yZa33j7/v9duPkyNM0uTo1Rr8DKubo5JoAAOM8pM3MKiIi4XC0iug0TRQbv4WqWeGSAzcbPI3jKw8e7Ha7/Wbb5+758+fPnz174/XX+n5JiPvdVo122829O3dff/31X/3CF/pVP4zj5eXSEaapFqngFHNGnVpkgIFjmFlm9SBANLdS7Vb8C/Dww/+04zZ8a/+2aIaJc8eAgME5OrG3iQEz1WmaxulwHMF+QreXpm4tVCWAiJgJM2NCSiG2YikGVubY9aHv8/KcY5fzKlCq7pubK9dqU7Hddrk89+UipgQpACJWoalAVSjSOFooBu1TOF/z3fN498JXC4nBOTh4k9VsnYeGhiF3AAgktOBF6JMhAsQUV0wLcyoF3AAQpmkgKQBzJFucmCP1S8y90hUKMiAbAtqtyT2t+7cgd4bZKhEjgrmBnTqAuZFw6i3gkEkcts0tjv40A3CfewYE2KQ7W174EY/2ME908tpZvTKl5AeOkWO4NzsBJgDghv85ZADEND/nEwcAH7r+JnPhJ5IULy3QuU2MaO0EpoCzj6mljNOYYxIgEx3ckRk4jAghxsCcYyelWBEoMg1TirGUevnq+Wac3IzMmQlqmapACG2pjiJL4pSzqgjSzXaz3+8QrD1cToEUxT0Cp7wyRFxkzVFGDGKAlgll3Ouzp4aEr76CXR61MAScOf6gjYAhIjsDHGwpttwTDhiehhpTYgYzRjR3LQVcWn6H4GrWSmjQ9DLbVENgNwMKiAhExMTMrRBh2nrs1MQJaq0A0EiD6Yhtd3XV2XnPy8OJQMX8ROvqGJ0cH+jRkcyVfQRo3WMic+eDPWqjWK6Wc8aUCLDBnwghRmYA0+oqbdI4NL5dcDQPFWg3lMePysO38/YZF6UyuY2LDrYk5znug9VRINJmL4iaU3r/62ZF+PE7yr07l7UWjLwfS7/splLWADnF/TCkPlOKv/xLn//pz/3cww+ejM3rIgMaHDrwbk7Eu/1OBMMhAwghxAZwAKgH0oV2c1pb2N2beAAzq1mtNee0Xq+bzAMRLXK3fX5dsATm999//7XXXl323dnFxfPnzy8v7+53m3GxPLu4dMQmH7/b7fq+r1VVVUXEJIRQpTYfEDhR8zohICITHUVH0I6bCz8ywPr/63j5lYRtNL0ptLijGpgamCq6mpvpNAzjONRaa614GAPSFqg4ADoCBCQHZyRGWMSQiHOITdeUmA0cmGmxSot1XF3E5TmlvpWatRS2/XBzfWXO497O7/jyrF/0njsMCVVxnHAsXio2is0Y8OIc717wnUu+vCiLzmKgFBDJUNDRDdG0zRyxO5qHpScBC8DqbsDBKYRoQk5oXkEbCetkUoiWDurASNExNIGeBn1velcnqdML0e5pAeRovk9YMLU9SndQVcZwauJnaLndGutDT3juoJobEWkVtJlqZ/bAKqoKPrchRaQx8LSK/NEHNMQbAPCBLmK+vCMigvkANAsIDAf0SyMwOHqLj7Tvh9C4OYuDsvPx9wckKxBSI+MTa0Fx1cZ5xjebvQbmnFHqYrGaEEPi6lZFTZTMmfBmt+1TVrcKtjhbPbu+ArQYQgAUB3SPMZpaYDYRiryfhswsTkAUAsfAUqVIcSdDI6L9zfCx114PkUeWfJ6vrp7cwRAilWlygHGqHGO6cwFmBOjmgK6qIc5A+FkpzK2Zg1bvOMbmAcHMiBHcXNRnr2CiUwMi1jLlnFTETB1cIYR8eGcOgIx0BB01ZVJkJnckkpYKtgcKAK3C03UdmMkktZZpmlbLJTB7Q5EjMUdXMxATIQfgW4qbo1rWMaNFxKZNeJwDwENZCSm4zyUjZgY7Qs6NHMykFX7MBADdlMzYzYcxSdWnj+HZo7TfYNmTB0Apslcp3SrigmVbCKCWgjS5ldWy/+3/3Tf+tfFHyt/cXvxoWvzTabffSswKhLPEI8ZAIfFuu//FX/mVn/rsz77/wbPqLoDEsVZhotT8lmpDYcWZaRumaUop0aFX1+A97Zsyc9/3jU2273t2Y2ZVRZr/Oo7jIucyjHWcTPT+/fvXV1cpJTTfb3br9bKKPHny5JV794dadvvN2fri/PLus6vHq/OzoUwhp7zoEVGq7XZbPaF6rbUGxBBCVXV3OUwIERGcoK5PLcxLlvw2gXsx0X/pl6528l6g4AKm4EaIIUkVJ2pqFA4uqtM0TuNYSpmBzofPYmZ2MlcyMHAECMSBOMfQkXUxdimHVs6MQdxi10F/3l/ej2eXtDiL3ZKBUNTLiNu9mow3VzfTxOOAZzs6O6fFEikGw1AFSmFzQIQUPSdbLvjOJd65qItcE3tkAEDwufQBBmaoxuDsju5hbTSZR4cG9SHHVqZHCuzBQcnUTWPD/KmhOTm5OxNNqmhVG0GMwzEW9hMH8EJofIT5+wHI5w7myKgi7spIYI1i+aALZg5NxOrFopAdpB5alaBl1s3VNPkYJiKKKq2COWM03f2Ys7dNDocC0elSOAzsgLnBPObaqOvm79geP79YO/rIAw8dkOOHfmg5zsVlAKDA5t7gIcTBsSh66LrrcRzAuxgxEDHtrp6/cvf+brNZdblMU4zMiSvx+cVZRS+mHiiFSKLDfuTAOaaWS5l7CKHNODx88tTc12erGLmUyVQUHIgRfNV1Z31fdHherl+/E+g5TOOG+MxCwIBIoYAEAFAIHlrTI+csOhfv5uYINI2zim06bm56tzlLPY7CHZAzJlrInQi0VkFzVTN1ACHnECAAACFFIGohB2HTf0Ckxi80x+Ii/qM/sQaAb/vWPSLOFNBugQg5OKuJzlo2gIbS5hNaUCC1NnZlmuUnb7f08YEei5s4CybPh73Ynbp9lZq5uhma1jKhKaBLrZkAxzEM+/rkYXn4Dm2v2NQ4VDODIjAYjCF1NVrIVdVSDF3HaWKR8sZn733jf3D2zvvT4m7ucri5uuoXq6nIvX7Z94tSpv128/Tps3fee+eXf+WL7z97MopOqhjSVKRKxVZ5aKK45rUWCMzcHR1bGQf0F6i226NU1ZzzdrttoRIRwaHvZeYYsFFGa5VhGF558ODZ06fDdvf48ePVctmvl2dnF7/8i7+0296A27Dd9f3q3v1XHj159+rmerFaF6kdRwBwhNTlAAHAx3EyBA8Yc44xeuP/YW6eqcWRcIDxfOROfCmhv/3Di0WC+TQEACCfNVgaQZkTArMTOzUIM6mKqooU0SaYSA3D2ppPAIAOoaGTXFE9hJg4JOYupT5xjjGlxMxIhCkIQVosw8Wr3cW9sL6EfsUxJUQsU91hwPMJAIZBh10BGM1Z1UtxTuroCqzmDhSRcg6rHi8uwsUlrleSosUIHAiJEdXFvU3/GpiCKqiCSFg6R5VJ3QiLmYMyGwEjMCCji9dKaihqVK2KlkmnsU4DuQGogzq4AzEFP+F39ENV8djIPd1F7t5QdO3nlvYBGDOf9JLhkCKYt1ltbVTm7u6NL6g1f4kI1NqZ6GDuJ/X/w74lQnh5KZxmJHhgHj211IRMgRqyZV4mTEj0gkl48Tj5y21NHACOw2unRQY8yNrNHfA21mTW2EKcY7cKEwB1qe+SEOxKoeXy8vxuLcVUr6+v+xhy3zn6RH5x73JCr2Bg4GaohmocY4tGDczMOIYqgg5jmbbDSIsYIzEChxBSCohlu7u3Pu9jHKab63J9f7WKF+zPJcREKXsmDIFWS+46hxAgAlO1NmQbiKiZQVUFOCm/HA29mUvRWtvCaG5AmkowNylXMxGTCdoUBZEQJO9o9uDBiYECITJoSwT/Xvrhf2P9Z75j+vY/efW/aXXCH/7RBQD8+l+3e2GHu7kJgqkUbOrLgqwRg3No6FW61SlzR9VW5T9akNluyAGGiHha6pxb/c3RmoHN2aS5upqbuupxKIwJqAoPW3r6UN76Jb55TiLuMKoV9ApqsXKntNKRdpQqVwu4CsEZbdhvi0YTefWV++d3LmJgJl4sl9UpdX0VqzL86he/8MHTRzebm5thDyGYghmo2jhWQJ3Uln2vTfKVYJoKpXR2tnz+/HkL8I82kYjA5/ColDKOY9d1jfEiMJVSDKDrU0651trHlHPe31y//fbbH3/zzXEcu5iYGR2urq7ee//hncuLJkEArqLi7sv16s6du8+fP3/llddEZPQxpdSIiQKHs7MzxN31dhODxJyb0awH+fjDJjo8IH8hQHzh0X9oMBM+lAEcfj5tHQKHgExOaOBGbC0oBGutRnXzw/Zt73CKPkInQicACxRizCF2Ifa5yzm0RgsxAxN1CXNcXlyGO2+m87u4OsO8JKbkavvrqqNJB9MEVaMIisg4DECuDiFHQEDO2Ib4EsSAfZcvLsJqZSlXIgszhp0MtGHd1UwrqrqYVfEqYQFI6qBmwFUqOIVYkVnMwLydZ8MwbTeKIqPEOtk06Lh3mUyrqSi6AzZOUJx3u7SSziH+nYP0YzgMDn4Y7cG2qVrRTOeBr7Z5mmXHA6r6NLY6xI+KTarleIY5gKO5oqlKKwGZ3cYyqU+nb3VkL7ht2bRnP+spoh+agcyMODsz5sayPi++08ji1AEcik6IgHqcdHuR9P9AfgYAoKpm4AgEpAS11twvx2kERyfaTAPkrpoSopsx4lQKpSSmCp4vzgv49X4rbomDqzLCul8oeplGsGYEnIhKrQayG8YY43K9BoBhHFoYXqq66eX5ReJkZo+fPn7jgu7fX6hOUIMF1hCmwHm95K4r5lgNCEMMqqrmMRIAICETmc1VFFPTxsF7mL1pkpBd1zETgBOCAzCSuJiK1VonQ8LIgQI5AhISM4UATIgETNiWjhs4/Jvn/9e/n37473c//B3jd3z78OvbKC8c6mwigoDgLlLLNLaBMjkoFpgqiMVkABAamlOhgUEcIaaISG72Qm3Y4egAXowh/YAzbKL0hzWvLaMzMDOVOu4JPCHBfrd7+G556/Pp+lFv1RwKZSMqMghWzJ7OyJfu0w5IKQdyCCH0/WKxWGLsXn3lld00Pbh718ymIp9548307DrGvB+GZ0+fPv7gsQMqwFSKtZCIUKZGdxjKNCIRoB8mNCg37uU2wXDAULR72Oo8R+hUS6pq63IjulkpNYcopiGEzWZjtYoIIHZdF4ikVKkyDOPTp89yCudn5zebmzuXd/aTlFKW6/7u3bu1Trvdbr1eB4bmAMzdQRGx7+16s20ZebMJMUY3q7USIDXwT8PsHaDb8OJx3KEvxaBt6AE+4uxbH1BFDIBCDLnjVMWrqbuazwrCyBwwBAAHVQQIIRwpJUzBRZmwTzml1MXUxbTo+tjn0KbeiCBwWPZptTy//wAuX49nd3CxxtwHQqx7JRUXMRVTN4+lBEdQrdOEQBhVG5AtNskuCsuuuzij9Rl2nQbGGOc5Wnc3b3A0MwOdMwBUtVpCmHYLg2gwiQbEMlWHbeg1w76oCKJux8AbwIcYljKKo9i0setntL2JUkOb8yRmAyBERzMnatLs6OClpYrEdsSAmrt7wEPhxQGBZ40icwd1MGxFJTQO6G5E4FUQGv8bNpS5uyEYIZhqE1hkBGtUNPNkGRxquNzMBTNrFTwMBBERcwAAcyOeIYkN3gPkTo6IDIGIW5kGAzqBuiESErWqEyAg39b08UBvh7PIOyKSAxLdMkDggcCWkACo1IoNJdgEI8xVJIToGOpQwB1DqA55tdY+3khJYEvCcbNdR5r2u7Baeei61YUBgzta9aKx63Q3YhWUwqsFRdAq4N6ltB/2I8LOJiNYn52VKsW9uKUQO3NcRspd0c6l/6vf9vk//w0//b/+6a/5LntjvC7ES+DzkLpucVcILYeKHsmtjPv9GEI4WzNScKnVHZERQIs2NwsAM+mTWUoJwExlmAoTtuh0XwRBSKfgKiaiVCGGnLnrKHcYEwRCAEcjUEA0RlMwh+8ov+HvpR8CgO+Ub3d2xoiHkj01ihMzAmMbfdoFDExRagXXagKBQI1yF1NnyiF3TXcjhCilgAAAMBE6ipobEiO6Ec0SIgjQConEhBTImy9uqYkRkbmyTKCuJkgIXqOOvRYcdvz2r47vvRf2O6ggxAJltCs1W5SwSSNcCt+vJWw696rRqJvGPnSrsxSWy3sxr65utuPDxwlJijKn87sPnu7FQ766unr4+OE0jR9c37z13qNn19v9MKqDGiKQqwogMRcViqENQJCBF5lkS6qRsJbSiHlVK6LHEFp/u2UAjQECAELqJtUmiUoh2mRVrZYdSH3zzY9tttuLi4uU86OHD7uUzc1r3Ty/Wa3Ob7bjYmXDMK6mYcDGBbsYxvHBK68Mw7CiJRGgo2jkGDsMfb9veuKtr25uhlhKSSk1PbLqmkKEkwDrNBI/pgV+0suBkzjfAYAarT0AohGbmaOZK6CZs0AvuBp5bym5oVZBMrCRmcGLJUOkGADU0GtwdDVzrxGQiNUXnPrQ9V2fuy51GXPqckqBY0weIvWr5YPXujv36f4DXq6g6yllcochmGEVoiJF1BSdRq7CbsGVZRIKOTABMFrI2XPU1cLuXExnC+ozxOSOPGepZu5U0KqSqteJRWKdaBxstw8olQFbIYeQDVQnd1dCIjcUgrgFCpNoWt3hSR2qDpu6eQa7TRBp8DYkMLUW8M71n9khAzG1DnFAMp8JfttzOU3Zbp/TCWam1ehbetbK/Sfw5MPzmws+DgBIDRWAQAAnXJzN1h+y+xnXfEx1G9MAEbV5dKCjsBe2L9IKQ3Nlgz8C8XlcZ4gfqXX8cq8JTyZjCQwQzKHW6oDEoZW2TbXh0U0EEFNKylTGkZm1VlU1tVFqcbi7WGLXO2AgqqXGwAGpTpOOYzQjsGnaTWXI/QImdcUQ+/24E9XlYnG+Wj+5uen6HosmjjiVftETh81uv/nW/Q/95rcA4M9+g337k3u4RnMEoLhcUkwV0F05cONYTym10nlTcWu52Eu3qDEWoKmqtp0YiacyoEMpRU2k7BOqTIOKKsVunQIzNorNBgYiauw7SG0kGMD9X938b79t/Lbvmr4T5hLaiw9gpuxXRAJiB1azaZxUpiJDDRyYwRXBOSZlNA1oqqIE5kam0oZcGLlNHpqpGTTa5EaYnFJCQNc6LwMD8Za2Uq1SiyICuMl+SDKGcRgfvzs+eYQP3/FhjAYgMmqBYIBiXpyh0iZdUkmT2BjTIlreVe4WZ4hgnrp+EVO3Wq1U318vVzGQIU7DwIBPnzze3NxILbWMT589++DJk6kUnyU22sDj3LYws5bANGGGMk0cHAECs87EhU5EDWrZTGfj+WlaCESUc+fo4zgyo6oxERHnFOvgwzAg4qNHj+7cuTNNk4i89uCV/TisztZ5sXj+8OHrMS7P1g0AUGt98803v/CFL5RSGtf0crmUQ5+GiFerVXtD90YRbs0JHTvwqlpqzcwvrbfDjvvoHoD7LWilhargAAROs1wTEQGgITqyU4SYHAwMydi9UghIQORsLkhoDmTmbfrLRRUCJuKQaJX7Vb/oF33quthl6lLOOQXimLHr4/mdxYNXurv38PIOL5aeMoUIKo5oqlIKjl3qSqusO01kig5EyI7BgdwBIeSIyz6ul7xcSE7I3Ayl2UxBZmbU6KOlYqleiwwDD6NNJVCt4AAGbk4M4FZUrRYkCoRIjqBehhKe0/Z5ayb7uLfttQ0bqxVCMvBWeacTfwuHrq+bu5kDEFIrjMJM/vMR1r/Z8Ze28dF7H0mg7FQ98cTDz1XXE/zA8QE304yITKwH4Wk4lHH4IIWKh1YA4pECbv4lACBhk/fDF9P/Y2j/Ydt/ehwDk+M8BCI2/AAHChynIk5QRAwczIuoMVPgkNO2ToMA5kBTDY6gvh8mM1/fuVyen29qcakRc2BOzLXWOpU+JRn2IbiomLsOY8fdbphSjNfbcRjG8zuXgVmrNK2rYlBrXWM/7QczvfNTuV32r3t+uYGr1N8BU1XlHDSE1pMnN3AlZI6BKNRp5KaLgNymn243mDu5IaA0NwBgZlKKlIqIqiLTrg5bszKNAyJRXqAbI8SUWtsd5p7cDCnGpiZsDu7fNX376Rp4aeW0oIJCHzpiJBOx/U7KJNMOGT0kq1VVOHXRzTmQBQ4WU25SlA5mCogGDetwwCC0ww9Esy2IdCQ/qNAAgAFxCDqNwSRLhefP5PE7w9tfLFcfJJuyc1C0KsFdXQ2qwVSX2+VrWFejxhHEpJg6c+y1MgKklFPKDQ6PiCHyuN/H3L/79hf3k17fbEqtZRx2282zp88bb7OqIXG7FGasOo/4NmjDOJS2HdqYCMBH05gfcX3t5PYOzeuLFGZmgGkaycPFxUVKsXWMh2FopHJ939/sttvttnX7aq05Z3fv+17BQ0ivvfbG1dXNpz71qWmaVJ25cX1r+5Raq4jM3HM8ixXXWhtr6THkf8G43178C4HXS1/twz8jNYQ3zhjQkDBEiomyOjoYOoq6NdowB+ZKgITkaKDYav6M6ugYYuhCXHX9arHsFn3qutRlSpS7jkLCnMLZRXf/1XTvbr68g+s1514DIzEJuRSfuEbmGGrKLuYORNwKOEQcMSbiFCjlnnOm9TKuV7joOUZnAoAWi4E5qIMaiFBVUoGqOFUYRx8mmEqIbYQSURBVBMEZQcEdCBgVDbx62TJH2F/lkFHN6wTjBLWgO4VYzYmcDxw4R1PYHkOttW1g0cqNjHfuDN/Sup3+iwf60Bd2mlrCubFMRO0959NOX/si9evx6R4mg5p8h9xCPE8s8kx+4s4xtHr9IdgHgEZW2gAvMzkln0Qch7GDVu35ssfxwtquaJFUI7VXQSBcnq1VTVRjSqRIqoPZIBN4CDEGhFLFdqMBQgwx9/txCn1fXHfjPlJQVQSopY7b3arLLkbMFHW42TN6VacYqnjq0n6qOcZV19dxklKmSdRsqpOaRYr77bZfL7bD+Ju/Of6ef++f+M6rEM6mWvZMogU0UWm3wsClEJODMsU2ioeoru4uJ3iZ222JiATYYDENA8rM0zCWMoJMaLXsd1pHNVymRU4xp4xE6GBmpObooAZMTVm1/euHQE/hFirW7nZTfSIiANKqGDJzQJxy18l4I/tt1WoUYs6drntwDgSeiJBB3cQ9mNc2W9Ck8NrYDjOlPEvihMiq2ijEHdEdDQiRVRTdSJ3MoVYatuXJe/L+W/jk/dXuRobdqINTrBWsKAeaYF+5eC90f9JLr/3eaRIBczJP5pkpM2vfrRaL5X6orWc/7Pd1GO7cufvWF34FOO7HEmK8uXr26NHDxx88nmfyqOkXtYg+hMRHU35kLiqlEEdEdNBSCjMd13mK8bg18DBk19oAw7RfLBYhBCYm8FolhyZDtkwp3Vxdl1JWy6WIVJG7d+/u9vvFYlFq3Q/DcrUKIahb7jtgOr9zef3WW1ebm+VyWVQCBnBu6JrW+G1a1mbGJxZ/RiK1LXxEmsGMNmxRGp30AF7ajKeO4cR6gDMCoRNiiBQCpUwpezB3QwWExjsqJg6OTExoDTESAphJCoHMA2EX8yLlZbdYdH2f+9jllHPqU+o6SFm7Pt65t3jwgC4u4vlZWCwoddJStKkgk5MjQQocmS0mVyQg58ZAxdkCEabIse/CesXrNa5X1nfOZA2+aADYSN8MRL0WqBNWoWmi/ei7AcYJphJy7EzUXIMrIpEDuymguLoqgeioTs4cAUND/LC1ehFxiGoaQgKcc43jPT0G1E15soXTKuLukVhFEX3G8R/kX2ZbavqSI2nLznTu9NoBaNH+i+n20foJ79D8RA2IqA1kITT44C0lQPMl81o5fKIdRWnm99Tb0j2Ram3Y9sZJ0GIQJmpswwRQ9HYW4Rjmv3RP8CBUWUqhQCnlUsQdpmnq+wUzE+I0jpP5pkyFvIvRwGIIwzh0AGWqAjiJG/Hy/NLAl4u+MpmZliplDMTgriJdzmp7MyNkBKxFFqv19X6YzHJID+7df3r11KquVqudwW6Ycs6lCZsQXV8XmWTx97V+TQDYV7hiWKfFA2GwNpiNju6mEmNsYnVuZt5YUxFgztJa5ae1DR2oVdPwYFJdvc3+UK1Wq9ZapwLUAswuhgTIcsDPNPbORvrU6hrMrDN0SvXY9TkAxI6fHgITJXBX1xBTTCmGGJCHcTO5IqwlUCVExNSDgVEgEQwB3JAJmGOtU4slkaGUsQUxtYrPgqMIbgBs5oDB1cjUawky9T5Z2e0fv7v70q+EmyerMkQpQIQYwdDRjXQrW82T5CldslxWXRZNUxUBii6MmkE6MyRMzPGzH3v7v/xNP/HKTy8/9asLB6hiT548nar0i6UC7adydbN79MGzRj9hJogMyADWpJcpNFHMebYWZux/JgZVNRdmRoQQYilFRFKMXddN09ROjjEeN0ibfmJGR1LR1WplOlM1fMVXfMXbX3rryZMnsFyq6ma7iTmJyJ07d549e9aGZsdxDDHE3OfUIeL52eV2s18u1kTEFEX06HKYueUB7dOPBdt2Ga1U5YcewLFgcAy5jt7iuA1PLdVL57Q6RBNqdSTgCCF5iEB15lIzcApOZOCRCQsECmgGhAYeUzZRDpFj6FPuc7fuFot+GXMKKee+C5kxROi67vJOvPeAL87p4pwWfcgdRE7IIApoTIAEETwgVSYjgkDoqZlJQkqBQwihC7Tqeb3Es6Ut+ib2AjTDrUMIqApVUQSrsGiYKuwH3O1hN/q4h1IDcERgRiW12KgITMm0IWsMnN2tChQzn9CAmCNzpEAOdMjHAeyliO/oUa2NCx3csou2WbIZl3piGV9y0afFnBl7f9jPJzBTOIVtvfQOp97+xO3TMbc4Di6c1g3gJFRv795M/0vveVSbOlr5lkd/OPJ96RqON6el1VKqmpphiAHNb66v8eCWoLHfRAo5ybCXWve7XRilX6yrWl6s7t+7E1K62V4ruGd292kYy7g/W5/JVBIxElllwhSZh1JTTiHR9Xbcl/2y6y5W67ff/lLX5RFwvV4/n2oOUcVCx5vNZtxV8vjo3e03fuaM2JD2YluQHbBSI0exJpiKDc1pBghN/bENat2yNwNAy9mZmYER0UREpJZJpDQmOSlVplpKrVWdEDn1yzOMqU39gJuRtiLMHOupEnOdJqAAhO22t/mMYxvpWKLR6omiUat0auqXU8qiVsZCiaQMhYCZvXF8eLIaIJIrAjKgmgIjObi16UIAOMwbt2UQOAAc2kXuBBa0et3juPXrD/aPH5Ynj7rdFe42YKKqjuRGqoJEhaWEceg23auUX2Nd0xRsAhF3K+g1si4zndeQmShw/C9/04//wiff+4VPQv7vP/3q01cp5c3NDTPthwEolKLvP3q8HabWhnOfR+iZIxGpmpg0G6jqKaVyECMSESKypnVw+GuLnNrzbcH4sZfmAA0SaiZEVFr2TKSq+/3+vffee/PNNxHx2dOny+XS1EKKNuzff/RwLFOWTkxrrY5YREi167qzi4t33313mKblconMZIfBT4A2k3GKKj4G/jhjW4yZDHymXaIZPNaqtse9BidB2KmHaPt3Pmee9SdkopQoZYoTxi4kVxBUI3atlYgiIhgE5rla7AbEjASAjJRi6nPX526Zuy6mkHJIKadEiaBLuFyF9Vk8u6DVOS1WtMghpkZS0OZb2JTUgiu22JrY0ZCRHACJmCMTpxgWkdZLPFvBcuF9ZykZuDf8IaFVIVGogkW8TlgLjIX2E+yGUCYvWoYhWIhABsREDT7T7DWGBtZpdM9Aru5G7mBuAULAwESITIgA5uDot3xMfrDELeXHQ4RPDuqtXWDmCgcUzeElL3aDT8Gg/9OO+TF/aNL7tBZ/6jyO+SMAOChzADpcIba0aoaqMXND16IbApo74D/aAcABpAgAkRndsaW60sQlCjEBUU6p9+QBDMHASlERxarPnj0rRPdf/1i/PAMwq5pyLIgNG7fo+kgMMUYOohUpIcYYc5g8xZS7NF0P+7L72CuvjsNIgDHE4igiakYxNaL/cRxVADW+88UnNr5BHQaaqk3uoirm6iyhYQkRzFHFsHHlOSEoOCDOg1R8yMBcpJQC0ERopXnOHON2u23IP1UTdXWcioa8oNjXxgRBh8hOzQ+gb5ohbYqEGGa2Tm0iwIAAUEppTGEAgO5kSkiKbOAAFFMHGGo1xoquBeZAcnDn2qUYAaM7ELXIoE0akotRRJq1sdzMYmRmEikuTdoBCDS5sE26ez48eR/fewt31/1+h8NGdTKASmSOru4AgiYdaufxHtOrdbe+HlxHKwWcABnzNKHVEMICOGCMRPyZL77xC598DwA+89bHrLe46FcXwWrdbreU8Orm5mY3bofSvEzbgqoQuxg4TtPIaU7LpqmKCGFo89JIYGZITb1udnJHViU+SIC1o5QSQkxdJKJa3d1DDNfXN6s+Swzu/vz588vzi7Ozs91229DAALBcLt09pbTf7zebTc5ZVBb9srnSvu8Xi8WjR48+/elPw8HowyE2v+V3Om0Knozut+O4eefthtCY2BqM9aXA/2j94eASzAwJDYgCUwjEATkgRwoxRy8ygSqgASADGZI7RqDDnCoQNvgj5xC7lBddv8hdn7oYYgyRYkoxeXLscliv4tlFXJ3BYum5oxCZZ1UyUI1mJEIirOY6Z1zN7pNTy0khAmSGRaZVj8tO+yyBWwcbDrNSrgLVqKqpkipWwVJwmnCqstlDmUg1WLs/iE4KxOQUndhDkQrWQNrH3hchsARrujTEAYkRoXVGTq2re9PcgFbkmR2Ae5OPRyI1OU7bwUnk/uFUoKGMHE0P3eMGTIZ5HRifkIG/FGWfAnLw0ATWQyxwhDbzrFoOxzLU8S0AGjjgkBM0qJi3KdAZiHKaprwwRvIPPVoOjoCmaqrMXMbJgcAczU1FDHbDsCPwdU/uu91+fXF5s9l0PclQFqsVBn72/FmOPO4GMFWKZfLAPA3Tql+I+CSjg7txLWbB3cBMd/vddr9LfbdYdNvNDSLGEKHUWmrX5X1V5jzVKrWChWkYnrx3s3tewpl517BiUsvIsScJxo1TvPWQgKiNAWqrxBLezli0u5dzHobBVatIKVNOCRpfP1JVNQNpZWkDoLBYnzmxmJMrORkYulc3O0AM2MHUMHK1GprYBYKqkvoP/Q/dt33rHr1pHujc1lehEGFuUEvMnRMPRaJN0PXIUqZpsbIcAwaSWhASBjBEDBBjUnMHIZwZMemg7aJmbiYi4ICops6gLmXaPB0/eKc8e7S8eUrjnoadDFtQEaIRsTpmZOxwrBvrbf2xM7uPm/SopqGOcb6hxrK3/fVkLv15FkQO0Rx+59/+lq/8wutnPxL2y/1qfeZhuT4P73zpS6Kq+/H6Zvf86mY/iaEHjIjUgLlteNZa5xxn8xdCaBS5RI4zFW4LsYHaGErOcBCAhEOBpd0BIG/JtLubG/os2NmogVJM77333nKxOD8/3263u/3uvNbVei0iT548iTE2GI+KqqoDqLsBnF9ePn7yZLPd3r9/n3zOsY6XOruBA0Sn+aE5yGCuNiMGmciwfRHEA4QDwE9x2P4CR/3tv0TkbjPJO8cYc4xlFt5gRSQHnVv8RASkgCEwCBg7gAcgdgiEXUp9ysuu77quy5ljDCmFGGOKmpC6Li2WaX2GiwV1veVMgQM5ODZ3BiogglJBxc3RZyprAkBqvCNokTAzdAn7DvuOUoYQWhTjTfFXlAzIHd3YXGuBqdg0wjjBMIAIimqZQnRDRlGBhrUzB3M06wKbAACrCDAampmBQ2hpIJOjGxogMQVEPML4EZFmDpxmdrUJoSEiBnIHNWncx3BSKTrW4OZF1ri0gcyUcJZ/gRedfzPRpmpuLz1U90YtfMSxtfqg+TG6P9HpVdUQWL1Ca0wLxJjcgUNqzqapQzIzupMTKJATMFLgKhJjnAtTSMdZoGPWcuuT9FCCPDQtQorDMDhjNQCtkRh0ZrfWqiKVAjNgqaJjQef9bhyHQgDUx+68f3z13idfe7Pshkg8FUlpIEwiNS0WHqlOwqSRaV8UAsi4i2DLRPtpGMqIKRrD9fOri4vL0bFuRgQ2rUihhjBtR8asMCHxMNLzd/nCXpc7BShGLmo3iNkoAi3MKfpkbqbuHIj4MHNHik4cFLxKnbvu5hhYtQJB6pKISCkiFV3HaT/dPCMQ0TpM5fzug/X5ap4KMQCApq3ecATSYk5pK4fdQMDIxZnRnR3+wY90f+IPPyRXN0UAQkAnBAPXNh9iakCIkSxSsQACjhoC2CSQAYlcmajeXD9PXb9an++mMXZ960wER2x9bKnQODXNtJqBuk8dUVLx66fj+2/h9dN+v+OhwlisDFK2HECRHBhCKLFOtIdXJLwKcrnf0TPhyd0QJnBgj7jv5EmkZ6k7X4fQFVZMQcWr6ae+8MpDfQLUIXeryyU7hhAmw3E/3lxf78atoiB3RQGJTOqk0zqcuQuShtAhYjOd7q4mjROJkGKM2uRtD1m5qfqBFaP10kopq9UKEcdxlz3HGLuYZCpOLFKLejWvYjl1Vm3cjufn57QOV9dXV9ebfrEahqnvl2aWc7/dbof9SECp77tFT4wcaNl326urVy7vODPHUFUixZBiKSWE0CoOiDO4F3Gm/CtlaqFh4NCSd5rpxxGArQWS6IiNJFjB3eE4q3SL/QN3gOpuRKlL4Gw5ZIlpkeOYJqqOCKZK1OiUmSmx7onMGcghAgT1RYiLELqcMQbuI+RAgF0O3LFHCLzMyzt8foHrBa6yZwwBmJyRzSqbqIxsxa2IVTMN6qzo5jwTHzm4hZCAFWOCvrPlyhZLZUYgdlUAxkiOIAqlkinp5HWiqcT9EHeDjXvTsdYhVs0VQ4ugmQ8Gi2nmyzwYLGiG0trde8Go3aZaLx5+gIH6IXeDQ9fo9qRDeHiE9BwrcfPis8aiZfChDv7p0cgdjzXBkxCbj/zAp386fkpD8sw1YlWOPDPEOM3m2w/s9sfvO/8PG289nKQRx+DoNEF5KW6imV5RAUBVF2kBXT/pKPX2lkqtLo3XKwp64DCqIyARj+PUdQsvJS9Xzzc3MaYupfHqJudQpiGktROqSuoXUquZklWEoEYObuiL5aJbdNdPd6rKManpJPV8udjvpmo2lMIx5hD3YxnGfQKcTFarJWH0HWzf2V6c35ksqZuzV6ukE08IAB4UEdroqB5mQQBMtIK2jiKKyAFwwi3GBDdxRwRzkalMpZi3YNABcbleoYPWqVY1aOWxpiwAqg4u6I3YllzBzElhGgWJQgjm3K5EiiKSmysAIyggOs7pikNLB5vQYK1Tir1ZnaaBhxyAmNnQck7MPI2jIaY2ymAy8zwejgaPcTdTYQRTHfbb8uwDvblK+y0NO/Wd6o5MKaRSCkRiJkPZX16lOxwvWRfjhAOocSUSRHSGKLs8PfLyyHhKoOBuHCJxJDdUTylj4Ivz9TBOuN+SoVSpVR9+8PTJ1c1mqM7MHEqd4NCiIEJVi43I2t3MDoT+R1RPIUIOXGppAzHH6oqI5JxbG8DM2iD3cSZgtVi0GAjY1MzcWiFuEbO7D8NAMRDze++9BwCr1crdG2dOQ/W4eZmmGC4dMaV0cXHx3ltvv/rgQbda46Gv1uBANPNu3ZZ6jvv6tOxzWuc57Np2suGMJGyT/3hEA76wx2ne/sQcc9Zcteu6Re73xcbJpc5i44hAiE4JGA0QnJGoWkbsU1p2XU7ZUuAYY4iZKQaGpvey6Hm5jKs1LBeek8fATNgQa+5gbVarQqlQxUW8iqs25iLEAz6VEANzSpCT5+jMPt8cJG/Gs8Xxjqou4rXQVKAUmEYvUx32VicQQrUAhxrfafnl1MSfgp1PzOttQ+YjHcBLVZ1j6+zWLH6o4OOnRX9sXft/BLL+H3L4ySjZ6VW1YiaAqRrMQmZGB0VpIgKntuZmwqkTaMFxnbW5h3na88AAftpROJr+27VF6Cfz6My83W5DCDmm1cVyvx/HYQAFZPI22xw4MD/bb2G13A+zHtOyX0z74Xo/UJ/W69VuczPtN1PBuOgGrSl0lNikgHsfYhupBkKMXKeSmABxLKXruu7OxfV2E3KuABpoMFFGYyxSxv1GreBqcXZ+D/bT5/7Qs3/tt//gH/qvPv5tb6f1axcbAe3ASINVdCCDak5MKo6IIaQQ4lz2aZ7yAB+MB/pMc2hgMJOqKuSAiF1Oal0pg2Nmw+Vi5WYyDSZmAGYBwxz7tQoeOpgKOIJJA/tIi10sl+rHR+mHaQ8kNkAXc1BC0zq5FESMMYbELszMYGpaTSerbDmCQMjJXUWMQhqH0YljjATQhDEA5i8yL2kTRHKrMg7sgIBk7iLqFSOZh2mqTgyok27X95fl01PpyhCqwARQXQsroUZj912Ex6RvO191IS1UgdEYE1NGLAi63e04cO6TE47jUEfZ7PdPnl998e13t2LVQGCm5Wi7qRnoUkrOuR5QajHGUspisWgWOefc1mojhW5ZwnHW4bjCT9d5Q+ZsNhtGWq/XxdxNVa2B/QW5wZ2r6TAMue8AIMbYZOKvr68fPHiw3+9Xq5UhbDabszuX7n52drZZr58/f36/6/BETOJ0UudYBviH2v3b43AWId62J8Fvp1ZfqEDMGx8hukYJOcU+575f5cmYJvDDKwECERJXAjAGTETM1nNcpC6n1KfsIQARI3QpxRAtRu96WK3CesXLhedkOVIKyNRsn7uSClXBYcRxgnHCqaIYaev8UkPBAhMwQWrFnwXmvoY4QyFa7dCsYf8bH4uXAmWycQvj6NMA4x5rITE2R9XQNslpn/0w2IKnnXQwRG/9tBeqZl/uph+PtmhO73VbUnzQ22pwrnZmi8qJqDUPCGfCP39xwOcFQ3/in04vpj3ztnqOnsbbXMzhtCNRnZoCHGqjBzbQRuAMJyH87fsjuLVu+yxCewwl2nWeYgzmV3ATzDrUr9QYUKZSi02IZ6tz10a1V92dUwLk3TSKGrinrtuO434cM1BenW23fnn3TkIo1zeIToSipVss1JxDqOO4zJ2JYNXQ9XWcgEjAjaG4FqkxxC7nzX6fcicIV/vdoFbdBzVOmcGJ/eLe5ZPnm6tvvn7vX74BgL/8T+nX/7uXhEN89U5xc3RnCcABcHQzAxE1a3pQM95ODVJKzFRrdYdaBQ8C7tM0uYq7UZviMCHE0VwMQuwiRjUf9nsgcnN1Qw2k0YjcsFYJIYC7q5iDI4oaBjYkZIZQRBAAXEXrZGpSqrs7B45ZpKpWBjMZwYq7hxD7LgRErSO6IphqRSkqhZhBzQCZIwAEbhgfd4cDd+FttGSmVqqBB1MQ1Wm0qVCtNlUWqJM7giYqVDXvV6+EcH/SxbaGscA42diy70zMHrB08tTsXeQPUtLzGvqhCFsFJ3dyI3OqYvupZrHtfr/dbK6vNm+98+7bbz98th0shGroxK0u2lZm13Vtm/d9D1NpPXloHK7z/Be4exNTU9Wm6Nv3/W63a8tbVRuOq+u6ljdMKsw8TRO6m+nNzc35au1utYzQ920jtDcca1mtVqo67PY5phxTnYqUWqeyWixvbm7uv/oKEDUm6hjjYrG4vr45v3s35Xxq7lv9IAQ+eqB25ac7/ctZoeYm5sbwjAPE0/j1NmIDBCYwpECxyzapVcnD6Iuu7AJW0oBWDAkQnRESB3cIAD1w6rjj2OWcYupTtsgQmQNFQiKCmKFb0Pl5OFvTotecnBtI3tFblm6kylVwLDhVnKqWqkVcFH2m0kJCb/x0KXHuOHeeszFDID/g29Hc1ciMzFjUa7FSYJpgHBv2H0olUa+okwY8QUSdQhthBjjPBuu2C++3lJ94UpxpY03Hk1vNriH/7ED8e5qvucnpE6ID8focUp1MZ7RLmldbe+3JASeZxOn1HAPzdj0Hu4wAVqUAAAdWEyIKkc2Mw2Gwy28/t91ROykEHX9LhIDk7s1b+AEpgS+OpB+XVxtKcgRTI4dSawxBzQi9Sr2qz3PXGUPqqKpUUSd0YozRkBarddnuHCjkrlstQx3MbKqlDgM7xJS6s4XHpFMZ9rvMjK4AUMRIzBDEXdAhhqFO6r5ar6ZxcgMKyYk34xAXfRFjsRgTEy26xWazud7e5B+eh4G/5RdewV24ee9mvXiABBAUVCnNAaYcRkljzK22EEKQak0dpWWvKtJCASm622xyTugmbuCGZlIrEeduGWKKANv9np8/iTGGGIdpZA45d6aecmdiIowAZmqqjqTuIAxIiKiI+ac+6/Cdv+kPwNd993zz/+DP/3NMxBxUBdxUKqIT4lfAg6/cvZ4WKQXWiRtbp6gQqKmoVFOdqqSuV6BkRiFEyI6gUmDeEaiq4DMblUkVE1YxVXd1U1CTG3Mwz7IP136xX36M7XLzDDauQiJIldAVICYoRUmxPHJ7H/ADiuOichoNueuAiENwB6IAruOkz683j55c7fb7hw8fXl9tnj673uyrAQEGQCOnI4e5zyMLddVmr/bDcbk2WH37ucVe6/V6HMfNZrNarRoMtO2FxnjR3me5XB4KX55SAxVZe+4pBkdov5exNPpoioECX19f73a7WuvZ2VlTlWm4/lrrMAwUwvryfL/fx8b9sN9vt9t7fV9rPTbqPhzy28kg2BE1hCd5NrbO0+FFjbakJRZ+kAQ+BRkys7mzo4BTCGSQlr2b5WmC/biaFl720+B9n8w1YGAjGo0DJcPslIhTjDnlmVQmsjOnLjEypuQpx/W5L1fQLywnSJFjaOEtgZlWKIWmgsPAU/H9EKrYVEkNj0g0cAMgJk5JuiUu1tZ1FdE5eIjE7GhzL9+A1FgEpgmnCfZ7LBVrpSouCqIgAOI+aTg1o8ebe3Safhi7mH/vjVbqIzztMeM+Wtvbju6HKkvwIbTM0XDDCYDn9FkeL+/4m/mZEQH4R8H58aV3bqB/1ZcLWS9865Pa4gF+NbcxjhkG4qyodERTHF9IRHbitG7T0qY9f/KdubUuHNE9AKrobr+jmCmEWieKgTmfrRK5bQiGaYo5B0QDuNlcxYhSi4+j1FpVXMIyZuZIWNHcrRghAizWKycuN4OihZzSsp82uyI1IbpqCtkdRMwdxUzd3dzEcl5uNs/RLVMAhW9+5f5v/5Pf8r947xMCD6cbef7248tuXaloCjubXIGYQozi0ob7jw+L0Am9TEPDbyDYQW/dzs5XLjoMU+P+VFUk6BaLlLsQ0lSqSN3vdmXcxcAVLHBECmfrc6vF1M2glkKEgfnPf/3f+OE7P/tHfv73/vqrbwTAT/2f/vT6c58DgO/52d/9yQttjLPf/83/yYeXKwDA13z0rwHgD/7M74whTKVWlZhySpk4tAf8Rz7/z7dzWmNjDm5UGV1dXcVU3LROo4x7rCMGGW2D/RDvDnR/gvuywWfVpjR2QM6MkQAV2JPuaP9cpnc8PqW0C+a0c506Xp+dEXfm1mSQ1e39R49+6Id+dDMUNdtsB0d0B2kI9mbx21DCia1sBZ8DgjOsVqvWB27hSwhhGIbNZnP//v2u64hou92enZ21PyFizllVm0uotS4WizqNZpZSurm6ijzzo6SU0GSapmEY1t1cXHLC9fJsGsYWJVw/v7p79+44lXE/LPvF8Qpvbm6IaJhKzjml9OTJk5QPlhROATwvzJe8tHmPO/H4tvji729P+FCOPv9plpVvYE/CGGLfLc5WWMdqg8qSdfLNjtmTAwOGmKJCNOicEoUQQgyRY2QOHggYiQADQWTsO+gWtFhQlyFl44gUkJzVyEFNSZVq5VJxmKBUnwrWijJzKQIgBUJEYMIYsO+t6zFlj1GZgeggvA54APKQKNYKpWCdvFSbqhXxqmhoaiqIegBrv2RV/dB7aaH36Z3yF33m8aADR9sx0j8dvjj+5vb8k9eeRtwNCoiHOYLjy09dyGlhR1Vn7t0XuxRHetjj95p/RD/or+CxzQUA6OGwY47qXR9BZuAHbGj7v9MFdEiAZusPJ+Q/AOB4CzJt39ea/JBZ0zwEhCpCTP16NZWy3e32m80YaEyJ1svcLzZVF8vlk8fvFJPc5QcXd57vpq5f+iIp8Hi9rXVih/PzM3LdjwUROIRJKnYBiG/2Oy0TpyhS26wvxnQ1jrXKfpw8pDqV9fJ8KK7FyaULcQLZqdgPaviuB9PzD9h9utmVZ5sUOgtYzY04z7upfXc4RgAxBDhYyWNi5+6BCBwmESaUqgAQA4UQQk4GRCktuoVO44/d+Zn/x2f+6lf+4r1/8r/+urPzi4uzy3G7XS7OHBCBpJq7/OQbv/znPvOfAcC/7//vb/+/D1/7b/4ZALj+zK/57P/hX31jnH7f3x1N1Mx+23/xdTdXV+PmSS3j+fl6fXb2+a+9+qYPvu6XP/P0s5/4EhChO7qqVJ9lgen7v+kHPrzC2/HnPvVXPvL33/Lka77lg8+wO6rI9kY2N1QGNlWavvcfPOD1ni+2vtjfjNeYCRUFpyYazkKxZr/O/pTq+6M9zThRMK6ZdEH965fx/EyMHcQM/tpv/LGffv2Ld/4v8b2Hz4uBAVRHbD0zN2ZkV3Jj12Nlsj0CEWm93BbOt93azmnX36Ter6+v7927d0u8g9hqRMeHCAD7/b7v+9YQnll91Nx9mqaUIhEuur6VyNqbi9s8MM/cXMJ2u229h2EYkMnMFou+2MxL0RiEgvvV1dUbb7zRko/bgOyE6+UYkL30LI4nwItdxMP588/Hl5+aPkIydySkBqp3AfOoHdjKQNAlu4g7uceirEZujJ4NslHmtpQjcuAUPaJHx4AQwAPxYkHLBXUdx84pGBICsGMABDGs6lPFYYT9qMNApUgZTQppOLKSOXOTqOSUas6QkoWgNCszOs6UytTGktRB1KfJx8GnYlW9KlVDI3eS6lAdBAO8aKCP965taTwYrKMF/HIbww+VlqMD8BdrMv5Sl8ZfeO3xCbVUbu40HKhDAVr6BojzAA5Rg+TcMsf5S3SvR8lF8GbrAdwM6KRCc3RaL0TrL3wi0qGEdTynLRx3OwZZp+1fwlujf7yexjWIJ5MJBDjP2DVIkhswEZOqjmXiEDhGrXszJISrq+snu73nRIwpUp20TPtnTxXAkYIAt2wkIg2mm+ure/furlKHMVHK8ATVvZXmDdyaQiRSJMqLxcNHH5RamdiRz8/OTbVURQrrvkt9/+TqCskfDdvlx1/f/coXQhVV0Js9XaoBGrAzhxDMtGEEmaO7IQY3q7UgYggsIq2/4vMst4g0Qn6LHDBibERHIThQyD0ze5f/0jf91z9991d/+o1fffUnuvs/monC137t16OBVAckd3DwT/3cPfgdAAB/6k/Vr/2LfwYAfvSP/9FHn3oDnjyahnG32109ffbs2dOrq+dW61nGnAPD9H3/3n8MAL//R3/b9/z87/v28p3UJVAhl2m/rcNgZkD0vT//uyMYUyCOogbMHFOTi/wLv+Y/uY0qHADn+Y8fu/e5v/jVf+0jt8Zf+p1vvfiLGRDxDe/DN7wPqEBFdKO+D3XnriWY//7/8GIKcPbmA793OQFwCID+uY+9/dd/4w8BwKN/MabvR3MwDEZkPkufOqAdqPxb+eVo7gEgxth8wDAMTY+hFViOXavjGm5/6vu+pQKt9N9YC1NKwzDUWplDzunq6qpLKaXceCOmaVpEUpHFYtGCd20qQO5EGAiVyZkYQWupZYrnZ7txHPb7lLOoAMLZas0Ow36IMbVYkHluJuNJsfpoTz5s/Y+W5MTQ3I4ctb17fF17B7fbndn+wkCG7gQeQ0YKgThq7OL5egV37owPP5Anz+T5je325JoEOqXkFEPAwBwjxYCBPYAzEGPIWbvMq1VcrqHrQ9dpjM5BzQKTm7soFoFSfJp0GHGqXkVLcbWABOCNB7fNayAzhkC5w5QhJgzBqA0ggzu6WWOtBRPX6rVAESiqRVrpH8XdyFVEvXEWuYNpw4QRHIS5AYFb3bpBIRvM/6WY96Xi+Kkdf/EZvAjxbK89yQF01vUmcED0owKMuR3z2gP4t1G7zITDTbmifdBLqSLQwXOhm1cHDxxEpImWA4B746RpDWdgxuYPmOaMh4jd3Rp+qbFBEik4uIcYvII1QFYbgkJ0RHU4zRt8hpqBmSVDMxN1UmME0YpozjCpYqJaFcBi6KZhyimYCDtlxkkmECSTxL48X2431zH1QS3EsExpP9xsd/vc3XGP47Bd5Ji7jtGmKmOVvGCVUQiIKAOgo7bGtVgACISllM04VAATA6mX5xfPd9tJR+jCHmwYt7lD9vh0NzyDBJ/61O6X3lopxQoKOJCYYxzJOiJmM3H3Mg0I4NI8CrUgsU3n1CpEjIAGo4JUEXMLMYUYKHcUAgTi2MXQEUU3+bbdt/zI3Z8DgN/w8KueLp5vd7uf+9nPfdVXf3Xul5vdDgECcpmm/+73/x5+9z//7r/zhUcf/9hnv+vbP7hYwuba1LbbzdNnH4y7LRJc3l2geQ4ppvSFg5z6Zz/+Vv7iKuXOEjEnLSUxAyUrU2v9UxM8IYqRcA5+HVy/7+d+DwA2Vug2qUCIHOh7+X9pZi4OirLb7J7/chcepe6DunzrL3/Du6CVQGFW4vBqAACfe43+yre0HdHg0U1QcACA/9f3tOv8wkdat6Iy/mm3RvgIMlv8v+PwgwzEiphzZwBVbbVa7cepqlGIRGSArtqKPK0DfOzStVrQYrFoomBtT63XazjpDrp7wwhN0wTiXcyLvFApSM7gedEt+oxq4264vrq5fGMdA4VIu5vtebc2pzKNGHEcBlBf5MVuvLn088R88+xq1S/BTVV5uQ4hOMx0C2UcY4waOKW4G8VcGWailJajnCYEh003Q7/m+bWZlnyGcCMiYkACbVSCbW8zos8TtKAWAOe5oRg4oTsyLM7tQtVMFaucb7f16aPx0fvXb78FX3gr3cjCUuTsfQc5RoAFhzEFQEdCRy4UaXkO3RrzuvbJI0FgCtHMVM1FEQjVqBQcJtwPPE44mQmX6pWREOJccIbKDDnjaun9hcReOXiM2kb3DFwRDNWEXdQGqHsSwWo+OI/VipZJuCirJ3GpVUxDi9yPhfujKacDWNNuiZdno39q1j+8Ol96Hl/uOI3WTz8aZkboNpRxfFOHF73Lh6/hpRLWiTcCgNapUmJ66YRTX/VSDnE8cw7ticSNkFocTczH37/g+U7dHpEewqsqAm1MjtnBnAkafyajmJo7IY3jyMRWxBDMPaXUeRgDZyAs1c2mqTJamUZXdqYyjcv1+TAM3bJTlSp+c33d55BzdkBTnbQy826autVimMo0TTkmQkIDjvFmGIdSRLRMsl6fP/ngcVqvXn/tlUcfPN7ttyHg5dlKp3Gz223204NXX50ePh+e37TBcVF1wARJRNDQZK7+obmBKhHHfOwelTIRBURwQEckxoTJEYiYQ6IYMYSQAofMMRMGhPCvvPsHfu2Tr/w1n798fPf9yRBT/qk3v/gXf/df/o7rb/wtf+Nr9rudF3v93Ye/5b/6WwDwQ9/4tT/y674xpZS2G85pKtNPvf75v/V9n/30L977J3/ga7BVAxWI49e998o/+0PwC59+5w/+wu+NORExMBMDhACIYUnCPEvVN5PhYMcBTXd/EQQhqoho5nVUjuRgrohKFHl194zx2VT3gOVf/JmFli2DmFlVN6CqhNLjlu0p1PeEN5mmiBpUnRPvKPyNPxFpfS4hKKBYWzk8lfpLn37/8598t/5Gh98Ih0rmIXj916ApvQLADmY5zBu4AoD8b3RwSFdVlJlzzhWK/G2Bv93AWtxgNo30LefcyjWtLdy6Be3lrcNfSkGBhiZS1Qq11hJDqLV0IVKM+91uu92aSVXJOYG7mTo4IapK12UiLLVc31xfLC9F9fmzZ6nLrRXRqN+22+2dO3eePXny6uuvH+2Dqjo32Qk4toU/2r78ow6c1R/bfic8bF6H0ABCQBhDciYKkZDRSZtOqAldTut7D/TVj+U79y2l/S++E8cYavAQnBmhWU8EQmK2GLDvcLng5YIXfQ0BQnBGbHTDberJDKTqVHwccBigVC/VRI9GyhERwRExBu762C+U2Ykc6ZaEwRzc0cDNXKtJsWHP44BjsWkiVXJvEBeT6lWkFhEJbb6jvcMtCOfQPZ8j8ROE5amdPb37L5lUeNEK/yMexotWeP73xdeevv9Ltv4lfBF8FEH/IY3A4zc9/RNRq9w0LskXrm0mIGypACEQHqUqTrOfl/798EGBG9+Ngksp7h4IGu9/DhFzrLUCOFEcxkHNDHmo0wBucWmMVTXUmiJ/8O57F/cvEfzJo/eDgmtZnS26RRcZTUrO2aweqqVQRUQUEZoO2jRNy36lqomjId7sd2OZigoRgfv11fP7y/7i/KzWIlKKjIi0Xp9BrY+ePLn/idcuPvHG42kSrxfgruZuAtIsjjdb38Lhhj8hV5sn/5rsWqv8uCMCY0BECjFSTDFG5siEREw4M/9wSN++++bpfJO+atXfvfP40aO/98//nS99xfMvwd/5+M/deeXHF//M3/hv33z4wVuv3PvBr/uqt165l7Sa0TRpGXbDOP6tP/y5L3zVB1/4zAe/5guvfeqX7iMi53R2cWd9cfkHPvvViy+dL1ZnkKIzNqAzEkUKjuRi6pOa0YtzKreIeG+4TxvH8cgK7mCNSwGdCJyCAojogFxNq/g0+h7Q3IAEg3RpTPq8338w2HPlbUCJ7J0ZAcJN7JavvfG9P/LJfV5MuSvg0zSACXLe7ofv/Jv1r//A3/qZX3q7ANhc+rMZn/FdDt8NzawhYQixceCo6vR/HF9ajQPsAQD+lfbz7C2Wv2O1/vl1s+mtfHRsFbTv3pghuq4TEeK5PWA2q/yUUnKKAJi7jhDHcbx7ed5hZ6Bdyvth17Rw20pg5kaTAA5936vqdru9d+/e9fV1COHs7Gy3mfUDpmnqECEAOdQqFaklKw28floO+sh999GH44EzHwDIzA7ytWgUQwwhZorBiR3RZ9OQ8CD1wObW7bm/OF+cxz4+xeXw+ffPSiBAJHbQytCCcowJcuLFEpcLXPTWBYwRAwMSoJEDmrko1olKtbHR7ItMxWoxVTjSyxMikxJCjJATpISBnRmpcccBmYM7iJFZm/zCcfIyWSksFVRsKqCKaqCKNrdMVTU0/NbRqd6W733G1XxksPwRt/SjbP0/5MG8dP5JHenLvdVHP8q5infSdYATiNjRHzTGq/ZdjnMJ85TQfBxgSy++f/MtSNSKPcx8dBCnvYfbm3OiCaZuLedQMycERuQQnXKOqmpaZTICEhFUn0oxA/MqIurm6KWUEc1K0Bwv796ZTJ89eeq1oggzLrr0/NETQE4ppot1g13LNBKwmbVxFkR0tW7RYeCnT54G4kAMZsvF8rqUfSniLmarxbJMA5hqGbc3V6tlr3Z5tbm6ubm+fPPNZ19/9Sd/6//tn07f/YeH39K/8eBme1OsSUybaEVo8w0WQmAkPSws4AMsD/j4RFLKPqt1IiDGmCkkDoGZAxEyIzEQgWvIGXwBgJDreUrd+fm3bb/pl+B9APjH/67/U//RXwGAt1+9/5/+tu/6wlc/+fTPBzPb7XZqVgH75eof+5XXvvBVjwHg17z1yXiWc879crU6O+8Wy5i72C2475ECcmgDxQCETOgRQ0WL5AiucGL9/cBEq1KgNfyZiPm4ZWbKKzRHqFIQisHkJI0iUbFVUyHV5Dd5eoL6vtgGQonBInlwogncQk4f+/T6k58qKVWORgSmrfikqur47sMP3nn49FjsmGeaWwj43wP+3UMIhZAWeV6ZSuH/HOlkmNbMFosFM4/fNlx/07WoLBdLZqb/gXe8Oz8/B4BxHJu5b43itn2O/VgisqqNFqLrOlBrCUTO2UWmaUrdIoU47ocQY+piDmm9WN1sbghwtVhOw4gOKUSpMpRhlVLOeZjGaZpSl1vX+uLi4uHDh13XzU0/AQBQ1QYebX3pYwT2PzLQfMFuzHQX5AjMjdiQkSikDMQYAvDcWmv0jk0ozJAc0c0desgZAjF88tLiFhf21tNclQkriLeaEpOHqKkL6zM8W9siewqQGAK38WQwAxGUCUrx3d6HPYwTVkFVUHNHZJ7tCaERY0qQs+dkMVmjfT7UaQDgoI9kaJWKYK04FSzFawGpWgqbuVSXimKqVeuktYbTkBkOiZXZzO7UAhw9UV87ZglH+wuH8Lwtr7ZPTv962mW6fQAfnq46ecn8E6GqMpHaUe/hqATwArFfaxMdPwsRW+R+TFqP5ZpjNnOc5ZlB0AeUwimP8fytoanlheZvcW5+nFzmMZ9AaAOHx53mh26wIYQQ3FzKqCalFHD1NrPnLi6MbbgcBSCFuB0mM6sgauqcploNQUUCh/1muzxbxhjfeOMNSn24uFAEEXm2vXGpXeJaq6HlDlUEERe524x7rXJ55zKnHsxCivvdbhCRudaU6zD0Oe22m+VqPan0XUrd/Xfffmucyue/5/3HX3/1F+C/+KZ3P/2N5fUde1GL5jGwuLsrUtN5dOKgKogYKYK3CDECqs2MY6wqDZcXYsj90h1DjCEmokYk2gIs4xDQiVMfkUXKgmLM/R/91X/2Wz74zO/4sz/7lT/w1wHgP/uff/fn+vT//e0/8YP/3BcB4E//M7+1lLJYLvP6vFv2v/sHv+sbH3/m6979dHojc4whppBSzF1IXe4XHKOaMWMDraMhIqo6gAMRRkYEdjS9nV9pXk1EGrrADzMrx8CiMWi2r0mg7qJeTUtCNGMvgdBhCHDTbd/z6QPtN7jEXkURyZkGUOnS6tUH4eOf3KXOY1QiIGSjlNK0Vycoou+893A3TnIoxx7xIcduXKvP+Isjli1Ybr8hoqurq6bvSH+Xz//OxfPnz5f3VmdnZ7t+V0oZhuHs7GwWqjsQ8TfEZ/uhNQmkuqpM0xSYTK3hvjbbzcVyTeiNFHrRJQRcXpxdnp1tt9dorqXmECNxjslFp/2wWMRhGFJKiHh9fX0v32fm/X6/zH2Xcq11t93FGLHJKFU5HbuBF8GgfphYPtYtjp3t9ptwkPNDRLdWWgEHbAlTiBE4OEUMjMiAANg4UAMisFUAAUIILGKOYAJx3TO/asKrQldDpWcbFHUHbXwNIVgIlrM2XesuYQ4Yg7YqqjuYgFQq1caBhgH2I5cKpVhtHN1IROpKMQGhMWJM0GXoFpqzB3YCYPJmf9RIHd1BhdRQxIfRxhGnglVchMy8CKubmNYqU5kzgJcd44lVhUPmezSIR1sPh8j3WIGhFxQVbo/TqTH4MseXc+CnbqblaP/jXf1p/n5sYR1/aNd5Oul2+0Gno86I3qo+jWO4rS0EZCK4nSG4rXpBYzsGOTbMDycEcyu1VjEtbmqi6Opq7VLMwMBT7MSBidoe6zglr3i2upJiiLvdfhqndQzb7XZ1frbZbEg8LSGvVuNgMpZFTkaIaDHGatDkWHOKUgXd+5wBAN0DBzC/GcZ9qUUViEIgd69lCphcq4G7oYG//vrr0zCe//jy8ddfAcA3PfuakW/O7t+VUkjdqRVE5iWhqgTz4EitFYgAKEYnCk5OGNytiiJxiJk4qnpIAYmd0AG8DQmwgaNCY1VP5JQoIBACrH/yi9/zH/0368/+/JOv/MQP/Au/c3q+y0+fvvMN1+3O/8JXvP/mz5w5QEypXywWq/W3Pn8F1yF0OYTIMSFS6roYE8ccQnBiQiQKrg3NNc8eNs4JB8TqiLcc9E2V0N2a7JiqihQ8GF8iagxOTRYWXR3ADFXBRLVw9ksYoTzXm4elPkUuMUpsA3TKPoGX3J997I2zj3/yOneVGBApMCKpCxqC034YbrbDB8+uDpgqaDy9L+Wjx73WFnmM0Q8HHBqkx0W73W5Xq1WbxhrHsQ3iNtPf2CMa4rPrusbe3N5zv9+fnZ1BcHc0s0kkcVgsFlKrqlap7EjotdacUiQed3ur0tBubZKAiKZpakEbE7cZhaY30CJIBBiGoe/7enNzfXW1Xq84BK21Gf2Wux8L13BSP2g/HHkjmj8+/v6Y+iOiuCITcUAmjplCpMCA6MjUpKdbCAgEYAQQEBC8iRkRmwEKgCFJXME9DIbrcRo/98tys2VMRQrnqCl57mh9gcs19gvMCWOw9nTACRzNUAWlwDjBfsRhD+PkpYJqy+scAJkATYEdiWLwlDxGCGyzbBnMoHR3VEd1MHGpWCYshUqlWqFOXiuZuSmYNnSQaVUV1fqCA8CTo4Fh/GT8qp1wHC/8SJvrH+JseMltfORx6htOz7p17zALNRxs9Ef0IT5cbvITHKoduOeO/x7jgjmgw4Pa+4lNn2HDTe0ScabHaB/qL0CJjx/avEUD0R7rpyYK2kSrjP2YtyMhYgjuLjbPXqi6mUmtk9gY2DIRYuo6cBqG8Su+4ivf++IXq4ICX++Ge2eXFLvQLQBsuUp95N3NdUuQt8M+d8taqrNDcBVdLpYtXA2JrVkyQgMMMZjbfrvpUlIwJprBVe7TVB+8+lr49+PqH+Q/+91/ijLF5VLHfTjQsmPA1s9odB37YYs2ZzzIkbltOUdEDhg4AgJSBERkijkxR2ACx2PbxxAckQy9kXgCkxsZrn7q5z7xv//XAeDt3/u7fva3/AZ+8jhmvnvv8nf9N9/0A/Qzn/jsxVf9ygNfeMohNMnwLofcAQdOHQamEJlCjB0zIzIAuagYgsvs/g0byQkgIwMCkZIf5ktOdgdJrUcEYUsizSwENq9MwR1tBlCwKJWKYDFDTzsaH43TwxGuudMISo3kcDQtxrVfrd78ZH7j49dpUQlCYgqsZoRoam5GTmrw5OmzRx88UUcABnQCbZd8XO3HwR08KZGHEFo9Bw9gHj4crUXTdR00+QTmxWLR0DVtqbTorQFJx3EMITSr3Yx4SzUWfY7EdmBjBkQRWS5WrkoGIfB+t3v+9Fkk7rtusVjUUgCgscvlmERlEWMre65Wq2biU4wyFJlKg64O+6FfLswMXiy3Hq3T6QY8/Y2Z4WFI7QVbBA4UMDClSCFhZKBohIAUZkKdGbHRkILgaJAADKGRDJMhOoAjUIglqp+vu0+9kYZx+vwX63ZPzMIIibHP3Pe8XGLfQUzObHQwGu5gClKtFJsmnwaYCpTitYIKOjtSGze1VooKhDFSzpqShQBETgitCOhA5t7q+6pWJhtHGsdohjaDwLk1Vc3BXFtvUEREXs4AjnfwlFvjyHB5OtEz27t5Aug2xPAX5y+OWcJLhvIFo3nSkj3Sxr1wSTMJ/3x1L13t8aNfdCQvZyrt3+OIytGTzQB/oCNWrH0kzBnAHDLMMujc6sP2kU0JRFAwN0A3UECAmeAbAc3aB5gZuqM6ETigzAQ6qG6qNhVFosDBwDdaHNN+HOLF2Zd+9R2pcufszur8Iiy6izt3V8vVtB08RY4pgul+xzmqiRpbUW4jHOgIECKP10PqlwAemFOI23Esak1jIuZuu92aWmSKKTahx3YHV+vVfr87OztLP0tvfertr/yqTyIxcmh8wY1rBkIopZh7rRUBGoMYM3OcO8Pu2ProECnlDDHElFNMzUk2dk5zV28c4e7eGiYO6ioaHD72L//v+p/86d03fO37/8L/6ulXfiJvr1erVREfd/vPfPH1j/9bFyLC5+wAfb+Iy8ViuUw5U2BMKeaMxBxigBBCbn0RQhIwMgMzO+g9OHkAOkogIRPoXHQ+MiKYGTHWWlp1yM0aVl2FkB3RRcmcRMbI6p7QeivjuIXhnZ09tjwtaLQYooI6kxEVqKtXXz/7+Cf5wWvb0FckogJgCJQCllJVxBUQ6Rc+/vbjH3l6fbPlENwUzQ+L9XZH+KFUhYhEwExtfPeIiWg922bHW6DQCvd2oFtoz66pvQ/DgIillK7rWv+g3QciGodhkXpmFql6gJc0Lfgq0qc0TdNyGffDPucciKdhFHYmdgcOAQFSSpvNJuVUVVu+m/tumqYWbOXU5gtxmqYY47Nnzx6EQIFTjEzUMOt4ovMFL/qD9i0AgeAQ1R3szPyfRN1qQYEpRuQAyM36Gzi6EcIcIFE4gIWgWpMlQnJAQEVXOnRhYi4pYA7dxSqer+swxsCVKXQZlwvsO4wJOfphiMEPGHUwc1Wo4nWycbK5bVtJvdUXDKFJwCMhhQgxYEwUoxL7gfoNZl/i7gqqZAZVoExWqklFrSDVpKKYVfEqOhU9OYLJbS+lEUiBOQE2UeH2F9WKiI1VvxmHI3nIqTVv9vTQ4AAwF1PHA9mIlHnIq0EqDxwdL5ns27D9BNhr5kTBZ9Hv5nLamp4F2Y+L+/gSbrO37pEQ3AgBTZs29qmnOTowxNAgKkjUaOEMHRBCSA2jCe7uCAqASMCMaK3Wz2108LbaSEjg4GaBQyvxgLsFMFFoypat6CytdBarFPMamF01ICBQmYoiYGBedJPWznHJ6d3HT5+vrr/0zhfPLy7eeve9EAMTP7g8q8N2uLle57zfFMcqWjsK2d11MpDc9RBJWHOygOYCQDQ4bNRGsYhM7vtpgEBueJ5XTICM7K5IIOXs4uLxo8eu9iuPvvSJz3wCHHLq1SdzdXdQnxGE01x3nmEbXdfkYcQ1phQpUYjUKhsxU8weQhPZcvNWxmgToaBOTgyOaGra/diPvv7H/gQA7L7p6774b//rMk1xnNahM0g3MUAk1LBMZ2ogZgAY+z4vO8pMOYScMSYj5BQ4peBsaBCIAlWtyGCu1ZQR3c1EQ2BAdhVEEhFXRSYEJ2eQAm6moiaKomRuig4uguZQChAWKqSdebQQKlaZZAnrvHsFrvD5+499C1RBZIqBXQZCHolqjKtPfsXqzU8MXSeETsKETAsDFTUinKSKaXX5q9/1Q/+f3/xj8Mfg3nkAq4FdwQGDmcWYGnYTD2Wfw1AexkilVNUa41w5iSGXOjZr3nKFxu0zDENLWBvpWyPdan2COpU+dzmmYRhSiC2ZqFUmGGIMB75E77pUS4kxIJl6RcRd2Y/1TERSSAnDuB89QF71N75TUxYBgForpm4/7i4vL81kHPeIHmOsZaxWPUBIXOq02Wy6Li0Wi37RowOoIbGrtaS9ZasREJsAJJG1ai0AoKsLABNSjHk21zHlrpcUIAQKAQ85U4sWUci1zW2GJkgxxwNYWy5ghmZuhwhzAgC1rAE9125Z1ivZbnyqHNgJnZlzh31vMYWQiCMpOjU9CcVqOBTYbWmzpd1AU4Vi5OwHDnxCcCRn1ECQOCx6Tx1wRkpKDaPUchIDFUYDKFSmUKvvJy1TI09H0+gNI+qo1ryFilbTSv4RGcDRWx4L5acNdzrISb8EmT/+FQ43x0RM1ci4qaifME67+0mS8II0I+Jh8pZZTeZ87fAhzbyf/HzLrPDS9Z/il46hAQAgh2MKefwi7t50ERCJkObpsmbSifAwgz4PIh5KQC99d0QERD6IkgfiVhZHgCriaO4tikA7gZq+NL2AgGCOjuM42CqHFHGyd995x5S63DHTol/0uXtw/z4AqPv18+fabjWzITAxg5dxZIpmTSqHxFTdHAwRDRyIikqRCuBNzlDqxITuaiqJyc0Qoe/yVGudytn52eZm88tf+OXf+k/8Fq+mpSUvCK7gTjybEiJqQ3OqOgyDJ08pu1MVt73FLqeUA0ZsNRg0gKaKeMwFiYiaHxVTIrr4C99//ue/HwDe/XN/ZvtNX4dSQY2ih+SpW+RxGJ0SEMfEIYi4mMbQLbrV+eK8WywoZA/BkJCYnJuPwcDEbO4ByUWtVENq08muiim1B8FEWquIgNmsbg/uru6mptB8PHgVmfaDVpE65fMEjoTgACGQO8kg09O9PdngAFECVCFHjEkiTGa0urx45ZXLj39qSFkR21RXQOIQ0dBQXdXcilQx/YVPvtuWyPQdxn+P2Q2Rpehxkx4X+TGBDoFrrQ3ut1wud7vh/Py8qfs2IqCcc9d14zi2+9913fX19X6/PyV9A4D9djeOYxsQOyYNRHMwTTRzLE9lak60AUAvV2sV3e53d87O3bxyDBRkbp+FYRpTYBGp09T3y1LmbkqbUm7VKjhAOdz97Ozs5uZmuVzWUqmF0mbwIuvi8SWIc8ze9iOBI6IDKjiHEFNMuacQUpcbYd7R7sxBJ4K3xv+x5gxg4OpynIZyPyAB3BHZXMAEQD0g9JH65OCQA/UdLxa86D0EJELCVjRyADNFMagVS8Gp+FihCjb0nwFRoxCilqwAIcZAXYYUIQZjNiKgW6s3Qyfd3NRUoFYQaegSA0dwaiO97jYz5thxhvbLOgD80HG4y7f/+dIx35ETZ2BmhESAIuJot7RC/qKG5Ife5GjTb5/Nlzu+TI/h+D7wIumbHJyNH/g7j6nDyTedCX2OO6p1qPxFOOyxX9DuF8CMAmqDhIR02g65vZrDt8NZz1pPwzeAudrGKSDTNBU0311vnj27CV1HgK/df2Uax2ePPri+vn79zY8tF/31zU1iVrXUd6mPw+a6jjUsO6JAHBBRRAk5cpKqgbtqdrXdlFpUJHDSUgOxoyJirZWncnbncrfbNQzJEXj3xS996b3333v9/iuOisiIpg4GqlX80GVpX6qVj6cyAhiAUQiUoFYHMArcL9c+F3qOxQrCA+dMW7LdT/zUnb/wl7of+4nxW3/to+//d8E9inKo4IQUnbOI6jiw4zhN7hRSdEc145i7fr2IixgWxJFSduIm7CtolCK3Rp8rOgYISk4E6vPukdZmVCNEOOE1IQa39oTdpCIhAJhqE7ECIIfgAFIlcjBABM0UscLNkxu8GXrHrBGMHKlyvAbpX31l/epXLO/e2xNLigCgIsGAmFqewQEnUXc0AzH47r/5Dc9/4678t+PyR+IeKyKhAaJHDlXn4vtL638Yp1LqarWCA9QNDia12dlWeGlbo9nc9Xp9c3PTikIxxgYWauPc7TEdWSVaAtHuTzUlB50qIzGhVgnM4zCSeu2rqsYQ20sYvWHDAIAomNkwjkvE5ldKKY1n9Pj+y+Vys9mo6nK5fPTokbvvdrvFYjXvRJ9VyGkuWB4bSXO1+GDXzYHaN8cUqeshJ8UQT6z/EVBkasCNtOWFqpoDiB+bnA2BZdgWjbvKiDYxipB6F3DdO4GFjvuOFj122VOgGFrP1tDMwE2gFi6Fp+JDgXHysXpVaCHpjIY3UEN0N0YKlDLk7ClqZGWEcGuE27d2NVPTWq1UEJmrz+ZoAI4+w2lNzVpEaATO9GUdgJ90Sk9tsaodO5ynbqBF09aYKJrhOwTODYhph/8EAHjR/tOBNK39tVWK/AA5nWe0vjxS6FRN/ngcr/lgWOfrJ76Fgr102nwCUSuF4YzvpNu1dWr9D5Hrce+139kRoKbGzK4GACGwmGtryJxcjDftnuNTnN/NHGC5XnVny3fLTkqRaTpfrrjvEfz6+fNaSsgxhxAAyNyr5K4TcFFLiK5GgIQ01bobhrhcunvk0MUM4E5hOwzVHRlALDIqobhNdVz3FzExEYHZcrEwxwrgomY2DkOp8ou/+PlX7z1AYjdBZAR3he1u13V55okspU2ZImItY6mGhIlRraI5GwEImICR+9wSh8bviHPsT0T5x3/i1e/74wBw/cf/8PN/6Q8FIFNDq6ieY0+UgEWrwvmEFDBl5uiAHCISxZQtdBSiARIHMQQicFYwTikERkI1SzGCmKk0mvXWGXPwao2XsdGoMbOZSK2l6QSIFpHqbmBoarVWcggpMlG/6AsWK4aI4EoOUBUmIAkBu4QUEJyhIA4hnH3s1cUbr2q8ex2iM2JgB/C5zcD7MoJbwmAiUkXUR7Gzn1i++e9cPH76rI3bIYqqpBgj8VSm02U/86+JmDXtwCBi2+328vKuqqbYVZlEpO97OMF8L5dLbHOCbbXE2Gr0bXQcDkDS7XabUmqjAG37xxgJXKYCR+oFtb7vc0w+Van1/fffv1if3b97t1udXW020ziBo4sTYOKUODKSuu53O0RUESba3NwwUUMNnZ+fbzab9sPNzU0IoaUCSJi7Doiw6XQf8N/uTgjAtwFfCBkIMca8XITceSCPiVrplui0jNEsCRGDOxxLPA2nB27YqGcMzK1K8wzgLq46FbIJyD0irjLJylIAT7hawqKzlDBGYAJCANA2XW6KUmDY+37nu9G3I1TxKm0dEvOMRm/mKDDEiP1CU9YYJaDNg2bYuo6zeTQDNRe1WlEUvMkMNEojAyBvEmEGaqAwazzekmgfbeUxKPuw1TOzdmHH9osf6MJP7+N8ZsNjiQKAlgoAhkZEzAQOdqDIP/gVPSzfW/mto+KKf4jW9fYcxGNMrfNovqkq+Qu01ccvcgxUj9/r+JWpUfqceAJEBL9lGToCRt0dYe4BzJCJRlyF4UgFdHQMBw/U5qtnomxTg0af56ZqxDAHWUXbdV1tt4JayXKIq35RJru+uSmmF6sFr/pHjx5d3LnDBMN+GwhiZBFdLJbTfkdOzLHLfXVzQOKAYu5g1tSueZSpuJdaY4yuFgC9SOI5TDO13Wab+y6mLsdUQPu+r2Mpk/zET/3k4nde/PpnX4sEDgbAQNC43Tl3zIwpWZUZbDevJhMRACT3LvchRkYigFrK3ENqzUmCNjH3yvf9S92P/+T0P/u1mz/+R/a/9psjEjurQYTQSrEO8INnP/nNu39M+kVGQFFEAiQKIcbEIaozczDi6n4ATAJyjESMwd0pRC3V3ZEYgGoZVBXcRTVxqLUykoMRM1FgljayB17dK6LPemDukbGZ2pC4NZFzjiY2T8YBmKJbIO6aqjTmICmtX3uw+OTHSt9VX4ylgllyRre+79t4KEdys1IKIYLBVGo1eOfhB0+vNmoYck4h+jQxBgaUKjBr692utDnYB3D3cRxbjeWIs3SYZz9bKrDf74/a60SUUmq0bn4QzW7cnLvd7tg3PuwjbW6gz+m4lYjobLEkRDJIXb/MnVUZy4TEdy7vDOM47AcwZ+Rpqm5o5oG4WqnjxMy0AHLY7wdZLjnG5nX6vt/v9znn7Xb72muvuRqYiypTNbMjpAkP6jcU2JsAS7NpiH2/iIsOQvRAHDPFREQBXihBnNiHtm5g5mhr2D9V8ApmJmJVTdVUwZyQDATdHcwCQpdQluhAXc+QsV9631tkTgFCIx1BEXMT0ooyUhlpLD5NQQzUmnIGENVZtyA4QDGJacGL3mOymITJmCgGjjDXfgDAAQGola5UXZWQAkUHFDTEoCYu2oybgoubEhghpUNl42hP8aC+8pFonJeOlrkf7emttzgk+cfixvH82fy1c+l2duPkMfjp+afv+dHXAACH0077E2hzneGY/374OI6KENFHv/vhtOPl4fFooMGD42yfDggtgnB3awZuPpsQmpyewxxbztd2kp3MsGU3MDMnmKaJ+0QUguPNdp9yzDGN43j37h0gqrXu9vuYk5gi4urszBF3u2GJVMaKBgKGTDF1+5urFBMBiahZvdptJ1Nx7Sgkogm8MSQhuYJ2IaipVDEdY5dVpt1ul3MCxr//u37ur/7jPwoAf/8//0sA5OBIGGOEQwbW4CXNoebUqVnDKDOnmHLOfQy51km0tpGiA2YxMlP3Ez/1+h/9EwBQvvXXPvv+P09MyR3FuVY2o6oyDHUY/61P/j//na/+TwHgZ//af9zl7u+d/8yf/9q//uuefO0f+/zvcycz+/6v+Ws/evez3/u53/OtV99sjgHYiYmYDNjRCBEZIwK7lCrTVIaxLTlyEBF0cKJIDNwMZRWpKhO4AKq5EHgVad7ruNgIkYnREBEwoKE7hbhY5tU5jV5KVcK4WPX37/evvloX3WhOHFICcGN0Ym5tx2rzNoTWZHckjrv9/t0PHpth7pfF7P9H2Z8G25JlZ4HgmvZ293POHd578SIiIwdlKkelRArNIKQWCISaFlAlNVAUVU0DNXQb1d30YNVthln/KbO2aquhC6ParFpYFWUM1Q1qKEAIkARIDDJJKZSSUqlUZKZyHmKO99695xwf9t5rrf6x3f2e+15Eku0Wdu3GfX78uG/fe6211/rW96nWfpFEBkgu4mp62m2zLCg1gyrjzszjOFbGhTrsqxZYznkhWBRcdFdqIr7u3UvKtUsLllCpnuw+B2H1IxVUOJpZaC4uLskhT9O69B4+fHhxfvfOxd1k+cVXXxYJZSo5jbvNJucEABXtU9k1zKw/9tvzM1raNtfEADNXci1GcvcYAiwLsFah5rVMN4o3sW2laUJoQNiQgIQQacH2PLbAETGZgpqqutZqr3nRUrJDTmnSlaneHADMlYmcHIiAGdvWgZwYUiEI2LSwbbFrjAkIEAydwBRygTzhNGAebBpsTDZmKKpuAGAALFRB4k7gka0J0DQYo4ZQZSaB3KpuwWKYame+m9e0spgDeIX+w8xrCq6e1Yq6ItXWVgzhhmd1zcO8uSV8wvieELSuewK8fRGqgNnFJVSrCQC2KPGehuT1pNnULl9R4/g3vbHV39w+4TRaf7P750XK0cyQ3thJrKn/xy5Yfa8vaKV5/hGdNkFYnUALWmn2sk+MYW0erq2k9XAAiYEZY4ivXV1bLlePHr3tPV+fEK73V92u3Z5tmrYxVA7MxgZ2eXGxH46bdoPjSICqOuYksVW3lMvu4oyRDTyZZXeYIyZiJHKPxHOXgzuY1X5LAAA1ESmHQ5AgEo+/Y97n/cpTn/zW196PxOgoZDBz4dQd9ywx5OrMRMRYQT0o7pSzkdQ0ZE28gwMC+93/7q/f/ct/DQBe/8s/qt/+bawOOXvRaZxgzDpOOozT9b5M08994y/Xe/gZ+7nvvfqW//a7/96vPP3JX3n6k9/25fd9w2ff+ZFnnv/RD/wYAPyl9/2ND/3E2yk03G0lNtJEbAIJGJAjYSBCQiYDa6EtOZcpFdWatQs0Y+QrzXXTNIfU5zQQg5lCAdXqvcCsABMwGNTMp6srAhYwB2+6TTy7UJgsBOq2m2efjRd3BxSO29qf2YUqOl20FFUwDjm7YkGwkrOWUhRS0a+89NLLrz4AZEAhLtt2W0o5Xu93bUNCcCKst64CIkTkWqqsvqrG9RbmDejK6EBLtwqetNNXmH99obUjrCbix3E8Ho/n5+d13laYkGmpfS+1UA5qnkuq8gMXl3mc7t27JxJee+21brfbnO3apk05UQgEKBK8GBMhAjpY0TylikKsNKXrpKp3+Nprr905u+NFnbAMIxFxkBBCuIm0ZgeIiLFpYtNw07IIMBEKMVV+BkRAsNUHrO7NAbQq26u6GhTVUjRlVwUdTYubIRMxo8whIzsCsHFVdQQ0QmCIjk4Qo8XowsCMhAYOZuwI5lAKpsmGQYfe0ljDdkNAIiMArggUAgJvhTaRutabCBKQhZiIsDaurLLpVjHNqlAK2LK4KvADCUkAk1bUspsjABHFIE0jq93XRRl4RQ2/md1cj5VLp76t+VNrzM7EcCP9uO5PZ3O/0hMuF1kLpDfGkdDN4U3D/zU9dQNCrVFD3dSfvt03PNZ5T0R+Qxo+exxwh5MSQg1XlyK6wcKTSpVOgOZChdPcU0a10Wax+7MzqJUZNVj3W4v3UlVCzmbmWPOTpWQzOx4OWuzy/OK1V171NgBZyfl4PHZdh8zHsUfiuNkcx1FYECDlBOAcxMsEBMM4IVLbtqQem2acChIPwxCDIELFs3VtA0TSRmcS4ZRzTcTlortuk1LKucQQ3vL/PNP/1cM/dvmHvvnVD/giQYFOIkFzISI3pWWuYy0VoTgioTRNF0OLgGbFoLJhI7if/drHn/v//O3tRz/ef8uHXvhv/iI54NXVX3zHX/2Fs1/9Dz/2I+//1HN2HKBocOCiOk3/3s9+n3+ffuOn3/aeX73zenjxmz71tn/19PMA8HW/cPb6+JV3fv4MfhgA4Bt+89mHX3ghtF1oWpTAQeB82+y2YduFbevCxuQE0kbwCO4l5YqHBtUESd0AyaygW2X8n6aJGIjQ85zbrMYRpSoiGDmZKRKiELg5M4dWzs7H8Wrz1FNyeUFn5wMF5OiIm2ZjUx8ZHXQcJ0Q2ByF2UnegmbzWUrJhnF548eWpqDSbbrNBZnW7vnq46bpx6LVoUV9BZcssIgAgptplQYsYwApnqDmf2vRbmwDqZ+tfKlKoruh1EtrKALHgiNAr44uLNJqyiDAiI7EEZskpmZoX3Ww2MTZdt2GPV4eDtF3TdMjsbq5GyMUUDKri2DiO7s7Cauo5+5JMZuaqZPD666+fd2dmFkI0opyzQ22tBUJxJ3cHJyEKsWnaVmKgtgFEJKmzkSr739xBfVNEVbNSipqllM3Ui7qqTtnqxHBjz0JEEoCwuM0tju5UG3aJjAUEwQUpkDmZOweMwYWBqlFxM2UFLwVSgpR8SpYzmBNjQUBiFAZ3Z3Skyg0DQSBGjMFDmH0JUu1P9hl3soSVZmDqVrls57QQASMCkjny3LgPCLVBQgLHKGawdlX47BrwdDeAN3lzgNoMfRJolKJmHgJXNUqbG59mu4dMruRm7pUUzMHJrcqmGIEhoFbXSwiISMB4ghYFAAJzN6tqAQ6gDgCujFjX2xxWI+KiNzBP+sXvANSE9RK8oyGSuyLSsm10M0V0qM6GasmBgAEBasaXmd21FF2cClQpRwdEdQ4NAC+U4rikgKyCb8GdzAWo0giYOaiZGVccBSi4C0lRrToxBXIBzbk44pgLt5vjuE/TdByOKnD53J1xf7V1TFeHyJclynZ71u3O+zHrNAXHbNBb2UY67McpcN/viZmLuaEC7lMyCiUbuwHrmLNZbgxbllwKxZYRVYsDjamM07HZdESu2ocIdz/S7v6dO7/3z35bfLcUTZOO7aYljeYqoTErxELcqGVyJ5zbRFJSZCJhIESkomPKKU8JkS5/89Pv/U/+cwB45U/80df+1B/X117SMX3kzsf/wjv+CgBMX7f/z/7RH1eTGCI1YcxTnsZv+K3n/vPf+renKZkld/hT//T7vvm33vahz359SoMUSzn/zT/3Hz///q/89i+828jKNFrOuRRApAdRgjTbzW++78v//Xf8+O/sv+M/+MK/a27OmBEcwdw854yOzowSKuDNHJwlbpoup3QERBIy8xX5Olt/YkBWKATCxAwC5L07Pf10c3FHmgAIBSFIKJpVJ0eiQJOZmhmFGGNQQ/TInpLmNAG6OiTwVx5cf+bzL5jFzdnW3NsQSNUUhilPSWs2dZ6TsDTLqzYxIqOw5JytKDODzamqmrE5Ho8V2VkTWSugYy7kLlmREAKhM2NJYxbabDZCoHmaBmTEGENRRQQWYCRAz9OUwsaQtufn++uHhg5AhEGoywlje3l+57kHX/pi6DYkPvmDEgUd2hhzKaaa89RtNwqesVDl01FEJllVypn3V/uuCtM3bK4cWGEySyFHppak4dBgaGWzg6ZxCcjOzJVnFrmaMEMgzcbE9Q1n05zVvFJ3TFpSmZKlolNCQKmQdaJKvwwAgQNARRvNSQ9yQCIVB0IVyKWAEgo5uVthbLD2bwMUOIAlzgn7yfoJUlErZoW5saLgVT8EmBgBicTbrXcba7sSgzdSBFGoxvVWA2OsKLWCJXHJVHIGz8zmRMVIiYqaejLMcxMbsIjHiN3Ou07WwPw0xfFVkic1jljD7TWUJr9pEl4hYkWVlqutkXiN2WnxvbO9pqXOvMzFepEaltdXcCqr6+64NFXfus7Nbd80DcxJmOXvuFR6/YTpuiYGT3cL1YzDyXMtbo8QYKG0XMjyFj2lNd6vFPlQNxCqi6bOzRanxh1ui9aO1qqYzx6Mnanmrv1wOKRpbJpY2ymPh/65e/ev+qEhROZ207386qtB2o0QS5gqE4DbOE0km5SnTkSI1RwQh3GcaiSIJBLcLLlHiW2IgLZqP6SU1X0cx6urK3BDgKZtPOlkwz/75//8/e99dx4zcoXJGnNtE/V5F4fGLhUQW18gC9eBVc3TdByGIU/pu/7Lv3TnE5958L6v/9IP/8HrD35AXnl56ofDw0eX1xm+HwDg3b9+cdg/kmbL7Ie+d/eUpwDB3aeUci5TmpqU3v0b90fuUyoVPShRvunz7zKCIGzu49jXmmfeFxHhR/zf/OG/8fGnPv8R+I33fu65b7/+ZmOwlDVNeTy6GRCAQs7oIk1oicTdo4QkMk2QUuJFb70SqwFAjLGoktSmOl8Bcjjj63fuXkpiRGGusic1GergS78JEcEwDF4V01QdIKt+/G1fePHnXx3GiaRFxPPzc1V9+PBhSmmapnXHejNjwSsqBhGDSGiacRxrZpGZp2lS1aaLKyGEuzdNU6GWdUXEGOtpRDTrtiM4gKrWluC6FVDVTduYaUoJXZoQEBHcQgxEeOz77aa5c+fO2dlFQ9Ecm6bth+P24k7XbSU0m81mGPc5qakFZgJ0c7IaL5qhejYXEpF5r1w3kwCbbnO4PtzTu7A4vVxy07VISBQcGBBZQtN1IbYUAklgVuYbtM+CGDQKkotr7Ucr2UxNdRwHL8M0DmVKoMaAXPtIbkBDJzTyy8/VvjGz05zkJQKn2peGVgpU+h9zKQVytmEqw8ipWCk2+3EEImJxAKo8vgAYhJuWmxZipBiMGZnmloLV+VQ1UIAZpgTgxM4AtdUf0BAVsDbBASIxgwRoW2ga7jZzCugU4oIn8JUnHYAQrRbd3Wk1sTPs1ADAzepOw83MtQJgFuwkABoiFjUwq3b/FM71NR5LVH7Lu9BtptL1YObazoOIdsIp9K/9CquCVjOgyrkK35diZkJYJ+XtkyHrAoOp3mipL1UQ7uxy6skrXeiadqvJ0DpMBMnUMRwOB0Qspo2E7dl2GhMb5mLtdneYxtAEaWKeUiMzPTwRiogVNTUyD4hCzEQF8uHYG9iUxnEYzrsQkJQYRM63OybKJfk8sDKllIqKyOF42HZt0dI0m6bd9GH86Md+/QtfeeHpZ+4xQ2WcX1Ov9UXTvFy97ntFaupMS8l93/f9g+2vP/97/+u/BgAvvP0tP/lH/oAw4m99MgBoSlcPHqZh+q/++B/64m+7/uAnnn5ED/14FWJ0c0RStRhbXHRuzYz7yvPKOWuMsW1boZhLzjnV6mI1dqplSsfhWBzg63/j3sff9XkAePrn+OXdZ7vLHSOCWhqOaZoADAmQOYfgG22aDpyYMcbYapuSo5JwCBJ46YIlZGYCQp6V5nwdEwAAAyISiUTgpgBUKZIq4L2eU1t5V3paB8hqf+93/9I/+n0fgf8Inrt/2TS82WwA4OHDh/v9PqVUCR6m6RYGtF6QiYnmUu1ms3n08Lpmq+qXBpMYY9/32+2WbhhwscpsbbfbU6hPKaU+Sk2rrqV7WuRRyUFVjTlW0A5zKmXxBwQOu/OLMtmU9Oz88t79+23XdZvN/ftPf/YzD882O3bYhoYAspe5+TUXIDNC9wISis2DWXdaIYaiZRiG2LZgyIHVzB2qeCeHEJqu7TYUYuX7R4I6GniCUqlhmAIl81KSq1b5lJym4XicxsFUESAQz+39TEzsC8Xvk2bi9I+41EGhOBL5rECu6OhqoE5Zq94LTNlz8aJk4EBOBFCRP25IDoCEEiM00WNAEZBQtQSQCGhWtay7kHXaeMX9EyGDMyqZIyCZITiAGxoRhAiBsWu8idR1sua14THUzZscdtJhe2orZ3Hek3+aB/02NTSseHxHAwBzZFoLwQ433Jxraf4ND3dn4nXr+tVvuw7O/O0nsqK4YD0fe5zTa56CxexEeaY+af1HIjKfmVOr94bT2WYGZnAzPL7WbWbX70smz7xGWNlVLjbpeBSW47EHxNg0BZwRQugCQwbYnW0Pabw425lbmqZziSWNaCqEImRmTQil2K7rGB3d3K24inBKiQkji2VNw5j7MVzcA3Umkq6diocQhuPY90O36frjsGkbcBiHgVGI6JjGf/FzP/fDP/yHmMjUYmhOqHJO4Ftah3ceYVUtpb++fvRd/8X/6/5nvggAv+dnAR+eve1jH37u184bCaEYE0/9wIDMfP8X5NgNiJjzRIQxNm6Ys3bdViSa+jANqto0TQixlNL3o3Bs2qZNA9yMNcQYc06lFPVkOacpfc9ffuuzH47v/cxzLzS/1ey24ayLbRTifjhoKlkTC3dtK22Tx2mzPYuhQUZ3CCEAORnPbc/uAC4iZYERr5Nk5eAEAEBmFvRipogEpcLH8XSl1CKtzKxKJWsZUvnE183dv/l7ffcxqf3Vjx49sqU/vxI2nJbHEDBIqGmcCujsui7GWCP6Gr+ve+VV26viOysJ6G63WzuBQwjDMKjDSh0BALUSEEIA80CsRFaKUsEYa4sdEgCTuvXT6I4X509N2YgEmM3x4vLONH3y1ZdfvXt+ORyvnjo/20p0NYas4CVnJaOAlVapdlohEbhzLU+673a7KSVkYmZiBoCcjWMoQE1sm802bFogIZ5nnlWwTCVCWDg+3WEoaqZFi07Jyzj1+zIO0ziaAjMLMzoEXh6cbrDmj9mW03TCjembqXTc3MAVCgAoKEAxHwYYE0zZU0Yz8hrtiQIioBEWNUYwQmoCbjvoNtC02DQYA1Trzzd3cZp1qF+viE4C7I4FUJ2AEIzcgRRQUUgAmoa6TptGuo2skQguhMm1IHPbet6YRazCYycxbz3I0czJYaZSmRu+nKhChlcbfUPlOtfRZ89lwOwLRfPpFqTurbjCFbSs1nz9ltMX4wvpFcyAqAog41XUb00c8aL2fvry5gidb1w9IznMVBpQoVX10U6IMGoRY50r80WqDztJ+FSDj4i+dDYgVOZQNDVm1kWlQM1ACJiOQ+8IaZrcfXN29qg/3n3qaWmkmClxaOLu7Ox4vW8lNOjX/T4ETnlSMzEDg7aLLVMTozA5GDOSYZrGyOFis9uPx4hMLI3EqQwppQ1vdZqQGBGPx8Pde3f3+6vj8Yjg05i3u3ZzfnG973/+wx/+gR/8vRe7LZsZzgOScw6BVRUJiCpEct4P1CTM5fO/9YEf+4mnPvPFzz9z93f/rH/hGx4CfKrWbP/97/6mHbeCjIiBGTwHEYBEhJ/54Cvv/NVdkVyKlaKpn87OLtS87/el5Dy1MUYzKCmNpdfcTalv287dh6F3gCCScw4xmquVMo2TlvKOXz476EMI7K8/8IakiSxo7sNw/NI3PQKwn/+3vvDezz33B//xt+12l5vdebfZxDaYQwhRcJa6nLVziRGMmZHWLvt5URARIklo3J08AKKZArF7LUrNfVi0dNjmnBFBi6rZ9XH45r/5rld+4AH9C5J/SeVMx3F88OCBLKwqRKQ213tPjzlDa8aBY9uKyMXFRd/3MLfXSi0CV6+ASxNsrQRM07TKAKzSjDqNa4/nGgClKRk4AcQQrEApRZCUKOUcYhzHUS3fv3yKkR8+vHrrW77utQePnn37O+48df/Tn/703bt3H73++u5yNyTtpOFikZiAJ1MmUYJiWkwlREuFRMjmpUxELNJexn4YiLnCopomZlNzaLpNsz2TtgVk4kDMVU3FFnBHFaR096KlqKl5ySWPo6Vh6vfj1RVoAXeWKEhCzEhcdYqW41b+53bc+VgAWg2ILbaB3N3As0FRHUc7HmEYSM1ywaqOjghCtYgTmLMqCHsMJbA3UUP0IBbYmJxXUZIZHOM1FY9zOKvODgCV/AK8QlPUrGQDIAjigXHTWtPidudtlNOEzwoLeywo1qUpV4uGBe3ypIdYl/qJ+a5u++b6dSaVUmYLiog6415sUZg7HWVf9QYqdc9sQB1PQuzH7ufJ49SHnbqK017wSm6OT/QEvOG3rJdZ/VzFFnhlO6lZ+HwC0IN5g7Scc3MULVFm0gVDFGZVd/esRdp4PYw1fDaAAp4JEiEx7XZbiPHO+cXxeIwIkBMJQ8mOHoL0/VC/cxNadEWzUrJqDk2YjkfVEiSmfnRVMt9uNpuuS+O43WyYBTGVkkVE1Q6HQ9M2h8Nh28U0pW7jaq4I18f+F37xl576Y09/+6vvQ5wDCF642qspxFlMgwCglPJ1f/sfvOvv/CQA/Nrv/s5//MF3vvP5X/nCNzxcB+Ejz372mZ/vNm3XxHi23cUQWon9kH/hz3z55/7MFwHg//yt3ywSTG2gabjuu67Nlsx8yvpb73/5vR+/P40TIY5mdtSy2QDA8XgkIqiN6CF8/luu3v6RM6ttMiGMOeVeRy0cxQgUvUD55T/5lY/+6ZfrLX3uA6+/5Ve3H3rhPXXpIwMJigiDENXJ7ABEJCvOebX+67ZyCSwq6pzc1a3Ok3m90ELmo6qllJSmYjnlchyn8Sf7i78QDEWaJgS+vr5ec0Rd111fX7/htF9N1TRNtUlq0+1SStOU27YViZWIv55WNys1m1Sz/HVXUUVX1sVSl3+9w/pcxBSYcs5RQk1pqioCECKASQyquahuz87f9a73PnqwZ2kkNLuLM3hJnjo/v9hsber3iukwENj27l2JhmrD1EsbiQVdCZEcUM3ZgwQ167quqMamUbNjf7y4eyeEiMRBQttt4uaMmxYlIAsSITNLdZMG834LUi7rUBfNllM6HMbjIR0PmlJAEGZwqKl/Zn7cu77R8Zj1X7Z9WJnjKrErmJK5m4IqlOw5e0qapgjgQArghM4CPoMjiRligKaBrvXYQBNUxImhimdQLTvPX/gYpQ5hqBtwczQFnLnrFB0NCSR4ZGxbayNv2ub8XG7d95scK1cGLSwVdQpXasulaowAYLWB4obO02fayJkYeYYhVz7medSw1ucJCIgoq56gknx1AMVPOGfmnNdNcP2YB37smGP/k+PJTcabPfv6jPVC4E6Ip/oEsNj09alPVv7j9zDfyZt8V9M0NiVNikyK7kixaXbb7a7ZUhDYCNnu4v4zjURyvzpev+WZu4LYOVw/fEkBIhEJAaLE4CvBgmlgKVpSzsdxmtLUtg3HoCkheB5TiE2VCowxFDNCLKU4CCIcDofzi93YH90DswSJA2Z1jEH+0x/96wDwZz7+h/+95//N6raZuWqkwMwTwGt56R1/6++/6+/+9Ovve9dv/P7v/fJz93dX1z/0T77jG774dU1of/qHfv3dn3r27Vdh/+x+GiYUcY5Nu62ELNX6A8A/+1Nf+Y7/6rKoTtOkpUig7cXuLc8990/+5Od/9k9/EQD+j7/tQwgUY1TP+9dfr8iWldLjl/6j13/hz74CAP/xt3+nO0DSUfNQ0r7vh6lX8IyawT73gUenr+MbPvesdDiOY2i62AZkdiRb0hFNEFUlmdvBKjW03+46LKUgBkRyB0cwQAM3rxnZeVNY7dEitlXGNEwGX3nppc984YvJPLax7dr9fp+z73a7/X5fAZ0pJ1hKmuuxWn9mIhEASCkJpxhjzjN2Y8WAunvbttM01TLAqgBTgaFrjUEWEGC91bpXCCLM3IYIAG2MZpqnhOTMHGIMgUfNU0r7/UEkbLqzzeasH4ePfvQ3VPUtzzwDJe/H1DXtJrR6vLYxdRIU2ViAWKlS/M7iQrBAgEi4toufX1zsD/0F3AFEQG5i17YbjNGJDZEQFaoy4rw59cU9V4x/zllz8uGQpnG8PoxD77kE5sASRYCYieuKqKNqM3Dy8XFeFvZtO7B+Cn3V7UEwcEMtXoprdite+4IIgRmEyNFmVqlKJ1PRn4IxYNdCaCAEZ/GqS8lVpWAuud2yXY4MDK613xfN3ZxM0VzNAZmEsIsWg8fIbSfb7a0dQH3Hj6WAAGDVmWMi1wJL4RdgnclerG7FZgoHWO3liSmsocQ8QFY5D6r155qRrDF+DY187TOo9aichdgJNRdamIQe24h8FQfw2Ju7ZY5nqch56dYU0JOfvWXTEdfiNwDALGVeXR6UUmbCHwCHGe0Bi8N67BZZpF6UWfp+qEITAJCLodDhcESifuwjtQ9eeTgwyNkdj4iujjgNA4oc9j0Vq7SjBNi2zXVOKacYQiOsU2pDHBSK6pjSlCYRbmIQ9SaGKY0xyDAMxBybtkQ+TtnNc8nM3Pd92zaIWIoCUAghhti07f47DvXmf/ne83/K/lB9O4i1XjejvGyWSQdV/cy/8ftLKR/7ge+ZprFMuek2bbN55vqtXbv9oZ/6veBw9QPXV6/3bWyOh8PFdvfsU09bLtuue/RL53/pO/8+APy5D/9w/y2HBw9e219fjf1xf3V19fDR4Xr/m+97UO/k41//5bv/DAnR3Nq2aZqWmJgltk3bdb/wZ5+vp33kf/fwe/67r8uuCC1oLkgUwnHsm01z99mnnvsn9OGnPvPez7zlvZ965r2fvuRdIA4xhlqhUVUqGmJTsyiIWG2lLTj6dfPqC4C9lCJ8YjzWnCegA+RS6jyq664auimlh8fx+U9+6tH+gGETmrg/HJjo/HzX9wMRVX78ebb74z4AZlwRNW2TiyJi5fusTjpGwjLf2KmybtX8SilVXbBK6LTf76WSdZzIsNRyharmaSKHrutyGnNOm7bbNg3MLoeIsJTiAa6urs82d3LJ50/f74fh4aPrBw8eiuv9u/deuH7katumS8PYXZx3sWWhCS15YSCRoOAK1eZYTZMiYM75zt27j/YHA0SSENvNditNW4gr8R8yI83gdV8i5Mrj6uAllzROOQ169WA4Hsd+dPUmxEYaQiRkCoErMOnNY+JTs4vL637sZy0bLMGmgat7ccuVVpCEKUZ0XfCBCEB114CAwuIhQBO5bTQEClGZndF5oSiG1fH4LBy2gpLcwdCKeVafMqbsKec8uQMgonAllZPtJmw7iEFOYxZfyJ9hKZCuO6b6pea+dEmBYyVEZHBSLwhKN0Js1Vb6mvqH2/3WPpcrsOJqkzoR5WKIKDXKKsW01KxYRckEMFcFcCHwufiN7kuvljsAVHGVZW3cGO4q9TrDcgAc5/+gdiC6qxsBmzoQEouDqwNWIgNcUlI4A58AnAlsBvBVFWB3zQp1W40LstMIyVXRqzJBXeqz25BKJADAEtFRS3ZHJlakCcZM1Mh2GHrMPk5TjhS69u757uzyjhK98OIL3bZ76u5luTq0m83VK69hymPbTAWbJiTngRBBW4JNSXvImqYmNEJN8jKaAto2+DBMAh5RCdWoGBYCl6wBaRObvj948bFPYzttt2eMXtlpyjQK+vYXu4v/LPn387/x0h9IWtompsGiCDl6bXjUOd9aW61LyZ/8g9/n0wRogEUCNU236c6CNE23iaHtdpf3n2V3VNVttyOAs905E/+fXvpzP/iRH/rO1z6EfxpfefnFV7/85asXX5gePOofXh36ay35589/9WV4FQDedu8t73r7GQKZxKbbNl0XtxsQ4aZxwj/8d/zHf/jDAPBnPvYn7VsVwHPJKaVDfzhYUigXl2d3nrpso/z+H/vefjwierjD7i4sEqIEBnfBQDbTXtWoubIpVH/gBjG0NcRmRhRE4K4N7lrnLSIwgRVHdyRK5sihqJac6zZg6qeU06j86S+//OXXHxWJoWnHpFr8/lN3D+M05RSb2A+Dzy0KTkQ4b02dGUUYdBasKHk62571fe9gakYkhISuUULOOU+pjY0VtaJNiF3TDseD5kSwsZJV9Xg8uruEYKUwo2oOISB6bX/MZRIRcSrKhvMefUxl03WNxCbUmNbBxTFuzrqXX33prrzt6ft3VO3zX/zcN73vPRfb7QMODQkoRAkB4zj1EXm32eyH41Cm0GACL4QGCm7ComVCUGliQQ9t06dxc3nJXWNBXCQGYVpoJQF1TtO6FDPAoj5lVZ2gpOn4cDxclcOoKZNjaKKIUGAioirXTnOnVM0+YM3xEa+O8MbIAKjfsg+zUaopA8S6DSAmN1cmCAwheYtegqdGLbtWmhhAE63kXUTGHpqWm43EJklwIRcAMaAqllqFaWuuf7Y1ZFAU3dBRVTNkowl9cJksD6ONgzlRbFxIJXjTWttgF5tNuMUGuibBT8PkOeu3yGkx3iDs8QR2OQP/ZqN/Qvx5Em6vl1qhPk8eVPNX7pXuAxHdwXBB8jzxqTWErz2KKxtipOju82DBzf246lx9BbRyUuueOUfBzaDSvb/R7a23dBrJL8/iAIjAUD2lw5Qm8FoYxzVvVj3uipxBgFJUS2FkNUtWHDE2rUmYhimPEyIwS1EzS/2LL5NwwwJm0zietY0wXV0/utyedWe7vN9LjBCDDVhKPpOoWmptQkvx2p2HIEToClAxux6CSAjEHELIqlpKSkm1CHEIMecyjuP5bus+AUCMkYhC4Hv/j81r/9frq//FQ/t9fnXYNyxuxQGKGjJIILAZU6CqpeSajanoERHZbLbbzS5nRUIOIpHyAOi4vbzMSb0SMrufnZ3/jsO300XAIG+53D79zrelR/vrF1/uH133w77k9Gc+/Lb/YfszH/rsu34Avmn6piHEaKGLbYfEm/PzuNlI0yDLB778u77nf/z4d++/yz5Y0KyopjQ+evjwrV27Hw/IsDtr2y4Wn4bxSA0TuACvi6KaezNDM8I51QMnqVFf6klrhXbNmfjSaHILPucOiKXkUoq55ZxLLln1OIwP9uNnP/cFVQixIWZyeurpuyXlcRxqar4mi25PvGXtEG26tvYTjOPYtZsY4zimdd4yEzLVjBPcrtyISNM0Oeca4BNRVQQDqx2/sBKuMXPtqgkhhCClQEGs2aEYY+TYdRHAygiEnFK+enT10ksvNpv773v/BxCxCeH1l1+5eMuzz95/WsCDGap3sSlNO4y95sxAXWyIGYGYICNWdVA0IEBCDiFICMMwhCa2bYuVbX8xWWaGSGimC72EOWY1yylNwzRcj/sHqT/kPkcJVQaZiKqsRYUw1zd4Ory3L34L9PlY1mFJCcwVwvl3RCdEJjeChkkjqEN2K+AFQMHdCIFqih0diY0JmZwFkB0RYG3ixVPT40tCfqYpLWZFLWWYMo6TT1OZUknZSgGuUqyMIh4DxSgxUpA3pYNeZ/ZXOeE0mb4OkC9mbnEMN0N5upf86l9az1/L0eZK83biq93PnERyFxHLtl4Nl+/0uakY18TXWhWYgbBWBdsIarc1AvqtbBi6IdQmDV41JOs7qFbesHocM3dh9GKVBZpOqoLVLFa+nT5nQXEiLeoA6sZBpI1X4zSOY2yacrg2hkD06muvXl7cabF5eHjEDT919yJrfu3q4ebyHIn6NG0uzooZN8GZpnFokYGh7uhVnaqFKhqCCGCQ4Evvj7u3bcsh5mEopZhajV9qYRDAznfb2iJU0SPqWEppm/iTP/VTv+vbP3jv8szRUkriaOBmLjEC1CrOTDSW8iyPHGMTQoihYWYi6fs+xiZKAwz/7W/7Ox+5//F//9d+5LsffMuwvw4cenePsmnOzUyatjvbbi/vNhd3y5gINKX0Hv2dP/Jrf3w89tN3DWA+5dSrtd1Gmmaz2cSmzWpEDEzfX571nYtwP/Sp3zuFs2efYsQNbhBdBIunaSzg3rYtgUO5CfdukQm+UdGPiNxmqMxj09itrMHT6bqoCdecJ1M1syGVT77zxZ/6/b+y+XDz4CdeBW6CBDV46t59ArvaH8xMTqga1m85XU31ypeXl9M4NNL0fX/37t2ctWJ7qsluN7u+7ysMb77BpbdrLUdXQ19xQYxeJ2oNWSpIjxYxpbXs0XUdM09TQsFhsN2uGzXVAOL6em9md+7cabtGAJ66vHzrvXuvv/LSluX87MyHIZdEsGtiBDcQDo07Y0JngqnqVxm51mwAVRfYtu2rrz/cdDtwrM16VM1iLTAiOgE6qLsbmlmaxjT1w/F62D9Ixyuwwhjq7m2GRoks5RN+zEadRsPr/64/T+fG+joQYO7orCaCCNnRa2go1hhbQwUwKxS3KTuqIOKcNSJgAmEPrELORJW8rqYOYe7pmmNiczCrKARUw2KYFVLxYbShh5QsTaq5ZuaBqapgFkIKwsJAt/UAVmPtS5vV+qgzFIcITgxixQacTvgV6biOyIp1W83ubJTfxA1UvBcs1n8Z0LUF+PFJjwtSqH5qpTOiEx1gmGXYwd0ZqSoWzK4EEWlW+wQA4IXLyGup/VaQdet7b9/zTfpvRcutwhFvVGSuUy3ljBX/YwZMiE4o0jAyl3GMIfTjYEV35xevPHhAgIKs07h//cH7P/TB4dg/df/SU0KNl5d3uvMLUx2HQdOUSpYQsMZlKOBzcizlJMxdiJYKApSltacuKnWMsYGZRoZWMteU0uFw6HZbItrv96WUqpJHhK+8+upP/MOf/BP/1h+RAAoFAYjYVItm8soz6KfvHQGJA5Ko25QTAnOQ/XHfNuUTz37hR7/xxwDAP2Tf9VPvB8fhcMCcsA1HTWGzaVjUMRti7AI3rto1UHI5XO89wN23PROYVc0CAZGITFMmkgCg6vv9PgoP03DcX6c8uhsxENhH3/rJb3nx3YDggGaKiLGJKFhyRgZbyHPqbAR3UEWuc77Otzm7z4yAN6jidQnU7MFjSQMzM1P1Une0OaeiltX+0e//1c+95xV4D9z5G9L+UphSOb+4IKLhMJRSHKCUcjwe80KSswYx6+Hu0zR1XXd5eZm1DP2Yc64yL6XYiuPcbreHw6FGvvUidUNQga21ZnDyIL6KtKzVDvcb4YFTIJObB5C+z/fu3UkMF5eXlxeXVw9fz6mol4evv17SdOfs7C1PPWVXV9evvdohnMeQS/aSsJirx4ab3RaEDmk0QkYjV+Vq+dEBzKk/jt1uN03p6vrq6WefS2ohNoi40L5Y1e6qsQg4l5TGfj/1h/764XR4pGlogsS2EQkiEmOEZTN3arjWQV6MBK+jvY7PY4v6xgic/JxDQ0QgBCGHCECABRyxGKpVpXbLBgZcM09MzlQEPRAQATEAgxMAgRMC4Zw8qHxvrinjVGBKNiXvJ+0HP/Z2PPA06jSVnMyNAxDVNlHiECQGiVHiEgisyZnHHsaX1vYnHxUX/n1EtNtxuS00y34C/aSF3LUO3HwCIuLsw1eDvDamrx7FwWTRD3gsfVRPWN/f6rROA3yY+/FgbR4+fUnzXTkgE1bQqoMj1jT/LOFTQXsL0zoBlGLEsNRvuZbCAcFBzRTMaabom0OqGrTVkKGScJVSSs4VM1xsxmqRsDIlLWM/pCkR0lN37j4cBitaSk45ccnPPn1/07VDHvr+eLHZhHghQfqxd/UxTU5mqmrWXux8KqYahNRz1lJUmagNMV/vXbg6nrrsU0rqWeame1qrPrDQh9nxeH5+PnuLlIlomoYYws/9wi997/d+z9ueubdpApQM4CJiOjc4uOs4jqWkOY52CLFBJPPaIVAbDoaU83s/8wz8HgCAD33p64fjXkjQPB20ScGH0Ydp6ksyUAN36poOHMZxUNXrh4+apjGZClJRtQBIhBLzMLpDzgWRDw8fWBqYycCEHNgY8S996Mf+h+/6BwDwT//7vzROycFE2AEVlJgRfa79VvXpaoAQajacCOrm5sZMzCJyVANtm4UfFBFKqXopWIPohUm/OFiVmTSHPufnnr//ufe8DADhF1pnuXt5T0Ic+6nv++MwdNvNMAzDMKwWav0F58xMnfM4jiMTtl1bsj58+PDu3afatj0eh5xz3/cksW3bKuBTc0o1qwMA9bZrU0LXdW3b9n1PBPUva8eoiGjJXtfpkumqKSARBoAgwZ1CjMdD37y1UbVhGEspTEhmpLZhaZAuN1tUK+M4Hg+5bSuVoRs0TavoERxDcM0Gik0AwimlupRibM52F227ubraP3UfhIO7W6mtVICEDlC780opWjRP07C/Sofr6XhdprENEiXW8H8N/OEkqD81L8t2zStt4+kJN/H+yQfXf+Wa+XF3AlWrOjWLRj2ZA6hDaRhBGZFBj5MXR3ciQAYP7MJKVCFEWtO3lU3ZbQYOVABuUVRDVSyex8mPox/7crim/mgp6zSZKQQxcGBCYUPgKNJECqIAssbOj0UT6zbTToD5j40LvQn1AiwNTacepY6RLQSc80WqCa7FW5jd2jq+q62vdYUnXS7c5iZaf3H3pS9/vdvFe/tNFk0r7W1to2CgSm+JaK41FwRQO9qXvO0Ca1Iz5HA6Gr72KxDUGgbAQomnhkTrnfjSeV9DuVqQFJGixoQTgTOZW5pGITrfbF4f+/31fpqyIbQhvPL6q88898zheIyd5JwAu+P1oXcoJPfu3uvatnfVXErO7d0QAkOMUOs6wqUUy2UT21FGo1mcr76mGOMwZUsTMxcdQxAY0/pmVTWPWiHkpzuzonZ98B/7//74//5/8x9MKTUEqo4IzHEG75abZgict9JY7b4ZENXsM6UpHXP6yf/6P/uNt3722154n3kqJZNjDI0dJ+JwfHTt8JoBIQoga2jU8jRNgGgpDQB6Fee7JVJTllhMU7YyAxJcKhsHqjQ09r209LG3fqLe2C9e/spvf/n9SOCGSFABrAizuND6ZuvPEHhN9N9aCyc9WWu6f2b5MKvomtU6mHvRolpMk2k5HMer4xT+b3j+o238xaBAm82ubTZmfhyO14d91zVE1Pf9G641WAKdEEIbpC6uUkqV9zoejzXLV4/aHlw1Xtq2ra++Rl3V01d/UFF5zFx1LBZGjbke0DQN1TFZTF5VGQsh7trzp5+50/cHN+y67h3veOdLL7xw7969vj/SU/ct5U7k9ZdeDu5N0zJaOR7INPXj5eVlCdFRECiGMDochtGjxLahrjHwqVgIjbLVe75///7QD6oKQEGCm9Y0iQMUU1UtZjklL2U8Xh2vHqTjAU0jcdtsm6YrJ/IJ6wC+4diervF1tJ+M9N/s1QAA0IzXckdwBkIT98YYGgd3S4ZCpmXIUDSgzDVWJEA0JEJGYAAyBXAwBHKo8H5Uc1MvCqlASmWYsB/KsdfjAYYBc9actdZSsApYARKxCDEDEyDeSpi84TM89nc8MbKrgSZalMm+5sMXi7jGTQ6EiDPM9Ik7qak0v91+vL6PulbXbQcA0CzluOZwF3xuuXWj6+PXcv68kzA3nPGs6+ObGRFU+p+KLVsbxmgWIkUDV1NzxZnjxyvMr9YIVuvPJxoDQKxl3pwDoZqa46RFRBzgMAz76+tpGMzpzr27U0qOvru8eO3R6zvYbdqYxmno+1aEN7Ft2nEcoaRd0yXkSAyluGqxUhWOEFFYGgkgYfRiZnMFjOhwOEhsa6A7+9ST8KeGMCsApjJQEiERg9GvfvT5H3333/rie77ypz72g7/9xffUsveKuT5FfwGimqEAIih4ySNp5dPXIU2Wyzs/eW+P15vQQlFLNhAHhSaGPCoTW3FCBocSGmebptHdZ+BXEEQkEXPKpXAI6l7cFbC4hRinXFi46DSUVLDQ6H/s579Xf2f54Je+/gNfeIfFgkiMgishIFN9qeBOvEw8NxYCNLVc45haSHdAAD6dKjerBs1npb5ZbVStysfpOA6ep3Gc+nF84aXXPvWZz/NvtRRj07S77bmqTVN++PBRbOJmszkejymlN1tNq/2qldi2bbKWNU2/Vq0rom+OkJhxQbJW0ZjqD4ioKojVfy1p9AXVWr8rpeTCzbKZrkF0hZYy8fn5xVN37z//yitP3Xlmtz27urpyh8OhH8fx5VdeAjNLOfVDKyHEgKbH/RU5TmOfps5Mh5TLA2rPd7Jt716cUxsOJYVNm3MuauZGbBIaIhEOx6Hf7w9nl3fcvYZ7cyBZ+VRynsZRx+vxcJ2O11BK2zQhdhQ64Ch4U64/DeS/ir16A6N0Yve/ysdtBh8iABAgMHms8TyAslkEMNcCVszBaREqmFPIDmbqFVJhYm5VkA/V3byY5Vr1TTaMUz9wP5bj4MPA0+ClgCqI1MY0B3BADgx1Y+HmbuJuiHST4v+qTz4XOJa/zhl/AGK2J1oH4Indgy9F4JtckIODPwa5WQ3lTeQFNoM2nzhwYR+7ZWgAkAAWIgY/2QE8dpO+PIijVcY4qoH7olYGtsZ4sOrqISy4TkAALyUvoH9AN1Szmax7dSDmjrboPc0C6HVylEJIRYvEqITgDsRQFBEP19dZpHYVSBB3m6bx8u5dCdI07XAcImMyZ0IEPNvugshk3nBgpK5toGhJqeXOka1YP43mLsxVbATACTE2jYio2cK1MhuLnDO4z+SlDmpKJDNPJJIIllIIqW3b/fWUfpf9/d/1LwDgr8BPf8vLH3CDkjIFqh6SmVRv0nFqMMt4mpppThOzpGl0L0WTZRsUJu7ZyYqSg/ZTE8Kvv+ML3/H5d7OTFzW1GBuMrG6+IO5cg8886KRmHGQ0NUQlNMKrYzEzJHRUjEgNlim989P3//zn/jhzF7fR3RCAhGpe3mZe1JudKFRv7dUOIi4ChLjyv/oN38kNFGJmOMS2aWuXjalplXoBKDmXlPtxfPW1hx/7zU8cU467XQih7baOWLJePXy47TahCVXXd9lCvcFMRlz6imv+QXh3djYMY865lFu4jJoI2mw2h8NhmqbdbldRQ3UtVMYhXyrDu92O0cdxbNt2NvcstIjCmlklMi21ZGgWRALL/fv3P/lJSil3Xdc07eWdyyn3w9insQnCY39sd7vgClrANTC7hBACITASgRHRZrPB3ZbaJqNv226y4gS7izspjcWTmpdSYmyQxqvr64s797RUq+jm4OZZNU9pStPQH9P1gzIeQUsjIswxNkACLAQ3ojf/2vD/scOX5I/fhgO82UXmE8DdgRF9jqLE3cEjuSMhuQMxslIBwxmmjl4DKXVFL+YIRm4VaY1mZmBWpQw8ZxsnHScfhtwfvT9inlC11CDUlJfAlQg5CAkDkRMKkiM5gFW1ezMjJlPnGeQOaip0wg+qTg4AOEuSVmo9V7zxCHYaL6wl0IqHW/sYwAkcay+luSKieiYidKclDHN3QiRmc3Sw7DZH2gvxii/FalvaFGGpQBi6kwMhYeWmnvcZxDNFD1EN3B1n2igxc3BkEqyFdQBwYHAHNwR0AmQA0lL15wB8pqJDsDUdTFDvcAkG3RAdEBlcCFU9lwzEtmggkJlqAcJjGjVEBQIlyD7tByjmkLxkRGi7AORuenH/Lce+T4chpzF02xACdhJjpDZOw0AFck5FC0dMpW8wsZqRTm5TpbUEOB6PacrA3jA1UZAABSedYrsZx0m1aMkOVqML9+BeKyEKWvI4AlggMTBBJ3C3DD87v+sPvvhuZLI8NMKGCGAxUM4F3OpkcnPQsaQszMiMZjpNzkRgWZN6KqbTlI6Oph5YCFHI/+h/8RcB4If+9gf/5z/+2yNKIyFYpLFhDhVdGptGU0kpOQA5mPvxmBUtQzGCj7//K+/+5P2MCowOwEVCbpBRQmjbDbZtIReJEoREZkQdorsigqtBvaa5laJFWZBjlOrfFAhZtSZDSp3ZiFjFmYjIK8G0OxqQo6YMYJpTKlOZxjSmPtmLD/KvPv/lL72yx9g2IWyaDZi7lb4/UIDYhq5rX3vttWEY1jVFC79epVlFAkBLVZ1YyAiGnBFTjO35OSPuh2FgxpxrY5SSYNY0TOMZnEtorB9zLpWSMaVkCy9kKSXnJIRmxax2QkS00jASUlM1Bip8PggRMaA4lOnw8JVXS58tWGhwex42592l3uv7R3uYzrlpt/eEzaY89X0kAuTtrivTiDZ1ITpzbIUZC6ECeGjGnItz2zSes3AsJEPKJXtouq4r4Dwcxs1uO3l2ZK+yd6XkXEo/pKur8XBA8KZpYztLg4VAxG52Ixy/wn4QcdW2q8v/xOrbWiAmojkhDOBL/vwNs0DzpayWEwnIDWvpxxARWCCCOjpRLI6UjVKZ1JEQnYBJqS49L4yMzARAChUXxaCgSctQ/DBxP8Bxz4cr3F/Bcc+aTBOY1n6pKMbBKVb+JCYJJNHJzYvUJipEZJ6FKBGReJbMWev+60+wW0+5tAS8gcdb3eX6l1O36ebrWevwvWF0M5+Dt7pqV9+7fuAmlVQVDk52MzWCm4mG9I2RvETk+MYo1dp2XZWhkLnKAdW0ADwRkbnfIoBb/0hOqsV0hgS4u7khgFT/VPMpEsQdJIzjQzUz8JSNg6BmFB7GAZmF5MVXXo4s6JBTtiZuNu3FxcXV9VUxZCNzczPygIBt27Wbzb7vzVSYwX2WiyI3AFPLOV+eXxKisIzjWFQlVJnoKhzJNQhg4rLgSEopTZRKCamqbooEW4K7P7L7ge/+rsPFcRPCKWRrbQrxJVuIUAuhdXunpeSUkuWsqo6O5Lmom+acckqfe+8r9VLPf+Cl1/76I1KPIm1sY9hU8PZnP/Tgg596DhxSTqamuSjYmKcCKo382b/2NwDgB//eN/7gP/xGYnKkAAEQt+0uNh3WzCKzBOEqOXtT4aCq94OIlTXe1KZp6rjxpR7gJ9IXFam3hpM1Hgeru1A0M8/ZzZKmlFNKOeUy5vLoevzoxz/xqc98Dpvu8vJO7NoyldqDPYx927YhyDAMVZO9JnPgtpa1mcaq34msxT3gMKSzs8s0TjmX3W7n7uM4LkVpE6TKJl2XQ60DT9O027arNsC6CkopyLhCP2v6F6Hu3xSXJbaG0me7M1P9zKc/HSQA4sOHD770xc8d90dGyNO4n8b7b3mraxn6vgEAU4BaFgVCLDlvuk7Ux3HcIABAkJAQm6bdBNGcKEBxc5opAwyAQ6AgV/t903XF0dBVs5nmaZyOh+nq4XS8JiBmiaEVaZiZSQiZgBztljlas/kny/Zr3Bb4SSXgDU9YrwwzLgarNgAJAyA4GCKpQWBiwmiqSCFUunGfsZ6OthDbzcbDrKhOWceJsto0lX4o/dEOhzz0wRVVwRWqFAc6MJAQBZEYSZb6qIEgsBsAIjFrUXdHwZrUXHeypwv4tAbwtYzO6apYP1XNwjpet/7+NVz19A3Z3EY/A4RxgR6teU9ErGlKWBwGnTjt9Trrz9OnBpjzUzXXYwiByHDZ2J9sdJ68Qz9pGzGbC/fuAMunasaAROprVvCSUnNxft33/TAYugP1Y49t03R+6Idm0wHi8Xjc7/f37twhYQfoYkPmj159DSyFZhPbZpwmOyYkLpZps5vGyVQDsyBAKRSCqSJgLgncmxDPdjt1cPcQwpgSS6z9/8xU83iIWNEdjyVMmTmnbFhTc3799w4/3f/Mv/NHf0StkqDMSFtcQOVPuvkKw6gsI5UmmRBI2FKq2R11e/vzl9//d97/ufe/9v1/+71FTDUfx0GmnuCqbdr/w//44wDwB37sAz/4N99v7tVLIaOCAePnvvFh/aJPve+l3/Pj74scYwhN1zVtR8L168yUfa6EAUAppdT8GN3M9Gora4akvs1TQ7zAEG6m+umkcncAd9CiOec0luSISDLm8Z/8z57/tac/439+gk/z+cWFhJCmCZ2IqJZwK0T90aNHKSXmNzYuoUbfyz7YzNq2vbq6unt+0fd9zfaEEKZpMjMH77q2lnmri6p5fzOvH6xso4urppQSRanooHUmE5GpmXsTBQD6vm/btj54LnnbdE6Wk6ahv3N+FpmjIMfmxf642+26ELZN9Jyymjh4Ucs5hNCEyEIA0G037qBmuRQvxVAoSNd2kxm4VU7jIDKaQZBi2jH30ziWrIFVVXO2lMtwPe2vxsMjssKha9q2aVoRgblUg6owq4PdjuEes0iPoSKftD+wvvh/nbdY/5XnBDUBg6shEzkDgG4MhIAQg2ECJ64t9VapBdzRXM3IHdAdjMwgK0wZxgnHUftjOe516CGPNbemJQM6AxEREJU5yckUhUQcEc2JUFYY75qXX631mtZ4zA2sEdAb1gweGyBcnn+9zrzYHB8b0ye3UW82pu5z4xWeklAuhnXmLLx9/qnTWlfm6rfxBLv9BOZ1vtQcQbkD1ILzDVPpkw9y+kT193pXiKhmWntEkBFxnCZHIGYGzwBEHGLMqkBsbH1KYdMQxaHvA243280rL78cWDabTQh85/zMzMb9AdQ6tqwGzEVzK3HLTXBvYpcIwD0QReJA3DATugdmYAfYdh2Zj1NqmyaZcwh9ylVOpZIj4VJa9CXPRkuXRo3f6ym5uIj8wi/+2u/49m9//9e/UzWj6ekL8hso8A0rny3qIsysOmOEEIGEU5msmLo6wvf93fd/T/56Lzq5GYGRjzqB2cc+ODPmf/wDL3xr/1TFrtSOTkck5Lc+f/59f/vdX/jGR9//4+9DIRTGIBwEmUkEmf3EZK9Al2UCIOBsU2v6VkS2223d7tqSgfSlc+pW6mAJMsxMTdENwA29uE45G3PK+vy7XvmZP/AxAOA/D3c/vEWUXDIzdc3m+vp6s9lUV1SbMNYVul68jp6ZbTabaZqapjOzEKiKDTRNc3V1dXl5WT+73W77vmfmKKKqxBxjrDu6dbqGEIjiYys6lxyFmibWmvBJnOuIlHOm2YlLKWV7cXnnzt3x0DdNBzDW2tXVo4evvPLqnctLdivjGAnPupamPB2PbdOqKgHWwNTBaj6ZRBTcwUsp0raOaKqRJY0DuaO5sKBmJgZACaLjdHXYh+2ZatZp9KlPh6t0vCrjoWvaIDGGTjiCw03rA1hViFrX7I1NWPVVbkejX8UBnNqTN7RX67jNnhXQEWr7EQAgE4pO5MgEjBgUgqML1KQpWEUgVPo4c0eqFeHiU4JxhH4s13u73pf9XvuDDQPkXEPcYkoQnNiRjBECQxRqIggjobuRubhjbQerL3iduOA30KC1xEpEsMAubel+cr8hpFqvsA7iakROI2siAj9pDVs+a2Z8I9pwYq9ncOhMugnLB22RIDltU8TbnTi8qJ7WnCmerHk70cLkRR7ATxg/SilWHSRhEHYgM8NFiWIdtDVRVsdtnSLrAN7wm9qcZgOYi8gODojmVtwNYH/cl1pUJz4cD+12M5ofyxS6VtrmbV/3ri+OvxWiIFMueUqpaMnH4bzbiCsxZ/LJM4FthGHKCBZjpNEDYgCIiIEZUXO2CgU72+zYsWEh8gK2CoLXjXkNFXNJVYGrWv+UCy8TxsxEeJqyGajbo8PwT//Zz739rc+FAKImwo8ZegBgpnUmrDEHEUnkUqCk7ITMxEHMEiNNORlqtpxLsqJoULWp3PTeL8t3/pVnX/jtx+/6q8/2ZcCCSDi31LM4GJr+7r/7bvmHAYkpisQgISCTIRhBFCEmW9rEa3arTvW1mAQLeKZOaCJy0BXbuu4Maj1pfe/VX1bIDTOrq2pRy8UKEI1TGXIpP+vwvwUA2PzSdnd+WQei69o8VdadeQ73fV93SCsMel0U67dvNhtcNLMQcRiGnPMmhgcPHpyfn1eWf1o0vHLOSMTMtb93XcgiAjBrHdfVREQxxHVF0PKpqudcBYFhadwpqbj7lKbjcagy4+Dl5ZdfjCEEwv76atuECBjBh/11ayhmZBqFhlyktjAgeEUfBGERiNGDuBs4U1WKNYCsTIZuAVlI2rYZx7HdbK4PhzOOpqkMh9JfTVcPdDgKQKB5FwsL+XadhLikgB4zVnVNr4ZbF70pXHqeTq053N4x4Cm2ZfnLOrVuzONCM2cI9XdHACZqGwhiRE4TCUJhNwJ0RKwc4l4UmRAA1V0LqmIu1QFgP8Cx96HX44FLIrA8TkhARA7AMWAQZ6ImhG2HjYCQ+SxYKcxhNbYrjMHdGfENkTOPRc2LZa8Oag4oVkN8Ogqnc3c1nqdm9LQksNqX+X9xbrq85Xtv39Wp2QWYlcjWi6xv+okvvXmRq0Nac6wigoLkhIgkrMWrhmWNfuHEya23+lgMsHoyr+g7AwNHFkT0+kiCyUrRCtIkYnn19ddCjGqg7gXwOPSJkbvure94x3HoD4dj0waJ0rbRETSXgCQGxDRZociaycZMqgzuqjlndCcALCoApFa0xBimogRQ0eyBGAjQEiBqKUg3Q7S+wQp/qhaNmVPJyyNWQQtCEBb6xV/+9e/8jm/90De9b7Usa1FxmTM3U6JpmnEcZ8csoQIFoDh3rYhMzGmc5j4sYShkZKbFXIHR3MD9O/7KffyrT7v7BAkRCYgcyIkdCFiQiwEDxRA5CAVBYRCmICxCwiuZ1bKhudkEVxrz2g4dq8KXmlmFid0cazrx1JQsi2J2/JrSMPYp9cVhmPJQ4ItffuVffvhXokD7P93e+ehTzoLgIjyOo5WZnGMcx67r9vv9k3O+XrmOW0qlbTfLkNbgzNxhmhIi7Pf7VREsxqhmxaztuooWrY6tuj1VrQ4AlsAIAJBumTwiqs0rIiwiWGEkIjHG+lYfPXpUkoYQtm13TOlst+lik6dUUoohnDftWdfpoScSdGNTqq33asWVAiFzMQU3EqYYhqIBEInymKgombk5F+PgKuRqEXkyCwDjOBA+ZNd8vB6uXx+vHzJ46DoODRIgOZIRI2CFoKH7reX/VY5TO+YnUfzNX762GsCt/zm5lDsYIPiM08QoBmCkSISKcwtrlasHAgRBAjdQs5xtTDZM3g9w7O2418Ne+wPl2rJe0BEYkbkCzzEKtZGaoDyjKdEBi8npza2eara5b3I8Zi4REQBVZ/jqY6OgJ6qNeHJUsZo3nNzrt6x4+cqrUH2Ur7wfb3Q/Tw70+tVwslBPf8ETNfl6kbVh2N0rfN4RbKEmNwA3k9sSyje+7fYD+bJzJ5yFngHnNkWYDY0BQBUfktiqiLnnUhTD2eXlsL9SREU4Pz/bXVx8+Ytfefrp+5eX59k1Rrk4PzMWHqZd02ZL27vnV4GPJUlJ7NpFEC5DUgBnd8sZVZ2xbULXdQ9eeYUcCXDTtI/2h3jWRYIQAowJZl7VORisY9I0DS3ssHEb+3FuSS1F3cABihMYqun/+8f+zm/+yW//2NOf+Hc/8v2/7cV3IWIIoe4t3J15zilXzSlexK3MHZlCCMaguVCQYAbgUHsvaoQBNpO8AORstb2l5t4BAImICWZUHbHEEFtEYpIgjcRAzAauqhJqd6WjGwCvqNz1PZoZM/miuFTfLFXiz3Ijw1s7p0opTdMI3cwZAKjmNeesWpshMqCbqiFcXx/+1Ud+7cVXH4LEzS9fWCOVrbbGv0INMz98+LCKPtbWX5zhRTf5pZzzdrvNOdclW4d0NSuqhmBmWmUd1yLBceiRxJeczypdWXd7IhxjvL6+9ptNv1dFdli2OyklIcYZSkDFbzr8ReRsu3vw6sNaWnjt1VfTOHVBhCC2zfHhUdrGS0Y3L0XALWWgwhhFpOQ5/1Z1dgxAiJjA3eqOFa3K6zqmQsgNS8q6aZpp7MNWvJTpeEVWpv2j4dEDTSOEUBxTsSbWhhByhzUUAQC4rcp5s2DfxBZ9Lb/Dmxyn/4TLVqz+NKiYaGdlZDQARzIqQIAFZ+KHtfqiaLV8rIbFoGQYkw+T94P2g48DlOSlEg4bzquAkRCFQxND13ITjdHQGQHdQU1Oo57VUFa1gTlJAXD6y6n7WlOT7jZ/DgBOsEPuzk/gahZLvWwLwBcrP0OMVlN+Y4XBgWHty4InxhpXJE812rU7YTFYa9+mma2dxusjw4kLgZNNAyKycNZqAalSYVcQj1V3t0ygGxtBpKcMo8vNAMAcOWJVkoFFLZcQZ+bR7FpMHTjlJBL2wzROU2jiWRvz2KecAeDq6tGm2Iv9UdFMsz37jKRM/RjO78SL7ejgzNm1jSJMTK5WiXsIEawUArecm01X4UA55VwyITZNo4BqFkIIItUSocTa/l5Lv6sjZ2JhdrtZPEQIIIikbmD2hfe9+pvf/I8A4K9/68/8pz/xpwlotf54km3vuq52ls7EqEAhIMXIKOMwTlVJVoQQmNBNl7B01vQLLAigpZSqvFbrKMzIgAjMMYRWQmSUIJFQHBCJY4ihCVCBWGt7pptWHoF5Fw+qRsTrjrYivnye5zdzT4QRa0Nc7VmZs+rV+o/j4A4pZ9OSS5lSOgzjftAP/6tf/dyXXnIK5xeXEps6D0Ngdw0hMsrrr78+TdPl5eWDBw9sadI8jW/W1dc0bc5asm26mDRhjTPAzYuDV1YfAKgOuEYzgK6qOZemaat2JjOnNE3TFMI2xqimMcT6COYKyy6n5k+qO597IJiweJ3zm9g4QAjxmaefKUs78aNHr59vOjcf04DgVvRwfXU3dGgGBrmMDiiRBCm7F1UPEtsGuw4Q05hAwjCMLYkgEiEgghkUpeACmIpJi2WYcOdkbmnMUz/sH43Dng1cAiAboHohR3MCs9rhOY8n3NCgnb7TxxzAaojW0xaXufz9a6gBnB6EK788OM5AM6h6IsgkYFRtY0XlI1WQb+3LNAUkMEM1zcWmrNOkw9GHow69pYRmWFkn6ltDZBZDBGaSRmJDMRpRtaBoAKaCpuuTC9EK2iPwymtfiXmXlWJKaOAIwMwl55rlVQWkaGYOikhmZR3MNb+/DnZ1GqcGd96TnNhluJ04QwCstwMIJ9lPv72HOAUwwAJYxSoLN297UN1sFiaDuXUA667ZicgJAeZGLa8KNhzca8UIce7+9dPbO50ZeqKmefoTAGwGP4KIEAsiIvHxeCQUBhjH4yiIXejLGDZdOkx6POSSH0zDw5y9CW9929sevPDi9QsvcNvFGFohdN+4o3nKSXXKuBn6gQKGYhJC75oQtzHimDphJQuQW4b9lBAAFFppN3FDFBQpmblRSToOYx1SEZlUEcjAK0IjlSJNbGK0IblqzXY5ghmYO7MT+TBlFs4/O6fIv+GFdzkLAkBJoA6OTmRQyQGrYKQA1OBXwEIVuXWHbbtlGEcHVc2p1gWx60KMkVkAPKfsxVxBp6y5gMOUy6QFmSTEmq0yBJJILFVNO6CQEkcGIw4kOG8rkOrammfqauZKGhlXWShDBEMrJQchs9Us1uZwKGUSEXBwVyQslhHBUR0gexqn0Qyvjnkq/NHf/OxHfvNzk/Fms+mazq0Aetdt6k4ihDBM4/5w2G63RXWcploqrA5S1YhIJNSdWSnWNILEqiWVCRndzREksk7FHA3o0I9N0xTLRKRqaiACqkoYwIkpjONYdAIsqmWapqZpmHiNnAC823XTNK1VsRBCrRZ4hBDYkyE6WAGPKeWr66vnLp969erRHl0a8cAupKVMYwqIZ5szO6b2fNe4T9OwOdv10+io2VIBoxCxaTJxtzkLzdmoQBhT2u8uSBAom7uBFmbOaWq6hophcegTHMZLjtevvUyQ0zR4GiEEEZxZq0tCRsvAIUANvmZhLa+1/BrerUvV/KYn4NT6nx7rPyEiuN8Es7WDZLZphJVl8DawxZbTEQHmjHH1SwCA4IxEKOTkxqWoueW6cyZgcaGMXCBPSYv6mOxwrVevw9Wrtn9kxyObCgibA6BlC5uAVXkmRt497fHSYAMWRFjcxDSPx8f1AGCJZL0sTfxrmAyIhHriI4kIHbCKGNRTnlDSOXWMp1FMLd/Syf6g1hxo4XuwhaRouc7N6K+h91dxuaf78fW0GuytOBZ5gg179R+26gOffC8spYXHvvp0B7DWBtZnx3lXrsy8adtpmtTVzFgiMaNTSalruz4dGeFw2JeUj9eHYRr6KY2lAIKqPfv0M1/+wucZKY2jAIA0IQiLpHH0wBDFzYnQUonIXYgIFqXbdhvNqoiVE6BtG+k2iMghNE1rqiIypckqW7UZ6LJ1MwMHJIwcibCoalVCN8sp6aL6WV2pMDZtk5MCQlET4aaz9/4v3/bD3/z9vU+7GLTM+fWaValG1swqGe+8QnTeiaaUaAG5p5SEMUbtuk3NQdW9SM4ZihMgmkPxoe+zA0ocp5GEJYi6p5SKak33IxGzEJOauWkF3iGiIOFt5Vczqz1cQryu/5Uaj4Xdb5BL7ovm4Pz2a7UFagPmjBSynPPU98Mnv+5F/xn/lV9/flJst2dnZ+dMVMwqTLMy85hZJfxpmuZwOOgij+onFQVfBhCWYkC9wxhj0zSzch+zpmJmRYu71z7eZd6CqoYQmqYNIYxjXw39ujybpgGANdePS0a0PnI93K22jBBxzhmBtptNhXjde+qpV159pQ5Q2zQhhP56z8xiSIBRhNTR3IrWC6KDakFEkWhEROwGU84Kkobx4vwcAcy0pEymIuwFhHhKGYRrA2sep22zeWSqJSFS122dgJcNIkml9qq48LoYcU0YzHiqE+Af4q0UzVcxL294zsnfb35/s4uslqTe0KkZMTASZkQvgFVfrzZjVm2xnHwYyvGox6MNvQ2DTZOVgma1dFvTocRSA6Cm7ajpODTIQsSMyO5oCjndsoCn94rLX776QNRZfnoFMzvFkp3mSW5vn2fwdY0317+vgPG1AHB6ndWermP3pvf/Rvdc1wYt5H+rL1n/Ak84/PVLF39ws8M4vec1Ilg4IG6y/+uiRcTa0QMnnqaMBQHSOBKjAJJ5GScoCu7FDMCJZLfbEdGjBw+aGLiUcRozlK5rzu5c9EKWkwnt2iZZKqquWbzFYg0ylhJZClHt2VdVikFCIOFSyjiNZyVvmyYiGdGcinFPKeWSJXQiXLRYLk0bgJCZM0CM0d3crYJhRMAd27Y1Hc0MCcx8s+m++Nde+Acv/tM//Ad+3zhlNEVzYEaawSow4w6JiGYymTwvQuaaliRmCQGaRbJjxcaklHLOlgsBkiG6S2imok3XknBxZGE1m9J07PtcigMRB2laCcGryJdEImEOzAz0xnNblmKALah/IiKmKlBXZtkcXW3iKXaIF93EcRrTNByPh//LX/ibALAdSf+hx27b7c4QaRzHEMIsvihSIf+Hw6Ha6+PhUJfGaVh2GnvOUYUIM1ecz5rTv3ESBVS1Uv0gosOM9zezruumaVLTpmnMiGmmdwaACvqsD5VzXtX06pqNMfZ9j+jTlNEBnQQxTTlIHMfx81/4PBJtdztk9tpLCEgAEaWTuJE4TlOl1K7tdQgIjsxISA7ELISsxZRsmIazO2emKid7dBLmKIbIQmp2586dcUpte37nqaePx0dBu1JG1ULEWsw9s1Wh2Tpo1Y0hIoKDkdVnXAcWEd1ubMub2ZN/rf35KjbqDW0LEZ02qJ7cD7mTQUUi156xUnIp04D9AIeDHY/WD5BypThDYpqp2glDACQjDtyEZkNNw7UgXCWqrXhKNo23HMBqEM1M3ggb4+6nC6Yujtm+12KF3xD6Pzk066Cs0/TJ0amAhFNA1ZODuyaUv4qDXY316oHmESdc13N1NnS7SlHPvwEC4o0uwmrT14s/9iJPx/Ax16KVrGJ2e/Mg55yZREsx98AixGmaAnGvZhWD4ahu57uz436vuTBAydp0TbdpQxuGkq/6A4E76JnZNIzIEVTLNLYsAj7uD0ZszJWQIGtJQ39nszkOw5gm5Hmj03XdqNlyQYBpHBEgMBuYqYpwzSoyz52obdsCopnlXBCpqLVt3G63+/1xGXk0N1X46Z/5+fe/9z3vecdbAiKic+02hxv6v5qrmV9BS9X6cAwVQClNJKJN09bLVgLtnDPLJDmvHGuenc9iY+7EsYkKld4VN+Ddbkw5p5zMXJo5r72KQNVu3VPYFiJWybNSCi6kaafvFPyW8T2dWrh2/wJM05RSWlD8x0+888V6Tv/dxshddyZNl6ajiOx2u+PxWI3y4XC4urpy98vLy7krW6TueABvHGfFYlYUUA2iY4xVvUsXlaFpmvREmmmcxhiiiFTgARFVoFHf9xKIiKYpSxPqPzVN4+7Vo0ioWKMQQqijt91uq3twRxFhkDRNIcYYYwjN2cW2DSG27TCOKSVwn4YRzZsQzzjUQVS3Yg6I/TiSsHNF+nAxw1q1DFKAOQTMqZQiQkwIJMBmJUsI3HYU5agFJV5szq6//OXNdpvKXWdWnaaxB9OcJncPJKDuapUjHdyBGZ2IZziHuzoAMtf3B4i+FF0fMyyPmYj1nDf7e53nT57z2LH+k1W6HZx/AiASkhoqFAB3QDcAM89qqZQBhn3pr/W4t7GHnF219vNWwgokDBJcAkjEppNuCyE4oTugKYBjKTiNMA5SAxY8xVzOuZ0bbPvpMyy/z0ovQL52TqkqUiXJunnCU0O/5lWIbujn1pm9+p51e7tGVbdGamm/vAm6T4CejxlfX7qCcamGrQpN65fS0sx5+uIrL259gjVNsZ6w9kOdhn6PXYGWbp36FTMztFaKGFgdQ3FjEQRFpoqnKTmXUjIpMLlqjLHr2mlKhLhtOmlbCYEij6nfHw9ZddtGjiFp3mzagybTEpgFsEwjx5hzghjVLca4pWb/4FEqeZympBmdOAiLZNMqKtSEGGNiBCvZGGJsCBGZ3L3tGnBQVeE5uSEixTUEOjs722w2JRdCqv3OAJQU3PPf/fF/9B/+6T9xuYmBK4QTCWZqAT6hRGVmJCEOZiYBYAlFmbgJoWbVRETEECeRmFKyUsBU00xN1UkERgVQnEUN1Ixj05plLaUUIq9WrxpQVRXkIBH4Jt1nZm6g5uBVAOTk73VyuhK4+80bP7UUtVti/TkMwziOYypn/6q591/Gh9+e8D+B2Habzca0MkuHGGNN/ugiw7vZbDabzaNHjyrP2kx7sBx1o7D2rNQptJAC2UrMycxYu6xzQsBTquq657iJZpzqx6s/qzdfvci8V54LD+LuMYTdbqe5HI9HUwcnFj4/u2BEkbjZbHLW6zSZ6ru+/utfeenl4+GQzy4Y6eLs7Jzjo4ePLu8/jcJV75sJSQSIgAVFMAQIgiJTKRaFouhBS8pdswUrCJBNJQaXSE3gro2m2XF7caFf+XK73bUwYdNYyWnsyziO/V7TWCu0qopVrmdu4XQ3h7n2M59AS6F77edYhxdOIvonLeFjf19jgpk2+A2uc8v6nwYQT4azyIQBRAHQXB3BQBypOCTwKU+HUgbLI2lOJRFCcXBVAA2MEiI2LcaOui22GxPWqpyJgGZiOu735XC8SUc89hirWV8t7GyUa0xULfUTMS/OhrvGTfCGx/J1s0tYw+Qnj9Oxfuzva8S9roQ1WIPb3mK1Nb7c83qmLX0M8ERWpy77J2/ssevXy1YftmbD1u9azUfOeY4sZpwJY23JYSruWYuhO+GQJkOYcmIR8JS1ECHFeHl5+epLL4HDcOzPzrZTzq7TdteRAwO+9Zm3vPLSC4lz2HbTYVLXuW/O3M2aEEYzdVDVlFXd1H3KSWIMInWp10IOI6mqEFXioLjdkNRxg1CtJCAzi0g/jFapnBwQ8f79+6+8+kCrHDli04RcsqFkL5/8zFd+4h/+1L/9R/6wTmPXdaWkKI0/kRvFBZpd8zyr1SMigrmpKhUrpagBIjfdxkrOw+Rck7bIIsACYBI6rswflaXHLasWLcUmV2tCqPl9Fw/EMycirDHKGtTXIuGtRhZ3R8Aq4E4rBdAS9a+rpsrq9n0/DEM/jF9+9cFHf+P58rcyFwAOm8uzIDxNEwKcnZ0Nw1BTgrXhCxHPz89TSsfDAZZ0fO2zNVVcXAIs4QWdAIRwbV08bbxYHmFNVdVrNk1T+aXNSymFmQhvnA0i1gbjnHITZtKI07BMVSWKqlJsRYSciASAzIqpjnl66ZVXcpq2u/Occ0TsmhaKOcJ+HHahEUREGTWbsZAIggTGJhYiYKIYFMHdiTnn7EXBdC6tEVmgIsxNnCV7glzef1oZu/NLlz73w1ncTLIXpIlQdQK3mUsHARYJLYAZ7IKIq6wrgDsY3IZp/v/78zFD9+Q5a8H41IwsX++r3Vx/n9klAQDdwEENg2MEi4qNQ3BlzZaAiFkqRZBIR03UIMBMTePdxtvGqbYWAwCwG6TEmoMWObWhp8dp/vqWh5h7Qx4vxjIxIiI5AKjmxzzn6aAsP2/WFbzJ8WYOoOYi3uyDeCLxUx9NF4YvInK70bpa5/Rjhr6eXHfBb3Z9XDL7j9kIOlmWAFAJ8Ymo6IwfcveidRcCCJDARKhrd9BFBQ9t0219PDysD9g0zejGxMdDjw5m1o+DmsU2RIl5GC93Zw9ffrX0o3Vdn6ai6ozICIYOaoZujICIMPTDoaScVYI0XTcOEyB2uy0qpGlC4RiilTQOPQJ0bQtUIfZGNRkF7g4zGzYCM6kBugGiqj569AgRweewsRQzZM0lCv7Sv/p1/z3w+f/19Td+5e1/7MPfs8YKcOLIERGRkXgtCwNypc9GYACv8y0EJtKUkqoJosQgKK5ARCTBiRgduQURVZUggGgAbFq0EHcpTYQIakzMzFJpjQnXxjc+YdSBcrMpPJmNaGsudJmZtiA1a32iNuJWCP8rr732689/9uOffmFQL4Znu7PNZkNgjHZ+eVGj/pqLryXfpmkq/F9VJQQiqnptZoYnFax13uLJftqWtrs5Clmkfdccd430c64szc3Dh4+YuWmias55rPu89VKLNgAz37TLVvVEnzfuoZblc9ZnnroLxUsp45TOz7psZX/Yo9oYpjRO5+eXu+12eHS12e2UwAIbOCo0MY7j1EgohMRMQsoETArgIurWdZ1rLjnX1BUxSxRtG2uYGmEJQOQkZ/cuFRmFKJbST11soSiZgo7TkFLR0ARELKUQyRr2ud4s5PU9giMtMTreDs+/lt9PrcTXcs6t/32DLAsAgHGFGVX9R3M2CA7BoQXcCG0DbaIdyAPNAARwCayBgYlilE1H3cZiC1wVrwDNXS0Pg00T5HyrILnGvLaQIqwl2Zv7rMNnM9Z+fRI72QEsxhYRUfVGE+r20BgtgLP6Z7hpOphPXL63Bmi3Bm61uaf3fPqvq/legyOfWUJvvHG9xdoJ+eQm40kHc2q2qrHA0+pITemUvI7nNE144g/MZiXEmlvoulbdBaCqTx37fkAoqup2+dS9KcX91VUhyqoPHz3MefI8dSwAwEHatiklx20HRV994cXARNtue75JVog5tk0oFW/KLCGXzEgibNkdQFg2XfdoGDebjZYiwFRxvYSmc4mVI9fNigQh9CCSgExPPSW6aSn6jre/rXbzmhsALrlp1GxBYiqDCPzj3/fR6Tn4jec+9w1feuu3vPw+uF3SB0QHFJE6H4jIzRABwc2tGJo5AEqIZk4sU8rTNDl5TokcozQhBJTgTORoIoiUS/a6gwZHJAYGhoq2dDQzFyJENlU3I5ZaDDC1SlE5xzgLpO0mUll4yussON1ZmrmZTtM0jmON/V999bWPffz53/zMS0P27BA32267DSKWpzaQMF/v9zWcr5rssWl2ux0iXl9fI1HXdXW0q2JXztkXNHOVcNBS1rRPRZHW0av/a0uha3UDVeSLiJummaYREZjnEmAI0dXNbLPZVLXIVfwnRq6pKkKse5GZF4iQWXIu23az2ewOV9ebbvf2t779y1/5goS46Vp2RMcQwnaz4xA5xoDoJXcX56AFSjHErmvdBJsATYAYKQRs2wFs07W1EXrstagGEUBiCRQDdE31ExTFgMyRJDgCCcfYDjxKbD1NHDuIneXRTS0XNFwo7Qhr760BLmmam9V9k4KHx1/91/D7LTv5Jj0EpzuAWwehndzArZtBgEpwEtnBzY27QNqGvA2aJA05l2J7TF7781wYglT0JzUtNqI8Z38qcttLKmNPU/KUBNDqTh4QAGeMfEXbVztV8Ux1MbgDrIwPBg6gaszsPttfU0BgCdHrijCvSwYXq3oyQOYGtlD8AyBVnEnJvjR84TJYCOBAvpTgiGZ+SgAAKCfXvMnXN7XTfW0aqCdA7fGpfC9VDQaYgzsw38hcVCs2c2GSI7mDrol7QCS+Ecg+/cXdAYi5dswDc9WGrZ2WiGg+Y88UnI/HAQACooI7SknOEmmksdfDcNgHO3/q3otXV6HrJrfJSxMlF9VJ79y5RKac8+Xl2Yuf/QxDwQKeATGoURNiSsbJmFxIHVO2PDWRoqSjMfOwH7a789huHCA6BjQHTVk1T8CIcWdw0KxnXZhKDlwbRzkyjmUiQUUtXrJmd9t2zeX55Wc/93nTAu7CiFawMkZYQmCmkFTxZx3+Jw4A733hPZWBEys1et2NQ0COtTm/vgRAtZxdlZAAyVyZ2TTVRdE2XJKipohgAEgAzBhi3SeAgblGEncjJCdAQTdBbBAxBnDwKtTsBhzjNlABVahsW+au7hmKOoKCq98Qf7q7m6InZnfTylmAwGZe1AqYlTT0xzRNx75/5eH+Nz79xU98+fVDRgUExDaENkpKIxGdnZ0fjn2l/JxSyqU4UbfdQuCkltQcCSUYIscGWKwoSnBVR3ISaVqdJhBEXVQolm0B0aznXCf5ulFe0zhW/Hx30fc9uIJDnjIYhNAYA4cICzozME6leDGMXds0iBiIQwhCXDgHCYYBOLSxQ6BH++tpHIAebs42CoEltM2mIfJcLu49XZo23nvaRMa+D3I2dJuuaYbjUZDPznZmaWLy3YbbrpCEbStMCctUUttEJzyOU7hoHQEIuYmOKMK1jQ9dg/D1NIjbputG8E0TS07IYgYBuMMGoYxaik3AIEHcFcAZBEDWrAsCIC0MXVZq+IrI7o6OAI5IDnOvYPWLuBYgT8y93eICMliyS2ufASLOPPvzp27sPyLwwnhW0wNW9Ulm+0cAruAF0YWpawFNwDIYoYGbkMPV3o7JPSpxkIZiCxJj15AgkiE4gQYAKpMNB04TpYypyKnRXB9gjX8fC4Tdb3jfvsqxwKMRwNeA/8ntT3VKi7k31Zsofq2gnpzPa7L+5O+37oZPiCfhJMb02xikGgo9meLHZedy61mW66yPsET0s8N47OLrZuKxwvJSaMLFoNzEHRLFHTUVcyqpOEAqetRkbiBydnGZVQ/DCMIdMRIXUzZ861ueefjgYd8PDQAiFXBDcEQJQYv2+2PT7lBqx7tmTCVnIkSDNKXNxjeb7dQfcsrbbavCKeVScrvd6sOrUpRjEJFU8lyqnXnfZJomDjKlqT7mvXv3pmk67PdmswxOxZnMY2KGhCGE7v/u4V/mD7309pd/5PW33b8LyKKey8QqzoakdaKbWUXeMIGVUmGpITiY5uxmXv8SY2QUhxJi8Bpg1G5hdbeiZoBEwoSMDhIiERfV0LSIRPVNmWsuZlZxdQRV1mOO5QnZCZDcDWpO3JcD3BG4bn0WZAGWUkrRYnp9da2aP/l1L7Q/T7/56S98/ssvPTomNQbErm3btq2vO8bogDX7b2bDMKSU2q5NOXGUnFLF1YQQKnxzPUrdPoI7QIjRpinbTX24tvveLOTbqd0pTW3ThhAuLu5st9tKMTQLRs27YakcovUidXWIcIW01rqx5kIBGSk2MaPUnvDIgogikqb0qU996v7Tzz391N3XX345A33TN/62t779nQ+vDoeC23tPe3cEhyPAU888t3N/+OBhuHPRbvjY9/HsjGJLLBQbdzRzbqMKdWe7w/XeGFEEGFWYBCkEEnbCqrYdo2jJqI0gBEJXRXcwc3VUZ8QoQatmkxozI6GZuqP7HGJTbfirHtTVHQBWjpwZ8/K4iVtz+m9eA3jD89/snFOTu/4FoCqguCMQIDODu811HQD3ii1p1DJCAU2umAHRnBwJ264NIaJIvXtyAFPNyaYJU4KcLSdZsz2rCZt/t5v9/mlt800f8eRYzwcErb0JJ6n508e79Y1POIlTBwBop7Xo9aOPpYbWq62z//Tm4aSv/bHKR80yr75wvaDdtu+nC2y97KkPON0TwOJU7Ebbsk4FKkWrL1VwAiTm3W53SEWC2OgKHrvNy4fD3srdt7/94dWjZDBk25x1m7YxL9OUmqb9wpe+5FlD4FELEx7GYbZKCp4KcBHigh4QyTwCQVEkmlPMUUZ3AFfVruuuh7GUwmqV2abdbk6HS01Tyixci8Brmvjy8vKzn/l8DWXCTDFIgGgnYGoiBITwL/AT8MV/8JM//cf+zT945+JMohhi1hSMiRjRagbTajZFZ3gxIg7DQVWnKbsDghBJCNQ024zUj2PJpW1a98nrp8yGnLmJLW9EGomNAxFy27QgTHPbkQJYs2ncbBpHUzWHauPJEZwVDMDcCpiCFXRFmIM5d7QM4ITozNU9lJxTSmkYxsP++p/+0PP/7A99Av4cvOfZs4f7cTJwcEI6Ozs7OzurBD4hhL7vEbHrusPhUMe5ZleISDXV8u9pOFIhmPXl1iTMbrdbSdzq1FqxVfVIQ7+C31S1luhyzpvNZr/f04kG+Bo2rTKu7g4EMcaua+oVBGku/3jdJXuI7O5WFEhcbRrGy/Pzs+322WefuTy/+OJnP9/euQcSu8unvL1jyNc6XN5/5vLichyGR+bgvnnuufbinKPp1aPcbkLTcQix3TTEx2MfGPtx2rVdd+fcRGLbgDAQGhkzAYdZaNdLYBmGQxlHdOSSy5ggJ0yZVNGMHCNx1Rez2eivHCA365dwXb/VjBRcpEMQbhBfj9mfx2wFvMnxhuc/+ZHb5mjZYVQ1MQNHIEeo7MUITiJO7OSI6ipgOYBsYn549IIUAQJ4pUAnJmKozFfFbBwhZcgZS0bThfgFsW796tp2dzQ4tYan9/2vPU5Prt71NB22HnYbwEMzL/zNjvvUYdTutjca6NsblGX41r2Y6i1ynprhqYvnsdtetwun5QQ4cY0rXMzMbFGhOfWdsGqlniBHTz/uC+GiqiKTIxBLaGJWH4dxqkvaXZqYTK/H0dv42qOrwzgWgGPxC8Rjmrq2iYGnlEMI7iZCTYyyaftptLqTVRMkG5IjK2mNZgQZDdquRQkUpOu64/WjWloD8NruX7N7iFiHaA0Oqn0xNyKq0uSIuNlsXnvttXEcSwEiRCKoTBgAZk5e5yoWUyEo7sLwa7/+6bt3fv4Hf+D705TOtx2xixmA4aybPZs8rUG1qoNpnsw8p4TAIXCUAIbb7da6zTVeF927u2tJJVkpxMQiTIAEtQ7OHIikKKAwoQACGihC7TvjEMmsGLiCegYD1ypWZkXzygV0a9461/R7xfuo5nEaxrHv98NhmD75zhfqWa9+Wxr+sTsKIZ6fn1do/2qmiWi73Y7jWAe52vdq9MdxrD29te+hTtrauFDnVc55HMeLi4tZ0XqpsdWkJS/k52tGor6sauU3m03btsMw1Jlcl8ZcZCbu+7769ZQS+IKMdO9iRAQhCsKIGIWbIBTY3cEUragDgW27lliY6dGjB5d371zeudttz49DarZ3Nrvz6+tXrrM1SM2du5cXFynl1157NRDfuXPZxohIcbOdpjS6B6Kw7UAwlTKBMYGBESExWuXSIa5ZBgCwVNDUSyn9KEA4TjAOPiUYB0oqBkXV0AkYIxuAmtkcSt+ser9Bn7vVGNdkMQYI5HB7D7AG8nVmrL+/mQ84Pf8xg3P6+2PmYn137g6EYK61hwaRWSrLvzM4O4OZILaEmxCC5DEjNtyFsGm4iUZsQAEMAVELpOTTiGnylDwlOUWyPwatsROU5E32Y8mhr/vE1Xz7gqmv06t6T0Ryn3ORdaqtPSynYIZ6/ZWI/DR1s4zQrc3RGl+r+mnwbre7Fk4dyWqs7QnkKCLyktZ/bHNAC95udSfrHmK9Pt7uRahhWr34mkCoI5xL5QEFZiZhcx80R+zGaco5TUPy2AzTaCJDyooIJMeUh1SSw1kro6pbZubIfOz7KeUuBHODEFQ1W5kbLxGwIoJVpQm9Jg6RSJk5lWwGQ05kcRkKMIMqButaOzRLtfI119l13bE/qluUWCuc9VWKyCuvv+7uAG4KhMUMRGTMCRHMoahWjSMFR3J1cIN/8s9/eXN28Xu+53f0qaiaO+5ig75kWxeUYR3S/x9t//Yr3dbmh0HPYYwxD1W11noPe3+n7q/b3elujJ1gBStKFCEFCRILSCxFQATiCqH8AQghIXFDrhHccYPgBiEFRARCJNgJBCziYJLY8aHbdsft7ra7v/724T2stapqzjnGeA5cjFlz1Vrvu7u/dmBKe6veWrOq5mHM33P6Pb9HpKq2IyEzZyZmctcqtevHcdh1KYHW+XyqZTGt/dAH7vq+T11nQCrqINQFAgRQs6ZvaAyGjGYqtRI7GZgrqrlJQHR0JSL1KtXM9CKmz8w5FzDMuagWNcl5yXle8jzP5+PD+atvP3zvf949/qsR/xLO/3YVQ3fsh7W029QaYozLssBl3lZD7RBCNY0xmjuu0vzr2ms/3XVdkwVtTlKzAcycc8bL0tp8mpYOaum7tZ8rhGYDdrvd9kzlnNtcz+aypLhme9pPbO0aSAiuhOQmpRgD5rxw4LEfSy4ECOZD6pbH03Q6930/n4/LNL2+vZ2Oj1Jyl+LDx3eI0I/jNE2Px+l17B3DuB/o4XGqQvNCIYaUBGC8ua21FlEEDyEMu7ELEdQaxYAwIEKK3drMBMCuaEAq0UymJQSmUmIpms9QMlTxqj2F4qaGZoSBHF0BzTxs6YEL1KgqInCjhKFBm7y1quHgpyi/Atf1POHvQPzrz25/wpc1g2fOq29Sm3CpIbQ4Gd3ViFmdIAbEzl0RjQKEFLxLFJIfZy3koaehwxAcMRAjGrnJMuk8wTxxzihF87JOBLNLk2FDLmY2eTIGn754AcTXZ+4XsXIzYyZE3xpuXxg6v9Sv7IrJ88cKNV5s1xdxa6Z+lke6sqvXUcK1I39tIaDVpj9n2K+N0PX9vv7+7QvdfVMQY+aiT2m30KWlllrXZm4H7/p+KnmuUpEC8ykXca8AS1WCshvSXEsXwzQvSy5oYTemas6q6sKcpFawwEi1FrPeEJCp9d+nrlNmRbZIeVkQsREW2wH3w/DudG7Q346cQ4gxnk4nc1O31HUNnZl5f7jdkDpGAnWzVTcUANyALl4TokNL1TkZuCj+hX/n33vz6s0/8Sd/9bd+4ff/89/+6nLOLpA6ovjUkIhr9V5BWUTQoY8dgUuZ3YHJVZSZuxCrK8dQKlRTqtalUBdBlG7oAahq0QoYgssakgC4uoioqzFgkblMcy0F3BCdQzCr3oT7zFRERWrzWkSWeVbVUmobZZxzzjmfz6f7+4evvv3wB9+8t7+vX/yb48dTrurE1MXU931KKeecUrq7u2uRjZnlnDepbRFJfcfM59Ox9WG1mb34nFJ83W9Ya2371Fq2yZ106a9uT3F77rZPhRDa7EYza43KzcDknFvWKMa43++nky/LkroYQiC00DizSESkpa5zIRBcSs1zN+4iYS0LoQeCMp3rMt1/+DY/PnSxK8cPNwm/vv9m9/Y1MwMB1FyOD19Pp7tXd1++vuMYlpo/PDy8ffvGicUBERhM1UjdqphjFyMTLaU097G2GRbU1KEV1CBnKkWLKRPOk02PsBQUIQdwtOpMTW4bDAnRnuiGn+Ppt+KtOwJqmwfrrrDOkvRruLgECFf1gO9OBF3t89LT/67tCUkAAIAADAwNjJAulWvjCNBhQENCDhQScqJhoYyBehwGD+EyutnNKkjFWlgUSrFS2D1sQOxPfaquqvi8FeDpND45xM2t9ktbXdMkAWhiBk/RA1wFClsqGa6A+wVYv7iCL373s/ts8cSnQLx99jo+eIHUcDVxe/3TpYDxXXcIPrGL17bk6h24kPQwhFCLtkaw2I/zPLVvq6VATMC0lGxEjhj6fqqVQnCiWSyQ3g3D+cPDPqmKASIRm+Nc8o16ChxSFxGX09IhAGKupWbDXd8myhqBooexX2wVZG5cwOZO9jHa4xEAuq7bKootWw2wUgbneTazm5ub/eHmJz/5ScsXQuNMAjzJHCGiU9NQNXRAM0BAVORqcH8u//v/w7/5P/v4rwPAv/If/HP/3d/4r5lhE5ag5i7YGoGDA1OEy9RPAKtS3d1nMZ3AKaZAhCKCMSUOKQ2BOyB2gfl8xtC4iO6yYEDnQIRgDu5WK5gDM4CKlmU+WS0xhdBFARWzVWlapNZCRDnXpo9Wa6m1imjOeZqmUurHj/d/8NOvv7k/P861OB+zZPOUUi253+/GcWie+OFwIKKm2YCIW0YIL9nXzU+iy+wtvhpX51dD6zaW2haoNcRv7Aa4CuXb97QV3uik7eluzN3rx6G1sG1Wp1kXAgyMkSml0KeYYY2H+r4DpBSii/aHDszrtNRcuhi9ZnadHt5biI/vfnL/09/5/k1//we/ncbDYX+Ta6lSSq1Ja3x1R30fVN4MA5d6nh98Pw7jyIRLKVbclrJ4htSlmOppQlEP3CbyERGCsZuXCkvFIlasaIU86Xn2sqA6UEQHQgjOhME4CpKCKRgAPnmaDffXl9f1SCKCqyDg8zXCF6+3B/8aMb5r/8+C2LO/rijWSsFARI6rUWrtWMxR0KAyAhEnDwPEPg4ZF0+QIg8Y2jjwtf7rJUOtUAtIBRFUCdtaac+biLSy1SXB1Y7hjzBWfqW74O4tkCSiNlPgum+eLsIM/lxXZzMS32UDLrSq9WZcDgmf7/OZC/1ZS/s5I/GZiOfaWnz6DdehzHVtYKujPEUAm4NmrZkr9/1oBGrmZlJlrXGrdTEioYEDoZoCorr3fY9ECgbMVbSIIOI8z1IqdinXAgi55NCNCJBCYpY8TWNg6lPoQkYAZnfbH26qyXB3+zjNh/2ABedlmWNoHl4upZRCSBzXuDBc0sSASOSl1JzLsNt3XX9/f9+o4iLqDo5ABM3wqxoTuq7Tb5DAHb1RkKFFgfDtnzm1y/jrP/oHp79ydoN+10NxQmhyUrxKPYJXDSGa2TItIbBoNbNFlawDx1oYkIAopESRkIMZuuoqFipUrcYupZRAvQ16N7PEAdf4WsUqojGDiyFeBq66upletlorAuS8tMmOpZS81GnK87K8f/fxm2++ff/xYQaqRselzEsBZJW6G/q+tdeZIWLf961JuOu6nLNfiVDRRZynrZq+71si/kUEsD0dDcTNbFkWvpTumvfWrEJbllvmpwVtwzBspZ0tNeTulyyQLovaRaePmd2NuElSkqqVUpuxZyATVTNw4xAfHu47DiplOtXhzRtGHFOalvOYuDx+/Pp3fvNP/NKv6pR/8g9+98e/+CeWXG5ub+s81YD30/HNl18Qx9N0HsbhduweP36o52PqupjSMs1UBNwRMcWYEEF06LulVAwMTOymtXopep59ya4+T2cuM5YFa3FDZ3IHjoSExsFDVLSmPedXnuwG/u1fW91rfXDd3aWhIBFv+2++b2thh+9O9L/406XI/IfVDJ7ABwDaiKk2OaD9Ye1k0DbdjChwFw0YqAOKFgLGStmCBlJyJ2QENAdFURfBKlpKNEPwKhJQMWJwcWb2TeneDbAN5wEAA9wQEUyb2s+T49wWmau5mTsw0mqwzImpioQYtovS6lqqKhcBE7qCc0Ckq9lM10a1zdpdL6i2sSqIT+5+g/J1BzOHq9kd26Eys5k0HLi6E2s3w7VZ8if13adasZm5NzL/k1IpXipsa0CDyCGAqoj41XJRd6klhq6JvBe3MPa1lFFxMSiOwCGGGDkuRSSFWjIEYgYwHbv+vQMzxX7I2QJFdHItgajWmvouDv0UBC3vrcunuhNGSjBEO3TZ/FRUuri7vc21vmV69/Gx5sX3e0N/PJ262A1jDGnYsYePH4BQTPN57rqOQ3DTy2UMx8cjU2JKp+Oca3VjqQUpSJWWGCBAN2P3qlbRIhOGldzM7u6GrgTmBvCXMP5ryP8l/rN/7VdnO7NkmXeR4tjtyClQqOocOowOzupuAMWgZGEOS8laPTGAe5bqZiFEE48xOtniuc28ZSCiEMz0NEknGNlwregU06eajZk7UkwxBCIUlSqqInUppRRQQ3OXUkpB0JqnqpZL/Yv//G/8/X/s21/5X77WvzGfz4sTF+VTns5LrqrmFij26dB3+y7GeZl34wimeZ7A1KSCqbWCDXprgmOOIuIGWuth3BEgAwYkE00pgdoqCGFrHT6l1Oa9LHXZ86GahhYumDFRLYXAUyBmJgJ0iIEYncCWUlS11jwMAxGo1tUMJBKR6XR0rV1k05pSiiGEmJB4leEDDByBuA0cixxAxUUNLAXUWqXO5ZGJm78g8TwPj0f46e/5Mskf/OSbh98/3L3K93tGkuVosft4/z7c7RH1+NUp3hx2gLkojfui7lq1ZlfV/T6Pe6ZgoYMADOSKZhpDwCI+LTQvcp5AhWu28ymYaq1EgSIBoDM5h9DtMzEFJK2k2Vy8oQ4amCIyAqETOq21KPVWBmhEf0QEJ3Rz9ebKtcwmXvFbVgz6JGvywiQ0uWn4RHtmS128eI0AuGVZLgYECNAjgZMDEZmKMxkoYkQ2SkwKkk2KsRlqIQdQsTJxnUlndhHJVYqgh2s6IxEZ2IX34m32Xvv7dvzb8bV5eNsJbK6KP9feCTESPc2Tuj7hFxC/+ePbP5+FVFefNTdc9Tv8RRDw4ieuf+u7drve+UWA5hfpi+3Nz6Z9NscKLrUdv6Ri4RIB+NUlChyWWoXhcHNT789No6qUAoCl1JiSldNS8pBSzjkSqwiYdSnmZXHkjhgAa5FE68DT2HU1YugGdX+8P6LCj9+8DRFmyYbEHCwEB+xiKlLRnYjKskBj1gO6Qy6Vxh6BUkpTzsw8jqMj1ry0ltRc1s7txtBZlkVEEcltlVdrvPV2gZqrj9QW7/pfy700d8aBwv/E+V/Tv/GLf/1P/zd+7kc/eNOBYIrn6bxLo4o7IYXAIYBRXhYiQqTzdEZEVVUxCCyyllWKCJXcjkHBkail0ZunvHaz2yr/+WIdqra5F4iIDpZLKWVxs5wXEWnSCqXWKsVNaqn3x8e//ysf/tK/9PcA4PjfOv/y/3HngOCUSz2dlxZmmELXdbvdnojbSNEmP7dRA66z9ubYirHLsrhD3/XXbnvXda1PGBHbGmv5er8MnYdLJIqX6vHaiQ0QY2xhRysLN8vBHFviaMsItQefAF+U/VS12+0IW9ckmxmYq+g4jIjY9X3NxdAJkYkUkZncDdBiTORuJuyGpdz/9KdTmet0OqtqKSE9hG5X5xJSX85TOH4kU9Ly7ic/YXcwqMNYqqgU5hBSrP0o/Rh3t5ZGkuCJnVBF3CwB2rz4tOg0mQpIhVovXZtuIs4BKYQ0YOo9BQoIElBAK4hXAMc28LUJaTZ//jlwb346P9eapKu1tOHY9f/hP0Ut87u2J7cbEQ1bwoocABkRDd0ImcBrQHMgo4RYVBZRkWhVygxlIamgSopspIJhOwe7bIjIHFUrXIVJ1wexXYIt9jSzQKsXvF1BImImR7kUA1/WPVoOFK74oNf/h6sRjwBwPbSBrirv+ixl9Ow4r1k9f6QBeFb4vaptXKPFZthenMvGmOSLKKOqNh2I7XscoQk7EaKu+VxfptlqDSEkws48BHwoJcZYq7i35kRyk8eHx8iBAEV0Pw5kMi/zm90oeeLUIUfn+Op7X055qXMBN1CfTg93dztG1xASByPKtYoDMQ7DCJIjcS355nCDhBwiUUicdsNez9+KyO6wd3c1a679siy52GrkLpPEN9PbUg2tPHDJBCK1+BTQ3MhXWw2tdxcRAd0Q0X/7d7/+N/7P/86f/xf/+R98L85zPQy7FKuLGlBTp+FPEoNd10GHdZZNuazdvnmekQiZADGl1Pf9FpmhVJI26oq2+BVWK25uJlpUxUzNRKssy4LmLmLuVXLOOZcF3Odcz3MO/26G/xEAwO7/HZDZHee5Ho9nRABvkjvpcDiIlDTsRKUp7s3z3Jg8myPfllCDZriEkl1KRNTUoVsNoCF+uDxEWwa12TaOK4eCkNy9CTmICFxCWAAYx7GdbEpJHTcK3+b0NFUfM0shIHKeFyA4jLtSSuSw3+/Pp5OZRWK4KOBO08RIXZ+01EZG6lPqUgqB3Gouy0gcCRKa5WJltipC4qrkOMQUkBnQl4Kl1PmcvJb5FLSiVHUvJYtBNw5pf6v9iMOhe4NhxLK8w7c3IaVacsmLquFSIBedFxABFc/Z0cEMEmoVDpG7nnc773tIUU1CAgcFMxd1FwBDAmvzBhDBDZ8/4PhJ3h+eO394UVq93ufF/n94qudn366d7DZbuElbkjdXy4jIAdSBDN3VXJHREwKg5wJarGatFYpiUxRdPMBzs7alQa4P+vpkmg/4Ai5DCK5rRbe5G1sE4KANKNoHry/K9UJ8ka7ZzMxnnfdry/xd2ws0/yO37X7D1f178eurH/TJ1/qlQHcNSSufejtgIqBGWkUEYMQudUVqyxvVaiKCGE+nk+86d0eHFMOi6mpIfnd7e7r/qGqIEEKYpvMPXt+plDlXr5Ju76pxqY6iPVMCL8v0/v0cD4NioNhFZnZA1SpiTszsVQMHNCtiMC1LrgVmVTDz5q72fd+MU9O3aTwjWKeCaEuxFJVm7eCyOteuInATbU8G+VW5xtHRial1pahDpPB3f+v3/f/y7/5L/9X/8g+//GJeFnAdUieSgdAMWLVZoBZerKGkN5eMpTSSzoVFJqZtSFkOpWa6DENnZgxEvILpWqBaC/7g4KpSa2ncHtEKsFYARMu0LLXW0zQty3I8Ht99eH//ePrn/tTbD/+UDX+ZBSHnejxPtTp3aSkLANzeHmJkLYoEKtIP+0bcbE12cBEbv7Q6r8FKK4+lYUDEpgrX931zI1S1acxtK3DjL2zPC12EQlemMlEzBtcLFRGn89R+dLuYrQJRc9ZaASByyACpCaWopSGVUtrFTxzCZRorbEwtFEIigK7rUteZSOiCSa1W6zKb1I55AWdqd4BSDGCeOPRd7+okpePAtc7TPAagMpEUcJ2roSyoVU59dweLx/2bzpXsdI6jYa06TTIvVDWocq5Y1aVqnq0RNyh68MgRh56HocYAIaBhhECA7ADeqvrW5oQ5obshrjpUfuF208XxV9PNGGwP9dZh9wJA/KKavOHGzwJBf+T27FY+yeSgtbRQ46/HhEjYOo6Qjdo0AdOTALkTiKlKZTGrrtnClq+A55T/K6k3IAobFL4AyheH6JfSE150ycWkHdz2wfX7L6AJV/IJ9LkOg09Dh+vvATS/2GGkq90uk3Ga1dksCuLTw3PNetqsK11E2OFqNA9cgqTr03/xZtvsogINl4ih3SVlUnNvLRfqANA8zbQKsq+iYGa6LAsRMWEX4uPpDMil1tc3Nw/2ntogctMsOi0ZOeScD69eCRC5cYwyTTFwMCGAWoUcQ4yx69Q1InaMJ1FmMoDj48Pt7atFimPB2CkxIFdpTuW6GFTVcRU0dbjQyUMoRRBRRJlZDUQ0BEBEUWP2cRxLKVkUkSKxqm8KmqslcDBTBiJCcyfiv/v3flf/T//Wn/nv/5N/6V/4j/7Jb3/1v/NX/4sqXtVUnExbX1i7sBsgmkJjszTcFFmXk5gCgGoVKS18YeYmY6lZiahNtaVLOx4R1ZrdXbWqaa1FVaVWRii11FrnnE/TaZqmjw/Hd+/fz8siasDx7q/SglpVz0sxwH4Ycq1qnvpuGIZ5Oe+HfYwMlPq+b5NemqPdsL5IbZ0B7TGpl5kHzTidz+dmqPQyFbKxhra1J5d5NRt5v/lhrcnA3ZuAT0sltRnXdBm1xBcdw2ub3aJ/Rqq1diHuxwEAht0OAFqxoX1Do4d1XYfMfeqask3f99C4cwABUXIJSFVyipGIHUHNnJCYa5V5miMPeVkCRwAsUg8pmnLsOoKMVuv0QCZdHEstnpE6grpEt2V6HGKc370f37wmM1kyLgVr9VJILAC6ilfhEITA3TiE0KUaAseAXQ+BIziaIhiqurCYr4PG2wwjbIHqZzz9xjp68f6Gci+ihNU3veDGpyD5aR5y+9oNBrcXePnC7c0VzRAb4Jkb+kq4AEJwIkZzpYjA1KZJmjl3wSVZDjYRMBAYokPgsPn7L3xqxKc6Z5NjbCVx9Cfx2xdntS2sDQqrVKTv5OF8+sKuSiifNTkvbgys7CC/fjYuvw7bzfDLuPYQQluym/e0fepTEP9D7tB2tFvF+MUBb/3Ma86BSQkQUF1U1AzUvUuJEREQwNujNU0nVRM0IgpMqevk/oFTBECpNYWotaQunR/ukVHchi4N+0Pa7YybPhaGyFhzjIEBMHSx3w37vXOgrDeHQ1mWzjX0w0OeSq1LnheVihiZIEWIaVGrImPfhRSbEHFd57UGNaq1dl2ntuaCrpb7esti4K3TFdyHlIjIELk9PrpKA6IjOaTI4K7uyKCOv/U7v/93/nNfnX+x/r1f/Mmv/vb3/sxXv6JFSjUy8efyy+21gedalpJhI6EhbAeGiG0kS7MBKaWVyk6kpW7kyForUuPLq4gAuNSqVmutSy1/90/89C/+ud/40W/c/hP/my8/PDw+no5Lzo7sRO4o6kX04Xiac4lpAItNxaFJPrh7jOyuDeKbWicAxBjbXzfJtsaH7rq+lNL3fbNPrW8AV5Wep06dLSnagLvdo1aqa8TQWkopJcaw2+1UhS+UitYB0H7aL9mh9v+G6VolhZhzdtHDfh8jlyXjlZ75Zk1benPs+3br21MfmEspMYQxDZrneSlWaxiGOA5qYjGI1GLaM4UuAdOlt9kNXRC73U7ms4Mb0DLPskz9AZGj5pI6dRMCzcskaSBX4XsA93nyXNgdq1guyMFFrGR1ga4DQkAURE/Ru4RdCiE2r4FVkEQAuelfXrj8gNAESTbQuMb05nD7p+bhOUY9fepn0wj6R96aOlAbFQmErT8AHR249S4Bm0t1YHB0YNXB0NzEtEJ7hEWVa9hOxp6Lo20Kdn6leu/urk8Aen05WonNLvTHzSReF5mvT+AafK+/7QXuP1nFzxuA76RebZHEi6u/vePPQ5DNhGzxx2fjmxcGwK/aDq5NqV3EfxokqRsOvYOrqmkrmJGbXeZ1rHMC1mNWiTF27uTgonEXwfx0PHYxOsK0zKWWfQxAlIvsbu6mUgIzgufp2Lt0zPPj+W53M9zc+tCfp6mocUrT8cRd2o27HGM53iODIUBkJTrVEsYBMTpFAFDVMe1UNddqFzZkCw5qrVW35AMgQBuhTo2PlJK7f/nll19//U1gPhwONRctFRAZWtUKkAKYgQupuLd4nYgg9t38by/wTwMA/Ohv3079ZEYqIHlqKLNVPqdpEhEkqrUQtUhFRFyVt+WHT0L5UmuuNcfIDp5SGoZBVKvkhoAurtoQuZZSqmQzq7WolL/45379t3/l/W//yrvw/yz977moUYjuxGil2nme7x/Pp6ne3N4C8OlhybXe3d50XTcvS5dCCOQXBb2G/luC3t0b0Ldtu8jNMgGAiMQYm2pTztkuU/BePBrNb6i56TNTi3fbm9za6ABwbfjY3B3xSyN3e7OxOdy91hqQdnd3MYQ8T9tzMY5juLQp+BVNrpTCBAGpWafAvN/tuQI6I9Kwu03DHtKQl3MNQRBipNBHdcfAFAMQxhBT5MicT2cKfV3EFYm6fc/uAQxBDIp2Dj4v4360aQqB9HgiQiwZc0ZArJWKOKmbgok7ihkTYgqUEqQEMWGIwKFNRnMKjhyRK64Cw+aX8u+FAArP0XxDp+vQH1ZT8ZSo2PDzGhv//4H+sBGQDAyRkBydjNzao+ZAiGYKhuSEyRnVUNER3LyiiWtRrVk0bAUoeA6j22G/cG+3c2sOyLa/Y7tyT5KizAzoDrJ9yYtrsaH/ZmOa47ztfO33weevY7voz/TX2vtbqLvFue37m470Btnbb31XIPKH3IMXx7lZvhcRFRE1cVIzUzMmcocYQhFpyUIKwQBKKWoG4KVWjxBTbJe3S/F0/0AAr9+8nk/HwFwAAXDoB631q2++8Zi+PByW+VzzvI/RTA6HQ4pDCKk4qRoAqENKfRxHA8u1BI4cEnEIhAJBHHa7/XnK1d0B1dTd53nejJuZqVpzIVtbTLuY4k8msN363W73xdu3D/cPIvVmt3/Ux/lqCQFACpHAJbtrbd0DHAiYreKr/2kqf7n8+fRP5T9d6vIxxQGcpZaLod1iZ2x5KnMHwlKqqeWSAYBwnbUQOITAbRaFmrGyORGCmdZawAFpC9vt0kXVWryyamv/mr/8j/vf/hUAgPEvgzggsVoL73ye88PjMRe7vbtFjqfjPC3zOIxb1r5hrqO7W4PXRvWZ55mIztPUdFLpMuy+XDrwN8eimQoiavn35qe3ZA5clCQatX9RbV+OiKra912KsdayhjiXXP8wDOfzuT0Ozfw8FbRavL7kcRz58rwcDocqpf0iAohIFyJcuhaQyEzcgSOD6rIsdzeHvu8P/eBARIFDpJQKwiyiSGkYDFHcAd0JW6ql6zvPhQEodWU+B+768ZXVYudjXqoC9PtEAjbnlAyWzBFqgQWNmbWWJuuNYmi+uAKYqqIHc2AO1KcwdDUmDMGajAIhKoIjOLSB0uaqoBgYyL3dLm9Cm0/dwgDgDg4vzcD6p6e+gU9aAb7DN/3/yfZUAXhCLgKCNdOK4AjIBBQI3RnNGhHY0QqqRQQiKChhw9xrEAQAa7rY2ERSV+k9AADitV/FIaRuC04FrVH/mvjb5X0ndrvMUL22in55Ac8LwqsCyVUZAJ/nv9rH/CkEa5fhaX5vwyZuXakADqucQ2vtoTZn8MKv3WJqoEszF3iTadN1HILB2ivofpnO1rgjHFpazIihDWAEdG8gYeoGpuvdCBQChSLlMt0NQ9/Nx2OK0WoRNQjQBOjN3cFT7Mo8KepuSOQVTbquk1oRaTfu5vtHMJxPi5upWTeGmPh8fgzmVqTrxyqotfbzwtormafU375Jd2/P5ihCZR68Sh9FDCiQ09jfHm6+uJ+/eaxa3ALiN+/eNRJhI64gQEqUSzFAM4TGfGACcUTq+26azwQWGdh9ejwtp+nVzeH7b99Mx8eAJNAGUSMiGagjWmSMq4tKHjruIFDJ5+Hfx9M/Xcf9HqXm8xFZGOsMAAEAAElEQVTNwUmr/IU/9zf/3q98/S/8W3/6l3/zC0BAIK3BwU3NTVUEqpiZYesyACFqDJrNeISCXZdAuZp6m1yGmEuRNhYcsKiqWqlVVKdpmpfjL/4vRv5/fHn4D6I4EKciBgCidVnK/f09OB/2O05dzrosC0RKQ4dEUOvQ94mTiMUYteY8n9E1hI6IgHiZ564fHVzUQ+zagg9mdZnDMCJiU1uCS3fuSq6NCOSIaKDYeNUMsQsEzIAu2o9DLUsMEBgJlDk03E8plVJ2u11L5oAzAYFCXWqzHwysLqrCiWPkUisT9cMIQAgcQjRzU0+xC8xmzhw4hLTbTadjDNEJXQTcwH039t9/+wunv/9bTH0cdhPgx/OCigMNoetLLWZIgZkZCThiTDQXFTMHsQBiUm2W+YjTidUMqHKAOGoVz5khkCqwSV6YIyyVkRFRxAxAyZptqcLWRUgDDXsfekhBYF2wDffZzHINS4lZHQwR1AQIuM0HtXV4CqzlX1RrlUDbkASeaUIYAro2lKAWCCC2HmTYRM2217pKTXzCKb94WwDgLcgGcDXA9YMNN54wsM1jaWDYWpoIwCF4a3QjQ8DQmSk4E5ilDJjce/Rbp6AxSWALl5FAF9D/TBeuX1IlF4f38xZpxWEHB1ARAnR30RoQAXz1Iz5J+Fz/yrU9+DQi+c6tWedLS4CptnyKXRrHrn38J62CT37Xr+K+je75Ys/viuau97w6BQihBc7ovlbV1yARL4P6ADlFDShuxcwJFRyZqSkEICIgmh+GvpQ6z/Mv/vjH03TEQA6oCNOypDHdvXmdhv6bD1/fpNANHQIyI5hrqUDEQ+h2e2NWAIpdwJiSH25wXk7T8Xx7uD2f59Npsvcfun5IfYeIS86llHEcm3BN3/fmVqQwM5pV1RCZmVt5gJlEqqvFFALTMPTzNNdS97vh5ma/2+2OxzMTg6+5nm3SOhGhkYhIVbccU+pSYvPpfKq1vN7vb4b+4cP9NJf/5Je/+gv/lb8FAP/XP/c3/9Vf/y80A08YrjWm9NKHoSCAgIZqtN16IpKitWRe5YDWO/X3/rFv/u9//j/58d+++2f/jV9URwestZ6m+fHxQa2I6M1/mLzRDMybVl6u+cOHewA8HG6MWI1O50dR7cedg28U+63xZVlmvtJbXN35kOoqcsetKtDyPy08bfmfUkrTGlo9oeqRV5KPqRJi3w996lqs0FL8ugqCErpt4+Ybp8vdW2giVbuu2/RaWgjy8Hi/LEsIa2EgMMcYXa2Up9hldZXW7ChJrV3XBeK6zHWZb8fBwWNIudYQYynFYbcsedwNqMbMHJiU3N0cFdA5xH5H3Zgcjw/3iQkQRSvXoiIMzkwAKKqMQOYmAlBcTKO76nlaWMGZEXjOS+gGIFRVcQyIFBPGBG1O3OrpAYCDOpq5ikvFolgEW8c4NK0qB2j/akmV9iDTOnHiWdrn87n+a0i5rhm8QDP/XE7pP/2GSABPKffLTyC1nkgHIzYkJ3ZgJCIkoRD8EzR8sbUVtgHid8xvf7YRESOZGRm5KTE1usWWf0dEvPqi6wf1j3va7I3EC434bO7gzkDLhS5NVzLXABAu4P684IFbXRg+V3D+9COfXqv1LJ7swRoGuaMDtEu4XZ/2YBuYOyhSUROwooqBA9EkNXBwpLs+VYCHx1OpIlViCMMwjrsdFLFAHpmHDlJ4OJ/WjrCYOoBkrlq7ng09DX23v9E0augUmTsqp+kXfvlXH3/3dx5mxdBnnUIMv/t7v/dLv/YrIXID9O2KrUEYILg3pxLcsYn9iLYSvEpFhKGLfd+52ePjQ2R6fXunqjGQu4KhQ+sZAgRgAjMn9BAZvDVqQckL92EY+qHvVUSlxBC/+OLtw+P5T/7uetl/6TfftH4Vkaqam53+rV959//6r//2j//2q3/mX/8xIsg6jeiJSvF7f+rhF/7Oq8Rrfvx6Mfzf/sW/+w9+7ePv/tr7t381ffHX92peSpmW3Fh8zWsQNQASAwAotb579wGJ9/uDA7nDvMyllNilsKbdranoqOpKPVKFy0h2gKZyscUlKy60mcB+xdxvK6RBdkscGdpFLsJaoNxyPjnnYRha6mlZlhS567r90Dem1lab2dRDYxxa0N/Up1u7Yr0UxtvhtcJ1yVlE+KLQZ2Zaa5+6GCMhqtQudeAuta5hMvL+9s4Fqko/Dn3fV1MATF0KAFUrOkhRZg9pCP2h291hTCBWBUJAdA8IUpaxSww25UohzaKsMhCRG9SqouKuKjJl4GBVHEhUjBYEVgPjYIScIsVAHLBh39qZBQSGpiRCop4LZEGvyOucAEMABGqLFQAdgVcGyzXiX2P9Z19fw/13vd72vzYqf1zoe7GtjvWlRvvsfQdnJCRzdEBHBg5AXYzpmQH4FPjadk11+lkOhYhMzd2JyWGtX70otL74yGYD9DLA/Wf5LQQIRG6Obg4A5t7aPoncDDYO78VVbNlMu2hE+1Xi6/rn7DnJ+o8MRK5v5DajyR0vYR0hYakZEB3I3WPiLGX93S5oxKK5gjmjVFX3onLY7dIwfvX+2zlnU+0Cg+HH9x8EJIQASFPJxshdMkIVa2MftMr7+4eg9fXtq6wy3O7m0C1GHPvKkfudI8esuzdfdA+nvoIQVwxusOTlPB3n5bzb7T5+/LANJGkJhJUg4GBqTe8BzEUUwGOKKpXAVYWgV61gHphTCruhk1oJUd0Y0AkIkS6SG37RBGz3hYhLPj8WfXz4WEtm2kstIaW7u5uui//r//F/76//4Hd+8Nd3aiIq7kZErQPgL/3Lv/UP/+T97/7JD9//6+OPf+Oumlw0dJGZ//3/5j/8K//K7wHA/+Bf/mfhiuzQlsT3/trwD/7kRwC4/Sv0WB7V1hUIAOIKgEiByICCFJnm5f7+vh+GmBJyVMVlzsfjGZh340FMG8oPw9DkPxFxWRZ3LyU3YnFb233f56XShZBqZg27m7feCj8b9b4dp6oyIzmYeSRGDszchYjmZrYbBwBotKLD4dAGCZxOpwbcOefWE7fGcx2vPE7EVgdelqVVRJjZzZuZKaWA++FwAHJVtUvT9X6/b+aECE3VRNy9S70oIMdazWv5+uuvu773JuitcugHKwUcGFGdiHgYD91wCP3BzHMWM9dSglZSYaLpdNwRe4hxHHFa1kS7qFtx86pQS3ZRUiciUeMUaymqTrFDTsZkRMpRiAn4iS/vZqVQzp4z5BmLUlF0JQZzd2DlhgPsBOjevFFt/PoLXMAnaO7Xr68rgvB5U3Ft+P8YeY4/ansCzKvv3OiaDh6QjQkQncg5GAUMgQKHa8P1Wcy9xsHNPfELsXL77DWYElKbmUeETawRAJr+1BO4P+/UbTkBuCRJ3J+Yne1TetUJvG0OYLZqaLV92m8FWoFmw/r2AMCWlbsiCPml5PDCyF2/2P60+W7XFKD1YC6Twp6+tlnflh0DdG9TZ307AHNXk6aDOY4jswZHKctUwAwklzzPXdfPczbzXTcs02yohH5zc2Mm1TSNQ0xxqRnAE8fpNHPVGLpsGEMMqe/uvoR+1Ljrbt9UTtx1+XHq7774pf/M7df3f+Wc593tm/cfvuGU7o+PLYnRiCgNzjYOuKuqmIowdYhoqjGwuYMZuSEBIyIBG1TwLsWh76fz+Xx6ZAJENEczYMDATYS99Yu4o4dASDgMQyC1Mr1/9yEvi5mkJsYI2vUBsP+z737p/GqapnMpLgIi5iIO/vO/cfsP/9Q9APzc39qJFY5rm0K7Hb/3n71vd+e3f+3dj/7mYVsPDQ3/8f/Vq7v/gL/4j/vs+VJGAmYWVUAMMZqCky+LzEv++PGhG/p+HMzAgcQ154rEYzfoZeJFc/y3fGmDUb70HrdIelkWcAL3Rqw0s3meW0+AiEzT3L6qlNIO9TKAIV7HEH3fX/ijnV7GJ7Spk/M8L+cTUTgcDq09ew03zVo6CK4mPbQWM7tMSdr1AyIej8eWpzczd2PmZgBaZbsdWGQ2ra7OFN3wcHub+n5eilVbSvny7etEMIzj+Tyx6i5EBECHm/1ekfK89MON1CqisswdOZcleoF8nh/vbclnNby5q2LEcS3klGxGCKRatZRAUerCHB1BBdW0qiFgN+yEgEMQxMTRkAAY2jREdxAhESvZl0WXTKKsauRqjugORn3XpkO0PuW1PQifHvNr9F+f8avhJRtI4qVIuX3KLhzLa4/zGuUAXjri629dqR586qxfw3JbdYz0+b+2fBUTUhRqE+ApcXrq8ILnXvD1tjnvRLQSpq7oj+sHr8xYW0+IqCbU0k+rU/yZYS9+JaX5Ana3b/v0eLbX7mvLmiMYeuw7AFAVoqfQlS8jwMyMnnflbUab+Bnt9dML/eKYr2+SXUifZtaKH8+/vyW+oeUWr3+95YuQmWBNbZzPy1ny/fFxvH3FiK6eQuxTJyI3u/35fOr66G6nh2PoOA19P/TzvEQO1fz+/v6OQqBA3RgOr/Cwr+NBeBBL+8ObcPMmG6XDzd0P6bES716/+cGP83TqE3317isgfPfh21xyzktzThvtZPPTc5ndMRA7ACMFYmcoKqJCjIEgdenVzW1ZSl6OgZOZfv31N9Pp7AhIgQANFMBMXFW7rhuGYZ7nFKKqjsNoLjf7XVmECUqeTQRTYiJnBENmJMKui8z7Usqy5GVZzMCq/jP/u+///G/sf/g3d2rVzGquALCR8/7s//Z7/t+2H/yN3Zd/tS9etkeu+eMG/v2/MSo8UchU1QCRMHBkikBYj9PD4+M0zYfbm5R6dRWr7nA6nZecDZlCyLluNHkza9ybiyonNM5lMzmNFUoYgNYjmee5tbO1uKGNZluWpfX90tYLBi17RjEEERmHgZkfj0fgYG6tbNAIna3nYL8fW+jWgo+2/kMIpquQVzMhrfygorhe4a7NBdvtdmA+zzNH2hygtpVSWiqv5hJCSl0KyLd3rw67w7fv79F9HEciYsZhGI7n03madnd3ecrMIS/LsLtZzo8pxD4GmbPPD6HOXCc/P8737zDPVmvoehFXUHWotXJU8eyKMSaVAmoqGRzBXRxBpbgqIoeQTQixgDuiADGxuaERuYIolGrLYstieVGpVsVqcQSv6h5AyRA9EnPwhjmEjk7mCE1zBz6FSn+evXmKEr4j+fPC29+A5Q/Jd7wAn59lu0bRNUphBW8D6ZGBwcEcnZ8XgV8g16dft/1pO8/ruObaGV45dmDuawv19ZVyd3tuuNaq4MXTv97zU1C+3ozAHBwBASjFxnqkFF2uK/XP6zOfnON3Wb7rj1/7+9e35Mnmt8hANyHoNcRhplLrGgZcnRRewiniENzIwapIqeDWxdCl5ETgXpaFAfthNNEuJja/ubuda1EQZj6dz+fzebcb3M3NiMkAuv2djwcbb/jmFXQ3nPZ887bygH3fvXrrp/J73x5/6U//iZ//Zf2P/j//3l7w7s0Xv/sPf1O9AD6dS5sVg4gtqe2i2EgXVWJMDURE1U1TCjHxYRxfvbrNc7n/8FB1+eqnP52mcwg859L3QcxpdRMMwFIKXRfbLW108i+/+P50erTKXYotjwluZhUhEkOI5BCqZHNB8tQxQNfMqrv+/G/smyYWEeeq211DxB/9rcP3/4cjXBnpa5sNCGYXFSxwpAtFmNCJDOHx4fHd+4+I4c3bLwOnpRYHULVpWaZ5McfUdWa+lHLb7RpeN9InbUral1hqzkv7p6pyjE1aoJRyPp9bFbcFB61Zd0uZto6wtmC2wnIbMbZO8rks4xa3AUDO+TCOXdedz+ct+akX8V13jDG2kQ9NoAIR+6GPTIfDXnLZuuKbsHmksB1Pq0wg4jiMkhepdehGIvrie9/r0nC4efX+/f10fEyRT9N0++VbimEcB5smM0+pq7WC26ubg4iSLI/f/tRE+nqW873NjyGfyvl+h6hEORfm3qsAkpSaQxYnNRT3vJxDk+8BqKUqOoRY3YzRYpRaIgIgBuJqFgzdAFTdAKSyqddVE19UtVYp1cAVxVzdAhIJMADyelWJWuMoAPkzvv8T0D///7bwPoX+F175NR7+Ifjzs2DUp5C1Hcnlt1oA0NrcGgMSA0YQDp/Yipc/DFdAb/aUC9v86/XjhHQ5yDYHBgCYQyklxNBaQTcQXzG9GYDnEcCLGsD1tfvssQHgJlvq7qui9SXmalt7LZ/MAb525Jtq42frHNul3E7Brqb+brBygRF/eRkR3U1dARuhAJ90QhDBXKuIqKlKFXDTUgOziiDirh8EYK5Ll5KqTOdTQGfGueRznb8//FBq7WLUqvtxiLHf9fvb/gCc4v4NHG6933c3byGNNO674QY5KaW4u3n4+PvA4df+1D/+1U9//6e//9s/9+Of//Dw1TQ/ZDnjOotRQgjTNB0Oh3EcW8cpIAeAUguAgxvRyuNMKfYp7MZh7IeaRVRS7JZlynlx99iaTsEVzB2YV9GC7TFonJnpfH779jW9Obz/6h+epynn3BGu+lxIm0ZCSmme5+PxuPqkTY5GVUVKrSJiTiJCzLS5F83yOm2CFHhhIQO0gYOqZuqWEocQHEndSqlzLu/ff0ip3x9uG4sJwc3cHM7nyR1CTP0wPB6nptEE4MxUSgkhiFQzL6XEsHZHNgjOuRBRjMGqENE0nXPOSMjMyzK3lMs0LcwcQmjJn3aJCH3LkV4qNLDf7+aliFvXpbbC5+nU9/0wDM1+tyz/9YBPR08pxRQBPOc8z5OZxdANw5Bzno6nYRgO+/08z0tey+y1VrjUBgKH25ubGMK3D4+MfHO4MXOppuTfvvv2dDp3Mb598/rx4cMwDGBOxNVM3MCBKAzDEIjm+XysdTeMZEYykyxazvnxPiKgeb8bvYICuSESmnsuBSiKg5W13ajkWdWByInR0dDFwU1AlQGBGYjUTM3AGivdUc2qeFksL7UsbS2YWWtLRAZgQAlexYmd0B2Z0Fs/5lWP53ch5DVOrg7g52oA9hz9r1Hus9s1Rv1MNgBhm8G1/ROAGjulzcRGcEJCMgwUEOzaL99O45J7ajB3qS8grOUgREKqUjfSC0NTAQMARKLGmldVpuQGxERo0HCZUVUbkwQBdbu4CG6rVYCL7drO+DoNdZ0UQiduDFgA9xatOeiT4Im7r1Tri8LPdkH5avYAXRlCvkoTPVm452bA1RAujF1v5QhfNcJXfhg1yCsmzqTVwZ0CA3hVaYsPA2sKzInOR1tEwTWiuHPgZT6N4aZjIrBd3yWE8/GYAMBMl8yBxt242++n+eSiu2HMYrEfcxpPYdftXmN8PR5+qDHp7Wsl5n5nhPu7m4/TdHh1Nzw+LtVV4Qc//Lm/8+t/jbBjxiK5kaFqrcMwtKJig6Hz+SwGxFCkGhgyKFqVUl2IAyHu+v77b968vjk8PDwutUAIS56ZcRy6x+PJrE2HdndFxxgCAaQQBCClFEIgJgo4zedachxvqodqLlaDORrxlV5T86Zb8AFm3q65Q2uBdyQTYXRQuchHuDuYuxG5XxrnwR3QkNxbmA9I1IVIHEstHEKtcn9/LKXcHW6HcXT3qm5WCUwhHuezYjS0oe8dcc4TMzMBgoEruDJFVVWp7uKUnDxLDpFUpeYlpWRa+sDo4lrn6RgCE3upc5ZKTkzABKa1ifKHwIGxzeFoS1KkmGkLl10rg7fJ7KY6jmPXdVn0fDxuC9gu7TXu3vf96zc3RF7ydH58sFLGcTzsxir14/v3LRA5nc+thkwhtTBr3I8pMDrsx+H7X3xx//4jLL4/3ECBEOKu3y215FKMgJil1h+8/jIoIFhIne53Zxcy3/e727u3YNSHrpzP6DAMEdDQHbJ2GKXMxQFSwj5K5iKOFBACYlAgABb3IDLlRbQCIUGMcZdzBgwykDkSBjEOQlacqye10iqParhUWkRLMcmqBQHQnNTrMgMoePGK4JXdCdwteErijh7AkWHlbful1vgExxeq4Yuk0Av/dXPGr7n817ivbghNABgdrszDVZrh2mzolRO5GRlA1GvNhCcr4ATNAbJGAmrCcA7+LAW0nWHDOW8qBe5EbHrhn/GTGgl8x7ZVpZpHzsSIIGIbhG4PZfN9Sq3MDIjEBPpdE8GeLCFdJN5CCK7tLC8X4eofepmJ2rDjBbJf34MXpvXTqgN8QtvaPIIX12G7OOZOlzkBrQ5BRAbrR5o7VkQsMBOAr8JkJh44hJRymWrJppWYd/1Qc47EbmpIudaYhtvbfQzh4eGBiLqhj9iLokKMu9t0eNW//pKGfdwfoN8xs1Oo5uJWcnn1xZc3+93x/kPAuhv729vD+3c/uXt193s/+W2DRu1nd2/8QgBoUwwBwNxyzjH1MUZi8mruAOjjMNzd3f3wRz8komWeEAHasmFSVUAIxE0NO9dKhCFwjOH161en08nMDod9jKEbu1rL+/fv6pSXXJAYiUrJjeG+XfPm/4pIsWJdDw6NFG8Xv6Gt4RYIXjoWHdpzhEBIl6lkRACI1OhY7VaKCgB8vL8/n8/qsNvtQgjg7kBu1c3c7Hiaa5VSZRiGGOPD6WRmd3e3iOtYxxACrqpE2q5kexBKafn5iohd1zV6+fl8VpXdbkQEEa1SUFZr1052E4uOMcbY1KGbghCpaikZAYkJcGUBtXRNq+u2To7m/rcOmDaXuI0kyzmbaghhN45EeDweQwjDMIQQGid1HEciBNfAvOsHEw1E+3E3n6e65LdvXxPSMp2Hw95MSp5VtU8B3B/u77//S2+8ZCLuhr5IKVKhys2he/Xmi+PHBw5xGMZc5hRAcwmOISQWi4fb8/EISIEDdCEkyqIpBXUzQGkKf8tiJgaGgBzoPB3BEwQrC4bUJ/NSageAhOq2lCwcg1MQY5G6zDovmguomoC3eF1Nrao5ePBSNWRgIiYANQMgBSB3aymgbXuRvdlAYH32zYCeQco1jvgnKaBP4civ8kjX+1+//13bZ//Wyr6I1ETdmm4QOv6RNFBvIWTrR2Pmi6/9Ugzu+nu200DEEGOt1dbuqpVMBgBtBKO74x+f+/+5322xx9P7LYnh7q2Ydm2WPz1mfF6Ff3F98WqDK/R/YefbtlGv1r5pIoOn9FdrwCmiLQWcYhTznLOoDONQl4wVmUjdtVaOaTeOcRjfvXuXc6XWtwxQXVPgru+neVYzJKpqANZ3QxxuoN/z/pYOtzLseH+AFOcljwNHCqfzOQQ2LaXMKUUt/PVP/sEPv3zz4Zvf+eLN9/sumeNpqXhpyGhQuyxLSinGqG7M3ASNcVV7xcPQM8IPfvD9vu8/fvx4Op0IsI9h6JCQzrUyIgdU9RDYfc0mbyqYzZaHwNM0MdOXX3757qs/AGhCCB4Bci49rV7/NE3tagdm6nu4elQ2cgFdcvrXHoODX0nFXifuVHRVynTAqvb4+Ph4moZh6LqOYzIzRzZTcyiipzkfj2c1izEOw1BFpmlqes6RGS7yoltqlJmQuTl9ItImQbZjizEBQEPnlnPbhuXhpRLWbMyGAgAQQui66O5mslpEePJpWhlg+/VWUWiuRst/juPYRsScz+daSiOtIuL9/T24p5XgL4F56PumOj52sYuhTyH2fYrx4f5DxwEM9t3eVCet5LqcT+fHh1evX4/DECnev/uWmavZkgsTIUVHN7TQdUZB1PvU911/vJcq3lFyNPWgjpFjOtye5jOrptTlLDx2SgDMJi5ai1UPQBgBGEyO85mQA5KJU+i0CBiGEKpIVUWACFRNHcxr1bzgMtuyQBFSEFEwIEAAYMBaKzJCFg+CSUEElB3cFYDQ7ZmjDJckcAMLuELOK3B4cqavHesXluMF5rzAk88mkT797M+yrfREA2DE1vjQsiOfAvfm3j89P+5PLvZlbvKnnu/2+hox20xBxLYudfOan7ptL5Qhb5f1O07Ar0oFz18/Of3Xl6W5PHA1fQk+V7L/1CrA8+trn8jJbR4+XpisL/7avDBzxLWvMuac2wAPURvHUayGGAGgqpioI1WRXAWZUow77ir63c0NxCBuZZqsSgCwxlIn5xD2u91ut/u9P/iJmYmbgrODY/TYQ3eA8bamgcbR+o5TXI7nqP5w//7mbg+I3/z09/d9/PDuD7zuyvxAVpfzMc+HoU/V0P0MABvQN85fs1siuklUtr6hrgsB8bDfHw6Hjx8evv7623meCbHvYt8zuLunYRiIwvF8ahPtGslHpT8+3jPzfr+f53m/G8Tt/fv3ZqrL/PDwMM/zTb9b+znMHWyTqzRVXINjh8tkK75MM6+yFlG3JbouZoBLh0YLTNd8esDQlmIp9XieVPVwOOx2O/fWvh7EXNWBuGp9PE1EBIix6929RTAtXRYARGpTYdsyja3gdokAirdsPpG18TW1IGLrF2szF9WNaRXoben7Zia7rmMM2GR/zVOM52lRkRSiiLWwo61zZm5yQ6ZrAbl9fwsIWvFgnuecc+QQYyKix8fHUkrTLi1laUFGCGQmN4d9AGOkfJ6H21uv4kUg0tD3XRdVqS/JRc7Lw9glr6UAcLLXd3cRyYlqzrzf73a7r7461iXPot9+/ECA5s4phpjycu5TUAMB4BjFVM2pHymlCohDMqQ4Dhg6rRJ96CgAsUiZzw/L8QgMiSgvmThKZe6AmVydOZq5VBVTgOimVgrMM8yTTTPkgqLogITe3AYHK5XAzRVDMG5lTsehc1QzAhLyZ5Z4A3r4xCVfPRIwvCRzWve7g+OaffxOLHoB8dfRxksL8ce3AQDghOTgtA7YRYB1kfkltwVX8L3l3EMIcGF/+gUTt5GHK9A/B9ONzt8WZeuKbTuvaJLXTiizCyOInqoieiXQf11xhefG1t3beN523VQV8RnXqIHCNYhvjaB+NboAAOAS4b3w7rcy8vad6zHgminyK1bJdv+ICIFanm7lTcfYdR1cyKkO6u5mCgbE2EQ05nlZSsa+X/KcS/UF+v1+ztNu6M+nKQUGgN1uF7qIDsvxNB9PitYNA4eQ0ujEgtHTUCgS8jiMRpyYDf3bd1+djsf9Lt3fv8956YdhOX578jNaLsvxyze3H7/9djcMp0mnaRrHsWHiNE3NeWzA0Tz3KrrB1vk89TG8fXXHzF/ff/zm/bucSxfwZuyHIYnUnPOr2wOFdD6fq0sM65iEZVkalaVRFed5nsssIqVkVDmfJyKqpfTDQIA1l5QSXtrQkNhEG+ptGbZtkWxr75lmNbhuc2kuBqwBdKOZ11obbu52O47dlswBYkcQRxN/PE3WckjqjWPTmmwbAXQrXcGVX9/agwlwmia6jIhoechaS1lmbPMUVauKqvplUbVLfd1R3HB5ixIuyaV1wpJe1M5bG8c8z36VQVLVFkwg4uPjY3u4YowB6XQ6lZyZSUVC4Bh4lYw2DSGYADN3kV7f3kYKZVkSYVnmm3G42Y0AACrn02no+xQCA1rOpZZuHL3OfeCP99P9B9sfDiICBA56Oh/fHu6CYy3VVGrOswqoAUd1Eavq7o75PKc+hNRjTHG/85ASRI/JgbKB1SUOHQ5Dfnh8vH+EomMiCxBDdGAABgMTMzFXgGpogrnAPNvpBEvGWlUEKIA1wTQCwJ6jVgFViwsCgbsRGgKNA4o4ka5WAfiiJnINdxvOwEu/+YIGLar2JwB5AVMvfP/r9/GqXPy0z89gAJ45sqtYDxgCOgBhK1i+rAFsB6craOLq/vvTwX16rC82vojH4oUypWZ6UZ0LMVyPBnux2UUat3l2n/XQ4QqITZ8K18TUtF3NDJ7fG3yeUNvig20fB782WtfHAxebd431eHUvN/S/9jrNLypy7nDRVUde5X9NK7a22Fr7oXvECRHVLcYIxJJLLRWZGDEwm/vdzaHmHEKqqXP35XQmHzrkx6XgwdEdQ1DECl6A3HGMiZgdoZSli/zw8RG0yvxYp4cynbwEK8dyLmiS2HdD+vD+DyiiVQmRXwgFbx2qLVPReAG1lGVZEODVzf7V3eHjhw/zUqqYVH19u/vxj34wzxOnm5b1vhmGEEjVmQIRmKmULCV2MYx9B33HgRUSIAK6ZVPVWqsPTUIHVLVRHhuVfnPwn9z55wvDN7rPdr/aslhvLqWUCIO7q5qD11qnaQohtLtDITYPTik4sYqr6seHx0VMHFRtHEdVXZZs5uOuX10KWKOQdX7OhX5XSnHAeZ7P5znGiMAhhJSSB6rTeXOe1npVCAQsIi0HtRkYRAQz5sAhRuZaa5kXZtZSOXWbQ9a+p/UBkMOmAt2S+zc3N2Z2PB6bdISUenw8NpGuUnJAeHVzo6oMGFNydzA3FxXph0GWMpdTH9IQ01zVRfsu1lojQiTsmLVkJKqlhMTi8lCWm90epETspMx95CnX0/lonG9TSpym0zGCTrVko4DqLio5uKGblrLrBiYEhGI6iYZxwPGmu3nlIYIInE9yfuCYyNBO2Uq2EDElZ1IANGUOjFTmZexHNEMtcJrgdLLT2c5nNEFafWAEIEA1x6pYBbAxEQ2sa+wADwwhUOA2PvjJ8X+er/8UN/D6X+armBCujuaGS0/7f0eu/8X/vws2/+gNYRuhbgjkq2zQSzG4z4K7mSG87I36bKV02/+z5uGZ0ftDDvXSdbJ9BJ8HWdd74hootNKZEK00nia60Ha7pp/CVYhzHVJs9+PT2sYGJdfdDH7FDrq20k+3ytGuiiXeMiBPwccq3gu2hqGGQMRDSlOt5DD2qZiY6u1+//7+nonQIRKdl8VMd+POq4whzThD47u5hECcEqfEIZhDmSdKrGAlz4kh17Kc7zU/oizEkSxPpxOYgQkjIPrx4WhugXizji1wab7wPM+N4hriSgwXkRTjfjdIKffH87KUZVmYYDd0BP7mzSszexiG4/G4LEt/yR3ZZWJoU6dh5t1ut9vtu914//CgKszUVGvMkpsRIl1mtzXikBOBmcjnlx9eRbRXuVcLITbt3PYIbvdrWeac8ziOxMEAiciRAICY3UDca62n83ScppY0DoGY+TQttdYQeLfbTdPU912zTC3l0jyYEAIR11rUntrmmzErpTD6MAxmhkSllObmV1NE3O12jY3TqgtEhAB97GNkEZmmSS/bOI6GT3OzW2dv6+Qa+qEpyjHzzc1Na85qE3K6rjOzjx8/MuAwDNP5jIh9F8/nY0oppYgITf07BN53PZha9cQUA0kuY4pa8nw6qurp+GBmy2S7YUgxsusuUQCtp4fFZIwxgi/no9fSd60GVI8PH41iUgGtXfBcZoiUIgXqgtRayy5FFJGcw27fH/bpcAd3X+DdW9jdTGqAON7c+XKX378zNX48mziEgF2EFCEwIiMgKUJVmZYgjDXDcbLHY308Wp4CcwiduiIir8JlaAYm6q7urZHHkBgInQg6A+yM1K8QjK4aWj+Lzp/6JQCAhKZr9ubFxzeMwueJoBdu9z/i1sLTi1gnXGwAAISLzDM2us5FYBqrNtZ8e5wAYA0ItsP6NDm+bVsTY/P9EQGJGKA1VayjTf0z0g5wSf6sj+6qnYmA6M9xecPcVbfL18B5a8mmEMCdEJHwYl/Xz25eOl1YWYgI+JS2ur55eLXZs2Yi90uMtt286+yzA+FaEF45UUSEl6YEvQz3IMSaS0sopS5R192fzn3qZikppLwsFINVgY5vbm7O50lFui6h6nKejaDjEJC6mHJZqCullvN0TKG/2e9VSK2Ylpqn8/GxLo9jUp3PUhe0oHWZpokRAmFkSinJfaXALRW3qRG0C3I6nUKMYlaq8GVsAyLGEMB8mqeh6x6PZybqUuz7HhF+8P0fVJE/+IOvbm5uTB3R2+iY1PiITcRJteRMjbtC7ma73TgEjqjrAHpEEQkh6mWu4RYBbF7Ci0VIhG7o17cMHI04ctNXRWRVNYVSa8kll2UcxxAiICIHALS25s3BrFaZ5/x4PK1JSqBhSKWUJvKz3+9V6kqQ2mratbbJDxAA3EMIeZpLqWaOaIHRzEop6Eolv337dsmZiPTiM22F38Z5bcOBu9SR+vl8asUkRAzEKSU3U9C2nEopW515GIYudc0g7Xa7ZkXmeW7DI8/nczt+QBSpzBRjKGXp+67V5Jt/1nXd2PcMOJ3P4zB2KZUlt3FT4zB8vP+Yl9ynhO5WNRLrkgNCAI3IxijLFIcxL1ZKkVoT91JmMCzmXexQFEzQNCU2rUuesC5yOu5DIkNUD2ARiUIM3eC7w4TBQ0f7EUGxLkAeSw6nfRx3msU51KZaYcZmqsZqiYMuGQtCme14tMeH/HhPbtR1FdBDAGrsZHQHU/UiqtUVtY1SYUAGByBPCQkoIDwjoBMh+JMu/UsP1f0qCHAkhCZXBs8MwKcm5NorffH6H90G+IUgcxUHtC24N5u5IiM+EYYckexJvNDM21ddQgFCusy83UxCS6SEFAEAiUwVAqmZ2yps3a4CAACBg9mluuturk8iOTFGUQ1MYmoALV6hTzSI2kEDQHu0RVrBmRBBwRzccQUJVXcCYm4kVEQgpNZmAk0x1R2czAyBnw0AZZCLwg+ukR2Kmdo6ckCaVJYatRG3ju5gthJdY4xksPVw2janjAIRqRoQVZOQEtQcY5xKDUTo5IyKGAIS0A9/+MP74+Pj9GhuTjqOO12E3JhScQ2xz1WRcTo+IA2GfNuF6UTBdxyYdPIys52BxWRGdlBSc/Jscg5dCl2PqX919/p8XkotN7vRXFMIOataDbFjJnfgbjwdH7MYsO36XvUsBF2kYb8DAqkzQR46kGxp6Ib94fXd29Px1Lrf3J0IOaC7dV0PgCKi7lU1gGcVXaYUwzj07saBmFDcFtFO60hBa4lMpRRRaWkotSaybc1lQ2zRuQIYu5lJaM8MQQVnhJY7cXBzBHB1r1qLSXV59foQYxSxru8NsBXvl6UY4WlZaoXjaTFlNCcAIqzVipi7D0MfmJZ5ijH2KZRJUmByKEW8alNPlqU0jmqkgGYEhIbujk4GEDCULGO/W5bF3Eyt6zsOKz+q7/uWBYUWwnrNdYGWukDoukFERJTiGuk2+eiW6N+GHu/3+2ZOzs3N7/uliJuqKoAWE7QABKXmoe+duboSIIHtun6MYUCWWoBIwJZS3HTg6OZlXk46dyEOiUkd0blOIJJS8orOIOoBqVRJjmjO7skMSn6YZ+0L0H40Oj9O+xDFz5bnZLXX2ouGfGIiN+A0jsMBdq9y6AUj3dykN6/j/rBMJyuMpGU5+hDp0PlEFczYELyI9kBoaFVBNEDMdQn5hMf3dnqn53sjcvQQAiEDkrs2lHM1dMeqJC55VbI0RAcgcgs8ckdubupdBAAGBzFgw5BeoPMK6PTSIAAYGBBFBGgDScAMWoIawFVbFmKNTQFaeRnXqcAtmXnVH3CtrHxlGNSvHeWn99GezZEHgDWgvz7Gi6kBvExfeiqjPSXQnzIz19tGsd9YEOt5t9k0F299szS+KYMCooNby6m38sRaf149bQQD5y353uTdtz6A54UXuOSF1tNowOCOhAioqgEvc94RfAvEwLepC88sLV5dl0uggIit7ad9gIiQoeWcVRWJm2daLx5rgz+E5zzi9oVrTRFiSiOMH07nx8cjh1RyAXcOxBxT1xniYdwxoCMSKTAqiBMA+es3X5TAyphS4BgpwuEwIKiUSUA4xQi5lpnZVOt5KiFw14VlmR2UELA1WIXQ9/3t3c3xeJxLPJ7PqesaY72dQtd17z5+nOY58KrshGAxcNclMWXnru/8oyFACNz3/d2ru6EfHx6Otzd3qY9fffsNMycOS1ncbLc/lFJO01RKQaZ9jLvdngliTGaGoKfT8Xze6d3e1CDC1sOxrSt3N/OWbW/l0Lb8mLnaYkSNUKDuITAAI+KlCGbmCGhtYvCXX34RA5h5jORA4EaNg2uaq5nD6TznUok5BBJVsVLL+mC3btvGNm7HRERuT8Pp2mskboPaGy53qXnZ6uStKXorYscYx2EU85RSQ38AaOKg9w/3XssmMhpjbPJBzSVq5+KXdqTdbhdjRPNWA9hmUvZ9r6rLdFqTbwQpJQIgwDSy60ouAcQU4mG37witCBPuU69mapJSBMCAnHMG15iii4wpmbvUMsRExHlZqKdWwLjEuESIHZMBELhaEa3IHSUutbqUYNb42lqWISQTYWJgVgAAp5iceTgc0s2+AsZ+FFfn0Pw2EVGpw7CbTHm77FUAi7miVc2Lzkd/+KgP9zadOHbISWN1iuygTXCoPbu11lqySkUX6A1NvBJaYKQQKueIDshgriToTADN8djSxJ+6859un4YL6ztXr6+/B76j1Pqz/NaL/T89DHxRBN48a1+x+Nmu1//ftu2D2z/bi03RYRu0gogqsj0h25f7hRK61dBbPd0v6aANlz97qtf8nC2kAndoCtj+FPpAs230dMzbzzVIXsf2PK/feCMCXe5yCwXAsVHyN5uEn2sKI6KWRdmO/8XNdDNwNKvAKKXe3dzE1B+nWdX6kJxwlnp8eHw4n3b7/X63O8/T69ev53niLoWh85jGu5uSp27fiwqxho7uTx+w5DAfIXYcuU8glt3rkk/MoGaqBo4cLCZWUQ7mqn3f3ewP7779NpfcqOIigoRm1nXd+Ty5KbgRBXct2YioT10XAzn84MvvffXVV12I5GBRfvT9H+zH3TTPRJT6bhz7w+Hg0HiNoKKuNo4jAORaU4jQYC7QEEJKqZZlOmoTQG02NVyGIF5dQmw+yqc92y1gBVpvRwvm3F1FDWGNy6qo6o9+8P0QAjE0oQtRN0ORKuYiVqudztPpNBElwOAOoGpm5tCmtwNAI9fTJa2HVxVgWPn4WrI0pbZWznWDnHMpNfaRCJtEbuMRdV1HREOXWteFu7eZwMuyxBiZukbrbAWS9tSEEI7TcZvbvs0ZJqLEHDh0qTPRQNwN6Xw+n8/npWRE7LsYYwyIKcQQyc29moITAhOnFJkY3dBh3w25lFxLSLG0kXDEUsuYwkjRq1R1MrNSQ5dCZNOIiI1xW7S4u6shOKhLXfZ9h4iquSAwq7lFgTJNCHIbOaZuOU+RWMDCSAaESMQBmYoUzbOHREBgpGJWtUzZ11k3Mw8HRKi1dmYq4g6qFSriMvnpXh8e7OGINfPA1DkruoGBgRu4NR15d3UVLTWDVCkqs5twcAgcAhUkQidKZghGiqgA4EZXzPXrPD58x7at4Q15ttV8/f72PS8wYwN9usKxT3DlM9v1IV0D6csGhw3IzO0p/Lz8CRFVn9VRX3zq+tufjNhlf2Zuyj20CkO4qrqtkh+tB9gvqpzwpNh8yetfaFh26cKwS3+2XzE+obHiLqRSv5pottGBNsi+Tt9vOWV9Lj3dzrOZqGYcmimwltoC2ChSzX9sDh3A1Zuqpoa4jp1hJri4fqJqDoRQpeokQGFI0UWnac4mFZ37rouhLvNJZTzsU5dSl+AOqujDfIYAWoHcxAtR9/D4ocIZQj/c3IWuR2bfRSRbyrHKnGI43NxM51lEatWu6+8fv+2HfUjxQqvRm8NhziXPc7vU7j5N05KX1gkYCZkwhGY5+Obm5ud/9HOtrfRwODRr13Xdbrcz8yJ1t9uNY//N+3eHw4GZP3x4b8VqzTc3+8D0eHx0NHDtUhjHEZFVTdWIw5KXWqp0SVnM1k6Ojepu7rWums+NQb8tj5U+QJdCPT0pwjYPUQEq1i/evIpdb2aqFYFNgTmKlVqkmqravORlKUgBiImClVKttIGrDZ2vZ7uLSGRu6alt8duFpdTSMsxca61FVZWIG1K3I7+5uWmFMUQcur51yc3LUnJ298jBRFVLY65O04mZh6Fzd0SXXGop+/3ezIaub+rQDNj3fesERsSc8zRNpZRpmhz0cDgAgOQMMZjWpDFGFlEAwC70MY79YKrmNgz9EKKUpWMSFUPgEMWl61OPNDATMtSaQiRXNGNAYjJwyaXrOgQAB2TqU+ojRUrneeIYqpQTTB3wGKJb2Q+pw4BlkVKYyEQppDlXkEoiUAuCSs56PnlMVsHOZz0+Lsdjnae6LDnPHlOW06v+hgCs1rosRFRLFrKuTHZ6sNPRlwlEMHSkgNrmw6z+IbohOIEzAZNTVa9FrSKTRzRmI3QOkCLG4G3qaBM38xWb4BPO/nfZAHvOJ3zyub9jtrDbE7hvqHXt+L9E/58tGti+5FmT1FP06q17/mWPQ3sIN4mFa+8b4FkRdXPqiWkDSjMjWMuhl6fjSdehASVe/dbG6Wu/e12Dxa1d4Oqq2UXzhJvgmnnj3qg5ETWdDbvaGS/1BlWlGBrztSkzbKdGSETUmojwUot2N+IgInh1k9a6JYf2tNulWAqXOsd2e4io9Ym5OwKaFi2UmGa1aTrnUh3ApCI5IwbGGEhEmGCMEdUoBorp/XIfYkT0QLjME3cBEZcyF9chdqljJ5vmc86WIlaZVQsfxjyfQxt8QTEvEyEs82kf7piwifKkfS/mdj63w+bA5/O5aSoEhC4l1drOtwvhzd1dn7rpeIoc9uPu3TSP/RCIwXx3ONwfH29fv3r//tu65C+/98Xd3Z3V8nB/YmYpZRhHAJjmqXm1hOH+4eHu7m6aZsJQi9aqZi2Tt/ZDNVcdEZHIAPNlWjoAtIRVCKHt3zKhBmCwWv2130q91HJ7c5O6LueKAL6OXyURUbkoPxosc1XFEBNQnHIppaipEwRa12Hr3d10+cmf+UBtPXBgUnX3Wmutioi1rI3QzNzK2jHG29vbVp5NKZlBKaVFYP5U8bIY2J43uK2hgBojDd3KRq25NAPcx+Siza+SXMq8TNMUkF5/+bbWWuYZzMC1i7E5b4wYUoqRh2EwVS2SupRCKHkhohTYazGAPM+7fuxi5CpWKgJEpD5ypP68nCkSXAYGAAAxI0AphUpe1NA9EaJKH0Mi6gP1BF0fMbvludaCUgMQRzbzJU8hZ5gnOz5ASlXN5hP3g6tTKXZ8hOlcjsc6L6qKHZVSxSy6m6ksMyG6FHXRfKwf38PpEeaJDSWUzhyB3NHMYwgAooSg4lBNM5iyG0m1sgCYgYXAymQxGJO5BtxBF0wAkJ1hY3MAQIu9Wt4CrnIMzzD6CqCfMhbPU0DXTvO1LtD191ybig0PP339AvfhQpN7wvNtp5eW5Pl2dazfYXl+ho2I0C/VAnMwb19El2Ni4mbwmBmJTJ+d8HZdNvt5fSH8aupC45C2unVzrPCSBWoNEG3/a97ndeQOF2NGFznYF7X+lTaw7W9NpBAQsco6iq9ZC2YuKkR0XZu5nEo7HkAAERl34/njPTOs3T1uDKxmLkoGh92+73vJ5fj44Twt/c2+OEgkYCKrHQUV11xydkHs0edlgUBtqEU2BbRhHHJeYgyvXr06Hs9LnpZl6bvO3FUKUohM+/04Sdmy7TFGUWvEG0COgURKDAwAifnm5ubmcDCRmsvt4Sbn3Kgpr27v3MzRkelwOPzkJ78XY3zz5s0Pvvf9PsVf//W/nXNmpmU+m3vXJS2lzHMtdnf3+vb29v7jhyEmBCm1iKhILeVpmnQ7mNUhuHgDdNXxFGI0s3a5kXmjG4dAIpbPRw5p6FJVVSkcEhGvXfveFgMAwDznealmkFKcssxzVldzH/p+nuqyLC1d0/p+15hdvZQnLeU2TaFWmUtu6kOXQ+VhGPb7/Xk5j+PQ/PRmxtb6dhtOr4ruDGjmREjEOZ9FavtmIhAprU3v1atXbZhMW1f7/b6Ra5tflXNu5B8AuLm5+YVf+IVpPv3+7/9euyBdDCnFFMjdIXAgZiI3U9UAiA61VEaPXaiqqrWU0oXYBWqBoKnshh2YEFFK4VzmXDPGXty6EMWaLBISkQJIKX0KjGC1RgRQ6XYjmwCoeiG0LkUCAHUHRuYhRa2LT0fe7e34yABQsp4eiUnnuT58WD58M314P5+ORCTelGpRVV2q5MyIKpms1PODzCfKM9WCFMAdDFtdERvdpVUdm5YfKLiACotEs3I+K1gObR4qCVNA9xjAHYIDuSICI15yFVurk18/4Z/bPhM0PH9/+/8LR/wK8Z+h/9M+360X9Nn3nxmA7wpbNqxsBgB+5sTTi6059e1Bhee2Di7F221gS8tBb/tss7TaXze8hivbwJeRqtedaG17uqDwxPh8CiOI7KLV90yvFRF8TfUgIhOZr6VgW9t9V+kVtC1/t54HIII9SVvrVeXDrP0IAly0zLTejq+//fCxlqJVHIAJkUlMuxRCF4iozFPJuecAxDqV8WYMu52YPz6eBeCh1t3hbha8/fLOHb765mtL/OX3vqTFAX0YBikLE7rou6/fmYGhESAzlrns9sN5mWPoas5xSA+Pp2VZ+n5IKZ0+PtRaW+sTALoaRiZ3JNrvhhTDfJwQ8XA4NDxqk0aQSMz6vr+/vy+l/PjHP/7FH//COI7zdPryyy8/fvyYc765uamm9/f3olprfXP39sc//vGyLGYGwCKyLMXdaxXCsqncNDOvpq1nlC8KPHjJqPJKoAAACES2lbJMT8cHd9yNvZqrCiKCWwxJzc1cRMyAiJalnE8TIqe+m+acRZFQqw27UU1EaiPpI2Lf93QZLtbROlxlW5OqWmrZUouqzsx9NzZ6/qtXr169umsn1UT5WxATKbaCgao22r6Znaezam5lj4b18zw31YrIHIlBLYQw7vbDMLRrsszz+Xx+eHhoJYQ3b950XffTP/hJN3SvXr1SKX3qEF1rVvUUE1OMXccBU4jIzGqIKCJGBg7zMi/LEoj7mCIQOzBRpNAPaTnLXOchjpxI3a0KAGBgdFC3upRa681u1KJanQGCKEhl8Fwzd50hIYGDLzUnwFLK0I/LNLkwuQOxfWBSo1otBEPwDup0Lh/v5/fvyvFeSwYK1UvYDa1qKCpcK4BrXUBzmY6eJ/LK5AjWapt+YTySUxPTI3BERzBGYFcySY61CBDanGgcdZq865wZYnQgIgYEUFTQDdw2RMJLShyf55m3tQFX6L/lpZ85/k+1gc/k+n/G15/+6Kfvv6wB/CHb9WF9l6n4Qz4NzXE2QwRVbT27cCX20FBYRR1XgRe/+qTZ0wngVbPPtRlYq8cXO9EckGeGahXppAv5CqAZAGZCoIs6NG6sVndwtSYa/uzOgdkaAbQyBj3VJsEB1FaDIKohhDZmClY7j3blH7RX8zT3y9Kl+Hg6xUCqTjEAUQTbj7uPp0ciKjnHEHCpCYj7zpClSDHROad+uBn2XT/2YTiXepw+nE0gBgrvb0OXEr17/57Ybm727iii4JjGpCZm3vfDMPTMfJzOIcQpl9YWOwzDNM9trBUANAoKEYjIru+ZqOtSuxH7/X4YhtQlYjw+Pn777pvvf/8H8zTFlFoOer/fv3///uuvvq41j2NXSkfs03RExJRCdP7iy7c//+Nf/NEPf/43f/NvuzkxS7V5XpZSEndbqPdU+9E1f6hSaxUmUpGLKb3S5Lj0XpmZaZ3n+fWbN7VWNUghdKkTsVyrr5oQIaAtS308Hh0xdv2SGyMeESGmpKpLnplDyTmE6GAYYxPjZCItK/q3zI+o1jbz0BGxEXti13VNeb/rutgnZjqfz2vRAsDdQwiBOaVYq8xTdjNRdTNw4BiGLomKuTZa0c3toet7z9as4zgOXdeHEADh22++mae5tU/f3t6+ffuGmY/Hk7ufj8f9YXSjaTq5O4B1MXqAu7s7dzgv5zzNfYokBiEkYkNzVXM/7PcMOMSOzEE0xmCmS16QgSiIaUrdnDMyxpBUxQzM1FQRHMGHoYea3awLHA10mTgEsXm8u7NqCCmmYEuFKg/Teex35lXqYtPZDGVReDhhDJyChFrO5/LwMN0/5vMMFEUNGaj1cJiZaPXF3D3PpgvOZ6w5qLRR76vKjzu44aqJ6a3ZsMmFN50HAkKEXejO5r5Um2dOZH0v3MYyEBChgxpSn/y5fgwC+EV+5ru86g1JtltvV2h2XRvYxP2fhQufZGKe+bifq0M8/+zTFhwBCd1dzQKHFkSAQ1PLalvjq+FFKHgzANtpt92u6T1wSTaRUcAgXolQzYBYXRxRGZEILlh4ycYoMatbrdnMQoymGmJApHoR190uxGYJYKvTNq6I2bwsfd/7Va6fNrVIR3RCR7D1wWutSepKDNt50UXUE4ERUBFAzdEAWjLAwQDdzYyRbJUFdHd3Jm3cHnDRViqAqgYUfFX4Yi8ZCM3dwI2xlJJiPN8/BsegYE4ABkOHgXpPy7J0MeVSACCGSNEhssVwqhWYHIgollzv7u5wN34QPIn/5PGhunUxpIA85HpaDodh2PehD4bGjFI1Fwld2o03gHFeFgNUA4x4+nBCxNak2oR6Nq+WALsukTsTBLR8Pi27sdb89u1bQEO0YYjT5PPygPRFtKhiY+q//8X3EZk43uxuwDU92jI/nM6LSvn+j37u7RffO9zc7ve3TAO5n+7vEyO4AOFxWWbVXi2mNk6eQKuZoWsgl1pMlR3URKq6ChhAW8um4ObuYmru6ubu0zzv9nsAAvC+65rmWq2ZzIBCC1lK1YdpmbIKxqqiLg7KgQjDPM9SnT2AQ0CmJmBlzgBWJYY4aXEQMYsxGmGpYkSK1KWu74cms+zuXdc14RxGkFJCW/YiRBSZGSHr9O7bMyE1Bbqi1RQwRAJUYJUqJQcOHNgRcy0DcWAchiGlDtEf7t+fz+dW3N7t+rdv38YYj8fTNJ0ao9TBHh4euq5TByLuujHFeLi9LWomKtViSOqoLUdLTLVEwtthN8bOSwY1AOfIQwd5LrnU2/1NrapFARmNzZUCVCtS6tilQNgF7NFCJPUWOAOoq1a1Ssz18RwD1VIUoZp0uwOwOgQAsgolz/VBKBVIZ0cUJiEopZScrQB5Xw2qaQocIFlFYkZwtEJa2RadHmCaMVdz9xQNiAkBCtmMyARmxcgKZIlOaOweKnqM/SzgxEgwgIWs9P6RndGOLIbuyOBk0A2UCGpt7bLIyBy4cQnBFAwcEYmJbQVrag7llvBogNHY/YSIgATQSMpE5E5AhBBwU/j3p/4AcNuc8dXX2XjqgKvZ2CbDUCPbw8bJvDIAF4jkS1fXP0JuB65YTZuduS4Rb+Ko7TQAEduIGgQC3Dz3xt9AuxChLjbQL5SkJ+fuc1s7ACJqsfmWzb/+SGtJ9kvz8MU2rH0R27lsGSQ3dwfyy9zYT/JO2z/XTwLe7A/qwCEQByByRzVTX1V/53mmy3RvbEVpREBUdWQad7vztDDyUsr33nzfEEREVEvOu24YhyH1wynP53nhsVcA5pBSWnIppUZ1A7o/HR1pf9gPkR38/cf3+30fUxzHseuiqzPzMATB0nUDOCGTO0gtZiK1IOJutztPU5McgFWCuAMAQmdmNHP3ru+XXHLOgDzuDsfjw/5w2O3HfuxDTLkUB5AqTND36c2bVznnlMLDw/nxeJ6Wcjjc/fgX3/7Cn/ilu1dvYtcRhTyVb7755v7ho7sRABOBw1KKplhqbZPlwRQAwMTMCEGsNXi0oUWNvetVqruv0ysaXYtwdZlvbkRaDHGJZQkRWM2M0N1zraXUKmLIbbZo13VzzrlIrRWQmxq/yuLQ2gVRRYkI0EUEcZWerbW2R3O/36U0bqtlVZlmboo92+Jpcxdyzo+Pj+fljIwp9oBUS65VASgyxhgaRxMB+n6IXaymGDAZ7/f7JgM3z3Nj+zSd5yZT+vHjx03HyczGXd9I+k0cgoj6YRBVqJ7nxcy4kUOIHTCX0kfsun6IXUQ0tZColAyMISV3l6rVXB3NLRHd7G8+HD8CcJdSIEawS4ivOSs7MAUk8KwmaozIPJ/P45tXUpEIU4x5yin0tRgQGmHkVLOXJWuuogYMFqK5mbTnJoCLG1FDTr88ie5WK+S5LgvXCiIIXitgiK3AYqa8Nr06IpoqqKJDJDaR9kKYmzfuRUzE6RiJPJAHhBiAGICBuI0gJqKIUVBbxoYNnR2gVZv9KsP/LHf/DDpe1H5XzqE3DZ6rDPy6XTvffDX86roG8BSCuPtTH9iz7SlJsvEp/9EMwIttdbcvrMpLYLQOSiVCv3Sm4cr/WcPt6y95YULwc6HN9UaXyKsR7NrT+OkkyG17CrgIsTGxmmQjre132Iq6LeZwAIQ25viFGbi2HIgkIksu5k4hursBmbsDxpQamN7c3DSd/SVnNwFmFVlKxZiQGZjcLQW6f/9OzW5ub1D1MA4xhCXnh+PZmGIMmDqNwR0GHmPXz2LLeb4vUqqOu5vbV3djF9AlvT4cdv08nzb7iZGHYRSnGBNxGvo9Yfhw/77vut0wfDidW5J6miYMqxB/SomRqmAr3oTYKeDru1fD7tDF8TSdl1KLSKcWU//weBp302EXd+PYd917kcCMXfdwf//u/Tug7hd++dd+9HM/9/btFyH1YppzrWLzPB9PD1qrqiCmQOTu87TUrgvMlQARA60Lxp9mMD1F3ptFR8TWrdbuYFNZaH1bzK1W7ETIzH0/KOB5XlR9XpaHh6OaUohSpe+HUurpNAGt/fAcEgDkeam1xhifys6XUexEq9hECAxIAND3fdeNbXhAg+PN0fHLjLMYYyvVmlkVIeZw6Y3IObvjMKTD/lDydHp4vNmPXdcxU82FOr7ZHw5pRMBpmh4fHwGg67q7u7v9fv/w8GBm0zS1yoRdZKUDUSCmiFIqM3fjKKUqCgM3Ohwi3t7eSqlmFhBbQCtmXUgUAjGihSJqyCGNRaYiFpgDBXUH1b7rq1RrYTQ6AHII7pC6PgKg1LIsQS2l1McIqs08d11X8hKQLIQ5L6rIfSxqZgoxddSbU67F3AAJHMzBzR3ADZAocAQnBzRzMBNVrhVECVxVyV1Nq1vkIKJSaxABEbg89mu4r2Zm7EjmiQIhGbSH17wKnGcLbARIbkRAhBSAgzFRU/BGdlVHA0QjY28TEv2FAbi8fpa02aAfrhb05X293mGD9a2KifidNYCn15sExOXf2xY27/s6gfOHgOx3bds3NEC8zmz6mp2/bl4gQIPNOl3S96pGF+t3beKaH/ezHANe13Wv+Dzbdp0R2j7lashb6xBtyg2quqF/q0S7OzWlB3+6eX6VFlPVLNLScFrF3NzJEdRRqgBA6/1p9erIHGMMXeIYKesimgLvmXOtIUZVXXJ+/HAfU5wbacadHZB87Afr0tx+122ecjgcFMPxfKzIH9+/n2XZD2ns49jHWpexC33qTo/3CGQDhBBvbndDv+uGfS0+jjbNc67TNC2NyraNl4qxa+fVD0lOpR18jElVS9Wl6G7f55xTPzjinKuoxBi//fChi2Nrsp+m6cOHD6379Od+7ueHu1ev37zZ7/fLsoRusFIdbF7mh4cP5+MjEnQYCBCIwbzmIiKqTbDkIlfu2vxZv/QD42UoynYvttfM3DjpjXnZfP++75sWIiI2EQiZ8ldff6MQqhogxtSp+TzPIlJVvQ0lZt66o7dgt93KaT63NoNG6zQg4tbZgLvdbaP846XM29x/RGwmpAF9myRMxEPqALCUolW6mIZhiCFoWcoyvX59G/6/lP33sy3ZdR4ILrNNZh5z3bPlCyg4AgQhgAYSKFKgFWVbPVKrZX6YmBhFTM+/o4iejomJ/gNGIUtJLbVIkTAkRYISDbwpVKGAMs9ec0xm7r3XWvPDznPuea+qKE4GonDevedm7nTLfuv7gEoaTXG+mJ3dvgVo6/N1GlP1SURUvdEPf/jDegX2tLt1cm0cRylWu9b7cbO2bfu+n8/mjHR1ddW2rZnVVjOIBMdtiJGdivgYTSW0zabfrscyb1vfzmIIBFjGLCk30bvoLq8uAcA5x2gMGLuW1Ya+5xg9e6VMPiAYh0AGqJBy4qoSAOqcUyMrkAn8fDb0ShjM0DmvVY8aCYnImVO3GccCCMjsI8Ck9WYKqCY5WRp06HlnBEXEmZlKqai2UqZygKmJWFEEc8SlFFLwzAg45oRmIGpFnGW9WhcTjyZgSITkhNgIPaIClFyAEQxrf4HfJT74lI06/ABQGUPRbCrmENVsc1LM3dvSvQ+4Ln0/6TDsSddy+PP33NwhbmH/0/0en1r6/qjVvvOTXEDvbnbXte4nBiaeqb0fO/ga7GExu0XvifsrXHq/ADyoVuFB3aku6XA9T1303VW7vmQHPs9AgRBQzVQQdgUiqwx6oDapvWOdZDZTsZ3aw9QKrqk9UiUGAAQzMQOjOkRjGEKob369FIgoKoo29GMxMyUwG4chNB0zj2NfxkSmrNq4Jpn5GFQVFAVtu9kQY28aFstS8vHp6eVQVtut48hETcRxTMfH86OTI0fmCc6WcysiuXTdzHvvm4ZdNPQGTqw03fwE+e17bwpQrRvSjoyvVq4XiwXt5qOJCJgB4P7jcyOXC3jvCeuDS4BM7NXsnfsPKitGymLkPvmpTy+Xy34YZ2c3ACClUYzMMKUMACmlftigFV8JtkzdJOpOOWdrJmLka6q/XeoGQMwsZcKA7bO9kgsiMlUNRY4xEleaa3bOqU60KohIzJsh/eCNN4YxxVlLoKZSxIZh2HtB9s45l4vITqmx0quZWYVvMrExE6GP0cya2LTdrIpZmmFlattbf9jxptTHu5J31v045wx5HHoAWCwWs7Zl4u16nYf+7OTYs9Ocl0fHi+XMBbftN6vNGjIScc0k+r6/vLys0wk0Sa25uts6RQEAnh2odbHpuq5OqEXnucWcM7Cryu+IWMXgmJmssPMAgOwVVJFiGwJCXyQYkgsudqgyDAmZyDlCiyEYSBIxsKJqALHrcsppKnaZjX1OZRSDUljNEwx97wBFVU2GJEq+AImIb9uSaegzJEEiilHUkBhAh7FPquiDMimQZ69S5Z5NRVhNSwYV57jkpKU4wlrgYmZRpSpZboAmkouZgYGJmioCWJFihgYIWColrSqmDFtTT0BIsaE4kA/ZcUHwIRgYAAsYOQaVUpCIqgzdPug8BB8+ZWD3iMe9hVRVAgK8trpPGeT3tHLwJCXBQVYxHfpwfgv+/Cigp+rp+2O8v2t5j21KWMAQwXTqWli9QFOyZFJ0j93ewzpVdW+3J3r0A+m7/eu097pPXZp9aYiIzN57iGFqT+yu/vXZTRxFZjUWMJ0ASfV3T16KmtDgDmSGiKCmIqDGRGDGVJnpBAAQAA1MxKT2Kc2yaM6C2Xs/JqGd4jmJkVhAGnJWBY7eO1JEQnLeHy/njy6urq62CXmbi8QmtM3tW3dvnh2BjARCBI65jCMjWR2NI1SO6NvtqGIUQ9tySG++FZp5Q7BebwDAOZekqGq1FMNmZbsRBx8aSwU0j1lg0xONMcYYnaqJaJYeiXjW3b5956WXXnrxxRcRsJSy2WxOb5/GbnZ+eRljw+we3r+vKjmn9eV56jcA6h2VIsExMYEIGewHq1XVuZpWP1E2rYmjqiJW7cO8vynkeBxHqKAyIu89TFSGtkedqcjF+cV628/mS3C+T31KyWBC5qWUEXFn7mWfmNZwpxb0zazrulwYEULTeu/Zx2o09zWfyt68zxigAhZLqXmA7TXXRPrtwM51bds1MTo3rNep3x4t5ow4bDbPPfPsrI25pMvLy/WwMQBHTZ0/uLq6qq/DbDYjoupyKlS0vgITHQUYE1W6oTp9RojHR0f3HzySXNq2Xcxm9Uk+OTnJw1CGraqyD2UcmZi8Qx9IhQSFvPdBkJiAvSezlBMDOOIxZ1MdtaDomNPJ8XFYLmQcL/r+uG1KyWHW5ZRENaiaiFP13ucxkW9i06yHTOhLRRCxC7M4jqWIEiIEr4ZpHAs7ICxI6Bx4r5UD0gjUtAiUZGmElEa1wFxyqhDExnutMpnX/UWrhlnUTAQARFUADFBM600HEwAhtaJIIJ4JYwAfkJ0ykqmBgTkyNiUzVp6oZ3dB83UF/yn8/hMmaP/JDHY2Z29k/rxG9n2+OJ0vgoEeHvX/Pxjovl60X9NTruY9/2qXT+CuFUxm15E4vGukYIcImmL/aZKLeB/3/Rnp1XteqcOMaYcYenqjXWOwGpXrE5TdbZDaVqzWaCIQ2YOF9v3n2nkEBUNAQEYsZswcmm7Tb9+9eA8kFVNmZAQFRYbRSgERNiOiLIYigdkBMlgIkduGPEvbZCnEREw+BINNUUMgH3yzWKjZgwf3h351cjQ/nnUl59z3hEZE7JjYgYvN7FgEFbBpujGP3dGZv7icBxzH5JxjLl0MselSSiKl5LwLMXgYs5qyD8BODPptD4g+BkMTs8V8/pGPfPTGjWc//OGPzObz1erqwYMHMTZHN26J6NV6XbVK1ldX/XaDpkO/7TdrlcwE3jNYYccOSad5DhURJVDVcSyISNf9eNuBhOvnqZWlO8mBygjEoQbp10CDGGNVuEu5rFarq9VqsVwq+iSSi4oYMNiuRg+7zHJv/WtBqU6BhRBKKeyoaYNzHJpWVbNYHeUtpTTNvF63uqTKxb8XNwaACvmfohPA2axp2pYJyjiM6+3Yb5bz2dHRsm2bJsbAtLlabbbrIW2Dd8TuatWPQ6rjF3WFFxcX+85EHeAoE6rEvHMKhgCVO1pVj46O6uswm83ymKp/IiJH09y1b7txuyW16MOsazfb7VBy7GYBQ/ABVYuUtm27pl1fXCKo9D0zMVEqmR0Tcco5ldItl+vVFSTajCmGMGw2bfRmIv1QZ88UMXgvgEYYm9hnIYpIVNSyKniH3goAhiBZB9WCmAGVKDQNBG86WZJSCqmUnC2NWJIJ1LihbsyOiJgIEB0RoZGgqumus5dtZ+/NsoiBiIiBAKOBmagNhtuowbsQOEQLHpCRHGFtARmoAaqpCkAtTu7i0RqDXhula2NltUh/bcd2RgmMngDf753HvvLx1Oca6R+axMMDvbu08+dyALW+8RTIB97f6B9uB/nOdYkHgAx1Wuvkuivl81SBgV2j7xqOOTE7k3OuiFhtIuM0ivWUc3rqPO2A/OepS7xfJkxjartt37+pHsEU6+2H3cMC170K21Xlal3JrpMJQEQ2CCHkNJIqI0oRArCqFlsrlwZmwADZzDGnIloKwYQwrwFvHdmdAO8pjYLCiIFTGi+3m3a+nC+OSpaz2czfOLsY+2EcrAy+dgsXi20/pG1/cnJMLs4Wx8+98NLxrefPzm4i+r4f19t+u90c37gFzOeP3liv12bWtq0R5pRSnQzw3peCVbWKUJRUre97FHSeXQii2jTtnbt3X3jhxZ/8qc8UCethXPWPVPX07HYIoUgZ09aK+uBKypcXF2Q6Dtt+dSXj4ByJKBFUKg5EdOy8c3UAUNVU1XPFhk3VbVXb2+d9oF1vIrMTkVJVa5qGmZxz9cFrmgaRpWhtva63gxkAcUppyCoiSIRExUxE27ZLpVRIWP1v2zRHR0e14G5ms9ks52ymakWkjOO0N93NH8guSfXOiUjld0PEtm1rnG5mlaez73s1y2qyLsG7xrmm42fv3FzMuuB4O47bzfrhZoOmwYf5fDGW8vY791KuJ64xhFJKhQDVLPn4+Bh2IIg9UERKqRGVqi4Wi8oX1Pf9bDbPPuSU6vveNS0ipn5oHCPiMOa2acm7dj7LUoaUOTbofe57MhhS8kDomA3brkWmjlu4ulLUNjZoasTz41Ny4fLBfXHmPEfvMKeSExAiMIiUXIIL7F0SUXSEXERBhFyMTRyKKhizQ98pZdv2yBioUSYfW1GstKbXqBsVEEVVAMw5uVrBRDQAds4QuUZCYGgyQf4q/K8IEIFBLkVUDbSYgikiuFpgEsvbHr23puWml+gIydgBkdY5VwBTA1YCVKxxJ+yj3n2p+9AE1RGhQ/0A2AkO7zPOWleoGcTe2ti7Pr9bNwWmevt71MYBwB1SX+7tptkken5ts3frq9ZtX8+CJztv+/3si/WgVtmeEaGOAtQlEjolUi3AHsBEyyTqgrx3a1OeXg0rmYIQk9bE3SaZGq870YI6cqVa655PXYV919cmHmd86rcqlb22YndhUjeA6rhNTdQUCUwQkNWUEdHU1DyxqoIomuVhBHb7A9RL28y6UrKV0SMooKEBUhIDAEUUMKPKtKXsEZMRqWF1ClbAwIGB+q7ZDoMBhULoyM3j2PqhwsKHvNk8Sjx79uWXctf+8OpiLOOYR5M8b+YRdBZnijib3zx78aUPf+zjp7duH5/eQOecc/12u1zg9q23hqsc2+6jd29/8083r7/2g8XsqJSSS16tVzHGYb1pF50gOO+c47ZxrpTNdhOahSK2XdO24eTk7GMf+9iHPvThy8vL1WpAkpwSM8+alglSv12tVlKknS/Y8eX5wzGNWVI/rrJts2196IiJPSNo9GQISE6Y0XlFBvZZlIhApb6xwTW1AyxFpRQwA1MmUEB00xw4IwE7B+jIETp2U427lKwGuaTtsO3HAhwRGUxyEjLCUjyRUIihQ/YOaUxJwQyk7WLXNEhGDGbSdi2gOk/bbT+OfSm5nc2Y3ZB6UXPOI3sjBiQjFMAs4p2L0SOigGXJAlJKERBEzJpV1bPvus4hLLrmaLkg0JzWFxdboDiMCdgT4f3Ly3EcV6tVysmImDnEWOm0ZouFIwYA9q7URFZNVRjZRMkT76A+y+Vyz69lhkQeGdsuHJ2cgRQppY2NQ/aA/ihcXZ1fpZGtY98WzehoQPQA5hyqDDlz8EDIyJ0nEXXtvFA4X11pmKVhoKQn3FGEMBv7q8ePN9t5ZEe2hRxR0CxEj0nGIkZqTZsUQVgBFCjnRM5BE5i9Avp2Ybm0WJFX6pgYfMOtUjCqs2CZpaAIghAoe3bIqIrEyWwEcD4W75G5AETHZnXa1sS05AJAJYuwM8IiBgYi6GCSs7IatCWzPsM2qx98dIEd+YguGGGFeRIYFgUCNAQmZEKc2NzNrqdNYRcUq+lTAlkEqCaoTOgru/2+dkSVgMCutQRq2XlyJGJPhtsT3YVOil5mB5QK+BQd9PtttNMGAADk94ZUHm5PBNrXuYLtiZMQcYLhAu5sMNbRM36idnbtk65DvILAVM0/7qz53m9VasZKJXQdzb/PhgdNxcMyQi0s735E187zfQps75cJ2Q5TlFJiAKhlocOdHGgS1B8774BAFBicgQmCAcS2ySrBuVHTbDZLrFuVMY8cAgp47wFp0XWXjx/fe2e4N/ZbFWCctU0zWx7NmjA/euWjH/vET3zq7NbdZjZD9kNOOScxRQSx4gLPZu2jR+XBg/v37t2rBfo333wTAByzqRqSFFU1NkTgCT9tyMTeexU7Pj5+5ZVXnn32WTNbr9fb7Ri72XKxWCwWkvJ6vR62vap2bacq43bo+21KKac09Nux36gKEJZU6tgtIhAzMpPjmterGVVw104aCJFUc6Um3KeJNsGdp+ehkuRUXFOMEYkmeYO2u7y8TCnllBERidab7TCMjiMRjkPqt1vXdCGErJLGFGIopXDkGGPXdWY2DENFy1xdXY3jmHOK0TvniFBVEShGh8ghRh+PTKFIkpyapnEEIpLSWEquT7hnRtOccmBq57Om6YJz88WsDSGnYbNZq2rf933a1hT48vJyvV4jopo5H8hPFBTeOed9fQUAIFWOaEDvvSPGCaFKJWcf3F43pj6i8/msSPbBnxwtT49Pn7l95+rq6oc/+CGxB1NEdk0QyQZKjtN6G0Lk4C5XKywlIsxCIGYyM8ltN9sOIzl/dDIbFJdHx29cvo6uJLGmm5Vx6NdXQ86g6WTexdncqhgOunoraxmPHRt4MDFkF0Kfc86qnJH9UFbMLhfph2xmbL5WXaRyOYGAquREUkiVEJmJAMGUmckFdg6JEOto4U4OEQAAVKrQqRrgkMZCTOzGYSRis4JEhkAGVNXhZZIR1jFZzBbERE3UqEZtCCDAoCCwU2NnrEIwB5j9Q4Nph2sBBSQjqKpWdt0EvrafuzLDe5ijgx3tP+8RN/sj1jX8uRzAE+b4/b9z+HlvtUH3VaMnarWHPQ8RqYNWsEOr7usqewteWUUPgLJsVdWr7Hb35NL2f/jfrVPtbce1Azjs7u48FLxvf+X63iAeJlQTLqVYYmZ4Hw1bAAAmMqpU/TkXAwihUQEDYAQjBDNPPOu6IiKDjONYkMNigTFK1rGM8+X8ckyr7XY1pkIY53NDjO2smZ+88qlPfOpTn/rIRz4au1ZUtv3IBAaS02CqzGRFiC1GPr94+M2vfz0Pa0O4Wq+KStu2LqdxHAMHVWQOzN4MN5uRCM1IBI5Pjpqm6br55eXlvXv3u65rm9lsPnOxjSHknMe+rzlc27Zt1677fuy3aezTOJSSpwq1oWPXT905ZmZyjn3wzjvawXUQrcoGgZnZmHpVDSEwI+y0+gzAkYMdHdNms6kOgJnBZGL9cj7nXESHMfdjdr5Zb68qjFKB0phzzga27BpAK5sUo48xJEZEZM+H5dDNZlOVWEIIbdsAGJIzsy5GZGdmzvlK+J1z0lI8Y1E0LWBKCCHWdKQ452fdsus6Zq5oEQZYrVab9ZWq5nFAonbW9eP4o7ff2mw2bdsy1QFKqtie2ipLw1glJIdhyDk3IUItjCA6IkMspXjHMcYYY61i1T629y46180X83YWYhxS8bG7fee5q6tLlL5pOyAZhm0/9k3X3b5z4+L8UqSIiOUMYJ13OWePiEhjEkOPHF3TNTM5OjlrHj2+Wq/W2/6ZO7dXF+cGxC6mcbvZ9pgLqo5FGGvNxoJj54MZYtNZlqFUaL0zRCCH5JBcylJU2DsEJiJ2AdkjYA2zySRwnQpAM9NcTA1V0Mh5olr8mUoCVuMuMwNAdgzeZdA8Jg5+zIUck2MyBFGtcTygJwZ2gOQBWcEKQFbLxbIoMaAqIoCYTWLNlSeA9kE3XZfj3xUoP+kSascYKsH4NY99/QxU27p7aWLY/ffawRz+196LyOfPzgB0H6HX6k3d3s+MvacDsD2+ExEACWlXM38CM1p/O32w66ujO55O2HWxkWtRaBf/k+1TAJhg3RP07RB69WckAfvY/9BL7FKomp09/dv326Y7cXgFVZ1zcn1af9YfogEienJFpYyJGYkImZCpmBJzrpO3xsTsYlDHBpBL6WazYcybbS+qzrvgfWF3fHrjwx/68Kc+9cnP/txfjm2b65isAXoyMrHStF5yDt4PQ5Hcf//V73z/e98dho3m1Pd9xfsT0Xw+rxlMbBcxBOaqbyWIGFxz++adVz70oVpKds4fL4+6bn50dITolNExX11d1bSvaZoYY04pp2Ec+5SGvt/kcYCqw7Hj8XbO1Vy14u6JyTFOIADCSgNUH4xq8iqeqt7uCtKUIrjrZNb/YoXxOCYiZDa1fkxjLleb3silIY3jyMxEzOQ322ECPrEH3YrIycnJmHMbm9g2iDiOuYLrK64JAHaM0BMGLMZWDEXEu2BqqYw5FQCN3jnHOQ25Gs0m7hTBfNd1TdM0TTOOowoMfb8aR1V1xEQwXx6J6Nv3H2y223Ec61T2dUxGEGNsmkZycY4RYb1e5ZzbtmUmFfHB+apKpuacY74GI+7H2bz3ofEny0VF2wFRcM3xCzfv5Pz669+4WJ2zYyVQKOt+vUAgtqr0W4Yhtg0AikgMIXo3jNmIGKiJXdvp48vV8y+8/M1vfWPd90Ma5/NFf3m+HdYAkFLpvM8GjMTRNxTQOCuKCHHcZlGgbCpqisyxQR8MGdGBmSEbgg8BkAHRCCqzoa+Tf6mHkkCFEBwzqACiJzZRVCNDmuwZwDU1gqloKWIAzDyUibcitm0ZBzBBAkRkQIfELqDzHp1DJiOnCMUsKbIYMtYSrk34+moM1QGJwgH45ymjpKqHDmDnHtRAcTezYk8UjnDvQp609Qf9gMO5gXd1g+sfOtvXld71a5wakJX6X6qYHpDf+ZzrPdJu6qpu9c2c+k7XA72TxgA8qe6EExXXVKOvggGwayToTvpy12I1Bd2VkBB2c7n1cLX4s88eDn3dtTl+kpb5+nJr9Uk1G6hMw7WkMLFJH6z2elis9tMqxFt3k2tmBpP0GKqqIakqwYRzvb5E1b3tWD2IiEXVjAwQUHIhopIUHBliSik2TfDeuchsvg0phIx4dHLcj2XcbNS7YRgTmTn3wY985Bd/5a9+8sd/PHrfLJeiyowCAgSq5hCcJ6ekiCJZcnrnrbf/6I//29XleRrHlAYkgqqMaNa0La7XkrMV4YDDZlsRjYvFAgwW3azkfHR0VM80hCYn2W4GHzzHcLXZrFarLjZt2xJg7XMO/Wbo1+PQm+RSck0CzDQ2MeccQ+jziLtBkHpzoDKtgzGigVGVAr0mfVPnaBxzjYnRqOzUbeotqyWgOqKVxcZxRHIXV5s+FVFbrdc1ihTRMaVqOmez2dCvS0mztjGT6Nk3EQDGYVCdHoBKL9F1XaVhQLTF4sgQCB0QmGBKSdWQg5k0wTHT6uqilNKGEILXkh355WLZtm11Y2O/Xa/XpUyqMm0zC01crVZvv3N/vVkXgxDCUYz1eSulVC5FH9xs1qaUttsNIxKDmjRt8I6IIIaIquOYwNR518UQ2qb61yplY2YVHjqfLZ3z3odZtwzNbLE4JnRpHJ976QOvfu/bpWxD06yurnK+6vth1sy895YKeqdm4ziyd6pK3pMzF5uUMhGfnNz41ne+PetmMbYXjx7dPD5izd654HjYlpQzKc+abnNx7gA4ujIkQK8ZfOOAGiMXfLtJydgXJclCTG0bQBSIfXDEfqqvEDvyjtCpaB4lD5q2HtQ7RwqI5JkYyQAdMQE43rH/AjATM2fA+g6SAjM6NKnEv6a1CuHReQQGYCIyYGQC8EiETMYmKKJawKr0M4B5wmkXqKosqKQoSDgJmO+Nie06vfAkjlEn5P2kmVtB4wCopjA1K7HWROhgKhjR405TbB8EPxVxHloq95Qp3NtGANtXafBg3upAoOZ9YZd7XmwiulaBh6ejY0RE3I/d2qFHqf/dIyZVlWziAEAFcmQ1Nhdh4L2S8n5AjJn3N3i/PeUS6uf9UneHrqf03ue1+83kFA+tzOFRiKiSwV0PDBz+F5/YOxHVcjAjG5DuHD9PQsqEQBUQgAaMpGroiRwXlW559M75VRIoZpel4Hx+enr6c3/9b/ylX/iFZ59/4fzBA8/sydCUcceiQAQgFUwjKTvnzh89/va3v7O6XIno/fv3fXQxRkNoujaX0hDGtkk5bbcr52nbr83s+Oj47MbJ1dUVEV5drbbr7c2bN6+u1pfnV4vFYtiO77x9v7DGECpiEgCqbtc4DsOwGfr10G/ymECkDkOE0Dh2TARo3vv6dHvvvQ/OCuEUXOuEINAa2tfaN+64RlQ15Qw0acLszVyNLeoc0Gq9IRfWm9Uw5qabP3p8rqYxNmUiD7IYYwixEnW0MRLzmFI760w0SRWjp4q0IaLZbLYnHWnb1ntfxMwsF8mlMHvVApq7JhDR0G9KKU1VByNo23Z5tCSiksdxHKtyr0omoOV85kIUkYcPH15cXFxtNqrqYiimVoSIFCyruOARQVUeP34sIo44Nk2MEQMws+QCACA6pgRmgV0d/lKEihkNIVRXV085hnY+P+raeTObOQ4++jRm1/h5OPv4Jz/95puvv/PWD5ZHxxfnF1ISgAvB6hUuOWfTUcUBtN7P29aQc1YCCE147u6de2+/teiasd9sV5dHs8ahoQqZkAoUM8LYtSKWzYpZLctrUeyiirELZJQVgB37AEj9OBYx9I59NLPgY84ZiNmxStI8oiTShBMcxyoIBQ2pvvJqNQkAIkSwHQK0vraKYEXAgA08URYBNDZkch7IIzCiJ/YxYgjkPBJFc2ishiCoRQEJyAzUSMDIEEHJUI0I1QxVVfZ09H/GtrcQh4EyHpRx9mwF+ORU8L7msTd0k+U5/HzwW7ffIzzhBiroZ/9X19z6YNeO4f0cQP2y7JRx/rsbHkwF10T/Gv25c5J7669opKQ7gRXaMZXu1z9lEk8O3R3a/f1/ay5fA3kpqTpj2KVj7z415xzsiYjrMNcOfrr3LravaO2u9R48ZfsUYNfA0acqfwAI6ACBqJhyRcgSVwFNMiDvkmLKiTF6H1bbTS45F2Dnbtx69mOf/Ys/9fnP33nlg9TGPvWG2jYNWyETUlSzSrxeiiCAFQSg7bb/ylf+21f/5GvD0EtKktV5u3fv3vHx8UsvvfTaa6+ZWcW8kyqBzLumbdvnnnvWOd9vrhbzpp2f3Lt3r2m62hSVYuh0NpttS1+fxXqhav1qGIY09uPYl5xEZRxHQiRyi/mcqMpkCjN73gk1V4bkyQEAAIQQah+VEESx6nBVndH6P8TKYMQ1/tjX68dxHHNhdtt+ePT4fL5cvv3g0Vi062YAUKTEGBVkNl9uNltVdUQxhpRSbIKp5FJMlRFzEVWtFRtE7Pt+sVhUsoc0lpRSzgUdt+2s2vT6eGzWVymlUN1G15wcHy1mTb/drlerqvS72W5r6en4+GQ7pMvLy3fuP7i8WmdVJt+0rW+8mVV+1up7xnEUUbQCYG0bvXNoplpqlBA9p5QG1Vr5idE3TfCeU5EY42KxqJ2AxWLhve+62bw7bbtZ23XkHBCu1uu2bX0MJs3i6PjOM3ffeP3mt7/x1RhzGoachFk0Z78DKu4mJ0rwM/ZhzP3bP/zhrWeeWc66R2iESIGH9eWMlUFQM1khyyo2CEXnmS2romPHgcwRO2MPaMYucChFCjL7aEBp7MUUkXMpzE5MkZ3VXqcaaAZJVjIjOCRTBbU63D65gQo9fxIlaGZV8BcBIzspkg3YkNgDCLLzyKzqEZkwsGNi9M48A6IDQoVcDIoaqoAiEhgKGjK5yfhANdgEYCC8N3rv6gY/tSozM8v4ZA9gMmU01f2hMiBNNWtSRSKuX3uCqeHAecCBJ3Dvjrvr0Q+jZ9WJs/LPZ8+fCK6fALceYC8rXsKs0lxUxgUzM9Hr/H1vWGEHla29ElWtNAyEtK812Y52YndH6akVWZ2SsCe8Qo36VZUIS9G9y3mq43v4DzuY/KrrnEbVDlw0QCUkfvJmwr7jtG/67Ig+zKQoiKIaIDK7SmZACFgZUsFqdTI2QdFREwfUMQv5GJvmk5/8zEd/9a/f/ciHYNaNiGKy3a4ZwXuEUkxLvf9gRGaahZBEdBzTV37/K3/yx39K5ETUh9h1s6Fszs7OXn75A0hkgOOYmHmxWKzOH6vJiy+9+PLLL7dte35+fv8+qZST5VHfp3fefOvk5KxpmnkzZyAkXCyWpZQ6AzyOYx7HcRz77SaXMaehlNGkxODTOCDA7Tt3exUmAkPvPRMSMzM775iAQCu9m/fBJKtCjLGU7HYztPuQJ/ggOnnX+vMKnhORXJIBEePF5eXJ6emj86vtZtt1MylaeXhKqc/ANEiMBCWnxWJuBttxmO6hmooul8vZbFbzgOVyGWJQURHNJZkpEtbO6nY7EFHFCJWc2hBD8MHT8dFR17ZXF49r4C8lD1K6rpvP56pWiqyvLrfbrZm1bbuM0fkAgIKqO9mMknMljyNEx6ym3jnvPE14ukqrVYW6AqgF50OMTCQitWFQE6M64YyIXdsVgVSsRY6xNTRkFtPt0DvuIgc1e+kDHxqH4fvf+W4b2quLy36z6UKct11G7Ferhme0k94LxEeL+ebBo9XlBRAsuu6dd95EK6MWb2PHiCYIAiYmpoDrzWY563yMpS9IjOZqld6zG81C2xbRNGZCJiYbEXHiyzODvh9CjCJSFCIYIZoKiFSOWJ1YBtCokiSrI3SIWgqoq3VnQAKbWolVLpABPZELvooxiBoiOEBf5aGrcpr3EAIGD2agoEW1iCIYsbEBgopAHTg3Q1FDNFUlNBWs5JNUS98IB2bxCZuz294z0je9tmMHGPeJ0472xISHtv29fIADwokXdQeRr1eWgFWMiKo+br1UYBOV7mFWAjvytaeWvvvJvrwFYHU3zqxyqRMQAZhIASQwNbVK+UsAIloHqBEBd00MRGQAEJ1mOPYV9gNyt10+QXuHU70CIogCAddKGpgRmqgAoGoxUGZix6paZBqoq4SDVlNFUWYGwsoRUmv0eECCVKPdnazddQWNDNUUaC9VZQr1AJRzIXZ7bZnaa4Gdwq0pItPk1zyLFSGzGTZNkx3023Hk9saP/cRnfulvvfzxT+dFUCbRDCVhSbBZLxZzTQOAA3BEjBM1GDI4EyXIP3zj1d/4zf+wWq1ykTEn3yyEKfXDpz796ePTW9/4xneMuiTDsmEmyTE0TfPiSy89/9KLoNY17avf/I4M49gPvCOiIRc2QyrA3nsTVCMGWm22WsYxDSWNw7gpaQ2S2JLBKKbGlhiWt26cv/odNmHvVdWI2QfnpqKQGhUz71zWQoBgNmYBJEVA75kYMEfQnLOqMXpRRTVH4AicQyQjdoKN8+H84rJr2+2QLh4+WDaBELfsi+Z+HBGqbvsIJmlcO48hOO8AyaeUjJwJ9Gk8Ojrruk5U22bG3jVN04/DOGwkDyKSRZpuQYxZEjoQlc16TQRH83nbREKLnlHL/XferAi9YewrXLZkffjwIqVysV49fvx4Pl+klEIInohMU86DSqVrLjkDgJSiovNZF9g576MLIba1iiVqOReRsWtbRiio6FkJCiEAOLDtenP++Hw2n/V9//bbb8/n89lsMRR/9+4zxycnN27ejk0bYmy7LkQXm/moJcxnRdIrH/uJ+ez4e1//2ub8Ikhu0c+jB7940A9ZTIBHo2Lcj8oh3jy9sU09E2xlA5R1vTZTyrEfsokihKIaHDtqPXfrzao56jD6bJ65Q2wUELxDjqOP1jgXsomknF1sx2HMFWsDQJEVFRiiI86l5AwG6BgEshY0UzDvPSIj1FRa2EYmssrsbAJSAnOuzxmAkCGpA0TCPGYAY2Y1dUTOMTABB2CPwEx16opNjUwtJcRY0dGmTB4Z2SHhVLIHm4jiAOtAGEw+QBGJEPTJiLOWI1R5YiyVqVVtZgZqBuiqg0GadEOhChjWjMEYgEoSIkIXkIjrOHRF5RDBzpe4vencpxjvCnz3Ifh7NK8PKypP/XD6DNcdif25wb4PXE0iwJ6DrFbIdUfG8H4pkpRpeh4OHaBZHYJ3zu0ho+/+2/22yzBA1ZAq4xvUooftKs7T4Btg7RVcl5524CLacWfCYTPcdtlKvR5PHRhJVRCRmOXaJ5sRWo1bEKAGLfUkHXP0IQQl1GaWHK3B6Obpz33+l1/53M/HW88N4ICwWCEEz7wdpI0xem+gMjWxwAzqPC0hFZPH5xdf+cpX3nzzRy747WYwM+771Xr18gsvPvfs86++9qP1uvc+JElm4Nkt5ovzi4vlcllEuthojIv5HK+RV8H7sNls1LAZx9l8kQdp2jDkPPbblHopSaSYaUpJSyEkx04tIZHzPrTtdrOupAgV3lOxm0RECFgZ3wkBaj1Xp4tabx4TGyM4IjKDNFodGjcE55z3kRz3w9C0syI6jKMYPnr0uGnaGNvtMKYxr9abqYJfSkpjKaVpYoiuaRsiTDkTUR5GInfr1i0xTinN5vOu68achmFIJadS8jCaATnHQEQOVIHx6vIxoN04OatRTmxiDP7i4qLfbkJsamrF7C/OV33fi9jF5eWm3yLSzZs3a7WnKvqKyihS+eyqDWDApovOcQzctg0RjcNYVKaIBGE+X7RNs12vg3OsGplQSyl522/M0IfgYfaj198oBm1jv/8Hf4jcfetb31pvtic3zk5PbpzdvPXyyy8/9/zzJ6eyODoax+QdcWhe/MCHh21aXW60v3CxXfdj45z3PpfkaqPJlBzmNDrnrZQkufHcOFqLBCZAaJpmLJkBB5MkZmieyJxPqvNmZuJBA7JXZnMefaCm885zCyWX7WpV0ihaiIiIEaGUwp59cBNpIxiAecciBU2ZKiMbThxQiFJKzpmtMTM8QPdhtVNECEKADGhgFfkDQFTJoZjIMTvvfEPOE3ljLqgGJqYqkFISDMYOyLQAkAEZAZCvxX8EEESu8l9gSLUZUQ3d+9iop6zfPviukeL+n/vqUC1CWxWVsutZqHfH/nX7c80BHP7ZIdfEYXry7u/XTXewGz0gNd2Z/v1Ybl34E0QOh/DNd3mm9972k42qCnBdlnnqCtb/36+qVgngoKO7XwAgKljl6alf2EuYHSYcddr+ENo0OWq9HsJ+1yWdsvWxHytF0nR9EJQAFJ2vgtqoaEaGAf1ybsHL7GQDsGX/S//oH9/6xCdWROfWuxC9ehNBqhKV0sRohLvhiuuyFe7QSl/6nS//5m/956ZtLi4unHMIkMt4dnL8mc98ltm//fY7iNjGJm2vri43N44Xi/n88cX57/7u7/7yX/1V730iqnTHMfqITT8kIgrBDWPvnN9sVopW8oCEDMZERpiTmAmTA2Ktk7rsFOF4PuvaWRqzdwFs4sr2LngXcAq0pAJikcDEKv5nenCIYAc62HVx21IE6mmydz5utht2Xg3OLy6dC/ffuW+V6q4UNUvjyIhd05jZkFL03jMTYTtrXfBSNOeMSE3TLBZHY07e+fl8jkQist1u+77PKqraNouUUsq5OWkNeSxp6Ic2NLPGgwqAzWYz77nvt0TUtF0Fj15drS8vL5k8sx/HMeUUm+a4bZfL5aNHj8ZxXK/XwzAQMwY/jmPJmYii8zE2IkIU2rZVlUmO2Mx5T8QxxhvL40cPH6JaG3wX42LWtk3ouu5keQJIx2c3T07PkmKcLRTwbxr2Y97245tvvvmtb3/7YnXx9ttv/9f/+pXlcnn32eeee/75H/v4x196+WVlTqLzG3c+/Kmf+u7X/nCdh1mMGSy2zbBOfb8Ks3k/bJ1zXdvmIoHx0cUlOyTTlNI2J8f07N3boZuNay1GBpZLaYMz5zapmA2BHRo47zM7DEFji+1M0aEiaAIuKa1qgbqU3LZtSsl7P58vWFTRSnYQvHegppJERImQmB17x67WQOqzV4MiRATEao2RiZiYNDqfDItViCkSGldJLcfsovPeR28+IJMRGoCYZrERNJkJO3IAbtIcBKVakVCtbHPg0BBNUQnIcGrP/tnGbW9V9uarlij3v8J9fRvQJpr6Chy5LhyB4mGgv/8r9wR48dBKvteSzIwOJoH3bOPvF6cDHOA7n6TglwmiVP3u9PaKCKpUY7o/vffMA2rZfZ8o0c4QTE2/XWLx3qcG9bJDRZIgAjOzw8pWDbsxtJpP4E6bbG/9K0uD7io/+8xm7z/2h9vb9KcupqpWouJaqK1NGzWp4C4DUDIF8I6cYwocjua5CXiylKaBu8//xKd+8o9+dL/7yCcfuwY8WtliSYRgJmiYxqHOCIkITiTj1w2VmiG99tprf/hHf4zOb4aE7FPJoOq9+9jHPjabL996+x4RA+TNZq2SPcAHX375+OhkM/RvvPHGm2++2cWGmWezWUrZe68GbRsBLMbQuVC55o2sSAnEJY85J5Wc84hghKjIRA5YEUwRTk/PvA+V07iS2OwzAAOrGlh1chPNzKgCMXdPM5lZztl0p+CGSg6dC0AUm3ZMuSjMuvmDR+cppYePL7LIYn40Ztlerft+KJIWi1kI7urqSiTHGBHROeeCV7A9//NsNgOAtm3b2VFFYa5Wq8vVFQAIWAihiKaUj09O22Y2DEPuh0gUQii5b5rmxs0bKaWSUgXy37lz5/HF1dv37otIaLrtdkjbXsW8j7PFDAAuLi5Wq9UwDPViOu+3aUAA57iLDSISYtt0TdMoWEol59HM2uijZyJadM3YbxvvY9e03t26efrJj3/0mTu3ovdAgTncee652dGpUWjmRwKUxOo76Hx8fHHxztv3vvf973/xS1/67ve++9aPfvCDN17/+je++uILL7/8gVc+/OGPsG9e+tjHb9258af/7Q+vHt4PIA50ebTsry7ZZHEW0OGYB+/jrG2325DSAKIhRlHdjuMwZkeMoVHqt2PvYojBE2EaCyn6pjGNhYLGjpo5tXPujqRYGpKC87FNjoZhKzIpH4QQFotFCB5Fc2FkAiYRZe+YohVpwQVytOMeRiZgrpk+GthuwgkIgVAZJYtVuVDJRIRoRERoZI7YExM5D+SQ0JDFUBEUTNSKYalkw0iIbMiMBMiGYAoKsuctrBADVWVEqBUeeFoL6yl79ZQPMDOQyYLBblKyfqiTYdOX7YkNdp5m3+lERIc7oOjTiB2VPZBmn18cLqvusT6gcOAM4CAfgeu2J+wPX3/lfB3XKqoKUKd4ilWB5l1tfd/0OLSzsENBVT9xGInvvUItJ+2dx+GCGR0iAkKFnzvnzFRE9F0XGnZ1nl1aVe0NVF0wPKCe3vUYpnZIzQkqaq1ihnDi8ZjaTiIGgM65seRKe6mqgFhBjoYA3gGzb6NjtoArM5zNxrabv/jinc/+peUHP9LE7/ZNA+wxjzMgzhm9M1PNWsax65rqGc2salrWIlU9u4uLi//0G//p3sOHilxUDMHM0jjMZifPPfuMY//w0SPV/Ojh21oSltR0zSsvv3zj5u0333n78urq29/+9o//2MdX/cV8Pn/zR28yY0miZo7ZOQYE731KAxCaaZKsVrRkNQ1MRQoiee8lKygDmkO6ffvuZrMNPtbWWh3mCKGpeFAyAVMmcoRgQIxKWHaSO3WEIsaYU51WmW4eOScKxLzdDsvlSc5yfnnR9ykVWcyXwKRj3g59P6S27ZrYlJS1yHK+SCkRYhMbYFCE9WrD7GazORAze/auTv+WHcWm7uhdU8pNO1vMF0xQmU1Vy7Ado9Pj5UxLWl9dVF2w4+PTR4/P33lwH5FdiFdXm1IKEQOpj6Eq52w2m9VqBQBN0zBzEVkuZuwc7bhSPFftyXHMSUQYITgyMymJnduurgLQrOlunB3dunH2F37iEy8/90xK/dD37by7++wLy+NT5cCxVfTAjkVpp8p3erw8PT7+0Ic++Lmf/dwPf/jD3/7iF770pS89vPfO+aPzb3/nu99/7fXjk9O7d+787Gc/8/O//Ktf+E//8fFbP1wED46UYCxlm8vNtus3Q32wg4+aUxfb3MmYkwElVQ5NxuS7Oan1kiNR0zQGuagfgZhDaGZ+eSY+Yuz6rMjOeZ9qiR9kHDfeR7WiqrPZwgyGMXGlVTcAVRHRnANB13WcJKcMBdoYa/Ba4ziHVZRNwQyZjUAJ0TkULqJFAZCQjJi4CsezC00HhD425hhdEEIFU7SsZRA1HxUQkIEcoDNwhs6QDVRBa+cTDaoEcH1sVJWAqtDdoZF8v2D6sNVKta6glbsaiIicAyZCt2/28q4scehI4CDhsIoCereTgR1v+qHh3tvuw89m1ww/77kd/mo/osXMh3UR2+Fw9wbrKXdnBxJo+0NPVRe4Fnzf7weJDge+Dosz03V7Egf2Z2y7VQESWRE0ePfJHrrGvRMqIvs06qk/ISIx2YvDVLBgLoWcA0Y1IGZug2sjEmQiWczDM8/d+tiPvfLZz8rtm5dDvkzbEDCNWw/gATWD6kiEwzh4Rzx5UAQwKbK/YtVmfe1rX/vTP/3Tx+eX45iIoI0eEbuuffaZu6enJ/04PHjwzltv/+jy4uHp0eLGzaOG4N5bb/zUT//MK2++8qM33/zBD35w//7922c3zptH4ziklJzzaCCl5DwSe0RWNQXVkp1nR+i8s2KFyU1REhExsEcE73yM8a233opNwzRlijUDqP6dFKwS/JXMhN75SpArBwQpRFTJllVNAJlD0zSpyJDKbDZnF+7df7tkdcGfNV0SO3982Y8pJ2m7NnZdKWVMw9HxspQC2bpZi2jex/WwVdXl0QKR2Qcid3F1udqMqppLqXQ6UKtJKYXoT0+PAeTx44uSRwAY+/XpycnNk2VsYj+OpjIOY9M279y/v9lsvI8ppc26R0TvKxqHcy6qpZSy3W6JqG3bmo50zmVN9bOJRh9CCMNmW1LOWQykgqFVMnvWkmKMiya88oEXjo+XL7/4wisfeLlt/Ftvns+Xi2de+sB8cSyI3gf0BACGSlLSkJ1zlf+QmJyj2zfPbt08++jHP/q3/tbf+Nf/8t/8we9/BbT84LXv/tc/PO9ms35z8bOf/ZnP//Iv/ca//Tfj1UUCo6ZdbTZh299WgBDHYk2cMW+bqGayyalmV/2YfWxny+NLveQour0sasqkyOSCxAZdZ+3cd8c+NoNabQ8SoXM22CiamLHvN8vlcYyx5n9ggCpWhABCjGSCiJqG7Xrjkbwh1wqBKsNE0HxA8YLkmLy34kyV2NOkLobEDGBEEJgCMQeP5MAxsDdGQ1LQIlLMikIWMR+QGMmji+ADOccOEQUgwU7jl0mNCPZtTty1f3cm5NA644T+e49fmT0REJuZKhCy1sbFE1Gv2YQ6fA/b5Q7TgSeSAJXDA8CTkfjhT2SS+X1viOje+NqfWcdnZrRav35anBJ2UfZTjmpyDMz4pMQjvtdh9lcEdijS91vJU5uJVg/n8LoqVR+e/T07PMeyU01BgJqKYFUaeNeaRAQQqtZUVXcxqLgwi10bjjoALaYWY7h589YnfuLsp35G7t4FhfXjByeNa3XLVpBYMBT2pKNDAtAYwz5j0YNrVQ3rD3/4wy984Qur1TqLXm03DiGGIwC7devWiy8+3w/b3/+D//ra66/2wyrlse91+dzZX/zJn/wvX/4v5+fnH/vYx77xzW++de+d3/zN3/y7/8PfOT09VdXYhBi7MWdh08mLg6qoFhFhgkqBqCY44WXZEBUBvRNTcD6EOAwpxpap1isphOB9nByAgRY1s6rIzkw1e6tJY6141nhKRJDAkYuxccH3uRC52Xx5796Dq6uNCwGQFGjYrMacSintrGuaTlVTLm2IqMaAN0/PtHI4I6jq6emp802MrQK+/fa9q/XKxxnANEulYKWUJKVt25Pl0nu3Xl3l0hMZqj5799ZyMfOEpuny8aNS1Hfh4uJizGJmRWW96QGAybFjxyHnvNn2TZwoMdq27bou5zwMw2azNtLFYh4cI3NK49hvQghIBlg1EomZADinoW3CzbPjF+/eunvnbDabf+Cl5+fLbkyJQjy9fbc7PRPAVATArCQFBKBcioh67xjABWcG7LjWk0Pjb9+99U/+7/+3n/nMZ37vd3/3O6++ypAkw2/91m/+3pe/+FOf+uQHX3rp4dtvbs4ftd2iH8umyCaXxkWxFNk33WIwG4dtjE0fhmFIAigK5GO7OErFXOrBwIAKoACEEHw3525JoSvgkLRpXBq2RXrVvqTNMGxEy3I5b9tGitRMkZGhFCiiuciYLOVg5tkZEik4x1hAzVylwUBCxB3Eor7ASEzKpIhMQQwZQKvtB2NGZnaemD17zy6Y48LOCExNwMRAzARMDQkR2TF7cA15h2yEGQHM0q4Tp1hEKpoRkdQUFXfzQ/tA9sBkvYcRq+n9IdKmsiJoZd6hXUi8Q2ASEexMwVO1HLcXAzZ7gjPnKXu1t/hF5HCh+yLJ+xnQw4lZ2mlhq2olrT3cPyGbGaGb6Ll30277AP+pxdTquSFWuHzNCqrLtIMxZniyjkaIqjL1fwDgv+cJDnMLE61XxszgXeupR6m6j/vj0sTdaggHTsCMiEqpnNtETClnJCZmIjbG2dF8lGEz9BpCuHHjwz/5089+7nNXJzdX4E9UZLV99mhJw9ojDuLEsTCHUkSUwBhpkstWFRGmyo0BqrrZbH7zP//n3/v93085J8LKVzGM463Tkxs3bxbR3/yN3/jq17+NZKenc83j8VF3+9aNF198rl994t//+3/3t/7O//ihV175wQ9/8PDhg6997as/9pGPdrNOSu5OYtAwDiUrMPsimrMigvPEzGpSIWrOOXZOihQ0ImQCMfVN67xX1SY2TNMdrwxuiECEbKzghqGPbcT6/lTCS61pVmUBIecqlSxmmwhrU0rL5WwYxvVqW9FWs2627ofNegMAgLRcLnMuKjkGn3MiJPaMaCLZAEQ5+NC2bdMuhjE9fHR+cXkJCOw497k2gceciGixWBARMm42q5xTE4OkdHJ68txzz6wvL4Ztv+0H752P3A9DfSPWm822T0ikqm0bACClcRzzYrEg1JxznSTo+77SujHT8dHx6enJer0e+n673TYh1Ic5BG8mjpGJCcEh3Do9uXPjxrO3b83n7a1bZzfv3rh//0HKZXFyvDy9MRYdU/ExJBV2XId7vGHjG2Q3jiMCIRqSUxUwKCpMZKgf+dAHnrl18/zq8qtf//q3X331rXsPHj9+/OXf/Z0/ZH7xmTt3Tk/M+7g4vnj8+NHV6sZxcC5u+nExX6iWItI2TM6/+aM3U85DSqLWzWYCBgqqxiEAOhFnLhT2CdEpgmPv/TZtzco4bnDYlrxVzSF4crTtN961sWliiOOQWLRyAKKBJ6aioFAlFZ0P7IgBOAT0jIQVQrB785GJ1TvL3lyx4ggM0dhYEb2vYGRVUEUI3pFz6qgKlirswHsGAMTOkw8uRG4abFrn2TEgepWezECqnKAiIonWmE9x1869BgsiIk0Q9HfZomtrpraPYvc1c1M1VDRAUCSqncopDryecHoKBYQFiW1SSXW4o+OvrHKHFrCugQj2tf1qVJ0jM3saxwpGVXzSXUfH++yBiNTKnlcBAOtvKm4JkatdrhSzNGmBTc3M6u+m3ikREhdRdFzvqCrUngQdGP3pFOpVBiWsvrJycBuAEYIUYWYElN2QV52LqPAxQjIzqCEqghk8pVGPu5FgVUDkGgVPxERgzDgxQ4GCIRKIGCGYGFFx3jvyOSkIppL9WZtiDu9cjW17dffZ01/+ldkv/NKj+UIUOG3Y46OLex/8yIcShwKgatJvmtBwiJeXV7PZTHeYIqu9B1YzccTDdvzGN7/1xd/53QFpAIAsBqgKOcl8cTxm/cof/vH9ew+GTT6axxaYg7s1P/rgCx9o25Nf/NW//b/+r/+vb/zJH3/wxee+cXby5ltvff0bf/Tscze7ZYhOZ43PAoTOG1iRwAhZh5zZOecmGkRiB2YKUKyA8+Q9MWsps+XxZt1HH6NzKoWdGiAzMYIPTEgOTIqOvZZS2hiIyCSXMoIaIxmzmSpo0kIOmcnUMfv1dnAupJwfvHOv78e2m/djUeG0zaUAsZt1TARMwM4xcmaOTdOnkYOP3gFyUjCB2Mwurlbn55f90Kecjk5OQuOzZHY8jgMSLo/mlcxnux7ymInQiizni+VscfHwcRrT1SCiTETnD89zKW3bbjZbJAohjCmFEELw4zhutqsYGyRTExeZiEykSAaTNvrTk5PYhpyG7WZlZrHx7LhYQUcz12gpjOpAPcrJYnbndHk2j8vYdCHcPF1cPHrr0aOH86OTxcnRmLNjDcE5Que990GsZmjZAyBkClxMDdBMCJCY5hiScmYEDjfvPvvcBz/00isf+fEfvPHHf/LVb37zm+ePHpYxvfrDB6/98P7t27fu3r5ls/k767WbHx93bfCNBUdNhjGzo3mYd83FuF3PgstlzA5OjhZpezmWvBl7H7qkBKF1YZHEAYKPVLAIljRuQZQEvLqj+VJQVkMPLlBgDB7QB8eEZpYmqI46IlNDUSPGZOiZjIgCY2QXmB0RIzkHUNlatc5fInp2VIowGSJqLepb1RPS2DbkHDIJWDERBGAoogqMSMgOXPDdzNqW53NoPXmPhGrZClsZCAnygJBVq3ARKQIasBIxGakqEu0m0oDq6GbZEUo/ZWqQqzx5VSbUCo1lZJSpmgKCogJenfNqmaCKJVxzFtRdOazjA1PAej0AvPcSTzkNm772hAIXAPCTEf3eczxFmbD/7WF3Anf9STMz0d0I2+Tu6KCduwcI4a7Wr3D9w8M+gb3bgdYcbJLxkmrXYZcrHFaQ9msBgB0gaOp416+x48P97z/XLGRfE5NdtqSqOhFNAwCSC4gFgBBFUjHP6JgBJZcuOgRYX5y3zSzNFz/2sz/3zF/6XF4skmFgZAAp+fLqYr6YGyJUnkFmkyKI3ns4YHqql1lB2HEZ5e177/yzf/bPXn/jjW0uvmkNkmNnklVtvdl8/9XvbterNkZTdcyzJi7a0xdfeOG55573PjRt93f/3t/7p//0n/7P/+B/+rEf+/j55flqdfXaa98/OT65urz46Mc+frnqgVAAx22vUrwjRQ+ElYi+8vRVxC0pVxZMAAjsYmw2m03XdWwghKDSNE3wzAjEUIfumLltW0LYEzzEGEsanXOsNToRqFkFM1tk5q7rUiopFyK6e/cucbh3/9F226/XG2b2MYQQ+mHIOTXMauXk+EgQYhdjN1Owzbb3ygD04MHD1bZPYx7GMYQwX8yLgg++wvPPzs7m8/lqtWLise+ZcTlbdLOGEfq+R7BK8DiMabvd1rz28ePzUgo7BuTK67nZbDabDRG1bSMiBuadB7WsaqKnp6d3bt5Kadz26/Pzx1X3ka71OSznXLuUTLCczU+PjxazbrGYO0ZCu7q8OF+tnn/p5Weeezm0S+db9o3tVBdEhL3PWYhYpYACEDp2BgRAAmZqIiJ53G77GPzy6CirxKb5xI9//Mc/9an1ZvOtr3/jt3/rt3/nS1/ot9vz1dXD8/NZ6+7e5KOxHB81IDaWHNoOt2sCYKLFfLa+fGQmzJzLMI55Nl8aaFHJquCaYjCkwhzFLPUbRVXNJfcBSh63mgbQMZs454xciI0BqUHwXo2QmUOIVlCVAAi5qEKduyVC59A7do68I+/QefKMoIhmUoi9saITUCRDAgVk9kjoHLEjZA+1DFSByUAmJkVFDNXMgIjIx+iahpro2oaic94ZIQkqmFlGc1M8qaCojDUJYEM1xQkSOpFaVKsCANeE/odmbXrBrVZ4rukMAMAhgRmYAlZOhGqiJ4ZB3HWt9mUb90RacVAyBrvW5n3CnuJkYuo6dCcWfxgST9YH0Qxgpyz2Z5SJ6n7qmtj73YgP1mIR7Ipn+zO/3iECTBTR12NZe1ToUwZ6VwI6LCjZu792eApP5S77Q+CTnfr9BamfJ24y3MNAd2U4mNgwaqJQ/5/QDSklJh+DJyJQZxApXCxO7376L3z4L/+V7fJYiDSLAqCKgrRtu6/kERIAai6qGkLYX8n9GVFl0HT89W9844033wRyZtL3vQMroATKiG+//XZJY9/3s6YJnsBEpMwW8ebNG7PFfL5cGsKLL774+c9//l/883/1P/39v/vaa9//3ve++/r3X/OvcBnyOI5NE3UoZkCMjj0TSD+YmSeunMMVOilSKAY6uF/z+Xy9XocQUBRA1TTG6BgZoQqrevIl22w2MxVHaGZoqKqMkHNm5vl8brtQCJEMfEo5hCZnubi4unnrjnPh7XfupZwvLi4rb2WlLVLVtmtl7OfzWWi9DxGZkP3VekXMJZXVanVxcWHE4zjmnBeLzjsvKUcf0jA+c+du0zSryytVzZJCcNH5W7dvoMHFxeNShAg32+1myP0wwo4Or/LTVRoJz66UIkVmbRdCCM4nNWCMPuScCfD5558/PTp++PBhP2xzHmezGSKmlGr045yLEdVIS/ZkN44XgYyZ5rMZqAik2M5zLqenN27degbJI7qchP3uKVV1zqe+dy6MYwItTYyELpVC5ESLKhRTU1qvrwCobbsx9Y69c+y9R+9n1H32c5/93M997sH9f/LlL37xy1/+nTde/8HDq/LocuwzI8Xnb97UYkVHcx7SWBGPwfM4DuRaRkPG9XrjQ1genWTF1SpdrVbL5Rx9l/KIjoht2K516KUM/eXD83vvzGeN72bBNwO4GFpmj8TkA0PQkmoF2DtHtUBtZmae2VEVF2IjVmJAUkYmhhq2+sJZzKsWlWLABQyACKkiETwScgDyDhGNEBEqWbTWkgIAIpELLgYfIsXoQ6DA5F195QnBrJiKIJsigIKAgCChwoQEAXrCuB9YS8Kdbo3ZtaJUxafuA9NdtKr1nHdl6muzpnZttA+J5K4HwZ4K+eEgKD7camBbrUydmIWJawEPv7MvvMCTKMxDo7mvVDxhWwkMJuA6ICiCgSkYe2dmgFiHL+pesYIycYK97y/Hu5e9P7ruNkQ0U9gL0Rz4mP2uzIzfi/riKRCRHnBR7HGBorJzkEhEpTKDok0tJ5r8d023i2bJEsmlUiDBiij82Cc+/tf/h3xytiVORR0jpsII220fQjCtPHKECMRcxiQiVVr20P8hYp0Z/O73Xv2Xv/7rV+t1ha9ozqVkAA2OHj16dHZ6HBwDwDgmJgSQEPjmzRu3bt+szKDsAxr83F/5/L0H97/8O797enrWdW+NfXr7rXsvPPdMzSB98I4cA5hIBl3MZyknZmJGkRyCi9GLyFhG23WkK2KqlDKbzSwXAFWwGD2hVQcAZh5LySmEgGAmBRFNplvs3BRS1bolETl226GEwIZ8797945Oz4+Pj73//9Sr+NQxDjBGYmqYppcQYzXSxnC2Plt1swd4Pqaw3PZC7Wj1eb9Ll5SURDTk75xSsaRoAaJpmu92enp567yuo/+rqyrFbzBoRuf/OvRBcKcUAhmE8v7xi3xBR3/dEdOPGjWEYKsKHmXPOdQ8V67ndbmOMxJBSArUbN24Edu+88852syFCRmIkM1vM5kRUShERFRnzSFBR/MKO2ybGGGaz7uT0iL2bzxcvfuAj7fwEODrfATtEq8yw9cWpaHo1DT4COUNkqIopmK2wWdHSb1Y3bt0OwQFQkdIEH4IrBJFCtSw3bt/6B//4H/+1v/k3v/fd7//2l3/vi1/4wte++72c9PXX3/jwi89Hp2zg1RBsPltehUcpJ1cYyADZB39+cbEd0p1nXzi7ebxaCTlMuXfOgRizyrCRYbN9/NCGdXCwvVwtXCRP3WxOHIlDxUwDMTnHLvoglIwQ0UDBqhpa5aci59F5dB5cMO/Ne0REJpRirkDx5BQa4OLUdGqtk5seU5rUfsSwVKUuJMMKTDYk54IPsfVNg7HxTUMRmZ0BKBXLJuwVM6IHG83MyEAVTAHRtBhOI2PvikFrgvseAi9EtJP/rRX1p+ntYFLv3eNWuP4TAUy02jID2+cCVUnuukgET8b++4i4cjDUf5YDgWn2vh57Gss0wwrHHifGTdoRQ9Y/112D13YQz8l816UjTjjZerbMtMPd79czfdiZ4Lrbfclo74T29QebRjD4OtHZuda94a4rrB/qnzt2dUCs7nPvPGBP/kNUl4o7AQM4yBIOXSDV+RGtwsj1ywZKSBS8SzJmAGjjuej8pZc//mt/g557/grNfADTiUWEIKe0WCyZWXf1saprWJvPFRBZI83pxhs9fPjw3/2H/+O1N95YbwcXGlNAg9i0m83V5WZVUk4plaSllBD86cmiDJv5rH3huWdu3LrpY4xNawDIFNrmF3/lV//Dv/u3P3j9jVs3bj1+/Pj80aPlvJvNuiGpKQBzdPPV1WXTRCCX0qRQWFnhEBCIq7p9vT7e+6urqzpjVR8GH6P3rJKrU6kRTVW5IgRgqtJdiFC5JUQMjIgZDAgdkUfUtml/9PbbJ8dnN27eVoVSZBzTar2ez+eqOlsuJtfO3Lazo0VYLJbtbPH44mKzHfqUHzx4dLVaA3nv/Xa7bbsZGM7DYrk8RuaUiokuZvO+7z277XbbNe3p6cnFwwfb7eb09NTMcs7Mfsxlvlherjb7iYH6bMQYicj7uF6v26YhIill6PsqLVBKArXlckkG5+fn4zCoahdjaENKo3Muxlhl3Gsc59iBineMZkzUNsEhLuaztpvlXE5v3A6xM3BMHp1jdqK5hm5s2PdDTdAceiaPlXyWTCQDWAyuFHn06EHTxCa4EFypehVoAEJIYMbOV2OSSm5n8x//1E98/DM/+ff+57//+1/+L7/1H//P3/vjP7738J0PvvT86XJ2MzYKKiUsTm9cXd4voqjADAgWvOv77f1799r2eHl0OwYqqqZ9yUlBZLNKq/MybCyNAOqaWAwYmCk4P1NyhtOgbhV6NCIgQjPnGQBQuYgAouMA7I0cOE9Ni01rjs3MioHzwNmoKBI4JhAHCI7EDIgBnQGgqzNKXCfGAM1UBSCrGjkXg287Dp59cE1ThSiBDI2QPaoae2BfgAHQDEHADIgKqgGaGCJ63E8dHdTGiSbkKkwl6Mm4g+muCA/VRe2i0ZooXPdudyCf6RU72DMh4iSeZQdUAZOx24GknsoDDv1BHbuFHfi9HqnGv9eFeyJ4L5jQtQU/2KAGxLvu8FN9gnfvxHsv8t6Zyn6R1UDXSPP6cuzAsXsHsM9squncn2nOWXe6CnZwIntzv6cjrf88zJBsN3kwmWIzULLptckAyOyAfDAjLMROfXyEDB946dP/8B+FD31g4zhpIS1cCUTAAPhqtVosFmqGRAwkKiLCiCGEeoLVsFYHRkQm8Pu///u/8zu/W8wKQBrH5WzRdbPN+gIAxjE1wTdNs1ld1kt0tlzkiCcnx2dnZzdu3CAmHzw6b6LE7oUXXvj5n//8v/oX/7zvR1RrQnN+fn55eX56824/lmLkmefzGUgRQANR1UrXNt1EM8dBd9neXsCZmU3NOecImZHQHCGSM5HGQ8kJEU1Fp0dC9reMiAidTFigoApMTlVTSh/9yI8Vhe+/9npOsrpahxCapmnb1sWw2qyrIzm7cXZ6NCN2l1erhw8vhiSrTX9xsVGFMW+cc4vFop0vxiE1Xdt13Xq7Tf1wsjwaNlsVKaXcuXmraZrXXvu+pP5oMV/O5z98880QmtVm3cTu8eWFamWp0+Pj46onXJ0iGTik4EMppd9uj46OFvPFOI6h6+bzeRnT+fm5lNLFpoLK+s3GTINzaRiIKDin9YFkWh4tGERLiWHWNrFrG8nl8nL9/AsvN80SsSH2xI4ds2dLomDOuTEV772Yee9SycCOAPfX1hMDatYMps/cvVNETAohtjGMOeckLgYHiKBEpIYwkXGDlOHG2fH/+H/527/0+b/ye1/68q//q3/xha985Znbtz/10gfOlp2KKfuxAJh6Z865DIMnKAAkAiVfXTzcrjfsIoAzETQpwyb32zwOZBqaZhQTz0AUZ0ccWyZGxCIlMgMzIlcQPzti51RUDRDqYEkgH8gH4KDOkfPKbgrlXUHnXTACyskQC4KBdyBCHJgdA3kPFYIMdd4SbGoW1F6BD+y9j40LAZxDYmIlZgViARWGqlaJREYmUqwQkXG1JIZEKoQHVvHdhvfQBJkZ6h44OtEcvctKm4pUHnpE5GrYdwa3fglqD0BVifZa9QDV1RDvze5Ticl+uy41VPaFHXlZRbirmYn661TlvQ304blVNKjWWTAE4gm+Wpme9sRBkxFHRCba0Tvbk27msLi0r+0456pQxlMnBQfl/qc+w27QrGYS+6NMLRfnzKxmGLQTBti70ik7mS57lSxFACqlhBABIOciiljM+hFQC1s5OfnJv/v34qc+tSUCKN5zHTyul0SJVuv1M8/eNTMpBXka46hpSvVDldy4ggidcz/6wY++8MUvnV9crPqBfGw4eB/SMKxWq2HYhOCPjo7MbL3e3rl1pioxuJuntz/40ot37txaLhepIHsvAGPJQKhqH/nIR/723/47//Hf/1vIAiil5O9+9zu/8NIH2OuQJY9j28bUmydnRUopDCiiXHM4RGWcVDZ3SWHbtjoRHU8OAAwdIZIBM0KeevtEXKe9Sqo6TLUMIiLOhaqiDABEvF5v7tx+5vj49NXvv351tXrw4IGP4ejkNIQwn8/feXB/s9mUUp65ebNt2iHlx4/ujUnX62Hdp8cXK6JQJHXdjAhTSn3fMznn3Gazubi8nDWzGk+klGKMOec33nij5HT39mm/3eSccs6Lo+P1pj8fLzebXrVcXV3dvHlzNpttNpuUUn1s8pC998MwIOKdO3fM7OLi4ubNm7NZu1qtHj58aKq1S+y9H4e+yovvq0kxxnEczcw718SAmh1y2zTLxTKlMQf34u0PnJ3dQvQi4JB9CORQZKwg6cqcGkLIIuM4xqYVgwKKCqpS4fKSdez7+axVLd6xqATfKELHzabfWk7EDguyCwqoO0GGNqgppGEzm89+9a//2l/+hZ//1//6X/72f/7N//bd733oxeeeu7GUMoZ2YXlMSQly4xGF+vWY+y2DL5C8H2NstViNs1FVc6rvMIXYtlEoum7m5zMf2+Acq9goRAzo6gxhwMiqAFZECFwlFkdm9hWmGXyIFiM7JjNjLCkDMbJjT2pFsU7ucgyNY3bkyYywIKGYFVNDsFqYr2rBROwcsUOq8QsDEzOCYzZSAGJP5BQdAptCKaWUAgzOEYAiOnATrnBvwfYl5WuSt90s1JQB7CYEDizVgSmrVQpC20my14r0E8a2mkQirv3e/Y8mi0nX9AaHB6grO8wVauRemf3rfvYJgYpU2YJ3rxKfrGftbDoQE9ZgGQ649acDTaagFKk4cVWFyaruL8i0OcciohPwtpb+RVXtINFBxH3rYm9A9x2S/aH3HmXvDuuHWi+qHBj7DGD6JhExV7RpZYMjpMpqY0Z1DL0UzVlGEdACpbgm9KH51C/84u1Pffq+d8HAgZlIzWilIkoQkcj5EHwYpOQ8DZ0d3j7vvZSiqm3TXF5efuGLX/zRj36Uizrnb9+9613Yrjbrq2ImzvOtmzf77QaT+eCcc+N2bKJ/4fnnXnjhhfliYYChaQBJioQQxyEZ46zrfuqnf+b84cMvfeELkhM4/dKXvvjxT/6Fk5u3G+cc0Xa9dt4TUtM0laSsss8ToQIg055QDwDNIIbYb3uzyspCiOCcZzSD6fZVi1lpQQGgVHYl9FVSXgVyLgbQNI2IbtdXiPjMs8+mnB48fPjOO+8QU9fNmjY2sTm/uKgy7nfu3JnNZmYGhqJ4tdpstsNq0yNyxZaY5YkNlqCW+6+u1m3XnZwcA2LJWZW32812u805t00z9IMZXFxcdt3snXv3kNy9ew+c96WMVT+gpgI1CnHOFSybzaZpmlu3bq1WK1X94Ac/uF6v3nr7rZxzfZscIhGmMTnnFHGxWKSU27bz3hPh48ePl4tF17Zd15bR2KSNYbtZx6P5rdu3bt1+xofWhY69B+Tt0GMGchhcS4A5ldA09eGJ0ZWSObg6E4w1VkErJQ/b7fz42FQ4hMqP7n1U1a5tttst1TodOaqAEzAwKKln4iaEIiIAHMLf/wf/8NM/9Zlf///+829+9U+2m9O7R3PXzIqIiqpYkUFFchrFsOk6B6ZF+zxiHWlVYGQUiTGyj7PlEhdNnywulsiefAghOC1Fi6aR0Yid9w6kqBihEjEBE1IVt7DafgvexaDRMzsCMwJoGkmZFAkEkM0xAkxjLMQTe9tkZbS2JA2sYqWIjJxjH8h7YEfOcfAQg7nMRGAEAFphSFj1i8CyqhSwOqjAxESKAkI7osZ9DR93NPh7m1n/D0wBCaZhJtSpIwj7RKD+vVTGFFRCYmSsAHbEyatMTWDjXdcUAUy1IGIIrtaS7EBZZSrCUHUJ05hr9ShMbnKJB0G3makZAQLxvhNRQ+ac0/Sy12i6+r9aKlHc9ysmXzdB8gEB0BABGR0aOWZCTjBx9wMhs9tXW3JOFetZC/o6TaKhiYLW7j2o7DvjdeZAprIzUR2QMTNDmhIjBMAp8RJVfhewdQppwUopKsoYDFHVAImYRxsJCIG9j4ychgJFPYe1FsJMM7jsePYzP333F39tGxZBwVcfSSYIBkqMaGplEHYYW0UnuVT6wtrfV5wEQ8GEQB1DGbbf/OpX/+N//u0H51ez2cKV9Oj+Pe/Do8ePTWWxCF13NKayHodbN274Mj6+OL95srxxMnvphbt37jzTzucAjalXJUcAOSNoFt6oc0g//yt/09R/4T/9B+8obdd/8JXf+blf/CXihii07VHaDhCkiQ0nyqXy10vVQGZlYsoiyJTGsQ0tFQzKSIEdIRZmINQmUC6qDkmIPO9Lc4goNhFeBTcNy2y3PQIoWio5idy6fUtB33rrrfOr89DGsxs3Kh/Sanu1HTeh8cvjxWw+R0Q12vTjg/NVympIPoRIHplz0fU2VVqe+Tyoqve+a+LRYk5sImVM25TSxeVjAJvP5zE2VgDYUs59Gs8vr7LKICNZPjs+WSwWorrpt1XHnJmLynp9FUI4OTm6uHh8cnJy586dN9988+LiQiWpCrMzk7EM3nvf+jSO3MaMOBYwqyqxlfGboveaEowjswaU6HE2a89u3sToCopjLZBLsna+DLFRBTEBQPahBljBOQAgNJUxS0HHyIhgBLR+fNlRNPS+adC5Cr3YQ5ybtisqAKo5eV/fDwIAjw0AmBqBmhZnqsk+8Pwz/+T/+X/97d/6wr/5l7/+eEwvnJ1qWS+stEaAbSprYxXabvNjxEDUQiFN7JAsZ4eUUlFF4pIz8Zia5Vng4KbCtwFRbKLlK9UEebA8Qh5RzMAYnSBU+jZyATkaBwyNhWBMGJ2BCQg1UceRBQgooQE7RAQmwKrHhFYAnRczKUXJwFCsdr2Q0YGRoSPfcNtgIHAKnIWNCVhBzcSpeQiErNqPBVLGNCAqBGcQBkBq2KGqZhFBZeeYAawIMANOlRhArAz3FVCODJV4rlKiqMpkkFVtClVlss8AaKakCoBGjKRACEiGiORwXxJ6ctsH+LZr2dUf6gF0coelmSRj3s12gLsRg7rtu6zOOdOyPyw92f14cg2TX6MDjH+VHjKrC7hGfFaEFFX1ZNvRX1Qh2d0/D7d94KyqhrYv3B+6XETeA4dg13clIi1SGwD7q4Q7vH/9glTGQucMeZKyJ2jbpmRLKVVHmtPQIhXGNWN88eWf/tt/R85uCAKrEnMFO1VnbaqO6PLqyvngnM95ot6zfafk4OJ751X14aN7/+k3fyOXMp/Ps8rJ/KTp2r7v2fFs1i27cHF5iZzmott+iwjbvp8/f/v07OT5519o23a5PE5Fm6YBJEPIY0YAIFYVcD60/ud/4Rc3Vxf/7Su/1TTh21//xqd/8qdu3V2qsBg0s9lm+9g513WzYRhU1bHVzNfMABTJuq7ZbFaEICU5JnKOHSEgO2AygMLE3pGnkFJyngAg5wxmgKQABMjO1zwsNCAiKaWLq6tn7j4LQOvN5nuv/SCXfHR8HGO8cePG2/fvXz18KCLzxRGz996PRc7PHzx4eJ5SKapErib169XVOI5m0HVdlcM0s9ozcM6tVqv6wG82m5zTycnJyclJ3/cPHz/2IcQYN5ttiHFzedG17d1nnpk17TiOiNj3PSKGEFJKtehfwUg3b96MMb7xxhsXFxe5JEYw01KGGGMd7ECE0ARFNDUVudpc3rpxY7GYd51j1LaJ43YNUubLznnXNO3x6Rk7V0WyXFAfqJvNXWiQ2ADogK5q/1475lRKSmMbZgAABrVaNT86ER+QuApy798Lq6MwAiKiKqWMiExEiKy6q6+awY7m3sC6tvmrv/ZXb926+7//b/+f18d7L50ut+tzyjp33gyR2AdWySrStU0xMbFtPzBCAZRUxDi2zgAMHJIH9i40PjaEwGAMUrSAZC2j5uxsgu4pCIbKd1nZ4Y2Y2Hv0nmMD3iMoGVhRZG+soOiYTWtozmZW5VgRCKYEtEqCTO9+MQVHNJUmDCriAycNq0mXqpZcAEyk5Kw55WHIY0+opB7JgADFCUAlR1CCndpNvX7XFDgIqLuiPgBUjpmdZaYdPPSJcgvWygjqxO5mqgZkAFUm2dTtC0xPG28AuFamf2+en/0zZE+a1/0KEPHdZndneQnweqHvtx0WxeAALTqd6u5EqskvJe3TJ9jZ61qi2Zvv9xtGsCcbHgeX5b25LvbnaAf9c8RpKIGZi+xp7QzMvPexaVLKKjUDAQERFQ9pDLiZH3/6l3+t3HlmTUgEAaDC2q8Jh9QMbBzHSjxQWZ334ZiqwvXLScVgGNMXv/Q7f/InX3v78SWFcHR0VMmNgejWrVvbfvujN+9dXl6pqWoJDucNu2V8/rnbL770AWI/Wy6d91kSMwOSqBFxpKrVC84TsYuz9vO/8itk269/46vby9XvffGLv/zX/sb86IYPQQQEWkBwwbMUX3FZOVNhMFY1LblpmolcDyA0UcGI63sHjkFLcd4RAeh1677W6KZxsN1cWD1r7/1ms+m6GTl/eXn53e9+dxzHk9MbqsohPL68vLy8NLO2m8/n8262UKBxc/748Xk/jM4HUN0OfSlqUPp+QObFfFargpXrLefcdV1KqT5RdXTrhRdecM6t1+t79+4h+FkIF1dX6/XaBS+5LM7OSspv3Lvv2FWtm7OzMxEx0WefeVZSTindvHlzHMfvf//7ttMyqrDy2iGvyC4zI2YzTcOwWV8Fdp4hOD46uTWOm66bX8pI3mbd7PjkeHm0PDk9nS+Om7ZD8t1sFts5slMzUDEj593+VdpD3epT1NRKCJEhPXz4cNa2sWuzd7CrMV4HRgAG4IjQoGgxrVHmVLWt2j27oab6/CuYqtinPvnJ/8f/8r/8+j//5++cP3z29CxbLpINgxlJUjNNSU1cSUhCjOiZQXSUZBhC9E3b+OVJnB0hR3YNsVMpgGCqDAYqUIqWpFp5ccjQHKIjYDRCw6oRFBoOTfGNMiMYBLQs5gI4AxMTqLGsISFRJZcBRdOsWlREJBctUv8JSuwIkQkqgr3STFRQEkEFik480KoqpWjJksa83RIZa2ZUQDBidaQeEEBrI35HcQZgVfia8JpSjLCSJmiVk0EwM92ZimuhmMPA+gAYjriTKIP9HMC7o++9mdt3UKfvPDnwNRWgJ6jL9V/92UYWAHC3n/0hnqo47Vd16NP239kbXACoZrISNZvZXmAe62RR1YbVJ0L7yaheAzr5qRVfZzwHp79fgB5MVO+/ObVodmeESLzLMJgdkEkqDJhKZvYipqDIhiC98x/9xV+7+dOfezybFXadFg+Yq583A0ITIYDaUDlaLqfGr7smTTIzmiaNEQCK2Ne/8a3/4//8jTEXMRu221QyM1+t1wCQSk5jYnBMDASOgZmcxw+99PJf+Sufe/nOc/1mS+zVENjlnEN0YMLESI5ARVLR4B0LU3dy8tm/+PPfe/XVcX3x2ne+884nf3BTrZkds+/abrZZrwEohAYARMR7cj4O44gEDmg56whNrHjfOE8GxkwI5hyqJERkYgMxIHKhwvZhh9ZVVVc1JESQmADX6/Xj84tPfOITq9Xmnbfvv/7Gj55/4SXvfRIhovPz82HMbdvFJjbtrIidXz569Phitd4cnZz1fVIoVWNms+1TKd0OUiUi+8SlLqD+sG3b6ob7vr937x4RtbPZdhwenz9GREd8cnKCBpcXF1Kkbdqc8+npqXNuPp/fvXv3rbfeysN4dnZ2fn5epw0Qses65ziNvZlWOpP9La5NHc9MIPPZbBw2x8/cbKJHjVpy9K7xoWma4OPR8qRpZ0gM4NkF4iCqiKpQiB05BKJyPbxJug9RpSBi17TjOK6uLp1zs+XC9iRbiPv0/fBdrnoeZmoAolJl7BTo4EWr09BqKjUX//BHP/T3//E//t//3//b9x8+fvHOzYUPJAKby5S2nsghm4j3MZcRDbepBBfEBFFd8C5G8C24oOCQPHPQkhkATD1qARETMJEiYAhMk542AiEwGqAxE3mHLkCcGSOYkjobMjgHTkABgVAVEZAY6pgOqIGSFiuiJUkppaQCUin+zYTQGImujYYiABhU1IeZgRqqgRipaUq573O/ZTJUZ6hoCmpu1gExVnagXdIwcYiZ8c687lOLqgB5GK3ajrh+b4H3FZrDuHZvvqZguvY8D2P5w29fB/g7s7iPOvdHrZUTkUMR9Kct6eEq60u1N+h7Zv+6VWjHQWqzi4B3APyqGVKPqyJEFhxhZeUzgYmHssBeWdesMmodOoD9cXEH6SFyZrg7MgOQGao+kRnse7z7RKRGiM45AKgrh12KDQcOkplBERRVIdT1owKhoF06jB/44POf+7nLdtEzCZZ6RaFmagYmWjWMwGzYDrSDnNY5WESsQ94HtBNwuV791he++O3vvXp+tc6q7F2McdP3pRT2rkgh7ypkjZhDiI6dJ/rMp//Cyy+++MxzLyyOTsZUilZm/zLlMEjkmJhMC4OllJDZNc3ZnWc++MpH0zCuLx7/6PuvouT16uLi6nEq2cdYdikke+9jZO9j0zjn0MwTry6vQggcvBEyA6BMaDLEqldeVVSZubaR93ffOWd2nZia2auvvnrnzp0Q4ms/eOPV1187Ob0RQvBNM5vNhjHnok3TLJfH3jcKNKSx78fLy0vnPZJLJY9jMYAiambsQzub17HqCtz03u9VQr33bdsy83q97vt+vV6LyGw+R6JH54+RqfZ7GWnSGJjNyeBkeXTj5PTW2Q0r8t1vfTv1w8nJyXq9Pj8/36vfpJSGcXjqZanuZxzHPI5oenq87Fp/43Rx68ZJ45kRtSRTIbS2adq2beeztpu3swWy96ElcgCcRWtOsQ/2aYfe3ucBRARqoIpmVxeXUBUFo3fsDm3CfmMCQmMi75ix3iowK2bFNJkm02yaTYtpBitSiqmKFBV55rln/v4/+ocj4FWW4hvs5u3iuAhsx5yl5JLFsqqOeUySkxaO3s86jBFDIBcBPVRhDrPGOSujDlsYex22kc0hMJqaqBZDKyWrJAIxTSbJTI0IXVB2xsGcMyJgUgRRySJgBmqEBKqoZqKai+aMYEXSOI5pHEyl5DGnJCXJZK+ECBltJ8qlBIhqVlUKcrEiVkRL0ZwsjTL043rVX17mq7VstrLdlmGUlCUX0ms8SzX2JqqqNGEkEQAmGAQysydyAITIZlgOuN/hoBdrZiYKalqmBMZE60/c3pnbDo2zq2k8ze0z3XieAKMVFnkYEVzr+u5i9sMeKRxkBoioKrVSxsxP7f8wsn7KxT3lVABgmhSrvZEa5qtNlTq1eqoEdazIAA0J92b6cG8T53MVojq8cPbErPLuh1ahjU/5A5ha91Nesr8OIsJQ84O6EwUAYnBNu513n/jFX/UvvpI8I2QHBkgCHmDqe1cEkYkykkipr5scjNHVs3COSymmKIB/9Ed/8gd/+F8VOKUMnkIIY87r9Xq2mKspMTvnuYpHEDsH0ePHP/6hn/3cz966cepCc+uZZzebjaggcSlFSgFA8F4IQdEHh6AiSkhMrjk6+diPf/Krf/oVTes/+oP/cve5Z2+/+Ao5TrmoWtM0xFzdoKoyqZGJ5uD5m1/7KqosZx0HZ2B1xr7WDpxnmMA/vjbBSimG6IPf3TLIo6Wcif04DK+//gMf23a2+Po3v/Xtb38vNh0zuxiZ+fJqvV6v1fD45Kxpmpwl5dQP6c233vJNE3zIWQBZTVORcRzF4MaNs74fHEEdQKu1+/l8Xp95ckxEb775Zp0r7vt+sVg0TfPGW++MOZ0cHZuZJlVVhzRvOyZaLBZnZ2dEVHJ++623FvP5bDa7uLysmYRzbhiGzWaDiKenJ2ns6znWAKXCPb1z66srzzSbxdPjxUde+WBgVwYEE0eUTdum6arcTDtbnpyIASI5H9mHlMUFx84RY21yXG+V0kBVS66vmBS5Or/omnZ5cjTkLP22mfmaiOCT2XNV9J4qDwgGqLXOMxV9r1/e6QWxepMVQUqRlz7wwq/+tV/5rd/4zQXSIvqEjmJrqVdQHziLDHmUXM7OzqQoYJidnGZy0fumaXyIRowqIBkkYR4h9Tr2MA4qOYCVksSQiKC+kQSECqoAvtL8Gzt0Dl2tRDtjUjRAYVSVgmZY5xoRTc20gEjRlMeU05hLFlLTbKhADKpmNbkRM8Pd6A9OgT9M4b8ZqEIRKMXKWPptSSOQBREvJRjkHXCciKxYhfcBYQA2rEwOSlVi+F3bPnBHvJ6SObS3tqPUfLdlvu4B7GPJKWJ9n+L8YSrx1CKe2nu98WjTr6rZ3S0UqgA7HHRipwfryX7D/rE7RDo+uRwtqQBAFXFH3em27x4+gCcayPvp5b28Tl0eEYsIGKhMbYN6P2xqZFw/ylNRaOcz7KBKpqp44DgnXzE1Z6ZOjQCYKTGOOY1i80/9hRuf+ZlLCkYWrI+qADETO5OaztWyIKiKChMz82GWNx0F1LIaABF//7XXf/3f/rs333w75SKGnl0qpe979o6ZhzQiMzERAhEFzwTSdd0vff6XnrnzfBdYjX3wUQwAcinDMIjk45PTgsT/P87+rNmS5DoTxdbg7jHs4Qx5cqwBhQIKAAkQZJPNAQTYIK+uWjLp/sdrJrsP+gV64ZXJ2nhbfdkkGxwwFQooAJVZleMZ9xAR7r7W0oNHxNmZVYWWFFZ26gw7947BfY3f+j5CJCVEUwFFVECkveT3Pvjgu3/4hz/63/9Tt7n69OOPlydnzdofn9xNKRfRPpznuom885YzAJ2/enXv3r0QQlJBR0X1lwBVMxcYRnGmB2F+eYcyfqg5p5RSSufn51dXV9/85jefPXv285///Oj4eLlchqYJIVzfbG9ublLW9Xq9Wq1ETFG6Ln722Wfbrjttmn4YFJyZFXcvBsw8JAGiYeiXy2XXdbvd7uzsbLlc3tzclCBpu92WAeai217IIXZd1zYNMvW7vYg0oXLMdV0vFotSL/rkk09E5K233jKzq6ur/X5fRJVLO6HkDTHG1Wq13W7KdOG8ROu6DsTO4dGq+fbvfePOycnV+ZVJRrUhDoG5qWvvfdO2R8fHAOC8b5dHCC5nK1kqMQGize1FAHidN1BESG273UlMq6OjECrf1H3Km82mbRdvVALGpV3Y4/AAxg0w15dt6taU7oAAohqBmKlj2253f/G9P3n62Sc/+ccff/XhXecD142CdP3OJCEH9A4Blaher7PQJqa29lwviJxnBiJPiBJRIqbecs8qgACS9XUmGOTSFpRidRABmYE9OUJCAipVGLMMmhCUJpY2M7OCH0/JUjKNOaeccs4xmUTMWsbORpda7L6aCZqgkRVYnuK0tkphIlvKmlLuh6Hbkiu1IiB2mZi4bAMmx6XgMKoFKGiZ5EIDKezTdgh+KZTzAAogqOOE2KEVAgAo03olLC26P2qK6m4FTA5EV0TEfUnjtyxKm5RPpqcOzFwsb5Ggmn6PZjo7hvmUEBG50JbNhszglgZvjLXL+czZyetvMi3irDknnoLiksHZAV/p4XUREYK99stySwDmu0aTvNRo22We6bXDwyGVQhYzs3NmCqOC/BhjFcJpACiCHWAF2ypGRghZhJxbPrh/+r0fDKuj6BgtehUPmgkykrNJewAAVAFsiENVVQXGO1vDUhkzMyYzwO1u97d/+7cfffRLA+pi9sH7ELKkwlzPzmFKVRUAoHiBMkP0l9/7829/+zvLxYpADYmIuxjbKhSP+OrVCwWs1nfIeTBSyWDZgWdAUMsqoW2/9/3vf/yzf47D/if/+i93Hr1zhp4oHB+dppglC6EDIxUgZtFcQsG2bVfLpaGxI2AkBC60V4BFPAAAVLOV9MGwIEGnG2ulTXp9ff38+fNHjx69fPny17/+9fHxcduu28UC2e123TAMpfhz9+5dI765vNxut9c3291+f3x8jMBq1g99ztLHyOyrqvIuABgBcvCIWEo0bdvWdTPEFIJ/8erl+fl5yhmIhpja5dIAL6+uvfM+hM3Npg6hDpUndsxHR0dN01RVdX19XVXV8fFxjPHm5mYYhrLCu67LOZe6lqoCWp4KMkRcFM+9d91+T6aNr995+PB4tQDNhYvee9+n3nlXSPHW63VV18Q+1C0AKQIzueANeUw8X0eLqRkSIjEYoKpkubm5WS9XVQiIaIihrrynruuZR+7SW7MyMtsqGCG+qa4xB0bTVzArHTpDE8mpCpgk/Ycf/uBXH/72o9/89itna1Dz3lW4EDBiROfRCNgNMQ8JFsfH1WIJ7L3zzKwKmgYFVelw2Em/HfY7pwoqWcQ7LsB9M/PEKmqAzjOglesCLpxcY46NJqYJc7JspfJTNCVExEQ0JYlRNeZhSHFIMiTLQqZIzhwjMiLT6Gima4epDjHG/ihasgQVgawm2XKKUbLkpFlBrUQ2iGpWtY0RAiMIOvYlvTIyEC3DmLPbHs3swXFrM9XUbsvytxIpZkWCuJyrO4yObeYIdc5EDj9GNTOzqhFY6VogABNjgSWZgimNtklL62RaZDCqVoIB6hjRKiDOymilbkU6qhBz2eczIxscNGPhAPhYjDKqMJjlVJKvssQNjNiLyEhvW2aJzbIpOR79sY5qxqWviGaOC+KzUDtAzgIIpGiGJUb0Y5lFEECn6blsys4VFmgKvk89O0YkMyRkJEIEQ8jGXkgcdvXAQ19nuGmXzZ/9kf/gG0NwzjIrOF4oIgGyDBl42mUGAM7zzc1AtS/qxUUyQWSU/xERyYpEv/joV//5//33m24YVLkK0ZRsMBMicug8BUZBZHQeGByZs+GDdx/8X/76e3dO1kre2LMJMTP5rFSFyoSOVnp1fZ3ztT86YkdgTISGqtAjMjtMQ7r71jv3v/L+L372b+umev744+DweLnc3+RFuxhiRHAAnr3PYiIkmXM/OF+zDzmLsXlybBA4xBg9MxaoMpbiV2ZAQWIm54IBDkMPZo5c1u7xp0+ISDR98puP0TQ4Ojk+qZvm2fPnV9ebzeamqeuHDx8yuU+fP/v000+rut1sNkDkQ4gxI1FMebfvttttCdUBlBGjpOOT45TSMKTluq4Wq003CLqrbb+Puc9aL9cc6m13vVwuk5kCnR2tu/2+9RUhBnbL5ZKIlqvVcrm8urpCouVqtdvvu66LKcWUgvcpxjgMzJxTKiG/9/WQoqvqtl1IyiDQ1nW3T+dXL96+d/ydb7z91XfuNR62251KRs+aHLJj75rF4vTsbH18WrdLCI2QF7C68kiU1JjRrCAlXBkZGiPPkrVnQYAG8OX1taRUtY05yohgqGpMWNdBRPp+Xzbm2EIwhAPFUzNFVGZKKd8GWzoiaVJOjixJyrmw4YuZodrp8fGf/uWf/C//8/989+6RC03fiUdGEV/V7UkgAzS2TK6pl9Wi5aaiGn2TBRHEWcK0p7ST/QX2O015iIMDFBA1U0UjqtCcGBMgkalRMs4KqOIMUAG9mVPMgEaaKRtHSBIBQDQDOUSVHHPaSyp1/31OO5MMRJ5dMkJFIiziAlaoMBRBEATRQMgMQExY1XIGGVQFM1hGzWBisdtbZ9UQnSgDi2AyBGTylXPCDKCawRG5kgAT0lRhApuyw0MjiUhSQFczEB5HJ6Q2SaAh0IHugJtLIjOssBwHUfBrQffcOJ0LTwDFySlg0TVXR3wLAngdHjoiZb+ggjSOlR1ekk0NWHp95GquJpmpgxGBOjuJ+ZxvE5S5joQoIyyHZ89pn+txvY5K4unSsJC6lLjGORw9EEKWyMwKopINynQ4lOHf6XLMQJDRAUIWMIhEuj5690/+NFe1gsE4qE3lDowVstIDRVNVrqqr66sHDx7Opz2f5wSRdK/Oz//2f/1fnzx5stn1Uc2Q2mWbdEgxhhBMAJGcc0ZITOy4rfCkXvz1D3/4jQ++HkIoGtaoBgAhVNfX1/XJqfMhhGrRLtjxdnPjHC2WbYGxDkPXNA2g996TyHf/3R9/8snHl1fXf3b/3vbm6rPPHt+7/7Db70OzAGQkVybC0xAdcQZaLNqcRTUX0hGCWUfhVuPTDGXSvDYzySqlQw6277snT55cnl/cuXPnZz/9UDQ9uv/g7bffqRcnNzc3McbtdivZHjw8cxwur64uLi4AYOblJ3I59wa349wxxkITjYjeuxhjoec8Ojpyzm+3O1HYbLbXNzcxpdV6HVNConaxePLkyW6/X1SNqRbG0MVi0bZtWWNF8BkAttvtZrMpsf9isRj6frPZ1HWNk1ZzeZT9kBw5R37Rtp5o0TSbq1fLtv7ut3///a+8u2pqIug4Ss6mttvvVHJVLdar9WK5rNuWfcXOI1KoqnLfigLiVE3EqVgx/lzCKc2y33eIeHx6UmaRkGwilB8ZFcvlFFpvZq79yD0+AzrKM3LEhbyICHMar6vI8EEpi5gxUUrJMaeU//jf/eE//8O3Ly5fvffg/i5FR+ABwBQAYoqsjsA7R6aqWdCMiQ3MGZEqqGgcQDJILi5ORcFMRKq6dVWDRpayMQoaOyIwBiODbGqoAkZWXKGZCahaoSQHM6AxSsxRU5QcNeeUYplUMCAwxzhVbQgJiItFLbAnm+Cvhf49i4loFpFsdqBJIjmlIadsZkiYQdQROGeMjWsJvZARCRJKMQ2lxgBjxWKulLxu6MqE8FR3mQ2p3r4M5kVg4OapkMOSzqHRPLTIbxwH7mH6xswKm8L8L/A1WOfBu72RwtxONh+ab3xDqRgAXusHkIlN1zyTJY1ZTplQH9d6sZmIalN9fxq8LlnqG40FmNWPywSIqGqBtBQBT5l7v6UHVN5NRADRxEaMSnk2BoggnEGRzaqECv6a8O4f/lF48JY4BxN90Ov3VtHM0EgVwCSnvu+r4AD04NaNvWoAMMOf/PQn//wv/5JFrBSyqoqd6/tOs7nawUjL7Mm5qmmCJ5T+m9/44E//9E/ZBQD0PqRsSARgVVPzdrvt9m1VV02tquiKi83X11fM1C4adoBoTCUZsQ8++MZX3vvqLz/68MMPP/y//k//03/6z//IxHfO7vf7HbMHk1I+IgJm6vZ7IlJJRb+UEJidSj5EVZmVzM2VKqKIeM+Vr0Tcbru9vDj/6MNfAMDjx48B4L2vvL9arc7uPdzth5cvX17dbFX17XffQeDnL1+klGLMfR+ziHOeAMqM1eXl1b6LddPUdV0UxkvlvWma0vtdrVaLxWK/36sqAN3c3KQhrhZLz+56e51SQoM0RMfMTKvVKuccQmDmwj1XaDu32+12u93v98MwOOeOj493u91+vy8JaFmK5fumqYc0lMZjYDRwsd+bxD/7kz/++tfe9wTbbl8m4AxAckazyrsQQrtoj45PQ71kX1V1w74ymCTqENi5iUcLDGD2BgAAogowxKHv9s67um6zZjWkkorayCM/B5tlNKHrun63L0oPBQwyr/+xpGSmlpEsph4AyhjEuFeswA5F1URzXYXvf/8v/+//y//tsq6D8znF4NmyxL6XVArjjAYlGyQkVAGwwEwmkHOKg8tJY6wI2XsDIw5VqJhDVhjigIk4OAUzdASIBmBjYb4EysVYF1EtlpGjV0wBRTTnFFOKEmOOMcdeYlIQAIdmjOid84UGiAgBx9HhgjcpJRczVHNIMJJLY1I1zSpZcwZRTTnHlHOuPSADODayGtU779ChdwpGaGUSr1S5ZSLAn+PU+esc0U7TS3RguL/gxQBwqwdwaPEBYFaQ+Xx0fBg4w2T7J13e6ctsyA7ek8cay6ji/cZHT4Hta+BW+CL3M0N0RkcINn06weSHDvFH8xkh4mEffS5/0euMdYepj44cP4V3LCEhgIoITPQWimBmKUnW0h2ZndOINHXsiQlIRSMKVUA3SPDg/tt//r2+PRIreOVD6PSUB6GRmqERQNd1lSvDLgKzZNqBkM7F1eXf/W9/9+z5s34YRIF8WKxWfRwIuA6ND7WbDmJfN7Unceh+8P3v37v/MARfULAwNkXIO390fPrq5cvlcl0jq5roQITOtd67m831bidNU6k5yKCqjmixWv/et78TvPvVRx9ub26+9+d/9t/++V/A4O79h7vNNRGxqxAwp2Q5X19frprGu4oIHBMTeeeiljKIn62JiIgJFApldKJpGAbLOXbd49/+5uLVq7quT+7c/c53vnO9uVkuVs9fvHry2bPLyyvn3MO33mbyz148v7q6qRet9z7nHKpaVb2r+j6aoYiklNg5M2uaBgDmUbtC2qwK6/X6xauLYRiGmDebjWh68OBBkYg5OTnZ7/dd11UhqCgQFDXj4+PjpmkQ8erqqozUDsNQUgEiijHGGAvOtay9ogcQY0RANc0puuWS0ICg322/9t473/rgfUcgIm3bAlA/RCJWG5ZtYzrcOVnfe/Dozv2HPtQcKvYBySFAcT/rk9PbLQbTaH3Zj4BJFdT6fWeA7WIpqlXVpgJogZKE5Tc2oHOubVtNuVzX7MBKlqApOySDEUnhiVU19T0RohqqkYHkTAZ5iKVr+s67j37/9799ffHKkDb7jurg0AI7AvTkiFBFmTg475k1RQJ0TGxqkm0YIGeQnIYEjJCTZ5IhRo1ZQBWcefMkWdAxoTEYliK2KY6mongmRVMzRBUo5XtAkaQ5aUqSc45DTkklW5lzMGUER+iIXBG+Q2JDHBt2Ix7UJkwnGxQ2oqILbKomYjmBiMQ0dF3CaDkygAMSdok9A3Pr1InMAFAEG7FCE23n58zjbEuhxMfzaw5ef1jzcLMzOYTETDZ0BF3oJJM753ozukYnYs6cBYn4c3QQB+f3xqxA+TjAUWIMipTuG63gLzumugerGpTZ5oKNLXG0GU1w1fF9ClJ+7ITcpgs2gV9zSnMaPnugnDODiRQ5Q3OORbOZEI2dAzMbCZmZC1S89tVYZEAqJVQrYCEaOXU8V73a0be+YQ8eDtzQAf33fF2IyFgSHVERJNjd3DR1QFAgK/rL5bKIIaWMQD/56U9//tFHXd8nyYDOEIYYc8qeXaH34uBDVZGBcyyxR4vf+/73/ui733U+ILmyZJhZRMFMQbwPSJxiJqJmsVTxw9DHmJqm8d6nHIdhAIgOFRA1CwZ6+92vvnrx7OTk5F//+Z++/9f/8fe++cF//cf/9n/6Pz9aVNXu5ubo+JSRc4rsfep7t1o6IgIqPZaUI04trFJDEBFiUnWFgwG9pWix6yTnX3z4s48/+kXhzf/uH3zX+bBaUVb7+DePr66ummaxOlpXVfv4yeOnL162bbvf701h0S7PLy+I3PHp2b7vbq633oWqGlEPxbyWAYtSDkopNc0ixlhEK88vrpxzHqgO1cvnLyRlRso5B+fbpi0LabFYLBaLQvMpIjc3Nzc3N0Whoeyj8lnOOVMtrq5Ex8MwlG8csSItmpoACPXB2ekf/sG37hwvct9XywWgy2piTvRlTklyOl0vzk5PT09PkXy9XHFVI7kZoLxcLse7igBACsA4lSVFswqoxRhTjMfHx8lK95O98zmrphxCsNfjwjk2Kgu+FNDGglspIOdUNmapIdMofZNLR8156vuYcizDQCmlnJJneP9r7/8/fv7zt+7eDU3DnlByjmnYdT30tV8gyVIEzBAMUvJVYBUGNc2EhjmySiDKcUBJklElGxCgY/RgCpJ9IZoSNVVSJVU2A80gaCmBqKZEWSyDSgJA0zJmmHKMOQ459jnGYvQLMS+VGWOAKepHQkIzFCMDQirkC6OPUQU1yGpZAAxMEQ1NxgxgGERNr1IFpC6AC0oMVClVRkFrZuainlI407Aoqsot5l4PJBoPo3uRPNIo49gSPywWFat+O1Q102Ee+pBSz/kyKzybV0RgZsDCAX1oxkFkjqyVbjGXb2I9D8/sCz8Lp6r3oWP4HU7ijXsxRcy3/2o++fll84/F9JfbKmMmZDlLkVu3sYtAIklVgdAHHgsZk3yYiGQtILmRBTQYRsBMKKp0tF5+8LW+rbOgp+LOX3MD4/1SLTeUVFPsAUA1GfjZyRbX5Zy7urr6u//8d59++qlOXLXOuSw5pugU2VNKmGyvYLV3JOYQ7p2e/Me/+ZuToyMCLJSqAEAGBSdoAIhwcnJyeXl57+xuzjm4mtDtdltVYA5FZVVV4zCAmUgaBmLn2bnvfPv3/uHv/wv55nt/+YOvvfeVf/uXH/3ZX/xgGKJJSnlIMfa7DYI5ZkeEDgvlIiMVWGdh7ivhpPMe1IxQVMEkxiiSnzz55Cf/9q+Shq+89963v/MHdV33MXtf/+JnP7/ebNvlipm7/fD02YvL6xvnnKgNMaEBAFVVE3wNAH0XY4wxJRdC1/dl5c/xrKoWq71er1+evwKAgtNPKd27cxq7XlOufSCDfrcP7GofSj3kzp07ZnZ9fZ1zvrm5ubq6gqJcdjB2XpptPgQzyzkXhglEXK1Wu93WBweqjKSSV4vq97/x/p2jVcW4Ol4DcVZywN2w2e37nCOZ3Tk5un/v7mp9VC0WSh7R4YTsKQBcK4HOlBWPQaGUSoeiWez7pmm0sP+OW6Wwx0NKycgOS0Dz5qKDwkDbtsWgqypbiMMgImV6uVgPVe37vU0Iw3lzBefbyiH5D77xgf/bKilUoRrivmUiQM1iBr4NTBUTMxECeMaCRUNNZAqqoAompb6K43+AAIVGF6NoBiAzz6gKKiaiIqwGqCBAairi1cjMKWSREmHlLHl0AElzRlNJSUGcZ3RjoTI4Z1gGsYAmgBXOAamNBQotTKQAaKAiqmKikjOIQIoWM6ha0gzbRF7RI3qrlsZBnAeuhcgcYylfTSyggLeW7fNmcLJRrDZC1emgbHNYvHGl6DkLSN3ax6lpMC/cQ8M6x782taVNwbAIJN+mG3AwbwWAEyuoqirTbfWJDks9+MX2fS53HJp1s9KqGmN8uC0+mZVxudkRIZYeGILMVSZ4rY1x+/0h3t9UoMwYgIChqhgoAGjSCU7qFCznXNgu0RwRMREwgZFnR8RMjCIZMSPmmNqH76y++vYQfGVeLU2DAq+DZU2wKL2pZMs55+WiIcAMMg/zyKSw9uGHP//JT36y2+2GnPcx1e3aOdenpADee195ciwELngiCt45hP/DD//qg6+9r6pVs9AsY70QDWBUIEADH2ozFINQNSja+Eqydn0XAiG5uqrMDBynLH1CAPVV1bRLyvs6VJLjj/7pH8/uPfjlx79++tmTull99umTUDVGsF6u4naHAADK6J1DJJJ8q//s3K1UNfugKiq5BCOvXr78T/+v/ycBfO29r37l/a8u2oUie09Pnr44P79aHR0H77p9v91v+j4aQFU3hcknDblpGhFp1k2f8s3NDbPbX1+HSdJnVlIrIXPf9yGE0gwIVfPq1auYZL1ee+f6vvfeLxaLMgy8Xq8RcblcnpyciMjFxcUwDPv9frPZlPVfBtGrqmrbtuu6wvKWYqRJO6hMS5SUtK6r4B0zLUK4e+fk7PSYTMkkDoIcouCQ7fzycrfbBcam8k3l79+7t14fsQtAHuh2TGQMD82YSafNJHGc+QI159z25ialtGjbMlgIQIpEAMyjVFTZRG/UABDR9HYblr96783U4tC2dcmomH2ZZEbkpjkuo/IxxhjH/Fskg2lK8eTO6Ve//sFvf/mr+++81Z33KWcn2jQNgWuryjAQonOOiT0CF3ySiMUIOTlTAjARRmB2DGpgoqCikqM3b6qmQAWWrQWCmS1lAgRFTAmGTFmdGGUZi8iFHDJnTVFzgrEGnAGN0UERncGDzkThCx6LPDByNZRvik7CbNhKC1iy5aw5oRqBEqJX5/YJ3F7DzqotNFtzlYagFSOTgwIsAlTMpEiIwEBj7D/1Pl8LeUfTOldrvgjtYmauPKrDLVf+piI8CX4dHocfc2A6R7KAQgN1YMOnUsVksHDE2r82/Tuf8WsW8HUHMCcib3iww9ThjUxivuARUqIlnZW5XX34QUR0G/WLjPCenBlBREQzjuVCKEsfJshSzhmoINOR2aVBxz4IILPDkSTVAgfHIEY95YfvvIPH6y5LWxYLHXbz51uqZopqZtrv9zkNIax1hCjcjnOa2b7r/8t/+d9fnV847/tcSjdU5OW894wOich55wkKT5fpt775zR/+1Q9CcDlJSonJ4UglpfMZlMtYHx3tdruTkxMEzqqL5dr5arfdqKpVCKZkhgTOB8eUB3jr7Xc+/tm/ECEBPnz4cLsfjtbr//r3f/+Hf/TH+z427eLo6CgNMfjAhKqCwKURJSIliB4lHKhU6opQ6lhUffH8+X/+3/4OAb71zW/cv3evqVtAbNvF9c3mxYsX66M1s7u6vI45bbdbX9WrsIox56w5q4H1Q19XLRLt93uYcQuIzHx2drZarXa7HQAUWEvdNMz0/MWL3W7XIqWUYkx3z84sJ0So67r0nxaLVkQWi8XZ3bOu6169erXdbsuAWKgCAOSUC2B/uVyEEFR1sWhjTJJzgfmPoJq6jsMQfPDOu7piwjunx8frBRNWla9DiJJ8Xad92mw3u10XQqiZFovq7N79o5MTH4KrKjFEIACFW54MHBf2WIcwBCv7mp3fbjZ9P6yW61Gsih1MYV95Tc5iWFAtb1YC5mhs3nclZvLOmQohIrucMxgUCaaxTF4mdcxySqoKYETC5AH4m9/61o//9V+vd9smhP3VZmEc2HsOddsul2c+rNq2dT6gCJoRGIOqKiEE5x2CWUbNlhNk06RWTHAxSWgFC1UoiVDERCBlKGKMKVscII8FGSNRMxWVpJpjSjGniKaaI6khA6gxIgMSIpfeI5T6vh1218evBmDTIykeopiGMUwFAvTsGKnOBGLWRdj11uy13WmopfK5YkMTcc48Oweli2moAMXiwsiJeVjhsYNSx/SAPlcrKa93BVQwG8TRWSGiD+VfIWFB3hWzWpiVC/VEqUGN1va16wZEBANVMZvpIubzIzPAgyawlk8sq0NuI+LXTneiXhCRYvvhNtsqlwumikwAoKLg0Aio6B9oRiRXxg7gtvp/eIiI6ijtYpbNFBAQEplKjmCGVGwdi0EVqmEYo0URKe2yEgiwNyYGwkKyBQTAIGZJoU4xOxkeHtEf/N4unCBWBEl0IKKCRCMesxlTIwNSM4ls0m8vgyNiKkOAZKWRBQBkSL/99ZMf//gXl7sUEwoGJKqqBQAzekLOTpXAWAM5h9Q4bsn+xx/8xcnJqem4z83EDKQ8OGMEGNERxKFphyzZjFDIk6GRUbNeDH0vZnXwKQ+GDsElQwzu3oP3Xz5+eufkIRK2R3dWZ+sH79jTx79FlXsPH2Ddhnp19eqJYwbLAKqGbKSK5EBBDAK5yiT7KsQ8RMmQFBE05d/+5lf/5e/+U+xu/vg737l37+4ewC9Wq5M711c3H/3yo36/vXN29ur8oh/2RHR8tEJyMeZee83JTGLWmIeHjx7tuzjkXC8WXRfP7j9wTCWEjzGu1+sYY9/3PnhwxCFcX19z4By7fr+pq0piB1bKbNkUF22dUlocr8/unt3sb16+evnyxUsski/BxRS9c6yWUwpVnWKnks7unDCBSkJi7ypCiv2+8r5yvN/t6rqKw5B7uXPv9N5pe3q0iMN2vTrLgHVTsw+2y32fhn6oQ9C4u3fv0frB21YtgD2qBEdgCYjQNEupQ4y4NQBgRJ5RoYZ9SjFb1a4o1IBIaJP1V8WiygeKOiXUZmaljWEHVeI5DivWg5iSCQCKAZgaIwK6KsQYbSok+BBSzmU8DBEIDLKA2TtvvXP88GH0/tjXtt272LXVom6O0LWCtXP1IGIue2LnXW2ZhwiYDUDEwJg1alZMQOYJ2ZABSREN2BOjCRFSxeAAJVdDzmgGiaTjuIeUc7aUE5OgquSUVQeRrJJztpwdAiQFMEIkMQZkRGeAamQjRIcMQQtxnKEaOoRyeYSKAITKkCyXQhaOlVpgZjIwAE+uQm4ouE75poPmxmrKIWdvYFnbSp2RSnDeTDAjmUdEIEBE48nmmBUqOoTJRk6xok7E/Lfegp2q3tZhZrcw/gN7E+0zvmCiPp6zwjGoPzToJZcvicH0ofB6nf1NfzQfeMsg/ZoP+PImwSEF25yZliU5NYDnwpDRdCNKdjwuX1UQBVEDK5xtZgIIoGqmCMBEhuyY1NABAWAIVflEZj2Mg4r2FTApGDGX2psBYDYmFpSjRw9W9+7fIDNyShGDmuh4hmOwZePGFXGgZtJ1+8V6lXMm521MQBTK7AX5f/qnHz199qLvhy5GIqrbitllEUSqqmCk6NhzCM63gVO/+bP/8P0//O53JqC9/Y5ngYiFEH+7250cLQFspgIsqI8cB+89sMtKQ9IQKs94evfuk9/86tlnT7//P5zEXCHA177+9V/+8sOTh28lwJRSzqlyJCpIQIQxDezCSDVLHIJPmWKMAIagTLDdbB5/8pt//qd/qOrw+7/3x/fvnTl2dbtaLFdd13/8618XdcZnnz3vh4EchRCaetENfZ9iSilrKXgbO5dSuri8SCkbYtd3y7AqTdpCuMbM+/2eiKqqHjTvu64UhfIQqyqsVyszG2JKKTVNUyrsd+6chhCePv3sarfd7XYpp+VyWcCRTdv0fQ9UBnZsv9+v12sAUJUYh82mW7bLso+Oj9feuRR7Ux32fVPzyfH65OS4DQ5RkdCH0LZ1nzSmtNtuCGlIuQ7hrbfeunf/oQsVOZ6WOaqqIRb49ZRw3+I7dJqE3+12CFxVVSEVYL7N9e12A762HubVYl9Oq15qraUhWv4NEhITHmx855yOUsmCmMicC/Xx8fGDB/d/89GH9956GxHZ8TAMWXaiDTnxNQ5DYheCK0J50VKEFEFyQdQE5hL/8Uy9UlA5xowYmIgY2QOSqWkSdUoIIzFDjJiVDAggpSQp66jzmi2LpIwmoEAIBdjPyIREyAX8ObZiCwJyHHbF2zo4giEWkqAyjwZamgPIxMgFwkgVuRo5OO/JSR9ls9NADJagKhPiZOKbBgDIgA0Z5npL+axSkTDmN0sj88ODzxlenOmg55/LMy6ZxeHvb1/EE5oWYaSGfg32ebtWSg3x8A9l4KUAA77M6pRF/OaHAsycMPQ6d9CXvMlr8NOSjoyhPljhYnutalYGA8tdwmL/MwBi6c1MiY0oAJirakQkoylZfo3PbsRpIaIZFWlMhKJIE01i7c7efYfbNosGb4QqKjalaaYzMBkADE0FZej3OcfKBxFRkUJ2N10ff/LJ43/4x3+8vL4pAm6AwMwC5pxjR6rAPjCyI+eJJPWP7t/9m7/5q+WqImAiJyKqn1srB/ct57xery8vL1JK3o+DoAWWoKre+ZQjMTFzMPKMKsO9B4+2++7q8tITJ8fdbv/g7BiRXr582RyfVq5SzaFqJCUzEJGsgKRVFVRBVWOMIuId9UPvHe43F59+8slPf/zj1bJ9//3320XdrI8M0Fd1zvnx4ycxRjO8urxBROcdMlehEdOuG1JKMeUyBLDb9yd3Tvf7/fn5edsuXAglng0hlOkwZk4pTRRv+4xQSFjJgJmP10eqaiIF3SgiR0dHy+Vyt9s9fvz48uoyNDUTvf3WWwXsb2bb7bbve42yXCyJCCDXdcvsU0p9P4xt59iVwpdjrKqKEHM33L1z5+R4HfvueHHctksAaNvFkIfNdri8vNzv90Sccrx75+z07H7bLssknSGmJMjG5Ik5621QAq9H60S03e4Qsa5qIlI1773AbYXnjbbffHyeEu6LFs3rSMSyTIs86pwoEI09AyXL2RRTzoT43jvvfPzznw4xulBhlJxBs/gRi+iAHKNzzARmojkOlDOXioSqmoCiqaAWcV1GIkByyEwQgmMXwHlgBwUsbgaiJqIpa8woimKYFbOBABigqAxZs1g2VXVYVAILhQoxO2Im4qJON44oFNOFWKDmhjQC9hALE0+RxR6n2skR+8Lsz0hBMKDzRVkYSLsol1sQUKjErDTEDUBVHbOhs2JLCy+WgZkhE4ARkOGoIHZrlGDKCG5bjMU/f84B6CidSIcTv4evmdPAN15zaJRnR2K3cFU4fCuzQgvx+sIZ7T7MDuC1Mv3B+7xh/snxeJHTMDAhlXgIp8/F2ftlmcu/BmBFpUGVxSaEz0gDO58zMZdWPzELoPe+NLhsqoLBgWst2D4oj8q5ctqF+n+TB12s2gcPE7IBSE4gsdRODZHmpvr0pAkV0fabG8/MRKpQSjUGo/qGGvzbj3/8+MlnWbXvBwHzHMi5nDMyFUYXdMETVo5qZ2T4w+//xftffRdn4dcvyABub3SRwULEo6OjzfX50dERldAAsWma/X7vvM/qRFTN1EDMVLVZLE8fPNx315vNpjpa+Dp0Q79ar7r9fn12L6U+5wGxVhUkiDG6UANQVi3ttZSSiSKAaby62PzmFz/91a9+eefO2de/+c26XbALddtubrastt1uP/vss5cvz1V1uVgjMnu3PFrv9vunz573MYqaiAxJ+hjLZNaLFy/K0G8SKfw25ngYhnKZJeMpLG+G5pzzxDHGzfWNmbV1jUTL5TKEcHx8vFqtzs/PX758eX193Xe9IsSU5mS0tIL7rmMb2W3v3bunqn3flx4DIiIZCCwWDYzZDyLAalG//eDu6fFRzQZgMUYiuri6rpq6j/Hy8jKlWFVNCOHRu+/cuXfPV1VVVUOSiowcgVHJDedNNG+KcbMQlbm2uq6ZGBFLAgR0C/G0A7Gww6NAP97YmG8ctwahlHwPetFvvLLsN2bPRfUQ4MH9e8F7QDQkIE8OiSrna+cqM6xdTciBnQMpfM85JcwZRDRnoFkgBZg8MhVbymCEgM4ZO2Rv7Nl5dG4OW7GU7xVA1FLOKVsWMdWkkrKJkZU5LkYEJmZ2hIxjBsBKCON/hBMOBRHHhMFKgadEzEjE4388choSBkZk4IqpIheQyUwBYp8kZxCLwJwz5AFySpL9QkOozR0E36VxN35rAlYoj2bT9IbNfOPZOXmdFh8RR7bFg07v4VIo+P/So8QJwCOq4QBHdAilLyK/5fv5hMwMDxzAoX2G18W/bt/n4KRpInd7Y3GPUkRjnev23VQEbQz5FYqO3djsHYvgqlDok1SL9MDIeg0w9fkdESmSI0JywQVVc1NPojQDxghrulg/UlqCqoKC5gzBx7pePHp0CQ6MJPaBTU3GvssoXQmzfwKzLDEOXeVDSolcyGkcY2ZEQLq8uv77//oP3RD7IYuZmroqAEAR/xpyquvaMVeePYqm4YOvvv2D7/2FI3LoREHAaMJilWen06gzToDF8vsQgnN+t9ut12vNIxO1915E2dWm2QHH1IuKcwzo337v/f3li5cvXrx/710Bi7Ebeeic856H2G+3WHlyzjsfFICIHLuc1TQTsIL0+24Ydh/+9N9++eFPv/Lue++9/35VN+1iBcgxG/pwdX3z0S9+8erVxaJd9X2fkrRtZQbPn7+63m36vu/7gZizwjAkZl+ymZRSXdd1Xd9st1XVMLPzrlxgVVUFn1NSHMmp7/cAsNtsY4xtXa8WSwOrmqZuGjN7/vz506dPS8piZm3d1KGyLE2odtsdGXhibtq2XpqBc0HEmN0wpGEYUpLTO8f73aauq1B5ACuQ0zh0J+vVatEGwtWyDYxJdLk8alfL691+1/V9H5mIAO/du//2O1/11YJ9EMOcNdTgOAChIRkAH+y1uURpZmUkrW2XhzuIiGSSOTwYwzaYAr4CWDqkaiccs/w3DIqpUZk8AEwp4VwiPgARFYzv3FUWMTAN7N569OD+vXvXl9d3qxZNyBxzVdeLul0y1d6HwBWalVktAvWOSIuQuzMxs3Gk3NTGuVBmlT7UNYZgVW2h4mZh3ptjQMymzkxUEEBUHUCBaKqBCKScAUiyYBbnuBgUZg6hNmYcx5hGo1/iNi3EnFhEzuEWiIhU5isUEMkROwQOHIRTAHDkPLtKMRA7IBLNIilFyia2j0ioQpZTjiTSAFo2ahr2jIii6pyT0tjHcvuL4O84N4aT8S36hJ/P7W714fT16dzPH/N7zT/iwfcH/DyvF5sKQOhzjuTNt/3cL8sxUy4fejP83DncmtpiH5mzKU6KPMxcRBVUBQsYQrSgNseai5qMJHYAUKgAxzclwjJZY8QOEZCZGYgCjpWoEjzOV02ODYDLGRZQrBqaMdM+x/bhfWmXqUg5W1aUyVEV5vFJhAAsm3jGYdjHOITgS54AaIRGSDEO7Kqnnz376Fe/utlus5qAFpRnVnEuQBlqK7RROa6WwUP467/6waMHD1HFlA4jfZpYRWFy3s65EhjaOCNiq9Xy4uLiNgZU9d53ce+riko3SRhUsioTnz148CuiF89ffPU7AEyu8qGqrjf7/WYbWh/jHrAuyEt2ztARshkys2YD0ib45xfP/+Wf/+HXv/rlo0ePHr39lXZxVLWtCiRJyP7mevvRzz88f/XqO9/5znazf/bshapuNjs1ozoAQBZVszLuG3OqqgoM+r5HxMViAYBHR0c5q5mVYsiYDZgRUd/3wzD0cRCRZbvw3qPZydHxYrEIVZW1jCPI8+fPb25uyuxYGbAuXbW5E9hUtfcBgEvCVFg/CwCJmYfYnZ6e1nUwkc3mJjif8lBX4c7J0aptHKNjQoS2bUNdqWE2uN5sDaz2zkxOTk4ePHwLfVAzAqrbpuACbQz8+SDmG58vIg7DsOv2k9Tw6yXWyUN8HvZ9G9Qf5ItTpvq7jsPMe7YAOBHOT9aGkJUUMmhbhd/7vW/8+O9/5Ko6xX1g1yzW7WrtXFi0q6LR5Jks95YGHoESqiogMk7gG5eWCSAjkQG4ypF36lkdU91QFSAE9M6QwMikhP6qIpqz5WwA2UZrIGaKRExA6JxHBGbPTMAe2TN5QpZSSMAZiQIwjpuSjREhApUgkgpbBBbiT3bsQoVYsfMcnKhHKokSE3qwGLv9Td9bBo1gIjmyARFDa6yktTnnxlCYCRELRJEJp4Tg9oZDuUbTeT3Mz+hW7ud3P87xjQraB6c8Z66hE5HdPukZ0G1j1emLUD0gk5F/fSXZbcPqtRMjeq0KNDIt09isLnTWMJanso2eYOyUmmmWnLNIdnB7pYcJhCJouTQcaTQK4QKhIyJgx0TEpfNeyvy3WcjcllAzYCwDIFhacWPTQXJKydu9tx71zAlIFUizWEREMzi82HJ+ZlmBhm4PJgSlua3IrCaEwEgi8m//9m/XV9eillIqJYvihdh7IiLnvfeLtoI8xGH/Z3/67/79H/6RZQVkAAag23mCbADI5BHRQIovlwPNGTNl5xaLxW63Wy9X890jolTiIyukeMJMWQRdtd/tQ7dPKRFT3/VqxsQ5JUqKZFXlEW0Y+oYdO+5jZGPHvqoqJrx48fyf/uHvf/Obj977yrsffOsPj46P23ZRQqdhs9lcX378y1/dXF9/97vfrav2X//lp3Vde18tFgti/u3Tz7p+GIZBgZxzCmiKccgnx2sxjTHWjQ8hxJxTGsrTXywWVVUVPHRh7AGAQvLjj44XTVMdHy/bBQESUp+H3W5nZqWYQ0RlsCvGWBgduq7z3hdP2fd9znByfKoCVWhUdVzeQLvdbr1c1HWd4wAAxHB1dfXB++8frVemadmeeCYiWq/X3ZAs65Cl66OoImPdtN/45jcXqyW5gOSQKfhaYeJ+IbZD9z49qb7vN5tN1dSzwMtB3/dLj5IulwxgDhZtgnf8bqNBRHiQJcyOZA7UbLTZYKamBgx3z+7u9nt/eheHiij4qmJyIdRETgXYOUYVUxMFU9OsZRYMQIuaY5m7nCvghhQcVg6D1ypAXWlVUeXBeyRHjATRXNE2w1LEzwBJLatmwySFuhy16MgwEZEVvUhiQHwj/RklekuQXCwJAKIishbxzKKqTc65AL4iNQ8aMHjnAhsaWJasmkTEVNQk526/EY2mKcfWZTFgS8ZCAgY1FBdaatdohGBCRAiGb2rWFhqQ8Ue9PWunE7fP5yH/bxzlZToF3DjnPoVlU2RGsNwuEbsFrb+ZKs7M5F+eAcweDInktS7A7WI6PHQiqEDEWQu+BGU2FayKRPBhKbPEfQo6AieKjCiN70PARITsCdGAgMZni4BcJjwLbzYh4siOXVwBopnKSMoKJpL88XJ5/14EFAOzrJoV8iykMd3/yQGAqEhK0Xs/0jaaoikWmibAy8vLH/3oR/uuH5JYaVAVP8Q45fyFYVydp5N29X/8H/7maL327BUQzB2aiNk3lyz6sAgw7XnMEuu6LijJsV2Zcwhh0w3OOSR0zBgCEGSzdrlo21ZzLh3rkti0ixapiCwCAHrv4hD7vq/JM3PT1I49qD3+5JMf/eN/7Xfbf//Hf/KNb3ywOnuHyMWUYkxXl9cf/vRnV5dXOQ9t3X70i19ut9u6KkpYrfPh17/57fV+M8Q4DCnUtXPh6uaaHB2t1qd37vz6N78u7jillHJmZkJqmgYAt9sdgKWUYxycc0XuTUQWTcPLJRM5djoOMcUC8y9cCIXhp67rYmGLxksR+QKAIuw+kuRMA18pJbUyDRDLvgs+eMduUa9X7aKpz06P1kdriX3TNI7detVsu/7jj39zeXWtKbm2fevRg5OTUxFwtWfnHHsFY2YdY/8S+txut1Knurm5KeeTszjnnXOHzbTyuA+jmcOd+MYi+dJw0XBksx1jPkLTKfx7bS6nnFUuQQaWEnw2wwf37y+WyyHlqgoBQ1017Dwzs+O6qiEnkQSmJd6UlFmkIFtViwcs8hEOCJEdkAFlcIQhUFW5tqG2wbrGujZzqAQWwDkjHMO0wmtvmgvfPRE6x4yMVHQ7nWNixxzYOXROicpQrhZmmyntKnkAIoCBIYyx5EThRYhMRM4FaljNA3okLwZgCaSEtllFRAGw77ohp5yTDL0XRXKoxgCeoSidq2ppghZVcAUbP5FwnAcYbf5ttHr4xBzQwQAtjVVsKypvk9EmYgCbzWshpCciNWViANAcR+bMYjVg9O1mUKDr8HmpL2BVQAQaPdOE/xnl5cov6NY78G3XQbM451At5xx46mMbTCoHAGaeeKzpqzlEA9LCsexuq97ldpQ4zlQcOSJCJFVz7JlIAYxKfj/uK5uApTBppiG7sf8yvS0AIJqiAqqSCGXF5Cj1q2Z7dIe4qvLQ86CkYEQ0VqdEx2mC8iaMoqJiuaqbjAI4IIhZVoU6NCnKk8efffrZ831MvdlQJBVLKAPgiNgFQ3ZcLSBZTn/xJ3/5zttfNfRmRAhgyuzsoGR3uOEPv5lx3+Rqyblqlpfn5/fv11mEnVORynkzIOczohiASmCKw+bszvFNzkQZXPBhcTVcrY8WvcaqWjTtsfeNqjD5Agavg69Nd9fnH374i59/+POu677+wde/9d0/WCxXydSBJknPnz/99S9/df7qVY6pDl76zbDbfuNr30Dnzq83T188u7y62ex20UBUEbEMAG+ur5q2WS7b7W5/db0thJ3MUIewXC6J+GbXqZkBMXPqYj/IwlVZxHt89NbD4zsnXdf1fZ80xyGmnHa7brPZFOlQRNztdqenp1VVFfxokZ4uXEbDMHgf2rZxjuq6uri48N6Dabuo18erIfV1u0jJ+u3ABmdHy9XSrxoLlWfHAOaYFm0DxNng/OLm/Hybk4Hk9bJ56+FdQkVm5AqJkV2x2mRGWMp+UIRPSvShopvr6zo0ddsoIBMXmfQRcgaFuophjNlfKx0URhMbJSimnQameMs/U0S4xkx/YkkEKF1ZLHmAQcKR+EuQCRFAkB1bNlEtBBYeqKmqh++889knT+6tfOOcIxdCDd5j7R0BgUjcoHaovWliKsLdSEhswkhFMKuwLoiN9IWhaqGqoG2xrqhd6GIpzoM5LcYy7BwDwiAWs2mWlCUSMpgAgGfvjDwzcz2Wrrwj75GcEZNzxCXYBkVQsDJITI7MqZqhY1Qzy4SAaoxEjjxRXQJMNjQjBV/4tyV7AwYYRJOgQ29iSD73KUkX4yAqDrLX3lsvpqyqdYCmRvJmIFk8UwQYIR56UMWAkTrC4LYgXzb+rSAMTlRch6Hf54+5VTDWCm3ydjjbPoSD6B6n5s9hjwGxFCttAv/M37zW+71tGk9fiq2amlG38uuHx0T4PgUyOK0KImJSy0UoxwVful7snai6EKaEgkEViZE9IyB7MwMoQuST+iMVrNUX3B+cqv/j7Z7Iv2Mc/LL1i0WXEhMZiqKIMNCtcI8CgoCZiWQmi3Hw3iGMPQsEMFNEn1LKAv/tn//5+cuXBa4mOTdtRY6dr5wrFOVYpOh12D28d/b9v/jTtgkF/IWIZX7uMDGfj6mPDrePuDwCA+c8gAUfXr58+eDevVLUlgxiRYaOkBlMQQEMq6rN3ZWpWdY0ZEfOOaf7fQhVKc4SkYF6F/q+jzHd7LfnF+e//OgXBvbBNz749ne+Q8T7vn/67OX5+UWO6dNPPyWDlNL9u3fB9Ory5aO33z09O4tJPv7k08+ePY8pi8G+79vFolTbp1tBALbZbAHAe1+idVUtalw32/7o6Khwfzp2hJhTbur65GR1dHzUdV2J94Fou9/d3NxsN7umaRaLxfX19SwYcHl5WSaZCzfyTCjdNHUR0tpsNqXqcnNzc//+/TgMVVMtFu31xdWqqapm4ZjaunKEnpEJHVOzWBUIYcrw2bOXOee+706X9fHR+vj4qOgNmCmiG6vQCCLZJrLbwldIRMOQCtd/27ZiisilEH2InjB7czF/YYR/uFRsQlXMX+E2QrqFYhx8f5DQ49hQHaNu1BJv5pyrqrr/4P6TTx4DkPch+EBELnjnPReNAc2kigCOAMCojK6W2HDKaNSUkdixq5yrAoVKvYfgqWmoqawKxN4E1dDEkXMCoKBWqjwHLMhMxAisyEzBV8ToPbFnIC4Gdrakb1iCkQMObJrSBQAkREJ05CrnMQTTjCBo4jM4dGCCSIX3nw1caWIQExAjdjFtd73LUUzKR1bmgcBLLWBOxXuPVmQHEQioMDgBGSJ9rmlafhwdwHwNJX7BiWHu84b188etQbxtCgDACHsfFwSMtniUAZqOLyseGiEgKgIR2mSMbGooje9ZwtK5YzodMzfOG+sbEQ1hIlQtxTIgItCigEigig4ADIEBwDtfsjRmllLWw/KPxggdET8HY33tthweqiqqCSmsVkogJqAKKAqSkyCB2nTapd5SlC4ASo0FiBQKNzuYGYHFnIaov338RIAURLIwEyAUBYHSYPOM3qNHqb3+8K/+7L13HxlkQjYCLVWCg0bIl13IvL3LRWURADg6Orq4fLXZbBaLRakL6+SacUL7EfOdswcv94OKOS4oaOx2vSoysyNyRI7M162qXV9fDjE1jE+fPu267tvf/YOTk5ORVqHrtrv+8vyy7/sP3v/axcWF5Hx85/Tp06euWZ4+eHTdxR//9Gevzi+7mIjd0A1pwunP1Srv/TAM2+32+Pj45OSkKL3MiExEco4QLaUBQJ2jBw/uee9iGrquG+tFKeWcd7vd+fl5FeqmacrQACIuFotSUucDoelCmFzoRZlxs9mklACs7/er1eLm5irG+P7dr21vNmjSNM2y4dpjjBEX9fEyBDaVhFB3Q0LvfvWbx0+fPtMYPdnJyfHZ3bPQ1OwYC5PqRNJwa4zGXq4h4jAMm80uhGq9XqtMMfsBQOiNb75gGR+sjsPI0V5fPweBwhdv7HmVlWrYHG4CqSpOE6MgIndO73gfxCxmRecXy1Xw3jlHpoTACqwjfwoalIabqUyh6Fg+QEL2zlcBgsMqYNviYgl1bVVtwRuzCaEhiEPvwJEiKFppI3AhxkAiRw7Ak3kmHqPpSVihhHlaRLfG6d9C94aTAyjfoI3hNxXsJ5Bnj1ypy0SKIgGhUsxqqGTFMBb3g+SIGZiUNEvsh4QGRI6YkBI4IKhMjLBkY8ycFTApESEzIBoZ4PhXnCE8ZS51emquLKBi90uQ+zueIhwgCsocwFwXyqbz4jtcNgVYNoPA/rt+hSaS9MNXItzySGBBd6kS3fqxefEdmt1bn8EjIWKJtGlqABCxCz7n7LwjmldhkfAlIkfOleYNHHg7mBze4ed+/hzKENzsAHqk5vgoo4okQjLKZibZkG2mvhiLUVMPuDBNkyEAKo23l50novOLi98+/mzIsh/iNAFGRgjMyL4QkNaMAfM3v/7eX/z5nxAKIgOBYpHeIRqTgTcfx+G1TK56fKzMnLOY6unp6fnLl8zsnTMjJjIa2V3MDJEcOx/a1eoYgYau3282BBD7gRs/9L3mZCpZNfVdFImxz1l+8/jpRx999ODBAzN7/vy5qO52OyPabrqTk5NvffCNFy9eXF5e1nX90S9/GVNE5//Lf/3RvuuS2nY/5KzGmUPwJjHG+UEUKmlmPjk5KSJZFxcXxYKXC2xD7YlBTWJqq3q9WAZ2+90uWwH/wfX1tYiEEK6vrwt83jlXxoYL+fNutyujIeVr4fa5ubl59OhR27Y3N1sAWCwWr169apqmruvz8/NHjx71Xby+vj49WiEKAvXdfnV2fLI+qh2D5jj0uVnEpM+ePv7Vx78FIpR+vWyP1ovVelU3jffeEABKIxTBpBjWMohoZsRcWJq9r9q2hTJZMuE4YYLM/Y7jzfDqNR0OOIwM3sgDvuQYLU7pJ8/vM53P2BswheOT41BVSaOxR2IFBGZEIAUw82VJqppkMiPAQphVAqQyY0s0Ru/EmAk1OGxqXCy0aampsa6AWJOaonkGRxQcEBW1mllqg4pJRGBVZnLEMM31m4mpqmZTQkMYiYAmAbDC76VT7jNWN0qAR8xMLriqUssIApQZjIGUpMyUKc4vRyJywAjIiIF4t++h8NAZtEChjJkyAAEhmq+IFNHK2qaJpmG2pfOjP4jCzSHeFjf4dToHmtgC3ggu5hcUtwMHtYISmzNzEVJ5w5rMxhEAnK9mQzmfMTGhu4XPsxvHFGRSoi/vqWUk9wCHcLhWS+N3diDEnCcPR0SIbr4pI+TRs4GRw9KwoQL5L7ujpCNjS5VeYy19cxxt/NzXLtOs+NcsMhAtj9YRARAkD0bG7NBMcrJJn4AQVTKO4FdRVUbKIogMogiEjkxEEX/1m9+8uLgWcAZpJDcqYorkDImZPJO3tHD8/e//5dHRMTNLYQSc2u+I43T04YIAgMPMxg5qweWfMLMZIFnbtrvdbr1aFfBszimLIIGqDikBIrBn9jEOsU/97obNBJUdkNn11dW6rVDz0Hd9P1xtttfXN7/+6KO79+4SUTG4VV2v1+vr7XbZtI/uP7i+vv7JT35SmPrrRdtW1T7m/bDtUxYxcgyiIrlMn8/MhqXn2bZtTKmqnJrtdrvFYgEA19fXpaftPBlICAGpqutaVbPEEDwqlpx4s9k0TTMMg5kVrv8CAy3CL2Z2fn5elCCnqIIQsW3blNLV1VXxN0SwWDTHx8f7/f7oaAVg281mvVhU3ufYDTacnqw8OwDIqWf2MeWnz19stvHZy1eIJrFvA967sz49WhUPBGiIt3wys0mdH9nNzU2pRFVVM8UuqKY0AvPeaPLb/A6/w47PqwVK8Pv67+dtDgdx3hQTjFCL+SPmXc8ezSRlQUQRdRxWy9W9e/f67U3KVrfLUltU04JzADDL2XIu4XfWqKIAiiCigGaiTDaO9iioq7wyu7rBunXLlboA7BQBvdOkyKQAhMREgli4/lFNNHvvEJHBPBUF5FHjhRHFQHNG70DVo2dEAEJDJB4BQACgSsQlDyu3ih0DIrOHKlhVi2bJAxO7omxDmCSbqpiWdkJ5wKWFWTnfVnXqlbKmbdejY6QdWCloiyoYWAXOe8QRhQzl9o6KKV9g/ScH8/r+n79+XgZgtsuff42IAJPZAeBnWhNzxoCT8kyxI7PiWLHLMMb+NH/WYaqBiMCTGJnZeEmfW5e39aiDwRMzQ8eACLMQMo59b2K6DWcm3zcOD5KNYg+gJbYqsKL5IMbZIc0bYD6H0RmYlmi0j1GWNTWtIGRL3sREARAVEItGBBQywWJZGCFl8UVALSsxorFhkRuWlPXDjz7e7vt9n4eYkck59r6MkTtij0Rt5azf/Ps///Pf//Z3yQVA79jZFJUQ6Ay3nb+OJuwLt/40T1e8u1per9dFerepl9k0hAApGeiQs8ZEOfcxhiaIDNvNVR62KeXlydE+dleXF5vN9ZPHw3rRpNi/eHn+m8dPNputRyq8Q2VSqet77/1+6L/2lQ9evXz5/PnzEmsv1qvFYvHy/Lzv+yy5rMA6+Mq7FNPl1ZUA0HJJRCXMH53WzEFMxMwxxtVqVdf1MAxNVSPierkqGFBmJuau72OOU9KT67re7/flQaeUyso8Ojqq6/ry8tLM6rruuq68eZgOIirkz+UTC9LUzIpw0NnJ6cnJkeYuDZv1ugFTMGubpm5qZj9kvbzcnV9edfs9AbSB7hwfL5vgPTFjVsGcwQbMSk5UHE4pKRFKzl3fG2ApfxXTb6WyAGgHDmBG45R8et4+83r4HQe+Hv7Pvy9GYDYF01u9tqzooAY1ypuMLQFU1aqqTu/cebrbk6t83SAwIKmqqCEUHUcVUEZLmghA2dBAswAAGypAFmFgQzI0AQjOYaipWZpvMFTgHYNaNmUoFA6locFFDIPGYV9gh4gOlA0I1Ht2jgxVVdAh8USUaTCrNFkWyAqiKEpAMN3oIhQMCEys3oHz4Dw5pyBmYsJKkk1TGQ4CE4SMkKCkGIiADEiADhDUIEne7RNoQvOlqmRARiiGdcuBdOqmEpEe7PEx6p+eCxFZIYM7XArz4y+rFhGrqipZLRyEhMVqlwV9+GhHgzu1c7/wr3ZAI0HTUZYFMmWzEZg0ZYU6Vi2nhuRMRjivoc+1OBCRJgCSFpbNaVab4FZzHG4TCFUUA0NgQ2bHE6wLzMQQDVDkoLEMhSdudACHmRMetB9sUtoRVfUV1nUuLXgVsYyGZKRW1o4dnnx5Ft57zdkMVcScAzNFY8Orq83HH3+MzhuZKCAIcSntjbVA710cuq88uPs//s1/aJYnWYDYazYiIgMELfn04ccd7NUv3fBYYFpWrl7btt1tt/v9vlm0u24HiEjgnJOsOQ77fi+aN9eXnz35re6GzdUV1mEvcnLy9Pmzz+zsNA/74F3bVGj2ta+9/9a9B+TYey9gH3/8MSAuFouze/cuXr66vLgEgGEYFuuV9/75yxfnF5eiVCQGs6Q09OvVetdfB6YIMAzDvXv3SvN2sVh0Xbfb7Xb7uFqvAaCIOBa9KjNrmnoS792vVsvdbpeziKSry8vFaln+1Pd9jLHU+ssCKO9/c3Oz2+1mJ1H4RG2S0it/XR+t1KRdNCklQFuuFimlxaJZtet+3w3xer3whGAmjonJx2Qg6Wrb9zF2XW+SQOWth/dXDbJzTFR0ftAFJi7QBsQRuVs0yFQ1VFXTLmCa8h0te1m2Zng4pjMt1MMdeggA+bKAYLb7n08X5ndGvK3dHr7qDZPEzM6cambGrEpEDx48ePzJ43qxzGqLRatmXDZpTiNQE61U7QuLhKiWhh5aVssEICqkQEIOgF0wIDMsXws0k8tcUUFMqZECGKqhADpmNdIyWmRIoGiQYgRwSAqIIAJqkhOzMxEQMVFUlZxJxlFTBQEDBVQxmu8SU1H0VQQFEAQwVE0muUspSQJNqiJqyTQjCQFBkZykEtypKoHlbsgaIxoRArEqIjoyYmAgb5M5mqs48PpmL9+UvzqRPD+nw+I+ADjHiKgqqsI8loMm6giYTVZ5pGCF+GhElt2mmVNKPsf+h1HnmJyOmFMgfa3WX15ccoWyqlQVbQQQzaQLcxgyo/sRsdChECEXbiai0QcY4dTlNjCyso6JHWmpAJKTLKXBoEU+oiSGANP0u6oq02tex1SLzjSUOpiqiqQYRVTV2uUqrRZUhZiSQ3CmaoIopmg4ooBwqloAQIyxUJTEOLhQjyeAZmJC9vTp80+fPstZJ0InJC7kJOjZ1cF5ptr57//Fn7718D6gEwMFHlvphjSxJd6e/AHB75c2502ZSdUsC07or+Vy+fL5q6qpFm2bRQqTMDByFR4//uT0wemzZ5+9fP70uG4fPLy3Oj1p75y+/c4HP/vxvz26e8KgaYifPnvmHb/z9tuLur3/4P7V1dXF9dX9+/dPTk/run756tV+u22aett1TdMMMW73uyLXXleht15NgvPMaJJUIiOuFqs7Z2d9P0jOJ6enMcZnz55VVV2WbikilSvy3q3XR6vFYrvdOufWq9V2tyuP7+L8YrPbLNcrACiBzm63K+DOUvpfLpdPnz4tCUHhED09PS29tOJaROTi/Hy5XDrnYxw2Nxvn3XK5AoCmcU3T7rbbzc1V22DbrNhR5Zz3vuu6vk8xi68Xu66LcZCcHty9c//u6fbmZaAQgg/BGdXgVwAAdMdJREFUO+d4RGsJlBWGICLDENGs8t47V0gCDjPUKXy6tfVzNk/0Wjr4Ztz2ResB8baoe+gwDqMfxAMlwoN3mU/JzADUOacmIgkRmSmltF6vjo9PKqyYvRFlUfaMADknMtFSdC+amYBCkrNURCaQVSklA9NkCdFZrpvBq5oaEAGSETKN/DygiqomeYIyAo/xzQg/LwV9KwS8jCJZs5ChGKJz0cQxRyWHHrkDX4P3VEd0POpBceGXU8wpDRFiLAgxm2gdsypKtpw0pSEPOUfMOWsSsWSoRMg0T3RR4TUAdMgqOXUDIQI54MAuJNoRMCMhBOecDwE8AKAxECEY3KJX4BY8aWaOUIloGmgoNShAciJKI2QcmABBEJTQrDBLFz/qnKgAEDnWlEuti2CaBIYykuDAyAwKmXaZG8g5FxlaLdBgM/YOmQ2QuWgrFveFBkCucEXdhsYGwDwii3gSvi/pbZbsnANARI/ECKhg5NhwpNwE580gj0NVVEreBkCCrjQDJYKZSjQAMJkgagAAqIXyW9F0Epcv+WPxf2BmAoIGaOSAFTmhGyRHFHp4d2AMgpaikiQWlEydqI8yoYAAAAhFRVJkZtHo2NAGRDQjwgCAOcknnzzud50kGYYBiNAhMXtwNfIC9diph/69R2d/8ed/GBoSjQ4ZtGCCyQgNGACxPHE0gHE0oGRLr2/y25yAQMCAQJVM1Yp/BrPTo+b8+ad37t5jdmBmqUfLT5/99vLy1Xa7efDg/re//p2mbdAHDK49OoH6hKsm9fvVanmj9vz8+tE7Xzk7PXG+2ey65y8vco4nJ6dVCN1+/9mTxwzMREdHy67vU+z7PtZVhUYKVGrxpdo+xLQ+Om0XizgMu8sLQ2rbdlGHV8+ed7sdAt45uZdF9rFDg+Dc8dHq7O6dYYhX2433wVXV+fk5M7NzL16+vNnt+j5uN7v16qip26GPKlY07ETk9PR0s9kMw3B1dVU0HRGRfQiBum44PWoQ8fr6elEv7hzfAURDq9u6qmrn+Orq6u7du7ub3fbiAkmr5RI0AzggHaS/3F6u16ehcRevzq+vr7r97uT4+L333hPJ5BuuWmKvYpqScCRVMzEGIu7zkEUBoGpbMGLvit4ujgJhhIhaeDJnuaZxWY9WDuayqr0ertttrfVwPeDEx/Vmol+Inw1KtQaLyTAl4pwV56kAwJyzGSgokrF3WIb0JTHb0apaNe3uYp/vkPiQSRyDaBFUVRHRlLxODU8zYclUs2FQy33SlIm9IARPpHaz792JTfYQUNQxDUYEA6Utpi6lKEbZwBAEWCSLJkA0IgWQIgiIRmZkZKLmMeOQG6+5QxdS7Jx31DtFIMeASEbqa2A0AFHlrJZU+pi7wQYZYh7E+pQxi6YeckzSDXEjcXBGomJiipCzZFMA8i4wgFfzLMygWQg8GKbOEPYe2YiLELECeKm4adAQzFnhN0MFsGkWrfQ+s01VEOcci0jOI4pAJ5Y0VQW4jawLxJiZJ847RBzZAgwgi9BBPjiXkg6zCjwovJSdBgAlsZAyEjZF5TBRIxwuODtoOuE40TBmHjwLxUxJAxJ4Ckm0YH4M0TlXHImWKzKagANjYAwKhRZULdPIjKgAQGpz2D+7zRL24DR3TiPcFxALEsPATEVVLaWMRLuuc2gKaGoEqKKKglY0TXXGwJlZjDGEAFPyNIKdzFQFTAx4iPmjj351c3OTtQAiClsRkcNQ+SowQkZNP/yrH5ydnk7yPtNXHEEKJeeD/x8Om5Dc9tqGN2ubxb7pLs7PT87OJA7bzc3zzx7/64/+Kat986tffefttxFJwRJg1SyJfVbzoa4qIaInT56I6rvvvsvMptj3qaqq9957t6qq3X776tWrEKrKhSRyfX0lBsHXzWJF5DabzfVmV8A5pQ2wWq2891dXV1cX50dHJyd3jhHoyeMn5+fnRb7Vsd93Xdd1x8fru3fP2kXd9/uu73xoY0qvzs9LUes3v/3tfr9PKS2Xy7KuFovFy5cvEbEAeN59990QwsuXL0txDydVd+89ARY+ic1m0+33i8VCRYaUVqvVMAwFmbpeH+12+xiHoe+dx7qqREWV+r7PSdp2aUDX19vz8/M49HUdPvjae+ygHwYiZucQLMXYLEYGKxQRGXIBNiOPIsCgIgmRcs4gwhAQAJhwnOV8nfd/LuX/94gA5t0974IvfR2O64WmTPGNDGB8Fc7rcNTuKulUlOgcP3x477fbz3LOvgqVD3F3IzoiIwyMHFMSg9FSETpRQwNVTTmbZbBsRsoE25tQNWG3lW6HVeWZVEmJsiLGgfoe+24S/orS515hKKyuhFY6EwA5Z5A81o/ATCkDKyZVJ5yQs9MyzGzFLHJMGqKxAyJVYU2w7/K+6/Y76Lph6Ps0xDhg6qXfy9AP3Ub6vUYhNciFjZ+NrKBSic2jFwCfcxZhAhUBYACTlFPX7TcbZQ/skZxhNgBWYENgR0ZEhmBW+ApKXeugDOPmQvbhQ30D7zU3NmeLPJp4KnCLqcb3RiwAABOj5NxfKoWnUpf8fOZY2gB2MAV2eBp4cMyvKWMPAKMIThkKZ08qEEIwhALXAoBCzU2AZoWiB0wzmBXhdcnlzJWRJKdSlwcDSRmnfNAmaCnhWEcqN1RGsm6CkR7VsqqIjHwAwUu3LVlhVvEy+S8EA1DVkgHQxMh2EFipiBS/JSKGAsQX15vPnj7TkevCRgoKZgpOTUIgy8M3v/G1P/mDP9Iojitjmjst04X891t8nz9Knxo+t/NLRPzpZ8+ur6/63ebq4mK1aNumXtbVW2+91S6WXdelJFTVMaVAVAAzRG673V1cXH7zm99cNPWw36/W9dXNzdnZ3bt37/f9/uc/f/L02WeLxUINzs/PAfnO2Z0+5sVi9dnTp5dXVzHL0dFRYeI8PT0teJv9fl+FUMD+u+3+ZrcVkdXRum7aIfZVVd29e2e5XOacr66umHm1Wl9db6+urwsF9Geffbbf74sZJSLvfd/3ZR1WVXVzc3NycnJycjKR8pNzbrlcAhSFSGV2bVtfX19eXl4umtY5CsE1i/pms2HmUFXeN8Mw7LvtbrvVNJzdvc/MTFx4G5fLdc56+eri1auXOQ+O6ZsffG29XnT7LZMCISMws/cU+14BEQmJkYJzznPN3gESiBhiztkTc2HcVQMu1UIlpLLYDkzw9Hx/J/Jn/n42HDPg7Xcvm4MPePP30wa/xROW4KmYlKOT4/XR1gXHjoFJAWKWmhw7nxMhuiS9L9q4RGRGarHvVcUxxiHHPJC5rGrsparl5lKWq6ppJQRRHszQBPc72Oz0Zqe7PvUpDzENcQcSY4G0oYIBohqoSgJim2rVjJLYMltwPTC52sdMYphEcsbY+9gpNxg8OKdmKNmGTva7oeuk38d+H/tuGDoYOun3edgP+x30AymgqAPHZsxIyMRlLAwYwakG50ENCGMWBCBAU00xUj/gvkNfkffGHtkpOWMPpoXRhhCQxibu7MXLbXclipmf9CH0c47B35hzmZ86kxORMuoFB2Hsoe2e340PRORn0z+uA0Q5IIybP/0NPzQvvnnl4QFZRDmxEVGKpEQKxsQcPBYATzmZibUUrJAIjhoAZCgiOmYIJTUoE8U8n4ZN7ev5VCfHVjwqwfwrNVUl5n23T1EVQZ0z4iyKAkyqoghJFA0zQvFPSgBMPPT7qqoA6PBzVQRIEe3Fq6uXF9cxSxQB8lAmBhHZUdN6zX1d+7/+qx8cLZdsYErkCA4eZYnF8MvRPl922OThX9vVI7FlOjo6+vAXH5Lls5Pj68sXdXDL5Xp9fAw6UvOqWtU27HzTLBAoxuGXP/sZIh0dnXTb7Xq93nbD8cmds7NTIHp5fvHy/BU7rwY55uX66N69e1fXG1V49vz5btc5F8gZES2XSxE5Pz8vhA1HR0d3To4BcL/f73Y7IipEb957IO99YOZh6Pf7/cnJSd/3fRcL8mez2XRdBwBt25bK0na7raoqpXR8fIyI5cf79+/nnC8uLkrXd7FYzIZMROpQFUHgtm2buqnrmtldXV374I+Pj73319fXu91ut9v1ff/2vfuLRSs5A3DTLBBARHe7fnN1YyaO+SvvvHV0tBj6PWDOMqBhjLHf70JV162jnAwYSeomeOeYyrpT1WIPLYIwMxNlSSAElAmdEL4mxz1hh0oKcGidX3/ur30/r3z67yUNOLUKv8xPzOEjToDyFKNzLvfRVc5XDj2x9+ZcqOv++romzgCK5Jw3YlBz3lO2pDkOu5ySqmQ1JMoxQtJkmu2iKsJ25IRcyEJ1Y0SQOtxv9PomXd/IzVb2nQx9jmmjw5BjzoKEopJFFIyIOzGwMhSqwGCRIDlwTqqFQjHBe1ysbL/B3cLvV+YChRpcUKKcEqRe+z5ut9LtYreP/T71nfZb7fc29EPfe9FA3iE6V3li54IL3tg54GSqqVfAuuhNAoBoklT2NAJITKkfKPQ+VORAXAJO4jKiA0IiMECbHHbpac3Bqzt06Yct42LrZzAlTCQQNsHvcW7MFhsqt+Jft7ZmMtyz0SSigqfE1yXoiEd7V8xT2VGHwGE6GDqbhQmJSHVUmCurzXAUZxAVQiytAma2LFhSOSws3WpF7lFFJJsaIaukKcsZ9WoQQKbJ0hJCFwgqMRcJAThwSCMsSlVSHvuNKfbD0EuSwAKQERUgp2SUgTSDOihd69dyr/KGOWcDvfVqRqoKJr/+7acXVxtDAlQsLW4zZucZKocV4r/7zu9/6+tfI0DVkadoflJz4/eNfTg37g6fiB3QaZgpH0yBlt8XYGgRznnx4kXbVigch/3u6gIk3bt7l5wb9gMAITofah+8iKacVLWL/a8//s13//R7cUjs/G63HxJ85SsPzfSzT59+9ItfLharGPuSiR8tT1yo2Q27/dXNzTarMHPlQwhhu90W212YzpbLpZmJ5CLLlVSaprlz5w4SqXHX98PQ13V9dnbWdf12uzs6Pi6XX3QCChF013UFQT8ub9VCi33nzp0S/u92u4JYLZWf0revqpAl7fbb4F0IoQ4VM6UcQ/BHx0ci+fnzZwVQtFwul4t2vV6JxBBcXdUAkJNsN32MQ7e9atvm/oP7p6frOAwACpbJAME8Y/AewSQPZuZCFaoFgJnJVK1EZBMrfN2CYGZceAJVTTAVBUKdHuLBcx9xYfMCmGGBh6viMLCb65b4BqtEWWNlX8AsHAtwIC9xGNmMC+lAYyqlBIToqF61aKgEzN75ql0sYbdhX2lKYOBcRVpEybOpBXJIkk2jJFNTgL7rjMBnjmCNCwE4qy1zwmaJwWPq8/YmnV/Ctstd7PY7yymm/c5SjHGIsfRpx6KPKiSZCBKMGMARRgJmrZIik/fQVbLdYLugtnHbJbiKQ22hEnZqBlk0DhoHSTIkEdGYhI0KiSn5GlGc8x45cAgU6lA57wURBAF04T0lXyoVQ9cTFtSsMJFDJkASgygWJe4TuUxeNZdWJEkuChF6aM9vS0Bv2GuYYABlWc9lnzl+xwP4yDSDTmWRzcvntQUxOY85t5iXkaqCgKriQUz9eTMEU0H8MPQo1RIAMGBRmPiqaAxqkHxgK0Q8IpbFe59jUlUkK5JgIFm1jA4JmIkmVZ0QmWM5CAAtj6y2NJZOkCbDD4g4zYdPgbqaWpEXVlUVKXyI2Sx4n0TFAFXJJOcsiFkKG7nc3vnxNpZGqwEc+E7m62337MWFIgMrB0xiiFRVVVs1NRFrPl62f/OD7x2vFgBIPiiO5KVmb97eNx43fNEx33wAML3d83NJUFUlxsdPHjvnHty7/+zTx69ePR/67t7ZneM7d1KS3W4nYtVyFepKBHzlmHwI9Yc//se2XZycnDjnTbIPTb1sxXCz3f76k8cCkHMWw5j15OQOIu52XT8MMWYXvEUk56qq2u12haun4HMePnwYQuj3u5QkpQSGvgpnZ2dN28aUun1vIFXtY4zDEC8uLppmsdnsUkrsXIFyznDPAt4vBf2SEDRN8/DhwzLbFWOc8WlN03jvU04px9j3x8frstiauipEFMenR0WHUlXbtg7BOefqqtrtdk3jq7oGwP2+7/fDMCQmWizDg3sn9+6fpNgzVcEzgFdFkSgppjTw4LNouwzOOcdFw3wAqJgLkyKaZTVDxSHnpmlUzbNZAXioCY36RaZ5XgM2cdh/wb77XM73xvr5ssXzO445IlTVnEdaeJ4kYsquCk1YrBf9DSiYYybnuK4wRrKFpkhg7KuaHOQECJ6NPJAqkqlZtgygpbWJRLbfwOXzmGKVBshDOLqTCMlMuy5eXdtmLzHtNcfc99LFlFKMQxxSliTZphIBEatoqTgZKDGyY2KyLEXsBVyViWHocF/7dmsUMNRW1eorI4emKGqSVSGjE/Tma0BiMedqNGlMK+cqcA35gK4KgdiLGSiySdKcwZoqQU5OLSJ2kkpGgogMSGaYRWPiqiYhFAYlUDYlJUMDtFymEex17iY3UjKplnDmtVrB9LS4aIQdkC3DmPaO4SGOgKHxAb8xUXyYCthUpSkDILOC7hxNH66mQwM0IxNundD4I0xRxnhJZdVmFQBwNM4YS8o5Z8+cVVCtmP5CLWtmqAYFsGAgksvYQXn7EuHOnzh60YN1jIgIt4R3IGXl5ZxSVok5Z9V2sawXSyCHhI6cSS+SBXEkWvxc1SvFCMizjHF5BAh8fX396WfPxFAUvOdsycCIHAIuQnCS/vTffff9d99FM1Fh74wc4lhUxdchnm885S87JhNQgip74ybHGDcXlyJ2797pfnezXi2f/PqS8vDo4T0i2nV7I66r2nlP5IyxauoQwtXVdYz529/+TtO0xp6YHRqGWlU/+e2Tvu/NwAwLpp7IXV3ddH1/fb1ZrJaEfLPbdl33/PnzorJSDPFqtVqtVtvtdrvdlpnW4MPZ3bvr9TrmQuYTDez58+eLdkXEiLxarZ49e+Eqn3Iq3RoAqKoKEQtPXHm+u91ORL761a8i4tOnT3e7HQDMNSJm9t477/rYlQg3hLBcLhEghNB3/YsXL8qOKMWleagQRZhr790wxDj0acjeVUxw92519+4RQvK+YiRTBLWczHLKzGVtVXXjGdFUcjZgM0OMZh6wTEsWZlAwVZGAiCmlMt9eVnBhMTrcpGaA9Joh12lWYN6/XxZA/P/hAA5Lu4eG5XY4FEk0s6N9v7vDpKbAVNUtxmwYIbXeMQPwMJioITgGVjHnFDWr5izsXKgrViFKJkPaXWvKaAY5xf1WSqE8ZtntbBhiSgPaDvIAmQyS2iCWVGOWrCIqgIjskwiAMaF3jsRoqjogIZNHl8wFM7E8xDx4X1vsIS+11ozMTK7QU3DjKTA552saOnR1QHWqwYaa2Bs17AP4ynkgzmqiiCqoQwa1nIR7qwBVEhS6p8JBhFSiVgUGRxbQAponrpiCsSIamALYnGm9lgFQGX5z7jByFxHnfCmh0NhAAObytMbSXqmPg5moTricN4/PD0kRodnUBpjX1pfEobMFnDPNwxVDRGUtIZYscs4syrhwmRosYxrGhMPQAxiAqKhIIkADnSCQQkimalJSZC14OWaPeDD/RVgouGa/RcQFYapqqgaqVkYnRrFAzTlLzouqsZEUCk1n6lQzEyuOtOCSTQueEgutv6lIRvSMhMj7Xffi1WXfp13X+UVT8DxVFeqq9mh3j49/+IPvt1WFAOy9THn4/L83jy/1AeOztAnQZ3Yr7ANz7J9zt++S2aO3Hpnm2HfD7kZTWi6atlkMfcpJm7pumgV7P4g658Bw6HpTPTo+XqzW7Dw6b5qHoYtx++TTJ1dXVynFEMJbbz3s+g4Mr66uu76/udk8evstVT2/uNxv95vNTQnxCiP/2dnZ3bt3C/VNYb85Ojo6Pj6p27bIQKrIMPRX1zdEnFKqa+e9yyIxDkO2lFMR6oKitYBY+gEiUtd1COHevXtnZ2e/+MUvCiFEyQxC8MyUc1ILTV0Fz8F7NV22C0LcbrfDMOx3OwUgZu9DjOn6+qauq6ZpskgbPDGpQdd1KfaBveR498G94yMo/MxmTiRZ5knbwRX5+OKiRMRiNDPnGmJU1ZwHdg7JjRljUcWI0VcVAgCoGakqAzKQqsY0FKZSmGE7tzHWxAyv/19lAId/xc9987llhVimbxEARpYIHcVQp3cmrJyH9erJby8uLl4dn95nVRc8VCEO6Kuq9gySNSXnAppYVgZVMCXIAOAQEMFhzrkoRBIQaoZumx33sfPLlUCtqtpHTTmjZe9T8AKVSRJmwRIToqhlBSBMKY/tQcmUkieuHDOzxaE4U1IABVOVFEmSuqQugAIoUN0CMzomYhcqNtNQVSacBhq6ysSpetlXREGpIiaBQAEBo2oSRBMGJiKQnIeexKFo5pQzgikVeVhAJnLEjEWqLBB571r23siKdxfJkpOoOIRZ2MupGjONiRfhDKn0oQYYpWOKtA2NDPgCMIoNIiqXB2uAwHAQJn9+rSCagbBDgwxEGQznohCYlV60mQp47+eVR5Nv0ImYfn5PG0cui3tLjGCqIIDjBJ4ykVkGUTRTEQfeJIkmG6e2JrXi8oZmgJZVig3HeVoMScCQUAmJSLHQHvvMDgCJOUuRjnAmGdRUpDfZaExkSTWnjJ4HtNwua8NKBnPWqzkMaJo00cQeaFo2A4IBE0EWIss5EyB5p4qg9Oyz803fDWrkmhRJDZpFTYTBg0vb//jD/3h2dk+LXp0LBIYkRAGK/jvAhAY1ABgrmgCgVloaZoYIqnm6wzO7KjBTmVUwszJSoKKWEZUzOSO0uKN4HTcv79098dVipwya6jqEOqAjdNzUVRZzav3Fk08+/sW777xdHd91dZNF0LlhJ5988nFKkUGP7py8+5WvbjbbxbJ68eLFxfXNZtfVTauql+evXj5/7pgcaRS73m5Wq1XVNlXTDDlt97shRTU5vXPULpYh8BB7JjcM3X7fdftI6IMPQ4qYKDTVi/Pn+7RvQoVmYZpV1JxTjJX3hrjb7dq2dc6dnp4+e/asOIkkOWs201A1lecqsKUePC19HZxXgN3VjeHY4sqq5Ks+Ju99P0QFv1isVZNjDG3LPmw2WwYJZI3Pp8dHq0VuqS4aHaSCkL3HmCITG/qibKwiKllyIgRNZuQsG7FjRDCxbMrE7MTUACRHYGDn0NzUNCrYFiDGlBI5JnRmBnnAESmMZqoym2pXIgUsXFI2WgSdyIDmmkFZX3QrBGUwDYshkqIzUBtrm1RqrarKCDzFOoBKBESgoj4zOn9yuvzVr378NY1vPXhLsmDjZePUEhkyu7ppXVZzOccIDsl7SrHiFABSSsxtTrFhUxUFVGJDp1nJifV78ZqUIghWITGJq9kvpNtnvDHee2Lo9zIUkS1LAFD43xSQHCCaoWQm5cIgCoBmmmKHwWFwWbJ5RS+ErIrsAlatuRarxjVLQmBTSz2mPqQuxM7n6PLCgwUCD+CslJ+JslaqbN5SYkaGWPmMnDWZyT6CJshipIAZgZGIy9SwZxfYL311hKEyACMzrjX1gnuTPqmgglPw7F2h6pyrNJPtRjxEC3yR53/DuZdKxuEPh39DRAAjLtBJgFJEQoSpozi+zMyxmyshh+9wWJQ8/JOmsYBOM+qg5JdgooUo0FREVaOo5ASgAKNO12HGw6+jEcotQERg4pGojlWVnUPHaoDMhU4ITaEANkUAIOei35NTTqqlFYDomLy3sdurSKyWUS2rziiIObMpMSZM+jDO+dKhizF99Ktf77seiDy7mJUQPfOirryHrz5890/++E+890ienUPmQnpnBy7z8CmO+3UcYru9veV+z68yM5iZGqfnqGqmRoQ5xUVTD0O3uzjfXl3ud7vlaq1IQ5TlYlm1CyJ2oWHns6mh9UNvcVCVqq6rphFVZt7tdk8++6zr9iL5zundR++8PcT48uUrZHr27Nl23xFzXTeffvppv985ZjNBhJTT0fFxVVV3797dbDZXV1dmdnR0tKhDXVcFxGmiOUlKSVWdc0276Pu+lPtJ3BAHdjybMEQsYpClkkPOpZQK36eqPn78uNT9vfe73bauqjxErer1atk0DRMN2yFD7oa+73sjzCqlqeDHrA9ijKfHR3Vd9V1um9o7lpRUk/fQhvre6dGiCU3lnOMyLImAITgzLZM6CCCScs7MGYmIHTMDiEi2ErMjloCGzANA0QgDZhEFFLCxXGmKM/IeTEutaN6Go7LD4VKxkvBbWdtz3Qan6cHb1XTgBsq/O6SoY+ZpqY/71UxHpzuxqpSEvjyLsqvu3DmNg/38Zz8lsbcfPBpSZCbyjpI45x2id2ZcomPHObAL4oW4wDEspYgyFBckjoQ5MmZkQ0IEHzxWDbnaq3VdDymGekHepxDAOQWoiCFlzdlUyWFMCUyJSbKU1nARkmUgMQUyNdMyYRo8YgJgqjR4x+ycr33Thnblq5aJAIykcamrU1XFyqWhitkDBBBv5sE0mxooCIGyApmhaNW2ZhlVQDOUVqYCcEHC0tiPdISOyXn23oWK6tYIASwDGnHhgcnD3lQzJDBzhWjIRjNNs1v/Iiv/ph15zUYfrhn83OsRAUFtQgqZmWKZtCqzfDCbb4PSRMXDEylsq3MluxSJS8ZQykFQVNkQdZJ/h1GisoznaJZczBweWrrbo0yU2NyimPCpZYqyiFiTK4k0+OCHw+70VHkSFTEtsYIV+nVEJfRN7apQQE5j5FRWfBl7m44ZWy0iBASAjojJIZDj6ny3eXl+1ffRDNgxSq49O4A6kDP7Dz/865M7d6qqQqZyzlD40qcGwPwssLAMHhwH1v+12zKHBW8sCTMBUJGslhsX9jf77c2m63sgRnaI3LRttVh7XyFSNlAAUeyHhGgXz56dnZ0VSgZmvry8/OSTT/b7XR6G0zsnX/nKV15dXnR9RMTnz58X1raU0uPHj7Ok4BgQhyEa2GqxOFkfFStfOd+ECgC8d4kghOBDtVgs+qvrUq4ppfmUs5mVuH6322EZg0R2zhW6/5RSEXUxs33XFZhpVVUff/xx3/fHx8fOud1u19Q1AHjvj4+OzKzfd6rqjIecC1HEi/NX7N3V1VVVVYjWNu2w74PjOvjdzaaunWNCTUy4qOq28es2eId1HRCs1KDK7Nobz8LMco7OOUsIhETkGHKKqMasBkUQlB2AGACjIrIjUcnZmE3MEVLUXCpKpQOlqkCFhPwW5fXmHv8c3VZpg83GfU4CvrBShK/TAONBBxLgtZ4fzjw0RKrARGZy587pqlk9+fhxhXTcLpwjh440es9YppuMTcH5oGIsoioi4opBGyJD5YiQWYjEu4ExkkVCIMSq8VyDb4S8NSlLlpxy2+BNA+yLTpyHpJBQNYMSQIFvA4MWWWJQbyQipZasaAqIGYnYVQ7YMTtHnth750KoQvX/aexPmyRJkitBkA8RUVUz89vjvjKrEoXqQqEx0w0U0IPG9CzR/tDdT/snlmhpiZp6sTQzjW50Y4BKVOUVkXH6bZeqijDzfGBVdfOIyBooBSV5mpvboSLC5+P36jifcwhEwKIhb1O34TZyvyXbkIkTDRgMs9mmagGNkCwEAAUJpSIpUlLso0guQE5H7QcVzLyM424AInMVgUhMSWYR2VRNMmJQ60SLSQ5hh355t5W6owAHnzKDfnrdqQPu/LzTcJhe2RDR8BaOOnFsoWHJGUeU4UdvMX22yVAi3qKXhxlij2K8GO9qwOiTXgaiPEJIB7eyi1YirzUBxSAiMDaobUJHEJoZh0CBFZBwVFIjklL8KWW8JBcpRUXVNBtyZE6+pcBgnCtWI6IJEDfVuGzU+UQkNABDpigKv//u5Y/vPujQDlcEJeAmAZXuV7/61Z//+b9hjiFVAETMyN7dYY+oYMf6w+hrP7q3ZvbR+Z3O6uDmfEJCzUyJsV1vCQHy1vIWTDgkJQaOTbOIzQy5Mo6z+SLnIqZ9ty1Svvjixe/+4e+Pj499xurm5ubs7Kzv+xjj8cH+z7/62Wq56brODNbrdQjh4OBg2/U3NzfMHFNoN+vtZgOge/t7e/tHe/uL7XYrUsykrlPbtqXkqq7u378vCj4ZACOT92bTtl3vLYEpnp3N56Qw0Tu79fEftl137969w8PD169fT2q6nkwsFov9+WIxb5gZzYgJAbxKG6t0cXGhqpqzpwtVClYyqEbCdrtpqjRrmNES6aypFvNZJCOwqkpogkST2CQiukPy+VjmWw0i0cwaVIsSmhR2ZkJCQEYRYwZUBNKS/c9K7gFSQPTmLrlsOJILZHgx3g8jfGLEnXNrN0EcnjYdyXEjIX5s/qfh/An8vWsfpmTCm5NTU3D47tIzVbP57KbbHO4f7P9y8fJ336zo/IuTA1VRyUElBkJ1CAYSBCIgVjUll+kGRNzGADFEDqEw9gSpSplgLSUyQlVnqkuoIdRpgQGg5J5nyWJSAy0iWYMXfBVWeVsFRpW+ZCA0R4kCBNfXGLjCIHJADmCAijGkpp5zXfN8Hhd7cT73fxwTExGUlGvasmszWddaGaTudXKWgCJixMREEIJFzpEUQ4mQkmopKIDWe9lD1ZGrng8O1YwYLZCpgkbSqGZWRKkYFZOsoMGIwR3vR/5fDT53TT7/IwM9UK+5t9/p6PoHYmaOrFpEFVSJiCeggmYYq9NmisS4s5lsrIqMFE6ABoFGHhI1z0+9zYsjiQUigqkNQF6vuyggmN7RFZg+oaoisjd1RZUc8+qVHwwhBK95ICGF4JkBcVBVFUUzRCwlO9NTUS25ONJD+wKRUpOwSgoGhKomqjDwCpqp6EjF7tbHv7eIAIWIyO5wKOaC784vL1cbBeQY3PPVkfbn9aLm//t/+Ov5Yo9DACNkQr8/xLpznneTHhUdJq5tPHTDbRGnapl2wi1wGNCMzIp3Bpmg69aaM+SyvrkopS8iIcSqWQhgHavZ4lANBMAIy7bXXA72ZnUVm7qezWYXFxcXFxeuyRVjnM2ax48fLpfLD+/PV9tN2+Xttkt1dX19fXF17Ten7zuHr8xm88ePHqe6yjkjaGDs2n6zXrtrP9i/F2Pc3KxUNcbYbrsQwmq1vrq6qZuZl4ZUddNuHfWQu+zKX8w8zCLl7LjP4+NjH/pNKTVN41iJ0+Pjvb0FAZbSSy51nSRnxwIh4s3NzWq12m63CtY0TVVVBIpggbGZzQNzUwdiI7SjRbOYNzFQzh2CxjjjgADm7wI7ARmOeGsn4u77NlRJteRMiBSQQaWAkkUFCbECkSwCzCGEkjvnCil95waBmSa1JCQCU9Vipgh3Eg4YoRk0wp5hp0S8WzuFMcjDEeStI52M39IJeTJZj52tBaDoX63okDF7BkBExRSRA7Npqav0/NmTNz/88OOPLx8eHVDuanYrooBIMYEQEqEpqiIIETETMHOwFCtwHrLIHUFBS2hIGOZ7CIHiLIeEHAUxiLTBWCR1Wbdb67rin09kRrNt6RlwoOMGQ1QQ7xYSiDplMhkQYqrqlGZ1M49VE5o51U2o69TM68WCmppjImLUgoSgNUsuuacQRDIiFDBSlSJo4xoRWVEPTVJKqGh9AmYwI0ACiMzoPObEoEMThpkdvIdIFANaNIlBFaSYZM0dEoGUQDj2AMaOzWgcx4nZn77u/JZuI80pJYSxqk5EZjJyUCDRwHJnO4IwY1wAk2zx7rtMW8evyWgi4CD+Lkp+VNQGoTYbJ6xEYfSqWkbS82nqyovhZjRJ9uxOO4dAzOhfkAkAZCwTMbMaqExxf8k5FymuTAJqomJEoamP7p0WHRJEEf/mSIhmWFQmh4o7TbbRJwIB5V7Wnb37cLktWsRmi0XbbghxXsdE8Bd/9utf/dHPCBkpuPUHxKHDDncaObe3dOD2+XhBEXHEPX+C7vD6MpKZhYil77ftug7cbW5uLi+6riOOh6dHnCqmUNUNh2BFTERzl7ttu1nPEv2//p//jy9fPHeVFa91xBhPTk4ePnyQu60DLjebTZ8FAC8uLnzkysw0l27VlVLms9nTp4+bphGR7XqzXC5Xq9UQucdU1zUinp2dLVeb09PTYnBxftnl/vz8PKaZ55p1XTNzVVVVVeVSHP9WSnGD6yMFVVXN9/aWy+XFxYX7jNuLOXe9iBBaVVWg2rbtvJkBwM3NTZd7N44u2yJSAhOozOqUAovI8noVI56eHM6bGMkCWawCgoFmgBCIp1nLXYs5+WZVVSo5IzgPMoIpQEwAUFSZommxwZ2rSgEIiIYcAnPuWkwJiACc116BycAtDPuyT0dyOMKIDkeeEu5pF7Fr/PrWUHOxJDOYOFN3j/DnttlYDtrJSlUVp0JQJCtAwFUVSTgBz/YP+OGjs1e/++GH7w7qlBZ7VVXFlFAxd8WBkAROEo1ESExMIVWcYuU+AVNQpmLFtHCoqtmeAgtwamZUV0LYdS3KgXUdbbY2a2wdoAQFAUBVjMhAIG5VyCdrEExKKQxYhcjMIaYYU1XVsW7qehabWZgtwmLB80VczNNspolDZGIGAcRImqAkSlEZEcEjRxOP7DFnUe/fA3oT35hNSkGMIaYYCxQfLgJAAgADUiN1eTKbbqYRGQYgUqmMm0Ctcq2axYqbjFsZOVUFMFNDu918nzf/u9ElgAFMXM446apNzgDR1NXDFUBNgWRSC8IhzPdIP5DXtG5327BXph8AANDVOMEUzcsp7hVwKJ0JsZmWnZUycE2fkfPOHc/0+TQQBUZECuzBSwgBcdCGHJtoJOAo2mEUYPKX6qVHka7vSy5FiolWqcqROzBjjClmQtoZtkE1+ClVPjf+hAiEwGD4/v3Ztz+87MWMGIlKyTEQMxztzf/6r/7iYG/mGtJEjOw9LlT/+53VmxzzlNTD0I8AuI3L2OyzVO9og+KelVK6bltKX4zO37zKbUchPXz0KFSzUNUcIgD07dY9PIgkpr3To2+/+f2716/+zf/wZ95Q9YTJBdlvbm4IdLvd5pzX63XXl74vTgDrA7frm2XO+WB//9HDh01TEdHl5fl2uxXJDssE4Hv3Hjx79uzs4vLly5dVPbu5uVEkIuq6rqqqkCq12zswTX5B0Wn+yHvFXdc5wef79+9tFJV0xGQpBYqUkmMIHFn6vM1qgz6ddV3nDmA+n88Wc2dODFgYWcVy2wPI0cH+fFHPZ4mgIFgMVZNq0R4RCHyQcQiMdg2uN0qJyNEGTGQgZmymKgJBvQqsVrwqHiioDrQ/SIyQiSGl1LZtXddEgMgAKmJAiOZe/zZio2kwE3HKlHetv5nRjnbTZCXsLuvXbgDxU6YDpj3pP+yQSIsqgQTmi7OLGdWH9TwQPnhw74q0vbq8kgyzeY5N4uhq2OyMLOx+xTBgCGyEFgAcl8UgpAqGyFw1sZ7frLfUpL2Tw9BUvchmg12fJdUaYwgxJobMagCGKBEUwcSACshQVDAlM1QlpMCBmVMIKaW6qlJdN/UsNXOezbhZYF1TqmKMmIhTRGYQNihYyJgwMDELgmmBvlcRzEYKXV/6gBSSACKSWUEFFQ2AxCGmVKFIyUbjapmRGo1ugAwZiJCMWAgcv4gcYmystKX0ol0YDS8A3BZGbi37zkb86DK4VZdGJ9Qf2R12Q1oPu1R1hJTAEHnuPEHHwZBPA43pBT8KV6fJZM3ZX5MIdTridrtTzYZSp/fMB6nHsd4yxN0A5BklmJkxO+M6mQEGxsA83pPg6bkZEjnA33Sc/PIMoOQixXEywBZCkBgpJY6xLaJgIsoIKgKmZjq1AXQkcIchpx4OIwKFUL17f/b2/ZkANrOZGiDAvKnqwH/2p3/y8y+/YHQHxUCMyAbm2rATHSPsfGsAQEcZ2K0DmO6u2S3tG0zQbQAVURBRcZmzzXaV2+1yvby6ONvfP3z25Rf1fN8wZTUOVQhJSu62GzJjwlCFWZXevvnxYH++Xq9SSmdnZw6xTzGhgYkuNzdd17Vtu9ls1pv29PR+SPHDhw/ddmtm6/Vq1jTHx8cppeVy2fd9yR26RQYwM6/YlCLz2fzXv/7Ty6vrb7/7ftt1201bVXVVNct1K2pVVQFhKSXGkHNumka67AmfOyR/kIhWyyXuDJ04fKiqKs2FmZ39LRL3/TbEKCKr9QoJiKkONceIiG3XVTGI9Vp0vVwzwOHBfl2lJkVGq2JIMdQxhMBWmMCYXakBprLJZFvNzGxA1IgI+AAOFVVGlL7vESlEAGPUYsYAgFbEEAGZCBQURbttFYOPOlMwREYkG7jY1OVPpyPvBxTQwJlTBtLcW4c0iefeOaQAbduG8fqp3uF0zM0McBq6RGb21p2a+ogMkoVAMYb19ZK7DF1Ppb93fGTzJq9WbdttV1sErmLaaxpD40Hvz6c3FRELCKFSCBiwFyfdBwixzdatVs3+QXN8wvOZBSx9YbIUQg6c2YFORKSGCKiRSIhcatEDViUCAIbAZgEQAWLgKqYqVbOqSdWsaZo0a8JspjFCjBgCMxMD8yDKQSlAiZaiRQYmAxBRK5nNSi4gVsSkiLCIASKZCoJoKV4/CMQhxIgm6jSkhmCkRqKkhgpeICJAIMToQ9LBQgROypVSBA0hRjdAjhseALlmLjdqTANgEhEH8mdPFImAUA2Qh4AFCHRgdEYV8RoGIoAWR/sgkimNvSMAgCLFQY/MTDRIXLguxKRl4WGUms9OueqzMaCqjnnD4FqKmuHwJSC4Thsh4KCZCSCiTIQkZj775sIdFmMAM8YA6lrSjETIBOwkeqxoCANcEiZCUGc5B82SS9fmvi25V81qRYHAKATmqBoJq6ZanFqIBCa5TyF4mueUESDksw7uGAOzqqIBe1cLyJBWbfv92zer0klibpp2dcNYaugfHR78L//uL+ezPQwL4IpChegSoAhoZIYKcAd0MWV1CihTL88JUQGAkEgQDAnMgaiGKmYmGqwAoiIUs1KKtq1cnulmWR+dHDx4hPU8VPOuL2jcpBkgCZaUaiJs12sAuLm+WG/zH//qT4/vnbx9/1aszGb13myOiCB5s9702vd9++Hiw/X19dHRSV3Xbdsljix5uV4fzZt7Dx9UdbXertabtZrWiBdXl6JAYLPZ3v37D7uubDY3p/cfAJLYTYj1+vL6erne3z8opbRtB4h1Xec+E9H6ellKMQAw6fs+xBhDAANKYX8xa9sub7cEVqXKB8SNQNSFSYCJqiqKSIixK9mQslouW0PjCrfbFrSjEhSg7ftecL28wn7z/OHJ3sxmKSe0KlSpbphIiYqZkyrCwDmiqjLWf4ZxdFURcPZwqVKNyCYefyqBGJCRSUFiFDOw7LpfxAymyABIVhSRVIC5UgXLSsxEPpDJZsAIAApGRASGZoDgE7mZPKFU81Y3IhEz7YCUcIwive9CI9cv3UKHbz3EblHBDLIYGCEBMYgUQKDApWQMEA00d8rIc+3ObxIzLDfSbahmZgp11ZoISN9ubzbLZZlXMboYDiEwkkgJIXRqfRYV7DvLBl0xw8gpbBtbzBfVyQEfzJSwmCExcwCUWSKLZExIETBSBAO0ro+oAZRVybSAFQQloAKMGBCaFGLkOnDNsaJYx1jFmLx67OrNViIIxQQMyEYICoiBNVUhzoADsod9knOnWnLJpYgJAsAwyO3uzUiNwCByyJrZLCH2JTPHCKbQK3QqPZQMRcAQKQAyaGEkCGiBJYRAUS0Gi8Gp3DxCnjC5blB9F5ZSpnLk7XqboTrcE2EMEqdgYDc0+GxEvxsLTL8aQuwQZMTUw1imVzDRwba7hxodgDkF55R73qaodvsW0+dHIgEhJiAqpiEEZkSOI1TSq48MTO4JButpBmMoPRW1SimSs0f9ngH0Jfd9V1RKMTNK/uKBU6xjqDOOhHw6ngEcxm1x7D3cZs3uR1U5oCFdr5b//M23q81WILBp324OU9yf17/5iz//8ssv62YOyEQ8rcBHodmnl5nL2djuQwCOEg4AMBanRo03sCJChKglr5fQt/16eX19vb+39/D5cwxhvthnjiyWYmUGfdcZGgWWXIppQMqlnF9c/vW//+vvf/j23bt3h/sH8/l8MV8sb266rs9SspXr5frq6qqu68PDwyLSdZ3f5/3F/Oj0RFRjSq631bXbiw8fighzDCmenp6aWYzp2bOHAvjN77+9Wt6s15sQ4uHhUdd1bdt7jcO5P3POXdcNcCBUIiole9UxhLDerLuuizESMxH1JYcQeineKkDCuqm73McYu9wjkxFu+9a0iJRU1SHFvvdcUPtctm1pV8t7h7P5opnNmyqFlMJs3ngKi4gpVZr7O8nxzjKNZ9NXa8gUfXLKdx0Rk89WkYlkMEZEF5sAAENFYSJTICJAIysFkYHRzHLOwBwCsLGN+ho7h2is8k/H885+2cEUjExfu0Tz9hNAvo92JhKBDlBGHNlKiClwUEA1K4qxCkXzhw9vjyQyQOmzoiIqI1CVAkeprai1UrIUAggIjBAdfWQIhBpAQ9j0GUPdzJt6Pq9O7zXHR9zUBQEIcSiyABMVlwkDJYLAgdBArUdh0EE2CwlBDVyUDBmBwRiQDQJhDLGOKQZOTJGJmBTBqf39HyAiAQLGGCFm5SDMFIIyG7O56o2KSMklWwZTRaLAMcTKW55OXslIjMhICsoOohEFU0drIAD5dJShgY/pIhApkRGK222F4BVMt+Je+vd2sMEdKmbYMdO+LdQMCEF9kNfYgLwZATBAJF027Kdt0LADRmvlj/jwlGMqZNCl8RBVAad9MgBXAEy1gHcRPv20OyZ7sHrMaq5DHbxZQRwc7QNhYCgCzwDI2TUMR4AXjodjOBLuLYuUUvq+L6MyXy5SzJiYImFAoJCqJqYmA5kN2pZjqc0QfbHVoYfTHaahhMpicH29/O7l66ubZS6FU7LSM0hgPj05+cu//MsQY4jJgHFHtPm2hvu5e+7OHu8+blPRB8DQ5/IVFBAdrGXIgaz066vUr8/fvX3//ixUs+NHLw6OTjbtNqSkAsghVVXflyx9iOSmNsZ4uLd/dv4hxvjjjz+enZ3N6ubhw4d1TIjYtm2MsYhcXl29ffu2qpqnT59ut52pMCIgNnvzqqr6vt8/ODg6Onp/frZers7OP6CUuqpiqh48fBBS3ff902fPuq67uLp+//79+/MzZ44LIZZSHMeFiO6t+7537+L3f1qRuq7NbL1em1mdmr7vSykhxalJ4I3z1Wo1m828heA+u21b1bxYzEVss203bY+IRawUWa/WsxSPjw7rqkoxNk0T4rDQKaUY2b3ObUnkrg9wSwAwFOls7DbBWGcvlpEAIJipQ7fNzEAmXL8/WafWKwERMLENnQAopRQoTOqkWT5v7BKxZjRlkIAfO6ePfvb9dhtsfa5A9FNxCY5J8LiBmawoAJiaYariyf2T7eb91dVl0L6KTGSmvWoxMcLAHFNVxZQYsOQORAggi1jfLTdtTKGaN0S0t9jjerE4vrd3dNrvH2pVWQhVqoxA0ETMiNXAVBxFE2OEFKygFTFCJTRAUhCEYGhmZRikAkZgxMghcahDqFPiwDFwICLvPzMQYRjsIjp2lAmBGZlDCJSixgiBldl8zEIHcKMWNRALhFiQApmCKROYYiBiJjEIbhy1gAio+wBFMzRDU7RRqgSJiYy4IJiZqIY81NCH3YZTLSIMv/qolodD79BgyGxgoKgeC3m7GE5f0c9CxyYgza5h8laBP+iZx2ArpyLJsKsmQz8wIk1WbHqpqb4xbUoAA8LAlacCzAEAmIIqUAjKQ/0ViCgEz4dEJI4wOBshbg5A0iKlzz7Q5KDPPue264uqMytB5FAzVInne3G2B3gnGbIRdD+hPnCnmeYHopgxcEH452++e3d+CRSqKuWuqxjmVfjNX/zbL1+8aGYLNaQYcCTd/QPHbLrV8FFLZar0T7E/+pCagoGZuIz9dnkJ26t3r35/eXYW6v1HT7589PwrZAUMhKFoP+YxLYCTJhEAVE3dlXxxcTFbzL/97jvTfHx0vGhmfjNvlsuqql69evX+4kzNvvrFH6dQrdfbUgqBKqgaFpF79+7t7+9fXFy8+v6Hy6vL3PWLWU2Bnz572sxm6037m7/6y9zL9fW1TwXnnEOIzNx2XYzRDGNKOqr0ODzRFzSm2mUdq6ryHgAippS87uHPyTmHKqlqiJE5eGF4s9qoatu2HqnEgCGkq+vlarMVNRerKqWAyt5i73BvfniwP29CjBEAmOKk+0ZuI6b66t3F8jDDT9W0w0dU6HCsVBVRnDsIxz6X9yHGoEonZLZJASQzMWVmVMORTssQ3YUoABsoGCHa1EWawnO/do/zbgD3U4b+p8oAiDgVEaa/IkJUJhzHQQlSncLhXqDYXZyXkkF7g6Kl9H0OyLPZHsfUbbZgwgBgyoEDgRgumrqeN/W8wVhBPdNqFqrKYixgHAhjICYBIwA1IAMThSIIEgJRCpSjqGZTDKGIqopqCaqO4CYVn7gJCAGhClQxB8aAEMDTAkFTREUAQuMRrTOE3CJg5sMf4JKFbn9ixCIRsyAFxiw9AAQCBiRQA1IkBgIiRgwAgl4cGVSO0ZRM2ZDHuFxB0YANwRPeMdlS04A7eP9RExlgKNCDmfmczkc9fTQw72Q6WpmQ0BDUo36f5x5X9PavPsIC75YIcfhMpipTKDHFEWrGzM6yBgCo5ogxVSXEidvnNsId/xLGwM3DfyKyQOxVTiAiAgohkoEPRA+DiN5dQIOA5INb/gs08H/O+WxFNBcQ7aX0UrKPYfhIDpOSFYb6+ICOjrRuDLwfXty1+KdTVQdWmtnUz6SJWZWYYsUGN5s+FwOkwNx1m8Tw4unj/+mv/jKlxBwwRMMAdgvHxp26/yTzayOdg6p6MWHK96djKSJIU5JuCKBSUgir7aZdt9C3r3/47uL926ODgzQ/PDy5l5p5XzbIETl2eTuf77W5Ny/BEuWcxaxstzc3N5uu7Upe1HVTzf/oZz9307lcLhHxzft31+sVcXz+7NnhwfGbN28AAKRI6RFg/+hkf39/bzY/Ozv7+uuvz8/PAeBgb3++aJ4+fQIUqrp+/uXPUkofzt6+eff27OyibdumaUSsbdss5oCumJITefrX9C3t12w2s7EJ7D1SVe26zZQceFKVUhJVJEbE9XozhgIOZoO6mZ2dX7U5l2IuEZ3F2rabRz7e39ubN4tZk2iA+VPgEfpsIQQyzwKJiHz/T4s45HMIYuZMDKaQktdbfP+ASGYi1aKANoh2iAhNlnoCZZZSQkhmzmRgoghERAEAzINOLYiRyMfEoEhmlxMb0kqcts3HlZy7Gw9GCY3pCZ8OgsFYVkJE7zLuJOselBAzFxMVq2axiyhQDvbmpv16U7pt2bar3PYxVDFEAzRRVQGR4Hz5hCklZqoCk5oUQbUQI8YEKaV5g1WCFAWdM1JRFItYyQOqJwRhxsDYQ0WcsRgoghoiEmov0QDNAmIiiEgBqY6pCjERRx/cAgsDD7f3a4RUTASYvTELbBiCUEYi8oGfFCVG63pA0hhdhwCZRZTBCJQhwKBmDgoQCFNkFUWgLIVTRQCkGgxBCoqCZJCIJVBAMLUiWqTvupyLIihA+NQnf3TtRqaIiAoIoOiTt7f9AE8XfAmn+iaMxZJPY4Tdi+4oQtw2l6Y/JB6gCJMtu30pEbNBhndUB3OHe1sGufUl5CUu4sAA5CQaiIzgcFEYVJxFhgkpM+Rbkjt/36H2k7Pjf7qu60vu+74vOUtR0RADp8ANV0fzeHKEJ0dl1ujdqteY9SLCqGO861+90cbBKHy4OH93frVus6j1OUPJTRP++q9+8/jRAyYCREMC5J3ewU4mcfe68/iE+xvxwkO0CD47YGhgoJEod610PWv77be/uzi/fPTki6dPn19cb2I9K6X0WZHjtuspRPAowDOtFHPOIYSXb398++Pry8vLhw8f9t32eG9/s16b2fXNzc3NzWq7ubq6iikuDo9ne/svf/xxs1pJ6ZdX1zHQi2fPF8fHXdv+8OOrH394+eHDhyqlvb292bx5/uVzYjLFZy+eV1Xz7XffvXr1+ruXP6yuV1VVffVHf/T1178zM6edaNu+6zrfY1M660tZV2m6Y54feEWurhoYS0bMnFJiZjXLDhaS20sHm4vbLhPRoDcEiGhVNTvaiwd7s8W8qasY0FKKwOQuCREc2+PT+Ex+EO4IH/muUBdjGObcdUqO+75HB6FwRkEgNCBVmXJgGkcLb/eAFkAeulEKhBFBveDpuk4i/lc6EorcbqqPyoa7L3tbPNgJvHaf8IcygNG2MDPYQC8Z0IBNAdhQQZGFay5sedub9ozAwcg099tAHAJCLmBKoqASIQQyKmBWILH0mRBTaoxD1cziYo+bxqpkMbjwr9PUQFHLgjmTWWTSyJyC5sAhAmeygpHBrBhkEUVkBDECMEJiwoiIUtA0AiZEBAhgDAZoNPQAICLImG0jIhATM3DAGMCHA5i9KATMgVmJnawxAKYQkQYBRCMmM2Aqir1acDl4ZDZgM1ZDUFJDG+FAZiCGTPCJZQj6B6FaMJYaB4Nuwxo6jTLCMCnuUS8MwB90GhwvchvGKYb6w9DgP3ypDjTPvvs89ldV9Fbw3bCCHAJG444cxWoc3oPMgGHQcUTv9OqIbjMwn3kdXlFzAXchHhqrWhGf8/JGtJuAoqKqSJQ4xKrGGHiWmpODdO+4nJ50TaV3i1QwHhUV9dEzf3C450TExBwsVm/fn79687YX5Zhy7hPDz7988Vd/+RezuubISKRe1sU7cIvpXXZX+9Zruqsbl2L30JrHF+ZVINTSS85Q+nc//L7v1k+//PnpgyfcLLqbN0YEKkQBzXLfElPO2W1TjNGl1V2tpc09Mx8dH2vpqe1y2/VSbm5uPlyc39zcUOC6bmJVX19dL6+vQaVdrxD03vG9wLhc3pydn19fXi3Xq729vSqlxOHxw0eEVNf102cvttvt77/55vvvv3/97v12uz06OvrlH/+r86vLzWZzcHgwn883m03fl65tPcD3SH82m9V1LSJFhn6Ambl0OwzV+YhuZLtcVRUROdIXFEU0hFiK9r0nbVBVUQyqqulyzxS7kl3yqa5iU6V7J0cnx4eJNBCEEIx8IpdDYNWBRISZwXxMfRDbgRG/QERSiprP2tMUggzFfUKAQhYMBIwVigirqpMFwSeR+FA+AjBkQqZhrgXLMADoEZ0gBgCd6FuI6KdGVj7aWpPLwbsVranF9XkfAIgAZmNNWBSQApEAkAGaGkHV1EKgmkvXqmXNBcn6vg/c564PImBA4GjIErkKTMzUgZoWpnpW1TibSQhCEFIExzH6hxdRUfDij1lkhpgkJYnBOBQmcRJ4QmMkReCgImpYQA2pYq6IqhgThUQUmCITEjlLBJip6VCRB6WRknf83sPEMobAQyEoQAgWAooaCwVnDOAUgjctAUBBwBCRi3FQEjM2DIEBAbwEJIYmpIaqqOI8DaCGeke6EQDuaADsXrubZnyOoc8fjkXjXa/uHGd49wIDxQF2iSOh/51Yd3x9f76IqA5CHDjyEACAOuhN1VTRhk3qRR+P82934RhXj9hKRBw3n8fVIY2Db3CLe1bDYUxNQTyDH5o1EMIwcoa3ND4qYqa5751Gpog4CYT3TigQptgc7FWHh+n4mI4Pu7pSaO1O9X9MVlRdYMYPzwjHRA6MyLnIqzfvLq6WiFTX1XqzPNib/d/+w78/PTkiRhqGfoGQEAbqZk+oJ8v/2QQPbQrv7j4OOPKyG5iV3HWbzfL66ofvv91L+vz5i+rgNC2OkRPGSxGVnCmmLFlVVayqR7QYWpf7UuTly5dXlxceKTdNs1nLarWujqvlcnl2dnazWtazhpk323ZbbjbrTbfZLGYNe2ley9X19bLP27bNJYcQAnFK6fT4ZDFbnDw+nS/mbdu+fvvm22+/v1mvfM988eLFZr3+p3/8x4OD/Xv379+sNt7N27RbEWnbzus/rk2/3W68m+/Maz6cbCP7QmSuqipWyVHtnuMWVVFBo9Vm7crATd2cnJxslkszYw6r9baoOTysqeLpydHhwX5T1yBdjOwOgJgBIQR27B0QBmJVnw6nMEIDVERNi3cmAoFrH6GNgDFxylcPVAA8nxjFvtnJ1QVQYoxj1DkQgKoqACIZIFrfGZJRMC8IkZ/o2wzg1hTgwAyECLu7Z0wRxjM4PrhrWz5CEu7+LYzEjlOS4Q5semqMEQ3C3LYVt11b2pYDAlrfdbnvLNUmWbMxICEQYAAMzs6pxswpxCpVqa6paaSe5RCzn1YzBxGWUsD16AEjR4sBYqQQQooaI4VgMfgUmVkwLalmBsgiJAAcUggVcxVDlWIKaWAOoIkbwVAFVEDVxBElQ9PDxuQbnW4ysDEbEzKbJwGBg0YTFW/HAzkngaCpARFF5sBcRBWAORQDNEU1BBlGZQ0QFIzElPyUeow7GqAAVmBy8qIu72gGADJVKqYKHYDKtO4IxGRTcqBjDcJFiIkGFhH1bFgsK5hxCF6rmfLc3d0QQhjhPDZRxXnZBcxoh8CHiYY/z+IGGolMh7kqYmLfS4QACETMbADIDM6To+ABl0rPRCKFiVz9x3mihzEQJKJEISKTmKKBCZCZ5tzltuu3fe476dvcZecdItYIVEE8mPO9h/DgOT54YbM9QMAYwHqfUzYABi8Bs1kBQzNTEDNRRKJghEqdBbm6XP3un19JH8mwYl53myfPH/zrX/8iVhFipVwBMjMhFDRB8KYdkam4FSDWnRzAwN8cAFFhIBE0cAeEoFZENLKVwoRU+u7mann29pvff33v/v29B19WzbyZLThEA8jbVvYPOrAqoBUhlTqmSBFQjUlE6zhbdeuri+vttjfTerb39sOHWV0X5vPl8vtXP7ZtC8inJ/eXy+V2fenzuua0V5Q4RqWoAGgZRPO26/t+fnw8m88Pjg4fPX0yP1i8fv367bv3H87O1uvt0f7xh3Kxt6Cg/X/5+/9S2v7+s6dVDDeqfZ/bvlegrogB1bNZZG63WyIIgxK1+rgL+2ZhToGrqs5SqjoaEHMwxNyLIfgzc9dqyQRQp1jFEBCqSH1Py3XbCYoaqlnfPji8//j+fhUNoFAg34cxRkQLQQELMw1BFRMI64C4VyIixK5tTQGZY1UNhfjhCc7fCaVIT8rAVrxfHZjZJBMHBiMYlK6lY07GnBDAiNCGmR0AAkX1br0JYUCnFWMpCt4JcF3f4cSTm2XnBRzgguibSKfpwUGge4r3/QouSjLIBAyuwjEkTvAL3qMSQMQQUmdZQ7AiIaD2hZCtjnI8715zAYOSMasIIHCAoJ2yZAIKRBEwqBF0VVUFjpRmoZ5baCTWVs+taTBFI1ZD6QVQERAFJRcpuYBGjshVk2bSbopFQQ6pgj5T6QNHlR4CqShH6gAEGZATpSZVKaQ61jHVgRMABTAO1lsXrApSaZclFUNgUwIjRPVxGzRiNEYgwhCBGIiQKUZmC6aFuoxoMTAhqFrwiBZBQyyiZJiAFTRVKSOJaBKLIiwaTAMogsA0waNFTEV61QKgIIqiAXenDT3MHcrtQ8PnI2AC8R16mV1PPi05jmBH/wUMRaOhhAkAiugVGNsBxuwGXzoyYd12dz+Fyvj7Bh56RjigXB0wSiPBkQF6PaWoDiBcn5T1eqiqoZGZ5N68nQBOr21ANgjtMFFgNNJSvPqkIgP1mxQVsQJoxhiquqKGwmLWHO7PT+/H49O4d6TzPcy9mKPOh2hoJLYARPo4liICZFIiTD++e/3969fb3IVEebvar+N/+Ju/efTocV01IcSBOmAEZU3JmIGN/Zc7BJ82TLUjDvkCgAF5rOcenUBVAyJIvr66+vG77zbLy5999Uez+VzrRV0vUkwCBiOTewzR79hqtZqf3gMzJlaEvhQRe//+fdu2IZAqnBwdXFxc5G2rXXe5WnVdN5/PU0pMdH11BWazpum6ru97ImqaBsnHGGF5fdO2rZkdHBzMZrN79+49fPSobppvvvnm+vr67Zt39x7cT1Xz/v1ZXdcnR0dnl2erbffHv/zV4fHp1Wqz3m67XNqu67MwcrUXS5+7rgtj38XMUkopJX/riZh24jID5JxLFgHAnLPJIBmGiE3T1HVNRMvlErSsN5tt2xtGIu679enJ4eOH9/cP9uoqERETxJTCMGXuWj2D6hAAEJMBO5cJ4hD8+oyxd6I/k68BAEwtjaKqIQypJYKYSlENwTgms5J7s4AxRgNEVMJg+Ekw/tFLm1vnjx4BsOGsTUShw5FCwJFf1C/aobfSHbgt76oEjvvw4w8zCAea0xWpijHO9herFLYmFeB2te6WqxmlhiIVZeOAmJAiclO5dFrklDRVITXQzEI9K8SGDp0nRiakLKXvO8lFc2E1dlg/EiEBoDh0kjmGSCGpmgZFwKxChBzdRozAf05kGIEiYeQwovtMS6YooKpqqDpQMI4o8OHQg6EBgzdYPbMnJVZiCsHEKTQVgd2IIgCaEQAbRiBMdW8gAJGDJ8qBmIkA1Jy3uggYgikImIhIsSxSRIqEaWk/AtLs2qTdhdmN2T992rTY0yM8TgxOdSEdJraUeWDd2U0bdz/DnWsijP3ofWnIZoYhcET16MYFbdy+jsU+BUNxlZiiogAKKqCkIqjZxkrUMOzITBwwBOeAQwAb9H5zm/tiXvc3E2EDwzAQ+TapOlhUJ8fp5Dgc36O9I6zqPt+Md3eAP6Hu/DzAaUFVKSTCQBAiVP3GfvfN9xfrG4tArN3q4k/+6Ms//zd/nmJV17NROWMIp3aO552bubt8u79Cu7UACIpIaBYQtHQEcHl+/v7HH7Poi5//Yr43b/ucqoZTNEItnhpq37cAcy3m42JFBFREddN3McXl6kqtLBaLUvrcbVer1dMnj9++edO12+vry4ODvaZpVqvVd999AwAphbbtq6pyjuhptzilc9/3Jycni8Xi9PT06OhouVy+fft2tV3d3Nycnp5WVXVxeZ1SOjw5ZqK37y9+/otfPXjy7OWPrz+cXazWWyRSIzIBdlRbx47/MiBGguAVfy0lhVA5OqgUpZBS9EXJOfdlYHh1B2BmTdPM53MYgbw3q+Vqs+2LxSaR2axOTx8/PD05AAB3MCrZmz2IGAI72B3HcrnDH1Q7BN2Nnz46Yjsr/pnjqcNAFiBizhmZUBC5MEf/vY1qFIgCGAAAUAE+y7v++fnN3UBtd5tNPzMNs2BT3jAcW/l8qdk+cTzDS+mg7DRkBqgGUM1m8/unNzdXueukz9jbXlNXRlSgCqFibtgnsGIIHGPFKUhVUUrGAYjNhVXEoChHlIGPywKSK4IDjB4ACYiqVEnXllIQoOYkbCYGXEIMylCUDMiAAnPi6DwPkTggJwQDFDE0sKImaiImAqKqRmO1fJxqQkQcdH0BALD0mUUZMXEgLqLmxC1E6JzHgGQirBCRjDgMhA2gzD5vNtxEMVM1EShoCuZl9FxYQUdAY4AdU7u75B/9793N8bkF28kAPkL3T68zEW0iokNFP33O1Cj2H6b+87i572w+L1UaglfQ/FHSiQ18cLBDZVSVANDGBpoWAGecMhMNUMaOASOOXEbEOM4DS1+Gsa+cu77fat/2OXdd7kpRCFUKqaYY+GCvvn+/fvAQj+/h4TEs9oCS0EZlsPg45c1j75oIDQSUwHxgkBEC2eLs/Oa3X3+zalvBAqCziH/zm3/7+OGTplmoAvFATP3p6uxait06rI2wWo85AIyGT2EIhgwmpt223bZXZx9mTfPFF18K6KbvKNUh1YCMSDGiiKBZ7rYqWcRE9eL66vj4GAC2XWtmVxeXX//z1yGwmaAJAfabzcX7s7xtVzc3s6peNLO6rtv1Zn++WK/XOi7xV199FWN89eqVq8GEEKTvjo+P9/b2Hjx48Pjx49evX2+329evX7e5ffz48dHRkYK1bfv48ePU1P/pP/3/9vb2nzx/0XXl8nrVZxHV3BWKHDiacM79fDZjxkgkWkKonG3ft1ZKycH7qprqYZCtzz6EPjLmI5pZVVWLxQJHfpS+73tRY46Bm6aRrmXEFLAK4OE/IjqXLwM4p6hZ8fxtCgsGUtJyJ9h32CgiOozyUwcwnV/HpiEOLMIxekRCqqracazMuJSshsxDvsiEo5YSwA5xrA2p/9gNurt/bCzZ79qH3Q82fZ7dBx2C4u07rxbbTzSo/GJE8HaEAZgOMRxjc/+4vAz9zU00PJrtHVcLVIohBAyJYh1SCoEDU4whRYqJqpmlJBwMiWOlHARIRKXrZRJlcjJ5GIZ1hzo4OJEKBmYNkXsJQAIEEKrIRawIqiHHKhAHduoADkiISGoiaiLstETeYVYz8Qrw8L0REYZ2MPBgkFEB6phQTUuRQZ9tQNBMd5sQSc0M2DAiZYOIDEzCZMFZ6ZiJwAwcsE4CQmBqAlZMimpRLSqiAXaCiOltpu7rsBh3hd13N8QUle9G/Xdwn3eN+xTyI9KEZps2DYwohel/d53HbnIwWTjfTGpqxYiZmCORqMB4vFSVyVXcVEVdKtVHA8AM0UAUVNUE0K0qc6woROTgUAHmYEUMQESlFAfKiVgRzb0YMkeEECVQfbRPx8fx3r304DEcn+reITYLUUNiT1GKGgCKCI8NaOff9yiIOSBGwsicFNMPP7779tvvteTEIN3mi+eP/91v/nzWLAijKZovkTl+787k/Uedlel+0kjub2YMBIYICgiOIkc1k7K8urq5vjk9Odmb72WxLndczylEcJ5RMwRKjESwmDV9u53P97ddN5vNnAmqbprtdvv9t99t201dVb/4xVf/9A//0HXtl89fzJrqf/9ff2ia9PjxYyK6vr4u0l9dX6pqKbJ/eIKIi8ViNhuolR20A1K8015V1ddff/3jjz/6dPGTJ0+8/PL+/buqqo6Pj////9v/GkL42Ve/eP3uw/n5+dXVtQFsN5sQIhn2XcfMKhICEYB49U9KChEACLCKqbe+27aBmJjdrDsIR1VKKV3XcQx+b1NKiNh1nc9z9Tmn2TwpKXHOfe639/eb48N5k0KVkh+fqqqYOY2ILyKeOs9ECAYlawgx3yVBmQ6UjWD8KRKicb5yGC5jHjrAQ9es+PiKp8dqRcSJTqohAAAQyWbm8hKTCImbZZ8nICIXB57O/u1ZFpmc0xSTqSrQcDY/QqDi2E++RYIMfWOCkfJocjCOhmLyMhMVKKREgU01He7t3z+FAof1frzZpmwEzBADxYpj5OiiHTFF4ogxClGsagtRkVRNxSygKEiRodRrpmQhEoCYmmEfmW38ji7RFZCZArJycJyzhRAksCogJyYOCAAamJxjINDA49+LAis6ZkYURKdjiIai4qza4O5QVVUdauKpESE51FtUQc1nyEw1FwHTgEgh+KimT5AhkcXom9bUQA2LGBMQAqIqSNactfTOM6QCGCajsGvHdxfv04jjs9dHYcu0UezuvtlxEgP8eZqB9PLrFHp89L4/lXkQjNNbNAwEg0+0qcIgYq5alAFMQaQYDgUoMLOSccBfI2AAIuKIHJEihIQhITPg2IpQ1SKSS5f7bdd2uXfgp6pyqGGWaG9OxwfNo8d8/5Een8jeodVNSMm6PAmv3D1LQxMWh/E7lGKMYIaitCnld9/9kLs8x9C164rx3/27v3zy7Knz1SFObfxh3f4lazS5z8Exg6N4rZQSEETz2ft3l1fXJ0cni/keIBftQgicqlBVkg0VApGDS3LXEhxEIi2yXW9ijBS467rI4eby6uLsvIM8m9dnZx+ur6+amD68e1O63kr+8sVXKaUffvjh7du3q9XKQYrz+fzhgwdqFmNcLpfL5dJZ+0MIDCYiX3/99T/+4z86J8TTp0/9Tw4PD7///uXVzfXpvQf/+T//5x9++OH05PQf/vt/v7ledl3X9Z0v3MOHD1Jd/9Nvf+tjAItm1mme1RWnCKI0isBMBUmfGqvqpi29m6SqqlabzYSqrKrKqUqaptnf37+8vMy5LHO72rQCCKps+eTo4YOTw5PDRbOY1akCgBSZvefLHNjtwygqd7sxXF8i+2yBsxUhIg887Z9H0QyBgBmRqwcrIopmKF4aHerRzg/hdWYzMlPmiGiqCliA4p3XvE3HPxP8mdlHm/n2zH4uRxlecMx5Yfe/P7FzGUltmGggIoiBEEoRYTt98ODDj2dYbBaSdRkAAnOTqhRiCAEZAUGJjJEYLaVsoEjIsaiVosYqRMpj4xARmUzNAXXsBFhqBEAclFmIDMGpdokCsYChGgEwESMnJgyAAMUxVJ6WM4AYsEHxKbNbjn4cbxSMqbhnG+YqM0iIgVEZAEgI+8GbTqGb48PQrPC47oEDszEHYqHbS82G5KNoNsumRUxMxaAAFARx5q9d6zwFjzhWJz/Zdj9ZArp9xi7nwU5CMMhtD+mF9X2PI4HUZJum18ed2uIfupwKwiFWTCqDy1FVcvoF1aHjqgYiiuIsKahiosRAGBCRQgVMECKGpByQEnAC3xu5SJ+lz7fSLyJ937v2BnCwQFhXdLhI947w8BQPTmHvCBaHVs8gJcgZTHCC/o62e/QBCiPaComJAyKLwncf3r67PD/e32exdd8+e/7s3//N38T5jCj6rBwC/dRa/NR9m06pDVx+TvelaNr27ft3b1er1cPHz/fmi75ti3QcOMaghAaClMQ0EKtkEKmqar1eHR7sb7b91dVVNW+KSJ8zEb18+VKlUEXM/Pbtm73F4nAx/+Gb75bXl//zX/+1ov793//Xrus2m5VqcR2jpqmYyFn03r59693gpmmOjo40926ar66u5vP5ixcvjo6O+r7/7W9/+/r164ODo2Y++9u//dummf/sZz/bbreXVzcld/NZdXy0t91uA/HxwfxmuZTSI3HiYCCRQ4yx9F3TzPquVFWFal3XBaSQKkRMMRqYk6C0Xect1pSSo4FTSv4rVb2+vj4/PzfETiCrc33bwby5f3qymNWRoPIGgCoRMjMNVR3HRPo+30VV+JuWKcd1u+85hIdKnw3IphJQjNG5RYkHYl0mNBv032GIfkyhmDI53wPox2Trd8rCdx6czMK/4GTeKTneyhz+y8619wDIYHoJM1ODUHM8OMDT+3L9SnudVzXHyigwReTg/F3EwZgsMHBQJBMzQAY0IDVQBWASmCCYAECGhqw2YUSmY+J0yg4JZDdfbGYgiBiAInNFiOTQPiZkQCYkJ1Eaki8rai5UtVP0Bxg5tgGcQA2YnHzehgmNoY0OSIoGRCpe9TYTdVioW47bUjJTCAGJwJUiSsFSBMFMM3JxFRWAAlbAilk2C7tRISJ6WrpTz8GdaiB81LD/qeRglxRQdmr3/sq5ZBV1yNpu7OBP8137mVfefcBGMiIYmvpqJkVogh4R3cpFqhKQFTFTAixaBjwSGBMxgjl2MiRjghAwxBAbYFb29CpLkdz32vdd23V97w7AjFQzgsUUw6Lhg0Vzem/vwSO99yAdndjiAOoGUsIh4y84bTe/MUPqd3tjvRyIACLaW3l9frHatokj5lwZ/PVf/Obho8fGjEgjYctQw//o3sBP9/AnH0tAngORKaB07eb8/L2oPHvxLFZ7iiSAAKRqTEgEgAiBJHuzt5AKqG1WaxVFxG3bNnuLYhZSuri8Wq7Xs/lsmTeSC4Jtt+uLd29XV5cE+O03355fnanK3t4eIl5dXYUQDw8Pj09ODGyxWKzX67ZtRWSxWBwcHLTtdnl11fe9mf3yl7+8f//+6enp8fGxmf39f//7EMKLF19+OD87v7h68cVzChEAVjc3eycHN5c3J/dPrwG6rr2+vLi4vCSiru8xcrKGGDSXxWLBzCVLzr0ZiEiqkgFIEQBQtSFLBthutyEEIuxyrlMEgJxzn3PXtapaxGOQgBRAMzPdOz05PjpoqlQlx/8QAjATuajOT1fPAcyA3OF5EjCmxcPBHMoyquOaOx4EvH7giQKhFwP9TItP+49QAe+a+aSjiQghMNNo9e50ZE3NGRJ29hVMn6Hc5QKaKgdqQ1d5Min+HN3hn5KdKfRhX37iESbCOyYys5yzmCKhKTTNLJ0cX37/rgpcxYpCFKCBMJkAkJSQiI0ICIuKEgfEXkRYi898kWpEQGAacCLe0xi4BAZfhaWIQ0qIGEnB15LAxJkpmWMkDoQAhqTmph8JAWlApxigk4WogWOGhlNuA2qFcMxChhEwjFFxOx1YJJqcxiR54vYDEJ0BABmBA4eIIVgIgCQi2melDDmLmZp2pAJohFlVDMWsAKhZmBo9NsanZqZmTGFnjcZ6swHesgndGfS4dWtjngJT18iFqImKKQUe0L8yvI6jLFyhCSdQ5NjrGPYQYbFyu0349klFoEhBACQ0UTBDA5WcfeOaoVo2A3P3p0QqpRg43B6MgiJRTB0AceCYjAMGCsRkaKWAZes7kb7v2660BUqrfZv7PhMJpUoplbTgdHpY3X8Ip0/kweN8eIzNHEMVQyQEhSKgKAqiBKiOxUBkZFUB6g2TKoNoRCjtttT8YV0u3uWgizr1CPro8b3f/OWfV9UMMVIgg+Kbh9mLicZEY0Z5226BMZ/TYX3J0Z5gKAiBAVVAu+3Nzdu3PzZ7+4+evqAQRaAUMQ5GjIRiREZWALggSdu2prnicHhw8Nt/+qd/9atfrfsbYFt3rW3ri4uLvu+O7j+4PP9QU2iIl6vr7fJact/n7Z/92f/YdblOKYSwXm3XN+uUmv39g8Ojk8Vif7vdvH/z+uzsLCA2TY2IV+dny+Wy7dY/+9nPT05OfvblV0dHRyGkruu+/vq365vVk4dPXv3w8tuX3x+fnLTd9uzNq67dfvnk4Xq53Ht09PTx/eXNFShcnF+tN61JIVDJZpUkTjGFKqa+bw8OFyK66boKqy73BmSBKCYVlJyLDnO7pZSuZCdtzVI2m02smr6oIUFIfZ8LIzFGhRnD8aw6rOuEHDEmA+17IooUAqNHR94FmA6LjS0uRCxiROSwVByFMYhIjWKK4MLb/qcYYow2cnmpgTPXFs2Ro1OhiAGbAQIZai7ArFz8YAERGCKxk40aCwAyIYCiIqNLhaHYlig4wVcIEUxMDSmwF498ggFcfwjFR010mOCZSsGISIbTzFBAb00rAgAy0TB1XCDDZDdCcmfpnW1EY5/xZe2TpfuH4eFp9/JiphQggCuhMiEaJeK6Mg5AySCJCRAW1Vxy4aAxGZiBAkTGMBY8FNA4IhY0LAYCaCIFkRATugAUtERqSgRc0JDAOFBkMFEzAhDQxAGZAIMBZSRVoF41WGErBmCYkMHncYkAFSOqgAWwwAi1aUKs1SqACKBoECBkzEaBAkufDU0AlLmABsxqRhARIwMZsgCDkimDApixqeQiuQgGY0ZAQCpihmQISIGBg3GYXDTu0AgTkc8cjz5g6v7f8dI/lQFMCcRuQQlHlmNDIKZAt4gg2G157cQCNqWNO1mn169tCqCMbvEEjq9SM1MgvX0BURxeyYYJYBy/ZoxExByoGnS7gAM595CYqpa+z10vXS4555z73OecixYFhmhWB96v6Wg/3D/lB/f0+IgXe2E2x7q2FIFoolAcovK7ZhoRVURV1YgUFMWAitjNant5cbNetZqzWvn1v/7VkyePETBwwtvq4R/qzUyZ3E6JVdGcENCncUy03FxdXJ+f7R8enjx4hJSygI7TcMQ0wWPci+SSTSQQEVGzmLddBwBIKCUvb24+nF9e3SwfPbif6rTerLFtseR22759+ya33dOnz375y1/+t7//7wTQtdv16oaZD46O9w4OFWi5afvtZrVa+W3JOd/c3FxcXKQU7z+49+WXL371q18DQO6lbduXL19eXFweHh+9e//+1esf752cprp6/fIlx/Do9H673Tx58uj05MH1ctW221y0z31d15vcMTMBejO2qqqu6wAs5x6AUoqERIEVqK7rEKIUUgUxbbvOb2NTN03TXN1cl1K2223VzLMoB4pV3Y/gDgZtUnV8sD+fJSeQwFETm4lCYGZG9CHHzy8cETnnm5+d2yXQXW4r9G6h84hMuwt3Lu9n+A+EYfI0UgogO1xwPB5kCKoKKAPmBAOY+UaBsWbpypEATuhi+LkqkI1HdTQXO/+F2x4Yjv/AoRjTH3/0Wv7kO3fKApEixL1Zc3zQvrkWJQqBCWGYPXXJVJChlK+qiCIu2Oq2w4stQOM/dLZk9eE4IwAEIwV0Cn9AHiA+AEgMYOQ1HuNAMZgWMABVIqYQgBGJjEnAxsDLee2chIYcY47OGUWEpuq8uUzIAZmMMaSEKgSgauN8/1CfVymA6DJeYEYYx0SA/KMXVSgiORv1BYKWXDiAslJQAEVSMAWHv5qohY/2zRSPfLQpp4Uc1uFzfdrbVfq0xmdmZkUkhIA8jNt40urNrs+qx00OAABwCC4G1+JZhpkh0qD4qGae2bqHoAHn411138MAIGzExBSRiUOMKTnoHzi6vsJQqFFTKSX30vbaZ81Fi+Su73OXczYVDsCJdBbh5IAfPeBHj/H+fTg+5tmMqspCNB8jIAGEQdoJkZCMhvCH0OfU3Ew7HAgUoMv64fy6GAhan9t6Vv/6T/8kVbGKcSqqfva2/19eAw0kgHear2/ON5v1wydPmmZuEACDinjRwwEevDMtZTaQICENgoXz+fz65hoYVMp6s1l1/d7eftduz96/ffb0MXb91//0f7x+8zIE/re/+Q2I/t3f/d36ZtVvV+/ev1/sHdx7cB9D6opSoL7P52fvu3YLANvt1hn5/9Wv/vjZs2ePHj04OjpS9bgVX778/ocfXhHR63dvfv/N75mo67abzepgMa+ralbFF09fLPb3D/YP//n3/ym33WqzvX//YYzpw9UFh+A1K4+su1yqKrV9t9m0wMQU2r6jkJg557LZ9n3JzWwWq8CJSykKtlyvNpsNABjykCjj1J5VK4XBTg73DhZNZApMIQV3AN5bJnLqf/nsbh/2OToSHRG9DDKkxBNh1GTZ/fLUYYIJTa9Ddy8cQ7CPztd0ymz3f3f6cNOfj/OKdzhaPntNJd/bw7vjEj7Zk2MZ6BO4+W4tfnwUCFERhSDuL7az1K+LMhCTZBuQHYaqol6XcUS/jxqbOQSQyLkWEAKOIz4KhkCgpISDjLi5M2BEJQoBNBGo51KlmFFAZkUGNjIT1RgCBlYGdZgEiiIZqKAZI5ABI05BFRH4GjqIiZkDl0AQGSMbIzBqMUFlJpdpcZs8lPgJrSAaMAVAVEQEcpcqCBPUPbOYqQxaxqaeQCAKQAETs2w6cYkMiz1ZWN2hiZ4Cedgx7p9dzmm9p0IQ7pR0cNA58UkohJ2+ljuDn9pSMPKe6zhJOG36odgpamboDnPYUV7w3GEJRecKYQqBAwMFJOIQicmAKKRJYwcMUNRK0b7PfZ+7vnR96fqJ/RHAAmlsKj48mD96Eh49o5MHeHDCB0dYNzg6AGRXzIGBX9o/gxPNjzeQgMXDLiK0YIJ9tvOr9aZti4mAPn326PHj+zGSiAAghFuf/Qdul8PGiWgH6A1o48cA+/D+zWazfvzwcVU3CDF3YkVVTEFjjLvTecOt3hEh6UuJVdo7PFhu1idHB/12s16vT+89bLt8dvGh3ay/PXvfL1dv375u++7f/Pp/XG/a9fJm0TS5215cnKcU67oGAkXkwDerzWa7NZGcs2sCHx0d/exnP/vjP/7jw8ODm5ur8/Oz2WyOiL/73TeXF9ci+ez88v3l++Pjw4P9/cuzc2Sa19WD+/e9SRBTvLi4vDw/A5CTw4Mvvnjatn1d18QsuaSU6lRN9tRGDD4CIWKM0W9dLllUlqulmnV9yYMimHKsQgj7dR1iajoJKa7blkNIaKXkmunh6dHxwSIygCu3jg6ABv2iQfHiJyi4wGw4bkNF9FbMbsiYJxiou7Hp8E5Hb7C2w5Aw0UDCOCjnhRDciNuIuBu4wcfX3D3aZqYyktCpG3EdX/Ant99uKDm9zuQV7hj0n77MPu1MA7jFCCSq1fH+/qN7+uN5BuNBgRKRgBCLFGe3IOdPEDERJdExA8BpCNunRYFAxWljbEAnGaAheZsRkJE4GCgJgJGJEEcIZEimRRGKChMNEFGDomYIigZoCqKoSsiEMHLOgyuDOS2H9x54+KeMEBDIRZqRmNEAQIzNzBIHCkFMvfHMHBCgmA4NYQBRUQCDrMiFIpQsEkEEiBXQkBRUAdSgmInZLQpId5h27Ba9eVvWhx0nMS3t7Ua5C1XGIVedaKTGGgzccQZTiYJGgPO0/0ZvMUxFDkxtziNUZHIwaoWIDMxEPGv1JGA3+gBEIhSzwEzJ86/gHNxiAMghRgVCc+ZBZUApvZZecl9ydp2Qbdv2pRfVYkqRUxWrxV44uR+OH4WTJ+n0MSxOKM1x1misLCQgNkJEdq3w3Iqa0qBp6a0RMwGCgECqBoxmIEY36/5m1fYKFLjL7b2HT+p5LSZsSng7Cz0dqt3YaloCu10zMEUAYwRCEi2McHZ+tlpdP378NFW1GrvMUe57RHCo+/Sy0z10SBWodaVHxFmdHj998rt//m2T6Prq4t3788XewWa9mdXV+vry7P27slmb2Vdf/eLRk6f/9e/+TnMOBleXF0Xt4YMH88UiG8yapp4tXr97d3F2ztYub67n8/mXX744Pj7+8ssXs1ndttuDgwMfH/nd737/3XffIPKrV69yX774+bOqqjarFahUqfrTP/nV0eFhipWYtpvty5c/rG5u6iot9hZfPH/65u372ay5ur5xpODh4eG23XgVmsYRMFOgTH3fD7vRJKa42my8IpZ7WW+7m5ubEGix2K+Qbm7W264N5lsdI4KaHu3P7x8d7M+qGDlEUrAwro6qjjxrvnb8qTVUdSJ+MrMQnFQYXPN9WuWUko2AvamLNtl9GrH5sDP24XGLz4WVnJGCVwiHo+r5/fABFEZFv2E70WAcwMjMfKh4ONc2uA+Ygi5wPkqdjP5oTGCXhXvaoruOZLIwAIBERmBwK0V+axnMCqpE7Cvio0U+v8mdqpSI/o1QVAyJCQytlAzMVkRZIYJ7Y0NARiIIfp8UCB2eA0QQCJWgqIIJIQRmKIq+XgrMaALM7Hq4ImIqUjIjqmrXdZjYEJFJpKj3bEMkBEFDstuEjMlVOf10ARg605tbXDfort3GjAaeuTKzl7bZKSIGvhxF9SK4+Gqo+rOGn1UUVNmDEUAPgQXIDEwh0M7w111fextTfOSxf8r5e9jo413T5h5edvAlEw4FRGVyAB52xRh3p8B2fY+qeizvD8koLoHDeLuzOxgaEAx+ZbBiRECITKLKVQIA4OB07MjBh2k5JA6RkIHQEM205E66vnRt7rZ97ru+60vfSe6k9KAQODQ1zBs6PgkPnsTHX/L9Z3R4PywOQj3LiS0ECxGQRQvrIGg/NDHsLkQHwNFoOkbZWWm57re9FVNkik2czWsXiQshEIVPID+313TPJ1+uqj7LRkAEJqVnsDc/violP3v8Ita1GiHFomZIxAomnxID+MkmRFDr+95MmqYRsGrWtH0vuSt9Z5Jfv/phb3//annVrlcnR4eX3Qar+OTp06JWDED1zZs3pduePnpyeO9BCCGKlJJfvfxuu7xu18u+Wz588ODLL7+squro6Ojk5ISIcu637Trn/H/8wz+5FMz333+72bRHR4fatci4Xd2QyZ/++pfPXzw10b29/curmw8fPnzzu9/XdaUGR4f7s6ZyjqO+7+fNzLdZzjmlZCZEtFgsKIZ226lqFokxtl1rpp2PfouaOWNaiKlOVQgpAvBytexKCaqz+V4pRUVmKZ0eHhztz5qEBMLMHKNTI6h68WHgh5lOweTIPwqqpgCIiBxyyoOAzHBNJ2Xq2017YMiMw/Be6GUQGBJuUI0p4FjBv80YhkMHMFSZBndit8Sft28xvPtOtWd3E05f8FNDMX1NG+cb5KdSoc9dOIAysWeDKjSHi7g/x+ttFCzbjoiA2MiYSVQk9xBAzAzYi8A+2QtjssBoBKS38smgpmjGCj6tTAMBpTIAqjACOQrOb4WiiYCp2zIQRCYCheD+wcDHe1UJIBIwciBn6R71L2Ew+H6LyQzQnGGJbPimQxJm5nAAJPTRMDd9flNhaHl418Nr4UUhQxjMJhuiAQMrIKqUXEou0ovkEu7c3zsLdhvgT49/FG/+1LUbOQ5zXv4iPFEh+TwWeHb80QbadQC+aRyvtvvKt59HBfxe6LjfwYgMcMDVEpERohHH4IEsMAGNjR0KyGSIyAEA1YoVp0nqJefcdX3Obdf1fd9LKWBKiFUMi1l49KB6/qL+4qvw/Au799AWh9jMMUaqwEIATgBIClayU7ARouAQ/9+9WzSy5KmBlaKXV8uuF0UooEAWK+cgt8AMn4z4fvaeTyGhmSnAANhQAdVvvvldJHz+4jnGuigoMCArKJAQm6ngZx0AgOSS2y4wp1nNzKJZRJ49f/bf/ut/cR8QCN+8evXmzev/5T/8zxfv3/3w9c0vfvUnz188/3//f/6/ImZFmPDR02fx8GTv+JSJVqvl2x++P/vwvuQcWU4ePnj+/HnT1ESECGdnHy4vLz98+HB8cnh9fV1V1c9//vO//du/3W63T548ns8Wp/uz9XJJYv/6179+/uyZquwf7G+323bb/sN/+4f1en1ycrLarO8/uLde34h02+02xvjw4UMiWK/XBlZXdd+3fZ/ruupK3m63KaW87dq23bYtpTDA34opoBmKal3XSKACm+2m7fuqrgGZmfu+B7PDg4PHDx4czOdNikigUnKhuh4mM2HiF0GPfO/01W6PGDCOhX/HYXCMGfJEG3cnHB6j/t0XGY6Peff+tgIDABN+GnagYj6BRGGXvuU2h/afp885HU+AkX/qX1DP8Ut32Mamvfov/NvbFxERtk4LBJjNq+pgocvORJkp596AYx2n72dSRBTGHvgQBLsoG0JERgITF8gEMhUD1EFPkQAYmXEc9ddCZigDjARcDa4U0WwiDBScTVkIaORG9fNqhmCEHJkCEjqQd8R8D3fB8z4ANBzhKYhoiKBIRuC6jswMHAxAzBzojqhmAqgO7DQDNPaGPRmAIQO5nCEYoaECFlFSJAVUIIUwFV4+rcJ/ZP3hbrzwaWbgtt4pTaa9uBvU7OJh3KHpjsJ1znnKQqbIaDee3XUM02Zij3OdGs0D2cAGUMQ89gdmM+MUFDHGwMwIRIERmWMkCsiEHAAA1ERFSyk5y1D67wpYVskuEkbIVWgO9vYf3EtfvDj4o1/E5z8v959080NLDVQNEmBQ5GgUDDAGAsvgCfLQC/nEh8EE2TYpstmW88uLrs8UqlxK7rN3t1UV/q+c7u49H4yOqtrQMJe+++Z3X1eBvvrqj1SlKAAyUiwCZkbDSNqtkMBH12q9UpHFYtGVzt8ol4KEZ+dnq9WaEM/PPrx7f/bFi2eJ+ezD+8Vi/uOrV83+oZqtNusa4MH9+48fPjzv8dXbD7lrr84/XJ6/19wT2qyp7927t1qtttvtbDYjoqqqvvrqq+fPn715++PR0fMPH87/43/8j33f7+3t7e/vP7h37/L1y/Vy+fMvXzx5/LCZ1amqKCAwvHz5UkR+/etfI+Lf/df/Urq2SyGEMGua03t74BUVtWZWA4CP2hKR0/enuvIn+PGLsUrEW+yzWNf3IlLXzWqzOjqa931PzDHGEKuUalEouj3c2zs+PIiMCNY0TV/UW3ZDWYaAmZh5IMNFnna1p79m1vc9jDYdAKbhZCJyYdiPUgRf5WlHTYM1HqSnlABIRBDAEewGQDzoWsMI8xtP9G3w7qPmk6X3toQz+OAIR4Ep+cY7xQN/Nf95F4O2G6DsupM/sKU/e3kBXw0wMCVMi3kbr63viCxyRIJcetUMqRYEFVWKIHIrfIuAhEjIXpAHVAQx8YlkViD1kblhXAJUyJSBQgra94iATKWYoqGJWUFRLSImoEjMJjKIisQACAA+huekDjwE797vw/FuAHiyIOM68JjoICAyI7AaFCkxRqBQVFQlII/j1Z4BFANRUwQixMgBYhTyqhMHDsUQgRnUyS1ggAHB/wmnRN1xxzAX4AAAAABJRU5ErkJggg==\n" + }, + "metadata": {} + } + ] + }, + { + "cell_type": "markdown", + "source": [ + "# Citation\n", + "If you like our work dont forget to cite us!\n", + "\n", + "```\n", + "@inproceedings{Prados-Torreblanca_2022_BMVC,\n", + " author = {AndrΓ©s Prados-Torreblanca and JosΓ© M Buenaposada and Luis Baumela},\n", + " title = {Shape Preserving Facial Landmarks with Graph Attention Networks},\n", + " booktitle = {33rd British Machine Vision Conference 2022, {BMVC} 2022, London, UK, November 21-24, 2022},\n", + " publisher = {{BMVA} Press},\n", + " year = {2022},\n", + " url = {https://bmvc2022.mpi-inf.mpg.de/0155.pdf}\n", + "}\n", + "```" + ], + "metadata": { + "id": "QyWfeEzECTQg" + } + }, + { + "cell_type": "markdown", + "source": [ + "# Related Notebooks\n", + "\n", + "Tutorials | Notebook |\n", + ":---| :---: |\n", + "Image Inference Example | [![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/image_demo.ipynb) |\n", + "Face Video Analyzer Demo | [![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/video_demo.ipynb) |" + ], + "metadata": { + "id": "9cEL-x2MEHrW" + } + } + ] +} \ No newline at end of file diff --git a/SPIGA/colab_tutorials/video_demo.ipynb b/SPIGA/colab_tutorials/video_demo.ipynb new file mode 100644 index 0000000000000000000000000000000000000000..d5c34e7ecf80035250f65d1336aeb7f374850887 --- /dev/null +++ b/SPIGA/colab_tutorials/video_demo.ipynb @@ -0,0 +1,215 @@ +{ + "nbformat": 4, + "nbformat_minor": 0, + "metadata": { + "colab": { + "provenance": [], + "authorship_tag": "ABX9TyOF6rc4QkOxYUF0EKnbRAyL" + }, + "kernelspec": { + "name": "python3", + "display_name": "Python 3" + }, + "language_info": { + "name": "python" + }, + "accelerator": "GPU", + "gpuClass": "standard" + }, + "cells": [ + { + "cell_type": "markdown", + "source": [ + "# SPIGA: Shape Preserving Facial Landmarks with Graph Attention Networks.\n", + "\n", + "[![Code](https://badgen.net/badge/github/spiga/black?a&icon=github&label)](https://github.com/andresprados/SPIGA)\n", + "[![Project Page](https://badgen.net/badge/color/Project%20Page/purple?icon=atom&label)](https://bmvc2022.mpi-inf.mpg.de/155/)\n", + "[![arXiv](https://img.shields.io/badge/arXiv-2210.07233-b31b1b.svg)](https://arxiv.org/abs/2210.07233)\n", + "[![PyPI version](https://badge.fury.io/py/spiga.svg)](https://badge.fury.io/py/spiga)\n", + "[![License](https://img.shields.io/badge/License-BSD%203--Clause-blue.svg)](LICENSE)\n", + "[![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/video_demo.ipynb)\n", + "\n", + "**SPIGA is a face alignment and headpose estimator** that takes advantage of the complementary benefits from CNN and GNN architectures producing plausible face shapes in presence of strong appearance changes. \n" + ], + "metadata": { + "id": "zYVrcsnLp7D0" + } + }, + { + "cell_type": "markdown", + "source": [ + "## Video Analyzer Demo:\n", + "SPIGA provides a general framework for tracking, detecting and extracting features of human faces in images or videos." + ], + "metadata": { + "id": "6VGcBElYwZQM" + } + }, + { + "cell_type": "markdown", + "source": [ + "###Setup the repository:\n" + ], + "metadata": { + "id": "Pxj4tBskykGV" + } + }, + { + "cell_type": "code", + "source": [ + "# Clone and setup the repository\n", + "!git clone https://github.com/andresprados/SPIGA.git\n", + "%cd SPIGA/\n", + "!pip install -e .[demo]" + ], + "metadata": { + "id": "N6Mvu13ZBg92" + }, + "execution_count": null, + "outputs": [] + }, + { + "cell_type": "markdown", + "source": [ + "### Record Webcam Video:" + ], + "metadata": { + "id": "E4u69_ssyxkY" + } + }, + { + "cell_type": "code", + "source": [ + "import colab_tutorials.video_tools.record as vid_util\n", + "\n", + "webcam_video_path = '/content/test.mp4'\n", + "vid_util.record_video(webcam_video_path)" + ], + "metadata": { + "id": "Mck9eHXKYUxd" + }, + "execution_count": null, + "outputs": [] + }, + { + "cell_type": "markdown", + "source": [ + "### Process Video with SPIGA Framework:\n", + "\n" + ], + "metadata": { + "id": "JefR-lla9xEs" + } + }, + { + "cell_type": "code", + "source": [ + "import os\n", + "from spiga.demo.app import video_app\n", + "\n", + "# MP4 input path: Webcam recorded video or uploaded one.\n", + "# video_path = '/content/'\n", + "video_path = webcam_video_path\n", + "output_path= '/content/output' # Processed video storage\n", + "\n", + "# Process video\n", + "video_app(video_path,\n", + " spiga_dataset='wflw', # Choices=['wflw', '300wpublic', '300wprivate', 'merlrav']\n", + " tracker='RetinaSort', # Choices=['RetinaSort', 'RetinaSort_Res50']\n", + " save=True,\n", + " output_path=output_path,\n", + " visualize=False,\n", + " plot=['fps', 'face_id', 'landmarks', 'headpose'])\n", + "\n", + "\n", + "# Convert Opencv video to Colab readable format\n", + "video_name = video_path.split('/')[-1]\n", + "video_output_path = os.path.join(output_path, video_name)\n", + "video_colab_path = os.path.join(output_path, video_name[:-4]+'_colab.mp4')\n", + "!ffmpeg -i '{video_output_path}' '{video_colab_path}'" + ], + "metadata": { + "id": "wffMRr2T8Yvk" + }, + "execution_count": null, + "outputs": [] + }, + { + "cell_type": "markdown", + "source": [ + "### Results Visualization:" + ], + "metadata": { + "id": "v0k3qZ3YDlEw" + } + }, + { + "cell_type": "code", + "source": [ + "import colab_tutorials.video_tools.record as vid_util\n", + "\n", + "# Display video\n", + "vid_util.show_video(video_colab_path)" + ], + "metadata": { + "colab": { + "base_uri": "https://localhost:8080/", + "height": 471 + }, + "id": "I6o6piO-Dju_", + "outputId": "6f520b13-c6e7-4abe-8660-51d32f66524a" + }, + "execution_count": null, + "outputs": [ + { + "output_type": "execute_result", + "data": { + "text/plain": [ + "" + ], + "text/html": [ + "" + ] + }, + "metadata": {}, + "execution_count": 10 + } + ] + }, + { + "cell_type": "markdown", + "source": [ + "# Citation\n", + "If you like our work dont forget to cite us!\n", + "\n", + "```\n", + "@inproceedings{Prados-Torreblanca_2022_BMVC,\n", + " author = {AndrΓ©s Prados-Torreblanca and JosΓ© M Buenaposada and Luis Baumela},\n", + " title = {Shape Preserving Facial Landmarks with Graph Attention Networks},\n", + " booktitle = {33rd British Machine Vision Conference 2022, {BMVC} 2022, London, UK, November 21-24, 2022},\n", + " publisher = {{BMVA} Press},\n", + " year = {2022},\n", + " url = {https://bmvc2022.mpi-inf.mpg.de/0155.pdf}\n", + "}\n", + "```" + ], + "metadata": { + "id": "ZvuQLJPDGejs" + } + }, + { + "cell_type": "markdown", + "source": [ + "# Related Notebooks\n", + "\n", + "Tutorials | Notebook |\n", + ":---| :---: |\n", + "Image Inference Example | [![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/image_demo.ipynb) |\n", + "Face Video Analyzer Demo | [![Open in Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/andresprados/SPIGA/blob/main/colab_tutorials/video_demo.ipynb) |" + ], + "metadata": { + "id": "aQ_G5unzGmto" + } + } + ] +} \ No newline at end of file diff --git a/SPIGA/colab_tutorials/video_tools/record.py b/SPIGA/colab_tutorials/video_tools/record.py new file mode 100644 index 0000000000000000000000000000000000000000..c5a0168c201fb2867d6d08fc850fd9ccef7f46b7 --- /dev/null +++ b/SPIGA/colab_tutorials/video_tools/record.py @@ -0,0 +1,78 @@ +from IPython.display import display, Javascript, HTML +from google.colab.output import eval_js +from base64 import b64decode, b64encode + + +def record_video(filename): + js = Javascript(""" + async function recordVideo() { + const options = { mimeType: "video/webm; codecs=vp9" }; + const div = document.createElement('div'); + const capture = document.createElement('button'); + const stopCapture = document.createElement("button"); + + capture.textContent = "Start Recording"; + capture.style.background = "orange"; + capture.style.color = "white"; + + stopCapture.textContent = "Stop Recording"; + stopCapture.style.background = "red"; + stopCapture.style.color = "white"; + div.appendChild(capture); + + const video = document.createElement('video'); + const recordingVid = document.createElement("video"); + video.style.display = 'block'; + + const stream = await navigator.mediaDevices.getUserMedia({audio:true, video: true}); + + let recorder = new MediaRecorder(stream, options); + document.body.appendChild(div); + div.appendChild(video); + + video.srcObject = stream; + video.muted = true; + + await video.play(); + + google.colab.output.setIframeHeight(document.documentElement.scrollHeight, true); + + await new Promise((resolve) => { + capture.onclick = resolve; + }); + recorder.start(); + capture.replaceWith(stopCapture); + + await new Promise((resolve) => stopCapture.onclick = resolve); + recorder.stop(); + let recData = await new Promise((resolve) => recorder.ondataavailable = resolve); + let arrBuff = await recData.data.arrayBuffer(); + + // stop the stream and remove the video element + stream.getVideoTracks()[0].stop(); + div.remove(); + + let binaryString = ""; + let bytes = new Uint8Array(arrBuff); + bytes.forEach((byte) => { + binaryString += String.fromCharCode(byte); + }) + return btoa(binaryString); + } + """) + try: + display(js) + data = eval_js('recordVideo({})') + binary = b64decode(data) + with open(filename, "wb") as video_file: + video_file.write(binary) + print(f"Finished recording video at:{filename}") + except Exception as err: + print(str(err)) + + +def show_video(video_path, video_width=600): + video_file = open(video_path, "r+b").read() + + video_url = f"data:video/mp4;base64,{b64encode(video_file).decode()}" + return HTML(f"""""") \ No newline at end of file diff --git a/SPIGA/colab_tutorials/video_tools/utils.py b/SPIGA/colab_tutorials/video_tools/utils.py new file mode 100644 index 0000000000000000000000000000000000000000..924bccf06cd0db5b14024b45828c4448a6fce823 --- /dev/null +++ b/SPIGA/colab_tutorials/video_tools/utils.py @@ -0,0 +1,52 @@ +import numpy as np +import PIL +import io +import cv2 +from base64 import b64decode, b64encode + + +def js_to_image(js_reply): + """ + Convert the JavaScript object into an OpenCV image. + + @param js_reply: JavaScript object containing image from webcam + @return img: OpenCV BGR image + """ + # decode base64 image + image_bytes = b64decode(js_reply.split(',')[1]) + # convert bytes to numpy array + jpg_as_np = np.frombuffer(image_bytes, dtype=np.uint8) + # decode numpy array into OpenCV BGR image + img = cv2.imdecode(jpg_as_np, flags=1) + + return img + + +def bbox_to_bytes(bbox_array): + """ + Convert OpenCV Rectangle bounding box image into base64 byte string to be overlayed on video stream. + + @param bbox_array: Numpy array (pixels) containing rectangle to overlay on video stream. + @return bbox_bytes: Base64 image byte string + """ + # convert array into PIL image + bbox_PIL = PIL.Image.fromarray(bbox_array, 'RGBA') + iobuf = io.BytesIO() + # format bbox into png for return + bbox_PIL.save(iobuf, format='png') + # format return string + bbox_bytes = 'data:image/png;base64,{}'.format((str(b64encode(iobuf.getvalue()), 'utf-8'))) + return bbox_bytes + + +def image_to_bytes(image): + """ + Convert OpenCV image into base64 byte string to be overlayed on video stream. + + @param image: Input image. + @return img_bytes: Base64 image byte string. + """ + ret, buffer = cv2.imencode('.jpg', image) + jpg_as_text = b64encode(buffer).decode('utf-8') + img_bytes = f'data:image/jpeg;base64,{jpg_as_text}' + return img_bytes \ No newline at end of file diff --git a/SPIGA/pyproject.toml b/SPIGA/pyproject.toml new file mode 100644 index 0000000000000000000000000000000000000000..2a84a692b49a5c2e16d71982286cf10c3aa68d37 --- /dev/null +++ b/SPIGA/pyproject.toml @@ -0,0 +1,7 @@ +[build-system] +requires = [ + "setuptools>=64.0.0", + "wheel", +] +build-backend = "setuptools.build_meta" + diff --git a/SPIGA/requirements.txt b/SPIGA/requirements.txt new file mode 100644 index 0000000000000000000000000000000000000000..b3c1378c0b679aee593be8c766a0517c11c0ba9c --- /dev/null +++ b/SPIGA/requirements.txt @@ -0,0 +1,9 @@ +matplotlib>=3.2.1 +numpy>=1.18.2 +opencv-python>=4.2.0.32 +Pillow>=7.0.0 +torch>=1.4.0 +torchvision>=0.5.0 +torchaudio +scipy +scikit-learn diff --git a/SPIGA/setup.cfg b/SPIGA/setup.cfg new file mode 100644 index 0000000000000000000000000000000000000000..d5cd0f1c07c21389776337c61f5b5772c4cad950 --- /dev/null +++ b/SPIGA/setup.cfg @@ -0,0 +1,74 @@ +# Configuration of the Python project + +# Configure setup.py +[metadata] +name = spiga +version = 0.0.6 +author = Andres Prados Torreblanca +author_email = andresprator@gmail.com +description = SPIGA: Shape Preserving Facial Landmarks with Graph Attention Networks +long_description = file: README.md +long_description_content_type= text/markdown +license = BSD-3-Clause +license_files = LICENSE +url = https://github.com/andresprados/SPIGA +project_urls = + Homepage = https://bmvc2022.mpi-inf.mpg.de/155/ + SPIGA Paper = https://bmvc2022.mpi-inf.mpg.de/0155.pdf + Bug Tracker = https://github.com/andresprados/SPIGA/issues +keywords = + Computer Vision + Face Alignment + Head Pose Estimation + Pytorch + CNN + GNN + BMVC2022 + WFLW + 300W + Merlrav + COFW + +classifiers = + Development Status :: 4 - Beta + Intended Audience :: Developers + Intended Audience :: Science/Research + Intended Audience :: Education + Operating System :: OS Independent + Environment :: GPU + Environment :: Console + Programming Language :: Python :: 3 + Programming Language :: Python :: 3.7 + Programming Language :: Python :: 3.8 + Programming Language :: Python :: 3.9 + Programming Language :: Python :: 3.10 + Topic :: Scientific/Engineering :: Artificial Intelligence + Topic :: Scientific/Engineering :: Image Processing + Topic :: Software Development :: Libraries + Topic :: Software Development :: Libraries :: Python Modules + + +[options] +packages = find: +include_package_data = True +python_requires = >= 3.6 +install_requires = + matplotlib>=3.2.1 + numpy>=1.18.2 + opencv-python>=4.2.0.32 + Pillow>=7.0.0 + torch>=1.4.0 + torchvision>=0.5.0 + torchaudio + scipy + scikit-learn + +[options.extras_require] +demo = + retinaface-py>=0.0.2 + sort-tracker-py>= 1.0.2 + +[options.packages.find] +exclude = + spiga.eval.results* + colab_tutorials* diff --git a/SPIGA/spiga/__init__.py b/SPIGA/spiga/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/data/__init__.py b/SPIGA/spiga/data/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/data/annotations/300wprivate/db_info.json b/SPIGA/spiga/data/annotations/300wprivate/db_info.json new file mode 100644 index 0000000000000000000000000000000000000000..026b8df7468581a8451fda952adbf7c95cec15d9 --- /dev/null +++ b/SPIGA/spiga/data/annotations/300wprivate/db_info.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:f43605118e19366321fa01e24711cad6a5eefdc752bc4015ecdaf4f63018f477 +size 8581 diff --git a/SPIGA/spiga/data/annotations/300wprivate/test.json b/SPIGA/spiga/data/annotations/300wprivate/test.json new file mode 100644 index 0000000000000000000000000000000000000000..69cf8472bc518128058fe42f683e8825fd38dbd3 --- /dev/null +++ b/SPIGA/spiga/data/annotations/300wprivate/test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:3aaa393fae27480c6779405082dee93241de5cfee8990c88d2f336d877c14753 +size 1383019 diff --git a/SPIGA/spiga/data/annotations/300wprivate/train.json b/SPIGA/spiga/data/annotations/300wprivate/train.json new file mode 100644 index 0000000000000000000000000000000000000000..1d9835845de2ec726aa41a23d5986597d9e26141 --- /dev/null +++ b/SPIGA/spiga/data/annotations/300wprivate/train.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:cdadec43ccfe4b228ce46ff79c6b09c3b9a1f167294e021b6c9fcb592e1f909f +size 9940676 diff --git a/SPIGA/spiga/data/annotations/300wpublic/db_info.json b/SPIGA/spiga/data/annotations/300wpublic/db_info.json new file mode 100644 index 0000000000000000000000000000000000000000..d78d653c7ac7bb2b90d2a7296248a6e49277d5b1 --- /dev/null +++ b/SPIGA/spiga/data/annotations/300wpublic/db_info.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:8612f49ab40b9d9e863d4ac3b2f0b84eb13ea38a885137c966eeccd6150dbb79 +size 11680 diff --git a/SPIGA/spiga/data/annotations/300wpublic/test.json b/SPIGA/spiga/data/annotations/300wpublic/test.json new file mode 100644 index 0000000000000000000000000000000000000000..609f31098509c704532bcaa79602bc5d076e7da1 --- /dev/null +++ b/SPIGA/spiga/data/annotations/300wpublic/test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:c4147e9924e7c040e647c7f39a50f56324a51383d3c52d4d056694211f36d0b0 +size 1865129 diff --git a/SPIGA/spiga/data/annotations/300wpublic/train.json b/SPIGA/spiga/data/annotations/300wpublic/train.json new file mode 100644 index 0000000000000000000000000000000000000000..8bd4124c34132ea7d812933c30a87cf16d5298f3 --- /dev/null +++ b/SPIGA/spiga/data/annotations/300wpublic/train.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:d432d230fc093e87cc402b33c23acf943b1552ef17453405b75f83db01b275fa +size 8157361 diff --git a/SPIGA/spiga/data/annotations/cofw68/db_info.json b/SPIGA/spiga/data/annotations/cofw68/db_info.json new file mode 100644 index 0000000000000000000000000000000000000000..5fdbe527879e9fd6e41d1295dc692ab62abb6b79 --- /dev/null +++ b/SPIGA/spiga/data/annotations/cofw68/db_info.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:2087f472b64f914ba8db2c50f2c79b22af96b376abdb01bfce87d0571ba3c235 +size 5611 diff --git a/SPIGA/spiga/data/annotations/cofw68/test.json b/SPIGA/spiga/data/annotations/cofw68/test.json new file mode 100644 index 0000000000000000000000000000000000000000..d91f26676c4f5819aa8585dad85ad3d386618a64 --- /dev/null +++ b/SPIGA/spiga/data/annotations/cofw68/test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:87325157ca578b28fa8117b9e02fd09768c1db588a0878c546ced9a266e51061 +size 1897814 diff --git a/SPIGA/spiga/data/annotations/merlrav/db_info.json b/SPIGA/spiga/data/annotations/merlrav/db_info.json new file mode 100644 index 0000000000000000000000000000000000000000..74e87085d428290d8e8a6589ec3faa74625a0bec --- /dev/null +++ b/SPIGA/spiga/data/annotations/merlrav/db_info.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:ad7bf54f27fe816c0500f9318aa1df8a4ae90758faebbf1ba64d3ea037185382 +size 37851 diff --git a/SPIGA/spiga/data/annotations/merlrav/test.json b/SPIGA/spiga/data/annotations/merlrav/test.json new file mode 100644 index 0000000000000000000000000000000000000000..26d627957734ae99ad43c3fba290d23ac933066f --- /dev/null +++ b/SPIGA/spiga/data/annotations/merlrav/test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:cd1e358a29f95f869fa5fd09cb37c335a2220b5b478565459221921540aeb236 +size 11312227 diff --git a/SPIGA/spiga/data/annotations/merlrav/train.json b/SPIGA/spiga/data/annotations/merlrav/train.json new file mode 100644 index 0000000000000000000000000000000000000000..df943ed607c514a8389f2225a030e4be23d1fe18 --- /dev/null +++ b/SPIGA/spiga/data/annotations/merlrav/train.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:7e8bfb36c27776d8386dfbee682af65332b1dad03faaedb9533b6b39acb230e9 +size 43323888 diff --git a/SPIGA/spiga/data/annotations/wflw/db_info.json b/SPIGA/spiga/data/annotations/wflw/db_info.json new file mode 100644 index 0000000000000000000000000000000000000000..1f60eef6cf3b8c4d63c3ca73eb95992b2a56c348 --- /dev/null +++ b/SPIGA/spiga/data/annotations/wflw/db_info.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:a0d623edbf37625b180d596b71f753263f2b7c81e44af0b10023097f04e56958 +size 26829 diff --git a/SPIGA/spiga/data/annotations/wflw/test.json b/SPIGA/spiga/data/annotations/wflw/test.json new file mode 100644 index 0000000000000000000000000000000000000000..7d4be9a6ec48158c03234cf7f54e521363a0c712 --- /dev/null +++ b/SPIGA/spiga/data/annotations/wflw/test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:306005740c464241d50a0aff00821215c2edbd913c739e4666f5e0dbca6f031c +size 9755013 diff --git a/SPIGA/spiga/data/annotations/wflw/train.json b/SPIGA/spiga/data/annotations/wflw/train.json new file mode 100644 index 0000000000000000000000000000000000000000..0e156062bd61dbd879355517ecb9fd05ffd4179c --- /dev/null +++ b/SPIGA/spiga/data/annotations/wflw/train.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:95dcb0a2479e759da5e7051ad5c62eae90af3987614cfb0731802139f24e210a +size 28374603 diff --git a/SPIGA/spiga/data/loaders/__init__.py b/SPIGA/spiga/data/loaders/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/data/loaders/alignments.py b/SPIGA/spiga/data/loaders/alignments.py new file mode 100644 index 0000000000000000000000000000000000000000..9467ec9308475e876346efe199e1973eb154cd88 --- /dev/null +++ b/SPIGA/spiga/data/loaders/alignments.py @@ -0,0 +1,158 @@ +import os +import json +import cv2 +import numpy as np +from PIL import Image +from torch.utils.data import Dataset +from torchvision import transforms + +from spiga.data.loaders.transforms import get_transformers + + +class AlignmentsDataset(Dataset): + '''Loads datasets of images with landmarks and bounding boxes. + ''' + + def __init__(self, + database, + json_file, + images_dir, + image_size=(128, 128), + transform=None, + indices=None, + debug=False): + """ + + :param database: class DatabaseStruct containing all the specifics of the database + + :param json_file: path to the json file which contains the names of the images, landmarks, bounding boxes, etc + + :param images_dir: path of the directory containing the images. + + :param image_size: tuple like e.g. (128, 128) + + :param transform: composition of transformations that will be applied to the samples. + + :param debug_mode: bool if True, loads a very reduced_version of the dataset for debugging purposes. + + :param indices: If it is a list of indices, allows to work with the subset of + items specified by the list. If it is None, the whole set is used. + """ + + self.database = database + self.images_dir = images_dir + self.transform = transform + self.image_size = image_size + self.indices = indices + self._imgs_dict = None + self.debug = debug + + with open(json_file) as jsonfile: + self.data = json.load(jsonfile) + + def __len__(self): + '''Returns the length of the dataset + ''' + if self.indices is None: + return len(self.data) + else: + return len(self.indices) + + def __getitem__(self, sample_idx): + '''Returns sample of the dataset of index idx''' + + # To allow work with a subset + if self.indices is not None: + sample_idx = self.indices[sample_idx] + + # Load sample image + img_name = os.path.join(self.images_dir, self.data[sample_idx]['imgpath']) + if not self._imgs_dict: + image_cv = cv2.imread(img_name) + else: + image_cv = self._imgs_dict[sample_idx] + + # Some images are B&W. We make sure that any image has three channels. + if len(image_cv.shape) == 2: + image_cv = np.repeat(image_cv[:, :, np.newaxis], 3, axis=-1) + + # Some images have alpha channel + image_cv = image_cv[:, :, :3] + + image_cv = cv2.cvtColor(image_cv, cv2.COLOR_BGR2RGB) + image = Image.fromarray(image_cv) + + # Load sample anns + ids = np.array(self.data[sample_idx]['ids']) + landmarks = np.array(self.data[sample_idx]['landmarks']) + bbox = np.array(self.data[sample_idx]['bbox']) + vis = np.array(self.data[sample_idx]['visible']) + headpose = self.data[sample_idx]['headpose'] + + # Generate bbox if need it + if bbox is None: + # Compute bbox using landmarks + aux = landmarks[vis == 1.0] + bbox = np.zeros(4) + bbox[0] = min(aux[:, 0]) + bbox[1] = min(aux[:, 1]) + bbox[2] = max(aux[:, 0]) - bbox[0] + bbox[3] = max(aux[:, 1]) - bbox[1] + + # Clean and mask landmarks + mask_ldm = np.ones(self.database.num_landmarks) + if not self.database.ldm_ids == ids.tolist(): + new_ldm = np.zeros((self.database.num_landmarks, 2)) + new_vis = np.zeros(self.database.num_landmarks) + xyv = np.hstack((landmarks, vis[np.newaxis,:].T)) + ids_dict = dict(zip(ids.astype(int).astype(str), xyv)) + + for pos, identifier in enumerate(self.database.ldm_ids): + if str(identifier) in ids_dict: + x, y, v = ids_dict[str(identifier)] + new_ldm[pos] = [x,y] + new_vis[pos] = v + else: + mask_ldm[pos] = 0 + landmarks = new_ldm + vis = new_vis + + sample = {'image': image, + 'sample_idx': sample_idx, + 'imgpath': img_name, + 'ids_ldm': np.array(self.database.ldm_ids), + 'bbox': bbox, + 'bbox_raw': bbox, + 'landmarks': landmarks, + 'visible': vis.astype(np.float64), + 'mask_ldm': mask_ldm, + 'imgpath_local': self.data[sample_idx]['imgpath'], + } + + if self.debug: + sample['landmarks_ori'] = landmarks + sample['visible_ori'] = vis.astype(np.float64) + sample['mask_ldm_ori'] = mask_ldm + if headpose is not None: + sample['headpose_ori'] = np.array(headpose) + + if self.transform: + sample = self.transform(sample) + + return sample + + +def get_dataset(data_config, pretreat=None, debug=False): + + augmentors = get_transformers(data_config) + if pretreat is not None: + augmentors.append(pretreat) + + dataset = AlignmentsDataset(data_config.database, + data_config.anns_file, + data_config.image_dir, + image_size=data_config.image_size, + transform=transforms.Compose(augmentors), + indices=data_config.ids, + debug=debug) + return dataset diff --git a/SPIGA/spiga/data/loaders/augmentors/__init__.py b/SPIGA/spiga/data/loaders/augmentors/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/data/loaders/augmentors/boundary.py b/SPIGA/spiga/data/loaders/augmentors/boundary.py new file mode 100644 index 0000000000000000000000000000000000000000..8c10ec7f13c8ac12c68114ddd7b1e4b25a545689 --- /dev/null +++ b/SPIGA/spiga/data/loaders/augmentors/boundary.py @@ -0,0 +1,122 @@ +import numpy as np +from scipy import interpolate +import cv2 + + +class AddBoundary(object): + def __init__(self, num_landmarks=68, map_size=64, sigma=1, min_dpi=64): + self.num_landmarks = num_landmarks + self.sigma = sigma + + if isinstance(map_size, (tuple, list)): + self.width = map_size[0] + self.height = map_size[1] + else: + self.width = map_size + self.height = map_size + + if max(map_size) > min_dpi: + self.dpi = max(map_size) + else: + self.dpi = min_dpi + + self.fig_size =[self.height/self.dpi, self.width/self.dpi] + + def __call__(self, sample): + landmarks = sample['landmarks_float'] + mask_lnd = sample['mask_ldm_float'] + boundaries = self.get_dataset_boundaries(landmarks, mask_lnd) + functions = {} + + for key, points in boundaries.items(): + if len(points) != 0: + temp = points[0] + new_points = points[0:1, :] + for point in points[1:]: + if point[0] == temp[0] and point[1] == temp[1]: + continue + else: + new_points = np.concatenate((new_points, np.expand_dims(point, 0)), axis=0) + temp = point + + points = new_points + if points.shape[0] == 1: + points = np.concatenate((points, points+0.001), axis=0) + k = min(4, points.shape[0]) + functions[key] = interpolate.splprep([points[:, 0], points[:, 1]], k=k-1,s=0) + + boundary_maps = np.zeros((len(boundaries), self.height, self.width)) + for i_map, key in enumerate(functions.keys()): + boundary_map = np.zeros((self.height, self.width)) + xnew = np.arange(0, 1, 1/self.dpi) + out = interpolate.splev(xnew, functions[key][0], der=0) + + out = np.round(out).astype(int).transpose() + out = out[out[:, 0] < self.height] + out = out[out[:, 1] < self.width] + boundary_map[out[:,1], out[:,0]]= 255 + + # Smooth + sigma = self.sigma + temp = 255 - boundary_map.astype(np.uint8) + temp = cv2.distanceTransform(temp, cv2.DIST_L2, cv2.DIST_MASK_PRECISE) + temp = temp.astype(np.float32) + temp = np.where(temp < 3*sigma, np.exp(-(temp*temp)/(2*sigma*sigma)), 0 ) + boundary_maps[i_map] = temp + + sample['boundary'] = boundary_maps + return sample + + def get_dataset_boundaries(self, landmarks, mask_lnd): + boundaries = {} + if self.num_landmarks == 68: + cheek = landmarks[0:17] + boundaries['cheek'] = cheek[mask_lnd[0:17] > 0] + left_eyebrow = landmarks[17:22] + boundaries['left_eyebrow'] = left_eyebrow[mask_lnd[17:22] > 0] + right_eyebrow = landmarks[22:27] + boundaries['right_eyebrow'] = right_eyebrow[mask_lnd[22:27] > 0] + nose = landmarks[27:31] + boundaries['nose'] = nose[mask_lnd[27:31] > 0] + nose_bot = landmarks[31:36] + boundaries['nose_bot'] = nose_bot[mask_lnd[31:36] > 0] + uper_left_eyelid = landmarks[36:40] + boundaries['upper_left_eyelid'] = uper_left_eyelid[mask_lnd[36:40] > 0] + lower_left_eyelid = np.array([landmarks[i] for i in [36, 41, 40, 39]]) + lower_left_eyelid_mask = np.array([mask_lnd[i] for i in [36, 41, 40, 39]]) + boundaries['lower_left_eyelid'] = lower_left_eyelid[lower_left_eyelid_mask > 0] + upper_right_eyelid = landmarks[42:46] + boundaries['upper_right_eyelid'] = upper_right_eyelid[mask_lnd[42:46] > 0] + lower_right_eyelid = np.array([landmarks[i] for i in [42, 47, 46, 45]]) + lower_right_eyelid_mask = np.array([mask_lnd[i] for i in [42, 47, 46, 45]]) + boundaries['lower_right_eyelid'] = lower_right_eyelid[lower_right_eyelid_mask > 0] + upper_outer_lip = landmarks[48:55] + boundaries['upper_outer_lip'] = upper_outer_lip[mask_lnd[48:55] > 0] + lower_outer_lip = np.array([landmarks[i] for i in [48, 59, 58, 57, 56, 55, 54]]) + lower_outer_lip_mask = np.array([mask_lnd[i] for i in [48, 59, 58, 57, 56, 55, 54]]) + boundaries['lower_outer_lip'] = lower_outer_lip[lower_outer_lip_mask > 0] + upper_inner_lip = np.array([landmarks[i] for i in [60, 61, 62, 63, 64]]) + upper_inner_lip_mask = np.array([mask_lnd[i] for i in [60, 61, 62, 63, 64]]) + boundaries['upper_inner_lip'] = upper_inner_lip[upper_inner_lip_mask > 0] + lower_inner_lip = np.array([landmarks[i] for i in [60, 67, 66, 65, 64]]) + lower_inner_lip_mask = np.array([mask_lnd[i] for i in [60, 67, 66, 65, 64]]) + boundaries['lower_inner_lip'] = lower_inner_lip[lower_inner_lip_mask > 0] + + elif self.num_landmarks == 98: + boundaries['cheek'] = landmarks[0:33] + boundaries['upper_left_eyebrow'] = landmarks[33:38] + boundaries['lower_left_eyebrow'] = np.array([landmarks[i] for i in [33, 41, 40, 39, 38]]) + boundaries['upper_right_eyebrow'] = landmarks[42:47] + boundaries['lower_right_eyebrow'] = landmarks[46:51] + boundaries['nose'] = landmarks[51:55] + boundaries['nose_bot'] = landmarks[55:60] + boundaries['upper_left_eyelid'] = landmarks[60:65] + boundaries['lower_left_eyelid'] = np.array([landmarks[i] for i in [60, 67, 66, 65, 64]]) + boundaries['upper_right_eyelid'] = landmarks[68:73] + boundaries['lower_right_eyelid'] = np.array([landmarks[i] for i in [68, 75, 74, 73, 72]]) + boundaries['upper_outer_lip'] = landmarks[76:83] + boundaries['lower_outer_lip'] = np.array([landmarks[i] for i in [76, 87, 86, 85, 84, 83, 82]]) + boundaries['upper_inner_lip'] = np.array([landmarks[i] for i in [88, 89, 90, 91, 92]]) + boundaries['lower_inner_lip'] = np.array([landmarks[i] for i in [88, 95, 94, 93, 92]]) + + return boundaries diff --git a/SPIGA/spiga/data/loaders/augmentors/heatmaps.py b/SPIGA/spiga/data/loaders/augmentors/heatmaps.py new file mode 100644 index 0000000000000000000000000000000000000000..3cc3ede432e5ca3ad2d0fd8a5972426bf59e9c16 --- /dev/null +++ b/SPIGA/spiga/data/loaders/augmentors/heatmaps.py @@ -0,0 +1,39 @@ +import numpy as np + + +class Heatmaps: + + def __init__(self, num_maps, map_size, sigma, stride=1, norm=True): + self.num_maps = num_maps + self.sigma = sigma + self.double_sigma_pw2 = 2*sigma*sigma + self.doublepi_sigma_pw2 = self.double_sigma_pw2 * np.pi + self.stride = stride + self.norm = norm + + if isinstance(map_size, (tuple, list)): + self.width = map_size[0] + self.height = map_size[1] + else: + self.width = map_size + self.height = map_size + + grid_x = np.arange(self.width) * stride + stride / 2 - 0.5 + self.grid_x = np.repeat(grid_x.reshape(1, self.width), self.num_maps, axis=0) + grid_y = np.arange(self.height) * stride + stride / 2 - 0.5 + self.grid_y = np.repeat(grid_y.reshape(1, self.height), self.num_maps, axis=0) + + def __call__(self, sample): + landmarks = sample['landmarks'] + landmarks = landmarks[-self.num_maps:] + + # Heatmap generation + exp_x = np.exp(-(self.grid_x - landmarks[:, 0].reshape(-1, 1)) ** 2 / self.double_sigma_pw2) + exp_y = np.exp(-(self.grid_y - landmarks[:, 1].reshape(-1, 1)) ** 2 / self.double_sigma_pw2) + heatmaps = np.matmul(exp_y.reshape(self.num_maps, self.height, 1), exp_x.reshape(self.num_maps, 1, self.width)) + + if self.norm: + heatmaps = heatmaps/self.doublepi_sigma_pw2 + + sample['heatmap2D'] = heatmaps + return sample diff --git a/SPIGA/spiga/data/loaders/augmentors/landmarks.py b/SPIGA/spiga/data/loaders/augmentors/landmarks.py new file mode 100644 index 0000000000000000000000000000000000000000..f1d17dcf9b86bf183bfe974b305e5fc0f6ea6aab --- /dev/null +++ b/SPIGA/spiga/data/loaders/augmentors/landmarks.py @@ -0,0 +1,307 @@ +import random +import cv2 +import numpy as np +from PIL import Image +from torchvision import transforms + +# My libs +import spiga.data.loaders.augmentors.utils as dlu + + +class HorizontalFlipAug: + def __init__(self, ldm_flip_order, prob=0.5): + self.prob = prob + self.ldm_flip_order = ldm_flip_order + + def __call__(self, sample): + img = sample['image'] + landmarks = sample['landmarks'] + mask = sample['mask_ldm'] + vis = sample['visible'] + bbox = sample['bbox'] + + if random.random() < self.prob: + new_img = transforms.functional.hflip(img) + + lm_new_order = self.ldm_flip_order + new_landmarks = landmarks[lm_new_order] + new_landmarks = (new_landmarks - (img.size[0], 0)) * (-1, 1) + new_mask = mask[lm_new_order] + new_vis = vis[lm_new_order] + + x, y, w, h = bbox + new_x = img.size[0] - x - w + new_bbox = np.array((new_x, y, w, h)) + + sample['image'] = new_img + sample['landmarks'] = new_landmarks + sample['mask_ldm'] = new_mask + sample['visible'] = new_vis + sample['bbox'] = new_bbox + + return sample + + +class GeometryBaseAug: + + def __call__(self, sample): + raise NotImplementedError('Inheritance __call__ not defined') + + def map_affine_transformation(self, sample, affine_transf, new_size=None): + sample['image'] = self._image_affine_trans(sample['image'], affine_transf, new_size) + sample['bbox'] = self._bbox_affine_trans(sample['bbox'], affine_transf) + if 'landmarks' in sample.keys(): + sample['landmarks'] = self._landmarks_affine_trans(sample['landmarks'], affine_transf) + return sample + + def clean_outbbox_landmarks(self, shape, landmarks, mask): + filter_x1 = landmarks[:, 0] >= shape[0] + filter_x2 = landmarks[:, 0] < (shape[0] + shape[2]) + filter_x = np.logical_and(filter_x1,filter_x2) + + filter_y1 = landmarks[:, 1] >= shape[1] + filter_y2 = landmarks[:, 1] < (shape[1] + shape[3]) + filter_y = np.logical_and(filter_y1, filter_y2) + + filter_bbox = np.logical_and(filter_x, filter_y) + new_mask = mask*filter_bbox + new_landmarks = (landmarks.T * new_mask).T + new_landmarks = new_landmarks.astype(int).astype(float) + return new_mask, new_landmarks + + def _image_affine_trans(self, image, affine_transf, new_size=None): + + if not new_size: + new_size = image.size + + inv_affine_transf = dlu.get_inverse_transf(affine_transf) + new_image = image.transform(new_size, Image.AFFINE, inv_affine_transf.flatten()) + return new_image + + def _bbox_affine_trans(self, bbox, affine_transf): + + x, y, w, h = bbox + images_bb = [] + for point in ([x, y, 1], [x + w, y, 1], + [x, y + h, 1], [x + w, y + h, 1]): + images_bb.append(affine_transf.dot(point)) + images_bb = np.array(images_bb) + + new_corner0 = np.min(images_bb, axis=0) + new_corner1 = np.max(images_bb, axis=0) + + new_x, new_y = new_corner0 + new_w, new_h = new_corner1 - new_corner0 + new_bbox = np.array((new_x, new_y, new_w, new_h)) + return new_bbox + + def _landmarks_affine_trans(self, landmarks, affine_transf): + + homog_landmarks = dlu.affine2homogeneous(landmarks) + new_landmarks = affine_transf.dot(homog_landmarks.T).T + return new_landmarks + + +class RSTAug(GeometryBaseAug): + + def __init__(self, angle_range=45., scale_min=-0.15, scale_max=0.15, trl_ratio=0.05): + self.scale_max = scale_max + self.scale_min = scale_min + self.angle_range = angle_range + self.trl_ratio = trl_ratio + + def __call__(self, sample): + x, y, w, h = sample['bbox'] + + x0, y0 = x + w/2, y + h/2 # center of the face, which will be the center of the rotation + + # Bbox translation + rnd_Tx = np.random.uniform(-self.trl_ratio, self.trl_ratio) * w + rnd_Ty = np.random.uniform(-self.trl_ratio, self.trl_ratio) * h + sample['bbox'][0] += rnd_Tx + sample['bbox'][1] += rnd_Ty + + scale = 1 + np.random.uniform(self.scale_min, self.scale_max) + angle = np.random.uniform(-self.angle_range, self.angle_range) + + similarity = dlu.get_similarity_matrix(angle, scale, center=(x0, y0)) + new_sample = self.map_affine_transformation(sample, similarity) + return new_sample + + +class TargetCropAug(GeometryBaseAug): + def __init__(self, img_new_size=128, map_new_size=128, target_dist=1.3): + + self.target_dist = target_dist + self.new_size_x, self.new_size_y = self._convert_shapes(img_new_size) + self.map_size_x, self.map_size_y = self._convert_shapes(map_new_size) + self.img2map_scale = False + + # Mismatch between img shape and featuremap shape + if self.map_size_x != self.new_size_x or self.map_size_y != self.new_size_y: + self.img2map_scale = True + self.map_scale_x = self.map_size_x / self.new_size_x + self.map_scale_y = self.map_size_y / self.new_size_y + self.map_scale_xx = self.map_scale_x * self.map_scale_x + self.map_scale_xy = self.map_scale_x * self.map_scale_y + self.map_scale_yy = self.map_scale_y * self.map_scale_y + + def _convert_shapes(self, new_size): + if isinstance(new_size, (tuple, list)): + new_size_x = new_size[0] + new_size_y = new_size[1] + else: + new_size_x = new_size + new_size_y = new_size + return new_size_x, new_size_y + + def __call__(self, sample): + x, y, w, h = sample['bbox'] + # we enlarge the area taken around the bounding box + # it is neccesary to change the botton left point of the bounding box + # according to the previous enlargement. Note this will NOT be the new + # bounding box! + # We return square images, which is neccesary since + # all the images must have the same size in order to form batches + side = max(w, h) * self.target_dist + x -= (side - w) / 2 + y -= (side - h) / 2 + + # center of the enlarged bounding box + x0, y0 = x + side/2, y + side/2 + # homothety factor, chosen so the new horizontal dimension will + # coincide with new_size + mu_x = self.new_size_x / side + mu_y = self.new_size_y / side + + # new_w, new_h = new_size, int(h * mu) + new_w = self.new_size_x + new_h = self.new_size_y + new_x0, new_y0 = new_w / 2, new_h / 2 + + # dilatation + translation + affine_transf = np.array([[mu_x, 0, new_x0 - mu_x * x0], + [0, mu_y, new_y0 - mu_y * y0]]) + + sample = self.map_affine_transformation(sample, affine_transf,(new_w, new_h)) + if 'landmarks' in sample.keys(): + img_shape = np.array([0, 0, self.new_size_x, self.new_size_y]) + sample['landmarks_float'] = sample['landmarks'] + sample['mask_ldm_float'] = sample['mask_ldm'] + sample['landmarks'] = np.round(sample['landmarks']) + sample['mask_ldm'], sample['landmarks'] = self.clean_outbbox_landmarks(img_shape, sample['landmarks'], + sample['mask_ldm']) + + if self.img2map_scale: + sample = self._rescale_map(sample) + return sample + + def _rescale_map(self, sample): + + # Rescale + lnd_float = sample['landmarks_float'] + lnd_float[:, 0] = self.map_scale_x * lnd_float[:, 0] + lnd_float[:, 1] = self.map_scale_y * lnd_float[:, 1] + + # Filter landmarks + lnd = np.round(lnd_float) + filter_x = lnd[:, 0] >= self.map_size_x + filter_y = lnd[:, 1] >= self.map_size_y + lnd[filter_x] = self.map_size_x - 1 + lnd[filter_y] = self.map_size_y - 1 + new_lnd = (lnd.T * sample['mask_ldm']).T + new_lnd = new_lnd.astype(int).astype(float) + + sample['landmarks_float'] = lnd_float + sample['landmarks'] = new_lnd + sample['img2map_scale'] = [self.map_scale_x, self.map_scale_y] + return sample + + + +class OcclusionAug: + def __init__(self, min_length=0.1, max_length=0.4, num_maps=1): + self.min_length = min_length + self.max_length = max_length + self.num_maps = num_maps + + def __call__(self, sample): + x, y, w, h = sample['bbox'] + image = sample['image'] + landmarks = sample['landmarks'] + vis = sample['visible'] + + min_ratio = self.min_length + max_ratio = self.max_length + rnd_width = np.random.randint(int(w * min_ratio), int(w * max_ratio)) + rnd_height = np.random.randint(int(h * min_ratio), int(h * max_ratio)) + + # (xi, yi) and (xf, yf) are, respectively, the lower left points of the + # occlusion rectangle and the upper right point. + xi = int(x + np.random.randint(0, w - rnd_width)) + xf = int(xi + rnd_width) + yi = int(y + np.random.randint(0, h - rnd_height)) + yf = int(yi + rnd_height) + + pixels = np.array(image) + pixels[yi:yf, xi:xf, :] = np.random.uniform(0, 255, size=3) + image = Image.fromarray(pixels) + sample['image'] = image + + # Update visibilities + filter_x1 = landmarks[:, 0] >= xi + filter_x2 = landmarks[:, 0] < xf + filter_x = np.logical_and(filter_x1, filter_x2) + + filter_y1 = landmarks[:, 1] >= yi + filter_y2 = landmarks[:, 1] < yf + filter_y = np.logical_and(filter_y1, filter_y2) + + filter_novis = np.logical_and(filter_x, filter_y) + filter_vis = np.logical_not(filter_novis) + sample['visible'] = vis * filter_vis + return sample + + +class LightingAug: + def __init__(self, hsv_range_min=(-0.5, -0.5, -0.5), hsv_range_max=(0.5, 0.5, 0.5)): + self.hsv_range_min = hsv_range_min + self.hsv_range_max = hsv_range_max + + def __call__(self, sample): + # Convert to HSV colorspace from RGB colorspace + image = np.array(sample['image']) + hsv = cv2.cvtColor(image, cv2.COLOR_RGB2HSV) + + # Generate new random values + H = 1 + np.random.uniform(self.hsv_range_min[0], self.hsv_range_max[0]) + S = 1 + np.random.uniform(self.hsv_range_min[1], self.hsv_range_max[1]) + V = 1 + np.random.uniform(self.hsv_range_min[2], self.hsv_range_max[2]) + hsv[:, :, 0] = np.clip(H*hsv[:, :, 0], 0, 179) + hsv[:, :, 1] = np.clip(S*hsv[:, :, 1], 0, 255) + hsv[:, :, 2] = np.clip(V*hsv[:, :, 2], 0, 255) + # Convert back to BGR colorspace + image = cv2.cvtColor(hsv, cv2.COLOR_HSV2RGB) + sample['image'] = Image.fromarray(image) + + return sample + + +class BlurAug: + def __init__(self, blur_prob=0.5, blur_kernel_range=(0, 2)): + self.blur_prob = blur_prob + self.kernel_range = blur_kernel_range + + def __call__(self, sample): + # Smooth image + image = np.array(sample['image']) + if np.random.uniform(0.0, 1.0) < self.blur_prob: + kernel = np.random.random_integers(self.kernel_range[0], self.kernel_range[1]) * 2 + 1 + image = cv2.GaussianBlur(image, (kernel, kernel), 0, 0) + sample['image'] = Image.fromarray(image) + + return sample + + + + diff --git a/SPIGA/spiga/data/loaders/augmentors/modern_posit.py b/SPIGA/spiga/data/loaders/augmentors/modern_posit.py new file mode 100644 index 0000000000000000000000000000000000000000..34042c80ccfa78b92c4a1a59c9053d4ed3ee5a65 --- /dev/null +++ b/SPIGA/spiga/data/loaders/augmentors/modern_posit.py @@ -0,0 +1,197 @@ +import os +import pkg_resources +import numpy as np +import cv2 + +# My libs +from spiga.data.loaders.augmentors.utils import rotation_matrix_to_euler + +# Model file nomenclature +model_file_dft = pkg_resources.resource_filename('spiga', 'data/models3D') + '/mean_face_3D_{num_ldm}.txt' + + +class PositPose: + + def __init__(self, ldm_ids, focal_ratio=1, selected_ids=None, max_iter=100, + fix_bbox=True, model_file=model_file_dft): + + # Load 3D face model + model3d_world, model3d_ids = self._load_world_shape(ldm_ids, model_file) + + # Generate id mask to pick only the robust landmarks for posit + if selected_ids is None: + model3d_mask = np.ones(len(ldm_ids)) + else: + model3d_mask = np.zeros(len(ldm_ids)) + for index, posit_id in enumerate(model3d_ids): + if posit_id in selected_ids: + model3d_mask[index] = 1 + + self.ldm_ids = ldm_ids # Ids from the database + self.model3d_world = model3d_world # Model data + self.model3d_ids = model3d_ids # Model ids + self.model3d_mask = model3d_mask # Model mask ids + self.max_iter = max_iter # Refinement iterations + self.focal_ratio = focal_ratio # Camera matrix focal length ratio + self.fix_bbox = fix_bbox # Camera matrix centered on image (False to centered on bbox) + + def __call__(self, sample): + + landmarks = sample['landmarks'] + mask = sample['mask_ldm'] + + # Camera matrix + img_shape = np.array(sample['image'].shape)[0:2] + if 'img2map_scale' in sample.keys(): + img_shape = img_shape * sample['img2map_scale'] + + if self.fix_bbox: + img_bbox = [0, 0, img_shape[1], img_shape[0]] # Shapes given are inverted (y,x) + cam_matrix = self._camera_matrix(img_bbox) + else: + bbox = sample['bbox'] # Scale error when ftshape and img_shape mismatch + cam_matrix = self._camera_matrix(bbox) + + # Save intrinsic matrix and 3D model landmarks + sample['cam_matrix'] = cam_matrix + sample['model3d'] = self.model3d_world + + world_pts, image_pts = self._set_correspondences(landmarks, mask) + + if image_pts.shape[0] < 4: + print('POSIT does not work without landmarks') + rot_matrix, trl_matrix = np.eye(3, dtype=float), np.array([0, 0, 0]) + else: + rot_matrix, trl_matrix = self._modern_posit(world_pts, image_pts, cam_matrix) + + euler = rotation_matrix_to_euler(rot_matrix) + sample['pose'] = np.array([euler[0], euler[1], euler[2], trl_matrix[0], trl_matrix[1], trl_matrix[2]]) + sample['model3d_proj'] = self._project_points(rot_matrix, trl_matrix, cam_matrix, norm=img_shape) + return sample + + def _load_world_shape(self, ldm_ids, model_file): + return load_world_shape(ldm_ids, model_file=model_file) + + def _camera_matrix(self, bbox): + focal_length_x = bbox[2] * self.focal_ratio + focal_length_y = bbox[3] * self.focal_ratio + face_center = (bbox[0] + (bbox[2] * 0.5)), (bbox[1] + (bbox[3] * 0.5)) + + cam_matrix = np.array([[focal_length_x, 0, face_center[0]], + [0, focal_length_y, face_center[1]], + [0, 0, 1]]) + return cam_matrix + + def _set_correspondences(self, landmarks, mask): + # Correspondences using labelled and robust landmarks + img_mask = np.logical_and(mask, self.model3d_mask) + img_mask = img_mask.astype(bool) + + image_pts = landmarks[img_mask] + world_pts = self.model3d_world[img_mask] + return world_pts, image_pts + + def _modern_posit(self, world_pts, image_pts, cam_matrix): + return modern_posit(world_pts, image_pts, cam_matrix, self.max_iter) + + def _project_points(self, rot, trl, cam_matrix, norm=None): + # Perspective projection model + trl = np.expand_dims(trl, 1) + extrinsics = np.concatenate((rot, trl), 1) + proj_matrix = np.matmul(cam_matrix, extrinsics) + + # Homogeneous landmarks + pts = self.model3d_world + ones = np.ones(pts.shape[0]) + ones = np.expand_dims(ones, 1) + pts_hom = np.concatenate((pts, ones), 1) + + # Project landmarks + pts_proj = np.matmul(proj_matrix, pts_hom.T).T + pts_proj = pts_proj / np.expand_dims(pts_proj[:, 2], 1) # Lambda = 1 + + if norm is not None: + pts_proj[:, 0] /= norm[0] + pts_proj[:, 1] /= norm[1] + return pts_proj[:, :-1] + + +def load_world_shape(db_landmarks, model_file=model_file_dft): + + # Load 3D mean face coordinates + num_ldm = len(db_landmarks) + filename = model_file.format(num_ldm=num_ldm) + if not os.path.exists(filename): + raise ValueError('No 3D model find for %i landmarks' % num_ldm) + + posit_landmarks = np.genfromtxt(filename, delimiter='|', dtype=int, usecols=0).tolist() + mean_face_3D = np.genfromtxt(filename, delimiter='|', dtype=(float, float, float), usecols=(1, 2, 3)).tolist() + world_all = len(mean_face_3D)*[None] + index_all = len(mean_face_3D)*[None] + + for cont, elem in enumerate(mean_face_3D): + pt3d = [elem[2], -elem[0], -elem[1]] + lnd_idx = db_landmarks.index(posit_landmarks[cont]) + world_all[lnd_idx] = pt3d + index_all[lnd_idx] = posit_landmarks[cont] + + return np.array(world_all), np.array(index_all) + + +def modern_posit(world_pts, image_pts, cam_matrix, max_iters): + # Homogeneous world points + num_landmarks = image_pts.shape[0] + one = np.ones((num_landmarks, 1)) + A = np.concatenate((world_pts, one), axis=1) + B = np.linalg.pinv(A) + + # Normalize image points + focal_length = cam_matrix[0,0] + img_center = (cam_matrix[0,2], cam_matrix[1,2]) + centered_pts = np.zeros((num_landmarks,2)) + centered_pts[:,0] = (image_pts[:,0]-img_center[0])/focal_length + centered_pts[:,1] = (image_pts[:,1]-img_center[1])/focal_length + Ui = centered_pts[:,0] + Vi = centered_pts[:,1] + + # POSIT loop + Tx, Ty, Tz = 0.0, 0.0, 0.0 + r1, r2, r3 = [0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0] + for iter in range(0, max_iters): + I = np.dot(B,Ui) + J = np.dot(B,Vi) + + # Estimate translation vector and rotation matrix + normI = 1.0 / np.sqrt(I[0] * I[0] + I[1] * I[1] + I[2] * I[2]) + normJ = 1.0 / np.sqrt(J[0] * J[0] + J[1] * J[1] + J[2] * J[2]) + Tz = np.sqrt(normI * normJ) # geometric average instead of arithmetic average of classicPosit + r1N = I*Tz + r2N = J*Tz + r1 = r1N[0:3] + r2 = r2N[0:3] + r1 = np.clip(r1, -1, 1) + r2 = np.clip(r2, -1, 1) + r3 = np.cross(r1,r2) + r3T = np.concatenate((r3, [Tz]), axis=0) + Tx = r1N[3] + Ty = r2N[3] + + # Compute epsilon, update Ui and Vi and check convergence + eps = np.dot(A, r3T)/Tz + oldUi = Ui + oldVi = Vi + Ui = np.multiply(eps, centered_pts[:,0]) + Vi = np.multiply(eps, centered_pts[:,1]) + deltaUi = Ui - oldUi + deltaVi = Vi - oldVi + delta = focal_length * focal_length * (np.dot(np.transpose(deltaUi), deltaUi) + np.dot(np.transpose(deltaVi), deltaVi)) + if iter > 0 and delta < 0.01: # converged + break + + rot_matrix = np.array([np.transpose(r1), np.transpose(r2), np.transpose(r3)]) + trl_matrix = np.array([Tx, Ty, Tz]) + # Convert to the nearest orthogonal rotation matrix + w, u, vt = cv2.SVDecomp(rot_matrix) # R = U*D*Vt + rot_matrix = np.matmul(np.matmul(u, np.eye(3, dtype=float)), vt) + return rot_matrix, trl_matrix + diff --git a/SPIGA/spiga/data/loaders/augmentors/utils.py b/SPIGA/spiga/data/loaders/augmentors/utils.py new file mode 100644 index 0000000000000000000000000000000000000000..30fcc012790a7bb984dc8ceefbeedc2b8a234465 --- /dev/null +++ b/SPIGA/spiga/data/loaders/augmentors/utils.py @@ -0,0 +1,147 @@ +import numpy as np + + +def affine2homogeneous(points): + '''Returns the points completed with a new last coordinate + equal to 1 + Arguments + --------- + points: np.array of shape (num_points, dim) + Returns + ------- + hpoints: np.array of shape (num_points, dim + 1), + of the points completed with ones''' + + num_points = points.shape[0] + hpoints = np.hstack( + (points, np.repeat(1, num_points).reshape(num_points, 1))) + return hpoints + + +def get_similarity_matrix(deg_angle, scale, center): + '''Similarity matrix. + Arguments: + --------- + deg_angle: rotation angle in degrees + scale: factor scale + center: coordinates of the rotation center + + Returns: + ------- + matrix: (2, 3) numpy array representing the + similarity matrix. + ''' + x0, y0 = center + angle = np.radians(deg_angle) + + matrix = np.zeros((2, 3)) + matrix[0:2, 0:2] = [[np.cos(angle), -np.sin(angle)], + [np.sin(angle), np.cos(angle)]] + matrix[0: 2, 0: 2] *= scale + + matrix[:, 2] = [(1 - scale * np.cos(angle)) * x0 + + scale * np.sin(angle) * y0, + -scale * np.sin(angle) * x0 + + (1 - scale * np.cos(angle)) * y0] + return matrix + + +def get_inverse_similarity_matrix(deg_angle, scale, center): + '''Returns the inverse of the affine similarity + Arguments + --------- + deg_angle: angle in degrees of the rotation + center: iterable of two components (x0, y0), + center of the rotation + scale: float, scale factor + Returns + ------- + matrix: np.array of shape (2, 3) with the coordinates of + the inverse of the similarity''' + + x0, y0 = center + angle = np.radians(deg_angle) + inv_scale = 1 / scale + matrix = np.zeros((2, 3)) + matrix[0:2, 0:2] = [[np.cos(angle), np.sin(angle)], + [-np.sin(angle), np.cos(angle)]] + matrix[0:2, 0:2] *= inv_scale + + matrix[:, 2] = [(1 - inv_scale * np.cos(angle)) * x0 - + inv_scale * np.sin(angle) * y0, + inv_scale * np.sin(angle) * x0 + + (1 - inv_scale * np.cos(angle)) * y0] + + return matrix + + +def get_inverse_transf(affine_transf): + A = affine_transf[0:2, 0:2] + b = affine_transf[:, 2] + + inv_A = np.linalg.inv(A) # we assume A invertible! + + inv_affine = np.zeros((2, 3)) + inv_affine[0:2, 0:2] = inv_A + inv_affine[:, 2] = -inv_A.dot(b) + + return inv_affine + + +def image2vect(image): + ''' + Input: + image[batch_size, num_channels, im_size_x, im_size_y] + Output: + vect[batch_size, num_channels, im_size_x*im_size_y] + ''' + vect = image.reshape(*image.shape[0:-2], -1) + return vect + + +def rotation_matrix_to_euler(rot_matrix): + # http://euclideanspace.com/maths/geometry/rotations/conversions/matrixToEuler/index.htm + a00, a01, a02 = rot_matrix[0, 0], rot_matrix[0, 1], rot_matrix[0, 2] + a10, a11, a12 = rot_matrix[1, 0], rot_matrix[1, 1], rot_matrix[1, 2] + a20, a21, a22 = rot_matrix[2, 0], rot_matrix[2, 1], rot_matrix[2, 2] + if abs(1.0 - a10) <= np.finfo(float).eps: # singularity at north pole / special case a10 == 1 + yaw = np.arctan2(a02, a22) + pitch = np.pi/2.0 + roll = 0 + elif abs(-1.0 - a10) <= np.finfo(float).eps: # singularity at south pole / special case a10 == -1 + yaw = np.arctan2(a02, a22) + pitch = -np.pi/2.0 + roll = 0 + else: # standard case + yaw = np.arctan2(-a20, a00) + pitch = np.arcsin(a10) + roll = np.arctan2(-a12, a11) + # Convert to degrees + euler = np.array([yaw, pitch, roll])*(180.0/np.pi) + # Change coordinates system + euler = np.array([(-euler[0])+90, -euler[1], (-euler[2])-90]) + if euler[0] > 180: euler[0] -= 360 + elif euler[0] < -180: euler[0] += 360 + if euler[1] > 180: euler[1] -= 360 + elif euler[1] < -180: euler[1] += 360 + if euler[2] > 180: euler[2] -= 360 + elif euler[2] < -180: euler[2] += 360 + return euler + + +def euler_to_rotation_matrix(headpose): + # http://euclideanspace.com/maths/geometry/rotations/conversions/eulerToMatrix/index.htm + # Change coordinates system + euler = np.array([-(headpose[0]-90), -headpose[1], -(headpose[2]+90)]) + # Convert to radians + rad = euler*(np.pi/180.0) + cy = np.cos(rad[0]) + sy = np.sin(rad[0]) + cp = np.cos(rad[1]) + sp = np.sin(rad[1]) + cr = np.cos(rad[2]) + sr = np.sin(rad[2]) + Ry = np.array([[cy, 0.0, sy], [0.0, 1.0, 0.0], [-sy, 0.0, cy]]) # yaw + Rp = np.array([[cp, -sp, 0.0], [sp, cp, 0.0], [0.0, 0.0, 1.0]]) # pitch + Rr = np.array([[1.0, 0.0, 0.0], [0.0, cr, -sr], [0.0, sr, cr]]) # roll + return np.matmul(np.matmul(Ry, Rp), Rr) diff --git a/SPIGA/spiga/data/loaders/dataloader.py b/SPIGA/spiga/data/loaders/dataloader.py new file mode 100644 index 0000000000000000000000000000000000000000..f942510916fffb132762ab5e41d5ac96d6b54e7a --- /dev/null +++ b/SPIGA/spiga/data/loaders/dataloader.py @@ -0,0 +1,41 @@ +from torch.utils.data import DataLoader +from torch.utils.data.distributed import DistributedSampler + +import spiga.data.loaders.alignments as zoo_alignments + +zoos = [zoo_alignments] + + +def get_dataset(data_config, pretreat=None, debug=False): + + for zoo in zoos: + dataset = zoo.get_dataset(data_config, pretreat=pretreat, debug=debug) + if dataset is not None: + return dataset + raise NotImplementedError('Dataset not available') + + +def get_dataloader(batch_size, data_config, pretreat=None, sampler_cfg=None, debug=False): + + dataset = get_dataset(data_config, pretreat=pretreat, debug=debug) + + if (len(dataset) % batch_size) == 1 and data_config.shuffle == True: + drop_last_batch = True + else: + drop_last_batch = False + + shuffle = data_config.shuffle + sampler = None + if sampler_cfg is not None: + sampler = DistributedSampler(dataset, num_replicas=sampler_cfg.world_size, rank=sampler_cfg.rank) + shuffle = False + + dataloader = DataLoader(dataset, + batch_size=batch_size, + shuffle=shuffle, + num_workers=data_config.num_workers, + pin_memory=True, + drop_last=drop_last_batch, + sampler=sampler) + + return dataloader, dataset diff --git a/SPIGA/spiga/data/loaders/dl_config.py b/SPIGA/spiga/data/loaders/dl_config.py new file mode 100644 index 0000000000000000000000000000000000000000..962f883d6fb299d66b454366cbd906e2ae32d8d1 --- /dev/null +++ b/SPIGA/spiga/data/loaders/dl_config.py @@ -0,0 +1,170 @@ +import os +import json +import pkg_resources +from collections import OrderedDict + +# Default data paths +db_img_path = pkg_resources.resource_filename('spiga', 'data/databases') +db_anns_path = pkg_resources.resource_filename('spiga', 'data/annotations') + "/{database}/{file_name}.json" + +class AlignConfig: + + def __init__(self, database_name, mode='train'): + # Dataset + self.database_name = database_name + self.working_mode = mode + self.database = None # Set at self._update_database() + self.anns_file = None # Set at self._update_database() + self.image_dir = None # Set at self._update_database() + self._update_database() + self.image_size = (256, 256) + self.ftmap_size = (256, 256) + + # Dataloaders + self.ids = None # List of a subset if need it + self.shuffle = True # Shuffle samples + self.num_workers = 4 # Threads + + # Posit + self.generate_pose = True # Generate pose parameters from landmarks + self.focal_ratio = 1.5 # Camera matrix focal length ratio + self.posit_max_iter = 100 # Refinement iterations + + # Subset of robust ids in the 3D model to use in posit. + # 'None' to use all the available model landmarks. + self.posit_ids = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, + 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24] + + # Data augmentation + # Control augmentations with the following list, crop to self.img_size is mandatory, check target_dist param. + if mode == 'train': + self.aug_names = ['flip', 'rotate_scale', 'occlusion', 'lighting', 'blur'] + else: + self.aug_names = [] + self.shuffle = False + + # Flip + self.hflip_prob = 0.5 + # Rotation + self.angle_range = 45. + # Scale + self.scale_max = 0.15 + self.scale_min = -0.15 + # Translation + self.trl_ratio = 0.05 # Translation augmentation + # Crop target rescale + self.target_dist = 1.6 # Target distance zoom in/out around face. Default: 1. + # Occlusion + self.occluded_max_len = 0.4 + self.occluded_min_len = 0.1 + self.occluded_covar_ratio = 2.25**0.5 + # Lighting + self.hsv_range_min = [-0.5, -0.5, -0.5] + self.hsv_range_max = [0.5, 0.5, 0.5] + # Blur + self.blur_prob = 0.5 + self.blur_kernel_range = [0, 2] + + # Heatmaps 2D + self.sigma2D = 1.5 + self.heatmap2D_norm = False + + # Boundaries + self.sigmaBD = 1 + + def update(self, params_dict): + state_dict = self.state_dict() + for k, v in params_dict.items(): + if k in state_dict or hasattr(self, k): + setattr(self, k, v) + else: + Warning('Unknown option: {}: {}'.format(k, v)) + self._update_database() + + def state_dict(self, tojson=False): + state_dict = OrderedDict() + for k in self.__dict__.keys(): + if not k.startswith('_'): + if tojson and k in ['database']: + continue + state_dict[k] = getattr(self, k) + return state_dict + + def _update_database(self): + self.database = DatabaseStruct(self.database_name) + self.anns_file = db_anns_path.format(database=self.database_name, file_name=self.working_mode) + self.image_dir = self._get_imgdb_path() + + def _get_imgdb_path(self): + img_dir = None + if self.database_name in ['300wpublic', '300wprivate']: + img_dir = db_img_path + '/300w/' + elif self.database_name in ['aflw19', 'merlrav']: + img_dir = db_img_path + '/aflw/data/' + elif self.database_name in ['cofw', 'cofw68']: + img_dir = db_img_path + '/cofw/' + elif self.database_name in ['wflw']: + img_dir = db_img_path + '/wflw/' + return img_dir + + def __str__(self): + state_dict = self.state_dict() + text = 'Dataloader {\n' + for k, v in state_dict.items(): + if isinstance(v, DatabaseStruct): + text += '\t{}: {}'.format(k, str(v).expandtabs(12)) + else: + text += '\t{}: {}\n'.format(k, v) + text += '\t}\n' + return text + + +class DatabaseStruct: + + def __init__(self, database_name): + + self.name = database_name + self.ldm_ids, self.ldm_flip_order, self.ldm_edges_matrix = self._get_database_specifics() + self.num_landmarks = len(self.ldm_ids) + self.num_edges = len(self.ldm_edges_matrix[0])-1 + self.fields = ['imgpath', 'bbox', 'headpose', 'ids', 'landmarks', 'visible'] + + def _get_database_specifics(self): + '''Returns specifics ids and horizontal flip reorder''' + + database_name = self.name + db_info_file = db_anns_path.format(database=database_name, file_name='db_info') + ldm_edges_matrix = None + + if os.path.exists(db_info_file): + with open(db_info_file) as jsonfile: + db_info = json.load(jsonfile) + + ldm_ids = db_info['ldm_ids'] + ldm_flip_order = db_info['ldm_flip_order'] + if 'ldm_edges_matrix' in db_info.keys(): + ldm_edges_matrix = db_info['ldm_edges_matrix'] + + else: + raise ValueError('Database ' + database_name + 'specifics not defined. Missing db_info.json') + + return ldm_ids, ldm_flip_order, ldm_edges_matrix + + def state_dict(self): + state_dict = OrderedDict() + for k in self.__dict__.keys(): + if not k.startswith('_'): + state_dict[k] = getattr(self, k) + + return state_dict + + def __str__(self): + state_dict = self.state_dict() + text = 'Database {\n' + for k, v in state_dict.items(): + text += '\t{}: {}\n'.format(k, v) + text += '\t}\n' + return text + + + diff --git a/SPIGA/spiga/data/loaders/transforms.py b/SPIGA/spiga/data/loaders/transforms.py new file mode 100644 index 0000000000000000000000000000000000000000..6371657516cd766c363fd7ea51bf978a65c70376 --- /dev/null +++ b/SPIGA/spiga/data/loaders/transforms.py @@ -0,0 +1,84 @@ +import cv2 +import numpy as np +import torch + +from spiga.data.loaders.augmentors.modern_posit import PositPose +from spiga.data.loaders.augmentors.heatmaps import Heatmaps +from spiga.data.loaders.augmentors.boundary import AddBoundary +from spiga.data.loaders.augmentors.landmarks import HorizontalFlipAug, RSTAug, OcclusionAug, \ + LightingAug, BlurAug, TargetCropAug + + +def get_transformers(data_config): + + # Data augmentation + aug_names = data_config.aug_names + augmentors = [] + + if 'flip' in aug_names: + augmentors.append(HorizontalFlipAug(data_config.database.ldm_flip_order, data_config.hflip_prob)) + if 'rotate_scale' in aug_names: + augmentors.append(RSTAug(data_config.angle_range, data_config.scale_min, + data_config.scale_max, data_config.trl_ratio)) + if 'occlusion' in aug_names: + augmentors.append(OcclusionAug(data_config.occluded_min_len, + data_config.occluded_max_len, + data_config.database.num_landmarks)) + if 'lighting' in aug_names: + augmentors.append(LightingAug(data_config.hsv_range_min, data_config.hsv_range_max)) + if 'blur' in aug_names: + augmentors.append(BlurAug(data_config.blur_prob, data_config.blur_kernel_range)) + + # Crop mandatory + augmentors.append(TargetCropAug(data_config.image_size, data_config.ftmap_size, data_config.target_dist)) + # Opencv style + augmentors.append(ToOpencv()) + + # Gaussian heatmaps + if 'heatmaps2D' in aug_names: + augmentors.append(Heatmaps(data_config.database.num_landmarks, data_config.ftmap_size, + data_config.sigma2D, norm=data_config.heatmap2D_norm)) + + if 'boundaries' in aug_names: + augmentors.append(AddBoundary(num_landmarks=data_config.database.num_landmarks, + map_size=data_config.ftmap_size, + sigma=data_config.sigmaBD)) + # Pose generator + if data_config.generate_pose: + augmentors.append(PositPose(data_config.database.ldm_ids, + focal_ratio=data_config.focal_ratio, + selected_ids=data_config.posit_ids, + max_iter=data_config.posit_max_iter)) + + return augmentors + + +class ToOpencv: + def __call__(self, sample): + # Convert in a numpy array and change to GBR + image = np.array(sample['image']) + image = cv2.cvtColor(image, cv2.COLOR_RGB2BGR) + sample['image'] = image + return sample + + +class TargetCrop(TargetCropAug): + def __init__(self, crop_size=256, target_dist=1.6): + super(TargetCrop, self).__init__(crop_size, crop_size, target_dist) + + +class AddModel3D(PositPose): + def __init__(self, ldm_ids, ftmap_size=(256, 256), focal_ratio=1.5, totensor=False): + super(AddModel3D, self).__init__(ldm_ids, focal_ratio=focal_ratio) + img_bbox = [0, 0, ftmap_size[1], ftmap_size[0]] # Shapes given are inverted (y,x) + self.cam_matrix = self._camera_matrix(img_bbox) + + if totensor: + self.cam_matrix = torch.tensor(self.cam_matrix, dtype=torch.float) + self.model3d_world = torch.tensor(self.model3d_world, dtype=torch.float) + + def __call__(self, sample={}): + # Save intrinsic matrix and 3D model landmarks + sample['cam_matrix'] = self.cam_matrix + sample['model3d'] = self.model3d_world + return sample diff --git a/SPIGA/spiga/data/models3D/__init__.py b/SPIGA/spiga/data/models3D/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/data/models3D/mean_face_3D_68.txt b/SPIGA/spiga/data/models3D/mean_face_3D_68.txt new file mode 100644 index 0000000000000000000000000000000000000000..5640bd0df65fcb268cbc78c5d0b3eba6221f78c7 --- /dev/null +++ b/SPIGA/spiga/data/models3D/mean_face_3D_68.txt @@ -0,0 +1,68 @@ +101|-0.71046061493|0.39334543762|-0.853184236267 +102|-0.685409656726|0.169750713576|-0.878623094747 +103|-0.607672440834|-0.0597969416711|-0.922355056609 +104|-0.545664962607|-0.262499453743|-0.920836599126 +105|-0.446214526601|-0.439045175771|-0.863139209 +106|-0.334435950087|-0.566049889292|-0.728913281016 +107|-0.236168305748|-0.653698223145|-0.585459059996 +108|-0.128307367184|-0.712045321067|-0.488221730877 +24|-0.00354849146401|-0.73799619898|-0.461364289002 +110|0.131199109787|-0.733135962679|-0.466262199442 +111|0.257373771199|-0.666487934012|-0.560781626341 +112|0.359823738861|-0.569594984479|-0.666664889106 +113|0.455878939364|-0.475272786995|-0.762199581604 +114|0.583151236654|-0.255441185628|-0.895445263128 +115|0.635035270608|-0.076593055883|-0.925024981148 +116|0.688562921266|0.127095701882|-0.90624669312 +117|0.711883056933|0.332170073984|-0.901990426153 +7|-0.406302776083|0.360389456414|-0.383328256737 +138|-0.34477414508|0.384294131116|-0.310253684249 +139|-0.261521910706|0.396020592391|-0.286645173372 +8|-0.160787895282|0.371046071664|-0.330243237009 +141|-0.245621576158|0.334421719594|-0.323105980143 +142|-0.328092143154|0.331973054751|-0.339942994735 +11|0.163880511996|0.34074733643|-0.314140711047 +144|0.250844605212|0.392490504074|-0.279030578851 +145|0.340770354713|0.378980645804|-0.285841921386 +12|0.432352000574|0.348665008376|-0.377158168878 +147|0.333467711264|0.328033806608|-0.318530865652 +148|0.246621391603|0.335053488011|-0.313137199532 +1|-0.552168877878|0.483792334207|-0.466456539274 +119|-0.459810924979|0.561780416181|-0.308160933539 +2|-0.360178576451|0.566290707558|-0.216753374881 +121|-0.249770054109|0.530336745189|-0.148694799479 +3|-0.101941089981|0.482471777751|-0.124216132105 +128|0.00843526194116|0.416310824525|-0.139142361862 +129|0.00731217835113|0.267155736618|-0.106471830332 +130|0.00190174006432|0.142359799355|-0.0544539305898 +17|0.0|0.0|0.0 +16|-0.118903311783|-0.0792784542251|-0.23553779698 +133|-0.0504300242939|-0.104665185108|-0.171210015652 +134|0.00312657092554|-0.111845126622|-0.154139340027 +135|0.0687543983424|-0.0995458563329|-0.173275169304 +18|0.148988810614|-0.0737848514841|-0.23851346235 +4|0.0979764884322|0.465935806416|-0.131673602172 +124|0.214281256931|0.497130488239|-0.135680573937 +5|0.373011222167|0.520379035113|-0.223000042464 +126|0.501607216527|0.500371303274|-0.31925158046 +6|0.57362522379|0.457842172776|-0.465084060802 +20|-0.2229832011|-0.277627584817|-0.354306324758 +150|-0.157062857603|-0.248737641674|-0.270218764688 +151|-0.0816354856174|-0.23618498428|-0.225237980338 +22|-0.00391577759471|-0.24499812323|-0.2126098208 +153|0.0629421066443|-0.230774971512|-0.208501270489 +154|0.135507933036|-0.240646328001|-0.235471195707 +21|0.240381217797|-0.283709533358|-0.332281891845 +156|0.143706630542|-0.329461104518|-0.283978333058 +157|0.084139951946|-0.355354733249|-0.256464077311 +23|0.00813704018925|-0.360357397837|-0.250423014186 +159|-0.0778260690655|-0.349041413147|-0.26966136614 +160|-0.157111645515|-0.311971743234|-0.322383820174 +161|-0.182660017757|-0.278377925956|-0.341170846656 +162|-0.075943475389|-0.283519721316|-0.270854173882 +163|-0.0026701322545|-0.286917503123|-0.254428375696 +164|0.0685062003389|-0.285630836758|-0.257845545665 +165|0.194170296105|-0.279641061937|-0.314605542849 +166|0.0689862474833|-0.288076969827|-0.258696545259 +167|-0.00273913414372|-0.28915723747|-0.25622946708 +168|-0.0766989697362|-0.286311968999|-0.273027820051 diff --git a/SPIGA/spiga/data/models3D/mean_face_3D_98.txt b/SPIGA/spiga/data/models3D/mean_face_3D_98.txt new file mode 100644 index 0000000000000000000000000000000000000000..f5920400bffb6ecc8ae2afc39348ba63ba3805b1 --- /dev/null +++ b/SPIGA/spiga/data/models3D/mean_face_3D_98.txt @@ -0,0 +1,98 @@ +100|-0.710460614932|0.393345437621|-0.853184236268 +101|-0.697935135807|0.281548075586|-0.865903665506 +102|-0.685409656727|0.169750713576|-0.878623094748 +103|-0.646541048786|0.0549768859803|-0.90048907572 +104|-0.607672440835|-0.0597969416712|-0.92235505661 +105|-0.576668701754|-0.16114819775|-0.921595827864 +106|-0.545664962608|-0.262499453743|-0.920836599128 +107|-0.495939744597|-0.350772314723|-0.891987904048 +108|-0.446214526602|-0.439045175772|-0.863139209001 +109|-0.390325238349|-0.502547532515|-0.796026245014 +110|-0.334435950088|-0.566049889293|-0.728913281017 +111|-0.285302127936|-0.60987405623|-0.657186170535 +112|-0.236168305748|-0.653698223146|-0.585459059997 +113|-0.182237836481|-0.682871772143|-0.536840395466 +114|-0.128307367184|-0.712045321068|-0.488221730878 +115|-0.065927929287|-0.725020759991|-0.474793009911 +24|-0.00354849146405|-0.737996198981|-0.461364289002 +117|0.0638253091608|-0.735566080866|-0.463813244263 +118|0.131199109787|-0.73313596268|-0.466262199443 +119|0.194286440465|-0.699811948342|-0.513521912927 +120|0.257373771199|-0.666487934013|-0.560781626342 +121|0.308598755049|-0.61804145929|-0.613723257723 +122|0.359823738861|-0.569594984479|-0.666664889106 +123|0.407851339087|-0.522433885778|-0.714432235344 +124|0.455878939366|-0.475272786996|-0.762199581605 +125|0.519515088045|-0.365356986341|-0.828822422342 +126|0.583151236655|-0.255441185628|-0.89544526313 +127|0.609093253652|-0.166017120718|-0.910235122162 +128|0.635035270609|-0.0765930558831|-0.92502498115 +129|0.661799095895|0.0252513229862|-0.915635837119 +130|0.688562921268|0.127095701883|-0.906246693121 +131|0.700222989101|0.229632887961|-0.904118559673 +132|0.711883056935|0.332170073985|-0.901990426154 +1|-0.552168877879|0.483792334207|-0.466456539275 +134|-0.45981092498|0.561780416182|-0.30816093354 +2|-0.360178576451|0.566290707559|-0.216753374882 +136|-0.249770054109|0.53033674519|-0.148694799479 +3|-0.101941089981|0.482471777751|-0.124216132105 +138|-0.100790757462|0.429593539303|-0.13295377507 +139|-0.24861972159|0.477458506742|-0.157432442443 +140|-0.359028243932|0.513412469111|-0.225491017847 +141|-0.458660592461|0.508902177734|-0.316898576504 +4|0.0979764884324|0.465935806417|-0.131673602172 +143|0.214281256932|0.49713048824|-0.135680573937 +5|0.373011222167|0.520379035114|-0.223000042464 +145|0.501607216528|0.500371303275|-0.31925158046 +6|0.573625223791|0.457842172777|-0.465084060803 +147|0.500456884008|0.447493064827|-0.310513937496 +148|0.374161554686|0.467500796666|-0.231737685429 +149|0.215431589451|0.444252249792|-0.144418216902 +150|0.0991268209517|0.413057567969|-0.140411245136 +151|0.00843526194114|0.416310824526|-0.139142361862 +152|0.00731217835118|0.267155736618|-0.106471830333 +153|0.00190174006432|0.142359799356|-0.0544539305899 +17|0.0|0.0|0.0 +16|-0.118903311783|-0.0792784542252|-0.23553779698 +156|-0.0504300242939|-0.104665185108|-0.171210015652 +157|0.00312657092558|-0.111845126622|-0.154139340027 +158|0.0687543983424|-0.0995458563331|-0.173275169304 +18|0.148988810614|-0.0737848514843|-0.23851346235 +7|-0.406302776084|0.360389456414|-0.383328256738 +161|-0.34477414508|0.384294131116|-0.310253684249 +9|-0.303148027928|0.398970401478|-0.298449428843 +163|-0.261521910707|0.396020592392|-0.286645173373 +8|-0.160787895283|0.371046071665|-0.33024323701 +165|-0.245621576158|0.334421719595|-0.323105980144 +10|-0.286856859665|0.324384347457|-0.33152448747 +167|-0.328092143155|0.331973054752|-0.339942994736 +11|0.163880511996|0.340747336431|-0.314140711048 +169|0.250844605212|0.392490504075|-0.279030578852 +13|0.295807479997|0.39454861469|-0.282436250152 +171|0.340770354713|0.378980645804|-0.285841921386 +12|0.432352000574|0.348665008377|-0.377158168879 +173|0.333467711265|0.328033806608|-0.318530865652 +14|0.290044551442|0.322730607606|-0.315834032602 +175|0.246621391603|0.335053488012|-0.313137199533 +20|-0.2229832011|-0.277627584818|-0.354306324759 +177|-0.157062857603|-0.248737641675|-0.270218764688 +178|-0.0816354856176|-0.23618498428|-0.225237980339 +22|-0.00391577759461|-0.24499812323|-0.212609820801 +180|0.0629421066443|-0.230774971513|-0.20850127049 +181|0.135507933036|-0.240646328002|-0.235471195707 +21|0.240381217797|-0.283709533359|-0.332281891846 +183|0.143706630542|-0.329461104519|-0.283978333058 +184|0.0841399519463|-0.35535473325|-0.256464077312 +23|0.00813704018926|-0.360357397838|-0.250423014186 +186|-0.0778260690653|-0.349041413147|-0.269661366141 +187|-0.157111645515|-0.311971743235|-0.322383820174 +188|-0.182660017758|-0.278377925956|-0.341170846657 +189|-0.0759434753887|-0.283519721316|-0.270854173882 +190|-0.00267013225455|-0.286917503124|-0.254428375697 +191|0.068506200339|-0.285630836758|-0.257845545665 +192|0.194170296105|-0.279641061938|-0.31460554285 +193|0.0689862474834|-0.288076969827|-0.25869654526 +194|-0.00273913414368|-0.28915723747|-0.25622946708 +195|-0.0766989697367|-0.286311968999|-0.273027820052 +196|-0.291183407723|0.363024170951|-0.328919887677 +197|0.294656095888|0.353995131537|-0.31463990759 diff --git a/SPIGA/spiga/data/models3D/visualization.py b/SPIGA/spiga/data/models3D/visualization.py new file mode 100644 index 0000000000000000000000000000000000000000..49bf883d7194039d260ea1dfb70eecd2454c8fd1 --- /dev/null +++ b/SPIGA/spiga/data/models3D/visualization.py @@ -0,0 +1,37 @@ +import argparse +import numpy as np +import matplotlib.pyplot as plt + + +def main(): + # Input arguments control + pars = argparse.ArgumentParser(description='3D model visualization') + pars.add_argument('file', type=str, help='File txt path') + args = pars.parse_args() + visualize_3Dmodel(args.file) + + +def visualize_3Dmodel(input_file): + + with open(input_file) as f: + lines = f.readlines() + + model = [] + for line in lines: + line = line[:-1] # Remove \n + line_split = line.split('|') + values = np.array(line_split, dtype=float) + model.append(values) + + model = np.array(model) + model_xyz = model[:, 1:] + + # Show model + fig = plt.figure() + ax = fig.add_subplot(111, projection='3d') + ax.scatter(model_xyz[:, 0], model_xyz[:, 1], model_xyz[:, 2]+0.8) + plt.show() + + +if __name__ == '__main__': + main() diff --git a/SPIGA/spiga/data/readme.md b/SPIGA/spiga/data/readme.md new file mode 100644 index 0000000000000000000000000000000000000000..a30d1e2503c1f8a62d186dd183bdf769724e225d --- /dev/null +++ b/SPIGA/spiga/data/readme.md @@ -0,0 +1,72 @@ +# SPIGA: Dataloaders +Currently, the repository provides a pytorch based image dataloader implementation for the task of: +* **Facial Landmarks estimation**. +* **Headpose estimation**. +* **Facial landmarks visibilities**. + +The dataloader can be used for training or testing the networks and it includes general and +specifics data augmentation for each task, as it can be image partial occlusions +or headpose generation from facial landmarks. + +In addition, the framework provides a wide benchmark software in order to evaluate the +different task along the following databases: +* **WFLW**. +* **MERLRAV (AFLW 68)** +* **COFW68**. +* **300W Public, Private**. +
+ Coming soon... + +* AFLW, AFLW19, AFLW2000 (test only). +* Menpo and 3D Menpo. +* COFW. +* 300WLP +* 300W Masked + +
+ +***Note:*** All the callable files provide a detailed parser that describes the behaviour of +the program and their inputs. Please, check the operational modes by using the extension ```--help```. + +## Training/Testing +The dataloader structure can be found in ```./data/loaders/aligments.py``` and it can be +manually controlled by instantiating the class ```AlignmentsDataset()``` or by using +the ```data_config``` structure available in ```./data/loaders/dl_config.py```. + +Each image sample will follow the next configuration: +``` +sample = {'image': Data augmented crop image, + 'sample_idx': Image ID, + 'imgpath': Absolute path to raw image, + 'imgpath_local': Relative path to raw image, + 'ids_ldm': Landmarks ids, + 'bbox': Face bbox [x,y,w,h] (ref crop), + 'bbox_raw': Face bbox [x,y,w,h] (ref image), + 'landmarks': Augmented landmarks [[x1,y1], [x2,y2], ...] (ref crop) + 'visible': Visibilities [0,1, ...] (1 == Visible) + 'mask_ldm': Available landmarks anns [True, False, ...] <- len(ids_ldm) + 'headpose': Augmented POSIT headpose [yaw, pithc, roll] + } + +Extra features while debugging: +sample = { ... + 'landmarks_ori' = Ground truth landmarks before augmentation (ref image) + 'visible_ori' = Ground truth visibilities before augmentation + 'mask_ldm_ori' = Ground truth mask before augmentation + 'headpose_ori' = Ground truth headpose before augmentation (if available) + } +``` + +## Visualizers +The dataloader framework provides complementary visualizers to further understand the databases, +datasets and their difficulties: + +* ```./data/visualize/inspect_dataset.py``` +Focus on the database annotations and the data augmentations, which allows us to +understand the training, validation and test datasets. + +* ```./data/visualize/inspect_heatmaps.py``` +Extended visualizer version focus on understanding the heatmaps and boundaries features used for training. + +* ```./data/model3D/visualization.py``` +Visualize the rigid facial 3D models used by SPIGA to project the initial coordinates of the GAT regressor. diff --git a/SPIGA/spiga/data/visualize/__init__.py b/SPIGA/spiga/data/visualize/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/data/visualize/inspect_dataset.py b/SPIGA/spiga/data/visualize/inspect_dataset.py new file mode 100644 index 0000000000000000000000000000000000000000..2fac34324fa47f455e096644585a147400a19e53 --- /dev/null +++ b/SPIGA/spiga/data/visualize/inspect_dataset.py @@ -0,0 +1,181 @@ +import cv2 +import random +import numpy as np + +import spiga.data.loaders.dl_config as dl_cfg +import spiga.data.loaders.dataloader as dl +import spiga.data.visualize.plotting as plot + + +def inspect_parser(): + import argparse + pars = argparse.ArgumentParser(description='Data augmentation and dataset visualization. ' + 'Press Q to quit,' + 'N to visualize the next image' + ' and any other key to visualize the next default data.') + pars.add_argument('database', type=str, + choices=['wflw', '300wpublic', '300wprivate', 'cofw68', 'merlrav'], help='Database name') + pars.add_argument('-a', '--anns', type=str, default='train', help='Annotation type: test, train or valid') + pars.add_argument('-np', '--nopose', action='store_false', default=True, help='Avoid pose generation') + pars.add_argument('-c', '--clean', action='store_true', help='Process without data augmentation for train') + pars.add_argument('--shape', nargs='+', type=int, default=[256, 256], help='Image cropped shape (W,H)') + pars.add_argument('--img', nargs='+', type=int, default=None, help='Select specific image ids') + return pars.parse_args() + + +class DatasetInspector: + + def __init__(self, database, anns_type, data_aug=True, pose=True, image_shape=(256,256)): + + data_config = dl_cfg.AlignConfig(database, anns_type) + data_config.image_size = image_shape + data_config.ftmap_size = image_shape + data_config.generate_pose = pose + + if not data_aug: + data_config.aug_names = [] + + self.data_config = data_config + dataloader, dataset = dl.get_dataloader(1, data_config, debug=True) + self.dataset = dataset + self.dataloader = dataloader + self.colors_dft = {'lnd': (plot.GREEN, plot.RED), 'pose': (plot.BLUE, plot.GREEN, plot.RED)} + + def show_dataset(self, ids_list=None): + + if ids_list is None: + ids = self.get_idx(shuffle=self.data_config.shuffle) + else: + ids = ids_list + + for img_id in ids: + data_dict = self.dataset[img_id] + crop_imgs, full_img = self.plot_features(data_dict) + + # Plot crop + if 'merge' in crop_imgs.keys(): + crop = crop_imgs['merge'] + else: + crop = crop_imgs['lnd'] + cv2.imshow('crop', crop) + + # Plot full + cv2.imshow('image', full_img['lnd']) + + key = cv2.waitKey() + if key == ord('q'): + break + + def plot_features(self, data_dict, colors=None): + + # Init variables + crop_imgs = {} + full_imgs = {} + if colors is None: + colors = self.colors_dft + + # Cropped image + image = data_dict['image'] + landmarks = data_dict['landmarks'] + visible = data_dict['visible'] + if np.any(np.isnan(visible)): + visible = None + mask = data_dict['mask_ldm'] + + # Full image + if 'image_ori' in data_dict.keys(): + image_ori = data_dict['image_ori'] + else: + image_ori = cv2.imread(data_dict['imgpath']) + landmarks_ori = data_dict['landmarks_ori'] + visible_ori = data_dict['visible_ori'] + if np.any(np.isnan(visible_ori)): + visible_ori = None + mask_ori = data_dict['mask_ldm_ori'] + + # Plot landmarks + crop_imgs['lnd'] = self._plot_lnd(image, landmarks, visible, mask, colors=colors['lnd']) + full_imgs['lnd'] = self._plot_lnd(image_ori, landmarks_ori, visible_ori, mask_ori, colors=colors['lnd']) + + if self.data_config.generate_pose: + rot, trl, cam_matrix = self._extract_pose(data_dict) + + # Plot pose + crop_imgs['pose'] = plot.draw_pose(image, rot, trl, cam_matrix, euler=True, colors=colors['pose']) + + # Plot merge features + crop_imgs['merge'] = plot.draw_pose(crop_imgs['lnd'], rot, trl, cam_matrix, euler=True, colors=colors['pose']) + + return crop_imgs, full_imgs + + def get_idx(self, shuffle=False): + ids = list(range(len(self.dataset))) + if shuffle: + random.shuffle(ids) + return ids + + def reload_dataset(self, data_config=None): + if data_config is None: + data_config = self.data_config + dataloader, dataset = dl.get_dataloader(1, data_config, debug=True) + self.dataset = dataset + self.dataloader = dataloader + + def _extract_pose(self, data_dict): + # Rotation and translation matrix + pose = data_dict['pose'] + rot = pose[:3] + trl = pose[3:] + + # Camera matrix + cam_matrix = data_dict['cam_matrix'] + + # Check for ground truth anns + if 'headpose_ori' in data_dict.keys(): + if len(self.data_config.aug_names) == 0: + print('Image headpose generated by ground truth data') + pose_ori = data_dict['headpose_ori'] + rot = pose_ori + + return rot, trl, cam_matrix + + def _plot_lnd(self, image, landmarks, visible, mask, max_shape_thr=720, colors=None): + + if colors is None: + colors = self.colors_dft['lnd'] + + # Full image plots + W, H, C = image.shape + + # Original image resize if need it + if W > max_shape_thr or H > max_shape_thr: + max_shape = max(W, H) + scale_factor = max_shape_thr / max_shape + resize_shape = (int(H * scale_factor), int(W * scale_factor)) + image_out = plot.draw_landmarks(image, landmarks, visible=visible, mask=mask, + thick_scale=1 / scale_factor, colors=colors) + image_out = cv2.resize(image_out, resize_shape) + else: + image_out = plot.draw_landmarks(image, landmarks, visible=visible, mask=mask, colors=colors) + + return image_out + + +if __name__ == '__main__': + args = inspect_parser() + data_aug = True + database = args.database + anns_type = args.anns + pose = args.nopose + select_img = args.img + if args.clean: + data_aug = False + + if len(args.shape) != 2: + raise ValueError('--shape requires two values: width and height. Ej: --shape 256 256') + else: + img_shape = tuple(args.shape) + + visualizer = DatasetInspector(database, anns_type, data_aug=data_aug, pose=pose, image_shape=img_shape) + visualizer.show_dataset(ids_list=select_img) + diff --git a/SPIGA/spiga/data/visualize/inspect_heatmaps.py b/SPIGA/spiga/data/visualize/inspect_heatmaps.py new file mode 100644 index 0000000000000000000000000000000000000000..63527ccfe2b4a57b1fce81d01da8e2ba51b0bac1 --- /dev/null +++ b/SPIGA/spiga/data/visualize/inspect_heatmaps.py @@ -0,0 +1,92 @@ +import cv2 +import numpy as np + +from spiga.data.visualize.inspect_dataset import DatasetInspector, inspect_parser + + +class HeatmapInspector(DatasetInspector): + + def __init__(self, database, anns_type, data_aug=True, image_shape=(256,256)): + + super().__init__(database, anns_type, data_aug=data_aug, pose=False, image_shape=image_shape) + + self.data_config.aug_names.append('heatmaps2D') + self.data_config.heatmap2D_norm = False + self.data_config.aug_names.append('boundaries') + self.data_config.shuffle = False + self.reload_dataset() + + def show_dataset(self, ids_list=None): + + if ids_list is None: + ids = self.get_idx(shuffle=self.data_config.shuffle) + else: + ids = ids_list + + for img_id in ids: + data_dict = self.dataset[img_id] + + crop_imgs, _ = self.plot_features(data_dict) + + # Plot landmark crop + cv2.imshow('crop', crop_imgs['lnd']) + + # Plot landmarks 2D (group) + crop_allheats = self._plot_heatmaps2D(data_dict) + + # Plot boundaries shape + cv2.imshow('boundary', np.max(data_dict['boundary'], axis=0)) + + for lnd_idx in range(self.data_config.database.num_landmarks): + # Heatmaps 2D + crop_heats = self._plot_heatmaps2D(data_dict, lnd_idx) + maps = cv2.hconcat([crop_allheats['heatmaps2D'], crop_heats['heatmaps2D']]) + cv2.imshow('heatmaps', maps) + + key = cv2.waitKey() + if key == ord('q'): + break + if key == ord('n'): + break + + if key == ord('q'): + break + + def _plot_heatmaps2D(self, data_dict, heatmap_id=None): + + # Variables + heatmaps = {} + image = data_dict['image'] + + if heatmap_id is None: + heatmaps2D = data_dict['heatmap2D'] + heatmaps2D = np.max(heatmaps2D, axis=0) + else: + heatmaps2D = data_dict['heatmap2D'][heatmap_id] + + # Plot maps + heatmaps['heatmaps2D'] = self._merge_imgmap(image, heatmaps2D) + return heatmaps + + def _merge_imgmap(self, image, maps): + crop_maps = cv2.applyColorMap(np.uint8(255 * maps), cv2.COLORMAP_JET) + return cv2.addWeighted(image, 0.7, crop_maps, 0.3, 0) + + +if __name__ == '__main__': + + args = inspect_parser() + data_aug = True + database = args.database + anns_type = args.anns + select_img = args.img + if args.clean: + data_aug = False + + if len(args.shape) != 2: + raise ValueError('--shape requires two values: width and height. Ej: --shape 256 256') + else: + img_shape = tuple(args.shape) + + visualizer = HeatmapInspector(database, anns_type, data_aug, image_shape=img_shape) + visualizer.show_dataset(ids_list=select_img) diff --git a/SPIGA/spiga/data/visualize/plotting.py b/SPIGA/spiga/data/visualize/plotting.py new file mode 100644 index 0000000000000000000000000000000000000000..76661f33cf61807a957def360d07277bbd7db6e3 --- /dev/null +++ b/SPIGA/spiga/data/visualize/plotting.py @@ -0,0 +1,97 @@ +import matplotlib.pyplot as plt +import numpy as np +import cv2 + +import spiga.data.loaders.augmentors.utils as dlu + +BLUE = (255, 0, 0) +GREEN = (0, 255, 0) +RED = (0, 0, 255) +PURPLE = (128, 0, 128) + + +def draw_landmarks(image, landmarks, visible=None, mask=None, thick_scale=1, colors=(GREEN, RED)): + # Fix variable + thick = int(2 * thick_scale + 0.5) + # Initialize variables if need it + if visible is None: + visible = np.ones(len(landmarks)) + if mask is None: + mask = np.ones(len(landmarks)) + + mask = np.array(mask, dtype=bool) + visible = np.array(visible, dtype=bool) + + # Clean and split landmarks + landmarks = landmarks[mask] + visible = visible[mask] + ldm_vis = landmarks[visible] + not_visible = np.logical_not(visible) + ldm_notvis = landmarks[not_visible] + + # Plot landmarks + if image.shape[0] == 3: + image = image.transpose(1, 2, 0) + + canvas = image.copy() + canvas = _write_circles(canvas, ldm_vis, color=colors[0], thick=thick) + canvas = _write_circles(canvas, ldm_notvis, color=colors[1], thick=thick) + + return canvas + + +def _write_circles(canvas, landmarks, color=RED, thick=2): + for xy in landmarks: + xy = np.array(xy+0.5, dtype=int) + canvas = cv2.circle(canvas, (xy[0], xy[1]), thick, color, -1) + return canvas + + +def plot_landmarks_pil(image, landmarks, visible=None, mask=None): + + # Initialize variables if need it + if visible is None: + visible = np.ones(len(landmarks)) + if mask is None: + mask = np.ones(len(landmarks)) + + mask = np.array(mask, dtype=bool) + visible = np.array(visible, dtype=bool) + not_visible = np.logical_not(visible) + + # Clean and split landmarks + landmarks = landmarks[mask] + ldm_vis = landmarks[visible] + ldm_notvis = landmarks[not_visible] + + # Plot landmarks + if image.shape[0] == 3: + image = image.transpose(1, 2, 0) + + plt.imshow(image / 255) + plt.scatter(ldm_vis[:, 0], ldm_vis[:, 1], s=10, marker='.', c='g') + plt.scatter(ldm_notvis[:, 0], ldm_notvis[:, 1], s=10, marker='.', c='r') + plt.show() + + +def draw_pose(img, rot, trl, K, euler=False, size=0.5, colors=(BLUE, GREEN, RED)): + if euler: + rot = dlu.euler_to_rotation_matrix(rot) + + canvas = img.copy() + rotV, _ = cv2.Rodrigues(rot) + points = np.float32([[size, 0, 0], [0, -size, 0], [0, 0, -size], [0, 0, 0]]).reshape(-1, 3) + axisPoints, _ = cv2.projectPoints(points, rotV, trl, K, (0, 0, 0, 0)) + axisPoints = axisPoints.astype(int) + canvas = cv2.line(canvas, tuple(axisPoints[3].ravel()), tuple(axisPoints[2].ravel()), colors[0], 3) + canvas = cv2.line(canvas, tuple(axisPoints[3].ravel()), tuple(axisPoints[1].ravel()), colors[1], 3) + canvas = cv2.line(canvas, tuple(axisPoints[3].ravel()), tuple(axisPoints[0].ravel()), colors[2], 3) + + return canvas + + +def enhance_heatmap(heatmap): + map_aux = heatmap - heatmap.min() + map_aux = map_aux / map_aux.max() + map_img = cv2.applyColorMap((map_aux * 255).astype(np.uint8), cv2.COLORMAP_BONE) + return map_img diff --git a/SPIGA/spiga/demo/__init__.py b/SPIGA/spiga/demo/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/analyze/__init__.py b/SPIGA/spiga/demo/analyze/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/analyze/analyzer.py b/SPIGA/spiga/demo/analyze/analyzer.py new file mode 100644 index 0000000000000000000000000000000000000000..33b7514796661ea3b2dac6294aa32880dc4bd772 --- /dev/null +++ b/SPIGA/spiga/demo/analyze/analyzer.py @@ -0,0 +1,53 @@ +import copy + +# Demo libs +import spiga.demo.analyze.extract.processor as pr + + +class VideoAnalyzer: + def __init__(self, tracker, processor=pr.EmptyProcessor()): + self.tracker = tracker + self.processor = processor + self.tracked_obj = [] + + def process_frame(self, image): + image = copy.copy(image) + self.tracked_obj = self.tracker.process_frame(image, self.tracked_obj) + if len(self.tracked_obj) > 0: + self.tracked_obj = self.processor.process_frame(image, self.tracked_obj) + self.tracked_obj = self._add_attributes() + return self.tracked_obj + + def plot_features(self, image, plotter, show_attributes): + for obj in self.tracked_obj: + image = obj.plot_features(image, plotter, show_attributes) + return image + + def get_attributes(self, names): + + # Check input type + single_name = False + if isinstance(names, str): + names = [names] + single_name = True + + attributes = {} + for name in names: + attribute = [] + for obj in self.tracked_obj: + attribute.append(obj.get_attributes(name)) + attributes[name] = attribute + + if single_name: + return attribute + else: + return attributes + + def _add_attributes(self): + for obj in self.tracked_obj: + if not obj.has_processor(): + obj.attributes += self.processor.attributes + obj.attributes += self.tracker.attributes + obj.drawers.append(self.processor.plot_features) + obj.drawers.append(self.tracker.plot_features) + return self.tracked_obj diff --git a/SPIGA/spiga/demo/analyze/extract/__init__.py b/SPIGA/spiga/demo/analyze/extract/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/analyze/extract/processor.py b/SPIGA/spiga/demo/analyze/extract/processor.py new file mode 100644 index 0000000000000000000000000000000000000000..5e62fd89cce5031670c7a63c98a8f27df0dc332c --- /dev/null +++ b/SPIGA/spiga/demo/analyze/extract/processor.py @@ -0,0 +1,58 @@ + + +class Processor: + def __init__(self): + self.attributes = [] + + def process_frame(self, frame, tracked_obj): + """ + Process tracked objects to extract interesting features. + :param frame: OpenCV image. + :param tracked_obj: List with the objects to be processed. + """ + raise NotImplementedError() + + def plot_features(self, image, features, plotter, show_attributes): + """ + Visualize objects detected in the input image. + :param image: OpenCV image. + :param features: List of object features detect after processing the frame. + :param plotter: Plotter interface. + :param show_attributes: Selected object attributes to be displayed. + """ + raise NotImplementedError() + + +class EmptyProcessor(Processor): + def __init__(self): + super().__init__() + + def process_frame(self, frame, tracked_obj): + return tracked_obj + + def plot_features(self, image, features, plotter, show_attributes): + return image + + +class ProcessorsGroup(Processor): + def __init__(self): + super().__init__() + self.group = [] + + def process_frame(self, frame, tracked_obj): + for elem in self.group: + tracked_obj = elem.process_frame(frame, tracked_obj) + return tracked_obj + + def plot_features(self, image, features, plotter, show_attributes): + for elem in self.group: + image = elem.plot_features(image, features, plotter, show_attributes) + return image + + def add_processor(self, processor): + self.group.append(processor) + self.attributes += processor.attributes + + def get_number_of_processors(self): + return len(self.group) + diff --git a/SPIGA/spiga/demo/analyze/extract/spiga_processor.py b/SPIGA/spiga/demo/analyze/extract/spiga_processor.py new file mode 100644 index 0000000000000000000000000000000000000000..1e0ef38c20f807f310cd3d7b7bcc2f20f74f7149 --- /dev/null +++ b/SPIGA/spiga/demo/analyze/extract/spiga_processor.py @@ -0,0 +1,60 @@ +# SPIGA library +import spiga.inference.config as model_cfg +from spiga.inference.framework import SPIGAFramework + +# Demo modules +import spiga.demo.analyze.extract.processor as pr + + +class SPIGAProcessor(pr.Processor): + + def __init__(self, + dataset='wflw', + features=('lnd', 'pose'), + gpus=[0]): + + super().__init__() + + # Configure and load processor + self.processor_cfg = model_cfg.ModelConfig(dataset) + self.processor = SPIGAFramework(self.processor_cfg, gpus=gpus) + + # Define attributes + if 'lnd' in features: + self.attributes.append('landmarks') + self.attributes.append('landmarks_ids') + if 'pose' in features: + self.attributes.append('headpose') + + def process_frame(self, frame, tracked_obj): + bboxes = [] + for obj in tracked_obj: + x1, y1, x2, y2 = obj.bbox[:4] + bbox_wh = [x1, y1, x2-x1, y2-y1] + bboxes.append(bbox_wh) + features = self.processor.inference(frame, bboxes) + + for obj_idx in range(len(tracked_obj)): + # Landmarks output + if 'landmarks' in self.attributes: + tracked_obj[obj_idx].landmarks = features['landmarks'][obj_idx] + tracked_obj[obj_idx].landmarks_ids = self.processor_cfg.dataset.ldm_ids + # Headpose output + if 'headpose' in self.attributes: + tracked_obj[obj_idx].headpose = features['headpose'][obj_idx] + + return tracked_obj + + def plot_features(self, image, features, plotter, show_attributes): + + if 'landmarks' in self.attributes and 'landmarks' in show_attributes: + x1, y1, x2, y2 = features.bbox[:4] + thick = int(plotter.landmarks.thickness['lnd'] * (x2-x1)/200 + 0.5) + if thick == 0: + thick = 1 + image = plotter.landmarks.draw_landmarks(image, features.landmarks, thick=thick) + + if 'headpose' in self.attributes and 'headpose' in show_attributes: + image = plotter.hpose.draw_headpose(image, features.bbox[:5], + features.headpose[:3], features.headpose[3:], euler=True) + return image diff --git a/SPIGA/spiga/demo/analyze/features/__init__.py b/SPIGA/spiga/demo/analyze/features/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/analyze/features/basic.py b/SPIGA/spiga/demo/analyze/features/basic.py new file mode 100644 index 0000000000000000000000000000000000000000..f7d3dbae466c5aa3f33866b82cd51e470b7111b1 --- /dev/null +++ b/SPIGA/spiga/demo/analyze/features/basic.py @@ -0,0 +1,40 @@ + +class ObjectAnalyzed: + + def __init__(self): + # Processor addons + self.attributes = [] + self.drawers = [] + + def has_processor(self): + if len(self.attributes) > 0: + return True + else: + return False + + def plot_features(self, image, plotter, show_attributes): + for drawer in self.drawers: + image = drawer(image, self, plotter, show_attributes) + return image + + def get_attributes(self, names=None): + + # Initialization by input type + single_name = False + if names is None: + names = self.attributes + elif isinstance(names, str): + names = [names] + single_name = True + + attributes = {} + attribute = [] + for name in names: + if name in self.attributes and name in self.__dict__.keys(): + attribute = getattr(self, name) + attributes[name] = attribute + + if single_name: + return attribute + else: + return attributes \ No newline at end of file diff --git a/SPIGA/spiga/demo/analyze/features/face.py b/SPIGA/spiga/demo/analyze/features/face.py new file mode 100644 index 0000000000000000000000000000000000000000..cf15b49f2609be3f4d037994fbec50083294ca4e --- /dev/null +++ b/SPIGA/spiga/demo/analyze/features/face.py @@ -0,0 +1,20 @@ +import numpy as np + +# Demo libs +from spiga.demo.analyze.features.basic import ObjectAnalyzed + + +class Face(ObjectAnalyzed): + + def __init__(self): + super().__init__() + self.bbox = np.zeros(5) + self.key_landmarks = - np.ones((5, 2)) + self.landmarks = None + self.face_id = -1 + self.past_states = [] + self.num_past_states = 5 + + + + diff --git a/SPIGA/spiga/demo/analyze/track/__init__.py b/SPIGA/spiga/demo/analyze/track/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/analyze/track/get_tracker.py b/SPIGA/spiga/demo/analyze/track/get_tracker.py new file mode 100644 index 0000000000000000000000000000000000000000..b8495b47938dc557e01944b784f803e2b8f3db9e --- /dev/null +++ b/SPIGA/spiga/demo/analyze/track/get_tracker.py @@ -0,0 +1,13 @@ +# Demo libs +import spiga.demo.analyze.track.retinasort.zoo as zoo_rs + +zoos = [zoo_rs] + + +def get_tracker(model_name): + for zoo in zoos: + model = zoo.get_tracker(model_name) + if model is not None: + return model + + raise NotImplementedError('Tracker name not available') diff --git a/SPIGA/spiga/demo/analyze/track/retinasort/__init__.py b/SPIGA/spiga/demo/analyze/track/retinasort/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/analyze/track/retinasort/config.py b/SPIGA/spiga/demo/analyze/track/retinasort/config.py new file mode 100644 index 0000000000000000000000000000000000000000..b0c3ca78e73af40d4e4bd5500059986702c49654 --- /dev/null +++ b/SPIGA/spiga/demo/analyze/track/retinasort/config.py @@ -0,0 +1,81 @@ + + +cfg_retinasort = { + + 'retina': { + 'model_name': 'mobile0.25', + 'extra_features': ['landmarks'], + 'postreat': { + 'resize': 1., + 'score_thr': 0.75, + 'top_k': 5000, + 'nms_thr': 0.4, + 'keep_top_k': 50} + }, + + 'sort': { + 'max_age': 1, + 'min_hits': 3, + 'iou_threshold': 0.3, + } +} + +cfg_retinasort_res50 = { + + 'retina': { + 'model_name': 'resnet50', + 'extra_features': ['landmarks'], + 'postreat': { + 'resize': 1., + 'score_thr': 0.75, + 'top_k': 5000, + 'nms_thr': 0.4, + 'keep_top_k': 50} + }, + + 'sort': { + 'max_age': 1, + 'min_hits': 3, + 'iou_threshold': 0.3, + } +} + +cfg_retinasort_cav3d = { + + 'retina': { + 'model_name': 'resnet50', + 'extra_features': ['landmarks'], + 'postreat': { + 'resize': 1., + 'score_thr': 0.95, + 'top_k': 5000, + 'nms_thr': 0.8, + 'keep_top_k': 50} + }, + + 'sort': { + 'max_age': 90, + 'min_hits': 3, + 'iou_threshold': 0.3, + } +} + +cfg_retinasort_av16 = { + + 'retina': { + 'model_name': 'resnet50', + 'extra_features': ['landmarks'], + 'postreat': { + 'resize': 1., + 'score_thr': 0.75, + 'top_k': 5000, + 'nms_thr': 0.8, + 'keep_top_k': 50} + }, + + 'sort': { + 'max_age': 90, + 'min_hits': 3, + 'iou_threshold': 0.3, + } +} diff --git a/SPIGA/spiga/demo/analyze/track/retinasort/face_tracker.py b/SPIGA/spiga/demo/analyze/track/retinasort/face_tracker.py new file mode 100644 index 0000000000000000000000000000000000000000..cdb2e4e1af749098477734e6f9a0112d9dabeaec --- /dev/null +++ b/SPIGA/spiga/demo/analyze/track/retinasort/face_tracker.py @@ -0,0 +1,82 @@ +import numpy as np + +# Third party algorithms. Implementation maintained by SPIGA authors. +import sort_tracker +import retinaface + +# My libs +import spiga.demo.analyze.track.retinasort.config as cfg +import spiga.demo.analyze.track.tracker as tracker +import spiga.demo.analyze.features.face as ft_face + + +class RetinaSortTracker(tracker.Tracker): + + def __init__(self, config=cfg.cfg_retinasort, device='cuda'): + super().__init__() + + self.detector = retinaface.RetinaFaceDetector(model=config['retina']['model_name'], + device=device, + extra_features=config['retina']['extra_features'], + cfg_postreat=config['retina']['postreat']) + + self.associator = sort_tracker.Sort(max_age=config['sort']['max_age'], + min_hits=config['sort']['min_hits'], + iou_threshold=config['sort']['iou_threshold']) + self.obj_type = ft_face.Face + self.attributes += ['bbox', 'face_id', 'key_landmarks'] + + def process_frame(self, image, tracked_obj): + # tracked_obj = [] + features = self.detector.inference(image) + bboxes = features['bbox'] + bboxes = self._code_bbox_idx(bboxes) + bboxes_id = self.associator.update(bboxes) + bboxes_id, bbox_idx = self._decode_bbox_idx(bboxes_id) + final_tracked_obj = [] + for idx, bbox in enumerate(bboxes_id): + founded_flag = False + for past_obj in tracked_obj: + if past_obj.face_id == bbox[-1]: + past_obj.bbox = bbox[:5] + past_obj = self._update_extra_features( + past_obj, features, bbox_idx[idx]) + final_tracked_obj.append(past_obj) + tracked_obj.remove(past_obj) + founded_flag = True + break + + if not founded_flag: + new_obj = self.obj_type() + new_obj.bbox = bbox[:5] + new_obj.face_id = bbox[5] + new_obj = self._update_extra_features( + new_obj, features, bbox_idx[idx]) + final_tracked_obj.append(new_obj) + + return final_tracked_obj + + def plot_features(self, image, features, plotter, show_attributes): + if 'bbox' in show_attributes: + image = plotter.bbox.draw_bbox(image, features.bbox) + if 'face_id' in show_attributes: + text_id = 'Face Id: %i' % features.face_id + image = plotter.bbox.draw_bbox_text(image, features.bbox, text_id, offset=( + 0, -10), color=plotter.basic.colors['blue']) + image = plotter.bbox.draw_bbox_line(image, features.bbox) + return image + + def _code_bbox_idx(self, bboxes): + bboxes = np.array(bboxes) + bboxes[:, 4] += (np.arange(len(bboxes)) - 0.001) + return bboxes + + def _decode_bbox_idx(self, bboxes): + bboxes = np.array(bboxes) + idx = bboxes[:, 4].astype(int) + bboxes[:, 4] = bboxes[:, 4] % 1 + 0.001 + return bboxes, idx + + def _update_extra_features(self, obj, features, idx): + obj.key_landmarks = features['landmarks'][idx] + return obj diff --git a/SPIGA/spiga/demo/analyze/track/retinasort/zoo.py b/SPIGA/spiga/demo/analyze/track/retinasort/zoo.py new file mode 100644 index 0000000000000000000000000000000000000000..19a95c06d4ba7587fc1fe97f3f9f4a74be120ac9 --- /dev/null +++ b/SPIGA/spiga/demo/analyze/track/retinasort/zoo.py @@ -0,0 +1,22 @@ +# My libs +import spiga.demo.analyze.track.retinasort.face_tracker as tr +import spiga.demo.analyze.track.retinasort.config as cfg_tr +import torch + + +def get_tracker(model_name): + device = 'cuda' if torch.cuda.is_available() else 'cpu' + # MobileNet Backbone + if model_name == 'RetinaSort': + return tr.RetinaSortTracker(device=device) + # ResNet50 Backbone + if model_name == 'RetinaSort_Res50': + return tr.RetinaSortTracker(cfg_tr.cfg_retinasort_res50, device=device) + # Config CAV3D: https://ict.fbk.eu/units/speechtek/cav3d/ + if model_name == 'RetinaSort_cav3d': + return tr.RetinaSortTracker(cfg_tr.cfg_retinasort_cav3d, device=device) + # Config AV16: https://ict.fbk.eu/units/speechtek/cav3d/ + if model_name == 'RetinaSort_av16': + return tr.RetinaSortTracker(cfg_tr.cfg_retinasort_av16, device=device) + + return None diff --git a/SPIGA/spiga/demo/analyze/track/tracker.py b/SPIGA/spiga/demo/analyze/track/tracker.py new file mode 100644 index 0000000000000000000000000000000000000000..0199ca826820bb92511a242c350696690500ed73 --- /dev/null +++ b/SPIGA/spiga/demo/analyze/track/tracker.py @@ -0,0 +1,25 @@ + +class Tracker: + """ + Object detection and tracking interface in a video stream + """ + def __init__(self): + self.attributes = [] + + def process_frame(self, image, tracked_obj): + """ + Detect and track objects in the input image. + :param image: OpenCV image. + :param tracked_obj: List with the objects found. + """ + raise NotImplementedError() + + def plot_features(self, image, features, plotter, show_attributes): + """ + Visualize objects detected in the input image. + :param image: OpenCV image. + :param features: List of object features detect after processing the frame. + :param plotter: Plotter interface. + :param show_attributes: Selected object attributes to be displayed. + """ + raise NotImplementedError() diff --git a/SPIGA/spiga/demo/app.py b/SPIGA/spiga/demo/app.py new file mode 100644 index 0000000000000000000000000000000000000000..659ec537f986a11eac66bd2ec84955e7b8f8f70e --- /dev/null +++ b/SPIGA/spiga/demo/app.py @@ -0,0 +1,107 @@ +import os +import cv2 +import pkg_resources + +# My libs +import spiga.demo.analyze.track.get_tracker as tr +import spiga.demo.analyze.extract.spiga_processor as pr_spiga +from spiga.demo.analyze.analyzer import VideoAnalyzer +from spiga.demo.visualize.viewer import Viewer + +# Paths +video_out_path_dft = pkg_resources.resource_filename('spiga', 'demo/outputs') +if not os.path.exists(video_out_path_dft): + os.makedirs(video_out_path_dft) + + +def main(): + import argparse + pars = argparse.ArgumentParser(description='Face App') + pars.add_argument('-i', '--input', type=str, default='0', help='Video input') + pars.add_argument('-d', '--dataset', type=str, default='wflw', + choices=['wflw', '300wpublic', '300wprivate', 'merlrav'], + help='SPIGA pretrained weights per dataset') + pars.add_argument('-t', '--tracker', type=str, default='RetinaSort', + choices=['RetinaSort', 'RetinaSort_Res50'], help='Tracker name') + pars.add_argument('-sh', '--show', nargs='+', type=str, default=['fps', 'face_id', 'landmarks', 'headpose'], + choices=['fps', 'bbox', 'face_id', 'landmarks', 'headpose'], + help='Select the attributes of the face to be displayed ') + pars.add_argument('-s', '--save', action='store_true', help='Save record') + pars.add_argument('-nv', '--noview', action='store_false', help='Do not visualize the window') + pars.add_argument('--outpath', type=str, default=video_out_path_dft, help='Video output directory') + pars.add_argument('--fps', type=int, default=30, help='Frames per second') + pars.add_argument('--shape', nargs='+', type=int, help='Visualizer shape (W,H)') + args = pars.parse_args() + + if args.shape: + if len(args.shape) != 2: + raise ValueError('--shape requires two values: width and height. Ej: --shape 256 256') + else: + video_shape = tuple(args.shape) + else: + video_shape = None + + if not args.noview and not args.save: + raise ValueError('No results will be saved neither shown') + + video_app(args.input, spiga_dataset=args.dataset, tracker=args.tracker, fps=args.fps, + save=args.save, output_path=args.outpath, video_shape=video_shape, visualize=args.noview, plot=args.show) + + +def video_app(input_name, spiga_dataset=None, tracker=None, fps=30, save=False, + output_path=video_out_path_dft, video_shape=None, visualize=True, plot=()): + + # Load video + try: + capture = cv2.VideoCapture(int(input_name)) + video_name = None + if not visualize: + print('WARNING: Webcam must be visualized in order to close the app') + visualize = True + + except: + try: + capture = cv2.VideoCapture(input_name) + video_name = input_name.split('/')[-1][:-4] + except: + raise ValueError('Input video path %s not valid' % input_name) + + if capture is not None: + # Initialize viewer + if video_shape is not None: + vid_w, vid_h = video_shape + else: + vid_w, vid_h = capture.get(3), capture.get(4) + viewer = Viewer('face_app', width=vid_w, height=vid_h, fps=fps) + if save: + viewer.record_video(output_path, video_name) + + # Initialize face tracker + faces_tracker = tr.get_tracker(tracker) + faces_tracker.detector.set_input_shape(capture.get(4), capture.get(3)) + # Initialize processors + processor = pr_spiga.SPIGAProcessor(dataset=spiga_dataset) + # Initialize Analyzer + faces_analyzer = VideoAnalyzer(faces_tracker, processor=processor) + + # Convert FPS to the amount of milliseconds that each frame will be displayed + if visualize: + viewer.start_view() + while capture.isOpened(): + ret, frame = capture.read() + if ret: + # Process frame + faces_analyzer.process_frame(frame) + # Show results + key = viewer.process_image(frame, drawers=[faces_analyzer], show_attributes=plot) + if key: + break + else: + break + + capture.release() + viewer.close() + + +if __name__ == '__main__': + main() diff --git a/SPIGA/spiga/demo/readme.md b/SPIGA/spiga/demo/readme.md new file mode 100644 index 0000000000000000000000000000000000000000..17368cfd467486f6979e9e67255b642956e654d3 --- /dev/null +++ b/SPIGA/spiga/demo/readme.md @@ -0,0 +1,62 @@ +## Face Video-Analyzer Framework +This demo application provides a general framework for tracking, detecting and extracting features of human faces in images or videos. +Currently, the following tools are integrated in a video-demo available at ```./spiga/demo/app.py```: + +* Tracking: + * FaceTracker : RetinaFace + SORT. + * Detectors: + * RetinaFace (bbox + 5 landmarks). + * Backbone Mobilenet 0.25. + * Backbone Resnet50. + * Associators: + * SORT: Frame by frame +* Extractors: + * SPIGA architecture + * Features: Landmarks and headpose. + * Datasets: 300W Public, 300W Private, WFLW, MERLRAV. +* Viewers: + * Landmarks, headpose and bbox (score + face_id). + +### Demo Application + +``` +python ./spiga/demo/app.py \ + [--input] \ # Webcam ID or Video Path. Dft: Webcam '0'. + [--dataset] \ # SPIGA pretrained weights per dataset. Dft: 'wflw'. + [--tracker] \ # Tracker name. Dft: 'RetinaSort'. + [--show] \ # Select the attributes of the face to be displayed. Dft: ['fps', 'face_id', 'landmarks', 'headpose'] + [--save] \ # Save record. + [--noview] \ # Do not visualize window. + [--outpath] \ # Recorded output directory. Dft: './spiga/demo/outputs' + [--fps] \ # Frames per second. + [--shape] \ # Visualizer shape (W,H). +``` + +### Code Structure +The demo framework has been organised according to the following structure: + +``` +./spiga/demo/ +| app.py # Video-demo +| +└───analyze +β”‚ | analyzer.py # Generic video/image analyzer compositor +β”‚ β”‚ +β”‚ └───features # Object/Faces classes +β”‚ β”‚ +β”‚ └───track # Task heads +β”‚ | | tracker.py # Tracker class +β”‚ | | get_tracker.py # Get model tracker from zoo by name +β”‚ | └─── retinasort # RetinaFace + SORT tracker (tracker + zoo files) +| | +| └───extract +| | processor.py # Processor classes +| β”” spiga_processor.py # SPIGA wrapper +| +└───visualize +| | viewer.py # Viewer manager +| | plotter.py # Englobe available features drawers +| └─── layouts # Landmarks, bbox, headpose drawers +| +└───utils # Video converters +``` \ No newline at end of file diff --git a/SPIGA/spiga/demo/utils/__init__.py b/SPIGA/spiga/demo/utils/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/utils/frames2video.py b/SPIGA/spiga/demo/utils/frames2video.py new file mode 100644 index 0000000000000000000000000000000000000000..eaba367ff17ba2ed0ae09ecd387a98c106d4e06b --- /dev/null +++ b/SPIGA/spiga/demo/utils/frames2video.py @@ -0,0 +1,62 @@ +import os +import cv2 + + +def main(): + import argparse + pars = argparse.ArgumentParser(description='Frames to video converter') + pars.add_argument('frames', type=str, help='Frames directory') + pars.add_argument('vidname', type=str, help='Output video name') + pars.add_argument('-o', '--outpath', type=str, default=None, help='Save record') + pars.add_argument('--fps', type=int, default=30, help='Frames per second') + pars.add_argument('--shape', nargs='+', type=int, help='Visualizer shape (W,H)') + args = pars.parse_args() + + if args.shape: + if len(args.shape) != 2: + raise ValueError('--shape requires two values: width and height. Ej: --shape 256 256') + else: + video_shape = tuple(args.shape) + else: + video_shape = None + + frames2video(args.frames, args.vidname, video_path=args.outpath, video_shape=video_shape, fps=args.fps) + + +def frames2video(frames_path, video_name, video_path=None, video_shape=None, fps=30): + + frames_names = sorted(os.listdir(frames_path)) + + if video_path is None: + video_path = frames_path + '/vid_out/' + + if not os.path.exists(video_path): + os.makedirs(video_path) + + video_file = os.path.join(video_path, video_name + '.mp4') + if video_shape is None: + video_writer = None + else: + vid_w, vid_h = video_shape + video_writer = cv2.VideoWriter(video_file, cv2.VideoWriter_fourcc(*'MP4V'), fps, (vid_w, vid_h)) + + for frame_name in frames_names: + if frame_name.split('.')[-1] not in ['jpg', 'jpeg', 'png', 'tif', 'tiff', 'eps', 'bmp', 'gif']: + print('File %s format doesnt match with an image ' % frame_name) + continue + + frame_file = os.path.join(frames_path, frame_name) + frame = cv2.imread(frame_file) + if video_writer is None: + vid_h, vid_w = frame.shape[:2] + video_writer = cv2.VideoWriter(video_file, cv2.VideoWriter_fourcc(*'MP4V'), fps, (vid_w, vid_h)) + + if frame.shape[:2] != (vid_h, vid_w): + frame = cv2.resize(frame, (vid_w, vid_h)) + video_writer.write(frame) + + video_writer.release() + + +if __name__ == '__main__': + main() diff --git a/SPIGA/spiga/demo/visualize/__init__.py b/SPIGA/spiga/demo/visualize/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/visualize/layouts/__init__.py b/SPIGA/spiga/demo/visualize/layouts/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/demo/visualize/layouts/plot_basics.py b/SPIGA/spiga/demo/visualize/layouts/plot_basics.py new file mode 100644 index 0000000000000000000000000000000000000000..051f7c074e73e770067ae44be8ca4b3b35d91434 --- /dev/null +++ b/SPIGA/spiga/demo/visualize/layouts/plot_basics.py @@ -0,0 +1,40 @@ +import numpy as np +import cv2 + + +class BasicLayout: + + # Variables + colors = {'green': (0, 255, 0), + 'red': (0, 0, 255), + 'blue': (255, 0, 0), + 'purple': (128, 0, 128), + 'white': (255, 255, 255), + 'black': (0, 0, 0)} + + thickness_dft = {'circle': 2} + + def __init__(self): + self.thickness = self.thickness_dft + + def draw_circles(self, canvas, coord_list, color=colors['red'], thick=None): + if thick is None: + thick = self.thickness['circle'] + + for xy in coord_list: + xy = np.array(xy + 0.5, dtype=int) + canvas = cv2.circle(canvas, (xy[0], xy[1]), thick, color, -1) + return canvas + + def update_thickness(self, thick_dict): + for k, v in thick_dict.items(): + self.thickness[k] = v + + def reset_thickness(self): + self.thickness = self.thickness_dft + + def update_thick_byratio(self, ratio_dict): + for key, ratio in ratio_dict.items(): + self.thickness[key] = int(self.thickness_dft[key] * ratio + 0.5) + + diff --git a/SPIGA/spiga/demo/visualize/layouts/plot_bbox.py b/SPIGA/spiga/demo/visualize/layouts/plot_bbox.py new file mode 100644 index 0000000000000000000000000000000000000000..96911b41fe4f678ae41d5a7eac1484700952b99e --- /dev/null +++ b/SPIGA/spiga/demo/visualize/layouts/plot_bbox.py @@ -0,0 +1,53 @@ +import cv2 + +# Demo libs +from spiga.demo.visualize.layouts.plot_basics import BasicLayout + + +class BboxLayout(BasicLayout): + + BasicLayout.thickness_dft['bbox'] = 2 + + def __init__(self): + super().__init__() + + def draw_bbox(self, canvas, bbox, score_thr=0, show_score=True, thick=None, color=BasicLayout.colors['blue']): + + if thick is None: + thick = self.thickness['bbox'] + + if bbox[4] > score_thr: + text = "{:.4f}".format(bbox[4]) + b = list(map(int, bbox)) + cv2.rectangle(canvas, (b[0], b[1]), (b[2], b[3]), color, thick) + if show_score: + self.draw_bbox_text(canvas, b, text, offset=(0, 12), color=color) + return canvas + + def draw_bbox_line(self, canvas, bbox, score_thr=0, show_score=True, thick=None, color=BasicLayout.colors['blue']): + + if thick is None: + thick = self.thickness['bbox'] + + if bbox[4] > score_thr: + text = "{:.4f}".format(bbox[4]) + b = list(map(int, bbox)) + cv2.line(canvas, (b[0], b[1]), (b[0], b[1] + 15), color, thick) + cv2.line(canvas, (b[0], b[1]), (b[0] + 100, b[1]), color, thick) + if show_score: + self.draw_bbox_text(canvas, b, text, offset=(0, 12), color=color) + return canvas + + def draw_bbox_text(self, canvas, bbox, text, offset=(0, 0), color=BasicLayout.colors['white']): + b = list(map(int, bbox)) + cx = b[0] + offset[0] + cy = b[1] + offset[1] + cv2.putText(canvas, text, (cx, cy), cv2.FONT_HERSHEY_DUPLEX, 0.5, color) + return canvas + + def draw_bboxes(self, canvas, dets, score_thr=0, show_score=True, thick=None, colors=(BasicLayout.colors['blue'])): + num_colors = len(colors) + for idx, bbox in enumerate(dets): + color = colors[idx % num_colors] + canvas = self.draw_bbox(canvas, bbox, score_thr=score_thr, show_score=show_score, thick=thick, color=color) + return canvas diff --git a/SPIGA/spiga/demo/visualize/layouts/plot_headpose.py b/SPIGA/spiga/demo/visualize/layouts/plot_headpose.py new file mode 100644 index 0000000000000000000000000000000000000000..ed0a39858dc7a813c103dd51829feac79e53560f --- /dev/null +++ b/SPIGA/spiga/demo/visualize/layouts/plot_headpose.py @@ -0,0 +1,70 @@ +import numpy as np +import cv2 + +# Demo libs +from spiga.demo.visualize.layouts.plot_basics import BasicLayout + + +class HeadposeLayout(BasicLayout): + + BasicLayout.thickness_dft['hpose'] = 2 + + def __init__(self): + super().__init__() + self.hpose_axe_length = 2 + self.focal_ratio = 1 + + def draw_headpose(self, canvas, bbox, rot, trl, euler=False, len_axe=None, thick=None, + colors=(BasicLayout.colors['blue'], BasicLayout.colors['green'], BasicLayout.colors['red'])): + + trl = np.float32(trl) + rot = np.float32(rot) + K = self._camera_matrix(bbox) + + # Init variables if need it + if len_axe is None: + len_axe = self.hpose_axe_length + if thick is None: + thick = self.thickness['hpose'] + + if euler: + rot = self._euler_to_rotation_matrix(rot) + + rotV, _ = cv2.Rodrigues(rot) + points = np.float32([[len_axe, 0, 0], [0, -len_axe, 0], [0, 0, -len_axe], [0, 0, 0]]).reshape(-1, 3) + axisPoints, _ = cv2.projectPoints(points, rotV, trl, K, (0, 0, 0, 0)) + canvas = cv2.line(canvas, tuple(axisPoints[3].ravel().astype(int)), tuple(axisPoints[2].ravel().astype(int)), colors[0], thick) + canvas = cv2.line(canvas, tuple(axisPoints[3].ravel().astype(int)), tuple(axisPoints[1].ravel().astype(int)), colors[1], thick) + canvas = cv2.line(canvas, tuple(axisPoints[3].ravel().astype(int)), tuple(axisPoints[0].ravel().astype(int)), colors[2], thick) + return canvas + + @staticmethod + def _euler_to_rotation_matrix(headpose): + # http://euclideanspace.com/maths/geometry/rotations/conversions/eulerToMatrix/index.htm + # Change coordinates system + euler = np.array([-(headpose[0] - 90), -headpose[1], -(headpose[2] + 90)]) + # Convert to radians + rad = euler * (np.pi / 180.0) + cy = np.cos(rad[0]) + sy = np.sin(rad[0]) + cp = np.cos(rad[1]) + sp = np.sin(rad[1]) + cr = np.cos(rad[2]) + sr = np.sin(rad[2]) + Ry = np.array([[cy, 0.0, sy], [0.0, 1.0, 0.0], [-sy, 0.0, cy]]) # yaw + Rp = np.array([[cp, -sp, 0.0], [sp, cp, 0.0], [0.0, 0.0, 1.0]]) # pitch + Rr = np.array([[1.0, 0.0, 0.0], [0.0, cr, -sr], [0.0, sr, cr]]) # roll + return np.matmul(np.matmul(Ry, Rp), Rr) + + def _camera_matrix(self, bbox): + x1, y1, x2, y2 = bbox[:4] + w = x2-x1 + h = y2-y1 + focal_length_x = w * self.focal_ratio + focal_length_y = h * self.focal_ratio + face_center = (x1 + (w * 0.5)), (y1 + (h * 0.5)) + + cam_matrix = np.array([[focal_length_x, 0, face_center[0]], + [0, focal_length_y, face_center[1]], + [0, 0, 1]], dtype=np.float32) + return cam_matrix \ No newline at end of file diff --git a/SPIGA/spiga/demo/visualize/layouts/plot_landmarks.py b/SPIGA/spiga/demo/visualize/layouts/plot_landmarks.py new file mode 100644 index 0000000000000000000000000000000000000000..4d91432a024ba4071166b0d43fb9f2f020640641 --- /dev/null +++ b/SPIGA/spiga/demo/visualize/layouts/plot_landmarks.py @@ -0,0 +1,53 @@ +import numpy as np + +# Demo libs +from spiga.demo.visualize.layouts.plot_basics import BasicLayout + + +class LandmarkLayout(BasicLayout): + + BasicLayout.thickness_dft['lnd'] = 3 + + def __init__(self): + super().__init__() + + def draw_landmarks(self, image, landmarks, visible=None, mask=None, + thick=None, colors=(BasicLayout.colors['green'], BasicLayout.colors['red'])): + + # Initialize variables if need it + if visible is None: + visible = np.ones(len(landmarks)) + if mask is None: + mask = np.ones(len(landmarks)) + if thick is None: + thick = self.thickness['lnd'] + + if isinstance(landmarks, (list, tuple)): + landmarks = np.array(landmarks) + if isinstance(visible, (list, tuple)): + visible = np.array(visible) + if isinstance(mask, (list, tuple)): + mask = np.array(mask) + + # Clean and split landmarks + ldm_vis, ldm_notvis = self._split_lnd_by_vis(landmarks, visible, mask) + + # PIL images to OpenCV + if image.shape[0] == 3: + image = image.transpose(1, 2, 0) + + # Plot landmarks + canvas = self.draw_circles(image, ldm_vis, color=colors[0], thick=thick) + canvas = self.draw_circles(canvas, ldm_notvis, color=colors[1], thick=thick) + return canvas + + @ staticmethod + def _split_lnd_by_vis(landmarks, visible, mask): + mask = np.array(mask, dtype=bool) + visible = np.array(visible, dtype=bool) + landmarks = landmarks[mask] + visible = visible[mask] + ldm_vis = landmarks[visible] + not_visible = np.logical_not(visible) + ldm_notvis = landmarks[not_visible] + return ldm_vis, ldm_notvis diff --git a/SPIGA/spiga/demo/visualize/plotter.py b/SPIGA/spiga/demo/visualize/plotter.py new file mode 100644 index 0000000000000000000000000000000000000000..e960ba8f4f1804495added79fd5cb3a2131d2cbf --- /dev/null +++ b/SPIGA/spiga/demo/visualize/plotter.py @@ -0,0 +1,14 @@ +# Demo libs +import spiga.demo.visualize.layouts.plot_basics as pl_basic +import spiga.demo.visualize.layouts.plot_bbox as pl_bbox +import spiga.demo.visualize.layouts.plot_landmarks as pl_lnd +import spiga.demo.visualize.layouts.plot_headpose as pl_hpose + + +class Plotter: + + def __init__(self): + self.basic = pl_basic.BasicLayout() + self.bbox = pl_bbox.BboxLayout() + self.landmarks = pl_lnd.LandmarkLayout() + self.hpose = pl_hpose.HeadposeLayout() diff --git a/SPIGA/spiga/demo/visualize/viewer.py b/SPIGA/spiga/demo/visualize/viewer.py new file mode 100644 index 0000000000000000000000000000000000000000..aa96e70a2d08ff13946ecedcd50342e3ae2cfca5 --- /dev/null +++ b/SPIGA/spiga/demo/visualize/viewer.py @@ -0,0 +1,163 @@ +import os +import cv2 +import copy +import time +import numpy as np + +# Demo libs +import spiga.demo.visualize.plotter as plt + + +class Viewer: + + def __init__(self, window_title, width=None, height=None, fps=30): + """ + Initialization of the viewer canvas using width and height in pixels + :param window_title: The string with the window title to display. + :param width: The given width in pixels of the window canvas. + :param height: The given height in pixels of the window canvas. + :param fps: Frames per second + """ + # Visualizer parameters + self.canvas = None + self.width = width + self.height = height + self.window_title = window_title + self.visualize = False + + # Time variables + self.fps = fps + self.fps_inference = 0 + self.fps_mean = 0 + self.fps_lifo = np.zeros(self.fps) + self.timer = time.time() + self.frame_cnt = -1 + + # Video/Image writer + self.write = False + self.video_name = window_title # Initial name + self.video_path = None + self.video_writer = None + + # Plots + self.plotter = plt.Plotter() + self.fps_draw_params = {'text_size': 0.75, + 'text_thick': 2, + 'coord': (10, 50), + 'font': cv2.FONT_HERSHEY_SIMPLEX, + 'color': (255, 255, 255)} + + def start_view(self): + self._kill_window() + cv2.namedWindow(self.window_title) + self.visualize = True + + def record_video(self, video_path, video_name=None): + self.write = True + if video_name is not None: + self.video_name = video_name + self.video_path = video_path + if not os.path.exists(video_path): + os.makedirs(video_path) + + file_name = os.path.join(self.video_path, self.video_name + '.mp4') + self.video_writer = cv2.VideoWriter(file_name, cv2.VideoWriter_fourcc(*'MP4V'), + self.fps, (int(self.width), int(self.height))) + + def save_canvas(self, file_path=None): + if file_path is None: + if self.video_path is None: + raise ValueError('Path not defined neither video_path is available') + else: + file_path = self.video_path + + file_name = os.path.join(file_path, '/%s_%i.jpg' % (self.video_name, self.frame_cnt)) + cv2.imwrite(file_path + file_name, self.canvas) + + def reset_params(self, width, height, window_title, fps=30): + self.width = width + self.height = height + self._kill_window() + if self.video_name == self.window_title: + self.video_name = window_title + self.window_title = window_title + self.fps = fps + + def close(self): + if self.write: + self.video_writer.release() + self._kill_window() + + def process_image(self, input_img, drawers=(), show_attributes=('fps')): + + # Variables + image = copy.copy(input_img) + img_h, img_w, img_ch = image.shape + + # Convert gray scale image to color if needed + if img_ch == 1: + image = cv2.cvtColor(image, cv2.COLOR_GRAY2BGR) + + # Draw features on image + image = self._draw_over_canvas(image, drawers, show_attributes) + + # Resize image if needed to canvas shape + if img_w != self.width or img_h != self.height: + image = cv2.resize(image, (self.width, self.height)) + + # Update canvas + self.canvas = image + # Visualize FPS + if 'fps' in show_attributes: + self._plot_fps() + + # Write the resulting frame + if self.write: + self.video_writer.write(self.canvas) + + # Timing loop variables + loop_time = self._update_timers() + break_flag = False + # Visualization + if self.visualize: + cv2.imshow(self.window_title, self.canvas) + sleep_time = int(1000 * (1 / self.fps - loop_time)) + if sleep_time <= 0: + sleep_time = 1 + if cv2.waitKey(sleep_time) & 0xFF == ord('q'): + break_flag = True + + self.timer = time.time() + return break_flag + + def _plot_fps(self): + # Plot algorithm time + params = self.fps_draw_params + cv2.putText(self.canvas, ('FPS: %.2f' % self.fps_mean), params['coord'], params['font'], params['text_size'], + params['color'], params['text_thick'], cv2.LINE_AA) + + def _draw_over_canvas(self, image, drawers, show_attributes): + for drawer in drawers: + image = drawer.plot_features(image, self.plotter, show_attributes) + return image + + def _kill_window(self): + self.visualize = False + try: + cv2.destroyWindow(self.window_title) + except: + pass + + def _update_timers(self): + self.frame_cnt += 1 + loop_time = time.time() - self.timer + self.fps_inference = 1/loop_time + lifo_idx = self.frame_cnt % self.fps + self.fps_lifo[lifo_idx] = self.fps_inference + if lifo_idx == 0: + self.fps_mean = np.mean(self.fps_lifo) + return loop_time + + + + diff --git a/SPIGA/spiga/eval/__init__.py b/SPIGA/spiga/eval/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/eval/benchmark/__init__.py b/SPIGA/spiga/eval/benchmark/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/eval/benchmark/evaluator.py b/SPIGA/spiga/eval/benchmark/evaluator.py new file mode 100644 index 0000000000000000000000000000000000000000..85ed64a7cc6cd3be4b4ed3fad5f1aa9ce1613c1d --- /dev/null +++ b/SPIGA/spiga/eval/benchmark/evaluator.py @@ -0,0 +1,108 @@ +import json +import pkg_resources +from collections import OrderedDict + +# Paths +data_path = pkg_resources.resource_filename('spiga', 'data/annotations') + +def main(): + + import argparse + pars = argparse.ArgumentParser(description='Benchmark alignments evaluator') + pars.add_argument('pred_file', nargs='+', type=str, help='Absolute path to the prediction json file (Multi file)') + pars.add_argument('--eval', nargs='+', type=str, default=['lnd'], + choices=['lnd', 'pose'], help='Evaluation modes') + pars.add_argument('-s', '--save', action='store_true', help='Save results') + args = pars.parse_args() + + for pred_file in args.pred_file: + benchmark = get_evaluator(pred_file, args.eval, args.save) + benchmark.metrics() + + +class Evaluator: + + def __init__(self, data_file, evals=(), save=True, process_err=True): + + # Inputs + self.data_file = data_file + self.evals = evals + self.save = save + + # Paths + data_name = data_file.split('/')[-1] + self.data_dir = data_file.split(data_name)[0] + + # Information from name + data_name = data_name.split('.')[0] + data_name = data_name.split('_') + self.data_type = data_name[-1] + self.database = data_name[-2] + + # Load predictions and annotations + anns_file = data_path + '/%s/%s.json' % (self.database, self.data_type) + self.anns = self.load_files(anns_file) + self.pred = self.load_files(data_file) + + # Compute errors + self.error = OrderedDict() + self.error_pimg = OrderedDict() + self.metrics_log = OrderedDict() + if process_err: + self.compute_error(self.anns, self.pred) + + def compute_error(self, anns, pred, select_ids=None): + database_ref = [self.database, self.data_type] + for eval in self.evals: + self.error[eval.name] = eval.compute_error(anns, pred, database_ref, select_ids) + self.error_pimg = eval.get_pimg_err(self.error_pimg) + return self.error + + def metrics(self): + for eval in self.evals: + self.metrics_log[eval.name] = eval.metrics() + + if self.save: + file_name = self.data_dir + '/metrics_%s_%s.txt' % (self.database, self.data_type) + with open(file_name, 'w') as file: + file.write(str(self)) + + return self.metrics_log + + def load_files(self, input_file): + with open(input_file) as jsonfile: + data = json.load(jsonfile) + return data + + def _dict2text(self, name, dictionary, num_tab=1): + prev_tabs = '\t'*num_tab + text = '%s {\n' % name + for k, v in dictionary.items(): + if isinstance(v, OrderedDict) or isinstance(v, dict): + text += '{}{}'.format(prev_tabs, self._dict2text(k, v, num_tab=num_tab+1)) + else: + text += '{}{}: {}\n'.format(prev_tabs, k, v) + text += (prev_tabs + '}\n') + return text + + def __str__(self): + state_dict = self.metrics_log + text = self._dict2text('Metrics', state_dict) + return text + + +def get_evaluator(pred_file, evaluate=('lnd', 'pose'), save=False, process_err=True): + eval_list = [] + if "lnd" in evaluate: + import spiga.eval.benchmark.metrics.landmarks as mlnd + eval_list.append(mlnd.MetricsLandmarks()) + if "pose" in evaluate: + import spiga.eval.benchmark.metrics.pose as mpose + eval_list.append(mpose.MetricsHeadpose()) + + return Evaluator(pred_file, evals=eval_list, save=save, process_err=process_err) + + +if __name__ == '__main__': + main() + diff --git a/SPIGA/spiga/eval/benchmark/metrics/__init__.py b/SPIGA/spiga/eval/benchmark/metrics/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/eval/benchmark/metrics/landmarks.py b/SPIGA/spiga/eval/benchmark/metrics/landmarks.py new file mode 100644 index 0000000000000000000000000000000000000000..6201394d4108ff26f20b018aa781de5df846f671 --- /dev/null +++ b/SPIGA/spiga/eval/benchmark/metrics/landmarks.py @@ -0,0 +1,236 @@ +import os +import numpy as np +import json +from collections import OrderedDict +from scipy.integrate import simps + +from spiga.data.loaders.dl_config import db_anns_path +from spiga.eval.benchmark.metrics.metrics import Metrics + + +class MetricsLandmarks(Metrics): + + def __init__(self, name='landmarks'): + super().__init__(name) + + self.db_info = None + self.nme_norm = "corners" + self.nme_thr = 8 + self.percentile = [90, 95, 99] + # Cumulative plot axis length + self.bins = 10000 + + def compute_error(self, data_anns, data_pred, database, select_ids=None): + + # Initialize global logs and variables of Computer Error function + self.init_ce(data_anns, data_pred, database) + self._update_lnd_param() + + # Order data and compute nme + self.error['nme_per_img'] = [] + self.error['ne_per_img'] = OrderedDict() + self.error['ne_per_ldm'] = OrderedDict() + for img_id, anns in enumerate(data_anns): + # Init variables per img + pred = data_pred[img_id] + + # Get select ids to compute + if select_ids is None: + selected_ldm = anns['ids'] + else: + selected_ldm = list(set(select_ids) & set(anns['ids'])) + + norm = self._get_img_norm(anns) + for ldm_id in selected_ldm: + # Compute Normalize Error + anns_ldm = self._get_lnd_from_id(anns, ldm_id) + pred_ldm = self._get_lnd_from_id(pred, ldm_id) + ne = self._dist_l2(anns_ldm, pred_ldm)/norm * 100 + self.error['ne_per_img'].setdefault(img_id, []).append(ne) + self.error['ne_per_ldm'].setdefault(ldm_id, []).append(ne) + + # NME per image + if self.database in ['merlrav']: + # LUVLI at MERLRAV divide by 68 despite the annotated landmarks in the image. + self.error['nme_per_img'].append(np.sum(self.error['ne_per_img'][img_id])/68) + else: + self.error['nme_per_img'].append(np.mean(self.error['ne_per_img'][img_id])) + + # Cumulative NME + self.error['cumulative_nme'] = self._cumulative_error(self.error['nme_per_img'], bins=self.bins) + + return self.error + + def metrics(self): + + # Initialize global logs and variables of Metrics function + self.init_metrics() + + # Basic metrics (NME/NMPE/AUC/FR) for full dataset + nme, nmpe, auc, fr, _, _ = self._basic_metrics() + + print('NME: %.3f' % nme) + self.metrics_log['nme'] = nme + for percent_id, percentile in enumerate(self.percentile): + print('NME_P%i: %.3f' % (percentile, nmpe[percent_id])) + self.metrics_log['nme_p%i' % percentile] = nmpe[percent_id] + self.metrics_log['nme_thr'] = self.nme_thr + self.metrics_log['nme_norm'] = self.nme_norm + print('AUC_%i: %.3f' % (self.nme_thr, auc)) + self.metrics_log['auc'] = auc + print('FR_%i: %.3f' % (self.nme_thr, fr)) + self.metrics_log['fr'] = fr + + # Subset basic metrics + subsets = self.db_info['test_subsets'] + if self.data_type == 'test' and len(subsets) > 0: + self.metrics_log['subset'] = OrderedDict() + for subset, img_filter in subsets.items(): + self.metrics_log['subset'][subset] = OrderedDict() + nme, nmpe, auc, fr, _, _ = self._basic_metrics(img_select=img_filter) + print('> Landmarks subset: %s' % subset.upper()) + print('NME: %.3f' % nme) + self.metrics_log['subset'][subset]['nme'] = nme + for percent_id, percentile in enumerate(self.percentile): + print('NME_P%i: %.3f' % (percentile, nmpe[percent_id])) + self.metrics_log['subset'][subset]['nme_p%i' % percentile] = nmpe[percent_id] + print('AUC_%i: %.3f' % (self.nme_thr, auc)) + self.metrics_log['subset'][subset]['auc'] = auc + print('FR_%i: %.3f' % (self.nme_thr, fr)) + self.metrics_log['subset'][subset]['fr'] = fr + + # NME/NPE per landmark + self.metrics_log['nme_per_ldm'] = OrderedDict() + for percentile in self.percentile: + self.metrics_log['npe%i_per_ldm' % percentile] = OrderedDict() + for k, v in self.error['ne_per_ldm'].items(): + self.metrics_log['nme_per_ldm'][k] = np.mean(v) + for percentile in self.percentile: + self.metrics_log['npe%i_per_ldm' % percentile][k] = np.percentile(v, percentile) + + return self.metrics_log + + def get_pimg_err(self, data_dict=None, img_select=None): + data = self.error['nme_per_img'] + if img_select is not None: + data = [data[img_id] for img_id in img_select] + name_dict = self.name + '/nme' + if data_dict is not None: + data_dict[name_dict] = data + else: + data_dict = data + return data_dict + + def _update_lnd_param(self): + db_info_file = db_anns_path.format(database=self.database, file_name='db_info') + if os.path.exists(db_info_file): + with open(db_info_file) as jsonfile: + self.db_info = json.load(jsonfile) + + norm_dict = self.db_info['norm'] + nme_norm, nme_thr = next(iter(norm_dict.items())) + print('Default landmarks configuration: \n %s: %i' % (nme_norm, nme_thr)) + answer = input("Change default config? (N/Y) >>> ") + if answer.lower() in ['yes', 'y']: + answer = input("Normalization options: %s >>> " % str(list(norm_dict.keys()))) + if answer in norm_dict.keys(): + nme_norm = answer + nme_thr = norm_dict[nme_norm] + else: + print("Option %s not available keep in default one: %s" % (answer, nme_norm)) + answer = input("Change threshold ->%s:%i ? (N/Y) >>> " % (nme_norm, nme_thr)) + if answer.lower() in ['yes', 'y']: + answer = input('NME threshold: >>> ') + nme_thr = float(answer) + else: + print("Keeping default threshold: %i" % nme_thr) + + self.nme_norm = nme_norm + self.nme_thr = nme_thr + + else: + raise ValueError('Database %s specifics not defined. Missing db_info.json' % self.database) + + def _dist_l2(self, pointA, pointB): + return float(((pointA - pointB) ** 2).sum() ** 0.5) + + def _get_lnd_from_id(self, anns, ids): + idx = anns['ids'].index(ids) + ref = np.array(anns['landmarks'][idx]) + return ref + + def _get_img_norm(self, anns): + if self.nme_norm == 'pupils': + print('WARNING: Pupils norm only implemented for 68 landmark configuration') + left_eye = [7, 138, 139, 8, 141, 142] + right_eye = [11, 144, 145, 12, 147, 148] + refA = np.zeros(2) + refB = np.zeros(2) + for i in range(len(left_eye)): + refA += self._get_lnd_from_id(anns, left_eye[i]) + refB += self._get_lnd_from_id(anns, right_eye[i]) + refA = refA/len(left_eye) # Left + refB = refB/len(right_eye) # Right + elif self.nme_norm == 'corners': + refA = self._get_lnd_from_id(anns, 12) # Left + refB = self._get_lnd_from_id(anns, 7) # Right + elif self.nme_norm == 'diagonal': + refA = anns['bbox'][0:2] + refB = refA + anns['bbox'][2:4] + elif self.nme_norm == 'height': + return anns['bbox'][3] + elif self.nme_norm == 'lnd_bbox': + lnd = np.array(anns['landmarks']) + lnd_max = np.max(lnd, axis=0) + lnd_min = np.min(lnd, axis=0) + lnd_wh = lnd_max - lnd_min + return (lnd_wh[0]*lnd_wh[1])**0.5 + elif self.nme_norm == 'bbox': + return (anns['bbox'][2] * anns['bbox'][3]) ** 0.5 + else: + raise ValueError('Normalization %s not implemented' % self.nme_norm) + + return self._dist_l2(refA, refB) + + def _cumulative_error(self, error, bins=10000): + num_imgs, base = np.histogram(error, bins=bins) + cumulative = [x / float(len(error)) for x in np.cumsum(num_imgs)] + base = base[:bins] + cumulative, base = self._filter_cumulative(cumulative, base) + return [cumulative, base] + + def _filter_cumulative(self, cumulative, base): + base = [x for x in base if (x < self.nme_thr)] + cumulative = cumulative[:len(base)] + return cumulative, base + + def _basic_metrics(self, img_select=None): + data = self.error['nme_per_img'] + if img_select is not None: + data = [data[img_id] for img_id in img_select] + [cumulative, base] = self._cumulative_error(data, bins=self.bins) + else: + [cumulative, base] = self.error['cumulative_nme'] + + # Normalize Mean Error across img + nme = np.mean(data) + # Normalize Mean Percentile Error across img + nmpe = [] + for percentile in self.percentile: + nmpe.append(np.percentile(data, percentile)) + + # Area Under Curve and Failure Rate + auc, fr = self._auc_fr_metrics(cumulative, base) + + return nme, nmpe, auc, fr, cumulative, base + + def _auc_fr_metrics(self, cumulative, base): + if not base: + auc = 0. + fr = 100. + else: + auc = (simps(cumulative, x=base) / self.nme_thr) * 100.0 + if base[-1] < self.nme_thr and cumulative[-1] == 1: + auc += ((self.nme_thr - base[-1]) / self.nme_thr) * 100 + fr = (1 - cumulative[-1]) * 100.0 + return auc, fr diff --git a/SPIGA/spiga/eval/benchmark/metrics/metrics.py b/SPIGA/spiga/eval/benchmark/metrics/metrics.py new file mode 100644 index 0000000000000000000000000000000000000000..b4f690ae75ce39e44e3219a898c3acee6928a4ab --- /dev/null +++ b/SPIGA/spiga/eval/benchmark/metrics/metrics.py @@ -0,0 +1,42 @@ +from collections import OrderedDict + + +class Metrics: + + def __init__(self, name='metrics'): + + # Data dicts + self.error = OrderedDict() + self.metrics_log = OrderedDict() + self.name = name + self.database = None + self.data_type = None + + def compute_error(self, data_anns, data_pred, database, select_ids=None): + self.init_ce(data_anns, data_pred, database) + raise ValueError('Computer error has to be implemented by inheritance') + + def init_ce(self, data_anns, data_pred, database): + # Update database info + [self.database, self.data_type] = database + # Logs and checks + print('Computing %s error...' % self.name) + if len(data_anns) == 0: + raise ValueError('Annotations miss for computing error in %s' % self.name) + if len(data_pred) == 0: + raise ValueError('Predictions miss for computing error in %s' % self.name) + elif len(data_pred) != len(data_anns): + raise Warning('Prediction vs annotations length mismatch') + + def metrics(self): + self.init_metrics() + raise ValueError('Metrics has to be implemented by inheritance') + + def init_metrics(self): + # Logs and checks + print('> Metrics %s:' % self.name) + if len(self.error) == 0: + raise ValueError('Error must be compute first in %s' % self.name) + + def get_pimg_err(self, data_dict): + return data_dict diff --git a/SPIGA/spiga/eval/benchmark/metrics/pose.py b/SPIGA/spiga/eval/benchmark/metrics/pose.py new file mode 100644 index 0000000000000000000000000000000000000000..3e591f00f71f26466d66545a5229663f116193eb --- /dev/null +++ b/SPIGA/spiga/eval/benchmark/metrics/pose.py @@ -0,0 +1,159 @@ +import numpy as np +from sklearn.metrics import confusion_matrix + +from spiga.eval.benchmark.metrics.metrics import Metrics + + +class MetricsHeadpose(Metrics): + + def __init__(self, name='headpose'): + super().__init__(name) + + # Angles + self.angles = ['yaw', 'pitch', 'roll'] + # Confusion matrix intervals + self.pose_labels = [-90, -75, -60, -45, -30, -15, 0, 15, 30, 45, 60, 75, 90] + # Percentile reference angles + self.error_labels = [2.5, 5, 10, 15, 30] + # Cumulative plot axis length + self.bins = 1000 + + def compute_error(self, data_anns, data_pred, database, select_ids=None): + + # Initialize global logs and variables of Computer Error function + self.init_ce(data_anns, data_pred, database) + + # Generate annotations if needed + if data_anns[0]['headpose'] is None: + print('Database anns generated by posit...') + data_anns = self._posit_anns() + print('Posit generation done...') + + # Dictionary variables + self.error['data_pred'] = [] + self.error['data_anns'] = [] + self.error['data_pred_trl'] = [] + self.error['data_anns_trl'] = [] + self.error['mae_ypr'] = [] + self.error['mae_mean'] = [] + + # Order data + for img_id, img_anns in enumerate(data_anns): + pose_anns = img_anns['headpose'][0:3] + self.error['data_anns'].append(pose_anns) + pose_pred = data_pred[img_id]['headpose'][0:3] + self.error['data_pred'].append(pose_pred) + + # Compute MAE error + anns_array = np.array(self.error['data_anns']) + pred_array = np.array(self.error['data_pred']) + mae_ypr = np.abs((anns_array-pred_array)) + self.error['mae_ypr'] = mae_ypr.tolist() + self.error['mae_mean'] = np.mean(mae_ypr, axis=-1).tolist() + + # Quantize labeled data + label_anns = self._nearest_label(anns_array) + label_pred = self._nearest_label(pred_array) + self.error['label_anns'] = label_anns + self.error['label_pred'] = label_pred + + for angle_id, angle in enumerate(self.angles): + # Confusion matrix + self.error['cm_%s' % angle] = confusion_matrix(label_anns[:, angle_id], label_pred[:, angle_id]) + # Cumulative error + self.error['cumulative_%s' % angle] = self._cumulative_error(mae_ypr[:, angle_id], bins=self.bins) + + return self.error + + def metrics(self): + + # Initialize global logs and variables of Metrics function + self.init_metrics() + + # Mean Absolute Error + mae_ypr = np.array(self.error['mae_ypr']) + mae_ypr_mean = np.mean(mae_ypr, axis=0) + self.metrics_log['mae_ypr'] = mae_ypr_mean.tolist() + self.metrics_log['mae_mean'] = np.mean(mae_ypr_mean) + print('MAE [yaw, pitch, roll]: [%.3f, %.3f, %.3f]' % (mae_ypr_mean[0], mae_ypr_mean[1], mae_ypr_mean[2])) + print('MAE mean: %.3f' % self.metrics_log['mae_mean']) + + # Per angle measurements + self.metrics_log['acc_label'] = [] + self.metrics_log['acc_adj_label'] = [] + + for angle_id, angle in enumerate(self.angles): + + # Accuracy per label + cm = self.error['cm_%s' % angle] + diagonal = np.diagonal(cm, offset=0).sum() + acc_main = diagonal / cm.sum().astype('float') + self.metrics_log['acc_label'].append(acc_main) + + # Permissive accuracy + diagonal_adj = diagonal.sum() + np.diagonal(cm, offset=-1).sum() + np.diagonal(cm, offset=1).sum() + acc_adj = diagonal_adj / cm.sum().astype('float') + self.metrics_log['acc_adj_label'].append(acc_adj) + + # Percentile of relevant angles + self.metrics_log['sr_%s' % angle] = {} + for angle_num in self.error_labels: + if max(mae_ypr[:, angle_id]) > angle_num: + [cumulative, base] = self.error['cumulative_%s' % angle] + perc = [cumulative[x[0] - 1] for x in enumerate(base) if x[1] > angle_num][0] + else: + perc = 1. + + self.metrics_log['sr_%s' % angle][angle_num] = perc + + print('Accuracy [yaw, pitch, roll]: ', self.metrics_log['acc_label']) + print('Accuracy [yaw, pitch, roll] (adjacency as TP): ', self.metrics_log['acc_adj_label']) + for angle in self.angles: + print('Success Rate %s: ' % angle, self.metrics_log['sr_%s' % angle]) + + return self.metrics_log + + def get_pimg_err(self, data_dict, img_select=None): + mae_mean = self.error['mae_mean'] + mae_ypr = self.error['mae_ypr'] + if img_select is not None: + mae_mean = [mae_mean[img_id] for img_id in img_select] + mae_ypr = [mae_ypr[img_id] for img_id in img_select] + name_dict = self.name + '/%s' + data_dict[name_dict % 'mae'] = mae_mean + mae_ypr = np.array(mae_ypr) + data_dict[name_dict % 'mae_yaw'] = mae_ypr[:, 0].tolist() + data_dict[name_dict % 'mae_pitch'] = mae_ypr[:, 1].tolist() + data_dict[name_dict % 'mae_roll'] = mae_ypr[:, 2].tolist() + return data_dict + + def _posit_anns(self): + + import spiga.data.loaders.dl_config as dl_config + import spiga.data.loaders.dataloader as dl + + # Load configuration + data_config = dl_config.AlignConfig(self.database, self.data_type) + data_config.image_size = (256, 256) + data_config.generate_pose = True + data_config.aug_names = [] + data_config.shuffle = False + dataloader, _ = dl.get_dataloader(1, data_config, debug=True) + + data_anns = [] + for num_batch, batch_dict in enumerate(dataloader): + pose = batch_dict['pose'].numpy() + data_anns.append({'headpose': pose[0].tolist()}) + return data_anns + + def _nearest_label(self, data): + data_tile = data[:, :, np.newaxis] + data_tile = np.tile(data_tile, len(self.pose_labels)) + diff_tile = np.abs(data_tile - self.pose_labels) + label_idx = diff_tile.argmin(axis=-1) + return label_idx + + def _cumulative_error(self, error, bins=1000): + num_imgs, base = np.histogram(error, bins=bins) + cumulative = [x / float(len(error)) for x in np.cumsum(num_imgs)] + return [cumulative[:bins], base[:bins]] diff --git a/SPIGA/spiga/eval/benchmark/readme.md b/SPIGA/spiga/eval/benchmark/readme.md new file mode 100644 index 0000000000000000000000000000000000000000..d4cb7c4d266816ef48e7ecec2e1da07f4d6f4c68 --- /dev/null +++ b/SPIGA/spiga/eval/benchmark/readme.md @@ -0,0 +1,24 @@ +# SPIGA: Benchmark +The benchmark evaluator can be found at ```./eval/benchmark/evaluator.py``` and it allows +to extract an extended report of metrics for each dataset. For further details, +check the parser and complete the interactive terminal procedure to specify the evaluation +characteristics. + +In order to use the benchmark evaluation, the prediction file must follow the same data structure +and file extension as the ground truth annotations available in ```./data/annotations/```. +The data structure consist on a list of dictionaries where each one represents an image sample, +similar to the previous dataloader configuration: + +``` +sample = {"imgpath": Relative image path, + "bbox": Bounding box [x,y,w,h] (ref image), + "headpose": Euler angles [yaw, pitch, roll], + "ids": Landmarks database ids, + "landmarks": Landmarks (ref image), + "visible": Visibilities [0,1, ...] (1 == Visible) + } +``` + +Finally, is worth to mention that the benchmark can be easily extended for other task by +inheriting the class structure available in ```./eval/benchmark/metrics/metrics.py``` and +developing a new task file like the available ones: landmarks and headpose. diff --git a/SPIGA/spiga/eval/results/300wprivate/metrics_300wprivate_test.txt b/SPIGA/spiga/eval/results/300wprivate/metrics_300wprivate_test.txt new file mode 100644 index 0000000000000000000000000000000000000000..132752a14125c287f1d0a664084ce4943a4b945c --- /dev/null +++ b/SPIGA/spiga/eval/results/300wprivate/metrics_300wprivate_test.txt @@ -0,0 +1,337 @@ +Metrics { + landmarks { + nme: 2.030598939445185 + nme_p90: 2.7880932616458525 + nme_p95: 3.0777544749713726 + nme_p99: 3.834184107657207 + nme_thr: 7 + nme_norm: lnd_bbox + auc: 71.00849804168183 + fr: 0.16666666666667052 + subset { + indoor { + nme: 2.034564559904317 + nme_p90: 2.7259855150065606 + nme_p95: 3.0092119632411545 + nme_p99: 3.713329759683323 + auc: 70.96381253891056 + fr: 0.33333333333332993 + } + outdoor { + nme: 2.0266333189860526 + nme_p90: 2.823638152094534 + nme_p95: 3.217040770610454 + nme_p99: 3.834184107657207 + auc: 71.05339689254487 + fr: 0.0 + } + } + nme_per_ldm { + 101: 3.6806610803182505 + 102: 3.3036602516363742 + 103: 3.339433875945013 + 104: 3.454702516496273 + 105: 3.611916041455306 + 106: 3.719966247876225 + 107: 3.548076775082098 + 108: 3.2518252416098865 + 24: 3.096658896153719 + 110: 3.331046674179755 + 111: 3.699712378619379 + 112: 3.7843353250872225 + 113: 3.6034097769479234 + 114: 3.398488809686842 + 115: 3.3141217781436625 + 116: 3.280323260898595 + 117: 3.544361895970207 + 1: 2.757092591472853 + 119: 2.242685122483485 + 2: 2.0915854137040806 + 121: 2.0586213715102817 + 3: 2.123266891475812 + 4: 2.078486972366517 + 124: 1.796939685624812 + 5: 1.9188959395054488 + 126: 2.1738624874122228 + 6: 2.624636921552657 + 128: 1.5520879573321433 + 129: 1.2549002865469516 + 130: 1.17669611982962 + 17: 1.4660272904294709 + 16: 1.4505750980043473 + 133: 1.029206611825485 + 134: 1.1578763764399964 + 135: 1.4523188926457233 + 18: 1.8149727805659837 + 7: 1.388113293070523 + 138: 0.9782280739323941 + 139: 1.4519658473793906 + 8: 1.9434955210694351 + 141: 1.579927226333795 + 142: 0.9795537257185432 + 11: 1.573585552070739 + 144: 1.009652358478732 + 145: 1.2587210616231412 + 12: 1.5793154047393527 + 147: 1.1712298544072581 + 148: 1.0158092454679306 + 20: 1.3654116942883525 + 150: 1.3991990474588623 + 151: 1.2462856085922873 + 22: 1.0382222181925866 + 153: 1.4298055400286076 + 154: 1.6178077717355814 + 21: 1.9146205126976596 + 156: 1.7453498742022029 + 157: 1.6858832552899667 + 23: 1.396568360761986 + 159: 1.5292370812850333 + 160: 1.5946255121363364 + 161: 1.3332901947302789 + 162: 1.1785447751601195 + 163: 1.0187335950212426 + 164: 1.3344807664948581 + 165: 1.736265138539922 + 166: 1.638976611962414 + 167: 1.3432143685181699 + 168: 1.4211731540502521 + } + npe90_per_ldm { + 101: 7.792348947260428 + 102: 7.084284783662423 + 103: 7.00267244505699 + 104: 7.11370360965358 + 105: 7.169040113179254 + 106: 7.2420085022388765 + 107: 7.0092655347920685 + 108: 6.653925085500781 + 24: 6.312629764258624 + 110: 6.454926282662611 + 111: 7.414894684684534 + 112: 7.8126541675676835 + 113: 7.415456624957532 + 114: 7.24509404695461 + 115: 6.912281722736787 + 116: 6.672501696370728 + 117: 7.217817998736465 + 1: 5.487776518419356 + 119: 4.454286064030085 + 2: 4.0134627911922 + 121: 4.088715377295195 + 3: 4.211052099955585 + 4: 4.037415662963983 + 124: 3.4469165471729477 + 5: 3.9864537671903637 + 126: 4.4751537271539075 + 6: 5.474239719648658 + 128: 2.834816765905374 + 129: 2.2342495378788207 + 130: 2.1759546821990923 + 17: 2.5418198758079984 + 16: 2.576833155505584 + 133: 1.9794875969490342 + 134: 2.098944179442805 + 135: 2.407073180794855 + 18: 2.9144263159065007 + 7: 2.7047079934870015 + 138: 1.8557917169522138 + 139: 2.457276944950026 + 8: 3.2924827521662205 + 141: 2.704159715833272 + 142: 1.8698923398185585 + 11: 2.683163668302068 + 144: 1.8304971688134921 + 145: 2.184512515479075 + 12: 2.912935303982953 + 147: 2.074820991655545 + 148: 1.8803985833925125 + 20: 2.4937956106514334 + 150: 2.591990835431721 + 151: 2.2625583999418772 + 22: 1.9780265158922163 + 153: 2.6224550571489877 + 154: 3.2408057855185093 + 21: 3.707365699795642 + 156: 3.1072768395751913 + 157: 3.1679371463471115 + 23: 2.510236952841339 + 159: 2.8718913632783964 + 160: 2.881251348014151 + 161: 2.524050295380916 + 162: 2.1275892848246936 + 163: 1.884137823110829 + 164: 2.432245754693854 + 165: 3.337998651440683 + 166: 2.9696817088203815 + 167: 2.316776125494591 + 168: 2.568779298951829 + } + npe95_per_ldm { + 101: 10.075572675677341 + 102: 8.818179377359794 + 103: 8.782133525632883 + 104: 8.643303594630462 + 105: 8.606411141514197 + 106: 8.641525601763867 + 107: 8.045215924441003 + 108: 8.435963345382614 + 24: 8.98978588560972 + 110: 9.209410203200584 + 111: 9.690509154913633 + 112: 9.528589159993023 + 113: 9.516280184903218 + 114: 8.806410992841911 + 115: 8.349939939616558 + 116: 8.306406512963349 + 117: 8.948843864453119 + 1: 6.607728795206713 + 119: 5.328839886207676 + 2: 4.719557597011315 + 121: 4.803093906639568 + 3: 5.066642833569373 + 4: 5.106882789323109 + 124: 4.405464649556331 + 5: 4.792967300757355 + 126: 5.312659675767809 + 6: 6.55777924210191 + 128: 3.309968146826916 + 129: 2.6825883040009937 + 130: 2.4823859073064334 + 17: 3.107821014772654 + 16: 3.104094496813284 + 133: 2.2987283138903787 + 134: 2.3965594095703406 + 135: 2.778131597510065 + 18: 3.417492367908234 + 7: 3.620758651495707 + 138: 2.5771490826818635 + 139: 2.983064731141363 + 8: 3.718558278089841 + 141: 3.1060236607485288 + 142: 2.382002241110809 + 11: 3.1854035291469387 + 144: 2.2942253082346777 + 145: 2.7631832911247534 + 12: 3.4466035286261287 + 147: 2.6992500039970317 + 148: 2.3485294437550133 + 20: 3.216585381779816 + 150: 3.0851452590040425 + 151: 3.0592010658988906 + 22: 2.4266778242787073 + 153: 3.38165515276341 + 154: 3.7832660988534497 + 21: 4.581001942866445 + 156: 3.8923444760487502 + 157: 3.7494216498115063 + 23: 3.3595885805903856 + 159: 3.6741936975782754 + 160: 3.5264543871919876 + 161: 3.1694861030365487 + 162: 2.515374327000464 + 163: 2.2866964953427025 + 164: 3.1082736052648565 + 165: 4.031899925586421 + 166: 3.578448574876227 + 167: 2.875831262261589 + 168: 3.232139784668087 + } + npe99_per_ldm { + 101: 13.801902428443963 + 102: 12.87712171046809 + 103: 12.402656213930339 + 104: 11.1057085602639 + 105: 11.353922785698465 + 106: 11.647547037817693 + 107: 12.83429625061474 + 108: 13.307141731654763 + 24: 14.618925151278201 + 110: 15.261628339432663 + 111: 14.14823585987817 + 112: 12.335533428069908 + 113: 11.802116552825849 + 114: 12.510726633232077 + 115: 12.69435364188939 + 116: 12.89529194227151 + 117: 14.120910351994045 + 1: 8.638311101530586 + 119: 7.535269476509163 + 2: 6.559870102583517 + 121: 6.630420572209065 + 3: 8.290823571978367 + 4: 7.6847786232321535 + 124: 6.822107522918532 + 5: 6.939187568926209 + 126: 7.608413202225105 + 6: 8.340906801308865 + 128: 5.072392719133257 + 129: 3.5758878270546597 + 130: 3.172918188296416 + 17: 4.218440531352108 + 16: 3.931176580980738 + 133: 2.919954597731364 + 134: 3.236737576939871 + 135: 3.415454133426117 + 18: 4.643995661949497 + 7: 5.772164810850686 + 138: 5.238776860999826 + 139: 4.208475684527024 + 8: 4.7641538901480445 + 141: 4.113162874534946 + 142: 4.625693800831237 + 11: 4.451128264439006 + 144: 4.168386107123375 + 145: 5.1101945338282695 + 12: 5.31672303499037 + 147: 4.523658333756621 + 148: 3.5122981836488223 + 20: 7.080964010381011 + 150: 6.377625659811748 + 151: 4.928590462504693 + 22: 4.701579190184112 + 153: 4.727943873063984 + 154: 5.465818611585125 + 21: 6.148406910087535 + 156: 6.786793649953492 + 157: 6.186824707078167 + 23: 6.837078051253573 + 159: 7.605776962432469 + 160: 7.235180906998915 + 161: 7.982744434560323 + 162: 4.656982439604284 + 163: 4.270483732934878 + 164: 4.6446884214498345 + 165: 6.0823676390136034 + 166: 6.9716680872367105 + 167: 7.432470055536447 + 168: 7.3663196613198 + } + } + headpose { + mae_ypr: [1.6090495251118835, 2.046698079387603, 0.955561359343095] + mae_mean: 1.537102987947527 + acc_label: [0.9183333333333333, 0.87, 0.9366666666666666] + acc_adj_label: [1.0, 1.0, 1.0] + sr_yaw { + 2.5: 0.7983333333333333 + 5: 0.97 + 10: 0.9983333333333333 + 15: 1.0 + 30: 1.0 + } + sr_pitch { + 2.5: 0.6883333333333334 + 5: 0.9416666666666667 + 10: 0.9966666666666667 + 15: 1.0 + 30: 1.0 + } + sr_roll { + 2.5: 0.9416666666666667 + 5: 0.9983333333333333 + 10: 1.0 + 15: 1.0 + 30: 1.0 + } + } + } diff --git a/SPIGA/spiga/eval/results/300wprivate/results_300wprivate_test.json b/SPIGA/spiga/eval/results/300wprivate/results_300wprivate_test.json new file mode 100644 index 0000000000000000000000000000000000000000..99ab6e8efbddc025cefb3daef201088a9269eb15 --- /dev/null +++ b/SPIGA/spiga/eval/results/300wprivate/results_300wprivate_test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:9c50536962725dd3cde6169f48fea7447314e17d1564ecf1921827704b6893af +size 2223550 diff --git a/SPIGA/spiga/eval/results/300wpublic/metrics_300wpublic_test.txt b/SPIGA/spiga/eval/results/300wpublic/metrics_300wpublic_test.txt new file mode 100644 index 0000000000000000000000000000000000000000..49e1f7cd1309fe4bd100d1b3f8aee063b1973e95 --- /dev/null +++ b/SPIGA/spiga/eval/results/300wpublic/metrics_300wpublic_test.txt @@ -0,0 +1,353 @@ +Metrics { + landmarks { + nme: 2.993687267871256 + nme_p90: 4.666037430932269 + nme_p95: 5.435113114011185 + nme_p99: 7.320552484553374 + nme_thr: 8 + nme_norm: corners + auc: 62.72750851023099 + fr: 0.7256894049346929 + subset { + helen { + nme: 2.5194569810704968 + nme_p90: 3.588651040403328 + nme_p95: 3.9771381372856305 + nme_p99: 5.038565693708802 + auc: 68.51294946769845 + fr: 0.0 + } + lfpw { + nme: 2.6867036799108392 + nme_p90: 3.8500450455085744 + nme_p95: 4.232240763191166 + nme_p99: 5.2672893244075185 + auc: 66.42133313963284 + fr: 0.0 + } + common { + nme: 2.5870801950420437 + nme_p90: 3.710404666983561 + nme_p95: 4.083736280045437 + nme_p99: 5.216315947831376 + auc: 67.6676731570753 + fr: 0.0 + } + ibug { + nme: 4.662282218592618 + nme_p90: 6.628041366327217 + nme_p95: 7.390973031124523 + nme_p99: 10.093415564142603 + auc: 42.44787101795513 + fr: 3.703703703703709 + } + } + nme_per_ldm { + 101: 6.160148291662601 + 102: 5.609969055309763 + 103: 5.639963193216567 + 104: 5.700234717877294 + 105: 5.62936644920689 + 106: 5.574676189493879 + 107: 5.349393371824218 + 108: 4.702542530122117 + 24: 4.168177272711497 + 110: 4.485507899065954 + 111: 5.208036708182383 + 112: 5.493830104918947 + 113: 5.586260490385025 + 114: 5.714415950920614 + 115: 5.442384369263486 + 116: 5.4538915292008125 + 117: 6.178730799959288 + 1: 4.165885001962012 + 119: 3.1921307867109445 + 2: 2.6405652171792697 + 121: 2.7692371208173987 + 3: 3.771312716404229 + 4: 3.915696771337146 + 124: 3.0583414383575067 + 5: 2.7836732387071392 + 126: 2.9600464424059627 + 6: 3.9325330705818566 + 128: 2.266086276562485 + 129: 1.879556319441715 + 130: 1.9706376235225898 + 17: 2.4439140053778123 + 16: 2.648478293025234 + 133: 2.1738938082518318 + 134: 1.9817528088827188 + 135: 1.7966616924282088 + 18: 2.1889880619377 + 7: 1.6798354870145646 + 138: 1.4525365591905652 + 139: 1.5444551246243863 + 8: 1.6622930186366096 + 141: 1.529130733663348 + 142: 1.461878641713216 + 11: 1.6372097638236516 + 144: 1.3940225437140497 + 145: 1.5293915903135549 + 12: 1.6939793028036296 + 147: 1.4966723651722735 + 148: 1.441845674425855 + 20: 1.81709289789314 + 150: 1.9693359999114588 + 151: 1.884337269187178 + 22: 1.4862224166931166 + 153: 1.9633109788224843 + 154: 1.9772138173842613 + 21: 1.9430947452720937 + 156: 2.5919972321865066 + 157: 2.561137981239902 + 23: 2.1950781821923164 + 159: 2.4901805745220082 + 160: 2.550118126201779 + 161: 1.9205944941018516 + 162: 1.7900476486146397 + 163: 1.3976363193641992 + 164: 1.9106126973833983 + 165: 2.0763873452059816 + 166: 2.1224747018434096 + 167: 1.693262532344654 + 168: 2.070427832570231 + } + npe90_per_ldm { + 101: 13.122683532466992 + 102: 11.837902215558064 + 103: 11.75616577370391 + 104: 11.875509248652866 + 105: 12.212341286473402 + 106: 11.149962035433145 + 107: 10.613398355229833 + 108: 9.389892873095325 + 24: 8.591199066081636 + 110: 9.421511135997605 + 111: 11.193086402244425 + 112: 11.707000001316612 + 113: 11.349684731339558 + 114: 11.811597643003372 + 115: 10.607833816884204 + 116: 11.243376754752148 + 117: 12.971478848872138 + 1: 9.23874231532177 + 119: 6.7372032763499545 + 2: 5.33974784249774 + 121: 5.732096724504876 + 3: 7.5062452089485365 + 4: 7.456439231223284 + 124: 5.8237217172512095 + 5: 5.37182931231504 + 126: 6.094696584923242 + 6: 8.17012872398533 + 128: 4.198385133649584 + 129: 3.3444779030854996 + 130: 3.5638768938015297 + 17: 4.429228974895804 + 16: 4.869116170096254 + 133: 4.157919854236839 + 134: 4.108282493143575 + 135: 3.522263446262345 + 18: 4.002610414280894 + 7: 3.2908041808066506 + 138: 2.7722779484559354 + 139: 3.1732425721021564 + 8: 3.466774533899654 + 141: 2.978701593114757 + 142: 2.7587386420612185 + 11: 3.2356256090137006 + 144: 2.69672824715176 + 145: 2.8984317775614516 + 12: 3.3750413338539142 + 147: 2.6896432032687887 + 148: 2.488745347966042 + 20: 3.4949560168183806 + 150: 3.615117113066581 + 151: 3.5894529408226603 + 22: 2.909838203155513 + 153: 3.7097208120818275 + 154: 3.919346282690197 + 21: 4.196338523026944 + 156: 4.950309881678925 + 157: 4.765821211342502 + 23: 4.117335074736717 + 159: 4.621291671397001 + 160: 4.736419766006695 + 161: 3.818460262745092 + 162: 3.385764999285364 + 163: 2.573588612350815 + 164: 3.785005840288626 + 165: 4.022827504716443 + 166: 4.00963166181946 + 167: 3.105493633989696 + 168: 3.9076308361907075 + } + npe95_per_ldm { + 101: 16.640887862533262 + 102: 15.73249785912902 + 103: 14.94766424497651 + 104: 15.524963676616089 + 105: 15.873365705127112 + 106: 16.417111507079138 + 107: 14.567853910225598 + 108: 12.510205643500568 + 24: 12.143881169760876 + 110: 12.089065625344906 + 111: 14.366730260926783 + 112: 14.740499149458255 + 113: 15.459087674693276 + 114: 14.599722757007777 + 115: 15.320290937083609 + 116: 14.708246193314626 + 117: 16.418629645261973 + 1: 11.937667692240536 + 119: 8.52572385838488 + 2: 6.659827131118409 + 121: 7.070926140929972 + 3: 9.409775342546114 + 4: 9.185034717032613 + 124: 7.160591484765116 + 5: 6.465838615220728 + 126: 7.2916218490559945 + 6: 10.085439984678748 + 128: 4.945152308750049 + 129: 4.240340551642683 + 130: 4.235830937943613 + 17: 5.07803313070256 + 16: 6.301010594644189 + 133: 5.3003686467661835 + 134: 5.39773858718444 + 135: 4.775021937005514 + 18: 5.647719520272081 + 7: 4.274205042229546 + 138: 3.594392271949664 + 139: 4.089779282378731 + 8: 4.741065197374902 + 141: 3.9364873945583154 + 142: 3.3173099248264215 + 11: 4.0045732629352635 + 144: 3.158413099972695 + 145: 3.6099848378771133 + 12: 4.872231016970969 + 147: 3.6122138787323426 + 148: 3.1785153515663076 + 20: 4.629010728226188 + 150: 4.8588032103886345 + 151: 4.64642981328001 + 22: 3.6423999181932727 + 153: 4.706447394770584 + 154: 4.916454492667414 + 21: 5.4326415927145755 + 156: 6.8671568682767665 + 157: 6.620902515780232 + 23: 5.608019225929798 + 159: 6.244705316060662 + 160: 6.2049492392703645 + 161: 4.621479019005777 + 162: 4.386075192468076 + 163: 3.4769696652222586 + 164: 4.58677707682409 + 165: 5.5239135136002755 + 166: 5.487065873148972 + 167: 4.446659252100746 + 168: 5.294582035532603 + } + npe99_per_ldm { + 101: 23.9472105829856 + 102: 21.712780306667675 + 103: 21.313324271514396 + 104: 21.368750734861273 + 105: 22.232228723373485 + 106: 25.08953794210005 + 107: 24.944096885619654 + 108: 22.96040182762928 + 24: 22.894704116944336 + 110: 22.614380914459304 + 111: 22.256763074721803 + 112: 21.25918241444815 + 113: 20.286955186210022 + 114: 25.694990732800143 + 115: 23.465421874951634 + 116: 23.351073650613607 + 117: 24.978511767730428 + 1: 16.4324939088724 + 119: 13.422956195988334 + 2: 9.618581533279238 + 121: 10.118878457527511 + 3: 12.82211476714369 + 4: 11.67716301954819 + 124: 10.797328353981431 + 5: 11.235362955909709 + 126: 12.247003662455013 + 6: 15.773704754299274 + 128: 6.383363322637416 + 129: 6.321260974342025 + 130: 6.300611559944998 + 17: 8.164659256640022 + 16: 9.51053078772321 + 133: 8.273369391152267 + 134: 8.076100532657165 + 135: 7.688675439981096 + 18: 9.79951835561599 + 7: 7.033074751907975 + 138: 6.423074083674037 + 139: 6.9446604878218565 + 8: 7.574534227892147 + 141: 6.5307976262292335 + 142: 6.341758670051268 + 11: 6.5760383486423315 + 144: 5.286412075946667 + 145: 7.240882514689094 + 12: 7.739950501196232 + 147: 7.44356729074967 + 148: 5.468215521283997 + 20: 8.286609944508777 + 150: 8.069308096570612 + 151: 7.411738191325378 + 22: 6.142237156302458 + 153: 7.701905468720823 + 154: 8.52986712064459 + 21: 9.300708464380659 + 156: 13.14337152729244 + 157: 11.376582767015504 + 23: 11.795090745823842 + 159: 11.10872358521376 + 160: 11.855785481682954 + 161: 7.618868444259899 + 162: 6.610868401789532 + 163: 6.220955897344144 + 164: 8.126455622376907 + 165: 9.37200137441875 + 166: 10.480683232603582 + 167: 8.139103679313033 + 168: 10.707529142440695 + } + } + headpose { + mae_ypr: [1.4116569256059106, 1.7011980952121855, 0.7716754190283938] + mae_mean: 1.29484347994883 + acc_label: [0.8911465892597968, 0.8824383164005806, 0.9608127721335269] + acc_adj_label: [1.0, 1.0, 1.0] + sr_yaw { + 2.5: 0.8374455732946299 + 5: 0.9796806966618288 + 10: 0.9970972423802612 + 15: 0.9985486211901307 + 30: 1.0 + } + sr_pitch { + 2.5: 0.7677793904208998 + 5: 0.9753265602322206 + 10: 1.0 + 15: 1.0 + 30: 1.0 + } + sr_roll { + 2.5: 0.9564586357039188 + 5: 1.0 + 10: 1.0 + 15: 1.0 + 30: 1.0 + } + } + } diff --git a/SPIGA/spiga/eval/results/300wpublic/results_300wpublic_test.json b/SPIGA/spiga/eval/results/300wpublic/results_300wpublic_test.json new file mode 100644 index 0000000000000000000000000000000000000000..52ec5e25f13fb246df02054310dba804eb4b6452 --- /dev/null +++ b/SPIGA/spiga/eval/results/300wpublic/results_300wpublic_test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:f0aa3529879d1f265f2dedc8cb3057e715fdf56b37c3380f7b622c0720f9bfdc +size 2556728 diff --git a/SPIGA/spiga/eval/results/cofw68/metrics_cofw68_test.txt b/SPIGA/spiga/eval/results/cofw68/metrics_cofw68_test.txt new file mode 100644 index 0000000000000000000000000000000000000000..6b4037dcbd6c0867dc7159fd305f46d455003b72 --- /dev/null +++ b/SPIGA/spiga/eval/results/cofw68/metrics_cofw68_test.txt @@ -0,0 +1,319 @@ +Metrics { + landmarks { + nme: 2.517048299761656 + nme_p90: 3.439260118578336 + nme_p95: 4.065583073314784 + nme_p99: 5.5576659368466075 + nme_thr: 7 + nme_norm: lnd_bbox + auc: 64.04980282900947 + fr: 0.0 + nme_per_ldm { + 101: 4.386618760988867 + 102: 4.061629839664334 + 103: 3.983745459766538 + 104: 4.059943179619045 + 105: 3.901502523065625 + 106: 3.6464161308997243 + 107: 3.3236750419605943 + 108: 2.88736723178498 + 24: 2.7423694672096457 + 110: 3.0635795053213557 + 111: 3.571088090891605 + 112: 3.9983500297313452 + 113: 4.0943322771194595 + 114: 4.255800757059301 + 115: 4.2912918761153485 + 116: 4.266023792408103 + 117: 4.530578189494549 + 1: 3.158660231370845 + 119: 3.4125315663662614 + 2: 3.352789113391728 + 121: 3.417363298999408 + 3: 3.668232431297081 + 4: 3.91431465693854 + 124: 3.840416726980644 + 5: 3.6046913869421213 + 126: 3.387491193444403 + 6: 3.0296136285985975 + 128: 1.8998212393466836 + 129: 1.516826726048447 + 130: 1.5100915342372372 + 17: 1.6919453984466715 + 16: 1.421215739597502 + 133: 1.5697432942669043 + 134: 1.4987569995929837 + 135: 1.366172570997096 + 18: 1.2916655495623037 + 7: 1.7581540811039842 + 138: 1.5428715462019915 + 139: 1.3632059460397556 + 8: 1.3302291252462273 + 141: 1.287550535022652 + 142: 1.4467690355725018 + 11: 1.2907119544949173 + 144: 1.5873275912342366 + 145: 1.9198143064375461 + 12: 2.2533648088916247 + 147: 1.747890660026784 + 148: 1.436164845643807 + 20: 1.991609432994987 + 150: 1.8109854987255802 + 151: 1.6953683686244805 + 22: 1.5060260323923602 + 153: 1.708202891919297 + 154: 1.6963691562752732 + 21: 1.87731093602303 + 156: 2.142094773425542 + 157: 2.240978526071491 + 23: 2.110667241896683 + 159: 2.2746052761540887 + 160: 2.2265284572934942 + 161: 2.1973066159601427 + 162: 1.7926476622155938 + 163: 1.5326108170595516 + 164: 1.729851588257375 + 165: 2.121233580025467 + 166: 1.9985535852655705 + 167: 1.845910843504295 + 168: 2.0797132242663703 + } + npe90_per_ldm { + 101: 8.018897558697356 + 102: 7.97010628672223 + 103: 7.566745648570134 + 104: 8.095347755811265 + 105: 7.756765075016777 + 106: 7.039911855937849 + 107: 6.288952271483205 + 108: 5.773784683107754 + 24: 5.945580939663232 + 110: 5.829576040208693 + 111: 7.112875146109584 + 112: 7.940662690831719 + 113: 8.250074675668332 + 114: 8.07748482264541 + 115: 8.233109448421368 + 116: 8.242831765389505 + 117: 8.687203940264425 + 1: 5.86847210127666 + 119: 5.243952556782381 + 2: 5.137097829449687 + 121: 5.2659079859150815 + 3: 5.857022822554752 + 4: 6.151300083812946 + 124: 5.789014437973446 + 5: 5.372824967591501 + 126: 5.475210902866383 + 6: 5.86178580377768 + 128: 3.2289389333211234 + 129: 2.622261396524905 + 130: 2.7304992712176763 + 17: 3.1572454384592046 + 16: 2.452719009880311 + 133: 2.627498132517079 + 134: 2.7312065493277164 + 135: 2.2973900896540504 + 18: 2.0929480199891537 + 7: 3.65244010654807 + 138: 3.1776907692766656 + 139: 2.8232017769140567 + 8: 2.450986276686096 + 141: 2.491367195541456 + 142: 2.914612560836842 + 11: 2.510987040195006 + 144: 2.9695834676241772 + 145: 3.4200280229584106 + 12: 3.949345153264541 + 147: 3.1944286922995526 + 148: 2.487523608598698 + 20: 3.975484769060534 + 150: 3.385725078332356 + 151: 3.285296446152331 + 22: 2.7130471412453243 + 153: 2.992534087755148 + 154: 2.9411914409794786 + 21: 3.4939899717823275 + 156: 4.021007684523546 + 157: 4.190985454904701 + 23: 4.130310029590604 + 159: 4.314667308966008 + 160: 4.272504657006288 + 161: 4.685153554561627 + 162: 3.203495263181351 + 163: 2.747330827383441 + 164: 3.0265766339171187 + 165: 4.500497180240332 + 166: 3.8905157693437964 + 167: 3.891106312239455 + 168: 3.8933988592268465 + } + npe95_per_ldm { + 101: 10.417038072470968 + 102: 9.991198289523819 + 103: 9.379720137555848 + 104: 9.799656008084403 + 105: 9.22207737018875 + 106: 8.829078350035305 + 107: 7.992799269180475 + 108: 7.4082148935339465 + 24: 7.413781438652343 + 110: 7.37361147503038 + 111: 8.709348785745767 + 112: 9.312892440791485 + 113: 9.77808155435385 + 114: 10.325717515744035 + 115: 10.033803637246558 + 116: 10.004145195487656 + 117: 10.821755638172457 + 1: 6.765196576889283 + 119: 5.947330615300408 + 2: 5.862662969499837 + 121: 6.152025258743905 + 3: 7.1670021067469625 + 4: 7.454245442904308 + 124: 6.756637702306873 + 5: 6.1635352411726165 + 126: 6.519119512853371 + 6: 7.1940984593611095 + 128: 3.6571416433436674 + 129: 3.056401499324455 + 130: 3.3808439264483634 + 17: 4.061928034301918 + 16: 2.9407680765002353 + 133: 3.0653183161807847 + 134: 3.180963980499353 + 135: 2.901656649057088 + 18: 2.840245418802563 + 7: 4.597797894095366 + 138: 4.3035882561965675 + 139: 3.7014036924353197 + 8: 3.5013324792600873 + 141: 3.2526250820240743 + 142: 3.9174824517972575 + 11: 3.63472057362023 + 144: 4.191612176955886 + 145: 4.520173157846678 + 12: 4.912688917799541 + 147: 4.356777295067304 + 148: 3.8592166644229673 + 20: 5.541101603402795 + 150: 4.834433689727549 + 151: 4.3500326868388095 + 22: 3.813502938654715 + 153: 4.389537008701319 + 154: 4.776232703613533 + 21: 4.980501036793917 + 156: 5.277853337613837 + 157: 5.740403588832144 + 23: 5.724463408255806 + 159: 5.932445207932544 + 160: 5.8883880784816025 + 161: 6.852697999733049 + 162: 4.380159191875369 + 163: 3.5470116495641206 + 164: 3.992186775614564 + 165: 5.563741112172766 + 166: 5.302063622441587 + 167: 5.434068653301774 + 168: 5.857697902700627 + } + npe99_per_ldm { + 101: 15.088755845432772 + 102: 13.073819615334575 + 103: 13.477893246441145 + 104: 12.545880504907462 + 105: 12.097862148538754 + 106: 12.268080481835584 + 107: 11.25379241268216 + 108: 10.828929543085886 + 24: 11.717651103815243 + 110: 11.699755871901786 + 111: 12.184678792172349 + 112: 13.34509981517936 + 113: 11.83952843526531 + 114: 12.853085381739312 + 115: 13.994438403474529 + 116: 13.081667763696956 + 117: 14.42657011217481 + 1: 8.916371368807438 + 119: 7.997584620353168 + 2: 7.610065164179458 + 121: 7.6362815228963035 + 3: 8.797749915381567 + 4: 9.865833274647276 + 124: 7.910805681261553 + 5: 8.048606667984895 + 126: 8.619571570257547 + 6: 9.183003733406897 + 128: 4.865828948220972 + 129: 4.287177166390985 + 130: 5.352060488383854 + 17: 6.229529147494782 + 16: 4.921147034354624 + 133: 5.357211627886322 + 134: 5.565350192932446 + 135: 5.716824998156575 + 18: 5.408026129580792 + 7: 6.784161819068971 + 138: 6.674934894826747 + 139: 5.596098482770631 + 8: 4.810708425032517 + 141: 5.29448127755881 + 142: 5.587101373823092 + 11: 6.561695360938204 + 144: 6.190677292735184 + 145: 7.575832280733528 + 12: 7.970272010646224 + 147: 7.102125471669491 + 148: 6.117951030854053 + 20: 9.733188811612486 + 150: 8.108968351347654 + 151: 8.053888878839329 + 22: 8.501392906622689 + 153: 7.842154498433768 + 154: 9.348911008680913 + 21: 10.794637315024282 + 156: 11.4410194218526 + 157: 10.844758689065458 + 23: 10.508751739629794 + 159: 10.397173521760807 + 160: 9.493416503817661 + 161: 11.033949636665236 + 162: 8.776212120745663 + 163: 9.80338512675157 + 164: 9.456915239371774 + 165: 11.727340045598552 + 166: 11.91779218298747 + 167: 11.234236463238254 + 168: 11.068899102792699 + } + } + headpose { + mae_ypr: [2.083062363064235, 2.475056062512911, 0.9064911102818425] + mae_mean: 1.8215365119529963 + acc_label: [0.8875739644970414, 0.8520710059171598, 0.9388560157790927] + acc_adj_label: [1.0, 1.0, 1.0] + sr_yaw { + 2.5: 0.6923076923076923 + 5: 0.9368836291913215 + 10: 0.9960552268244576 + 15: 1.0 + 30: 1.0 + } + sr_pitch { + 2.5: 0.5798816568047337 + 5: 0.893491124260355 + 10: 0.9940828402366864 + 15: 1.0 + 30: 1.0 + } + sr_roll { + 2.5: 0.9428007889546351 + 5: 0.9980276134122288 + 10: 1.0 + 15: 1.0 + 30: 1.0 + } + } + } diff --git a/SPIGA/spiga/eval/results/cofw68/results_cofw68_test.json b/SPIGA/spiga/eval/results/cofw68/results_cofw68_test.json new file mode 100644 index 0000000000000000000000000000000000000000..79eaaa13cbfce5b7b224305fd4757fbe98263ac6 --- /dev/null +++ b/SPIGA/spiga/eval/results/cofw68/results_cofw68_test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:03acfc2ede335aac354c9fe2c9bd008beb9d6d596210c74b4231a95b6687dd9b +size 1898116 diff --git a/SPIGA/spiga/eval/results/merlrav/metrics_merlrav_test.txt b/SPIGA/spiga/eval/results/merlrav/metrics_merlrav_test.txt new file mode 100644 index 0000000000000000000000000000000000000000..582c650e219abb322077e3608d40f8dd8bc7b533 --- /dev/null +++ b/SPIGA/spiga/eval/results/merlrav/metrics_merlrav_test.txt @@ -0,0 +1,377 @@ +Metrics { + landmarks { + nme: 1.5086804931543236 + nme_p90: 2.1635501319152364 + nme_p95: 2.466109589313714 + nme_p99: 3.455642125258591 + nme_thr: 7 + nme_norm: lnd_bbox + auc: 78.47397661438411 + fr: 0.051746442432087925 + subset { + frontal { + nme: 1.61560462312357 + nme_p90: 2.2463951142028145 + nme_p95: 2.572226598305855 + nme_p99: 3.6210860696886833 + auc: 76.9597525877967 + fr: 0.09111617312073106 + } + half_profile { + nme: 1.6828487909060967 + nme_p90: 2.272702728357507 + nme_p95: 2.5471145536327953 + nme_p99: 3.3987905213552203 + auc: 75.9657914896377 + fr: 0.0 + } + half_profile_left { + nme: 1.6593883465198958 + nme_p90: 2.3284338844722074 + nme_p95: 2.5693632263530124 + nme_p99: 3.278697689229699 + auc: 76.30098571769051 + fr: 0.0 + } + half_profile_right { + nme: 1.7054658859842966 + nme_p90: 2.220904448144333 + nme_p95: 2.491175396697724 + nme_p99: 3.5122625056995673 + auc: 75.64173351430159 + fr: 0.0 + } + profile { + nme: 1.1912121935927615 + nme_p90: 1.7318457133250305 + nme_p95: 2.04549650792864 + nme_p99: 2.878427460092048 + auc: 82.98987188287711 + fr: 0.0 + } + profile_left { + nme: 1.1429927541204028 + nme_p90: 1.6430975490859832 + nme_p95: 1.9478367509011818 + nme_p99: 2.63876055903246 + auc: 83.67867425299369 + fr: 0.0 + } + profile_right { + nme: 1.2370558577626498 + nme_p90: 1.810307762848865 + nme_p95: 2.1411266828074176 + nme_p99: 2.9389777318895325 + auc: 82.332208276089 + fr: 0.0 + } + } + nme_per_ldm { + 101: 3.3589768431762175 + 102: 2.7531280870845873 + 103: 2.859701002904713 + 104: 2.8634457682779235 + 105: 2.877658841330188 + 106: 2.720071048885179 + 107: 2.4629924994495793 + 108: 2.2467294961158877 + 24: 2.1288254355152607 + 110: 2.2724448767452325 + 111: 2.540627823930061 + 112: 2.8284471937158453 + 113: 3.012202614117622 + 114: 3.0464652090359206 + 115: 3.0443508364827943 + 116: 2.9206874592197822 + 117: 3.5246519565195786 + 1: 2.4989484892381864 + 119: 2.094527573540818 + 2: 1.9975862837642682 + 121: 1.9667532281958748 + 3: 2.1557279059194916 + 4: 2.036801626056737 + 124: 1.825762147391309 + 5: 1.9798960712376632 + 126: 2.205651215578999 + 6: 2.6494703945724276 + 128: 1.4815483716437434 + 129: 1.231528474400865 + 130: 1.247063433631788 + 17: 1.4741665492704437 + 16: 1.204987012197412 + 133: 1.0170302588663973 + 134: 1.0350961889009112 + 135: 1.0078531087065747 + 18: 1.229081438697912 + 7: 1.2964041628692098 + 138: 1.1803380166768218 + 139: 1.1907173974524987 + 8: 1.1245143408558638 + 141: 1.1016743161735143 + 142: 1.1321081964660915 + 11: 1.0727780654424217 + 144: 1.1618244167936957 + 145: 1.2171458580396803 + 12: 1.3729999278923841 + 147: 1.1778922447451972 + 148: 1.1254606806695924 + 20: 1.0895438485495015 + 150: 1.1152916781328186 + 151: 1.186922081665385 + 22: 1.0107909205470527 + 153: 1.1651654397855509 + 154: 1.1413200775970356 + 21: 1.1505719973688346 + 156: 1.2323070958056401 + 157: 1.2951471399634233 + 23: 1.3496263569400522 + 159: 1.3166097535695698 + 160: 1.185578952219307 + 161: 1.1289970069187725 + 162: 1.1741022347060504 + 163: 1.0222564924321926 + 164: 1.182969390549842 + 165: 1.1677089625147783 + 166: 1.4000000311093093 + 167: 1.1875541874658213 + 168: 1.3548409427314658 + } + npe90_per_ldm { + 101: 6.841303462812936 + 102: 5.871967061156423 + 103: 6.435313555001839 + 104: 6.0863414215710545 + 105: 5.856386610328998 + 106: 5.3515838953111325 + 107: 4.936905109240317 + 108: 4.35646958881554 + 24: 4.154501717080872 + 110: 4.366467634101041 + 111: 5.007177442427851 + 112: 5.75662407531498 + 113: 6.147574364558974 + 114: 6.5819160311808504 + 115: 7.242887674595011 + 116: 6.139449989740605 + 117: 6.913785566410088 + 1: 5.264989646117678 + 119: 4.281934194047823 + 2: 4.078521868372654 + 121: 3.9081540494658076 + 3: 4.243355566911822 + 4: 4.016214823124536 + 124: 3.688705902703632 + 5: 3.9564376406091695 + 126: 4.667716897467507 + 6: 5.730550741940217 + 128: 2.671781950666222 + 129: 2.191045192348473 + 130: 2.238379783884833 + 17: 2.608140372894774 + 16: 2.1748623755375593 + 133: 1.7634276968625462 + 134: 1.8924906144995726 + 135: 1.7874400893528062 + 18: 2.2361018447957703 + 7: 2.5174159955382107 + 138: 2.2777400322113186 + 139: 2.230048482303937 + 8: 2.191010919936544 + 141: 2.097821997361514 + 142: 2.139694713995162 + 11: 2.1575823638269345 + 144: 2.1801001764063463 + 145: 2.3478125097855127 + 12: 2.6692055655031304 + 147: 2.2042056800179175 + 148: 2.0837791212171304 + 20: 2.0762878643553657 + 150: 2.069576194472468 + 151: 2.2168224383982555 + 22: 1.8675655632850923 + 153: 2.2593226852473003 + 154: 2.169092157346306 + 21: 2.2776575357980002 + 156: 2.313307796442557 + 157: 2.4325564157550295 + 23: 2.466093276107024 + 159: 2.457834012145091 + 160: 2.2375426349501075 + 161: 2.2227197578057774 + 162: 2.2256901798461644 + 163: 1.9237306114380308 + 164: 2.2285056022065644 + 165: 2.2872963189685924 + 166: 2.6474074126240037 + 167: 2.266259572666768 + 168: 2.6563960731826053 + } + npe95_per_ldm { + 101: 8.441117987108047 + 102: 7.809974197367657 + 103: 8.914018643798276 + 104: 7.985589833529736 + 105: 7.657610856797052 + 106: 6.901529644151474 + 107: 6.003484363104082 + 108: 5.359714843390148 + 24: 5.237271616781721 + 110: 5.35817329527914 + 111: 6.093353283047422 + 112: 7.178776732921367 + 113: 7.864851413344902 + 114: 8.435585935405099 + 115: 9.31943075203189 + 116: 8.338565642906014 + 117: 8.844323862195974 + 1: 6.920610608658486 + 119: 5.579137925444407 + 2: 5.118546782224291 + 121: 4.9331439703683095 + 3: 5.3920267113612 + 4: 4.991568250091611 + 124: 4.567737138187528 + 5: 5.007922132090623 + 126: 5.8629287499286376 + 6: 7.279068497806011 + 128: 3.277869272288929 + 129: 2.6265009714322414 + 130: 2.598266674561741 + 17: 3.1108016117707487 + 16: 2.6423645953005237 + 133: 2.1061442879934087 + 134: 2.3322800165604987 + 135: 2.1330354379938354 + 18: 2.7965749304352037 + 7: 3.28428298493539 + 138: 2.9011942090088265 + 139: 2.8616896234789064 + 8: 2.965395206958521 + 141: 2.7671326920439228 + 142: 2.720548244959449 + 11: 2.7847408257771025 + 144: 2.8207150460715664 + 145: 3.0690144016397145 + 12: 3.5641601474934723 + 147: 2.9816894630361896 + 148: 2.7772131964014806 + 20: 2.9545877208209697 + 150: 2.676521986087967 + 151: 2.8397352668704365 + 22: 2.452843817529208 + 153: 2.786238880172479 + 154: 2.6948539822082376 + 21: 3.2014971657831786 + 156: 2.99331035258674 + 157: 3.099565507520246 + 23: 3.1536920132264137 + 159: 3.035724672323389 + 160: 2.8590697596373205 + 161: 3.18328939939261 + 162: 2.745295751539974 + 163: 2.491584206354821 + 164: 2.7848191019354513 + 165: 3.25229943328409 + 166: 3.384820152838584 + 167: 2.972183782174847 + 168: 3.393574192195915 + } + npe99_per_ldm { + 101: 13.306254348151949 + 102: 12.981243433347958 + 103: 14.194854214648371 + 104: 12.773848328599131 + 105: 11.310276344499538 + 106: 10.033189122433079 + 107: 8.737335443356818 + 108: 8.689656343619724 + 24: 8.813631497738173 + 110: 8.98053893671926 + 111: 9.200895008592042 + 112: 10.574307218972542 + 113: 11.80779942179725 + 114: 12.831817823579 + 115: 14.90723684715645 + 116: 13.403174325402333 + 117: 14.32637544856898 + 1: 11.107329717515297 + 119: 8.819292038261858 + 2: 7.998693376996145 + 121: 7.6630438328081265 + 3: 8.180601672453921 + 4: 7.1172156178272115 + 124: 6.883517943873057 + 5: 7.469622468883537 + 126: 9.260935533221096 + 6: 11.394333320505359 + 128: 4.985104181306873 + 129: 3.6610539607732746 + 130: 3.577669553046159 + 17: 4.282318668694788 + 16: 4.4367360979513535 + 133: 3.4077506728617175 + 134: 3.5073978351923065 + 135: 3.072085422485997 + 18: 3.8561367097286876 + 7: 5.243996543352382 + 138: 4.736214805102126 + 139: 4.658932237258348 + 8: 5.035769413543924 + 141: 4.859906333306005 + 142: 4.687698979363885 + 11: 4.754515314723082 + 144: 4.7954279914279745 + 145: 5.177008093991888 + 12: 6.376708713699464 + 147: 5.357222555071042 + 148: 4.726237540189613 + 20: 5.785803524452584 + 150: 4.7338985598610925 + 151: 4.626492612315765 + 22: 4.163245408353465 + 153: 4.496380103516062 + 154: 4.341338388123191 + 21: 6.061105262023478 + 156: 5.334943775605292 + 157: 5.152214838495613 + 23: 5.874569691242533 + 159: 5.791913011910687 + 160: 5.062634991173862 + 161: 5.835847336978609 + 162: 4.5226670212359945 + 163: 4.242683346393679 + 164: 4.30806562074895 + 165: 6.014068598402919 + 166: 5.471812890679048 + 167: 5.600333148651882 + 168: 5.405042102742384 + } + } + headpose { + mae_ypr: [3.2345458128780242, 2.2386364658267817, 1.7062846932804483] + mae_mean: 2.393155657328418 + acc_label: [0.8087968952134541, 0.8543337645536869, 0.8892626131953428] + acc_adj_label: [0.9886157826649418, 0.9992238033635188, 0.9979301423027167] + sr_yaw { + 2.5: 0.6530401034928849 + 5: 0.8369987063389392 + 10: 0.9340232858990944 + 15: 0.9707632600258732 + 30: 0.9937904269081501 + } + sr_pitch { + 2.5: 0.6763260025873221 + 5: 0.9099611901681759 + 10: 0.9912031047865459 + 15: 0.9979301423027167 + 30: 0.9997412677878396 + } + sr_roll { + 2.5: 0.8243208279430789 + 5: 0.9291073738680465 + 10: 0.9800776196636481 + 15: 0.9943078913324709 + 30: 0.9987063389391979 + } + } + } diff --git a/SPIGA/spiga/eval/results/merlrav/results_merlrav_test.json b/SPIGA/spiga/eval/results/merlrav/results_merlrav_test.json new file mode 100644 index 0000000000000000000000000000000000000000..e34420cc35f14668037cad7777bfdb5198213e14 --- /dev/null +++ b/SPIGA/spiga/eval/results/merlrav/results_merlrav_test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:490f620f568d5cced54f61cf9b0a449c7e414c0f90f659290935d39811cbe1ee +size 14445509 diff --git a/SPIGA/spiga/eval/results/wflw/metrics_wflw_test.txt b/SPIGA/spiga/eval/results/wflw/metrics_wflw_test.txt new file mode 100644 index 0000000000000000000000000000000000000000..e6438fcfcc347c37561e100f1d0530679468f224 --- /dev/null +++ b/SPIGA/spiga/eval/results/wflw/metrics_wflw_test.txt @@ -0,0 +1,489 @@ +Metrics { + landmarks { + nme: 4.060449569787332 + nme_p90: 6.765928760955893 + nme_p95: 8.197544910122737 + nme_p99: 13.090868491915499 + nme_thr: 10 + nme_norm: corners + auc: 60.55545281848933 + fr: 2.080000000000004 + subset { + pose { + nme: 7.1406786522793455 + nme_p90: 10.683591623734115 + nme_p95: 13.331614480116997 + nme_p99: 26.88728473439624 + auc: 35.30522609772822 + fr: 11.65644171779141 + } + expression { + nme: 4.457062543676477 + nme_p90: 7.023696522424334 + nme_p95: 8.14882559132701 + nme_p99: 22.37794722994855 + auc: 57.97977206967515 + fr: 2.2292993630573243 + } + illumination { + nme: 4.004404270660319 + nme_p90: 6.5263439186718575 + nme_p95: 7.9198072110541515 + nme_p99: 11.091641927095278 + auc: 61.30881713357479 + fr: 1.5759312320916874 + } + makeup { + nme: 3.809466022861384 + nme_p90: 6.319715813961875 + nme_p95: 8.290862588901753 + nme_p99: 11.568122626675834 + auc: 62.227636273476094 + fr: 1.4563106796116498 + } + occlusion { + nme: 4.951892714023863 + nme_p90: 8.090266937174373 + nme_p95: 9.927929968392291 + nme_p99: 16.439363635459827 + auc: 53.30944329221704 + fr: 4.483695652173914 + } + blur { + nme: 4.6502632721001484 + nme_p90: 7.309129270660999 + nme_p95: 8.694682218622555 + nme_p99: 14.421681667881499 + auc: 55.30994528611606 + fr: 2.1992238033635148 + } + } + nme_per_ldm { + 100: 7.499428096385048 + 101: 7.051152856495479 + 102: 6.689364840366089 + 103: 6.405394902267039 + 104: 6.184828312751848 + 105: 6.01289637200206 + 106: 5.825792191666405 + 107: 5.703581143874681 + 108: 5.558218880650258 + 109: 5.456541574926521 + 110: 5.356011590771132 + 111: 5.266801213177881 + 112: 5.1700746207919135 + 113: 5.11578920243509 + 114: 5.106880510341512 + 115: 5.225113359917539 + 24: 5.347111701530893 + 117: 5.193400965915828 + 118: 5.105516141121586 + 119: 5.1186167002866485 + 120: 5.154032577508115 + 121: 5.275157240183345 + 122: 5.389493979946993 + 123: 5.4938752374179955 + 124: 5.584092334651998 + 125: 5.705867605198732 + 126: 5.799339095880129 + 127: 5.954134417791037 + 128: 6.176961828664217 + 129: 6.455263479287812 + 130: 6.768471302761961 + 131: 7.125915842598694 + 132: 7.5666080900616945 + 1: 4.560765729125988 + 134: 3.7993917303919567 + 2: 3.4016672801102077 + 136: 3.345044810053455 + 3: 3.710503962280294 + 138: 3.6149551366473753 + 139: 3.2410971507433786 + 140: 3.291757973260253 + 141: 3.734225865973348 + 4: 3.72032794127556 + 143: 3.30955002587817 + 5: 3.4392003178872335 + 145: 3.8880208167570074 + 6: 4.752078564996328 + 147: 3.738086948109648 + 148: 3.3201253179463905 + 149: 3.2295749512632232 + 150: 3.647357521767312 + 151: 2.547342291744557 + 152: 2.283238387886172 + 153: 2.591598229160512 + 17: 3.0354855482365775 + 16: 3.2137738380189536 + 156: 2.518324235151659 + 157: 2.47653726483443 + 158: 2.5353874064282507 + 18: 3.2251412484538893 + 7: 3.1441893915300385 + 161: 2.4942204053480195 + 9: 2.6590371025659896 + 163: 2.3580909255854596 + 8: 2.8036185690133753 + 165: 2.3321001401925967 + 10: 2.591633267462054 + 167: 2.484735627041701 + 11: 2.7305098161561356 + 169: 2.4274079065187864 + 13: 2.7842155581430643 + 171: 2.52221107229687 + 12: 3.0657845511698607 + 173: 2.494593526480273 + 14: 2.6932726730687575 + 175: 2.3591528479046104 + 20: 4.112721320016711 + 177: 3.275914306275302 + 178: 3.42575723113226 + 22: 3.0927109768973287 + 180: 3.432414088055732 + 181: 3.2103207081848937 + 21: 4.432567252126953 + 183: 3.7233446858330366 + 184: 3.539979963579465 + 23: 3.6190759220532405 + 186: 3.4824407313700387 + 187: 3.6566723766201465 + 188: 3.472835226709668 + 189: 2.726895196789255 + 190: 2.930735583182004 + 191: 2.820444141794683 + 192: 3.7859629623364324 + 193: 3.1790111029427828 + 194: 3.3227123023323206 + 195: 3.0754071648176375 + 196: 2.2687775736645497 + 197: 2.3802949379562897 + } + npe90_per_ldm { + 100: 14.852445597799203 + 101: 14.18579862958194 + 102: 13.399793537733599 + 103: 12.718468904804915 + 104: 12.169341275908627 + 105: 12.01705017248965 + 106: 11.552579287899306 + 107: 11.519360109572814 + 108: 11.069713815819815 + 109: 10.974822012933272 + 110: 10.969423983927014 + 111: 10.643665463349626 + 112: 10.508696789450717 + 113: 10.509353382470481 + 114: 10.426225048917066 + 115: 10.77132409296981 + 24: 10.836704047501668 + 117: 10.227534559111756 + 118: 10.212154240626676 + 119: 10.343173662305139 + 120: 10.501815588300182 + 121: 10.60403011069595 + 122: 10.885667824449156 + 123: 11.223511777755174 + 124: 11.426450532559125 + 125: 11.731786380223648 + 126: 11.87994642089011 + 127: 12.347922569924979 + 128: 12.510717574506758 + 129: 13.203110126923216 + 130: 13.935800451738846 + 131: 14.65581284528847 + 132: 15.684327289240702 + 1: 9.145904257144307 + 134: 7.391833366795161 + 2: 6.557342516262404 + 136: 6.326639388017908 + 3: 7.123186160526489 + 138: 6.737679958469918 + 139: 6.122406459193663 + 140: 6.32844967785714 + 141: 7.423740406828487 + 4: 6.980971721786448 + 143: 6.45515651585541 + 5: 6.862006338881268 + 145: 7.679578611775045 + 6: 9.747986111715123 + 147: 7.334343333255734 + 148: 6.579826532395581 + 149: 6.304752067636323 + 150: 6.821268539263581 + 151: 4.755299967018147 + 152: 4.1313479515649725 + 153: 4.739782037447192 + 17: 5.5336191688254415 + 16: 6.437315379147384 + 156: 4.838950427255811 + 157: 5.138543963702374 + 158: 4.905267413061354 + 18: 6.107948731858525 + 7: 6.182595210311924 + 161: 4.856248707531849 + 9: 5.256125568483426 + 163: 4.51061528950398 + 8: 5.462974340475309 + 165: 4.517984859757126 + 10: 4.880297646197902 + 167: 4.851486229126095 + 11: 5.315306219280171 + 169: 4.753220539425407 + 13: 5.374371835997992 + 171: 4.852785312871789 + 12: 6.137253720508925 + 173: 4.902626446768939 + 14: 5.062119144586851 + 175: 4.477753808871465 + 20: 8.291468584753794 + 177: 6.865894383817322 + 178: 6.6278523121906945 + 22: 6.391876354854704 + 180: 6.737756386246774 + 181: 6.633701192824108 + 21: 8.828649325728422 + 183: 7.428439146636114 + 184: 7.215668900651159 + 23: 7.2506582758423885 + 186: 6.971699097467 + 187: 7.16787193303953 + 188: 7.134659063702044 + 189: 5.6504003691320195 + 190: 6.08694986471154 + 191: 5.698565063478801 + 192: 7.807921223112673 + 193: 6.27796544518223 + 194: 6.6953497695329105 + 195: 5.963853719652496 + 196: 4.42588286715022 + 197: 4.758802842487979 + } + npe95_per_ldm { + 100: 18.8274259243322 + 101: 17.91893820103512 + 102: 16.790440459339383 + 103: 16.36177051582291 + 104: 15.72781641631692 + 105: 15.041278647748332 + 106: 14.763833719969805 + 107: 15.025060221978926 + 108: 14.730682520252282 + 109: 14.643754841675316 + 110: 14.300136361811015 + 111: 14.654414320540273 + 112: 14.593583232262878 + 113: 14.47409072542243 + 114: 14.618637715471197 + 115: 14.530093031225332 + 24: 14.995606363223226 + 117: 14.448948156208589 + 118: 13.789274304854752 + 119: 13.832120269244403 + 120: 13.709518365737859 + 121: 14.129329077634093 + 122: 14.353242447422213 + 123: 15.16466545358333 + 124: 15.164929443920798 + 125: 15.113599392011784 + 126: 15.118919334522698 + 127: 15.493269395291685 + 128: 16.38552396477743 + 129: 17.243501461747186 + 130: 17.7726200230872 + 131: 18.733413340844084 + 132: 19.85817362564012 + 1: 12.282671457428942 + 134: 10.190266338206994 + 2: 8.627462529688064 + 136: 8.353884573498535 + 3: 9.149231954274304 + 138: 8.862645399076076 + 139: 8.214180187653598 + 140: 8.588138726132641 + 141: 10.198459485868906 + 4: 9.193189072829572 + 143: 8.508633703895459 + 5: 9.27580510928055 + 145: 10.66391353468443 + 6: 13.150535457623667 + 147: 10.295798054152893 + 148: 8.727375003658778 + 149: 8.139860884835961 + 150: 9.137884658727723 + 151: 6.1993757689099445 + 152: 5.379008416563386 + 153: 5.999217405852915 + 17: 7.471187849893246 + 16: 8.412519228071288 + 156: 6.511320139284012 + 157: 6.495503052291176 + 158: 6.4691245203276235 + 18: 8.046436081223744 + 7: 8.53023993361135 + 161: 6.5695540715861345 + 9: 7.06066679340818 + 163: 6.126827317718087 + 8: 7.391868149254668 + 165: 5.850762331953799 + 10: 6.392737721827344 + 167: 6.701751274702547 + 11: 7.108232079933884 + 169: 6.498765197817774 + 13: 7.377924918159498 + 171: 6.8661972583787225 + 12: 8.579455534855914 + 173: 6.604260017556539 + 14: 6.895344286814114 + 175: 6.07934878085839 + 20: 12.237940047506514 + 177: 10.415865290819106 + 178: 8.636449653407603 + 22: 8.548684956545552 + 180: 9.195403546434065 + 181: 9.307120855626186 + 21: 14.40623429205884 + 183: 11.136075208306705 + 184: 10.380179074464987 + 23: 9.900986672111294 + 186: 9.80179820389519 + 187: 11.26701817845163 + 188: 9.714741299910031 + 189: 7.997210438319446 + 190: 8.018485293706336 + 191: 8.152387130926519 + 192: 10.572139256377373 + 193: 8.829320776371096 + 194: 9.353915311261236 + 195: 8.770069844546882 + 196: 6.380411318934716 + 197: 6.925252704835688 + } + npe99_per_ldm { + 100: 31.796734331757474 + 101: 30.156823307914355 + 102: 28.085999280928775 + 103: 27.772409859859803 + 104: 27.063494458024618 + 105: 26.818097394520635 + 106: 25.30721172181605 + 107: 26.91752125832992 + 108: 26.856715591131337 + 109: 25.068096485672058 + 110: 25.487803402381296 + 111: 25.22568444548434 + 112: 25.97592571841177 + 113: 25.719255333824044 + 114: 26.344100968854626 + 115: 27.565684593896133 + 24: 25.958704292040675 + 117: 25.027316620457235 + 118: 24.153183750150713 + 119: 23.454696148177824 + 120: 23.650815452820808 + 121: 22.974733432539477 + 122: 22.7787999634705 + 123: 22.95454955539594 + 124: 23.536490612996054 + 125: 23.949973181222603 + 126: 24.156669818564882 + 127: 24.307258463774165 + 128: 26.230362982841182 + 129: 27.279179727007598 + 130: 27.658094700898353 + 131: 29.498087172293605 + 132: 31.031273144224297 + 1: 21.815528592810452 + 134: 18.552025618639288 + 2: 16.112806045145106 + 136: 16.26474105956125 + 3: 16.03098434863021 + 138: 15.331273499198128 + 139: 14.571579406397491 + 140: 15.17885461687226 + 141: 18.84639764294039 + 4: 15.14680909708014 + 143: 15.959472764350828 + 5: 16.782205693066487 + 145: 19.544102261096246 + 6: 22.703607587916377 + 147: 18.72768083165344 + 148: 16.949308129734572 + 149: 15.403991541464318 + 150: 16.53716758233348 + 151: 10.225916118065296 + 152: 9.87580178788986 + 153: 11.078951829537761 + 17: 11.432785302080758 + 16: 13.77854390122661 + 156: 11.423297506459893 + 157: 11.649539675840872 + 158: 10.298080549891448 + 18: 12.980837586206968 + 7: 15.380520840864325 + 161: 13.675989650355017 + 9: 13.996495073301666 + 163: 12.2974182120915 + 8: 12.70906602790459 + 165: 11.986475872557232 + 10: 12.564713827155238 + 167: 13.186734914311163 + 11: 12.050553315262324 + 169: 11.60835366208721 + 13: 13.926666792959946 + 171: 13.430274209070587 + 12: 16.136339266834494 + 173: 14.083254962467871 + 14: 13.786860675398353 + 175: 11.820493814517507 + 20: 31.456220720812258 + 177: 17.145310081719785 + 178: 14.383365993773618 + 22: 14.266997881870614 + 180: 14.767809590251009 + 181: 16.5761236909575 + 21: 34.75300701148773 + 183: 21.53482636836683 + 184: 19.21124669677774 + 23: 17.370155603691355 + 186: 18.523203073422827 + 187: 22.25607277080702 + 188: 22.550397440214464 + 189: 14.875857373605129 + 190: 14.056370833704333 + 191: 14.59218011999597 + 192: 24.578201317085025 + 193: 17.409549388507017 + 194: 17.03090444462318 + 195: 16.907666081457222 + 196: 13.586781795190145 + 197: 13.688773958708495 + } + } + headpose { + mae_ypr: [1.8035515527812418, 1.8859887869300525, 0.969774915452454] + mae_mean: 1.5531050850545827 + acc_label: [0.888, 0.8716, 0.9472] + acc_adj_label: [0.9988, 1.0, 1.0] + sr_yaw { + 2.5: 0.7692 + 5: 0.95 + 10: 0.9952 + 15: 0.998 + 30: 1.0 + } + sr_pitch { + 2.5: 0.7332 + 5: 0.9504 + 10: 0.996 + 15: 0.9992 + 30: 1.0 + } + sr_roll { + 2.5: 0.932 + 5: 0.9876 + 10: 0.9996 + 15: 1.0 + 30: 1.0 + } + } + } diff --git a/SPIGA/spiga/eval/results/wflw/results_wflw_test.json b/SPIGA/spiga/eval/results/wflw/results_wflw_test.json new file mode 100644 index 0000000000000000000000000000000000000000..720fbd0403efe72e152181962cf2e35eb80fc1b0 --- /dev/null +++ b/SPIGA/spiga/eval/results/wflw/results_wflw_test.json @@ -0,0 +1,3 @@ +version https://git-lfs.github.com/spec/v1 +oid sha256:943cb588521b73c0c8ddab4cf297a6b7653006a93568808c63389611a731f74c +size 13109839 diff --git a/SPIGA/spiga/eval/results_gen.py b/SPIGA/spiga/eval/results_gen.py new file mode 100644 index 0000000000000000000000000000000000000000..2c20995eaf1d174f729fae168cbc509c1732e2ff --- /dev/null +++ b/SPIGA/spiga/eval/results_gen.py @@ -0,0 +1,87 @@ +import pkg_resources +import json +import copy +import torch + +import spiga.data.loaders.dl_config as dl_cfg +import spiga.data.loaders.dataloader as dl +import spiga.inference.pretreatment as pretreat +from spiga.inference.framework import SPIGAFramework +from spiga.inference.config import ModelConfig + + +def main(): + import argparse + pars = argparse.ArgumentParser(description='Experiment results generator') + pars.add_argument('database', type=str, help='Database name', + choices=['wflw', '300wpublic', '300wprivate', "merlrav", "cofw68"]) + pars.add_argument('-a','--anns', type=str, default='test', help='Annotations type: test, valid or train') + pars.add_argument('--gpus', type=int, default=0, help='GPU Id') + args = pars.parse_args() + + # Load model framework + model_cfg = ModelConfig(args.database) + model_framework = SPIGAFramework(model_cfg, gpus=[args.gpus]) + + # Generate results + tester = Tester(model_framework, args.database, anns_type=args.anns) + with torch.no_grad(): + tester.generate_results() + + +class Tester: + + def __init__(self, model_framework, database, anns_type='test'): + + # Parameters + self.anns_type = anns_type + self.database = database + + # Model initialization + self.model_framework = model_framework + + # Dataloader + self.dl_eval = dl_cfg.AlignConfig(self.database, mode=self.anns_type) + self.dl_eval.aug_names = [] + self.dl_eval.shuffle = False + self.dl_eval.target_dist = self.model_framework.model_cfg.target_dist + self.dl_eval.image_size = self.model_framework.model_cfg.image_size + self.dl_eval.ftmap_size = self.model_framework.model_cfg.ftmap_size + + self.batch_size = 1 + self.test_data, _ = dl.get_dataloader(self.batch_size, self.dl_eval, + pretreat=pretreat.NormalizeAndPermute(), debug=True) + + # Results + self.data_struc = {'imgpath': str, 'bbox': None, 'headpose': None, 'ids': None, 'landmarks': None, 'visible': None} + self.result_path = pkg_resources.resource_filename('spiga', 'eval/results') + self.result_file = '/results_%s_%s.json' % (self.database, self.anns_type) + self.file_out = self.result_path + self.result_file + + def generate_results(self): + + data = [] + for step, batch in enumerate(self.test_data): + print('Step: ', step) + inputs = self.model_framework.select_inputs(batch) + outputs_raw = self.model_framework.net_forward(inputs) + # Postprocessing + outputs = self.model_framework.postreatment(outputs_raw, batch['bbox'], batch['bbox_raw']) + + # Data + data_dict = copy.deepcopy(self.data_struc) + data_dict['imgpath'] = batch['imgpath_local'][0] + data_dict['bbox'] = batch['bbox_raw'][0].numpy().tolist() + data_dict['visible'] = batch['visible'][0].numpy().tolist() + data_dict['ids'] = self.dl_eval.database.ldm_ids + data_dict['landmarks'] = outputs['landmarks'][0] + data_dict['headpose'] = outputs['headpose'][0] + data.append(data_dict) + + # Save outputs + with open(self.file_out, 'w') as outfile: + json.dump(data, outfile) + + +if __name__ == '__main__': + main() diff --git a/SPIGA/spiga/inference/__init__.py b/SPIGA/spiga/inference/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/inference/config.py b/SPIGA/spiga/inference/config.py new file mode 100644 index 0000000000000000000000000000000000000000..f6b881852fa1feed3ffe14aab9eb23cf89b750ed --- /dev/null +++ b/SPIGA/spiga/inference/config.py @@ -0,0 +1,58 @@ +from collections import OrderedDict + +from spiga.data.loaders.dl_config import DatabaseStruct + +MODELS_URL = {'wflw': 'https://drive.google.com/uc?export=download&confirm=yes&id=1h0qA5ysKorpeDNRXe9oYkVcVe8UYyzP7', + '300wpublic': 'https://drive.google.com/uc?export=download&confirm=yes&id=1YrbScfMzrAAWMJQYgxdLZ9l57nmTdpQC', + '300wprivate': 'https://drive.google.com/uc?export=download&confirm=yes&id=1fYv-Ie7n14eTD0ROxJYcn6SXZY5QU9SM', + 'merlrav': 'https://drive.google.com/uc?export=download&confirm=yes&id=1GKS1x0tpsTVivPZUk_yrSiMhwEAcAkg6', + 'cofw68': 'https://drive.google.com/uc?export=download&confirm=yes&id=1fYv-Ie7n14eTD0ROxJYcn6SXZY5QU9SM'} + + +class ModelConfig(object): + + def __init__(self, dataset_name=None, load_model_url=True): + # Model configuration + self.model_weights = None + self.model_weights_path = None + self.load_model_url = load_model_url + self.model_weights_url = None + # Pretreatment + self.focal_ratio = 1.5 # Camera matrix focal length ratio. + self.target_dist = 1.6 # Target distance zoom in/out around face. + self.image_size = (256, 256) + # Outputs + self.ftmap_size = (64, 64) + # Dataset + self.dataset = None + + if dataset_name is not None: + self.update_with_dataset(dataset_name) + + def update_with_dataset(self, dataset_name): + + config_dict = {'dataset': DatabaseStruct(dataset_name), + 'model_weights': 'spiga_%s.pt' % dataset_name} + + if dataset_name == 'cofw68': # Test only + config_dict['model_weights'] = 'spiga_300wprivate.pt' + + if self.load_model_url: + config_dict['model_weights_url'] = MODELS_URL[dataset_name] + + self.update(config_dict) + + def update(self, params_dict): + state_dict = self.state_dict() + for k, v in params_dict.items(): + if k in state_dict or hasattr(self, k): + setattr(self, k, v) + else: + raise Warning('Unknown option: {}: {}'.format(k, v)) + + def state_dict(self): + state_dict = OrderedDict() + for k in self.__dict__.keys(): + if not k.startswith('_'): + state_dict[k] = getattr(self, k) + return state_dict diff --git a/SPIGA/spiga/inference/framework.py b/SPIGA/spiga/inference/framework.py new file mode 100644 index 0000000000000000000000000000000000000000..a0f1f992539506b5743cf57ea30c5c8efdb6263f --- /dev/null +++ b/SPIGA/spiga/inference/framework.py @@ -0,0 +1,145 @@ +from spiga.inference.config import ModelConfig +from spiga.models.spiga import SPIGA +import spiga.inference.pretreatment as pretreat +import os +import pkg_resources +import copy +import torch +import numpy as np + +# Paths +weights_path_dft = pkg_resources.resource_filename('spiga', 'models/weights') + + +class SPIGAFramework: + + def __init__(self, model_cfg: ModelConfig(), gpus=[0], load3DM=True): + + # Parameters + self.model_cfg = model_cfg + self.gpus = gpus + + # Pretreatment initialization + self.transforms = pretreat.get_transformers(self.model_cfg) + + # SPIGA model + self.model_inputs = ['image', "model3d", "cam_matrix"] + self.model = SPIGA(num_landmarks=model_cfg.dataset.num_landmarks, + num_edges=model_cfg.dataset.num_edges) + + # Load weights and set model + weights_path = self.model_cfg.model_weights_path + if weights_path is None: + weights_path = weights_path_dft + + if self.model_cfg.load_model_url: + model_state_dict = torch.hub.load_state_dict_from_url(self.model_cfg.model_weights_url, + model_dir=weights_path, + file_name=self.model_cfg.model_weights) + else: + weights_file = os.path.join( + weights_path, self.model_cfg.model_weights) + model_state_dict = torch.load(weights_file) + + self.model.load_state_dict(model_state_dict) + # self.model = self.model.cuda(gpus[0]) + self.model = self.model.cuda( + gpus[0]) if torch.cuda.is_available() else self.model + self.model.eval() + print('SPIGA model loaded!') + + # Load 3D model and camera intrinsic matrix + if load3DM: + loader_3DM = pretreat.AddModel3D(model_cfg.dataset.ldm_ids, + ftmap_size=model_cfg.ftmap_size, + focal_ratio=model_cfg.focal_ratio, + totensor=True) + params_3DM = self._data2device(loader_3DM()) + self.model3d = params_3DM['model3d'] + self.cam_matrix = params_3DM['cam_matrix'] + + def inference(self, image, bboxes): + """ + @param self: + @param image: Raw image + @param bboxes: List of bounding box founded on the image [[x,y,w,h],...] + @return: features dict {'landmarks': list with shape (num_bbox, num_landmarks, 2) and x,y referred to image size + 'headpose': list with shape (num_bbox, 6) euler->[:3], trl->[3:] + """ + batch_crops, crop_bboxes = self.pretreat(image, bboxes) + outputs = self.net_forward(batch_crops) + features = self.postreatment(outputs, crop_bboxes, bboxes) + return features + + def pretreat(self, image, bboxes): + crop_bboxes = [] + crop_images = [] + for bbox in bboxes: + sample = {'image': copy.deepcopy(image), + 'bbox': copy.deepcopy(bbox)} + sample_crop = self.transforms(sample) + crop_bboxes.append(sample_crop['bbox']) + crop_images.append(sample_crop['image']) + + # Images to tensor and device + batch_images = torch.tensor(np.array(crop_images), dtype=torch.float) + batch_images = self._data2device(batch_images) + # Batch 3D model and camera intrinsic matrix + batch_model3D = self.model3d.unsqueeze(0).repeat(len(bboxes), 1, 1) + batch_cam_matrix = self.cam_matrix.unsqueeze( + 0).repeat(len(bboxes), 1, 1) + + # SPIGA inputs + model_inputs = [batch_images, batch_model3D, batch_cam_matrix] + return model_inputs, crop_bboxes + + def net_forward(self, inputs): + outputs = self.model(inputs) + return outputs + + def postreatment(self, output, crop_bboxes, bboxes): + features = {} + crop_bboxes = np.array(crop_bboxes) + bboxes = np.array(bboxes) + + if 'Landmarks' in output.keys(): + landmarks = output['Landmarks'][-1].cpu().detach().numpy() + landmarks = landmarks.transpose((1, 0, 2)) + landmarks = landmarks*self.model_cfg.image_size + landmarks_norm = ( + landmarks - crop_bboxes[:, 0:2]) / crop_bboxes[:, 2:4] + landmarks_out = (landmarks_norm * bboxes[:, 2:4]) + bboxes[:, 0:2] + landmarks_out = landmarks_out.transpose((1, 0, 2)) + features['landmarks'] = landmarks_out.tolist() + + # Pose output + if 'Pose' in output.keys(): + pose = output['Pose'].cpu().detach().numpy() + features['headpose'] = pose.tolist() + + return features + + def select_inputs(self, batch): + inputs = [] + for ft_name in self.model_inputs: + data = batch[ft_name] + inputs.append(self._data2device(data.type(torch.float))) + return inputs + + def _data2device(self, data): + if isinstance(data, list): + data_var = data + for data_id, v_data in enumerate(data): + data_var[data_id] = self._data2device(v_data) + if isinstance(data, dict): + data_var = data + for k, v in data.items(): + data[k] = self._data2device(v) + else: + with torch.no_grad(): + if torch.cuda.is_available(): + data_var = data.cuda( + device=self.gpus[0], non_blocking=True) + else: + data_var = data + return data_var diff --git a/SPIGA/spiga/inference/pretreatment.py b/SPIGA/spiga/inference/pretreatment.py new file mode 100644 index 0000000000000000000000000000000000000000..c2099056356301d2f9300b344f6273f4c75b5b31 --- /dev/null +++ b/SPIGA/spiga/inference/pretreatment.py @@ -0,0 +1,31 @@ +from torchvision import transforms +import numpy as np +from PIL import Image +import cv2 + +from spiga.data.loaders.transforms import TargetCrop, ToOpencv, AddModel3D + + +def get_transformers(data_config): + transformer_seq = [ + Opencv2Pil(), + TargetCrop(data_config.image_size, data_config.target_dist), + ToOpencv(), + NormalizeAndPermute()] + return transforms.Compose(transformer_seq) + + +class NormalizeAndPermute: + def __call__(self, sample): + image = np.array(sample['image'], dtype=float) + image = np.transpose(image, (2, 0, 1)) + sample['image'] = image / 255 + return sample + + +class Opencv2Pil: + def __call__(self, sample): + image = cv2.cvtColor(sample['image'], cv2.COLOR_BGR2RGB) + sample['image'] = Image.fromarray(image) + return sample + diff --git a/SPIGA/spiga/models/__init__.py b/SPIGA/spiga/models/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/models/cnn/__init__.py b/SPIGA/spiga/models/cnn/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/models/cnn/cnn_multitask.py b/SPIGA/spiga/models/cnn/cnn_multitask.py new file mode 100644 index 0000000000000000000000000000000000000000..c55694b513231d57fe2456b34cf2b65d82c7140e --- /dev/null +++ b/SPIGA/spiga/models/cnn/cnn_multitask.py @@ -0,0 +1,94 @@ +from torch import nn +from spiga.models.cnn.layers import Conv, Residual +from spiga.models.cnn.hourglass import HourglassCore +from spiga.models.cnn.coord_conv import AddCoordsTh +from spiga.models.cnn.transform_e2p import E2Ptransform + + +class MultitaskCNN(nn.Module): + + def __init__(self, nstack=4, num_landmarks=98, num_edges=15, pose_req=True, **kwargs): + super(MultitaskCNN, self).__init__() + + # Parameters + self.img_res = 256 # WxH input resolution + self.ch_dim = 256 # Default channel dimension + self.out_res = 64 # WxH output resolution + self.nstack = nstack # Hourglass modules stacked + self.num_landmarks = num_landmarks # Number of landmarks + self.num_edges = num_edges # Number of edges subsets (eyeR, eyeL, nose, etc) + self.pose_required = pose_req # Multitask flag + + # Image preprocessing + self.pre = nn.Sequential( + AddCoordsTh(x_dim=self.img_res, y_dim=self.img_res, with_r=True), + Conv(6, 64, 7, 2, bn=True, relu=True), + Residual(64, 128), + Conv(128, 128, 2, 2, bn=True, relu=True), + Residual(128, 128), + Residual(128, self.ch_dim) + ) + + # Hourglass modules + self.hgs = nn.ModuleList([HourglassCore(4, self.ch_dim) for i in range(self.nstack)]) + self.hgs_out = nn.ModuleList([ + nn.Sequential( + Residual(self.ch_dim, self.ch_dim), + Conv(self.ch_dim, self.ch_dim, 1, bn=True, relu=True) + ) for i in range(nstack)]) + if self.pose_required: + self.hgs_core = nn.ModuleList([ + nn.Sequential( + Residual(self.ch_dim, self.ch_dim), + Conv(self.ch_dim, self.ch_dim, 2, 2, bn=True, relu=True), + Residual(self.ch_dim, self.ch_dim), + Conv(self.ch_dim, self.ch_dim, 2, 2, bn=True, relu=True) + ) for i in range(nstack)]) + + # Attention module (ADnet style) + self.outs_points = nn.ModuleList([nn.Sequential(Conv(self.ch_dim, self.num_landmarks, 1, relu=False, bn=False), + nn.Sigmoid()) for i in range(self.nstack - 1)]) + self.outs_edges = nn.ModuleList([nn.Sequential(Conv(self.ch_dim, self.num_edges, 1, relu=False, bn=False), + nn.Sigmoid()) for i in range(self.nstack - 1)]) + self.E2Ptransform = E2Ptransform(self.num_landmarks, self.num_edges, out_dim=self.out_res) + + self.outs_features = nn.ModuleList([Conv(self.ch_dim, self.num_landmarks, 1, relu=False, bn=False)for i in range(self.nstack - 1)]) + + # Stacked Hourglass inputs (nstack > 1) + self.merge_preds = nn.ModuleList([Conv(self.num_landmarks, self.ch_dim, 1, relu=False, bn=False) for i in range(self.nstack - 1)]) + self.merge_features = nn.ModuleList([Conv(self.ch_dim, self.ch_dim, 1, relu=False, bn=False) for i in range(self.nstack - 1)]) + + def forward(self, imgs): + + x = self.pre(imgs) + outputs = {'VisualField': [], + 'HGcore': []} + + core_raw = [] + for i in range(self.nstack): + # Hourglass + hg, core_raw = self.hgs[i](x, core=core_raw) + if self.pose_required: + core = self.hgs_core[i](core_raw[-self.hgs[i].n]) + outputs['HGcore'].append(core) + hg = self.hgs_out[i](hg) + + # Visual features + outputs['VisualField'].append(hg) + + # Prepare next stacked input + if i < self.nstack - 1: + # Attentional modules + points = self.outs_points[i](hg) + edges = self.outs_edges[i](hg) + edges_ext = self.E2Ptransform(edges) + point_edges = points * edges_ext + + # Landmarks + maps = self.outs_features[i](hg) + preds = maps * point_edges + + # Outputs + x = x + self.merge_preds[i](preds) + self.merge_features[i](hg) + + return outputs diff --git a/SPIGA/spiga/models/cnn/coord_conv.py b/SPIGA/spiga/models/cnn/coord_conv.py new file mode 100644 index 0000000000000000000000000000000000000000..45e970ffd3a5b9b0d94870d4193afe64a1222b35 --- /dev/null +++ b/SPIGA/spiga/models/cnn/coord_conv.py @@ -0,0 +1,58 @@ +import torch +import torch.nn as nn + + +class AddCoordsTh(nn.Module): + def __init__(self, x_dim=64, y_dim=64, with_r=False): + super(AddCoordsTh, self).__init__() + self.x_dim = x_dim + self.y_dim = y_dim + self.with_r = with_r + + xx_channel, yy_channel = self._prepare_coords() + self.xx_channel = nn.parameter.Parameter(xx_channel, requires_grad=False) + self.yy_channel = nn.parameter.Parameter(yy_channel, requires_grad=False) + + def _prepare_coords(self): + xx_ones = torch.ones([1, self.y_dim], dtype=torch.int32) + xx_ones = xx_ones.unsqueeze(-1) + + xx_range = torch.arange(self.x_dim, dtype=torch.int32).unsqueeze(0) + xx_range = xx_range.unsqueeze(1) + + xx_channel = torch.matmul(xx_ones, xx_range) + xx_channel = xx_channel.unsqueeze(-1) + + yy_ones = torch.ones([1, self.x_dim], dtype=torch.int32) + yy_ones = yy_ones.unsqueeze(1) + + yy_range = torch.arange(self.y_dim, dtype=torch.int32).unsqueeze(0) + yy_range = yy_range.unsqueeze(-1) + + yy_channel = torch.matmul(yy_range, yy_ones) + yy_channel = yy_channel.unsqueeze(-1) + + xx_channel = xx_channel.permute(0, 3, 2, 1) + yy_channel = yy_channel.permute(0, 3, 2, 1) + + xx_channel = xx_channel.float() / (self.x_dim - 1) + yy_channel = yy_channel.float() / (self.y_dim - 1) + + xx_channel = xx_channel * 2 - 1 + yy_channel = yy_channel * 2 - 1 + return xx_channel, yy_channel + + def forward(self, input_tensor): + """ + input_tensor: (batch, c, x_dim, y_dim) + """ + batch_size_tensor = input_tensor.shape[0] + xx_channel = self.xx_channel.repeat(batch_size_tensor, 1, 1, 1) + yy_channel = self.yy_channel.repeat(batch_size_tensor, 1, 1, 1) + ret = torch.cat([input_tensor, xx_channel, yy_channel], dim=1) + + if self.with_r: + rr = torch.sqrt(torch.pow(xx_channel - 0.5, 2) + torch.pow(yy_channel - 0.5, 2)) + ret = torch.cat([ret, rr], dim=1) + + return ret diff --git a/SPIGA/spiga/models/cnn/hourglass.py b/SPIGA/spiga/models/cnn/hourglass.py new file mode 100644 index 0000000000000000000000000000000000000000..c3fb01c410c8df97c1ab0e2ab82b0b0ba04dcc91 --- /dev/null +++ b/SPIGA/spiga/models/cnn/hourglass.py @@ -0,0 +1,53 @@ +import torch.nn as nn + +from spiga.models.cnn.layers import Conv, Deconv, Residual + + +class Hourglass(nn.Module): + def __init__(self, n, f, bn=None, increase=0): + super(Hourglass, self).__init__() + nf = f + increase + self.up1 = Residual(f, f) + # Lower branch + self.pool1 = Conv(f, f, 2, 2, bn=True, relu=True) + self.low1 = Residual(f, nf) + self.n = n + # Recursive hourglass + if self.n > 1: + self.low2 = Hourglass(n - 1, nf, bn=bn) + else: + self.low2 = Residual(nf, nf) + self.low3 = Residual(nf, f) + self.up2 = Deconv(f, f, 2, 2, bn=True, relu=True) + + def forward(self, x): + up1 = self.up1(x) + pool1 = self.pool1(x) + low1 = self.low1(pool1) + low2 = self.low2(low1) + low3 = self.low3(low2) + up2 = self.up2(low3) + return up1 + up2 + + +class HourglassCore(Hourglass): + def __init__(self, n, f, bn=None, increase=0): + super(HourglassCore, self).__init__(n, f, bn=bn, increase=increase) + nf = f + increase + if self.n > 1: + self.low2 = HourglassCore(n - 1, nf, bn=bn) + + def forward(self, x, core=[]): + up1 = self.up1(x) + pool1 = self.pool1(x) + low1 = self.low1(pool1) + if self.n > 1: + low2, core = self.low2(low1, core=core) + else: + low2 = self.low2(low1) + core.append(low2) + low3 = self.low3(low2) + if self.n > 1: + core.append(low3) + up2 = self.up2(low3) + return up1 + up2, core diff --git a/SPIGA/spiga/models/cnn/layers.py b/SPIGA/spiga/models/cnn/layers.py new file mode 100644 index 0000000000000000000000000000000000000000..36bcf16c7812a6824b115272ef4a8712015709c4 --- /dev/null +++ b/SPIGA/spiga/models/cnn/layers.py @@ -0,0 +1,79 @@ +from torch import nn + + +class Conv(nn.Module): + def __init__(self, inp_dim, out_dim, kernel_size=3, stride=1, bn=False, relu=True): + super(Conv, self).__init__() + self.inp_dim = inp_dim + self.conv = nn.Conv2d(inp_dim, out_dim, kernel_size, stride, padding=(kernel_size - 1) // 2, bias=False) + self.relu = None + self.bn = None + if relu: + self.relu = nn.ReLU() + if bn: + self.bn = nn.BatchNorm2d(out_dim) + + def forward(self, x): + assert x.size()[1] == self.inp_dim, "{} {}".format(x.size()[1], self.inp_dim) + x = self.conv(x) + if self.bn is not None: + x = self.bn(x) + if self.relu is not None: + x = self.relu(x) + return x + + +class Deconv(nn.Module): + def __init__(self, inp_dim, out_dim, kernel_size=3, stride=1, bn=False, relu=True): + super(Deconv, self).__init__() + self.inp_dim = inp_dim + self.deconv = nn.ConvTranspose2d(inp_dim, out_dim, kernel_size=kernel_size, stride=stride, bias=False) + self.relu = None + self.bn = None + if relu: + self.relu = nn.ReLU() + if bn: + self.bn = nn.BatchNorm2d(out_dim) + + def forward(self, x): + assert x.size()[1] == self.inp_dim, "{} {}".format(x.size()[1], self.inp_dim) + x = self.deconv(x) + if self.bn is not None: + x = self.bn(x) + if self.relu is not None: + x = self.relu(x) + return x + + +class Residual(nn.Module): + def __init__(self, inp_dim, out_dim, kernel=3): + super(Residual, self).__init__() + self.relu = nn.ReLU() + self.bn1 = nn.BatchNorm2d(inp_dim) + self.conv1 = Conv(inp_dim, int(out_dim / 2), 1, relu=False) + self.bn2 = nn.BatchNorm2d(int(out_dim / 2)) + self.conv2 = Conv(int(out_dim / 2), int(out_dim / 2), kernel, relu=False) + self.bn3 = nn.BatchNorm2d(int(out_dim / 2)) + self.conv3 = Conv(int(out_dim / 2), out_dim, 1, relu=False) + self.skip_layer = Conv(inp_dim, out_dim, 1, relu=False) + if inp_dim == out_dim: + self.need_skip = False + else: + self.need_skip = True + + def forward(self, x): + if self.need_skip: + residual = self.skip_layer(x) + else: + residual = x + out = self.bn1(x) + out = self.relu(out) + out = self.conv1(out) + out = self.bn2(out) + out = self.relu(out) + out = self.conv2(out) + out = self.bn3(out) + out = self.relu(out) + out = self.conv3(out) + out += residual + return out diff --git a/SPIGA/spiga/models/cnn/transform_e2p.py b/SPIGA/spiga/models/cnn/transform_e2p.py new file mode 100644 index 0000000000000000000000000000000000000000..14c42534bf5f608bd34f576c5ac1f6e8c0eb6167 --- /dev/null +++ b/SPIGA/spiga/models/cnn/transform_e2p.py @@ -0,0 +1,257 @@ +import torch +from torch import nn + + +class E2Ptransform(nn.Module): + """Edge to Points trasnformation""" + def __init__(self, points, edges, out_dim=64): + super(E2Ptransform, self).__init__() + self.ones = nn.parameter.Parameter(torch.ones((1, out_dim, out_dim)), requires_grad=False) + edge_matrix = self._select_matrix(points, edges) + self.edge2point = nn.parameter.Parameter(edge_matrix, requires_grad=False) # Npoint X Nedges+1 + + def forward(self, edges): + B, L, H, W = edges.shape + edges_ext = torch.cat((edges, self.ones.repeat(B, 1, 1, 1)), 1) + edges_mat = edges_ext.permute(0, 2, 3, 1).reshape(B, H, W, 1, L+1) + edge2point = self.edge2point.transpose(-1, -2) + point_edges = torch.matmul(edges_mat, edge2point) + point_edges = point_edges.reshape(B, H, W, -1).permute(0, 3, 1, 2) + point_edges[point_edges > 1] = 1. + return point_edges + + def _select_matrix(self, points, edges): + + if points == 98 and edges == 15: + return WFLW_98x15 + elif points == 68 and edges == 13: + return W300_68x13 + elif points == 29 and edges == 13: + return COFW_29x13 + elif points == 19 and edges == 6: + return AFLW19_19x6 + else: + raise ValueError("E2P matrix not implemented") + + +# Database matrixE2P +WFLW_98x15 = torch.Tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]]) + + +W300_68x13 = torch.Tensor([ [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]]) + + +AFLW19_19x6 = torch.Tensor([[1, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 0, 1]]) + + +COFW_29x13 = torch.Tensor([ [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], + [0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], + [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]]) diff --git a/SPIGA/spiga/models/gnn/__init__.py b/SPIGA/spiga/models/gnn/__init__.py new file mode 100644 index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391 diff --git a/SPIGA/spiga/models/gnn/gat.py b/SPIGA/spiga/models/gnn/gat.py new file mode 100644 index 0000000000000000000000000000000000000000..d7816f22a4b3afd77d3f2d3e69bc65e45b026a14 --- /dev/null +++ b/SPIGA/spiga/models/gnn/gat.py @@ -0,0 +1,62 @@ +from copy import deepcopy +import torch +from torch import nn +import torch.nn.functional as F + +from spiga.models.gnn.layers import MLP + + +class GAT(nn.Module): + def __init__(self, input_dim: int, output_dim: int, num_heads=4): + super().__init__() + + num_heads_in = num_heads + self.reshape = None + if input_dim != output_dim: + for num_heads_in in range(num_heads, 0, -1): + if input_dim % num_heads_in == 0: + break + self.reshape = MLP([input_dim, output_dim]) + + self.attention = MessagePassing(input_dim, num_heads_in, out_dim=output_dim) + + def forward(self, features): + message, prob = self.attention(features) + if self.reshape: + features = self.reshape(features) + output = features + message + return output, prob + + +class MessagePassing(nn.Module): + def __init__(self, feature_dim: int, num_heads: int, out_dim=None): + super().__init__() + self.attn = Attention(num_heads, feature_dim) + self.mlp = MLP([feature_dim*2, feature_dim*2, out_dim]) + + def forward(self, features): + message, prob = self.attn(features, features, features) + return self.mlp(torch.cat([features, message], dim=1)), prob + + +class Attention(nn.Module): + def __init__(self, num_heads: int, feature_dim: int): + super().__init__() + assert feature_dim % num_heads == 0 + self.dim = feature_dim // num_heads + self.num_heads = num_heads + self.merge = nn.Conv1d(feature_dim, feature_dim, kernel_size=1) + self.proj = nn.ModuleList([deepcopy(self.merge) for _ in range(3)]) + + def forward(self, query, key, value): + batch_dim = query.size(0) + query, key, value = [l(x).view(batch_dim, self.dim, self.num_heads, -1) + for l, x in zip(self.proj, (query, key, value))] + x, prob = self.attention(query, key, value) + return self.merge(x.contiguous().view(batch_dim, self.dim*self.num_heads, -1)), prob + + def attention(self, query, key, value): + dim = query.shape[1] + scores = torch.einsum('bdhn,bdhm->bhnm', query, key) / dim ** .5 + prob = F.softmax(scores, dim=-1) + return torch.einsum('bhnm,bdhm->bdhn', prob, value), prob diff --git a/SPIGA/spiga/models/gnn/layers.py b/SPIGA/spiga/models/gnn/layers.py new file mode 100644 index 0000000000000000000000000000000000000000..31137f40b51fb73aee26fa5705dd3661b472fe37 --- /dev/null +++ b/SPIGA/spiga/models/gnn/layers.py @@ -0,0 +1,12 @@ +from torch import nn + + +def MLP(channels: list): + n = len(channels) + layers = [] + for i in range(1, n): + layers.append(nn.Conv1d(channels[i - 1], channels[i], kernel_size=1, bias=True)) + if i < (n-1): + layers.append(nn.BatchNorm1d(channels[i])) + layers.append(nn.ReLU()) + return nn.Sequential(*layers) diff --git a/SPIGA/spiga/models/gnn/pose_proj.py b/SPIGA/spiga/models/gnn/pose_proj.py new file mode 100644 index 0000000000000000000000000000000000000000..cfa37e9e8bb141671a33d019c206d6612a41333f --- /dev/null +++ b/SPIGA/spiga/models/gnn/pose_proj.py @@ -0,0 +1,77 @@ +import torch +import math + + +def euler_to_rotation_matrix(euler): + # http://euclideanspace.com/maths/geometry/rotations/conversions/eulerToMatrix/index.htm + # Change coordinates system + + euler[:, 0] = -(euler[:, 0]-90) + euler[:, 1] = -euler[:, 1] + euler[:, 2] = -(euler[:, 2]+90) + + # Convert to radians + rad = euler*(math.pi/180.0) + cy = torch.cos(rad[:, 0]) + sy = torch.sin(rad[:, 0]) + cp = torch.cos(rad[:, 1]) + sp = torch.sin(rad[:, 1]) + cr = torch.cos(rad[:, 2]) + sr = torch.sin(rad[:, 2]) + + # Init R matrix tensors + working_device = None + if euler.is_cuda: + working_device = euler.device + Ry = torch.zeros((euler.shape[0], 3, 3), device=working_device) + Rp = torch.zeros((euler.shape[0], 3, 3), device=working_device) + Rr = torch.zeros((euler.shape[0], 3, 3), device=working_device) + + # Yaw + Ry[:, 0, 0] = cy + Ry[:, 0, 2] = sy + Ry[:, 1, 1] = 1. + Ry[:, 2, 0] = -sy + Ry[:, 2, 2] = cy + + # Pitch + Rp[:, 0, 0] = cp + Rp[:, 0, 1] = -sp + Rp[:, 1, 0] = sp + Rp[:, 1, 1] = cp + Rp[:, 2, 2] = 1. + + # Roll + Rr[:, 0, 0] = 1. + Rr[:, 1, 1] = cr + Rr[:, 1, 2] = -sr + Rr[:, 2, 1] = sr + Rr[:, 2, 2] = cr + + return torch.matmul(torch.matmul(Ry, Rp), Rr) + + +def projectPoints(pts, rot, trl, cam_matrix): + + # Get working device + working_device = None + if pts.is_cuda: + working_device = pts.device + + # Perspective projection model + trl = trl.unsqueeze(2) + extrinsics = torch.cat((rot, trl), 2) + proj_matrix = torch.matmul(cam_matrix, extrinsics) + + # Homogeneous landmarks + ones = torch.ones(pts.shape[:2], device=working_device, requires_grad=trl.requires_grad) + ones = ones.unsqueeze(2) + pts_hom = torch.cat((pts, ones), 2) + + # Project landmarks + pts_proj = pts_hom.permute((0, 2, 1)) # Transpose + pts_proj = torch.matmul(proj_matrix, pts_proj) + pts_proj = pts_proj.permute((0, 2, 1)) + pts_proj = pts_proj/pts_proj[:, :, 2].unsqueeze(2) # Lambda = 1 + + return pts_proj[:, :, :-1] diff --git a/SPIGA/spiga/models/gnn/step_regressor.py b/SPIGA/spiga/models/gnn/step_regressor.py new file mode 100644 index 0000000000000000000000000000000000000000..c6396590490546e882eab987d40b1ba9078922c5 --- /dev/null +++ b/SPIGA/spiga/models/gnn/step_regressor.py @@ -0,0 +1,43 @@ +import torch.nn as nn + +from spiga.models.gnn.layers import MLP +from spiga.models.gnn.gat import GAT + + +class StepRegressor(nn.Module): + + def __init__(self, input_dim: int, feature_dim: int, nstack=4, decoding=[256, 128, 64, 32]): + super(StepRegressor, self).__init__() + assert nstack > 0 + self.nstack = nstack + self.gat = nn.ModuleList([GAT(input_dim, feature_dim, 4)]) + for _ in range(nstack-1): + self.gat.append(GAT(feature_dim, feature_dim, 4)) + self.decoder = OffsetDecoder(feature_dim, decoding) + + def forward(self, embedded, prob_list=[]): + embedded = embedded.transpose(-1, -2) + for i in range(self.nstack): + embedded, prob = self.gat[i](embedded) + prob_list.append(prob) + offset = self.decoder(embedded) + return offset.transpose(-1, -2), prob_list + + +class OffsetDecoder(nn.Module): + def __init__(self, feature_dim, layers): + super().__init__() + self.decoder = MLP([feature_dim] + layers + [2]) + + def forward(self, embedded): + return self.decoder(embedded) + + +class RelativePositionEncoder(nn.Module): + def __init__(self, input_dim, feature_dim, layers): + super().__init__() + self.encoder = MLP([input_dim] + layers + [feature_dim]) + + def forward(self, feature): + feature = feature.transpose(-1, -2) + return self.encoder(feature).transpose(-1, -2) diff --git a/SPIGA/spiga/models/spiga.py b/SPIGA/spiga/models/spiga.py new file mode 100644 index 0000000000000000000000000000000000000000..4c72a36f2a45a4344665980bcf90e94a62766e2c --- /dev/null +++ b/SPIGA/spiga/models/spiga.py @@ -0,0 +1,171 @@ +import torch +import torch.nn as nn +import torch.nn.functional as F + +import spiga.models.gnn.pose_proj as pproj +from spiga.models.cnn.cnn_multitask import MultitaskCNN +from spiga.models.gnn.step_regressor import StepRegressor, RelativePositionEncoder + + +class SPIGA(nn.Module): + def __init__(self, num_landmarks=98, num_edges=15, steps=3, **kwargs): + + super(SPIGA, self).__init__() + + # Model parameters + self.steps = steps # Cascaded regressors + self.embedded_dim = 512 # GAT input channel + self.nstack = 4 # Number of stacked GATs per step + self.kwindow = 7 # Output cropped window dimension (kernel) + self.swindow = 0.25 # Scale of the cropped window at first step (Dft. 25% w.r.t the input featuremap) + self.offset_ratio = [self.swindow/(2**step)/2 for step in range(self.steps)] + + # CNN parameters + self.num_landmarks = num_landmarks + self.num_edges = num_edges + + # Initialize backbone + self.visual_cnn = MultitaskCNN(num_landmarks=self.num_landmarks, num_edges=self.num_edges) + # Features dimensions + self.img_res = self.visual_cnn.img_res + self.visual_res = self.visual_cnn.out_res + self.visual_dim = self.visual_cnn.ch_dim + + # Initialize Pose head + self.channels_pose = 6 + self.pose_fc = nn.Linear(self.visual_cnn.ch_dim, self.channels_pose) + + # Initialize feature extractors: + # Relative positional encoder + shape_dim = 2 * (self.num_landmarks - 1) + shape_encoder = [] + for step in range(self.steps): + shape_encoder.append(RelativePositionEncoder(shape_dim, self.embedded_dim, [256, 256])) + self.shape_encoder = nn.ModuleList(shape_encoder) + # Diagonal mask used to compute relative positions + diagonal_mask = (torch.ones(self.num_landmarks, self.num_landmarks) - torch.eye(self.num_landmarks)).type(torch.bool) + self.diagonal_mask = nn.parameter.Parameter(diagonal_mask, requires_grad=False) + + # Visual feature extractor + conv_window = [] + theta_S = [] + for step in range(self.steps): + # S matrix per step + WH = self.visual_res # Width/height of ftmap + Wout = self.swindow / (2 ** step) * WH # Width/height of the window + K = self.kwindow # Kernel or resolution of the window + scale = K / WH * (Wout - 1) / (K - 1) # Scale of the affine transformation + # Rescale matrix S + theta_S_stp = torch.tensor([[scale, 0], [0, scale]]) + theta_S.append(nn.parameter.Parameter(theta_S_stp, requires_grad=False)) + + # Convolutional to embedded to BxLxCx1x1 + conv_window.append(nn.Conv2d(self.visual_dim, self.embedded_dim, self.kwindow)) + + self.theta_S = nn.ParameterList(theta_S) + self.conv_window = nn.ModuleList(conv_window) + + # Initialize GAT modules + self.gcn = nn.ModuleList([StepRegressor(self.embedded_dim, 256, self.nstack) for i in range(self.steps)]) + + def forward(self, data): + # Inputs: Visual features and points projections + pts_proj, features = self.backbone_forward(data) + # Visual field + visual_field = features['VisualField'][-1] + + # Params compute only once + gat_prob = [] + features['Landmarks'] = [] + for step in range(self.steps): + # Features generation + embedded_ft = self.extract_embedded(pts_proj, visual_field, step) + + # GAT inference + offset, gat_prob = self.gcn[step](embedded_ft, gat_prob) + offset = F.hardtanh(offset) + + # Update coordinates + pts_proj = pts_proj + self.offset_ratio[step] * offset + features['Landmarks'].append(pts_proj.clone()) + + features['GATProb'] = gat_prob + return features + + def backbone_forward(self, data): + # Inputs: Image and model3D + imgs = data[0] + model3d = data[1] + cam_matrix = data[2] + + # HourGlass Forward + features = self.visual_cnn(imgs) + + # Head pose estimation + pose_raw = features['HGcore'][-1] + B, L, _, _ = pose_raw.shape + pose = pose_raw.reshape(B, L) + pose = self.pose_fc(pose) + features['Pose'] = pose.clone() + + # Project model 3D + euler = pose[:, 0:3] + trl = pose[:, 3:] + rot = pproj.euler_to_rotation_matrix(euler) + pts_proj = pproj.projectPoints(model3d, rot, trl, cam_matrix) + pts_proj = pts_proj / self.visual_res + + return pts_proj, features + + def extract_embedded(self, pts_proj, receptive_field, step): + # Visual features + visual_ft = self.extract_visual_embedded(pts_proj, receptive_field, step) + # Shape features + shape_ft = self.calculate_distances(pts_proj) + shape_ft = self.shape_encoder[step](shape_ft) + # Addition + embedded_ft = visual_ft + shape_ft + return embedded_ft + + def extract_visual_embedded(self, pts_proj, receptive_field, step): + # Affine matrix generation + B, L, _ = pts_proj.shape # Pts_proj range:[0,1] + centers = pts_proj + 0.5 / self.visual_res # BxLx2 + centers = centers.reshape(B * L, 2) # B*Lx2 + theta_trl = (-1 + centers * 2).unsqueeze(-1) # BxLx2x1 + theta_s = self.theta_S[step] # 2x2 + theta_s = theta_s.repeat(B * L, 1, 1) # B*Lx2x2 + theta = torch.cat((theta_s, theta_trl), -1) # B*Lx2x3 + + # Generate crop grid + B, C, _, _ = receptive_field.shape + grid = torch.nn.functional.affine_grid(theta, (B * L, C, self.kwindow, self.kwindow)) + grid = grid.reshape(B, L, self.kwindow, self.kwindow, 2) + grid = grid.reshape(B, L, self.kwindow * self.kwindow, 2) + + # Crop windows + crops = torch.nn.functional.grid_sample(receptive_field, grid, padding_mode="border") # BxCxLxK*K + crops = crops.transpose(1, 2) # BxLxCxK*K + crops = crops.reshape(B * L, C, self.kwindow, self.kwindow) + + # Flatten features + visual_ft = self.conv_window[step](crops) + _, Cout, _, _ = visual_ft.shape + visual_ft = visual_ft.reshape(B, L, Cout) + + return visual_ft + + def calculate_distances(self, pts_proj): + B, L, _ = pts_proj.shape # BxLx2 + pts_a = pts_proj.unsqueeze(-2).repeat(1, 1, L, 1) + pts_b = pts_a.transpose(1, 2) + dist = pts_a - pts_b + dist_wo_self = dist[:, self.diagonal_mask, :].reshape(B, L, -1) + return dist_wo_self + + + + + + + diff --git a/app.py b/app.py new file mode 100644 index 0000000000000000000000000000000000000000..989104829628d28e387946e4bfd816c7feed5e9f --- /dev/null +++ b/app.py @@ -0,0 +1,86 @@ +import os +import sys +from pathlib import Path +import uuid +import gradio as gr +try: + from spiga.demo.app import video_app +except: + os.system("pip install -e ./SPIGA[demo]") + sys.path.append(os.path.abspath("./SPIGA")) + from spiga.demo.app import video_app + + +def predict(video_in, image_in_video, image_in_img): + if video_in == None and image_in_video == None and image_in_img == None: + raise gr.Error("Please upload a video or image.") + if image_in_video or image_in_img: + print("image", image_in_video, image_in_img) + image = image_in_video or image_in_img + return image + # if video + + video_in = Path(video_in) + output_path = Path("/tmp") + video_file_name = str(uuid.uuid4()) + new_video_path = output_path / f"{video_file_name}{video_in.suffix}" + video_in.rename(new_video_path) + + video_app(str(new_video_path), + # Choices=['wflw', '300wpublic', '300wprivate', 'merlrav'] + spiga_dataset='wflw', + # Choices=['RetinaSort', 'RetinaSort_Res50'] + tracker='RetinaSort', + save=True, + output_path=output_path, + visualize=False, + plot=['fps', 'face_id', 'landmarks', 'headpose']) + video_output_path = f"{output_path}/{new_video_path.name[:-4]}.mp4" + + return video_output_path + + +def toggle(choice): + if choice == "webcam": + return gr.update(visible=True, value=None), gr.update(visible=False, value=None) + else: + return gr.update(visible=False, value=None), gr.update(visible=True, value=None) + + +with gr.Blocks() as blocks: + gr.Markdown("### Video or Image? WebCam or Upload?""") + with gr.Tab("Video") as tab: + with gr.Row(): + with gr.Column(): + video_or_file_opt = gr.Radio(["webcam", "upload"], value="webcam", + label="How would you like to upload your video?") + video_in = gr.Video(source="webcam", include_audio=False) + video_or_file_opt.change(fn=lambda s: gr.update(source=s, value=None), inputs=video_or_file_opt, + outputs=video_in, queue=False) + with gr.Column(): + video_out = gr.Video() + run_btn = gr.Button("Run") + run_btn.click(fn=predict, inputs=[video_in], outputs=[video_out]) + gr.Examples(fn=predict, examples=[], inputs=[ + video_in], outputs=[video_out]) + + with gr.Tab("Image"): + with gr.Row(): + with gr.Column(): + image_or_file_opt = gr.Radio(["webcam", "file"], value="webcam", + label="How would you like to upload your image?") + image_in_video = gr.Image(source="webcam", type="filepath") + image_in_img = gr.Image( + source="upload", visible=False, type="filepath") + + image_or_file_opt.change(fn=toggle, inputs=[image_or_file_opt], + outputs=[image_in_video, image_in_img], queue=False) + with gr.Column(): + image_out = gr.Image() + run_btn = gr.Button("Run") + run_btn.click(fn=predict, inputs=[ + image_in_img, image_in_video], outputs=[image_out]) + gr.Examples(fn=predict, examples=[], inputs=[ + image_in_img, image_in_video], outputs=[image_out]) + +blocks.launch() diff --git a/packages.txt b/packages.txt new file mode 100644 index 0000000000000000000000000000000000000000..a3e85e905383c312f205afe014e8c601ac973a77 --- /dev/null +++ b/packages.txt @@ -0,0 +1,2 @@ +rustc +cargo \ No newline at end of file diff --git a/pre-requirements.txt b/pre-requirements.txt new file mode 100644 index 0000000000000000000000000000000000000000..e512b5e6f9ff21da877ab7baf6f9a65680818e20 --- /dev/null +++ b/pre-requirements.txt @@ -0,0 +1 @@ +pip==23.0.1 \ No newline at end of file diff --git a/requirements.txt b/requirements.txt new file mode 100644 index 0000000000000000000000000000000000000000..ee7aa7b1b972be9757e3410d2ee0b6816768a1ca --- /dev/null +++ b/requirements.txt @@ -0,0 +1,12 @@ +gradio +matplotlib>=3.2.1 +numpy>=1.18.2 +opencv-python>=4.2.0.32 +Pillow>=7.0.0 +torch>=1.4.0 +torchvision>=0.5.0 +torchaudio +scipy +scikit-learn +retinaface-py>=0.0.2 +sort-tracker-py>= 1.0.2 \ No newline at end of file
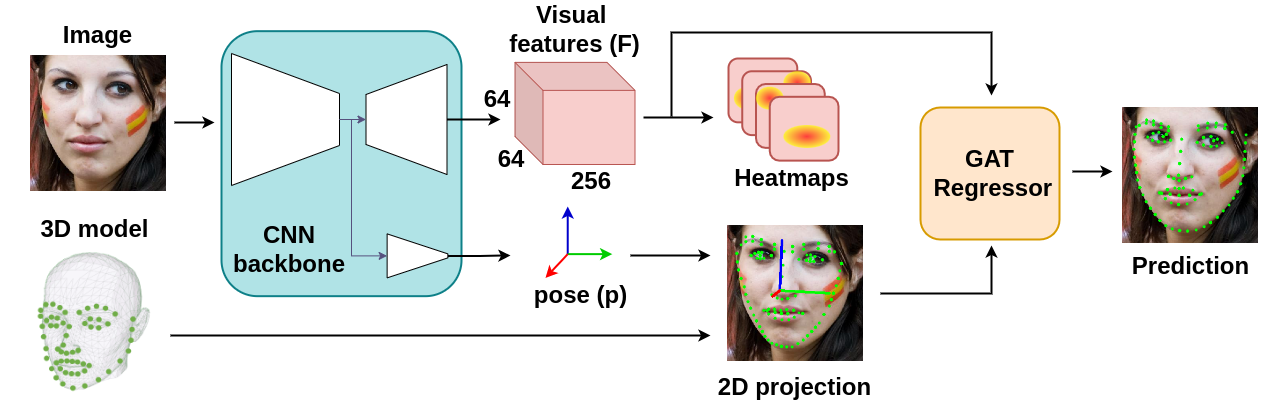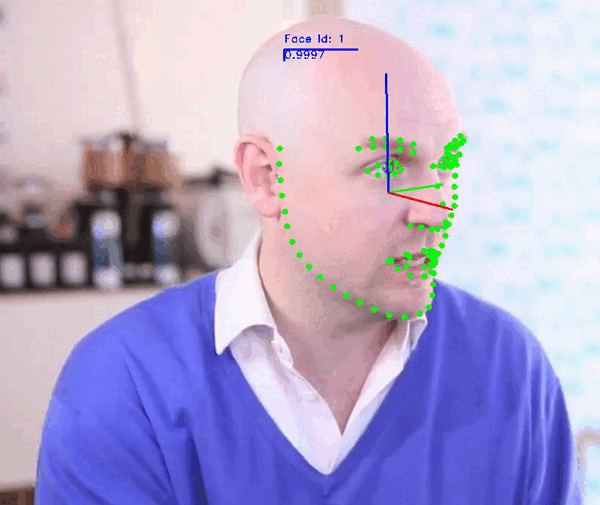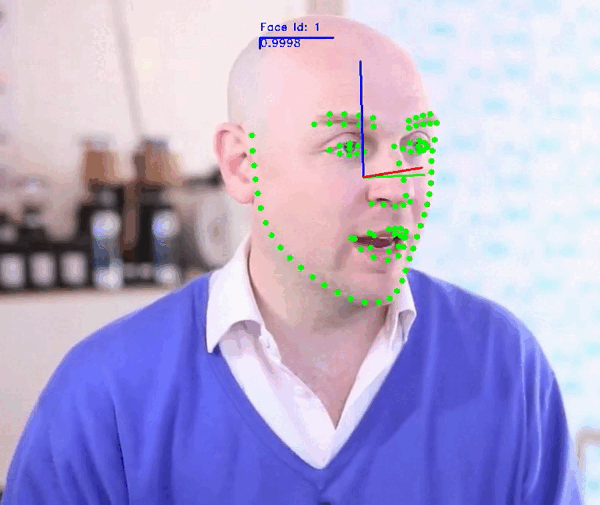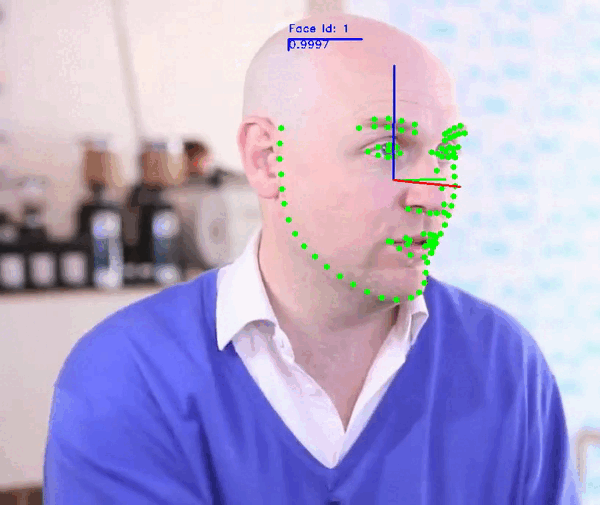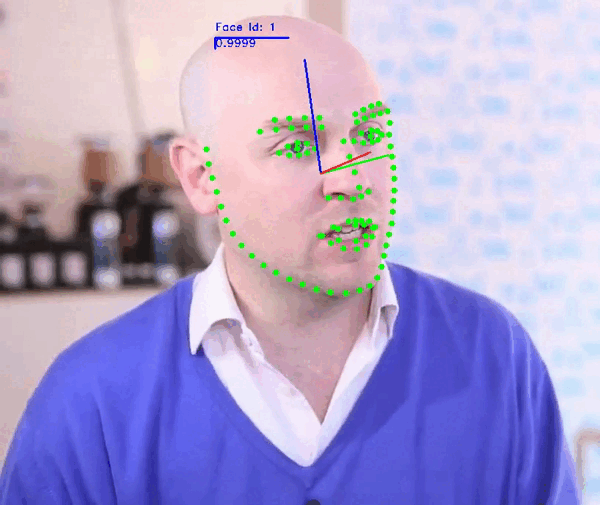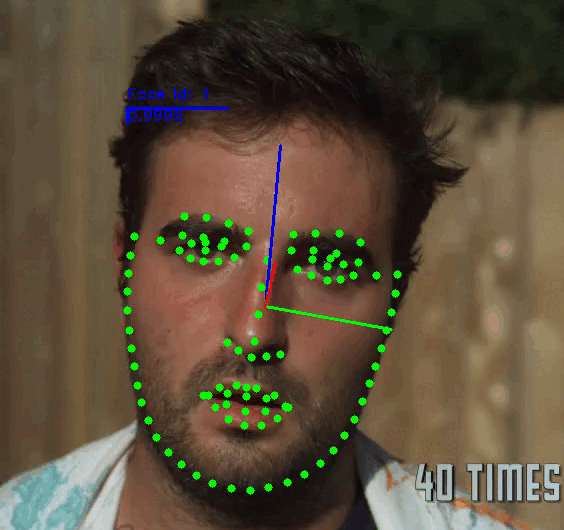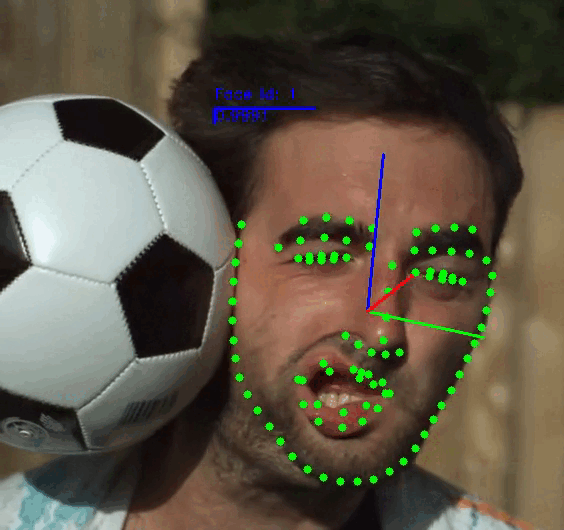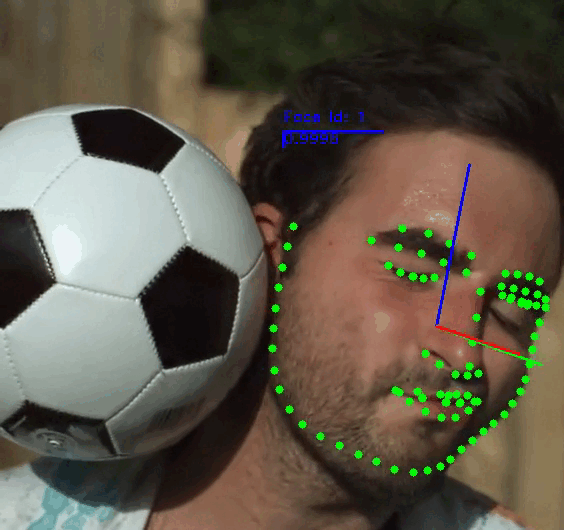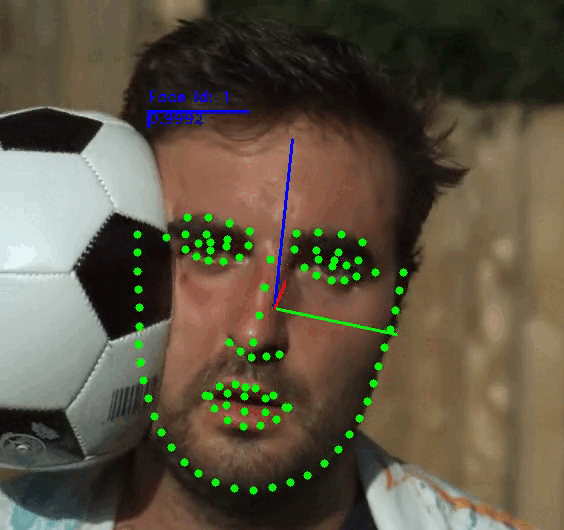