id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
34,546 | 2.1. Once, in a company, the following conversation took place:
- We must call Misha immediately! - exclaimed Vanya.
However, no one remembered Misha's phone number.
- I remember for sure that the last three digits of the phone number are consecutive natural numbers, - said Nastya.
- And I recall that the first five digits formed a palindrome, - noted Anton.
- Seven-digit numbers are not memorized as a whole; they are broken down into three groups: first three digits, and then two groups of two digits each. I think the three-digit number obtained in this way was divisible by 9 - remarked Nikita.
- That's right, - supported Mitya, - and there were three consecutive ones in the phone number.
- Only one of the two-digit numbers obtained by Nikita's method was prime, - added Sasha.
Help the guys restore Misha's phone number. | 7111765 |
34,550 | 3. All natural numbers are divided into "good" and "bad" according to the following rules:
a) From any bad number, you can subtract some natural number not exceeding its half so that the resulting difference becomes "good".
b) From a "good" number, you cannot subtract no more than half of it so that it remains "good".
It is known that the number 1 is "good". Find the nearest "good" number to 2015. | 2047 |
34,564 | Example 27 (Mathematical Problem 1434 from "Mathematical Bulletin") Let positive numbers $x, y, z$ be not equal to 1, and $xy + yz + zx = 1$. Try to find the maximum value of $f(x, y, z) = x(1-y^2)(1-z^2) + y(1-z^2)(1-x^2) + z(1-x^2)(1-y^2)$. | \frac{4\sqrt{3}}{9} |
34,566 | Problem 12.2. Let $k$ be a circle with center $O$ and radius $\sqrt{5}$ and let $M$ and $N$ be points on a diameter of $k$ such that $M O=N O$. The chords $A B$ and $A C$, passing through $M$ and $N$, respectively, are such that
$$
\frac{1}{M B^{2}}+\frac{1}{N C^{2}}=\frac{3}{M N^{2}}
$$
Find the length of $M O$.
Oleg Mushkarov | 1 |
34,586 | 8. Given $I$ is the incenter of $\triangle A B C$, and $5 \overrightarrow{I A}=$ $4(\overrightarrow{B I}+\overrightarrow{C I})$. Let $R$ and $r$ be the radii of the circumcircle and incircle of $\triangle A B C$, respectively. If $r=15$, then $R=$ $\qquad$ . | 32 |
34,587 | 14. (2003 National Team Training Problem) If the sum of all positive divisors of a positive integer is twice the number itself, then the number is called a perfect number. Find all positive integers $n$ such that $n-1$ and $\frac{n(n+1)}{2}$ are both perfect numbers. | 7 |
34,604 | In the diagram, $A B C D$ is a trapezoid with $B C$ parallel to $A D$ and $A B=C D$. Point $E$ is on $A D$ so that $B E$ is perpendicular to $A D$ and point $F$ is the point of intersection of $A C$ with $B E$. If $A F=F B$ and $\angle A F E=50^{\circ}$, what is the measure of $\angle A D C$ ?
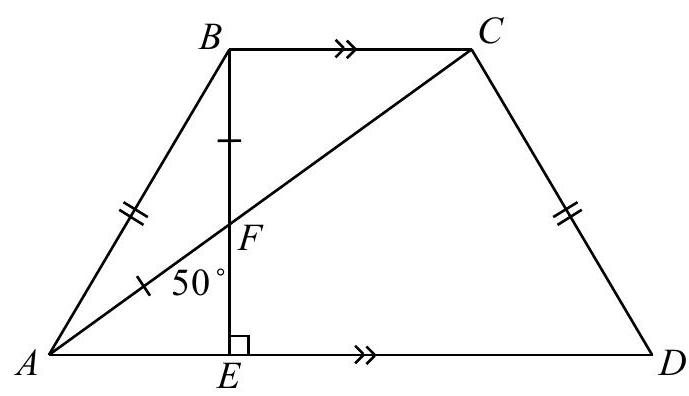 | 65 |
34,609 | Task B-3.8. For the angles $\alpha$ and $\beta$ of triangle $ABC$, the following holds:
$$
\begin{aligned}
& 3 \sin \alpha + 4 \cos \beta = 6 \\
& 4 \sin \beta + 3 \cos \alpha = 1
\end{aligned}
$$
Determine the measure of angle $\gamma$ of this triangle. | 30 |
34,638 | 5. In $\triangle A B C$, $\angle C=90^{\circ}, \angle B=30^{\circ}$, $A C=1$, $M$ is the midpoint of $A B$. Fold $\triangle A C M$ along $C M$ so that the distance between points $A$ and $B$ is $\sqrt{2}$. Then the distance from point $A$ to the plane $B C M$ is $\qquad$ . | \frac{\sqrt{6}}{3} |
34,646 | 7. Let $f(x)=m x^{2}+(2 n+1) x-m-2(m, n \in \mathbf{R}, m \neq 0)$ have at least one zero in $[3,4]$, then the minimum value of $m^{2}+n^{2}$ is $\qquad$ . | \frac{1}{100} |
34,654 | In an equilateral triangle $ABC$, points $M$ and $N$ are given on side $AB$, point $P$ on side $BC$, and point $Q$ on side $CA$, such that
$$
M A + A Q = N B + B P = A B
$$
What angle can the lines $MP$ and $NQ$ form? | 60 |
34,658 | 6. Next to the number 2022 on the board, an unknown positive number less than 2022 was written. Then one of the numbers on the board was replaced by their arithmetic mean. This replacement was performed 9 more times, and the arithmetic mean was always an integer. Find the smaller of the numbers originally written on the board. | 998 |
34,667 | . Find all finite sets of positive integers with at least two elements such that for any two numbers $a, b(a>b)$ belonging to the set, the number $\frac{b^{2}}{a-b}$ belongs to the set, too.
Answer: $X=\{a, 2 a\}$, where $a$ is an arbitrary nonnegative integer. | {,2a} |
34,670 | 7. Let $O$ and $A$ be two points in the plane with $O A=30$, and let $\Gamma$ be a circle with center $O$ and radius $r$. Suppose that there exist two points $B$ and $C$ on $\Gamma$ with $\angle A B C=90^{\circ}$ and $A B=B C$. Compute the minimum possible value of $\lfloor r\rfloor$. | 12 |
34,675 | 12. Let $F_{1}$ and $F_{2}$ be the two foci of the ellipse $C$, and $AB$ be a chord of the ellipse passing through point $F_{2}$. In $\triangle F_{1} A B$,
$$
\left|F_{1} A\right|=3,|A B|=4,\left|B F_{1}\right|=5 \text {. }
$$
Then $\tan \angle F_{2} F_{1} B=$ $\qquad$ | \frac{1}{7} |
34,677 | 1. Find all sequences with natural non-repeating terms, for which $a_{n}$ is divisible by $a_{a_{n}}$ for all $n$. | a_{n}=n |
34,681 | 5. Let $a_{i} \in \mathbf{R}(i=1,2, \cdots, 10)$, and $\sum_{i=1}^{10} \frac{a_{i}^{2}}{a_{i}^{2}+1}=1$.
Then the range of $\sum_{i=1}^{10} \frac{a_{i}}{a_{i}^{2}+1}$ is | [-3,3] |
34,701 | Let $l, m$ be two skew lines, and on $l$ there are three points $A, B, C$, with $A B = B C$. Draw perpendiculars from $A, B, C$ to $m$, denoted as $A D, B E, C F$, with the feet of the perpendiculars being $D$, $E, F$ respectively. Given that $A D = \sqrt{15}, B E = \frac{7}{2}, C F = \sqrt{10}$. Find the distance between $l$ and $m$. | \sqrt{6} |
34,703 | 16 In the sequence $\left\{a_{n}\right\}$, $a_{1}, a_{2}$ are given non-zero integers, $a_{n+2}=\left|a_{n+1}-a_{n}\right|$.
(1) Let $a_{1}=2, a_{2}=-1$, find $a_{2008}$;
(2) Prove: From $\left\{a_{n}\right\}$, it is always possible to select infinitely many terms to form two different constant sequences. | 0 |
34,718 | II If one side of the square $A B C D$ lies on the line $y=2 x-17$, and the other two vertices are on the parabola $y=x^{2}$. Then the minimum value of the area of the square is $\qquad$ . | 80 |
34,719 | 18. (1990 Japan Mathematical Olympiad Team Selection Test) A certain positive integer, when squared, has the last three digits as non-zero identical digits. Find the smallest positive integer with this property. | 38 |
34,730 | 13. As shown in the figure, in the quadrilateral pyramid $P-ABCD$, $PA \perp$ base $ABCD$, $BC=CD=2$, $AC=4$, $\angle ACB=\angle ACD=\frac{\pi}{3}$, $F$ is the midpoint of $PC$, and $AF \perp PB$.
(1) Find the length of $PA$;
(2) Find the sine of the dihedral angle $B-AF-D$. | \frac{3\sqrt{7}}{8} |
34,745 | [ Law of Cosines
A right triangle $ABC$ is inscribed in a circle. A chord $CM$ is drawn from vertex $C$ of the right angle, intersecting the hypotenuse at point $K$. Find the area of triangle $ABM$, if $BK: AB=3: 4, BC=2 \sqrt{2}, AC=$
4.
# | \frac{36}{19}\sqrt{2} |
34,750 | 4.8. Given a cube $A B C D A_{1} B_{1} C_{1} D_{1}$. A plane passing through vertex $A$ and tangent to the sphere inscribed in the cube intersects the edges $A_{1} B_{1}$ and $A_{1} D_{1}$ at points $K$ and $N$,
Find the measure of the angle between the planes $A C_{1} K$ and $A C_{1} N$. | 60 |
34,751 | Axis), $F$ is the focus, and $|A F|+|B F|=8$. The perpendicular bisector of line segment $A B$ always passes through the fixed point $Q(6,0)$ on the $x$-axis.
(1) Find the equation of the parabola $C$;
(2) Find the maximum value of the area of $\triangle A Q B$.
保留了源文本的换行和格式。 | \frac{64}{9}\sqrt{6} |
34,765 | Example 4. Knowing the fundamental system of solutions $y_{1}=\ln x, y_{2}=x$ of the corresponding homogeneous equation, find a particular solution of the equation
$$
x^{2}(1-\ln x) y^{\prime \prime}+x y^{\prime}-y=\frac{(1-\ln x)^{2}}{x}
$$
satisfying the condition $\lim _{x \rightarrow+\infty} y=0$. | \frac{1-2\lnx}{4x} |
34,829 | The Fibonacci numbers are defined by $F_1=F_2=1$ and $F_n=F_{n-1}+F_{n-2}$ for $n>2$. It is well-known that the sum of any $10$ consecutive Fibonacci numbers is divisible by $11$. Determine the smallest integer $N$ so that the sum of any $N$ consecutive Fibonacci numbers is divisible by $12$. | 24 |
34,894 | 5. If for all $x$ such that $|x| \leqslant 1$, $t+1>(t^2-4)x$ always holds, then the range of values for $t$ is $\qquad$ | \left(\frac{\sqrt{13}-1}{2}, \frac{\sqrt{21}+1}{2}\right) |
34,924 | 4. If $4n+1$ and $6n+1$ are both perfect squares, then the smallest positive integer $n$ is $\qquad$ | 20 |
34,946 | Example 2. Find all natural numbers with the following property: its unit digit is 6, and when its unit digit is moved to the front of the number, the resulting new number is four times the original number. | 153846 |
34,957 | Let $ABCD$ be a rectangle with side lengths $AB = CD = 5$ and $BC = AD = 10$. $W, X, Y, Z$ are points on $AB, BC, CD$ and $DA$ respectively chosen in such a way that $WXYZ$ is a kite, where $\angle ZWX$ is a right angle. Given that $WX = WZ = \sqrt{13}$ and $XY = ZY$, determine the length of $XY$. | \sqrt{65} |
34,977 | 2. Let positive real numbers $a, b, c$ satisfy $a^{2}+b^{2}+c^{2}=1$. Then the maximum value of $s=a^{2} b c+a b^{2} c+a b c^{2}$ is $\qquad$ | \frac{1}{3} |
35,046 | Find all prime numbers $p$ for which the number $p^2+11$ has less than $11$ divisors. | 5 |
35,053 | Example 4 When point $P$ moves along the line $y=2 x+6$, and point $Q$ moves on the ellipse $\frac{x^{2}}{6}+\frac{y^{2}}{4}=1$, the minimum length of segment $P Q$ is $\qquad$ | \frac{6 \sqrt{5}-2 \sqrt{35}}{5} |
35,065 | ## Aufgabe 1 - 290831
Eine Aufgabe des bedeutenden englischen Naturwissenschaftlers Isaak Newton (1643 bis 1727) lautet:
Ein Kaufmann besaß eine gewisse Geldsumme.
Im ersten Jahr verbrauchte er davon 100 Pfund; zum Rest gewann er durch seine Arbeit ein Drittel desselben dazu.
Im zweiten Jahr verbrauchte er wiederum 100 Pfund und gewann zum Rest ein Drittel dazu. Im dritten Jahr verbrauchte er erneut 100 Pfund und gewann zum Rest ein Drittel dazu.
Dabei stellte er fest, dass sich sein Geld gegenüber dem Anfang des ersten Jahres verdoppelt hatte.
Ermittle aus diesen Angaben, welche Geldsumme anfangs des ersten Jahres vorhanden gewesen sein muss! Weise nach, dass bei dieser Anfangssumme die Angaben des Aufgabentextes zutreffen!
| 1480 |
35,108 | Let $a$ and $b$ be real numbers such that $a^5b^8=12$ and $a^8b^{13}=18$. Find $ab$. | \frac{128}{3} |
35,202 | 1. As shown in Figure 3, $O$ is a point inside $\triangle A B C$, extending $A O$ intersects $B C$ at point $D$, extending $B O$ intersects $A C$ at point $E$, the areas of $\triangle B O D$, $\triangle A O E$, and $\triangle A O B$ are 7, $14$, and $21$ respectively. Then $\frac{B D}{C D}=$ $\qquad$ . | \frac{7}{8} |
35,219 | 2. The function expression of the image $l_{2}$, which is symmetric to the image $l_{1}$ of the linear function $y = a x + b$ with respect to the line $y = -x$, is $\qquad$ . | y=\frac{1}{a} x+\frac{b}{a} |
35,228 | 8. The solution set of the inequality
$$
\frac{4 x^{2}}{(1-\sqrt{1+2 x})^{2}}<2 x+9
$$
is . $\qquad$ | \left[-\frac{1}{2}, 0\right) \cup\left(0, \frac{45}{8}\right) |
35,233 | We draw a triangle inside of a circle with one vertex at the center of the circle and the other two vertices on the circumference of the circle. The angle at the center of the circle measures $75$ degrees. We draw a second triangle, congruent to the first, also with one vertex at the center of the circle and the other vertices on the circumference of the circle rotated $75$ degrees clockwise from the first triangle so that it shares a side with the first triangle. We draw a third, fourth, and fifth such triangle each rotated $75$ degrees clockwise from the previous triangle. The base of the fifth triangle will intersect the base of the first triangle. What is the degree measure of the obtuse angle formed by the intersection? | 120^\circ |
35,239 | In a country there are $n\geq 2$ cities. Any two cities has exactly one two-way airway. The government wants to license several airlines to take charge of these airways with such following conditions:
i) Every airway can be licensed to exactly one airline.
ii) By choosing one arbitrary airline, we can move from a city to any other cities, using only flights from this airline.
What is the maximum number of airlines that the government can license to satisfy all of these conditions? | \left\lfloor \frac{n}{2} \right\rfloor |
35,240 | A $\square\{1,2,3, \ldots, 49\}$ does not contain six consecutive integers. Find the largest possible value of |A|. How many such subsets are there (of the maximum size)?
## Answer
$\max =41$; no. ways 495 | 495 |
35,244 | 1. In an international chess tournament with 10 participants, each player must play exactly one game against every other player. After several games, it is found that among any three players, at least two have not yet played against each other. How many games have been played at most by this point? | 25 |
35,259 | 23. (USA 4) Find all natural numbers $n$ for which $2^{8}+2^{11}+2^{n}$ is a perfect square. | 12 |
35,264 | 8. Given a sequence $\left\{a_{n}\right\}$ with nine terms, where $a_{1}=a_{9}=1$, and for each $i \in\{1,2, \cdots, 8\}$, we have $\frac{a_{i+1}}{a_{i}} \in \left\{2,1,-\frac{1}{2}\right\}$. Then the number of such sequences is | 491 |
35,279 | 7. Given $\alpha, \beta \in [0, \pi]$. Then
$$
[\sin \alpha + \sin (\alpha + \beta)] \sin \beta
$$
the maximum value is . $\qquad$ | \frac{8 \sqrt{3}}{9} |
35,285 | 1. Given points $A, B, C, D$ lie on the same circle, and $BC = DC = 4, AC$ intersects $BD$ at point $E, AE = 6$. If the lengths of segments $BE$ and $DE$ are both integers, find the length of $BD$. | 7 |
35,286 | As shown in Figure 2, in the square $A B C D$, the diagonals $A C$ and $B D$ intersect at
point $O$, point $F$ is on side $C D$,
the extension of $A F$ intersects the
extension of $B C$ at
point $E$, the extension of $O F$
intersects $D E$ at point $M$. Find the measure of $\angle O M D$. | 45^{\circ} |
35,288 | Example 6 A square ground is paved with regular hexagonal tiles with a side length of $36 \mathrm{~cm}$. Now, a circular disc with a radius of $6 \sqrt{3} \mathrm{~cm}$ is thrown upwards. The probability that the disc, after landing, does not intersect with the gaps between the tiles is approximately $\qquad$ . | \frac{4}{9} |
35,307 | A class consists of 26 students with two students sitting on each desk. Suddenly, the students decide to change seats, such that every two students that were previously sitting together are now apart. Find the maximum value of positive integer $N$ such that, regardless of the students' sitting positions, at the end there is a set $S$ consisting of $N$ students satisfying the following property: every two of them have never been sitting together. | 13 |
35,312 | 2. Let $a<-1$, and the variable $x$ satisfies $x^{2}+a x \leqslant-x$, and the minimum value of $x^{2}+a x$ is $-\frac{1}{2}$. Then $a=$ $\qquad$ . | -\frac{3}{2} |
35,322 | Let $a_{10} = 10$, and for each integer $n >10$ let $a_n = 100a_{n - 1} + n$. Find the least $n > 10$ such that $a_n$ is a multiple of $99$. | 45 |
35,359 | Andrew takes a square sheet of paper $ABCD$ of side length $1$ and folds a kite shape. To do this, he takes the corners at $B$ and $D$ and folds the paper such that both corners now rest at a point $E$ on $AC$. This fold results in two creases $CF$ and $CG$, respectively, where $F$ lies on $AB$ and $G$ lies on $AD$. Compute the length of $FG$. | 2\sqrt{2} - 2 |
35,372 | 9. As shown in Figure 1, in $\triangle A B C$, $\angle A B C=60^{\circ}$, point $P$ is a point inside $\triangle A B C$ such that $\angle A P B=\angle B P C=\angle C P A$, and $P A=8, P C=6$. Then $P B=$ $\qquad$ | 4 \sqrt{3} |
35,379 | 15. From $1,2, \cdots, 2004$, choose $k$ numbers such that among the chosen $k$ numbers, there are definitely 3 numbers that can form the side lengths of a triangle (here it is required that the three side lengths of the triangle are all different). What is the minimum value of $k$ that satisfies the condition? | 17 |
35,396 | 3. Let point $A(2,1)$, moving point $B$ on the $x$-axis, and moving point $C$ on the line $y=x$. Then the minimum value of the perimeter of $\triangle A B C$ is $\qquad$ . | \sqrt{10} |
35,409 | 4. In $\triangle A B C$, it is known that $\angle B A C=100^{\circ}, A B$ $=A C, P$ is a point inside $\triangle A B C$, and $\angle P A C=$ $\angle A C P=20^{\circ}$. Find $\angle P B A$. | 30^{\circ} |
35,416 |
1. Solve the following system of equations in the domain of real numbers
$$
\begin{aligned}
2 x+\lfloor y\rfloor & =2022, \\
3 y+\lfloor 2 x\rfloor & =2023 .
\end{aligned}
$$
(The symbol $\lfloor a\rfloor$ denotes the lower integer part of a real number a, i.e. the greatest integer not greater than a. E.g. $\lfloor 1,9\rfloor=1$ and $\lfloor-1,1\rfloor=-2$.) (Jaroslav Švrček)
| (1011,\frac{1}{3}) |
35,421 | 3. In triangle $ABC$, the median $BM$ is twice as short as side $AB$ and forms an angle of 40 degrees with it. Find angle $ABC$.
| 110 |
35,436 | 4. As shown in the figure, on a semicircle with center $C$ and diameter $M N$, there are two different points $A$ and $B$. Point $P$ is on $C N$, and $\angle C A P = \angle C B P = 10^{\circ}$. If $\overparen{M A} = 40^{\circ}$, then $\overparen{B N}$ equals . $\qquad$ | 20^{\circ} |
35,438 | 4. If real numbers $x, y$ satisfy $x^{3}+y^{3}+3 x y=1$, then the minimum value of $x^{2}+y^{2}$ is . $\qquad$ | \frac{1}{2} |
35,467 | A snowman is built on a level plane by placing a ball radius $6$ on top of a ball radius $8$ on top of a ball radius $10$ as shown. If the average height above the plane of a point in the snowman is $\frac{m}{n}$ where $m$ and $n$ are relatively prime positive integers, find $m + n$.
[asy]
size(150);
draw(circle((0,0),24));
draw(ellipse((0,0),24,9));
draw(circle((0,-56),32));
draw(ellipse((0,-56),32,12));
draw(circle((0,-128),40));
draw(ellipse((0,-128),40,15));
[/asy] | 61 |
35,480 | 24. Given a word arithmetic puzzle:
Where different Chinese characters represent different digits from $0-9$, and the same Chinese characters represent the same digit, making the equation true. Please write one way to fill in the numbers to make the equation true.
| (23+91+20)\times(41-(6+7+8+5))=2010 |
35,513 | Example 2 Solve the equation $\sqrt{x-\frac{1}{x}}+\sqrt{1-\frac{1}{x}}=x$. | x=\frac{1+\sqrt{5}}{2} |
35,524 | Let $s(n) = \frac16 n^3 - \frac12 n^2 + \frac13 n$.
(a) Show that $s(n)$ is an integer whenever $n$ is an integer.
(b) How many integers $n$ with $0 < n \le 2008$ are such that $s(n)$ is divisible by $4$?
| 1255 |
35,547 | Find all positive integers $n$ that have 4 digits, all of them perfect squares, and such that $n$ is divisible by 2, 3, 5 and 7. | 4410 |
35,552 | 2. There are three numbers arranged in sequence: $3, 9, 8$. For any two adjacent numbers, the difference between the right number and the left number is written between these two numbers, resulting in a new sequence $3, 6, 9, -1, 8$, which is called the first operation; after the second similar operation, a new sequence $3, 3, 6, 3, 9, -10, -1, 9, 8$ is produced; continue this operation. Ask: Starting from the sequence 3, 9, 8, what is the sum of all numbers in the new sequence after the 100th operation? | 520 |
35,553 | What is the number of ways in which one can choose $60$ unit squares from a $11 \times 11$ chessboard such that no two chosen squares have a side in common? | 62 |
35,561 | We color each number in the set $S = \{1, 2, ..., 61\}$ with one of $25$ given colors, where it is not necessary that every color gets used. Let $m$ be the number of non-empty subsets of $S$ such that every number in the subset has the same color. What is the minimum possible value of $m$? | 119 |
35,584 | Maryam has a fair tetrahedral die, with the four faces of the die labeled 1 through 4. At each step, she rolls the die and records which number is on the bottom face. She stops when the current number is greater than or equal to the previous number. (In particular, she takes at least two steps.) What is the expected number (average number) of steps that she takes? | \frac{625}{256} |
35,585 | 1. The solution set of the inequality $\frac{4 x^{2}}{(1-\sqrt{1+2 x})^{2}}<2 x+9$ is | \left[-\frac{1}{2}, 0\right) \cup\left(0, \frac{45}{8}\right) |
35,603 | In the adjoining figure, two circles with radii $8$ and $6$ are drawn with their centers $12$ units apart. At $P$, one of the points of intersection, a line is drawn in such a way that the chords $QP$ and $PR$ have equal length. Find the square of the length of $QP$. | 130 |
35,604 | Find all positive integers $m$ and $n$ such that $1 + 5 \cdot 2^m = n^2$. | (4, 9) |
35,626 | 4. Solve the equation: $\frac{1}{x^{2}-10 x-29}=$ $+\frac{1}{x^{2}-10 x-45}-\frac{2}{x^{2}-10 x-69}=0$. | x=13 |
35,643 | 4. In $\triangle A B C$, $A B=A C, D$ is the midpoint of $B C$, $B E \perp A C$ at $E$, intersecting $A D$ at $P$. Given $B P=3$, $P E=1$. Then $P A=$ $\qquad$ . | \sqrt{3} |
35,644 | Let $a$ be a real number greater than $1$ such that $\frac{20a}{a^2+1} = \sqrt{2}$. Find $\frac{14a}{a^2 - 1}$. | 1 |
35,658 | 4. Given that $A D$ is the altitude of $\triangle A B C$,
$$
\angle B A C=135^{\circ}, A D=3, B C=25 \text {. }
$$
Then the perimeter of $\triangle A B C$ is $\qquad$ . | 30 + 15 \sqrt{2} |
35,663 | 1. The solution set of the inequality
$$
(x+1)^{3}\left(x^{3}+5 x\right)<10(x+1)^{2}+8
$$
is $\qquad$ . | (-2,1) |
35,672 | 6. The natural number $k$ satisfies the following property: in $1,2, \cdots, 1988$, $k$ different numbers can be selected such that the sum of any two of these numbers is not divisible by their difference. Find the maximum value of $k$. (26th Mo
将上面的文本翻译成英文,保留了源文本的换行和格式。 | 663 |
35,685 | What is the largest $2$-digit [prime](https://artofproblemsolving.com/wiki/index.php/Prime) factor of the integer $n = {200\choose 100}$? | 61 |
35,690 | Let $K$ be the product of all factors $(b-a)$ (not necessarily distinct) where $a$ and $b$ are integers satisfying $1\le a < b \le 20$. Find the greatest positive [integer](https://artofproblemsolving.com/wiki/index.php/Integer) $n$ such that $2^n$ divides $K$. | 150 |
35,724 | 4. In the Cartesian coordinate system, point $A(1,2)$, $B(4,1)$, and a moving point $P(x, y)$ on the circle $x^{2}+y^{2}=25$ form a triangle. Then the maximum value of $S_{\triangle A B P}$ is $\qquad$ | \frac{1}{2}(7+5 \sqrt{10}) |
35,772 | 3. In $\triangle A B C$,
$$
\angle A=100^{\circ} ; \angle B=50^{\circ} \text {. }
$$
$A H$ is the altitude from $A$ to side $B C$, and $B M$ is the median from $B$ to side $A C$.
Then $\angle M H C=$ | 30^{\circ} |
35,776 | Three, given that $a$ is an integer, the equation $x^{2}+(2 a+1) x$ $+a^{2}=0$ has integer roots $x_{1}, x_{2}, x_{1}>x_{2}$. Try to find the value of $\sqrt[4]{x_{1}^{2}}-\sqrt[4]{x_{2}^{2}}$. | -1 |
35,779 | Solve in the interval $ (2,\infty ) $ the following equation:
$$ 1=\cos\left( \pi\log_3 (x+6)\right)\cdot\cos\left( \pi\log_3 (x-2)\right) . $$ | x = 3 |
35,785 | 14. As shown in Figure 3, in $\triangle A B C$, $O$ is the midpoint of side $B C$, and a line through point $O$ intersects lines $A B$ and $A C$ at two distinct points $M$ and $N$. If
$$
\begin{array}{l}
\overrightarrow{A B}=m \overrightarrow{A M}, \\
\overrightarrow{A C}=n \overrightarrow{A N},
\end{array}
$$
then the value of $m+n$ is
$\qquad$ | 2 |
35,795 | A caretaker is giving candy to his two babies. Every minute, he gives a candy to one of his two babies at random. The five possible moods for the babies to be in, from saddest to happiest, are "upset," "sad," "okay," "happy," and "delighted." A baby gets happier by one mood when they get a candy and gets sadder by one mood when the other baby gets one. Both babies start at the "okay" state, and a baby will start crying if they don't get a candy when they're already "upset".
The probability that 10 minutes pass without either baby crying can be expressed as $\frac{p}{q}$. Compute $p+q$.
[i]2022 CCA Math Bonanza Team Round #7[/i] | 337 |
35,813 | Example 2 Let $A, B, C$ be three non-collinear lattice points on a plane, and the side lengths of $\triangle ABC$ are all positive integers. Find the minimum value of $AB$ and the minimum perimeter. | 12 |
35,841 | Example 10. (IMO6-1(1)) Find all positive integers $n$ such that $2^{n}-1$ is divisible by 7. | n = 3k |
35,847 | Compute the maximum real value of $a$ for which there is an integer $b$ such that $\frac{ab^2}{a+2b} = 2019$. Compute the maximum possible value of $a$. | 30285 |
35,864 | Let $S$ be the locus of all points $(x,y)$ in the first quadrant such that $\dfrac{x}{t}+\dfrac{y}{1-t}=1$ for some $t$ with $0<t<1$. Find the area of $S$. | \frac{1}{6} |
35,870 | Example 3. As shown in Figure 2, given the line $\mathrm{y}=2 \mathrm{x}$ and point $\mathrm{M}(6, 2)$, try to find points $A$ and $B$ on the $x$-axis and the line $y=2 x$ respectively, such that the perimeter of $\triangle A \bar{B} M$ is minimized, and find the minimum perimeter. | 8 \sqrt{2} |
35,898 | Example 3 The number of proper subsets of the set $\left\{x \left\lvert\,-1 \leqslant \log _{\frac{1}{x}} 10<-\frac{1}{2}\right., x\right.$ $\left.\in \mathbf{N}_{+}\right\}$ is $\qquad$ .
(1996, National High School Mathematics Competition) | 2^{90}-1 |
35,921 | 7. The integer solutions $(x, y)$ of the indeterminate equation $x^{2}+y^{2}=x y+2 x+2 y$ are in total groups.
The integer solutions $(x, y)$ of the indeterminate equation $x^{2}+y^{2}=x y+2 x+2 y$ are in total groups. | 6 |
35,924 | Let’s call a positive integer [i]interesting[/i] if it is a product of two (distinct or equal) prime numbers. What is the greatest number of consecutive positive integers all of which are interesting? | 3 |
35,952 | II. (20 points) As shown in Figure 1, it is known that $M$ is a moving point on the line where side $DC$ of the square $ABCD$ lies. Find the maximum value of $\frac{MA}{MB}$.
保留源文本的换行和格式,翻译结果如下:
```
II. (20 points) As shown in Figure 1, it is known that $M$ is a moving point on the line where side $DC$ of the square $ABCD$ lies. Find the maximum value of $\frac{MA}{MB}$.
``` | \frac{\sqrt{5}+1}{2} |
35,954 | Example 12 If $m$ and $n$ are positive integers, and $m \leqslant$ $1996, r=2-\frac{m}{n}>0$, then the minimum value of $r$ is $\qquad$
(1996, Shanghai Junior High School Mathematics Competition) | \frac{1}{998} |
35,965 | Four, (20 points) Question: In how many different ways can the elements of the set $M=\{1,2,3,4,5\}$ be assigned to three (ordered) sets $A$, $B$, and $C$, such that each element is contained in at least one of the sets, the intersection of these three sets is empty, and the intersection of any two of these sets is not empty? | 1230 |
35,975 | Example 1 As shown in Figure 1, in square $A B C D$, $E$ is a fixed point on $B C$, and $B E=10, E C=14, P$ is a moving point on $B D$. Then the minimum value of $P E+P C$ is $\qquad$
(2006, Zhejiang Province Junior High School Mathematics Competition) | 26 |
35,995 | Cyclic quadrilateral $ABCD$ has $AC\perp BD$, $AB+CD=12$, and $BC+AD=13$. FInd the greatest possible area of $ABCD$. | 36 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.