id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
33,496 | 7. Given a tetrahedron $ABCD$ where one edge length is 3, and the other five edge lengths are all 2. Then the radius of its circumscribed sphere is $\qquad$ | \frac{\sqrt{21}}{3} |
33,506 | 10. (10 points) A rectangular chessboard composed of unit squares of size $m \times n$ (where $m, n$ are positive integers not exceeding 10), has a chess piece placed in the unit square at the bottom-left corner. Two players, A and B, take turns moving the piece. The rules are: move up any number of squares, or move right any number of squares, but you cannot move out of the board or not move at all. The player who cannot make a move loses (i.e., the first player to move the piece to the top-right corner wins). How many pairs of positive integers $(m, n)$ allow the first player A to have a winning strategy? $\qquad$ | 90 |
33,511 | 10.255. Through point $A$ of a circle with a radius of 10 cm, two mutually perpendicular chords $A B$ and $A C$ are drawn. Calculate the radius of the circle that is tangent to the given circle and the constructed chords, if $A B=16$ cm. | 8 |
33,513 | 4. Let $Q$ be a set composed of several permutations of $1,2, \cdots, 100$, and it satisfies that for any $1 \leqslant a, b \leqslant 100$, $a \neq b$, there is at most one $\sigma \in Q$ such that in $\sigma$, the number immediately following $a$ is exactly $b$. Find the maximum number of elements in the set $Q$.
(Sun Gongchun) | 100 |
33,531 | 20. The five numbers $a, b, c, d, e$ are all different. The products of each pair of these numbers, arranged in ascending order, are $3, 6, 15, 18, 20, 50, 60, 100, 120, 300$. Then, the five numbers arranged in ascending order, the square of the 2nd number is $\qquad$ . | 10 |
33,543 | 11. (20 points) Given positive real numbers $p, q$. It is known that the sequence of positive real numbers $\left\{a_{n}\right\}$ satisfies:
$$
a_{0}=1, a_{n+2}=p a_{n}-q a_{n+1}(n \in \mathbf{N}) .
$$
Find all possible values of $a_{1}$ (expressed in terms of $p, q$). | \frac{-q+\sqrt{q^{2}+4p}}{2} |
33,555 | Let $n \in \mathbb{N}$. We define
$$
S=\left\{(x, y, z) \in\{0, \ldots, n\}^{3} \mid x+y+z>0\right\}
$$
as a set of $(n+1)^{3}-1$ points in three-dimensional space. Determine the minimum number of planes whose union contains $S$ but not the point $(0,0,0)$.
## Hints:
$\triangleright$ Start by finding a set of planes that work, possibly by considering the analogous problem in two dimensions to better visualize the situation.
$\triangleright$ Try to understand how a polynomial in several variables can be involved. It is important to keep in mind Proposition 20 stated below.
$\triangleright$ Consider trying to reduce the degree of the polynomial found, by using well-chosen operators.
Proposition 20. A plane in three dimensions can be described as the set of points whose coordinates $(x, y, z)$ satisfy a linear equation of the form $a x+b y+c z+d=0$ where $a, b, c, d$ are four real numbers such that $(a, b, c) \neq(0,0,0)$ (similarly, a line in two dimensions is characterized by an equation of the form $a x+b y+c=0$ where $a, b, c$ are three real numbers such that $(a, b) \neq(0,0))$. | 3n |
33,556 | ## Task 3.
In triangle $A B C$, the angle at vertex $B$ is $120^{\circ}$. Let $A_{1}, B_{1}, C_{1}$ be points on the sides $\overline{B C}$, $\overline{C A}$, $\overline{A B}$, respectively, such that $A A_{1}$, $B B_{1}$, $C C_{1}$ are the angle bisectors of triangle $A B C$. Determine the angle $\varangle A_{1} B_{1} C_{1}$. | 90 |
33,557 | (13) The line $x+y=1$ intersects the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ at points $A$ and $B$, and $C$ is the midpoint of segment $AB$. If $|AB|=2 \sqrt{2}$, and the slope of line $OC$ is $k_C=\frac{1}{\sqrt{2}}$, find the equation of the ellipse. | \frac{x^{2}}{3}+\frac{\sqrt{2}y^{2}}{3}=1 |
33,567 | Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
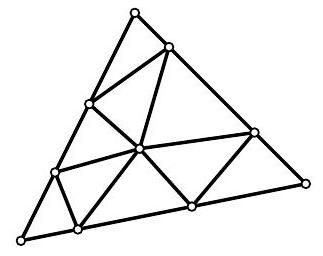 | 40 |
33,574 | Exercise 3. Consider an $n$-gon inscribed in a circle, and assume that any three diagonals of the $n$-gon never intersect. All vertices of the $n$-gon are connected. How many triangles are there in the figure that have no vertices in common with the $n$-gon? | \binom{n}{6} |
33,593 | 13. (1993 Putnam Mathematical Competition, 53rd USA) Let $S$ be a set of $n$ distinct real numbers, and let $A_{s}$ be the set of all distinct averages of pairs of elements of $S$. For a given $n \geqslant 2$, what is the least number of elements that $A_{s}$ can have? | 2n-3 |
33,595 | 8.30 Find all prime numbers \( p \) such that \( 2p^4 - p^2 + 16 \) is a perfect square.
(Leningrad Mathematical Olympiad, 1980) | 3 |
33,625 | 6-19 The set of all positive integers can be divided into two disjoint subsets of positive integers $\{f(1), f(2), \cdots, f(n), \cdots\},\{g(1), g(2), \cdots, g(n), \cdots\}$,
where $\quad f(1)<f(2)<\cdots<f(n)<\cdots$
$$
g(1)<g(2)<\cdots<g(n)<\cdots
$$
and $\quad g(n)=f(f(n))+1 \quad(n \geqslant 1)$
Find: $f(240)$. | 388 |
33,651 | ## Task A-1.3.
Determine all triples of real numbers $(x, y, z)$ such that
$$
\frac{1}{x}+\frac{1}{y+z}=\frac{1}{3}, \quad \frac{1}{y}+\frac{1}{z+x}=\frac{1}{5}, \quad \frac{1}{z}+\frac{1}{x+y}=\frac{1}{7}
$$ | (\frac{59}{18},\frac{59}{10},\frac{59}{2}) |
33,663 | 6. Given that $P, Q, R, S$ are four points inside the tetrahedron $A-BCD$, and $Q, R, S, P$ are the midpoints of $PA, QB, RC, SD$ respectively. If $V_{P-ABC}$ represents the volume of the tetrahedron $P-ABC$, and similarly for the others, then $V_{P-ABC}: V_{P-BCD}: V_{P-DAB}: V_{P-DAC}=$ $\qquad$ . | 8:1:4:2 |
33,666 | We wrote the reciprocals of the natural numbers from 2 to 2011 on a board. In one step, we erase two numbers, $x$ and $y$, and write the number
$$
\frac{x y}{x y+(1-x)(1-y)}
$$
in their place. Repeating this 2009 times, only one number remains. What could this number be? | \frac{1}{2010!+1} |
33,674 | $1 \cdot 200$ Write the number $1234567891011 \cdots \cdots 19941995$ on the blackboard, forming the integer $N_{1}$, erase the digits in the even positions of $N_{1}$, the remaining digits form the integer $N_{2}$, erase the digits in the odd positions of $N_{2}$, the remaining digits form the integer $N_{3}$, erase the digits in the even positions of $N_{3}$, the remaining digits form the integer $N_{4}$. This process continues until only one digit remains on the blackboard. Determine this digit (Note: Count the positions from left to right, for example, in 12345, 1 is in the 1st position, 2 is in the 2nd position, and so on). | 9 |
33,697 | 22.4. Among all such numbers $n$ that any convex 100-gon can be represented as the intersection (i.e., common part) of $n$ triangles,
find the smallest. | 50 |
33,716 | I2.3 If $X=\sqrt{(100)(102)(103)(105)+(Q-3)}$ is an integer and $R$ is the units digit of $X$, find the value of $R$.
I2.4 If $S$ is the sum of the last 3 digits (hundreds, tens, units) of the product of the positive roots of $\sqrt{2012} \cdot x^{\log _{2012} x}=x^{R}$, find the value of $S$. | 17 |
33,722 | 12. There are $N(N+1) \div 2$ dominoes, each with two numbers, and these numbers are from $1 \sim N$ (the two numbers can be the same). No two dominoes have the same pair of numbers. Now, arrange these dominoes into several "trains," where in each "train," any two adjacent dominoes have the same number on the adjacent sides. The figure below shows a "train" when $N=3$.
When $N=2016$, at least $\qquad$ trains are needed to use up all $2016 \times(2016+1) \div 2$ dominoes. | 1008 |
33,743 | Four. (50 points) There are 2008 students participating in a large public welfare activity. If two students know each other, then these two students are considered as a cooperative group.
(1) Find the minimum number of cooperative groups $m$, such that no matter how the students know each other, there exist three students who are pairwise in a cooperative group;
(2) If the number of cooperative groups is $\left[\frac{m}{22}\right]$, prove: there exist four students $A, B, C, D$ such that $A$ and $B$, $B$ and $C$, $C$ and $D$, $D$ and $A$ are each in a cooperative group. | 1008017 |
33,757 | 4. Determine the remainder when
$$
\sum_{i=0}^{2015}\left\lfloor\frac{2^{i}}{25}\right\rfloor
$$
is divided by 100 , where $\lfloor x\rfloor$ denotes the largest integer not greater than $x$. | 14 |
33,763 | 4.50 The street map of a city is a $5 \times 5$ grid, where there is a snowplow at point $A$. Find the length of the shortest route that covers all streets and returns to the starting point. | 68 |
33,775 | In a convex quadrilateral $ABCD$, it is given that $E$ is the intersection of the diagonals, triangles $ADE, BCE, CDE$ have areas of $12 \, \text{cm}^2, 45 \, \text{cm}^2, 18 \, \text{cm}^2$ respectively, and the length of side $AB$ is $7 \, \text{cm}$.
Determine the distance from point $D$ to the line $AB$.
(M. Petrová) | 12\, |
33,788 | In triangle $A B C$, point $P$ lies on the segment $A B$ at one-third of its length closer to point $A$, point $R$ is at one-third of the segment $P B$ closer to point $P$, and point $Q$ lies on the segment $B C$ such that angles $P C B$ and $R Q B$ are equal.
Determine the ratio of the areas of triangles $A B C$ and $P Q C$.
(L. Růžičková)
Hint. In the described arrangement of points, multiple triangles can be found whose areas can be compared. | 9:2 |
33,789 | 10. (20 points) Given that $f(x)$ is an odd function on $\mathbf{R}$, $f(1)=1$, and for any $x<0$,
$$
f\left(\frac{x}{x-1}\right)=x f(x) \text {. }
$$
Find the value of $\sum_{i=1}^{50} f\left(\frac{1}{i}\right) f\left(\frac{1}{101-i}\right)$. | \frac{2^{98}}{99!} |
33,794 | ## Task B-3.6.
Two isosceles triangles have the same perimeter and area, but they are not congruent. The side lengths of one triangle are 29, 29, 40. The side lengths of the other triangle are integers. Determine what these numbers are. | 24,37,37 |
33,795 | 3. Given $P$ is a point on the hyperbola $\Gamma: \frac{x^{2}}{463^{2}}-\frac{y^{2}}{389^{2}}=1$, a line $l$ is drawn through point $P$, intersecting the two asymptotes of the hyperbola $\Gamma$ at points $A$ and $B$. If $P$ is the midpoint of segment $A B$, and $O$ is the origin, then $S_{\triangle O A B}=$ $\qquad$ . | 180107 |
33,798 | 10. Given that the circumcenter of $\triangle A B C$ is $O$, and $2 \overrightarrow{O A}+3 \overrightarrow{O B}+4 \overrightarrow{O C}=0$.
Then $\cos \angle B A C=$ $\qquad$ | \frac{1}{4} |
33,802 | 10.4. Ten chess players over nine days played a full round-robin tournament, during which each of them played exactly one game with each other. Each day, exactly five games were played, with each chess player involved in exactly one of them. For what maximum $n \leq 9$ can it be claimed that, regardless of the schedule, at the end of some game day with number $k \leq 8$, there will definitely be $n$ chess players who have already played all their scheduled games with each other? | 5 |
33,805 | ## Task B-1.5.
A circle with a radius of $3 \text{~cm}$ is inscribed in a parallelogram such that it touches three of its sides. The measure of the acute angle of the parallelogram is $60^{\circ}$, and one side of the parallelogram is $2 \sqrt{3} \text{~cm}$ longer than the other side. Determine the distance from the center of the circle to the farthest vertex of the parallelogram. | 2\sqrt{21} |
33,810 | Example 6 Let $a_{1}, a_{2}, \cdots, a_{n}$ be an increasing sequence of positive integers. For a positive integer $m$, define
$$
b_{m}=\min \left\{n \mid a_{n} \geqslant m\right\}(m=1,2, \cdots),
$$
i.e., $b_{m}$ is the smallest index $n$ such that $a_{n} \geqslant m$. Given that $a_{20}=2019$, find the maximum value of $S=\sum_{i=1}^{20} a_{i}+\sum_{i=1}^{2019} b_{i}$.
(Adapted from the 1985 United States of America Mathematical Olympiad) | 42399 |
33,832 | ## Task B-1.3.
Determine the last two digits of the number $\underbrace{6^{6^{6} \cdot}}_{2019}$. | 56 |
33,839 | 8,9,10,11 |
Avor: Teresein D.A.
Points $A_2, B_2$ and $C_2$ are the midpoints of the altitudes $A A_1, B B_1$ and $C C_1$ of an acute-angled triangle $A B C$. Find the sum of the angles $B_2 A_1 C_2, C_2 B_1 A_2$ and $A_2 C_1 B_2$. | 180 |
33,859 | ## Task A-1.3.
Let $A B C D$ be a rectangle and $k$ a circle with its center at the center of the rectangle. The circle $k$ intersects side $\overline{A B}$ at points $K$ and $L$, and side $\overline{C D}$ at points $M$ and $N$, and $L N \perp A C$. If the midpoint of segment $\overline{A N}$ lies on the circle $k$, what is the ratio of the lengths of the sides of the given rectangle? | \sqrt{3} |
33,860 | 3. Find the side $B C$ of the quadrilateral $A B C D$, if $\angle B A C=\alpha, \angle A C D=\beta, \angle B C A+\angle C A D=\frac{\pi}{2}$ and $A D=a$. In the answer, write the result rounded to two decimal places.
$$
\alpha=\arcsin \frac{5}{13}, \beta=\arcsin \frac{12}{13}, a=24
$$ | 10 |
33,883 | Example 2. Expand the function $y=x^{3}$ into a Fourier series on the interval $(-1,1)$ using the system of Legendre polynomials. | x^{3}=\frac{3}{5}P_{1}(x)+\frac{2}{5}P_{3}(x) |
33,885 | Example 4 Given ten points in space, where no four points lie on the same plane. Connect some of the points with line segments. If the resulting figure contains no triangles and no spatial quadrilaterals, determine the maximum number of line segments that can be drawn. ${ }^{[3]}$
(2016, National High School Mathematics Joint Competition) | 15 |
33,893 | ## Task A-4.3.
Determine all triples of natural numbers $(a, b, c)$ for which
$$
2^{a}+2021=3^{b} \cdot 25^{c}
$$ | (2,4,1) |
33,894 | Task 2. Determine the largest real number $M$ such that for every infinite sequence $x_{0}, x_{1}, x_{2}, \ldots$ of real numbers that satisfies
a) $x_{0}=1$ and $x_{1}=3$,
b) $x_{0}+x_{1}+\cdots+x_{n-1} \geq 3 x_{n}-x_{n+1}$,
it holds that
$$
\frac{x_{n+1}}{x_{n}}>M
$$
for all $n \geq 0$. | 2 |
33,903 | Example 45 (1994 British Mathematical Olympiad) Find the smallest positive integer $n>1$, such that the arithmetic mean of $1^{2}, 2^{2}, 3^{2}, \cdots, n^{2}$ is a perfect square. | 337 |
33,928 | 32. [15] Pirate ships Somy and Lia are having a tough time. At the end of the year, they are both one pillage short of the minimum required for maintaining membership in the Pirate Guild, so they decide to pillage each other to bring their counts up. Somy by tradition only pillages $28 \cdot 3^{k}$ coins for integers $k$, and Lia by tradition only pillages $82 \cdot 3^{j}$ coins for integers $j$. Note that each pillage can have a different $k$ or $j$. Soma and Lia work out a system where Somy pillages Lia $n$ times, Lia pillages Somy $n$ times, and after both sets of pillages Somy and Lia are financially even.
What is the smallest $n$ can be? | 2 |
33,940 | 20. [10] There exist several solutions to the equation
$$
1+\frac{\sin x}{\sin 4 x}=\frac{\sin 3 x}{\sin 2 x},
$$
where $x$ is expressed in degrees and $0^{\circ}<x<180^{\circ}$. Find the sum of all such solutions. | 320 |
33,942 | 5. Nine pairwise noncongruent circles are drawn in the plane such that any two circles intersect twice. For each pair of circles, we draw the line through these two points, for a total of $\binom{9}{2}=36$ lines. Assume that all 36 lines drawn are distinct. What is the maximum possible number of points which lie on at least two of the drawn lines? | 462 |
33,949 | $14 \cdot 35$ Find the units digit of $\left[\frac{10^{20000}}{10^{100}+3}\right]$.
(47th Putnam Mathematical Competition, 1986) | 3 |
33,961 | Example 32 (2004 Slovenia National Team Selection Test) Find all positive integers $n$, such that $n \cdot 2^{n-1} +$ 1 is a perfect square. | 5 |
33,981 | 3. In two regular tetrahedrons $A-O B C$ and $D-O B C$ with coincident bases, $M$ and $N$ are the centroids of $\triangle A D C$ and $\triangle B D C$ respectively. Let $\overrightarrow{O A}=\boldsymbol{a}, \overrightarrow{O B}=\boldsymbol{b}, \overrightarrow{O C}=\boldsymbol{c}$. If point $P$ satisfies $\overrightarrow{O P}=x \boldsymbol{a}+y \boldsymbol{b}+z \boldsymbol{c}, \overrightarrow{M P}=2 \overrightarrow{P N}$, then the real number $9 x+81 y$ $+729 z=$ $\qquad$ | 439 |
33,982 | 24. Find the number of functions $f$ from the set $S=\{0,1,2, \ldots, 2020\}$ to itself such that, for all $a, b, c \in S$, all three of the following conditions are satisfied:
(i) If $f(a)=a$, then $a=0$;
(ii) If $f(a)=f(b)$, then $a=b$; and
(iii) If $c \equiv a+b(\bmod 2021)$, then $f(c) \equiv f(a)+f(b)(\bmod 2021)$. | 1845 |
34,017 | 1. In $\triangle A B C$, $A C>A B, P$ is the intersection of the perpendicular bisector of $B C$ and the internal angle bisector of $\angle A$, draw $P X \perp A B$, intersecting the extension of $A B$ at point $X, P Y \perp A C$ intersecting $A C$ at point $Y, Z$ is the intersection of $X Y$ and $B C$. Find the value of $\frac{B Z}{Z C}$. | 1 |
34,029 | 5. In a given hemisphere of radius $R$, three spheres of equal radius are inscribed such that they touch each other and also touch the given hemisphere. Calculate the radius of the inscribed spheres. | \frac{R(\sqrt{21}-3)}{4} |
34,041 | 29. There are 10 birds on the ground pecking at food, and among any 5 birds, at least 4 are on the same circle. How many birds are on the circle with the most birds, at a minimum?
(1991 6th CMO Problem) | 9 |
34,049 | 11. In the complex plane, non-zero complex numbers $z_{1}, z_{2}$ lie on a circle centered at $i$ with a radius of 1, the real part of $\bar{z}_{1} \cdot z_{2}$ is zero, and the principal value of the argument of $z_{1}$ is $\frac{\pi}{6}$, find $z_{2}$. | z_{2}=-\frac{\sqrt{3}}{2}+\frac{3}{2}i |
34,077 | 13.5.3 * Given: The hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>b>0)$ has an eccentricity $e=2+\sqrt{6}-\sqrt{3}-\sqrt{2}$, and a line $e$ passing through its right focus $F_{2}$ and perpendicular to the $x$-axis intersects the hyperbola at points $A$ and $B$. Find the value of $\angle A F_{1} F_{2}$. | 15 |
34,078 | Example 3 (APMO) Find all nonempty finite sets $S$ of positive integers such that if $m, n \in$ $S$, then $\frac{m+n}{(m, n)} \in \mathbf{S}, (m, n$ do not have to be distinct). | {2} |
34,081 | 9. (16 points) In the Cartesian coordinate system $x O y$, $\angle M O N=\frac{\pi}{3}$, and side $M N$ moves on the line $l: x=3$. Find the equation of the locus of the circumcenter of $\triangle M O N$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | \frac{(x-4)^{2}}{4}-\frac{y^{2}}{12}=1 |
34,086 | $(\mathrm{IMO} 2018, P 4)$
A site is a point $(x, y)$ in the plane such that $x$ and $y$ are positive integers at most 20. Initially, each of the 400 sites is unoccupied. Alice and Bernard take turns placing stones, with Alice starting. On her turn, Alice places a new red stone on an unoccupied site so that the distance between any two sites occupied by red stones is not $\sqrt{5}$. On his turn, Bernard places a new blue stone on an unoccupied site. (A site occupied by a blue stone can be at any distance from an occupied site.) They stop as soon as a player cannot place a stone.
Determine the largest positive integer $K$ such that Alice can ensure placing at least $K$ red stones, regardless of how Bernard places his blue stones. | 100 |
34,112 | ## Task A-3.6.
Let $\overline{BD}$ and $\overline{CE}$ be the altitudes of an acute-angled triangle $ABC$. Determine the smallest measure of angle $\varangle BAC$ for which it is possible that $|AE| \cdot |AD| = |BE| \cdot |CD|$. | 60 |
34,130 | Example 19 (18th All-Russian Mathematical Olympiad) Find the prime solutions of the equation $2^{x+1}+y^{2}=z^{2}$.
Find the prime solutions of the equation $2^{x+1}+y^{2}=z^{2}$. | 3,3,5 |
34,174 | 9、 (16 points) As shown in the figure, there are $2^{n}$ points on the parabola $y^{2}=2 p x(p>0)$, denoted as $P_{1}, P_{2}, \ldots, P_{2^{n}}$, and $F$ is the focus of the parabola. The angles between the lines connecting each adjacent pair of points and $F$ are equal, i.e.,
$$
\angle P_{1} F P_{2}=\angle P_{2} F P_{3}=\cdots=\angle P_{2^{n}} F P_{1}
$$
Let the distance from $P_{i}$ to the directrix be $d_{i}$. Find
$$
\sum_{i=1}^{2^{n}} \frac{1}{d_{i}}
$$ | \frac{2^{n}}{p} |
34,200 | 6. Seth has nine stones: three painted blue, three painted red and three painted yellow. The blue stones are labelled 1,2 and 3 , as are the red stones and the yellow stones. He builds a vertical tower with three stones, putting one on top of another.
Three stones form a set if any of the following hold:
(i) They all have the same colour;
(ii) They are all labelled with the same number;
(iii) They all have different colours;
(iv) They are all labelled with different numbers.
In how many ways can he build a tower that avoids creating a set? | 216 |
34,212 | Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
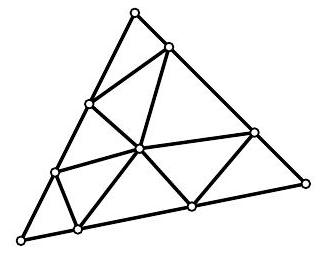 | 40 |
34,225 | 60. (See [34].) Let $\mathrm{P}(|X| \leqslant b)=1, \mathrm{E} X=0$ and $\mathrm{D} X=\sigma^{2}$ for some $\sigma, b>0$. What is the maximum possible value of $\mathrm{E} e^{X}$? | \frac{e^{b}\sigma^{2}+e^{-\sigma^{2}/b}b^{2}}{\sigma^{2}+b^{2}} |
34,226 | 8. Fill $n^{2}(n \geqslant 3)$ integers into an $n \times n$ grid, with one number per cell, such that the product of the numbers in each row and each column is 30. Then there are $\qquad$ ways to fill the grid. | 2^{(n-1)^{2}}(n!)^{3} |
34,233 | Task 6. (30 points) At the first deposit, equipment of the highest class was used, and at the second deposit, equipment of the first class was used, with the highest class being less than the first. Initially, $40 \%$ of the equipment from the first deposit was transferred to the second. Then, $20 \%$ of the equipment that ended up on the second deposit was transferred back to the first, with half of the transferred equipment being of the first class. After this, the equipment of the highest class on the first deposit was 26 units more than on the second, and the total amount of equipment on the second deposit increased by more than $5 \%$ compared to the initial amount. Find the total amount of equipment of the first class. | 60 |
34,239 | 12.046. The base of the pyramid is an equilateral triangle. One lateral edge is perpendicular to the base plane and equals $l$, while the other two form an angle $\alpha$ with the base plane. A right prism is inscribed in the pyramid; three of its vertices lie on the lateral edges of the pyramid, and the other three lie on the base of the pyramid. The diagonal of the lateral face of the prism forms an angle $\beta$ with the base plane. Find the height of the prism. | \frac{\cos\alpha\sin\beta}{\sin(\alpha+\beta)} |
34,271 | 15. Let the quadratic function $f(x)=a x^{2}+b x+c(a, b, c \in \mathbf{R}, a \neq 0)$ satisfy the following conditions:
(1) For $x \in \mathbf{R}$, $f(x-4)=f(2-x)$, and $f(x) \geqslant x$;
(2) For $x \in(0,2)$, $f(x) \leqslant\left(\frac{x+1}{2}\right)^{2}$;
(3) The minimum value of $f(x)$ on $\mathbf{R}$ is 0.
Find the largest $m(m>1)$ such that there exists $t \in \mathbf{R}$, for which, if $x \in[1, m]$, then $f(x+t) \leqslant x$. | 9 |
34,276 | 6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=75 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=91
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 40 |
34,303 | 23. In triangle $A B C, A B=28, B C=21$ and $C A=14$. Points $D$ and $E$ are on $A B$ with $A D=7$ and $\angle A C D=\angle B C E$. Find the length of $B E$. | 12 |
34,306 | 2. Let $a, b$, and $c$ be positive real numbers. Determine the largest total number of real roots that the following three polynomials may have among them: $a x^{2}+b x+c, b x^{2}+c x+a$, and $c x^{2}+a x+b$. | 4 |
34,315 | Example 10 Let $a_{1}, a_{2}, \cdots, a_{n}, \cdots$ be a sequence of non-decreasing positive integers. For $m \geqslant 1$, define $b_{m}=\min \left\{n ; a_{n} \geqslant m\right\}$, i.e., $b_{m}$ is the smallest value of $n$ such that $a_{n} \geqslant 3$. Given that $a_{19}=85$, find the maximum value of
$$
a_{1}+a_{2}+\cdots+a_{19}+b_{1}+b_{2}+\cdots+b_{85}
$$
(1985 USA Olympiad Problem) | 1700 |
34,325 | Problem 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1}$ is inscribed in a sphere with the base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$. Segment $C D$ is the diameter of this sphere, point $K$ and $L$ are the midpoints of edge $A A_{1}$ and $A B$ respectively. Find the volume of the prism if $D L=\sqrt{6}, D K=3$. | 12\sqrt{3} |
34,328 | 6. In a right triangular prism $A B C-A_{1} B_{1} C_{1}$, $A B=1, B C=C C_{1}=\sqrt{3}, \angle A B C=90^{\circ}$, point $P$ is a moving point on the plane $A B C$, then the minimum value of $A_{1} P+\frac{1}{2} P C$ is $\qquad$ . | \frac{5}{2} |
34,329 | 78. A natural number has exactly 9 distinct divisors, among which 3 divisors $A$, $B$, and $C$ satisfy:
(1) $A+B+C=79$;
(2) $A \times A=B \times C$.
Then, this natural number is $\qquad$. | 441 |
34,338 | Example Mountain (2003 China National Training Team) In $\triangle A B C$, $A C>A B, P$ is the intersection of the perpendicular bisector of $B C$ and the internal angle bisector of $\angle A$, construct $P X \perp A B$, intersecting the extension of $A B$ at point $X, P Y \perp A C$ intersecting $A C$ at point $Y, Z$ is the intersection of $X Y$ and $B C$. Find the value of $\frac{B Z}{Z C}$. | 1 |
34,344 | 6. [5] The elliptic curve $y^{2}=x^{3}+1$ is tangent to a circle centered at $(4,0)$ at the point $\left(x_{0}, y_{0}\right)$. Determine the sum of all possible values of $x_{0}$. | \frac{1}{3} |
34,349 | 3. For real numbers $a$ and $b$, it holds that $a^{3}=3 a b^{2}+11$ and $b^{3}=3 a^{2} b+2$. Calculate the value of the expression $a^{2}+b^{2}$. | 5 |
34,356 | Task 2. (10 points) Find the greatest value of the parameter $b$ for which the inequality $b \sqrt{b}\left(x^{2}-10 x+25\right)+\frac{\sqrt{b}}{\left(x^{2}-10 x+25\right)} \leq \frac{1}{5} \cdot \sqrt[4]{b^{3}} \cdot\left|\sin \frac{\pi x}{10}\right|$ has at least one solution. | 0.0001 |
34,380 | Example 2 Given the ellipse $C: \frac{x^{2}}{24}+\frac{y^{2}}{16}=1$, the line $l: \frac{x}{12}+\frac{y}{8}=1$, and a point $P$ on $l$, the ray $O P$ intersects the ellipse $C$ at $R$. Also, point $Q$ is on $O P$ such that $|O Q| \cdot|O P|=|O R|^{2}$. Find the locus of point $Q$ as $P$ moves along $l$, and identify what kind of curve the locus is. | \frac{(x-1)^{2}}{\frac{5}{2}}+\frac{(y-1)^{2}}{\frac{5}{3}}=1 |
34,381 | Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
Fig. 13: to the solution of problem 11.2
# | 34 |
34,389 | (12) Among all the circumscribed circular cones of a sphere with radius $R$, the total surface area of the cone with the minimum total surface area is $\qquad$ . | 8\piR^{2} |
34,391 | 7. In tetrahedron $ABCD$, face $ABC$ and face $BCD$ form a dihedral angle of $60^{\circ}$, the projection of vertex $A$ onto face $BCD$ is the orthocenter $H$ of $\triangle BCD$, and $G$ is the centroid of $\triangle ABC$. If $AH=4$ and $AB=AC$, then $GH=$ $\qquad$ | \frac{4\sqrt{21}}{9} |
34,397 | Task 2. (10 points) A circle touches two adjacent sides $AB$ and $AD$ of square $ABCD$ and cuts off segments of length 8 cm from vertices $B$ and $D$ at the points of tangency. On the other two sides, the circle intersects and cuts off segments of 4 cm and 2 cm from the vertices, respectively. Find the radius of the circle. | 10 |
34,399 | 11. (20 points) Let $a_{i}, b_{i} \in \mathbf{C}$, satisfying $\left|a_{i}\right|^{2}+\left|b_{i}\right|^{2}=1(i=1,2,3)$. Find $\max _{i \neq j}\left\{\left|a_{i} \overline{a_{j}}+b_{i} \overline{b_{j}}\right|\right\}$'s minimum value. | \frac{1}{2} |
34,404 | 3.28 Try to express $\sum_{k=0}^{n} \frac{(-1)^{k} C_{n}^{k}}{k^{3}+9 k^{2}+26 k+24}$ in the form $\frac{p(n)}{q(n)}$, where $p(n)$ and $q(n)$ are two polynomials with integer coefficients. | \frac{1}{2(n+3)(n+4)} |
34,423 | 16. Let tetrahedron $ABCD$ have $AB=41, AC=7, AD=18, BC=36, BD=27, CD=13$. Let $d$ be the distance between the midpoints of edges $AB$ and $CD$. Find the value of $d^{2}$. | 137 |
34,449 | 5. Given an integer $n \geqslant 3$. Find the minimum value that $\sum_{i=1}^{n}\left(\frac{1}{x_{i}}-x_{i}\right)$ can achieve, where $x_{1}, x_{2}, \cdots, x_{n}$ are positive real numbers satisfying $\sum_{i=1}^{n} \frac{x_{i}}{x_{i}+n-1}=1$. Also find the values of $x_{i}$ when the minimum value is achieved. | 0 |
34,455 | One, (40 points) Let $x_{1}, x_{2}, \cdots, x_{n}$ be real numbers no less than -1, satisfying $\sum_{i=1}^{n} x_{i}^{3}=0$. Find the smallest constant $c$, such that for all positive integers $n$, we have $\sum_{i=1}^{n} x_{i}^{2} \leqslant c n$. | \frac{4}{3} |
34,459 | Example 8 Given an integer $n \geqslant 2$, try to determine the smallest constant $c$, such that for any non-negative real numbers $x_{i}(1 \leqslant i \leqslant n)$, we have $\sum_{1 \leqslant i<j \leqslant n} x_{i} x_{j}\left(x_{i}^{2}+x_{j}^{2}\right) \leqslant c\left(\sum_{i=1}^{n} x_{i}\right)^{4}$. And for this constant $c$, determine the necessary and sufficient conditions for equality to hold. | \frac{1}{8} |
34,462 | 11. Given a moving line $l$ that is tangent to the circle $O: x^{2}+y^{2}=1$ and intersects the ellipse $\frac{x^{2}}{9}+y^{2}=1$ at two distinct points $A, B$, find the maximum distance from the origin to the perpendicular bisector of $A B$. | \frac{4}{3} |
34,471 | 6. In a regular $(n+2)$-gon, two vertices are randomly selected, and a line passing through them is drawn. Let $p_{n}$ denote the probability that the difference in the number of vertices on either side of this line does not exceed 1. Then the value of $\sum_{i=1}^{2018} p_{i} p_{i+1}$ is $\qquad$. | \frac{1009}{1010} |
34,482 | 6. The function in the form of $y=\frac{b}{|x|-a}(a, b>0)$
Resembles the Chinese character “唄”, it is called the “唄 function”, and the point symmetric to the intersection with the $y$-axis about the origin is called the “目 point”. A circle with the “目 point” as its center and that has common points with the “唄 function” is called a “圆圆”. When $a=b=1$, the minimum area of all “圆圆” is . $\qquad$ | 3\pi |
34,498 | 7. Given that the base of the prism $A B C-A^{\prime} B^{\prime} C^{\prime \prime}$ is an equilateral triangle with side length 2, the side edge $A A^{\prime}$ forms a 45-degree angle with the sides $A B, A C$ of the lower base, and $A^{\prime}$ is equidistant from the plane $A B C$ and the plane $B B^{\prime} C^{\prime} C$, then $A^{\prime} A=$ $\qquad$ | \sqrt{3} |
34,514 | 4. Let $S$ be a set of $n$ distinct real numbers, and $A_{s}$ be the set of all distinct averages of pairs of elements from $S$. For a given $n \geqslant 2$, what is the minimum number of elements in $A_{s}$?
(1993 Putnam Competition) | 2n-3 |
34,516 | 10. A city adopts a lottery system for car license plates, with 300,000 people participating in the lottery, and 30,000 slots available each month.
(1) If those who win the lottery each month exit the lottery, and those who do not win continue to the next month's lottery with an additional 30,000 people joining each month, how long on average will it take for each person to win a slot?
(2) Under the conditions of (1), if the traffic management department can control the proportion of people who win, such that the probability of winning in the first month of each quarter is $\frac{1}{11}$, the second month is $\frac{1}{10}$, and the third month is $\frac{1}{9}$, how long on average will it take for each person to win a slot? | 10 |
34,523 | 3. Let $f:(0,+\infty) \rightarrow \mathbb{R}$ be a function that satisfies the following conditions:
a) $f$ is strictly increasing;
b) $f(x) > -\frac{1}{x}$, for $x > 0$;
c) $f(x) f\left(f(x) + \frac{1}{x}\right) = 1$, for $x > 0$.
Calculate $f(1)$. | \frac{1-\sqrt{5}}{2} |
34,524 | Authors: Berlov S.L., Petrov F., Akopyan A.V.
On the side $B C$ of the rhombus $A B C D$, a point $M$ is chosen. Lines drawn through $M$ perpendicular to the diagonals $B D$ and $A C$ intersect the line $A D$ at points $P$ and $Q$ respectively. It turns out that the lines $P B, Q C$ and $A M$ intersect at one point. What can the ratio $B M: M C$ be? | 1:2 |
34,525 | 9. Given the parabola $\Gamma: y^{2}=8 x$ with focus $F$, a line $l$ through $F$ intersects the parabola $\Gamma$ at points $A, B$. Tangents to the parabola $\Gamma$ at $A, B$ intersect the $y$-axis at points $P, Q$ respectively. Find the minimum value of the area of quadrilateral $A P Q B$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly. | 12 |
34,539 | 3. a) Let $n \in \mathbb{N}^{*}$. Calculate $\int_{\frac{1}{n}}^{n} \frac{1}{x^{2}+x+1} d x$.
b) Calculate $\lim _{n \rightarrow \infty} \int_{\frac{1}{n}}^{n} \frac{\operatorname{arctg} x}{x^{2}+x+1} d x$. | \frac{\pi^{2}}{6\sqrt{3}} |
34,542 | 38. If $\xi \sim \mathscr{N}(0, v), v>0$, then
$$
\mathrm{E} e^{-\xi}=\int_{-\infty}^{\infty} e^{-u} \frac{e^{-\frac{u^{2}}{2 v}}}{\sqrt{2 \pi v}} d u=e^{\frac{v}{2}}
$$
Compute the integral $(u>0)$
$$
\int_{0}^{\infty} e^{-v} \frac{e^{-\frac{u^{2}}{2 v}}}{\sqrt{2 \pi v}} d v
$$ | \frac{e^{-\sqrt{2}u}}{\sqrt{2}} |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.