id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
32,317 | 4. How many ordered quadruples of natural numbers $(a, b, c, d)$ with a sum of 100 satisfy the equations
$$
(a+b)(c+d)=(b+c)(a+d)=(a+c)(b+d) ?
$$
(Patrik Bak) | 129 |
32,321 | 12. Let $a, b, c$ be positive integers such that $\frac{1}{a}+\frac{1}{b}=\frac{1}{c}$ and $\operatorname{gcd}(a, b, c)=1$. Suppose $a+b \leq 2011$. Determine the largest possible value of $a+b$. | 1936 |
32,326 | 5. In trapezoid $A B C D$, $\overrightarrow{A B}=2 \overrightarrow{D C},|\overrightarrow{B C}|=6, P$ is a point on the plane of trapezoid $A B C D$, and satisfies $\overrightarrow{A P}+\overrightarrow{B P}+4 \overrightarrow{D P}=0, \overrightarrow{D A} \cdot \overrightarrow{C B}=|\overrightarrow{D A}| \cdot|\overrightarrow{D P}|, Q$ is a moving point on side $A D$, then the minimum value of $|\overrightarrow{P Q}|$ is $\qquad$. | \frac{4\sqrt{2}}{3} |
32,342 | 6. Given positive real numbers $x, y$ satisfy
$$
\left(2 x+\sqrt{4 x^{2}+1}\right)\left(\sqrt{y^{2}+4}-2\right) \geqslant y \text {. }
$$
Then the minimum value of $x+y$ is $\qquad$ | 2 |
32,343 | 9th CanMO 1977 Problem 5 A right circular cone has base radius 1. The vertex is K. P is a point on the circumference of the base. The distance KP is 3. A particle travels from P around the cone and back by the shortest route. What is its minimum distance from K? | \frac{3}{2} |
32,344 | 54 Let $n, n+1, \cdots, n+k-1$ be $k$ consecutive natural numbers that contain exactly 1990 numbers forming a geometric sequence with a common ratio of $\frac{1991}{1990}$. Then, when $k$ takes the minimum value, the unit digit of $k$ is $\qquad$. | 2 |
32,346 | 8. Triangle $A B C$ has a right angle at $B$. Point $D$ lies on side $B C$ such that $3 \angle B A D=$ $\angle B A C$. Given $A C=2$ and $C D=1$, compute $B D$. | \frac{3}{8} |
32,365 | Example 3 There are ten birds on the ground pecking at food, and among any five birds, at least four birds are on the same circumference. Question: What is the minimum number of birds on the circumference that contains the most birds? | 9 |
32,405 | 5. The edges of the tetrahedron $ABCD$ have lengths 7, 13, 18, 27, 36, and 41 (in some order). If $AB$ has a length of 41, determine the length of the edge $CD$.
## Fourth grade - B category | 13 |
32,431 | 3. Let $m>n \geqslant 1$, find the minimum value of $m+n$ such that: $1000 \mid 1978^{m}-1978^{n}$. | 106 |
32,436 | Example 7 Let $f(n)$ be a function defined on all positive integers and taking positive integer values. For all positive integers $m, n$, we have $f[f(m)+f(n)]=m+n$. Find all possible values of $f(1988)$. (1988 Mexican Olympiad Problem) | 1988 |
32,453 | 14. Let $f(x)$ be an even function defined on $\mathbf{R}$, whose graph is symmetric about the line $x=1$. For any $x_{1}, x_{2} \in\left[0, \frac{1}{2}\right]$, we have $f\left(x_{1}+x_{2}\right)=f\left(x_{1}\right) \cdot f\left(x_{2}\right)$, and $f(1)=a>0$.
(1) Find $f\left(\frac{1}{2}\right)$ and $f\left(\frac{1}{4}\right)$;
(2) Prove that $f(x)$ is a periodic function;
(3) Let $a_{n}=f\left(2 n+\frac{1}{2 n}\right)$, find $\lim _{n \rightarrow \infty}\left(\ln a_{n}\right)$. | 0 |
32,455 | 21. [12] Let $A B C D$ be a quadrilateral inscribed in a circle with center $O$. Let $P$ denote the intersection of $A C$ and $B D$. Let $M$ and $N$ denote the midpoints of $A D$ and $B C$. If $A P=1, B P=3, D P=\sqrt{3}$, and $A C$ is perpendicular to $B D$, find the area of triangle $M O N$. | \frac{3}{4} |
32,457 | 2. Find all primes $p$ for which the numbers $p+1$ and $p^{2}+1$ are double the squares of natural numbers.
# | 7 |
32,459 | 8. Let real numbers $a, b, c, d$ satisfy $ad + bc = 1$. Then
$$
u=a^{2}+b^{2}+c^{2}+d^{2}+(a+c)^{2}+(b-d)^{2}
$$
the minimum value of $u$ is $\qquad$. | 2\sqrt{3} |
32,483 | 2. Given a natural number $n \geqslant 5$, try to find:
(1) In the $n$-element set $\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, how many different numbers are generated by $a_{i}+a_{j}(1 \leqslant i<j \leqslant n)$ at least?
(2) Determine all $n$-element sets that achieve the above minimum value. | 2n-3 |
32,491 | Solve the following system of equations:
$$
a^{2} b^{2}-a^{2}-a b+1=0 \\
a^{2} c-a b-a-c=0 \\
a b c=-1 .
$$ | =-1,b=-1,=-1 |
32,501 | 3. The sum of positive numbers $a, b, c$ and $d$ is not less than 8. Find the minimum value of the expression
$\frac{a^{4}}{(a+b)(a+c)(a+d)}+\frac{b^{4}}{(b+c)(b+d)(b+a)}+\frac{c^{4}}{(c+d)(c+a)(c+b)}+\frac{d^{4}}{(d+a)(d+b)(d+c)}$. | 1 |
32,507 | 11. As shown in the figure, square $\mathrm{ABCD}$ and square $\mathrm{EFGH}$, their four pairs of sides are parallel to each other. Connect $\mathbf{C G}$ and extend it to intersect $\mathbf{B D}$ at point $\mathbf{I}$. Given that $B D=10$, the area of triangle $B F C$ is $3$, and the area of triangle $\mathrm{CHD}$ is $5$, then the length of $B I$ is? | \frac{15}{4} |
32,510 | ## Task A-1.4.
Let $\overline{A C}$ be the diameter of circle $k_{1}$ whose center is at point $B$. Circle $k_{2}$ touches the line $A C$ at point $B$ and circle $k_{1}$ at point $D$. The tangent from $A$ (different from $A C$) to circle $k_{2}$ touches this circle at point $E$ and intersects the line $B D$ at point $F$. Determine the ratio $|A F|:|A B|$. | \frac{5}{3} |
32,528 | Example 3. Using the Kellogg method, calculate the smallest characteristic number of the kernel $K(x, t)=x^{2} t^{2}, 0 \leqslant x, t \leqslant 1$. | 5 |
32,540 | 6. (8 points) Let for positive numbers $x, y, z$ the system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=108 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=124
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 48 |
32,562 | 10.403 In a right triangle $A B C$ ( $\angle C=90^{\circ}$ ), the altitude $CD$ is drawn. The radii of the circles inscribed in triangles $ACD$ and $BCD$ are 0.6 and 0.8 cm, respectively. Find the radius of the circle inscribed in triangle $\boldsymbol{A} \boldsymbol{\text { B }}$. | 1 |
32,575 | 7.49 Divide a cube into non-overlapping tetrahedra. What is the minimum number of tetrahedra needed? | 5 |
32,595 | A math competition consists of three problems, each of which receives an integer score from 0 to 7. For any two competitors, we know that there is at most one problem on which they obtained the same score. Find the largest possible number of competitors in this competition. | 64 |
32,597 | 11.3. All cells of a square table $n \times n$ are numbered in some order with numbers from 1 to $n^{2}$. Petya makes moves according to the following rules. On the first move, he places a rook in any cell. On each subsequent move, Petya can either place a new rook in some cell or move a rook from a cell numbered $a$ horizontally or vertically to a cell with a number greater than $a$. Each time a rook lands in a cell, that cell is immediately colored; placing a rook on a colored cell is prohibited. What is the minimum number of rooks Petya will need to, regardless of the initial numbering, be able to color all the cells of the table in several moves?
(D. Khramov) | n |
32,605 | Example 5 Solve the system of simultaneous equations
$$
\left\{\begin{array}{l}
x+y+z=3, \\
x^{2}+y^{2}+z^{2}=3, \\
x^{5}+y^{5}+z^{5}=3 .
\end{array}\right.
$$
Find all real or complex roots. | x=y=z=1 |
32,636 | 5. Let $A B C D$ be a quadrilateral with an inscribed circle $\omega$ and let $P$ be the intersection of its diagonals $A C$ and $B D$. Let $R_{1}, R_{2}, R_{3}, R_{4}$ be the circumradii of triangles $A P B, B P C, C P D, D P A$ respectively. If $R_{1}=31$ and $R_{2}=24$ and $R_{3}=12$, find $R_{4}$. | 19 |
32,644 | 3. Given real numbers $a_{i}(i=1,2, \cdots, 2016)$ satisfy $9 a_{i}>11 a_{i+1}^{2}(i=1,2, \cdots, 2015)$. Find
$$
\begin{aligned}
f= & \left(a_{1}-a_{2}^{2}\right)\left(a_{2}-a_{3}^{2}\right) \cdots\left(a_{2015}-a_{2016}^{2}\right) \cdot \\
& \left(a_{2016}-a_{1}^{2}\right)
\end{aligned}
$$
the maximum value.
(2016, National High School Mathematics Joint Competition) | \frac{1}{2^{4033}} |
32,679 | Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?

Fig. 13: to the solution of problem 11.2
# | 34 |
32,692 | Let $M$ and $N$ be two points on the Thales circle of segment $AB$, different from $A$ and $B$. Let $C$ be the midpoint of segment $NA$, and $D$ be the midpoint of segment $NB$. The circle is intersected by line $MC$ at point $E$ (second intersection), and by line $MD$ at point $F$ (second intersection). What is the value of
$$
M C \cdot C E + M D \cdot D F
$$
if $AB = 2$ units?
Imre Merényi, Budapest | 1 |
32,710 | 1. Determine all natural numbers $n$ such that $9^{n}-7$ can be represented as a product of at least two consecutive natural numbers. | 1 |
32,722 | (9) (20 points) Let $A+B+C=180^{\circ}$, and satisfy: $\frac{\sin A+\sin B+\sin C}{\cos A+\cos B+\cos C}=$
1, find the value of $\frac{\cos 2 A+\cos 2 B+\cos 2 C}{\cos A+\cos B+\cos C}$. | 2 |
32,725 | 4. On a horizontal line that divides the plane into upper and lower half-planes, a segment $AB$ with a length of $72 \, \text{cm}$ is drawn. Using the endpoints of the segment, in the upper half-plane, a regular (equilateral) triangle $A M_{1} M_{2}$ and a regular pentagon $M_{5} M_{6} M_{7} M_{8} M_{9}$ are drawn, and in the lower half-plane, a regular quadrilateral (square) $M_{2} M_{3} M_{4} M_{5}$ and a regular hexagon $M_{9} M_{10} M_{11} M_{12} M_{13} B$ are drawn. Here, $M_{2}, M_{5}$, and $M_{9}$ are on the segment $AB$, point $M_{2}$ is between $A$ and $M_{5}$, and point $M_{9}$ is between $M_{5}$ and $B$. The lengths of the sides of the regular polygons are in the same ratio as the corresponding numbers of their sides. Calculate the length of the broken line
$$
L \equiv A M_{1} M_{2} M_{3} M_{4} M_{5} M_{6} M_{7} M_{8} M_{9} M_{10} M_{11} M_{12} M_{13} B
$$ | 272 |
32,727 | Let's calculate the value of the expression $P$, where the number of nested radicals is $n$ (>1).
$$
\begin{aligned}
& P=\sqrt{a+\sqrt{a+\ldots+\sqrt{a+\sqrt{b}}}}, \text{ where } \\
& a=\sqrt{76+24 \sqrt{10}}-2 \sqrt{19-3 \sqrt{40}} \text{ and } \\
& b=\sqrt{165+4 \sqrt{1616}}-\sqrt{165-4 \sqrt{1616}}
\end{aligned}
$$
Create a similar expression with the same properties. | 4 |
32,729 | 6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=75 \\
y^{2}+y z+z^{2}=36 \\
z^{2}+x z+x^{2}=111
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 60 |
32,744 | 37. Compute
$$
\sum_{n=1}^{\infty} \frac{2 n+5}{2^{n} \cdot\left(n^{3}+7 n^{2}+14 n+8\right)}
$$ | \frac{137}{24}-8\ln2 |
32,745 | 3. A trapezoid $A B C D$ is given with bases $A B, C D$, such that $2|A B|=3|C D|$.
a) Find a point $P$ inside the trapezoid such that the areas of triangles $A B P$ and $C D P$ are in the ratio $3: 1$ and the areas of triangles $B C P$ and $D A P$ are in the ratio $3: 1$.
b) For the found point $P$, determine the sequential ratio of the areas of triangles $A B P, B C P$, $C D P$ and $D A P$. | 24:21:8:7 |
32,767 | P.M.
In the country, there are 15 cities, some of which are connected by air routes belonging to three airlines. It is known that even if any one of the airlines ceases operations, it will still be possible to travel from any city to any other (possibly with layovers), using flights of the remaining two airlines. What is the minimum number of air routes that can exist in the country? | 21 |
32,780 | Example 3 Suppose there is a function $f(x)=\log _{3} \frac{x^{2}+a x+b}{x^{2}+x+1}(x \in \mathbf{R})$, find $a, b$ such that the function $f(x)$ simultaneously satisfies the following conditions:
(1) The graph of the function passes through the origin;
(2) The function $f(x)$ is monotonically increasing on $[1,+\infty)$;
(3) The maximum value of the function $f(x)$ is 1. | =-1,b=1 |
32,818 | 1.50. The center of a semicircle inscribed in a right triangle, such that its diameter lies on the hypotenuse, divides the hypotenuse into segments of 30 and 40. Find the length of the arc of the semicircle enclosed between the points of tangency with the legs. | 12\pi |
32,865 | ## Task A-3.2.
Determine all prime numbers $p$ for which there exist natural numbers $x$ and $y$ such that
$$
\left\{\begin{aligned}
p+1 & =2 x^{2} \\
p^{2}+1 & =2 y^{2}
\end{aligned}\right.
$$ | 7 |
32,878 | Example 13 (1998 National High School Mathematics League Question) In $\triangle A B C$, $\angle C=90^{\circ}, \angle B=30^{\circ}, A C=2, M$ is the midpoint of $A B$. $\triangle A C M$ is folded along $C M$, making the distance between $A$ and $B$ equal to $2 \sqrt{2}$. At this point, the volume of the tetrahedron $A-B C M$ is $\qquad$ . | \frac{2\sqrt{2}}{3} |
32,912 | 13. Given a positive number $r$ such that the set $T=\left\{(x, y) \mid x, y \in \mathbf{R}\right.$, and $\left.x^{2}+(y-7)^{2} \leqslant r^{2}\right\}$ is a subset of the set $S=\{(x, y) \mid x$, $y \in \mathbf{R}$, and for any $\theta \in \mathbf{R}$, $\cos 2 \theta+x \cos \theta+y \geqslant 0\}$, find the maximum value of $r$. | 4\sqrt{2} |
32,931 | 41st Putnam 1980 Problem A3 Find ∫ 0 π/2 f(x) dx, where f(x) = 1/(1 + tan √2 x). Solution | \frac{\pi}{4} |
32,936 | 7. Let $F_{1}$ and $F_{2}$ be the left and right foci of the hyperbola $C: \frac{x^{2}}{4}-\frac{y^{2}}{12}=1$, respectively. Point $P$ lies on the hyperbola $C$, and $G$ and $I$ are the centroid and incenter of $\triangle F_{1} P F_{2}$, respectively. If $G I / / x$-axis, then the circumradius $R$ of $\triangle F_{1} P F_{2}$ is $\qquad$ | 5 |
32,945 | 4. Let $S$ be a set of $n$ distinct real numbers, and $A_{s}$ be the set of all distinct averages of pairs of elements from $S$. For a given $n \geqslant 2$, what is the minimum number of elements that $A_{s}$ can have?
(1993 Putnam Competition) | 2n-3 |
32,953 | 287. How many solutions does the system of equations generally have
$$
\begin{gathered}
a x^{2}+b x y+c y^{2}=d \\
a_{1} x^{2}+b_{1} x y+c_{1} y^{2}=d_{1} ?
\end{gathered}
$$
In particular, how many solutions does the system of question 280 have? | 4 |
32,954 | 1. Given is $\triangle A B C$ for which $A B=A C=18$ and $B C=4$. A circle $k$ with radius 7 is observed, passing through points $B$ and $C$, and its center, point $O$, is located inside $\triangle A B C$. Tangents from point $A$ to $k$ touch it at points $N$ and $M$. Find the area of quadrilateral OMAN. | 14\sqrt{19} |
32,967 | 8・ 129 Let the sequence $\left\{x_{n}\right\}$ satisfy $x_{1}=5$, and
$$
x_{n+1}=x_{n}^{2}-2, n=1,2, \cdots
$$
Find: $\lim _{n \rightarrow \infty} \frac{x_{n+1}}{x_{1} x_{2} \cdots x_{n}}$. | \sqrt{21} |
32,978 | 29.2.3 For any two elements $a=\left(a_{1}, a_{2}, \cdots, a_{2^{n}}\right)$ and $b=\left(b_{1}, b_{2}, \cdots, b_{2}{ }^{n}\right)$ in $S_{n}$, let
$$
d(a, b)=\sum_{i=1}^{i^{*}}\left|a_{i}-b_{i}\right| .
$$
If $A \subseteq S_{n}$, and for any two different elements $a, b$ in $A$, we have $d(a, b) \geqslant 2^{n-1}$, then $A$ is called a good subset. Find the maximum number of elements in a good subset of $S_{u}$. | 2^{n+1} |
32,982 | 4. Let $A B C D$ be a square, and let $M$ be the midpoint of side $B C$. Points $P$ and $Q$ lie on segment $A M$ such that $\angle B P D=\angle B Q D=135^{\circ}$. Given that $A P<A Q$, compute $\frac{A Q}{A P}$. | \sqrt{5} |
32,986 | 9.2. Find the maximum odd natural number that cannot be represented as the sum of three distinct composite numbers. | 17 |
32,991 | C3. Let $X Y Z$ be an acute-angled triangle. Let $s$ be the side-length of the square which has two adjacent vertices on side $Y Z$, one vertex on side $X Y$ and one vertex on side $X Z$. Let $h$ be the distance from $X$ to the side $Y Z$ and let $b$ be the distance from $Y$ to $Z$.
(a) If the vertices have coordinates $X=(2,4), Y=(0,0)$ and $Z=(4,0)$, find $b, h$ and $s$.
(b) Given the height $h=3$ and $s=2$, find the base $b$.
(c) If the area of the square is 2017 , determine the minimum area of triangle $X Y Z$. | 4034 |
33,010 | Task 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1}$ with base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$ is inscribed in a sphere of radius 3. Segment $C D$ is a diameter of this sphere. Find the volume of the prism if $A D=2 \sqrt{6}$. | 6\sqrt{15} |
33,013 | 9. (This question is worth 16 points) In $\triangle A B C$, it is known that $\overrightarrow{A B} \cdot \overrightarrow{A C}+2 \overrightarrow{B A} \cdot \overrightarrow{B C}=3 \overrightarrow{C A} \cdot \overrightarrow{C B}$. Find the maximum value of $\sin C$. | \frac{\sqrt{7}}{3} |
33,029 | Problem 4. Find the smallest positive real number $\lambda$ such that for any real numbers $a_{1}, a_{2}, a_{3} \in\left[0, \frac{1}{2}\right]$ and $b_{1}, b_{2}, b_{3} \in(0, \infty)$ with $\sum_{i=1}^{3} a_{i}=\sum_{i=1}^{3} b_{i}=1$, we have
$$
b_{1} b_{2} b_{3} \leq \lambda\left(a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}\right)
$$ | \frac{1}{8} |
33,043 | Tokarev S.I.
The path from platform $A$ to platform $B$ was traveled by the electric train in $X$ minutes ($0<X<60$). Find $X$, given that the angle between the hour and minute hands was $X$ degrees both at the moment of departure from $A$ and at the moment of arrival at $B$. | 48 |
33,068 | A triangle's two vertices, the center of its inscribed circle, and its orthocenter lie on a circle. Calculate the angle at the third vertex of the triangle! | 60 |
33,079 | 6. [6] Let $\pi$ be a permutation of the numbers from 1 through 2012 . What is the maximum possible number of integers $n$ with $1 \leq n \leq 2011$ such that $\pi(n)$ divides $\pi(n+1)$ ? | 1006 |
33,080 | 4. Let $A, B, C$ be the centers of the given circles, $A B=2, A C=2, B C=3$ (see Fig. 1).
Denote by $a, b$, and $c$ the radii of the circles centered at points $A, B$, and $C$ respectively, and find their values by solving the system of equations. We get:
$$
\left\{\begin{array}{l}
a + b = 2 \\
a + c = 2 \\
b + c = 3
\end{array} \Leftrightarrow \left\{\begin{array}{l}
a=\frac{1}{2} \\
b=\frac{3}{2} \\
c=\frac{3}{2}
\end{array}\right.\right.
$$
Let $S$ and $L$ be the centers of the small and large circles, respectively.
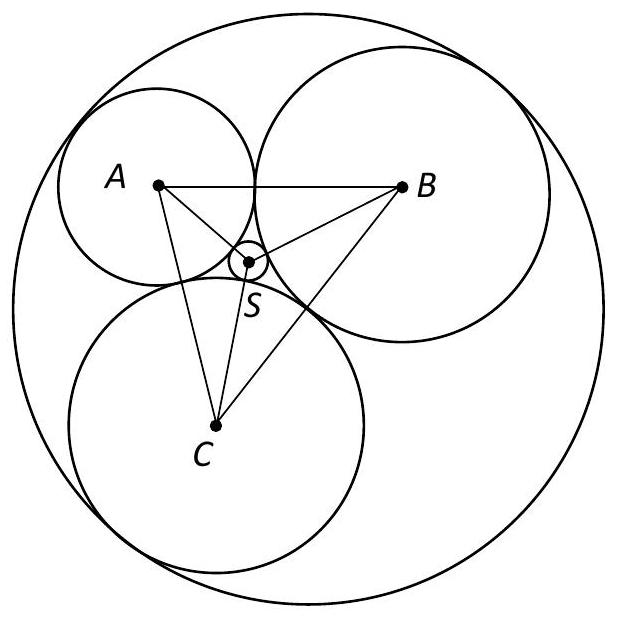
Fig. 1
Denote by $r$ and $R$ the radii of the small and large circles that are tangent to the three given circles, respectively.
Let $\angle A S B=2 \gamma, \angle A S C=2 \gamma$, and $\angle B S C=2 \alpha$. Then, by the cosine rule for triangle $A S B$, we get:
$$
\cos 2 \gamma=\frac{(a+r)^{2}+(b+r)^{2}-(a+b)^{2}}{2(a+r)(b+r)}=\frac{r^{2}+(a+b) r-a b}{(a+r)(b+r)}
$$
From this, using the double-angle formulas, we find:
$$
\cos ^{2} \gamma=\frac{r(a+b+r)}{(a+r)(b+r)}, \sin ^{2} \gamma=\frac{a b}{(a+r)(b+r)}
$$
Similarly, for triangle $B S C$, we get:
$$
\sin ^{2} \alpha=\frac{b^{2}}{(b+r)^{2}}
$$
Since $\alpha+2 \gamma=\pi$, then $\sin ^{2} \alpha=\sin ^{2} 2 \gamma=4 \sin ^{2} \gamma \cos ^{2} \gamma$.
From this, we have:
$$
\begin{gathered}
\frac{b^{2}}{(b+r)^{2}}=4 \cdot \frac{a b}{(a+r)(b+r)} \cdot \frac{r(a+b+r)}{(a+r)(b+r)} \\
b^{2}(a+r)^{2}=4 a b(a+b+r) \\
(b-4 a) r^{2}+\left(2 a b^{2}-4 a^{2}-4 a b\right) r+a^{2} b=0
\end{gathered}
$$
Substituting the found values of the radii of the original circles, we get the equation for determining the value of $r$:
$$
\begin{aligned}
& r^{2}+5 r-\frac{3}{4}=0 \\
& r=\frac{1}{2}(2 \sqrt{7}-5)
\end{aligned}
$$
Note that to find the value of the radius of the large circle $R$, in all the equations for finding the radius of the small circle, we can replace $r$ with $-R$. Then we get the equation:
$$
\begin{aligned}
& R^{2}-5 R-\frac{3}{4}=0 \\
& R=\frac{1}{2}(2 \sqrt{7}+5)
\end{aligned}
$$
We find the area of the desired figure, we get: $S=\pi R^{2}-\pi r^{2}=10 \sqrt{7} \pi$.
Note. The radii of the original circles are found - 1 point. The radius of one of the circles is found - 4 points. | 10\sqrt{7}\pi |
33,091 | 9. (This sub-question is worth 15 points) Let $a_{n}=2^{n}, n \in \mathbf{N}^{+}$, and the sequence $\left\{b_{n}\right\}$ satisfies $b_{1} a_{n}+b_{2} a_{n-1}+\cdots+b_{n} a_{1}=2^{n}-\frac{n}{2}-1$. Find the sum of the first $n$ terms of the sequence $\left\{a_{n} \cdot b_{n}\right\}$. | \frac{(n-1)\cdot2^{n}+1}{2} |
33,094 | 10. Given $f(x)=x^{5}-10 x^{3}+a x^{2}+b x+c$, if the roots of the equation $f(x)=0$ are all real numbers, $m$ is the largest of these 5 real roots, then the maximum value of $m$ is $\qquad$ | 4 |
33,098 | Question 81, In quadrilateral $ABCD$ on the plane, points $E$ and $F$ are the midpoints of sides $AD$ and $BC$, respectively, and $AB=1, EF=\sqrt{2}$, $\mathrm{CD}=3$. If $\overrightarrow{\mathrm{AD}} \cdot \overrightarrow{\mathrm{BC}}=15$, find $\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{BD}}$. | 16 |
33,108 | Ricsi, Dénes, and Attila often play ping pong against each other, with two of them standing on one side. Dénes and Attila win against Ricsi three times as often as they lose; Dénes wins against Ricsi and Attila as often as he loses; finally, Attila wins against Ricsi and Dénes twice as often as he loses. Recently, they spent an entire afternoon playing, during which they played six matches, with two players on each side. What is the probability that Ricsi won at least once, either alone or as part of a pair? | \frac{15}{16} |
33,118 | 10. The base of the tetrahedron $S-ABC$ is an equilateral triangle with side length 4. It is known that $AS=BS=\sqrt{19}, CS=3$. Find the surface area of the circumscribed sphere of the tetrahedron $S-ABC$. | \frac{268}{11}\pi |
33,136 | 6. A circle passes through the vertices $A$ and $K$ of triangle $A K T$ and intersects its sides $A T$ and $K T$ at points $C$ and $N$ respectively, such that $A C: C T=4: 1, T N: N K=1: 2$. Find $A K$, if $C N=\sqrt{10}$. | 5\sqrt{6} |
33,141 | 11 The sequence $\left\{a_{n}\right\}$ satisfies: $a_{1}=1$, and for each $n \in \mathbf{N}^{*}, a_{n} 、 a_{n+1}$ are the roots of the equation $x^{2}+$ $3 n x+b_{n}=0$, then $\sum_{k=1}^{20} b_{k}=$ $\qquad$. | 6385 |
33,143 | Example 3 Let the quadratic function $f(x)=a x^{2}+b x+c(a, b, c \in \mathbf{R}, a \neq 0)$ satisfy the conditions:
(1) For $x \in \mathbf{R}$, $f(x-4)=f(2-x)$, and $f(x) \geqslant x$;
(2) For $x \in(0,2)$, $f(x) \leqslant\left(\frac{x+1}{2}\right)^{2}$;
(3) The minimum value of $f(x)$ on $\mathbf{R}$ is 0.
Find the largest real number $m(m>1)$ such that there exists $t \in \mathbf{R}$, for which, if $x \in[1, m]$, then $f(x+t) \leqslant x$. (2002 National High School Mathematics Competition Problem) | 9 |
33,146 | ## Inscribed Quadrilateral with Perpendicular Diagonals Pythagorean Theorem (direct and inverse) Ratio of Areas of Similar Triangles ] Area of a Quadrilateral ] Complex ] [ Ratio of Areas of Triangles with a Common Base or Height]
Diagonals $A C$ and $B D$ of an inscribed quadrilateral intersect at point $Q$ at a right angle. Lines $A B$ and $C D$ intersect at point $P$. It is known that $B C=5, A D=10, B Q=3$. Find $A P$.
# | \frac{20\sqrt{5}}{3} |
33,148 | 10.8. On a plane, $N$ points are marked. Any three of them form a triangle, the angles of which in degrees are expressed by natural numbers. For what largest $N$ is this possible? | 180 |
33,162 | 10. Let $l, m$ be two skew lines, on $l$ there are three points $A, B, C$, and $A B=B C$. Through $A, B, C$ respectively, draw perpendiculars to $m$ as $A D, B E, C F$, with feet of the perpendiculars being $D, E, F$ respectively. Given $A D=\sqrt{15}, B E=\frac{7}{2}, C F=\sqrt{10}$, find the distance between $l$ and $m$. | \sqrt{6} |
33,177 | Example 3 There are $n(n \geqslant 5)$ distinct points on a plane, each point being exactly 1 unit away from four other points. Find the minimum value of such $n$. ${ }^{[2]}$
In reference [2], it is proven that $n \geqslant 9$, and an example is directly given for the reader to study the construction of the figure and its correctness. This article provides a construction method and verifies its correctness. | 9 |
33,210 | 11. In the Cartesian coordinate system $x O y$, the equation of the hyperbola $C$ is $x^{2}-y^{2}=1$. Find all real numbers $a$ greater than 1 that satisfy the following condition: For any two perpendicular lines $l_{1}$ and $l_{2}$ passing through the point $(a, 0)$, if $l_{1}$ intersects the hyperbola $C$ at points $P, Q$, and $l_{2}$ intersects $C$ at points $R, S$, then $|P Q|=|R S|$ always holds. | \sqrt{2} |
33,211 | A sheet of a notebook was colored in 23 colors by cells. A pair of colors is called good if there exist two adjacent cells colored with these colors. What is the minimum number of good pairs? | 22 |
33,220 | Yakob and Baptiste are playing on a $20 \times 20$ grid where the cells are square and have a side length of 1. The distance between two cells is the distance between their centers. They take turns playing as follows: Yakob places a red stone on a cell, ensuring that the distance between any two cells with red stones is never $\sqrt{5}$, then Baptiste places a blue stone on the grid without any restrictions. The game stops when one of them can no longer place a stone. Find the largest $K$ such that Yakob can always place at least $K$ stones, regardless of Baptiste's responses.
## - Solutions -
Translate the above text into English, preserving the original text's line breaks and format, and output the translation result directly. | 100 |
33,227 | C8. Let $n$ be a positive integer. Determine the smallest positive integer $k$ with the following property: it is possible to mark $k$ cells on a $2 n \times 2 n$ board so that there exists a unique partition of the board into $1 \times 2$ and $2 \times 1$ dominoes, none of which contains two marked cells. | 2n |
33,233 | Task 14. Find the ratio of the legs $CB$ and $CA$ of the right triangle $ACB$, if it is known that one half of the hypotenuse (from the midpoint of the hypotenuse to the vertex) is seen from the center $X$ of the inscribed circle at a right angle. | 4:3 |
33,263 | Task 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1} \mathrm{c}$ is inscribed in a sphere with base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$. Segment $C D$ is the diameter of this sphere, point $K$ and $L$ are the midpoints of edge $A A_{1}$ and $A B$ respectively. Find the volume of the prism if $D L=\sqrt{2}, D K=\sqrt{3}$. | 4 |
33,270 | Define the sequence $\left\{u_{n}\right\}$:
$$
u_{1}=1, u_{n+1}=\left(\sum_{k=1}^{n} u_{k}\right)^{-1} \text {. }
$$
Question: Do there exist constants $\alpha, \beta$ such that
$$
\lim _{n \rightarrow+\infty} \frac{u_{1}+u_{2}+\cdots+u_{n}}{\alpha n^{\beta}}=1 ?
$$
If they exist, find $\alpha, \beta$; if not, explain why. | \alpha=\sqrt{2},\beta=\frac{1}{2} |
33,272 | 13. Let $a_{1}=1, a_{2}=2$ and for all $n \geq 2, a_{n+1}=\frac{2 n}{n+1} a_{n}-\frac{n-1}{n+1} a_{n-1}$. It is known that $a_{n}>2+\frac{2009}{2010}$ for all $n \geq m$, where $m$ is a positive integer. Find the least value of $m$. | 4021 |
33,285 | A regular hexagon $A B C D E F$ is inscribed in a circle. Points $P$ and $Q$ are chosen on the tangents to this circle at points $A$ and $D$ respectively, such that the line $P Q$ is tangent to the smaller arc $E F$ of this circle. Find the angle between the lines $P B$ and $Q C$. | 30 |
33,288 | 124. Intersection of Great Circles. It is known that on a sphere, $n$ great circles intersect in $n(n-1)$ points in general. How should the numbers $1,2, \ldots, n(n-1)$ be placed in these points so that the sums of the numbers located on each circle are equal to each other. (Recall that the great circles lie in planes passing through the center of the sphere.) | [n(n-1)+1](n-1) |
33,308 | 16. (15 points) Replacing the larger number of two different natural numbers with their difference is called one operation. Continue this process until the two numbers are the same. For example, for 20 and 26, the process is as follows:
$(20,26) \rightarrow(20,6) \rightarrow(14,6) \rightarrow(8,6) \rightarrow(2,6) \rightarrow(2,4) \rightarrow(2,2)$
(1) Perform the above operation on 45 and 80.
(2) If the final same number obtained from two four-digit numbers through the above operation is 17, find the maximum value of the sum of these two four-digit numbers. | 19975 |
33,313 | 3. (3 points) Petya and Vasya are playing a game on an initially white $100 \times 100$ grid. Petya goes first and can paint one cell black with his first move. Each subsequent move allows a player to paint black any vertical or horizontal white rectangular strip $1 \times n$ on the grid, where $n$ is a natural number, and it can either match the number of cells just painted by the other player or exceed it by one. The player who cannot make a move loses. Who will win with correct play by both opponents? | Vasya |
33,314 | 3. For $n$ positive numbers $x_{1}, x_{2}, \cdots, x_{n}$ whose sum equals 1, let $S$ be the largest of the following numbers: $\frac{x_{1}}{1+x_{1}}, \frac{x_{2}}{1+x_{1}+x_{2}}$, $\cdots, \frac{x_{n}}{1+x_{1}+x_{2}+\cdots+x_{n}}$. Find the minimum possible value of $S$, and determine the values of $x_{1}, x_{2}, \cdots, x_{n}$ that achieve this minimum value.
(6th All-Soviet Union Olympiad problem) | 1-2^{-\frac{1}{n}} |
33,329 | $1 \cdot 60$ Find the smallest positive integer $n>1$, such that the arithmetic mean of $1^{2}, 2^{2}, 3^{2}, \cdots, n^{2}$ is a perfect square. | 337 |
33,331 | 6. As shown in the figure, in $\triangle A B C$, points $D, E, F$ are on $B C, C A, A B$ respectively, and $C D=\frac{3}{5} B C, E C=\frac{1}{2} A C$, $A F=\frac{1}{3} A B$. Let $P$ be a point inside quadrilateral $A E D F$ (point $P$ is not on the boundary). If $\overrightarrow{D P}=-\frac{1}{3} \overrightarrow{D C}+x \overrightarrow{D E}$, then the range of the real number $x$ is . $\qquad$ | (\frac{1}{2},\frac{4}{3}) |
33,345 | Example 1 Given ten points in space, where no four points lie on the same plane. Connect some of the points with line segments. If the resulting figure contains no triangles and no spatial quadrilaterals, determine the maximum number of line segments that can be drawn. ${ }^{[1]}$ | 15 |
33,353 | 10.3. The cells of a $2 \times 2019$ table must be filled with numbers (exactly one number in each cell) according to the following rules. In the top row, there should be 2019 real numbers, none of which are equal, and in the bottom row, there should be the same 2019 numbers, but in a different order. In each of the 2019 columns, there should be two different numbers, and the sum of these two numbers should be a rational number. What is the maximum number of irrational numbers that could be in the first row of the table?
(S. Kudrya) | 2016 |
33,357 | Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
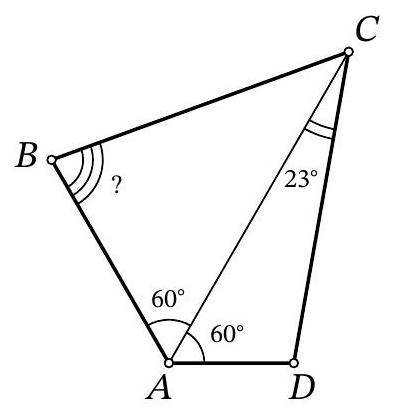 | 83 |
33,361 | Five. (Full marks 20 points) Given a positive integer $n$ and a positive number $M$, for all arithmetic sequences $a_{1}, a_{2}, a_{3}, \cdots$ satisfying the condition $a_{1}^{2}+a_{n+1}^{2} \leqslant M$, find the maximum value of $S=a_{n+1}+a_{n+2}+\cdots+a_{2 n+1}$. | \frac{\sqrt{10}}{2}(n+1)\sqrt{M} |
33,362 | 15. Let $m>0$, if for any set of positive numbers $a, b, c$ satisfying $a b c \leqslant \frac{1}{4}$ and $\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}<m$, there always exists a triangle with side lengths $a, b, c$, find the maximum value of the real number $m$, and explain the reason. | 9 |
33,392 | . Let $A B C$ be a triangle in which $\angle A B C=60^{\circ}$. Let $I$ and $O$ be the incentre and circumcentre of $A B C$, respectively. Let $M$ be the midpoint of the arc $B C$ of the circumcircle of $A B C$, which does not contain the point $A$. Determine $\angle B A C$ given that $M B=O I$.
# | 30 |
33,418 | 31. Cube. Holding a model of a cube in your hand so that it can rotate around its longest axis (i.e., around the line connecting opposite vertices), you can wind black yarn around it without any gaps. The yarn will shade only half of the cube (why?). The same can be done with another axis; there are four in total, and each time we use a different color of yarn (black, red, blue, and
yellow). The entire model will be covered with different colors, and from their mixing, mixed colors will emerge (the model of the cube is white and we do not consider this color). How many color shades will there be on the cube and which ones? | 6 |
33,435 | 6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=75 \\
y^{2}+y z+z^{2}=64 \\
z^{2}+x z+x^{2}=139
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$. | 80 |
33,466 | 10. (This question is worth 20 points) Let $a_{1}, a_{2}, a_{3}, a_{4}$ be four rational numbers such that: $\left\{a_{i} a_{j} \mid 1 \leq i<j \leq 4\right\}=\left\{-24,-2,-\frac{3}{2},-\frac{1}{8}, 1,3\right\}$. Find the value of $a_{1}+a_{2}+a_{3}+a_{4}$. | \\frac{9}{4} |
33,470 | Let $p_{1}, p_{2}, \ldots, p_{30}$ be a permutation of the numbers $1,2, \ldots, 30$. For how many permutations does the equality $\sum_{k=1}^{30}\left|p_{k}-k\right|=450$ hold?
Answer: $(15 !)^{2}$. | (15!)^{2} |
33,473 | 5.17. In triangle $A B C$, point $N$ lies on side $A B$ and $A N=$ $=3 N B$; median $A M$ intersects $C N$ at point $O$. Find $A B$, if $A M=C N=7$ cm and $\angle N O M=60^{\circ}$. | 4\sqrt{7} |
33,475 | 1. Positive integers $a, b$, and $c$ are all powers of $k$ for some positive integer $k$. It is known that the equation $a x^{2}-b x+c=0$ has exactly one real solution $r$, and this value $r$ is less than 100. Compute the maximum possible value of $r$. | 64 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.